Sample Entropy Combined with the K-Means Clustering Algorithm Reveals Six Functional Networks of the Brain

Abstract

Identifying brain regions contained in brain functional networks and functions of brain functional networks is of great significance in understanding the complexity of the human brain. The 160 regions of interest (ROIs) in the human brain determined by the Dosenbach’s template have been divided into six functional networks with different functions. In the present paper, the complexity of the human brain is characterized by the sample entropy (SampEn) of dynamic functional connectivity (FC) which is obtained by analyzing the resting-state functional magnetic resonance imaging (fMRI) data acquired from healthy participants. The 160 ROIs are clustered into six clusters by applying the K-means clustering algorithm to the SampEn of dynamic FC as well as the static FC which is also obtained by analyzing the resting-state fMRI data. The six clusters obtained from the SampEn of dynamic FC and the static FC show very high overlap and consistency ratios with the six functional networks. Furthermore, for four of six clusters, the overlap ratios corresponding to the SampEn of dynamic FC are larger than that corresponding to the static FC, and for five of six clusters, the consistency ratios corresponding to the SampEn of dynamic FC are larger than that corresponding to the static FC. The results show that the combination of machine learning methods and the FC obtained using the blood oxygenation level-dependent (BOLD) signals can identify the functional networks of the human brain, and nonlinear dynamic characteristics of the FC are more effective than the static characteristics of the FC in identifying brain functional networks and the complexity of the human brain.

1. Introduction

The human brain shows complex spatiotemporal behaviors when executing physiological functions. Characterizing dynamics of the complex spatiotemporal behaviors is of great significance in understanding the human brain. Since blood oxygenation level-dependent (BOLD) signals of different brain regions can be measured by the functional magnetic resonance imaging (fMRI) technique at high spatial and temporal resolutions, BOLD signals have been widely used to characterize dynamics of the spatiotemporal behaviors of the human brain [1,2]. For instance, the temporal correlation in BOLD signals of two distinct brain regions is commonly employed to describe the functional connectivity (FC) between them [3]. A positive and strong temporal correlation corresponds to a strong FC, and some brain regions with strong FCs among them constitute a brain functional network [4,5,6]. Alterations of some FCs in a brain functional network are often associated with brain disorder, such as schizophrenia [7], major depression [8], autism [9], Alzheimer’s Disease [10], and attention deficit hyperactivity disorder [11]. For example, Cheng et al. evaluated the FC between different brain regions in subjects with autism and found a key system in the middle temporal gyrus with reduced FC and a key system in the precuneus with reduced FC [12].

In most previous research on FC, only one correlation coefficient is acquired using entire BOLD signals of two distinct brain regions. The one correlation coefficient is called the static FC between the two brain regions. Recently, to understand dynamics of the spatiotemporal behaviors of the human brain more deeply, some researchers acquired a sequence of correlation coefficients by applying the sliding-window approach to BOLD signals of two distinct brain regions [13,14,15,16,17,18,19,20,21,22,23]. These correlation coefficients form a time series which is called the dynamic FC between the two brain regions. The dynamic FC exhibits complex characteristics which are effective in describing properties of the brain functional networks of patients with brain disorder. For instance, in one of our recent studies, complex characteristics of dynamic FC were described by sample entropy (SampEn), and the effects of schizophrenia on such complex characteristics were investigated. It was shown that the visual cortex of the patients with schizophrenia exhibited significantly higher SampEn than that of the healthy controls [24]. As introduced above, both the static FC and the SampEn of dynamic FC are effective in describing properties of the brain functional networks of patients with brain disorder. However, the effectivenesses of the static FC and the dynamic FC have not been compared directly.

Studies on the static FC or the dynamic FC are often carried out by first extracting BOLD signals of different brain regions and then evaluating the static or the dynamic FC between different brain regions for further analysis. Different brain regions are often determined by a brain template, such as the Dosenbach’s template [25]. The Dosenbach’s template includes 160 regions of interest (ROIs) determined by a sequence of meta-analyses of task-based fMRI studies which cover much of the human brain [25]. Furthermore, the 160 ROIs can be separated into six functional networks including the default, the frontal-parietal, the cingulo-opercular, the sensorimotor, the occipital, and the cerebellum networks, which were identified by performing modularity optimization on the average FC matrix across a large cohort of healthy subjects [25]. The six functional networks have been used in predicting brain maturity across development [25,26], parcellating cortical or subcortical regions [27], examining the influence of temporal properties of BOLD signals on FC [28] and so on. For instance, Zhong et al. parcellated the hippocampus based on the FC, and showed that both the left and right hippocampus were divided into three subregions exhibiting different FC profiles with the six functional networks [27]. However, machine learning algorithms have not been used to identify the six functional networks.

The K-means clustering algorithm is one of the unsupervised learning algorithms [29]. Since the K-means clustering algorithm can cluster different observations into different clusters in a simple and easy way, it has been widely used in fMRI studies [30,31,32,33,34,35,36,37,38]. For instance, Fan et al. used the K-means clustering algorithm to parcellate the thalamus based on the static FC and found that the thalamus could be divided into seven symmetric thalamic clusters [36]. Park et al. parcellated the primary and secondary visual cortices (V1 and V2) into several subregions by applying the K-means clustering algorithm to the static FC and found that V1 and V2 could be separated into anterior and posterior subregions [38].

The present study intends to cluster the Dosenbach’s 160 ROIs into six clusters by applying the K-means clustering algorithm to the static FC and the SampEn of dynamic FC, to analyze the overlap and consistency between the six clusters and the six functional networks, and to compare the effectivenesses of the static FC and the dynamic FC. It is shown that applying the K-means clustering algorithm to FC is feasible to identify the six functional networks, and the SampEn of dynamic FC is more effective than the static FC as the six clusters obtained from the SampEn of dynamic FC show higher overlap and consistency ratios with the six functional networks.

This paper is organized as follows. The experiments and methods are presented in Section 2. The cluster results for the static FC and the SampEn of dynamic FC and the comparisons between them are shown in Section 3. The conclusion and discussion are described in Section 4. Some supplementary tables are presented in the appendix.

2. Experiments and Methods

2.1. Participants

FMRI data for this study were acquired at Olin Neuropsychiatry Research Center and have been made publicly available http://fcon_1000.projects.nitrc.org/indi/abide. The data were acquired from 31 healthy participants (18 males and 13 females) over the age range 18–30 years. This sample was retained after applying criteria for head motion, from a total of 35 healthy participants. Informed consent was obtained from all participants in accordance with Olin Neuropsychiatry Research Center Institutional Review Board oversight.

2.2. Data Acquisition and Preprocessing

BOLD signals are extracted from three-dimensional functional images collected on a Siemens 3T MRI scanner with the following parameters: repetition time (TR), 475 ms; echo time, 30 ms; field of view, $240\times 240{\mathrm{mm}}^2$; slices, 48; slice thickness, 3 mm; flip angle, ${60}^{\circ }$. During the data collection, all participants were instructed to rest but not fall asleep. For each participant, 947 three-dimensional functional images were collected.

The functional images are preprocessed using SPM8 and DPABI softwares [39,40]. Firstly, the first 4 images are discarded to reduce the negative effects of scanner’s stabilization on the analysis results. Secondly, the images are corrected for time delay in slice acquisition and rigid-body head motion. Thirdly, several confounding factors are regressed out from the images, including 6 head motion parameters and the cerebrospinal, the white matter, and the global brain signals. Fourthly, temporal band-pass filtering (0.01–0.08 Hz) of the images are performed to reduce the negative effects of low-frequency drift and high-frequency physiological noise on the analysis results. Fifthly, the images are spatially normalized to the Montreal Neurological Institute space and are resampled to voxels of size $3\times 3\times 3{\mathrm{mm}}^3$. Sixthly, the images are smoothed with a Gaussian kernel of 8 mm full-width at half-maximum. Finally, the BOLD signal of each voxel is extracted from the functional images.

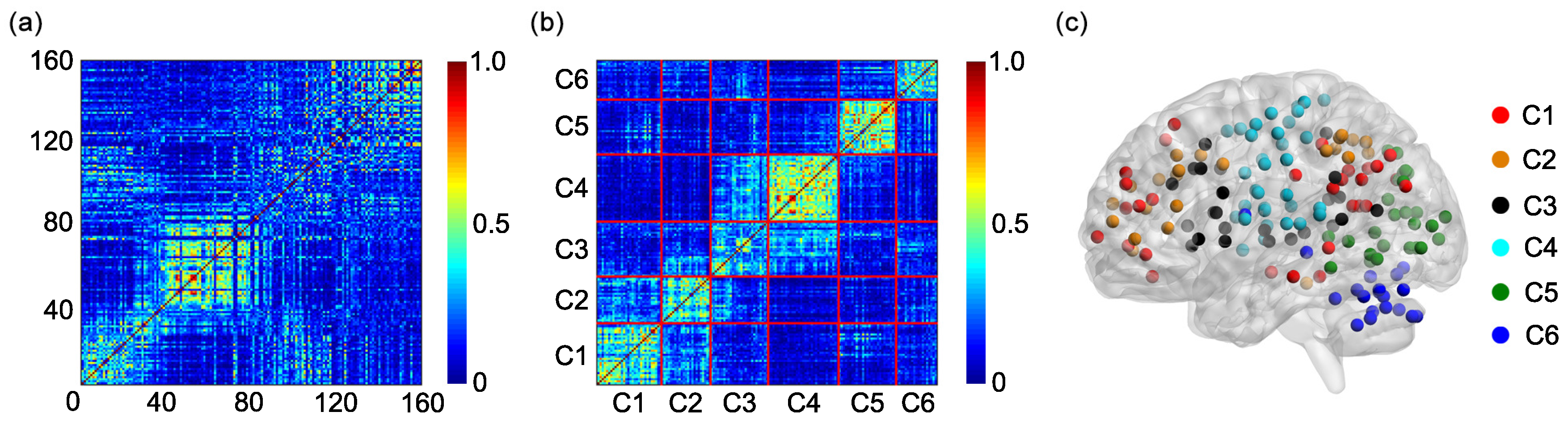
2.3. The Dosenbach’s Template and the 6 Functional Networks

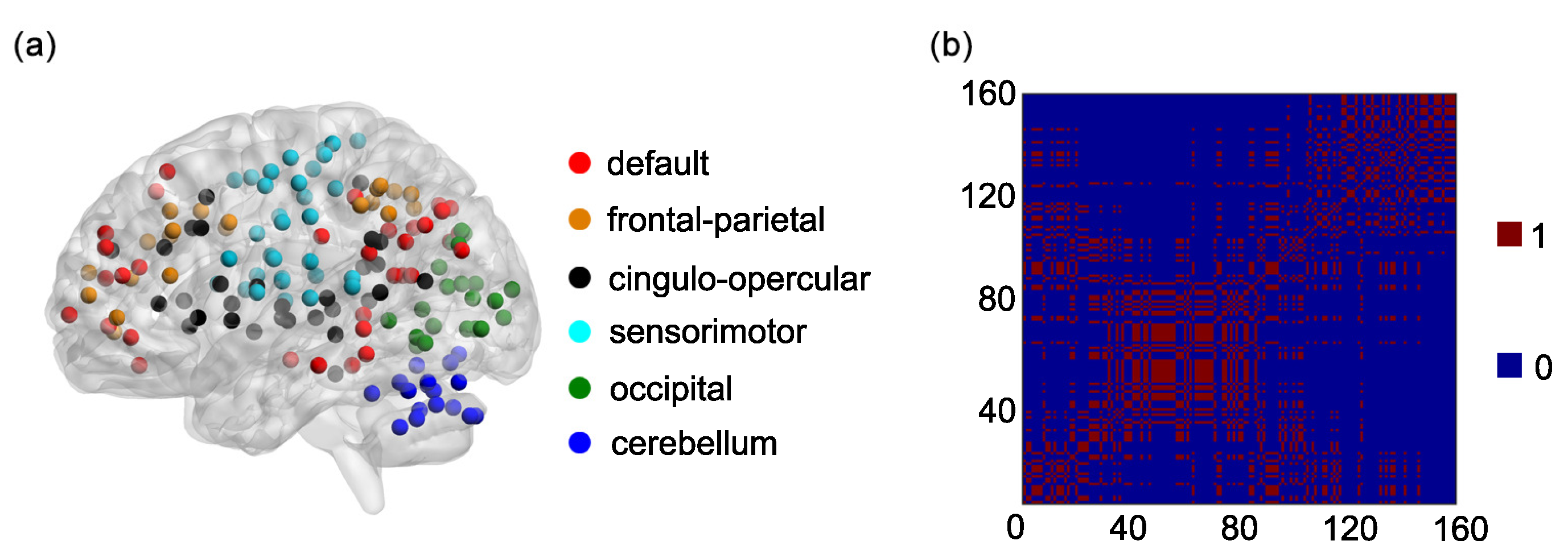
One hundred and sixty regions of interest (ROIs) are selected based on the Dosenbach’s template [25]. The centroid of each ROI is derived from a sequence of meta-analyses of task-based fMRI studies (Figure 1a). The radius of each ROI equals 5 mm (Figure 1a). The name and the sequential number of each ROI can be found in Table A1 in Appendix A. The 160 ROIs can further be grouped into 6 functional networks, including the default, the frontal-parietal, the cingulo-opercular, the sensorimotor, the occipital, and the cerebellum networks (Figure 1a). The name and the sequential number of each ROI in each functional network can be found in the first and second columns of Table A2, Table A3, Table A4, Table A5, Table A6 and Table A7 in Appendix A.

Figure 1. (a) One hundred and sixty regions of interest (ROIs) are shown on a surface rendering of the brain. ROIs in different functional networks are shown in different colors. (b) The adjacent matrix A of 160 ROIs in 6 functional networks.

Based on the 6 functional networks, an adjacent matrix can be generated [36,41,42]. The adjacent matrix is labeled as

$$A=\left[\begin{array}{ccc}{a}_{1,1}& \cdots & a_{1,160}\\ ⋮& \ddots & ⋮\\ a_{160,1}& \cdots & a_{160,160}\end{array}\right].$$

(1)

Each of the elements on the main diagonal of A is 1. Other elements of A are defined as follows: $a_{i,j}=1$ if the ith ROI and the jth ROI are contained in the same functional network and $a_{i,j}=0$ otherwise $(i,j=1,2,\dots ,160)$ (Figure 1b).

2.4. The Static FC and the Dynamic FC

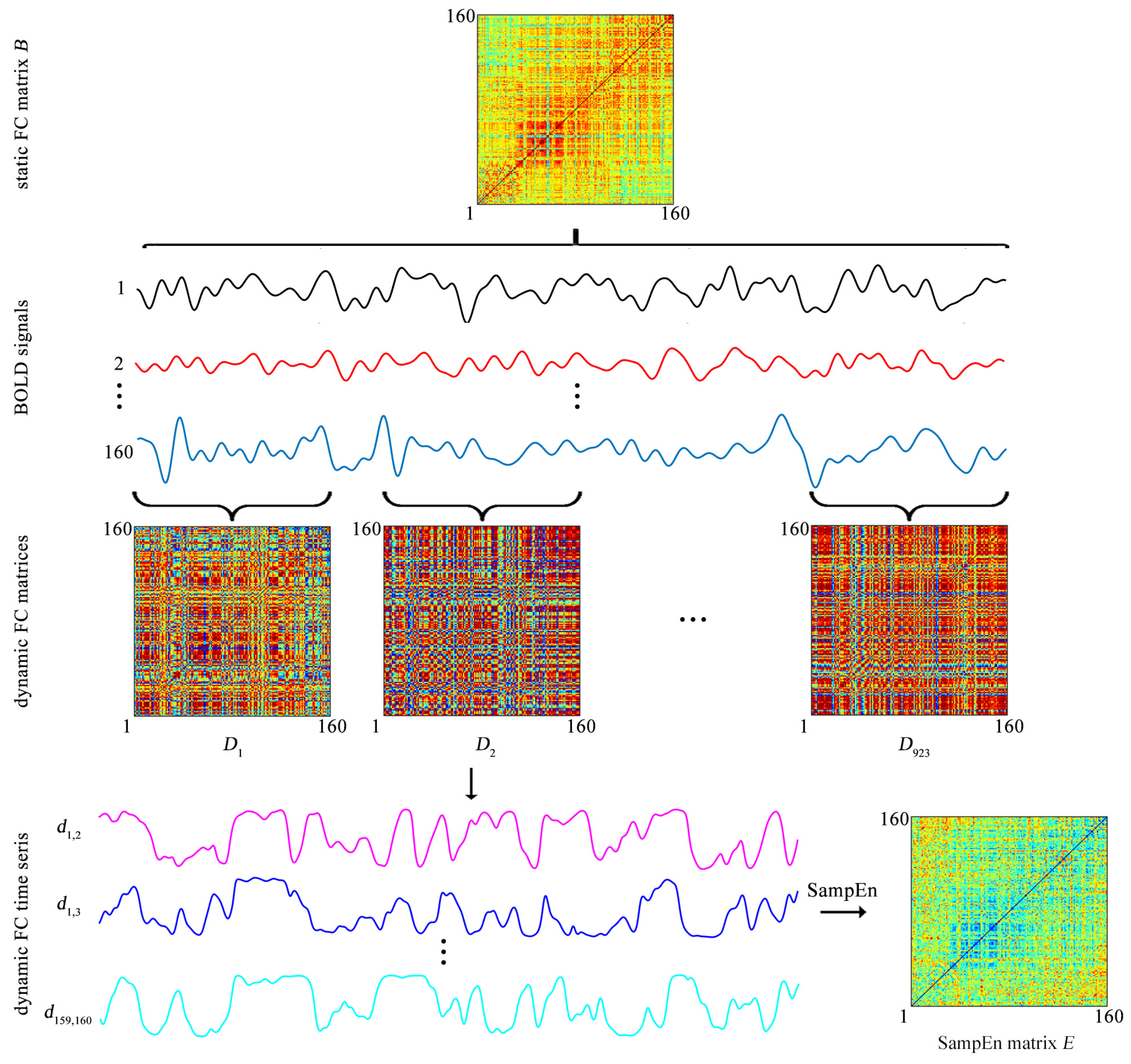
The BOLD signal of each ROI is extracted by averaging the BOLD signals over all voxels in this ROI. Then both the static FC and the dynamic FC are evaluated (Figure 2).

Figure 2. The static functional connectivity (FC) matrix B and the SampEn matrix E obtained from the BOLD signals of 160 ROIs. The matrices B and E are used to cluster the 160 ROIs into 6 clusters by the K-means clustering algorithm.

The static FC between each pair of ROIs is assessed by a Pearson correlation coefficient. For each of the 31 participants, after the static FC between each pair of ROIs is evaluated, a static FC matrix of size $160\times 160$ is obtained (Figure 2), which is labeled as

$$B=\left[\begin{array}{ccc}{b}_{1,1}& \cdots & b_{1,160}\\ ⋮& \ddots & ⋮\\ b_{160,1}& \cdots & b_{160,160}\end{array}\right]=\left[\begin{array}{c}{B}_1\\ ⋮\\ B_{160}\end{array}\right].$$

(2)

The ith row $B_i$ represents the static FC between the ith ROI and all the other ROIs $(i=1,2,\dots ,160).$ The matrix B is used to cluster the 160 ROIs into 6 clusters.

Dynamic FC is assessed by the sliding-window approach. Specifically, a tapered window is created by convolving a rectangle window (size = 20 TRs = 9.5 s) with a Gaussian curve (standard deviation = 3 TRs) [14,15,23]. The window is used to extract BOLD signals in a step of 1 TR, leading to 923 time windows per subject (Figure 2). For the kth time window $(k=1,2,\dots ,923),$ a Pearson correlation coefficient is used to evaluate the FC between each pair of ROIs and thus a FC matrix of size $160\times 160,$ which is labeled as

$$D_k=\left[\begin{array}{ccc}{d}_{1,1,k}& \cdots & d_{1,160,k}\\ ⋮& \ddots & ⋮\\ d_{160,1,k}& \cdots & d_{160,160,k}\end{array}\right],$$

(3)

which is obtained for each subject (Figure 2). As k increases from 1 to 923, $d_{i,j,k}$ forms a time series $(i,j=1,2,\dots ,160),$ which represents the temporal evolution of the FC between the ith and jth ROIs and is named as the dynamic FC (Figure 2). Since previous studies showed that the window of size 20 TRs captures more transient patterns in dynamic FC [23], the window size is fixed at 20 TRs throughout the study.

2.5. SampEn of a Dynamic FC Time Series

For each dynamic FC time series, $d_{i,j}(i,j=1,2,\dots ,160,i\ne j),$ the SampEn is calculated. For convenience, time series $d_{i,j}$ is denoted by $\mathbf{x}=(x_1,x_2,\dots ,x_N)(N=923).$ SampEn of $\mathbf{x}$ is computed as follows [24,43,44,45,46].

Firstly, constructing embedding vectors ${\mathbf{v}}_{\mathbf{i}}=(x_i,x_{i+1},\dots ,x_{i+m-1}),$ in which m stands for the dimension of ${\mathbf{v}}_{\mathbf{i}}(1\le i\le N-m+1).$

Secondly, define

$$C_i^m=\frac{1}{N-m}\sum _{j=1,j\ne i}^{N-m+1}\Theta (r-\parallel {\mathbf{v}}_{\mathbf{i}}-{\mathbf{v}}_{\mathbf{j}}\parallel ).$$

(4)

r stands for a tolerance value which is defined as $r=\epsilon ·{\sigma }_{\mathbf{x}}$, where $\epsilon$ is a small parameter and ${\sigma }_{\mathbf{x}}$ is the standard deviation of $\mathbf{x}$. $\Theta (·)$, the Heaviside function, which is defined as

$$\Theta \left(x\right)=\left\{\begin{array}{cc}0,\hfill & x<0;\hfill \\ 1,\hfill & x\ge 0.\hfill \end{array}\right.$$

(5)

$\parallel ·\parallel$ represents the Chebyshev distance, i.e.,

$$\parallel {\mathbf{v}}_{\mathbf{i}}-{\mathbf{v}}_{\mathbf{j}}\parallel =max\left(\right|x_i-x_j|,|x_{i+1}-x_{j+1}|,\dots ,|x_{i+m-1}-x_{j+m-1}\left|\right).$$

(6)

Similarly, define

$$C_i^{m+1}=\frac{1}{N-m-1}\sum _{j=1,j\ne i}^{N-m}\Theta (r-\parallel {\mathbf{v}}_{\mathbf{i}}-{\mathbf{v}}_{\mathbf{j}}\parallel ).$$

(7)

Thirdly, in view of Equations (4) and (7), we define

$$U^m=\frac{1}{N-m+1}\sum _{i=1}^{N-m+1}{C}_i^m,$$

(8)

and

$$U^{m+1}=\frac{1}{N-m}\sum _{i=1}^{N-m}{C}_i^{m+1}.$$

(9)

Finally, calculate SampEn of $\mathbf{x}$ as

$$\mathrm{SampEn}=-ln\frac{U^{m+1}}{U^m}.$$

(10)

The value of SampEn is not less than 0, and a larger value of SampEn means more complexity [47]. Similar to our previous study [24,43], m and $\epsilon$ are fixed at 2 and 0.2, respectively.

In addition, because $d_{i,i,k}=1(i=1,2,\dots ,160,k=1,2,\dots ,923),$ the SampEn of $d_{i,i}$ equals 0 $(i=1,2,\dots ,160).$ Thus, for each participant, a SampEn matrix of size $160\times 160$ is obtained (Figure 2). The SampEn matrix is labeled as

$$E=\left[\begin{array}{ccc}{e}_{1,1}& \cdots & e_{1,160}\\ ⋮& \ddots & ⋮\\ e_{160,1}& \cdots & e_{160,160}\end{array}\right]=\left[\begin{array}{c}{E}_1\\ ⋮\\ E_{160}\end{array}\right].$$

(11)

The element $e_{i,j}$ represents the SampEn of dynamic FC between the ith ROI and jth ROI $(i,j=1,2,\dots ,160).$ $e_{i,i}$ equals 0 $(i=1,2,\dots ,160).$ The matrix E is used to cluster the 160 ROIs into 6 clusters.

2.6. Clustering ROIs into 6 Clusters by Applying the K-Means Clustering Algorithm to the Static FC Matrix

For each of the 31 participants, there exists a static FC matrix B of size $160\times 160.$ The ith $(1\le i\le 160)$ row $B_i=(b_{i,1},b_{i,2},\dots ,b_{i,160})$ represents the static FC between the ith ROI and all the other ROIs.

The K-means clustering algorithm is commonly used to cluster different observations into different clusters based on the distance between these observations [29]. In the present paper, the K-means clustering algorithm is applied to the matrix B to cluster 160 ROIs into 6 clusters. Procedures of the algorithm are briefly described as follows.

First, select 6 rows from the matrix B and use these 6 rows as initial cluster centroids.

Secondly, calculate the squared Euclidean distance between each row and each initial cluster centroid, and then assign each row to the cluster with the closest centroid.

Thirdly, when all rows have been assigned, calculate the average of the rows in each cluster to obtain 6 new cluster centroids.

Finally, repeat the second and the third steps until the centroids no longer change.

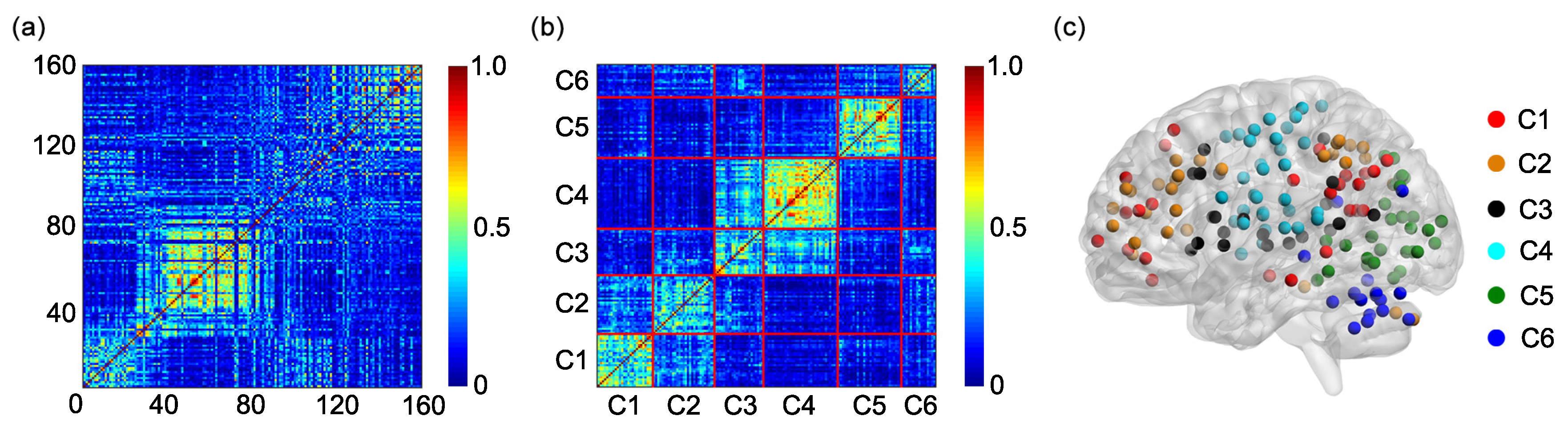
The algorithm generates 6 clusters, and each cluster is composed of different rows of the matrix B (or of different ROIs). Based on the 6 clusters, an individual adjacent matrix of size $160\times 160$ is generated [36,41,42]. The individual adjacent matrix is labeled as

$$F=\left[\begin{array}{ccc}{f}_{1,1}& \cdots & f_{1,160}\\ ⋮& \ddots & ⋮\\ f_{160,1}& \cdots & f_{160,160}\end{array}\right].$$

(12)

Each of the elements on the main diagonal of F is 1, and other elements of F are defined as follows: $f_{i,j}=1$ if the ith ROI and the jth ROI are contained in the same cluster and $f_{i,j}=0$ otherwise.

Since the study includes 31 participants, 31 individual adjacent matrices are obtained. A group adjacent matrix of size $160\times 160$ is obtained by averaging 31 individual adjacent matrices. The group adjacent matrix is labeled as

$$G=\left[\begin{array}{ccc}{g}_{1,1}& \cdots & g_{1,160}\\ ⋮& \ddots & ⋮\\ g_{160,1}& \cdots & g_{160,160}\end{array}\right].$$

(13)

The K-means clustering algorithm is further applied to the matrix G to obtain the group cluster result [36,41,42] and the 6 clusters of the group cluster result are compared with the 6 functional networks shown in Figure 1a.

The detailed clustering procedure is performed by MATLAB software (MATLAB R2014b). Considering that the K-means clustering algorithm is sensitive to the initial cluster centroids, we repeat each clustering procedure 500 times, and the cluster result with the lowest within-cluster distance is adopted.

2.7. Clustering ROIs into 6 Clusters by Applying the K-Means Clustering Algorithm to the SampEn Matrix

The procedures described in Section 2.6 are also applied to the SampEn matrix E, and 6 clusters are obtained.

3. Results

3.1. Six Clusters of ROIs for the Static FC

The group adjacent matrix for the static FC is shown in Figure 3a. The horizontal and vertical coordinates represent the sequential numbers of the ROIs. The sequential number and the name of each ROI can be found in Table A1 in Appendix A.

Figure 3. (a) The group adjacent matrix for the static FC. (b) The reorganization of the group adjacent matrix based on the 6 clusters obtained by applying the K-means clustering algorithm to the group adjacent matrix. Since the ith row and the ith column of the group adjacent matrix are reorganized simultaneously, the reorganized matrix is also symmetric. (c) The 6 clusters are shown on a surface rendering of the brain. C1: cluster 1; C2: cluster 2; C3: cluster 3; C4: cluster 4; C5: cluster 5; C6: cluster 6.

Rows of the group adjacent matrix can be clustered into six clusters by the K-means clustering algorithm (Figure 3b). The numbers of rows in clusters 1–6 are 26, 29, 23, 35, 30, and 17, respectively (Table 1). The ROIs in clusters 1–6 can be found in the third and fourth columns of Table A2, Table A3, Table A4, Table A5, Table A6 and Table A7 in Appendix A. Since each row of the adjacent matrix corresponds to a ROI, the six clusters can also be shown on a surface rendering of the brain (Figure 3c), which resembles Figure 1a to a large extent.

Table 1. The number of ROIs in the overlapping part between each functional network and each cluster obtained from the static FC.

	Cluster 1 $(\mathit{n}=26)$	Cluster 2 $(\mathit{n}=29)$	Cluster 3 $(\mathit{n}=23)$	Cluster 4 $(\mathit{n}=35)$	Cluster 5 $(\mathit{n}=30)$	Cluster 6 $(\mathit{n}=17)$
Default $(n=34)$	25	2	0	0	6	1
Frontal-Parietal $(n=21)$	0	20	1	0	0	0
Cingulo-Percular $(n=32)$	1	5	21	3	0	2
Sensorimotor $(n=33)$	0	0	1	32	0	0
Occipital $(n=22)$	0	0	0	0	22	0
Cerebellum $(n=18)$	0	2	0	0	2	14

The average of the squared Euclidean distances from all ROIs in each of the six clusters to the centroid of cluster $i(i=1,2,3,4,5,6)$ is also evaluated, as shown in Figure 4a–f. For each centroid, among the six averaged distances, the averaged distance from the cluster $i(i=1,2,3,4,5,6)$ to the centroid of cluster i is the lowest. This is consistent with the main idea of the K-means clustering algorithm.

Figure 4. The average of the squared Euclidean distances from all ROIs in each of the six clusters to the centroid of cluster $i(i=1,2,3,4,5,6)$. (a) Centroid of cluster 1. (b) Centroid of cluster 2. (c) Centroid of cluster 3. (d) Centroid of cluster 4. (e) Centroid of cluster 5. (f) Centroid of cluster 6. The error bars represent standard deviations.

3.2. The Overlap Ratios between the Six Clusters for the Static FC and the Six Functional Networks

The overlap ratios between each cluster and each functional network is analyzed in Table 1. The overlap ratios between cluster 1 and the default network, the frontal-parietal network, the cingulo-opercular network, the sensorimotor network, the occipital network, as well as the cerebellum network are 25/26 (≈96.15%), 0, 1/26 (≈3.85%), 0, 0, and 0, respectively. Obviously, the overlap ratio between cluster 1 and the default network is the highest. Thus, cluster 1 corresponds to the default network. Similarly, we can obtain that clusters 2–6, respectively, correspond to the frontal-parietal network, the cingulo-opercular network, the sensorimotor network, the occipital network, and the cerebellum network, with the overlap ratios, respectively, equaling 20/29 (≈68.97%), 21/23 (≈91.30%), 32/35 (≈91.43%), 22/30 (≈73.33%), and 14/17 (≈82.35%). These overlap ratios are high.

3.3. The Consistency Ratios between the Six Clusters for the Static FC and the Functional Networks

Based on the data shown in Table 1, the consistency between the cluster results and the functional networks can also be evaluated. The consistency ratio between cluster 1 and the default network is 25/(25 + 9 + 1) (≈71.43%), in which 9 is the number of ROIs in the default network but not in cluster 1, and 1 is the number of ROIs in cluster 1 but not in the default network. Similarly, we can obtain that the consistency ratios between cluster 2 and the frontal-parietal network, cluster 3 and the cingulo-opercular network, cluster 4 and the sensorimotor network, cluster 5 and the occipital network, and cluster 6 and the cerebellum network are 20/(20 + 1 + 9) (≈66.67%), 21/(21 + 11 + 2) (≈61.76%), 32/(32 + 1 + 3) (≈88.89%), 22/(22 + 0 + 8) (≈73.33%), and 14/(14 + 4 + 3) (≈66.67%), respectively. These consistency ratios are high.

3.4. Six Clusters of ROIs for the SampEn of Dynamic FC

The group adjacent matrix for the SampEn of dynamic FC is presented in Figure 5a. The horizontal and vertical coordinates stand for the sequential numbers of the ROIs. The sequential number and the name of each ROI can be found in Table A1 in Appendix A.

Figure 5. (a) The group adjacent matrix for the SampEn of dynamic FC. (b) The reorganization of the group adjacent matrix based on the six clusters obtained by applying the K-means clustering algorithm to the group adjacent matrix. Since the ith row and the ith column of the group adjacent matrix are reorganized simultaneously, the reorganized matrix is also symmetric. (c) The six clusters are shown on a surface rendering of the brain. C1: cluster 1; C2: cluster 2; C3: cluster 3; C4: cluster 4; C5: cluster 5; C6: cluster 6.

Rows of the group adjacent matrix can be divided into six clusters by the K-means clustering algorithm (Figure 5b). The numbers of rows in clusters 1–6 are 30, 23, 27, 33, 27, and 20, respectively (Table 2). The ROIs in clusters 1–6 can be found in the fifth and sixth columns of Table A2, Table A3, Table A4, Table A5, Table A6 and Table A7 in Appendix A. The six clusters can also be shown on a surface rendering of the brain (Figure 5c), which resembles Figure 1a and Figure 3c to a large extent.

Table 2. The number of ROIs in the overlapping part between each functional network and each cluster obtained from the SampEn of dynamic FC.

	Cluster 1 $(\mathit{n}=30)$	Cluster 2 $(\mathit{n}=23)$	Cluster 3 $(\mathit{n}=27)$	Cluster 4 $(\mathit{n}=33)$	Cluster 5 $(\mathit{n}=27)$	Cluster 6 $(\mathit{n}=20)$
Default $(n=34)$	29	0	0	0	5	0
Frontal-parietal $(n=21)$	0	20	1	0	0	0
Cingulo-percular $(n=32)$	1	3	23	3	0	2
Sensorimotor $(n=33)$	0	0	3	30	0	0
Occipital $(n=22)$	0	0	0	0	22	0
Cerebellum $(n=18)$	0	0	0	0	0	18

Furthermore, other values of $K(K=2,\dots ,12)$ are also tried in the K-means clustering algorithm, and the optimal value of K is determined by the elbow criterion of the cluster validity index, which is defined as the ratio of within-cluster distances to between-cluster distances [15,20,27]. The dependence of the cluster validity index on K is shown in Figure 6. It is seen that two elbows appear at $K=$ 4 and 6 due to the changes of slopes of the trend lines. Thus, the optimal values of K are 4 and 6. In order to compare the cluster results with the six functional networks already discussed in the literature [25], K is fixed at 6 in the present paper.

Figure 6. The dependence of the cluster validity index on K. The thin solid, dotted, and bold solid lines are trend lines of the filled circles. Since slopes of the trend lines change significantly at $K=$ 4 and 6, based on the elbow criterion, the optimal values of K are 4 and 6.

The average of the squared Euclidean distances from all ROIs in each of the six clusters to the centroid of cluster $i(i=1,2,3,4,5,6)$ is calculated, as shown in Figure 7a–f. For each centroid, among the six averaged distances, the averaged distance from the cluster $i(i=1,2,3,4,5,6)$ to the centroid of cluster i is the lowest. This is also in line with the main idea of the K-means clustering algorithm.

Figure 7. The average of the squared Euclidean distances from all ROIs in each of the six clusters to the centroid of cluster $i(i=1,2,3,4,5,6).$ (a) Centroid of cluster 1. (b) Centroid of cluster 2. (c) Centroid of cluster 3. (d) Centroid of cluster 4. (e) Centroid of cluster 5. (f) Centroid of cluster 6. The error bars represent standard deviations.

3.5. The Overlap Ratios between the Six Clusters for the SampEn of Dynamic FC and the Six Functional Networks

The overlap ratio between each cluster and each functional network is analyzed in Table 2. By evaluating the overlap ratio between each cluster and each functional network, we find that clusters 1–6, respectively, correspond to the default network, the frontal-parietal network, the cingulo-opercular network, the sensorimotor network, the occipital network, and the cerebellum network, with the overlap ratios, respectively, equaling 29/30 (≈96.67%), 20/23 (≈86.96%), 23/27 (≈85.19%), 30/33 (≈90.91%), 22/27 (≈81.48%), and 18/20 (≈90.00%). These overlap ratios are very high.

3.6. The Consistency Ratios between the Six Clusters for the SampEn of Dynamic FC and the Six Functional Networks

Based on the data shown in Table 2, the consistency ratios between the six clusters obtained from the SampEn of dynamic FC and the six functional networks are evaluated. The consistency ratios between cluster 1 and the default network, cluster 2 and the frontal-parietal network, cluster 3 and the cingulo-opercular network, cluster 4 and the sensorimotor network, cluster 5 and the occipital network, and cluster 6 and the cerebellum network are 29/(29 + 5 + 1) (≈82.86%), 20/(20 + 1 + 3) (≈83.33%), 23/(23 + 9 + 4) (≈63.89%), 30/(30 + 3 + 3) (≈83.33%), 22/(22 + 0 + 5) (≈81.48%), and 18/(18 + 0 + 2) (≈90.00%), respectively. These consistency ratios are very high.

3.7. The SampEn of Dynamic FC is More Effective Than the Static FC

For the two different measurements (the static FC and the SampEn of dynamic FC), the overlap ratios between cluster 1 and the default network, cluster 2 and the frontal-parietal network, cluster 3 and the cingulo-opercular network, cluster 4 and the sensorimotor network, cluster 5 and the occipital network, and cluster 6 and the cerebellum network are shown in Figure 8. For cluster 3, the overlap ratio corresponding to the static FC (91.30%) is larger than that corresponding to the SampEn of dynamic FC (85.19%). For cluster 4, the overlap ratio corresponding to the static FC (91.43%) is slightly larger than that corresponding to the SampEn of dynamic FC (90.91%). For the other four clusters (clusters 1, 2, 5, and 6), the overlap ratios corresponding to the SampEn of dynamic FC are larger than that corresponding to the static FC. For clusters 1, 2, 5, and 6, the overlap ratios corresponding to the SampEn of dynamic FC are 96.67%, 86.96%, 81.48%, and 90.00%, whereas the overlap ratios corresponding to the static FC are 96.15%, 68.97%, 73.33%, and 82.35%.

Figure 8. The overlap ratios between cluster 1 and the default network, cluster 2 and the frontal-parietal network, cluster 3 and the cingulo-opercular network, cluster 4 and the sensorimotor network, cluster 5 and the occipital network, and cluster 6 and the cerebellum network for the two different measurements.

For the two different measurements, the consistency ratios between cluster 1 and the default network, cluster 2 and the frontal-parietal network, cluster 3 and the cingulo-opercular network, cluster 4 and the sensorimotor network, cluster 5 and the occipital network, and cluster 6 and the cerebellum network are shown in Figure 9. For cluster 4, the consistency ratio corresponding to the static FC (88.89%) is larger than that corresponding to the SampEn of dynamic FC (83.33%). For the other five clusters, the consistency ratios corresponding to the SampEn of dynamic FC are larger than that corresponding to the static FC. For clusters 1, 2, 3, 5, and 6, the consistency ratios corresponding to the SampEn of dynamic FC are 82.86%, 83.33%, 63.89%, 81.48%, and 90.00%, whereas the consistency ratios corresponding to the static FC are 71.43%, 66.67%, 61.76%, 73.33%, and 66.67%.

Figure 9. The consistency ratios between cluster 1 and the default network, cluster 2 and the frontal-parietal network, cluster 3 and the cingulo-opercular network, cluster 4 and the sensorimotor network, cluster 5 and the occipital network, and cluster 6 and the cerebellum network for the two different measurements.

According to the results shown in Figure 8 and Figure 9, we conclude that the SampEn of dynamic FC is more effective than the static FC in clustering different ROIs into different functional networks. This phenomenon can be interpreted by evaluating the similarity between the adjacent matrix generated based on the six functional networks (Figure 1b) and the group adjacent matrix for the static FC (Figure 3a) or for the SampEn of dynamic FC (Figure 5a). The similarity is evaluated by the squared Euclidean distance, and a smaller distance means more similarity. The distances from the adjacent matrix shown in Figure 1b to the group adjacent matrices shown in Figure 3a and in Figure 5a are 2409.58 and 2376.52, respectively. The latter is smaller than the former, i.e., the similarity between the adjacent matrix shown in Figure 1b and the group adjacent matrix shown in Figure 5a is larger than the similarity between the adjacent matrix shown in Figure 1b and the group adjacent matrix shown in Figure 3a. This causes the SampEn of dynamic FC to be more effective than the static FC in clustering different ROIs into different functional networks.

4. Conclusions and Discussion

Different brain regions in the human brain functionally interact with each other to construct multiple functional networks. Identifying the function of each functional network and the brain regions contained in each functional network is very important for understanding the human brain. The present study tests the feasibility of using the K-means clustering algorithm to identify the functional networks based on the FC, including the static FC and the dynamic FC. By applying the K-means clustering algorithm to the static FC or the SampEn of dynamic FC between different ROIs determined by the Dosenbach’s template, we show that the Dosenbach’s 160 ROIs can be divided into six clusters which show high overlap and consistency ratios with the six functional networks identified by applying modularity optimization on the average FC matrix across a large cohort of healthy subjects. The results indicate that the combination of the K-means clustering algorithm and the FC can identify the functional networks of the human brain. The K-means algorithm has been commonly used to parcellate cortical or subcortical regions based on the static FC [30,31,32,33,34,35,36,37,38]. These previous studies along with the present study extend the application of machine learning methods in brain sciences.

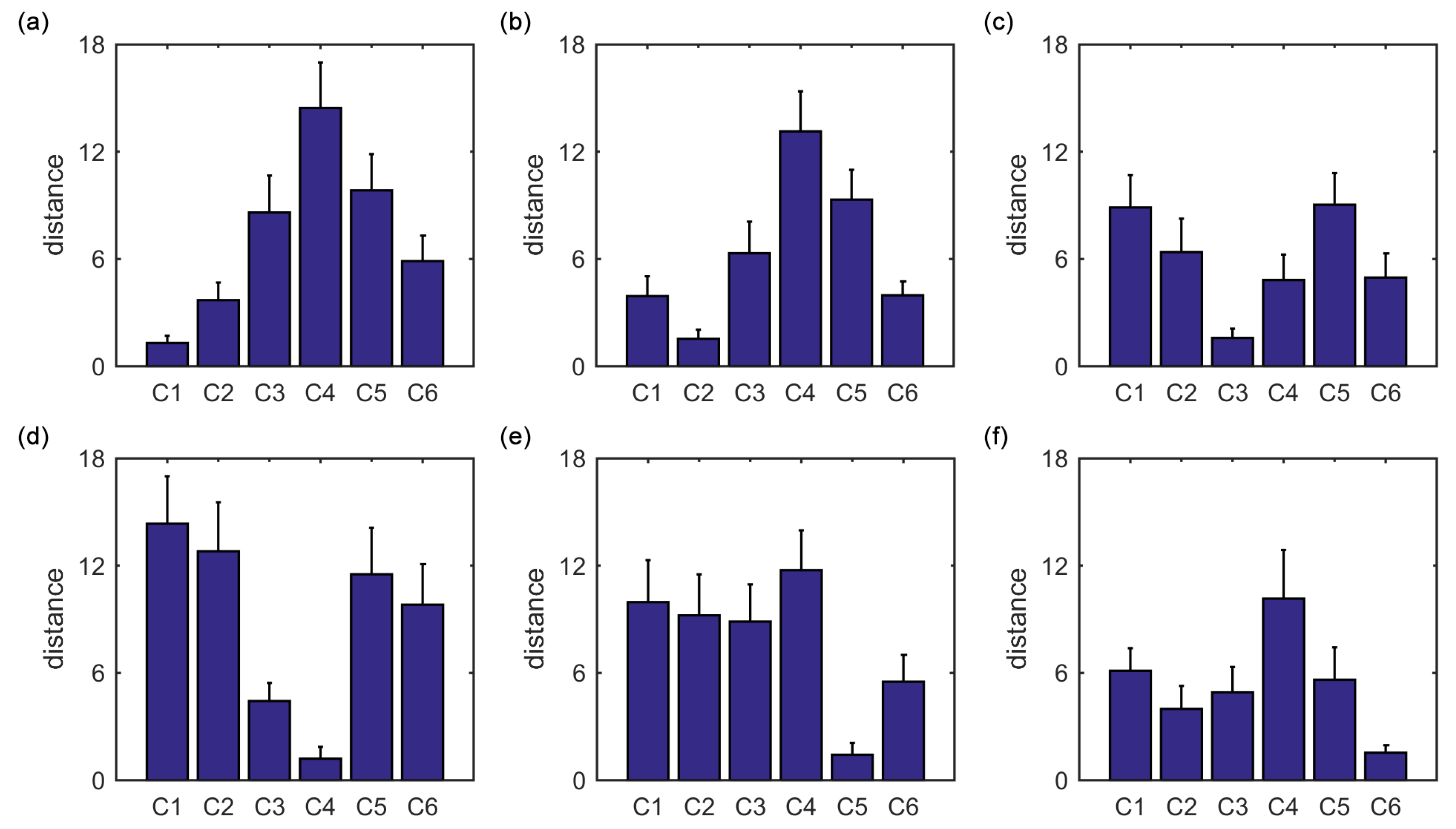
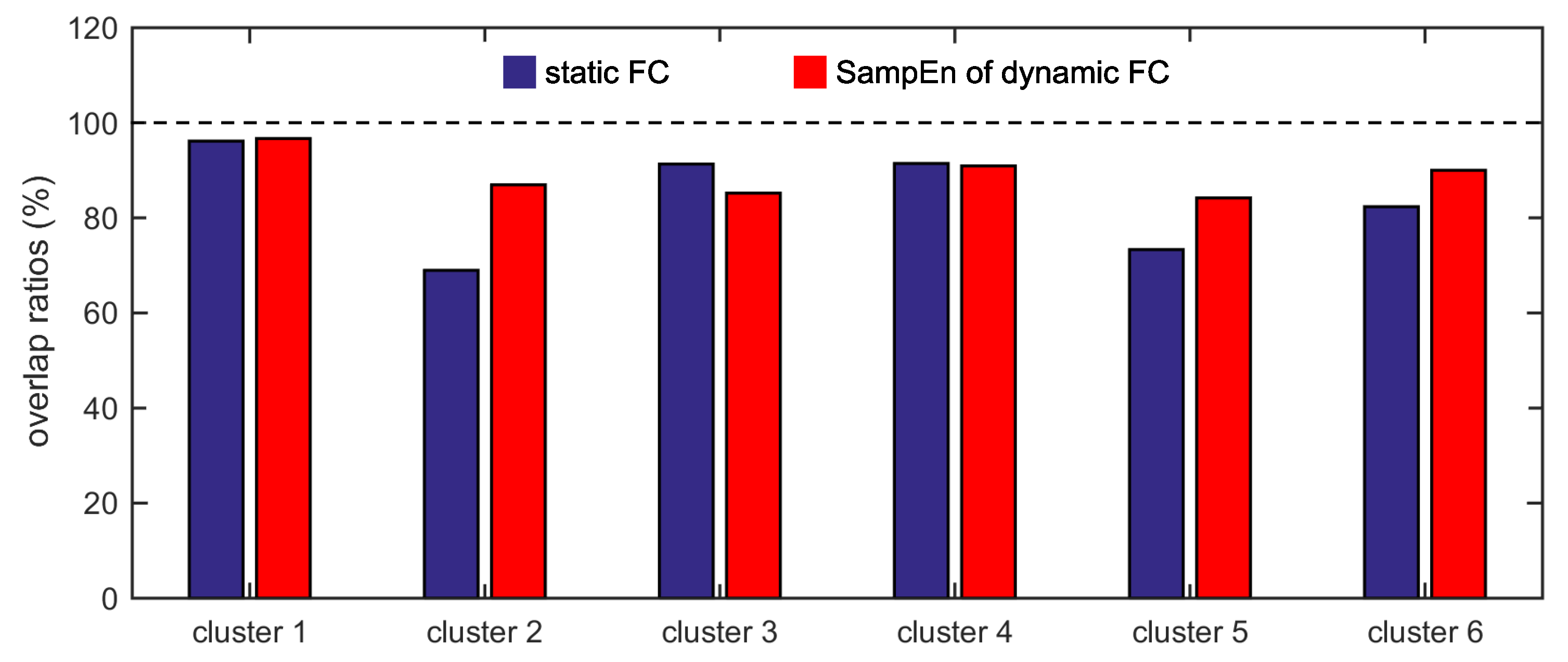
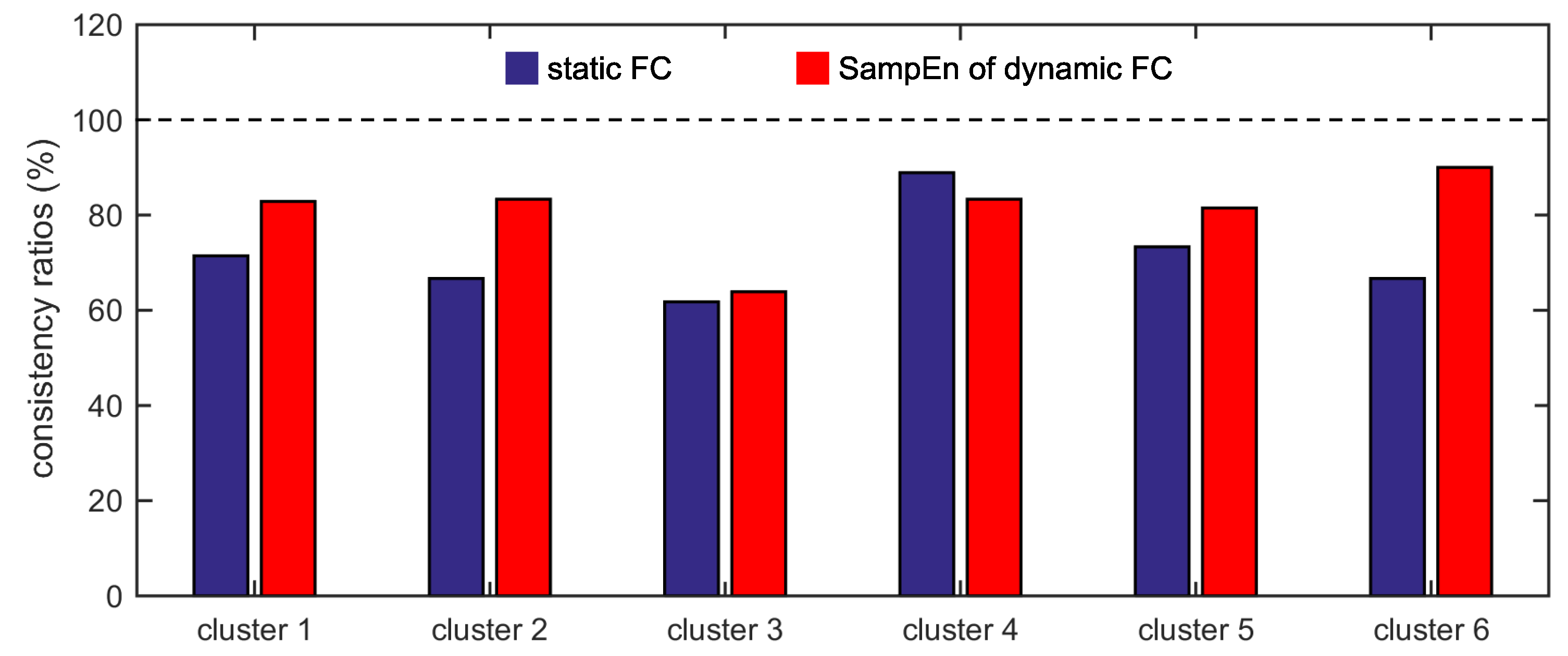
Furthermore, we show that, for four of six clusters, the overlap ratios corresponding to the SampEn of dynamic FC are larger than that corresponding to the static FC, and for five of six clusters, the consistency ratios corresponding to the SampEn of dynamic FC are larger than that corresponding to the static FC. This indicates that nonlinear dynamic characteristics of the FC is more effective than the static characteristics of the FC in identifying brain functional networks. In our previous studies, by characterizing the nonlinear characteristics of dynamic FC in healthy subjects and patients with schizophrenia, we have shown that SampEn of the amygdala-cortical FC in healthy subjects decreased with age increasing, and the visual cortex of the patients with schizophrenia exhibited significantly higher SampEn than that of the healthy subjects [24,43]. In the future, nonlinear characteristics of dynamic FC should be deeply used to characterize properties of brain functional networks and the complexity of the human brain.