1. Introduction
With the rapid development of network communication and big data applications, information security has become a more and more popular topic. Scholars have proposed a variety of information security technologies, including information encryption [
1,
2,
3,
4,
5], watermarking [
6,
7], privacy protection [
8,
9,
10], and so on. Among them, cryptography is the most basic technology in information security. In symmetric cryptographic systems, block encryption algorithms are widely used, such as in the data encryption standard (DES), advanced encryption standard (AES), and other systems. In a block cipher system, there is an important non-linear component called the substitution box (abbreviated as S-Box). S-Boxes play an important role in the security of symmetric cryptosystems. AES is considered to be an effective cryptosystem to a large extent. One of the important components of AES is its S-Box, which is based on the inversion and affine transformation of GF(2
8) elements. Due to the popularity of AES in communication systems, S-Box has attracted more and more attention. However, the S-Box component that is used in AES is fixed. If we construct this component dynamically, the encryption strength of the cryptosystem would be greater than before.
In view of the importance of S-Box in block cipher system, the design of S-Box with strong cryptographic performance has always been the goal of cryptosystem designers. Many S-Box construction methods have been proposed [
11,
12,
13,
14,
15]. In order to obtain a ciphertext block corresponding to a plaintext block, a byte conversion called the substitution byte (sub-byte) process is generated with an S-Box. In the sub-byte process, each element will be mapped using an S-Box. The S-Box is used to transform the bit input randomly. As a result, the output bit sequence has strong resistance to linear and differential attacks. Several approaches such as the analytical approach [
12], algebraic techniques [
14], Boolean function [
16], cubic polynomial mapping methods [
17], and triangle groups [
18] have been applied to S-Boxes construction.
In recent years, chaotic systems have been widely applied in the design of S-Boxes because of their good cryptographic characteristics [
19], such as random-like behavior [
20], non-periodicity [
21], and extreme sensitivity to initial conditions [
22]. In [
23], Lambic applied discrete chaotic map to design S-Box. In [
24], Lambic proposed an efficient algorithm for obtaining random bijective S-boxes based on chaotic maps and the composition method. The advantages of Lambic’s method are the low complexity and the possibility to achieve large key space. Çavusoglu [
13] designed a strong S-Box generation algorithm based on the chaotic scaled Zhongtang system. Ullah [
25] constructed S-Box with the help of the chaotic system and linear fractional transformation. Belazi and El-Latif [
26] proposed a simple S-Box method based on the chaotic sine map. In Ref. [
27], a novel method to construct cryptographically strong bijective substitution-boxes based on a 5D hyper-chaotic system was presented. Khan et al. [
28] proposed the S-Box construction method based on chaotic Boolean functions. Belazi et al. [
29] proposed an efficient S-Box method based on the chaotic logistic-sine map. Wang et al. [
30] constructed S-Box by using a hyper-chaotic system with infinite equilibria. Liu et al. [
15] constructed S-Box based on the spatiotemporal chaotic system.
However, these chaotic S-Box construction schemes mentioned above have not yet had a high score of linear probability (LP) and differential probability (DP), and the ability to resist linear and differential attacks were not ideal. In addition, the process of S-Box construction existing in the previous schemes is very complex and inefficient. Compared with high-dimensional continuous-time chaotic systems, low-dimensional discrete chaotic systems can generate chaotic sequences with higher efficiency. Moreover, some studies show that the complexity of discrete systems is higher than that of continuous systems [
31,
32,
33]. However, the common low-dimensional discrete mapping chaotic systems have a narrow chaotic range and unsatisfactory chaotic characteristics. Using such chaotic systems to construct S-Boxes will reduce the key space of cryptographic systems, and the cryptographic performance is not ideal. In order to solve this problem, it is necessary to design new discrete chaotic systems with better performance.
There are two ways to implement a cryptographic system: one is software implementation, the other is hardware implementation. The hardware is quite important when trying to expand the key space of a cryptosystem. Therefore, hardware implementation is an important issue worth considering. In [
34], authors provided the hardware implementation of a pseudo-random number generator (PRNG) based on three chaotic maps: the Bernoulli shift map, tent, and zigzag maps. It was found that some chaotic maps are more suitable for cryptographic applications, like the Bernoulli shift map that requires low field-programmable gate array (FPGA) resources, and provides high throughput. In [
35], the authors show an application in the encryption of very high-resolution digital images based on the design of a digital chaos generator by using arbitrary precision arithmetic.
To improve the shortcomings of existing chaos based S-Box construction methods, this paper presents a novel and efficient S-Box construction method by using a new compound chaotic system. It can improve the linear probability (LP) and differential probability (DP) properties of the S-Box, and enhance the robustness of cryptosystem against linear analysis attack and differential attack. The innovations of this work are as follows:
(1) A new compound chaotic system, tent–logistic system (TLS), is proposed, which has a wider chaotic range and better chaotic performance than the old ones, so it is more suitable for cryptographic applications.
(2) A simple and effective S-Box construction method by using a novel linear mapping and the tent–logistic chaotic system is proposed, which can improve the efficiency of S-Boxes construction.
(3) The proposed S-Box has a higher score of LP and DP than some old S-Boxes, showing that our proposed S-Box has obvious advantages in resisting the attacks of differential cryptanalysis and linear cryptanalysis.
The rest of this paper is organized as follows.
Section 2 proposes the new tent–logistic system (TLS) model.
Section 3 describes the simple and effective S-Box construction method based on the tent–logistic system.
Section 4 shows cryptographic performance analysis of the proposed S-Box, and makes a comparison with some recently designed S-Boxes.
Section 5 completes the research paper with conclusions.
2. The Proposed New Chaotic System
One-dimensional (1D) discrete chaotic systems have many advantages in applications to cryptography because of their simple structures. The general mathematical model of 1D discrete mapping system can be expressed as:
where f[
x] denotes functions with regard to
x.
x(0) is the initial state value of the system and {
x(1),
x(2), ...} is the output sequence of state values. For 1D discrete maps, the definition of Lyapunov exponent is as:
where, f′[
x] denotes the derivative of function f[
x] to
x. If
λ > 0, then the chaotic behaviors exist in the system. In this section, we firstly reviewed two famous 1D chaotic maps: the logistic and tent chaotic maps. Then, we proposed a new discrete compound chaotic system, which has better chaotic performance and wider chaotic range than logistic and tent maps.
2.1. Logistic Chaotic Map
The logistic map is one of famous 1D chaotic maps, which has a simple mathematical structure yet complex chaotic behavior. The mathematical model of Logistic map is [
36]:
where
μ is the system parameter in the range of [0, 4]. In order to determine the range of parameters corresponding to its chaotic phenomena, we calculated Lyapunov exponents under different parameters
μ and found the chaotic rang of logistic map was
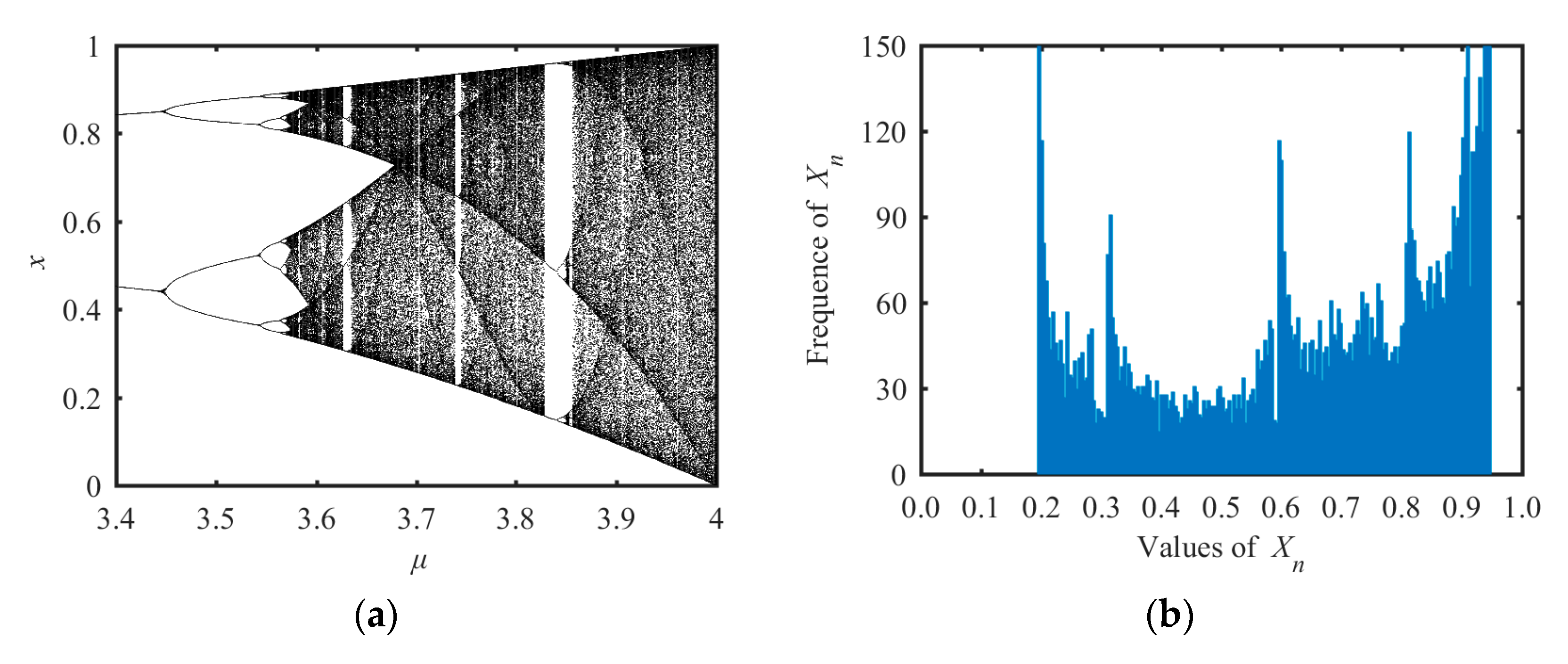
μ ∈ [3.57, 4]. The bifurcation diagram of logistic map is shown in
Figure 1a and the state distribution under
μ = 3.78 is shown in
Figure 1b.
There are three drawbacks in the logistic map. One is the chaotic range of the system is limited to
μ ∈ [3.57, 4]. Even within this range, there are some parameters that make the logistic map to have no chaotic behaviors. Another drawback is the non-uniform distribution of state values in the range of [0, 1]. In [
37], authors point out that the logistic map for
μ = 3.9 has aperiodic behavior. Instead of using the range of 3.57 ≤
μ ≤ 4, one can fix the value of
μ, however, which results in a lower key space. These drawbacks reduce the application value of the logistic map.
2.2. Tent Chaotic Map
Tent map is another discrete 1D chaotic system, which has the tent-like shape in its bifurcation diagram. The mathematical model of the tent map is as follows [
38]
where
μ is the system parameter in the range of [0, 4]. By Equation (4), we could get the Lyapunov exponent of the tent map as
λ= log(
μ/2), so when
μ > 2,
λ > 0, and when
μ = 4,
λ =
λmax = log(2) = 0.6931. Its chaotic property is shown in the bifurcation analysis in
Figure 2a. Both analysis results indicate that its chaotic range was
μ ∈ [2, 4]. The state distribution under
μ = 3.78 is shown in
Figure 2b. The tent map had the same problems as the logistic map: the small chaotic range and the no uniform distribution of the output state values.
2.3. The Tent–Logistic System
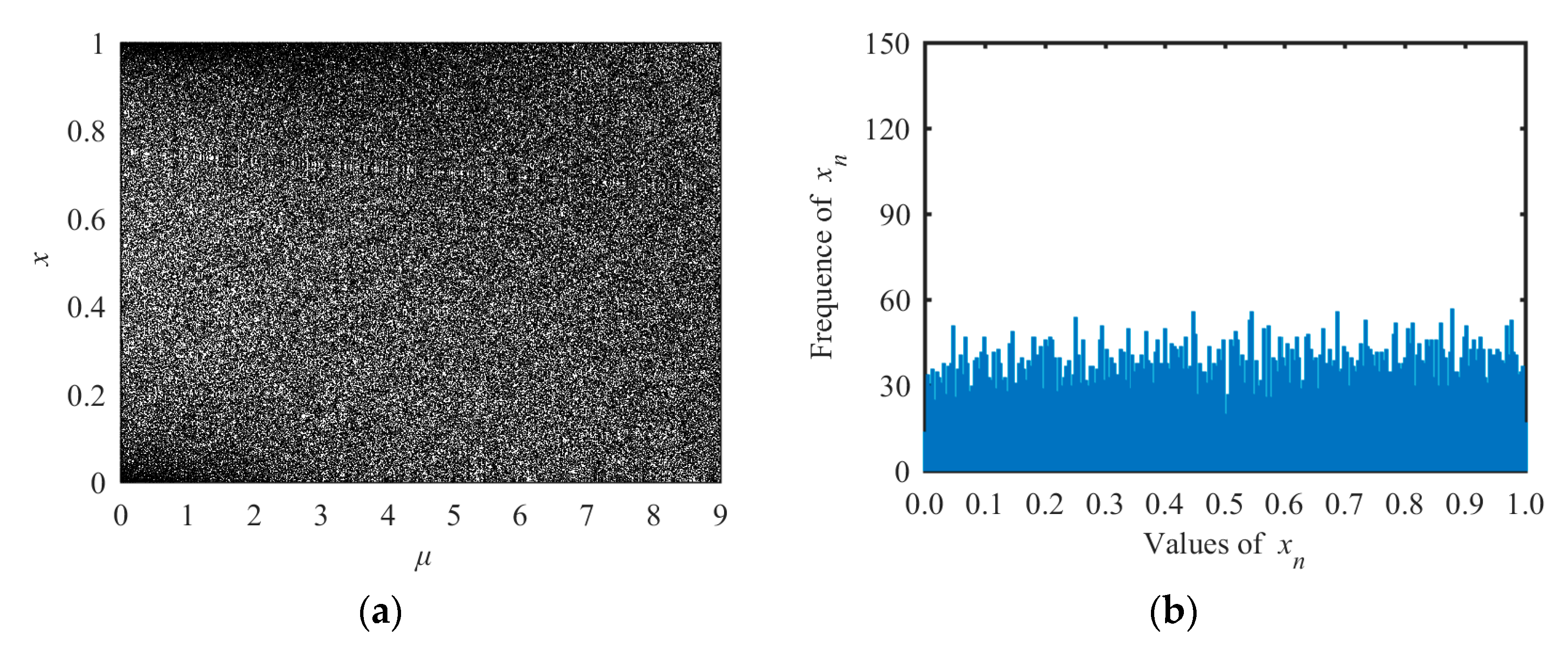
To solve the problems existing in logistic and tent maps, we proposed a new compound system by combining the logistic and tent maps, and called the new system the tent–logistic system (TLS). Its mathematical model is as follows:
where
μ is the system parameter in the range of [0, 9]. When
μ = 0, Equation (5) degenerates to the best chaotic logistic map, while
μ = 9, Equation (5) degenerates to the best chaotic tent map. Therefore, both the best chaotic logistic and tent maps can be regarded as special cases of Equation (5).
Proposition 1. In the whole range μ ∈ [0, 9], system (5) is a map f: xi∈(0, 1)→xi+1∈(0, 1).
Proof.
(1) When μ = 0, Equation (5) degenerates to the chaotic logistic map fL: xi∈(0, 1)→xi+1∈(0, 1).
(2) When μ = 9, Equation (5) degenerates to the chaotic tent map fT: xi∈(0, 1)→xi+1∈(0, 1).
(3) When 0 < μ < 9 and x(n) < 0.5, f1′[x(n)] = (36 – 2μ) / 9 – (72 – 8μ) × x(n) / 9 > (36 – 2μ) / 9 – (72 – 8μ) × 0.5 / 9 = 2μ / 9 > 0. Hence, f1[x(n) < 0.5] < f1[0.5] = 1.
(4) When 0 < μ < 9 and x(n) ≥ 0.5, f2′[x(n)] = (36 – 6μ) / 9 – (72 – 8μ) × x(n) / 9 ≤ (36 – 6μ) / 9 – (72 – 8μ) × 0.5 / 9 = –2μ / 9 < 0. Hence, f2[x(n) ≥ 0.5] ≤ f2[0.5] = 1. f2[x(n) > 0.5] < f2[0.5] = 1. □
The bifurcation diagram and the state distribution diagram of the TLS are shown in
Figure 3. From
Figure 3a, one can see that the chaotic range was the whole range
μ∈[0, 9], which was much larger than those of the logistic or tent maps. Its output sequences uniformly distributed within [0, 1] (see
Figure 3b). Hence, the TLS had better chaotic performance than the logistic and tent maps.
The new tent–logistic system has two advantages compared with logistic and tent maps. First, the chaotic range of the tent–logistic system was far wider than those of the logistic and tent map. If the system parameter μ was used as the secret key of a cryptosystem, the key space of the cryptosystem with the new system would be much larger. Second, the output sequences of the tent–logistic system distributed evenly throughout the entire value range between 0 and 1. These advantages guarantee that the proposed tent–logistic system was more suitable for cryptographic applications.
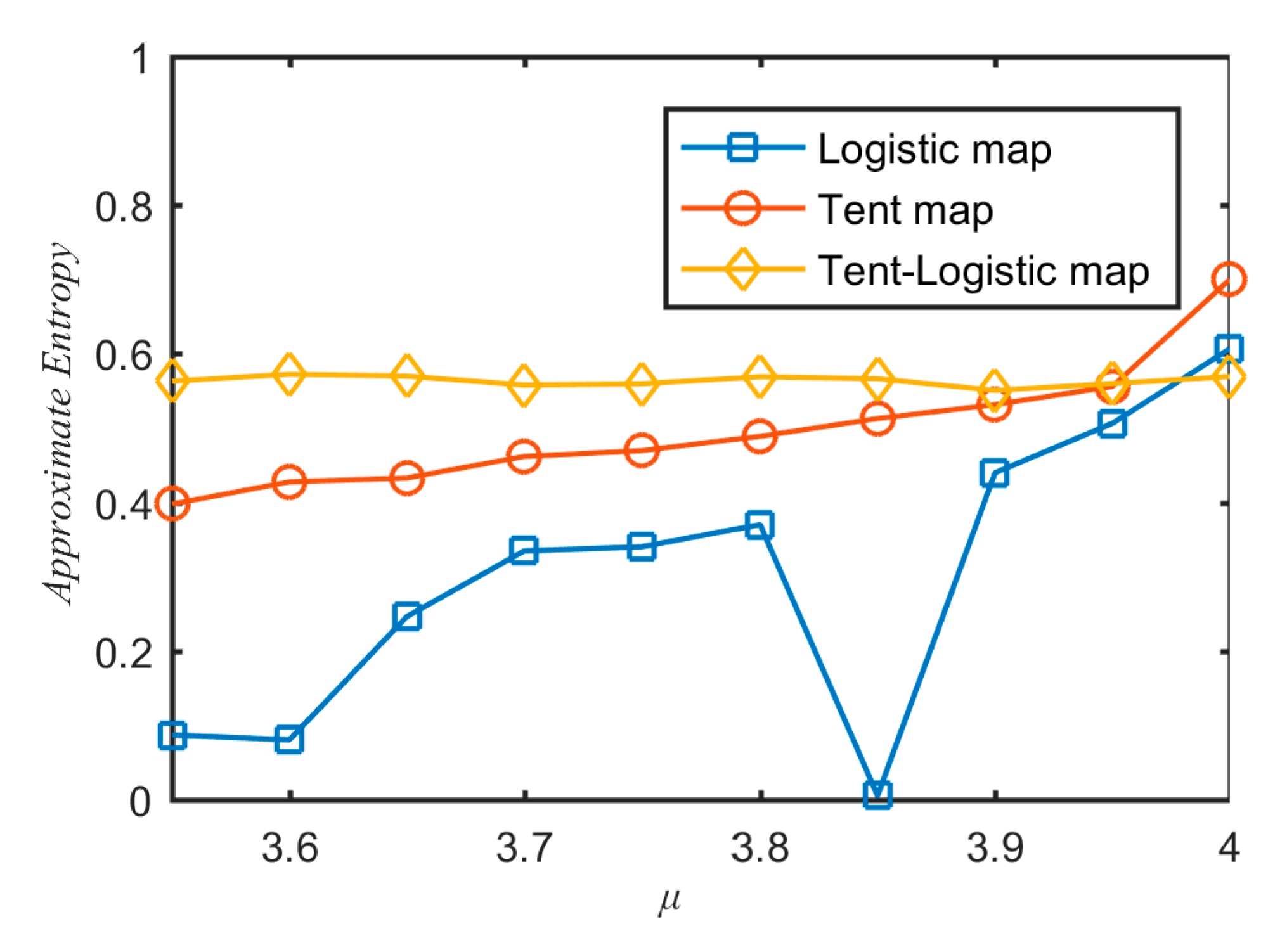
2.4. Entropy Analysis of the New Chaotic System
There are many techniques to evaluate the system complexity from time sequence [
39,
40,
41]. One of the most famous methods is approximate entropy [
41]. The greater the approximate entropy, the higher the complexity of the time sequence. To measure the complexity of sequences generated by different chaotic systems, the approximate entropy values of the sequence generated by the three chaotic maps are calculated and shown in
Figure 4. From
Figure 4, one can see that the approximate entropy values of sequence generated by the tent–logistic map were the largest ones among the three chaotic maps in the cases of most
μ values. It verified that the sequence generated by the tent–logistic map had larger complexity than tent and logistic maps.
2.5. NIST Randomness Test of PRNG with the New System
In this section, a pseudo-random number generator (PRNG) was designed by using the tent–logistic map. The specific steps of generating random number are as follows:
(1) Set the initial state value x0, the system parameter μ, and the positive integer N0 and L.
(2) Iterate the chaotic tent–logistic map (5) N0 times to eliminate harmful effects of transient processes.
(3) Continue to iterate the chaotic tent–logistic map (5) L times and generate a random sequence X = [x1, x2,... xL].
(4) Through the nonlinear transformation of Equation (6), the random sequence X is transformed into the random sequence Y = [
y1,
y2, ...,
yL].
where, floor(
x) returns a maximum integer less than or equal to
x and mod(
x, 256) returns the remainder of
x divided by 256. Therefore, each element in Y is an integer with the size of one byte and in the range of [0, 255], which is especially suitable for image encryption.
(5) Transform each yi to a 8-bit binary number, then we could obtain a bit sequence B = {b1, b2, ..., b8L}, which is especially suitable for stream cipher application.
The random number generator test standard is the Federal Information Processing Standard issued by the National Institute of Standards and Technology (NIST). The NIST test suite includes 17 tests, which focus on a sort of different types of non-randomness that could exist in a sequence. NIST test software mainly uses two performance indicators: pass rate and
p-value to determine the random performance of the sequence. The number of sequences to be tested is
m, the significant level is α. If the
p-values of
N sequences are greater than α, then the pass rate is
N/
m. The default value of α is 0.01. To test the random performance of the bit sequences generated by our PRNG, we set the parameters as:
x0 = 0.66,
μ = 4.5,
L = 12.5 × 10
6, and
N0 = 500. Then, a bit sequence was generated, which had the length of 100 × 10
6 bits. The bit sequence was divided into 100 sub-sequences of equal length, each of which was 10
6 bits in length. By this way, 100 sequences of 10
6 bits were produced. The results from all statistical tests are given in
Table 1. The min
p-value in
Table 1 was 0.045675, which was larger than 0.01. The minimum pass rate for each statistical test was 98 for 100 binary sequences. Therefore, the sequence generated with the new tent–logistic system and the generation algorithm could be considered to have high randomness. It is worth noting that the smaller number of sequences was used for random excursions tests in the
Table 1. It was due to the fact that random excursions and random excursions variant tests were not applicable to binary sequences with insufficient number of cycles. Therefore, only samples with the number of cycles exceeding 500 were evaluated for these tests. In our test, there were 57 samples with the number of cycles exceeding 500.
3. Proposed New S-Box Design
3.1. Introduction of S-Boxes
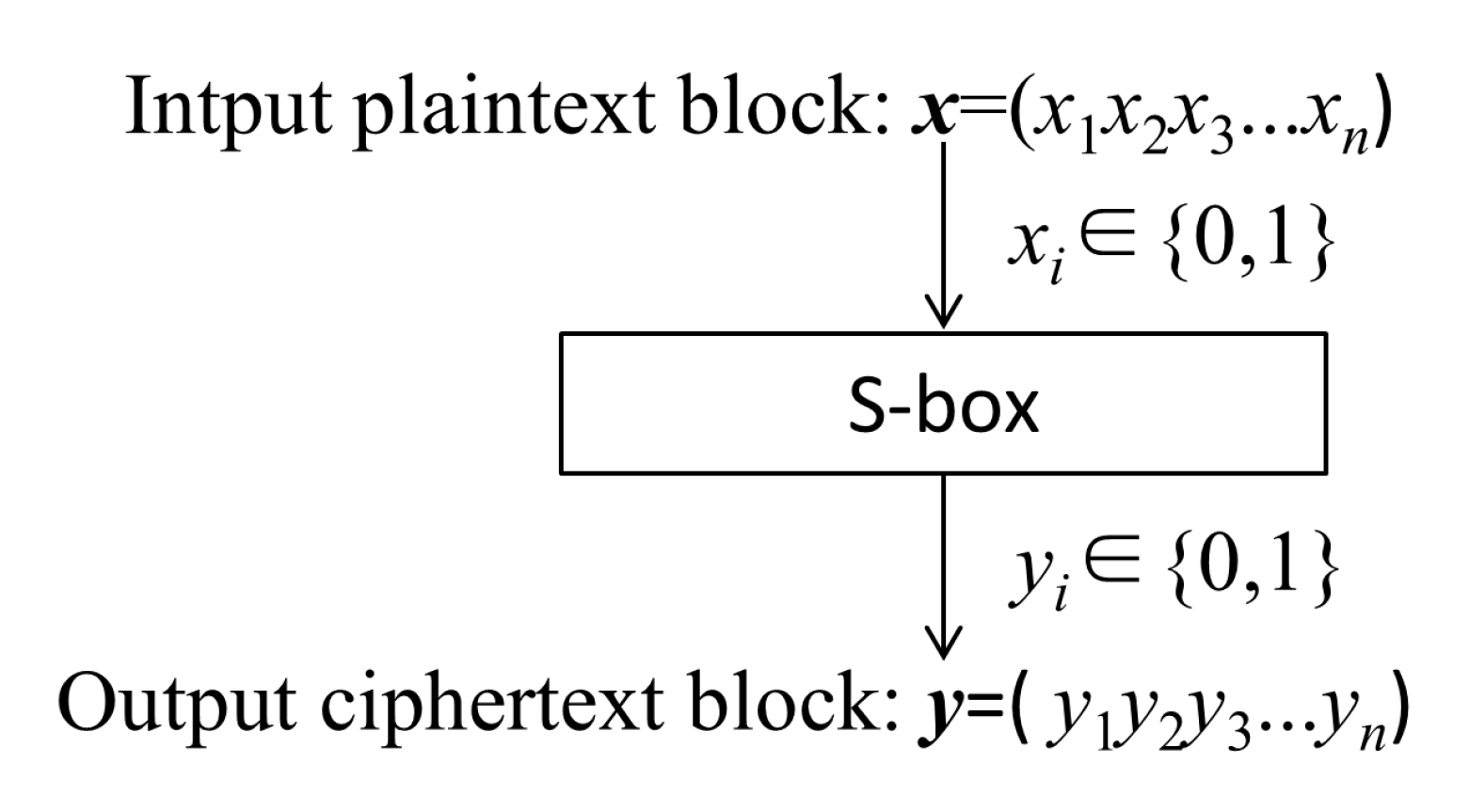
An S-Box is the only non-linear component in a block cipher system. It plays an important role in symmetric block cipher cryptosystems. An S-Box is like a black box. It transforms any input plaintext block into a ciphertext block, which can confuse the relationship between ciphertext and plaintext. A general
m ×
n S-Box is a map: {0, 1}
m→{0, 1}
n. When
n =
m, it means that data are neither compressed nor expanded during encryption transformation. In this case of
n =
m, the S-Box can realize completely reversible transformation. Most S-Boxes commonly used in cryptography are
m =
n. The function and basic principle of an
n ×
n S-Box can be shown in
Figure 5.
An
n ×
n S-Box is a number set of {0, 1, 2, ..., 2
n − 1}, which is represented by a 2
n/2 × 2
n/2 matrix Sb. S boxes that are 8 × 8 are the most commonly used type of S-Box, especially widely used in digital image encryption system [
42]. In this paper, we focused on the design algorithm of an 8 × 8 S-Box. An 8 × 8 S-Box is a number set of {0, 1, 2, ..., 255}, which is represented by a 16 × 16 matrix Sb = {Sb(
i,
j)|
i = 1, 2,..., 16;
j = 1, 2, ..., 16} shown in
Table 2. For 8 × 8 S-Boxes, there are a total of (
) different forms of variation. Among (
) different forms of variation, the simplest 8 × 8 S-Box arranges elements in an orderly manner from small to large values. As the result, elements in the simplest 8 × 8 S-Box has the form: Sb(
i,
j) = (
i-1) × 16 +
j-1.
The process of converting plaintext byte
x into ciphertext byte
y through an S-Box with matrix Sb can be expressed by the function S[
x] as:
where, floor(
a) rounds
a to the nearest integer less than or equal to
a. mod(
a,
m) returns the remainder after division of
a by
m, where
a is the dividend and
m is the divisor. Equation (7a) is a process in which each pixel value in a plain image is substituted with an element value in the S-Box. For example, if
x = 55, then
i = floor(55/16) + 1 = 3 + 1 = 4,
j = mod (55, 16) + 1 = 7 + 1 = 8. Consequently,
y = S[
x] = Sb(
i,
j) = Sb(4, 8). For the simplest 8 × 8 S-Box, we could obtain the following results easily as: S[0] = Sb(1, 1) = 0, S[1] = Sb(1, 2) = 1, ..., S[255] = Sb(16, 16) = 255. Namely,
y = S[
x] =
x. It is obvious that the simplest 8 × 8 S-Box can not alter any input plaintext value, so the simplest 8 × 8 S-Box can not be used in the encryption system.
Corresponding to the transformation
y = S[
x] in the encryption procedure, we defined the inverse transformation
x =
in the decryption procedure. The steps of calculating
are as follows:
3.2. The Proposed Algorithm for Generating S-Box
Many researchers have done extensive research on the design methods of S-Boxes with different cryptographic strength. However, most of these methods are complex and inefficient, so the time cost of generating S-Boxes is large. Here, we proposed a very simple and efficient design methods to construct strong S-Boxes based on the new chaotic map and a nonlinear mapping. The new method takes advantage of the excellent chaotic characteristics of the tent–logistic map. The detailed steps of generating new S-Boxes are given below.
Step 1: Set a integer parameter A such that A > 0 and A ≠ k × 257, k = 1, 2, 3,....
Step 2: Let T ← [0, 1, 2, ..., 255], then we obtained an array T, which contained 256 distinct integers in the range of [0, 255].
Step 3: Based on T and
A to obtain a new array R by the following linear mapping:
where
T(
i)∈{0, 1, ...,255},
A is a positive integer satisfying
A ≠
k × 257, and
k is a positive integer. (
A/257) is not an integer, and (
T(
i)+1)/257 is also not an integer. As a result, (
A×(
T(
i)+1)) cannot be divided exactly by 257. Namely, mod((
A×(
T(
i)+1)), 257) ≠ 0. Therefore, Equation (8) is a map:
T(
i)∈{0,1,2,...,255} →
R(
i)∈{1, 2, ..., 256}.
Step 4: Let R(i) ← R(i) – 1, then R(i)∈{0, 1, ..., 255}, i = 1, 2, ..., 256. We obtained a 1D array R = {R(i)}.
Step 5: Transform the 1D array R into a 2D matrix Rb, and then Rb could be considered as the initial S-Box.
Step 6: Set the parameters μ, initial state value x0 of the tent–logistic map, and an integer L that was far larger than 256. Then iterate the tent–logistic map L times to generate a chaotic sequence of length L. In order to improve the sensitivity of output chaotic sequence to its initial state value, we discarded the first (L-256) elements of the original chaotic sequence, and then we could obtain a new chaotic sequence of length 256, which is represented by X.
Step 7: Sort the chaotic sequence X, then we could get a position index array J = {J(1), J(2), ..., J(256)}, J(i)∈{1, 2, ..., 256}. Due to the non-periodicity and ergodicity of chaotic sequences, it will inevitably lead to that J(i)≠J(j) as long as i≠j.
Step 8: Calculate the 1D array S1 as follows:
Step 9: Transform the 1D array S1 into a 2D matrix Sb, and this was the proposed S-Box.
By the proposed method, the length of chaotic sequences to be used in constructing a 16 × 16 sized S-Box matrix was 256. The purpose of taking
L far larger than 256 is to execute (
L-256) times pre-iterations, which could enhance the sensitivity of S-Box to the initial value
x0 of the chaotic system. In the process of concrete realization, the proposed new S-Box was generated by the above S-Box generation algorithm with parameters were set as {
x0 = 0.66,
μ = 4.5,
A = 56,
L = 65536}, which is shown in
Table 3. The number in the first row of
Table 3 represents the column number of the S-Box matrix, while the number in the first column of
Table 3 represents the row number of the S-Box matrix.