Fitness Gain of Individually Sensed Information by Cells
Abstract
1. Introduction
2. Modeling Sensing and Adaptation Processes
Fitness of a Population with Individual and Common Sensing
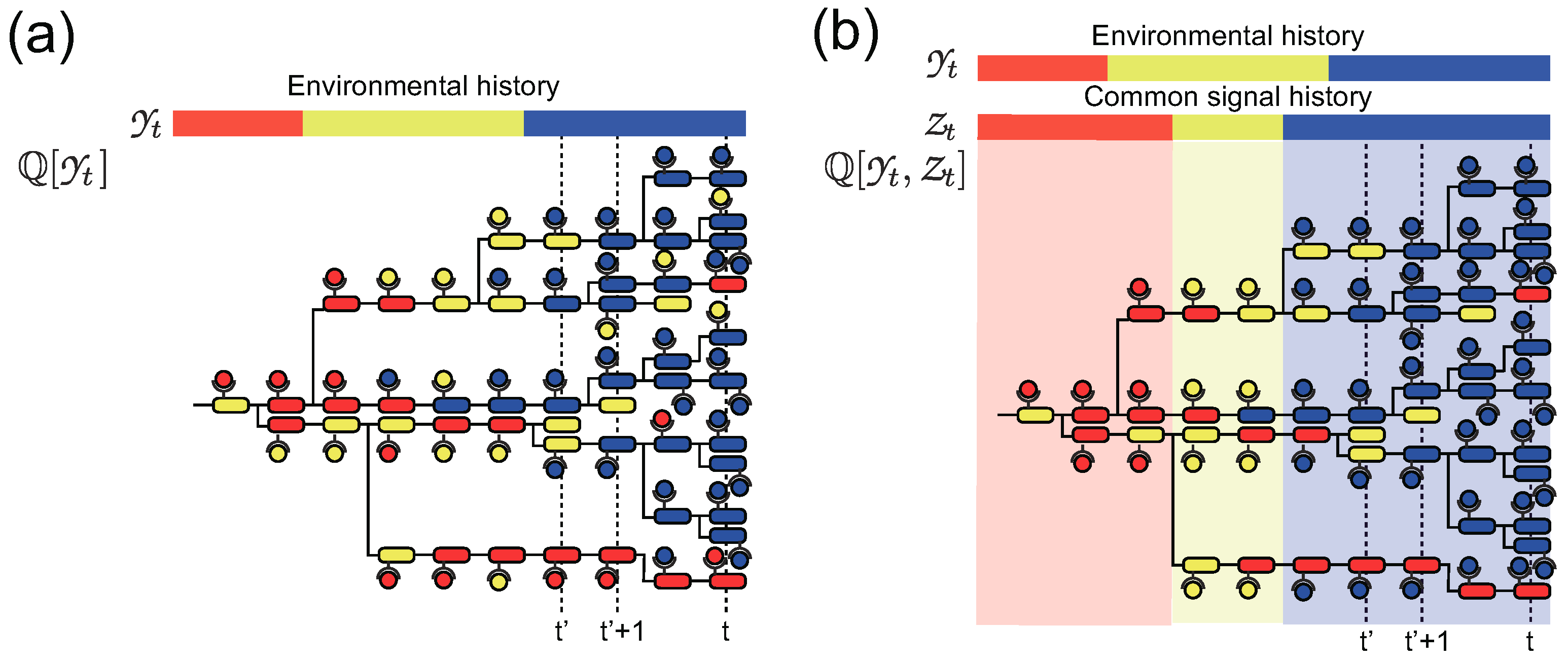
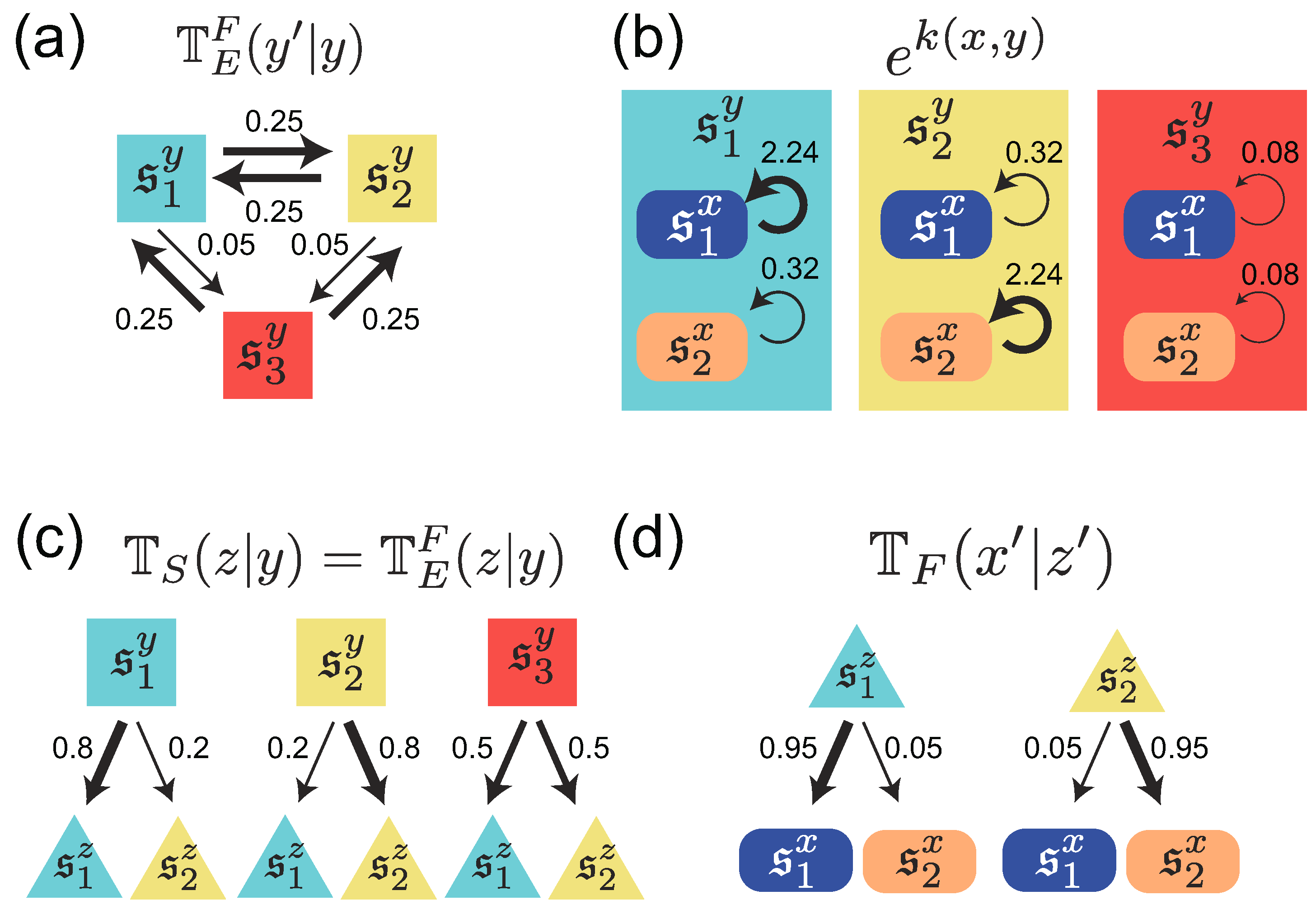
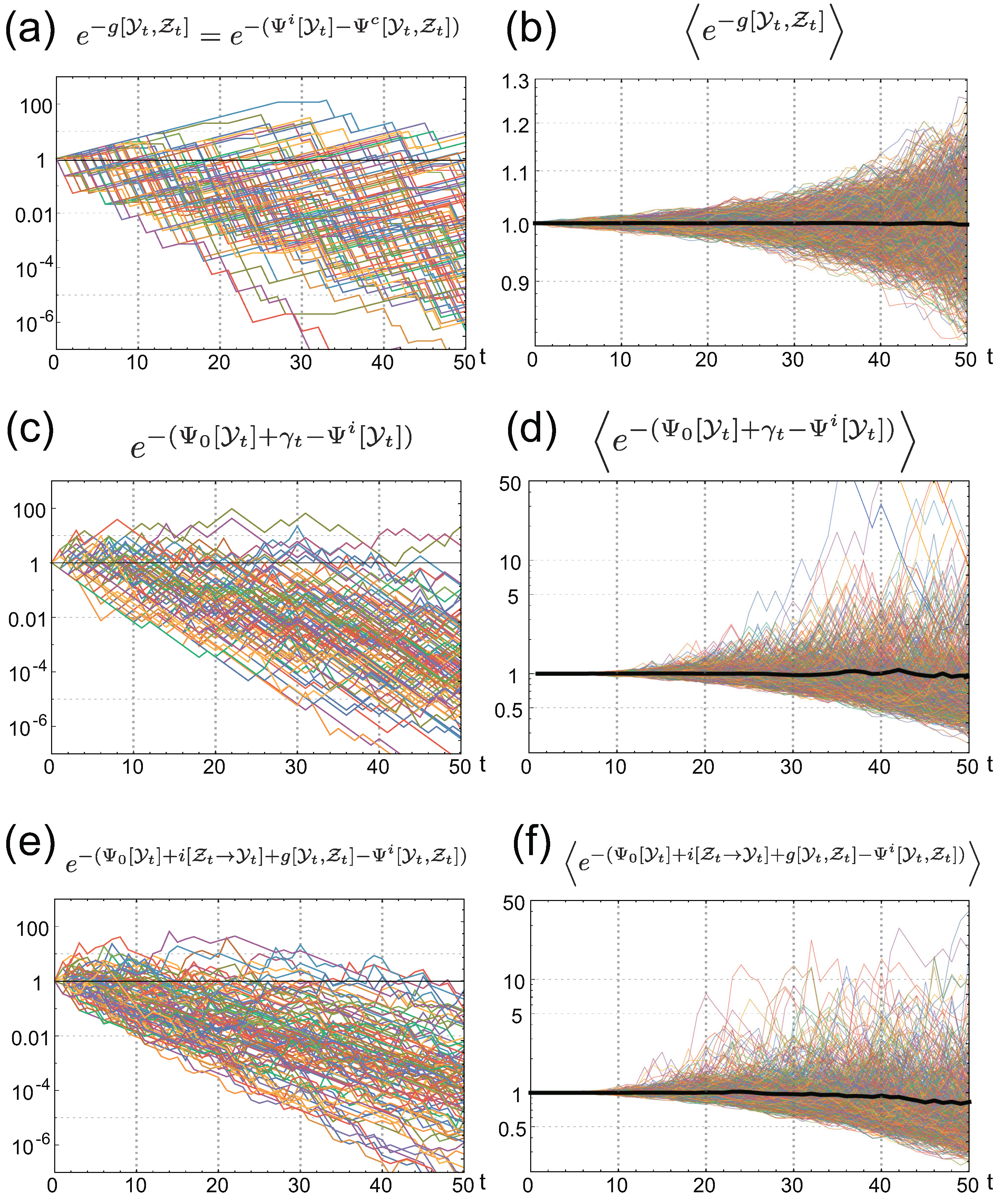
3. Stochastic Trajectories of Individual and Common Sensing
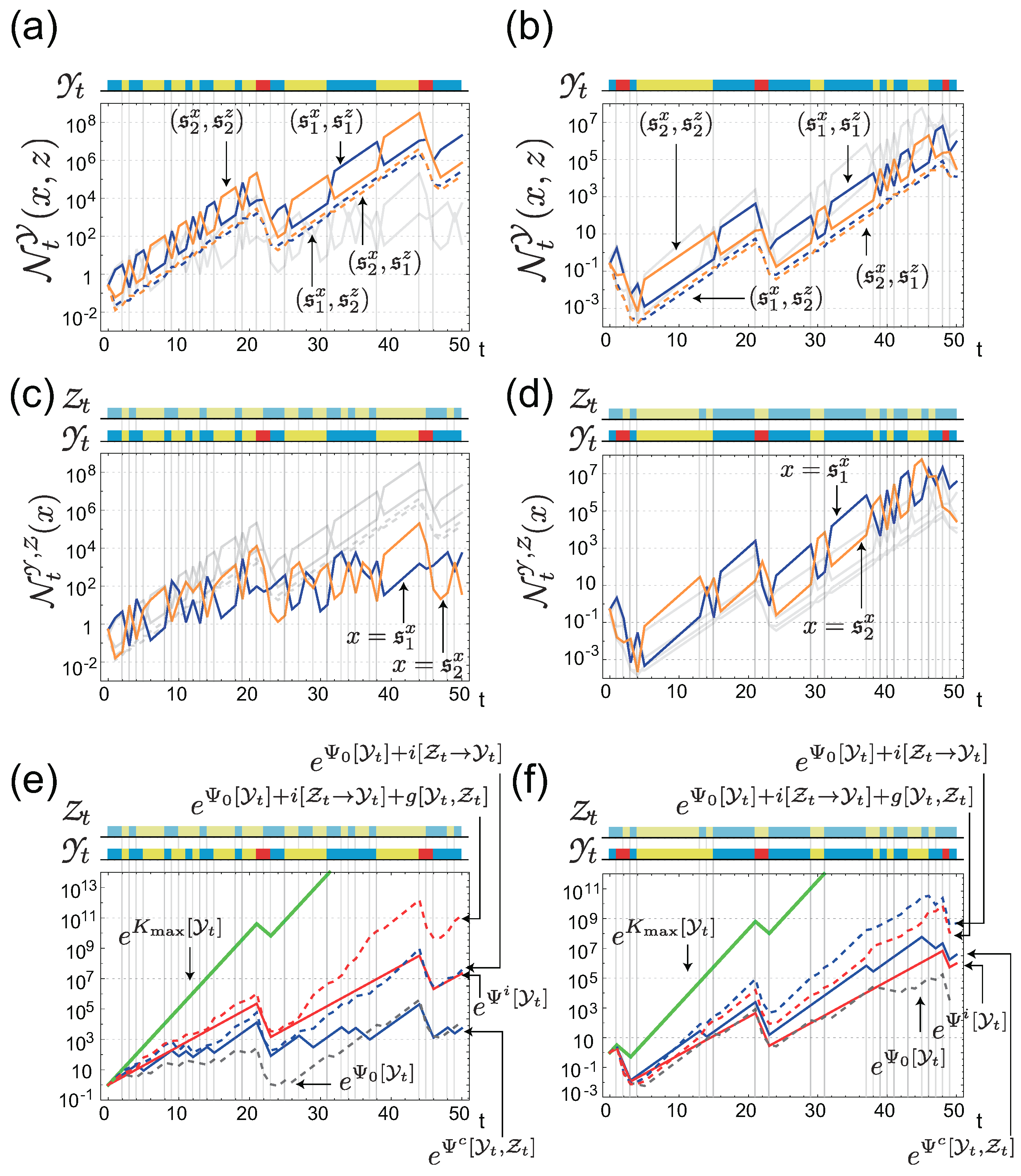
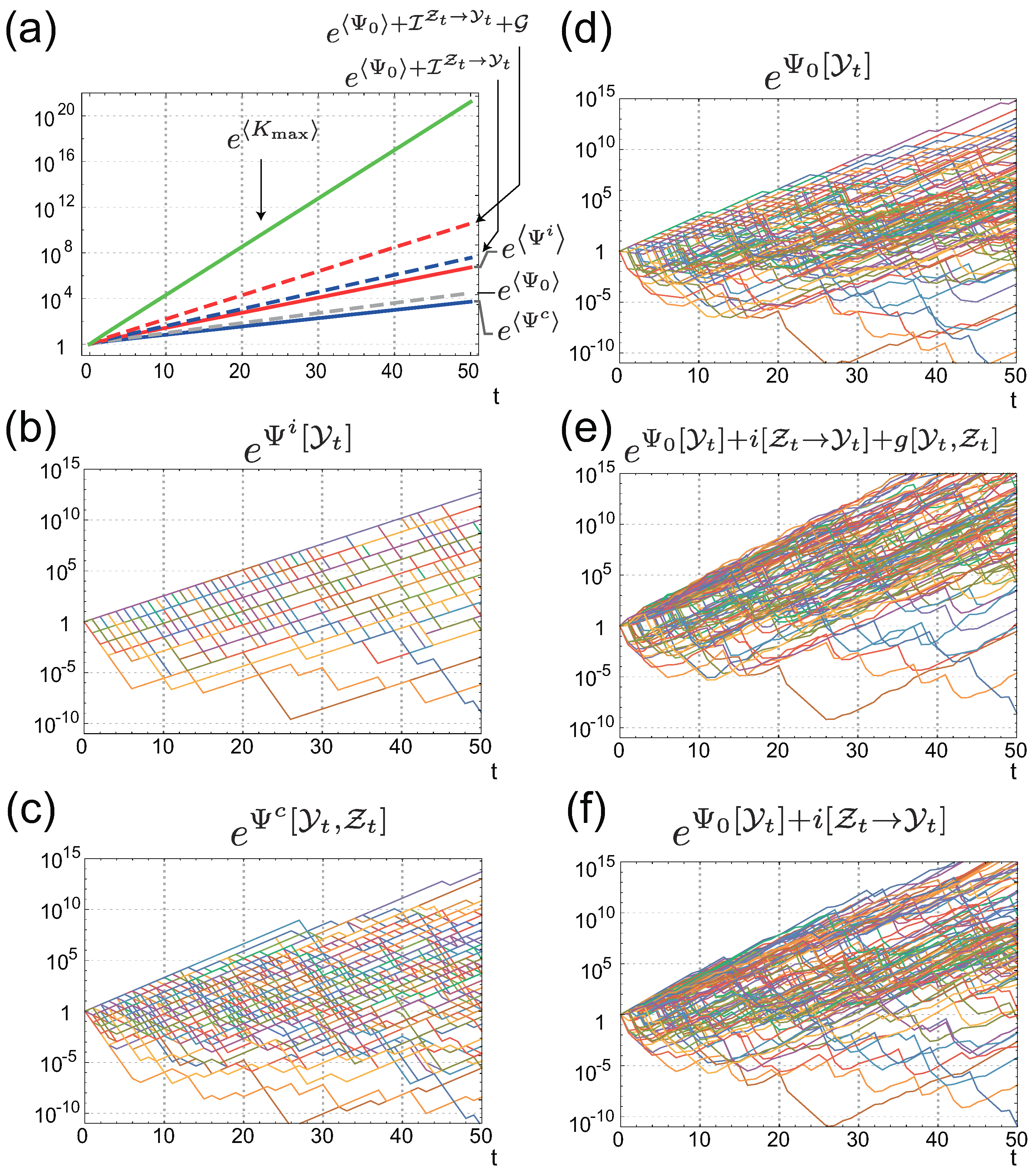
4. Value of Individual Sensing is Always Greater than that of Common Sensing
4.1. The Gain of Fitness by Individual Sensing
4.2. Connection with Other Information Measures
5. Discussion and Future Works
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of Equations
Appendix A.1. Derivation of Equations (7) and (8)
Appendix A.2. Derivation of Equation (15)
Appendix A.3. Derivation of Equations (16) and (17)
Appendix A.4. Derivation of Equation (21)
Appendix A.5. Derivation of Equation (30)
Appendix A.6. Derivation of Equation (35)
References
- Perkins, T.J.; Swain, P.S. Strategies for cellular decision-making. Mol. Syst. Biol. 2009, 5, 326. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, T.J.; Kamimura, A. Theoretical aspects of cellular decision-making and information-processing. Adv. Exp. Med. Biol. 2012, 736, 275–291. [Google Scholar] [PubMed]
- Bowsher, C.G.; Swain, P.S. ScienceDirect Environmental sensing, information transfer, and cellular decision-making. Curr. Opin. Biotech. 2014, 28, 149–155. [Google Scholar] [CrossRef] [PubMed]
- Tostevin, F.; Wolde, P.R.t. Mutual Information between Input and Output Trajectories of Biochemical Networks. Phys. Rev. Lett. 2009, 102, 218101-4. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, T.J. Implementation of dynamic Bayesian decision making by intracellular kinetics. Phys. Rev. Lett. 2010, 104, 228104. [Google Scholar] [CrossRef] [PubMed]
- Bowsher, C.G.; Swain, P.S. Identifying sources of variation and the flow of information in biochemical networks. Proc. Natl. Acad. Sci. USA 2012, 109, E1320-8. [Google Scholar] [CrossRef]
- Mayer, A.; Mora, T.; Rivoire, O.; Walczak, A.M. Transitions in optimal adaptive strategies for populations in fluctuating environments. Phys. Rev. E 2017, 96, 032412. [Google Scholar] [CrossRef]
- Tkacik, G.; Callan, C.G.; Bialek, W. Information flow and optimization in transcriptional regulation. Proc. Natl. Acad. Sci. USA 2008, 105, 12265–12270. [Google Scholar] [CrossRef]
- Cheong, R.; Rhee, A.; Wang, C.J.; Nemenman, I.; Levchenko, A. Information transduction capacity of noisy biochemical signaling networks. Science 2011, 334, 354–358. [Google Scholar] [CrossRef]
- Brennan, M.D.; Cheong, R.; Levchenko, A. Systems biology. How information theory handles cell signaling and uncertainty. Science 2012, 338, 334–335. [Google Scholar] [CrossRef]
- Uda, S.; Saito, T.H.; Kudo, T.; Kokaji, T.; Tsuchiya, T.; Kubota, H.; Komori, Y.; Ozaki, Y.i.; Kuroda, S. Robustness and Compensation of Information Transmission of Signaling Pathways. Science 2013, 341, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Barato, A.C.; Hartich, D.; Seifert, U. Nonequilibrium sensing and its analogy to kinetic proofreading. New J. Phys. 2014, 17, 055026-19. [Google Scholar]
- Das, S.G.; Iyengar, G.; Rao, M. A lower bound on the free energy cost of molecular measurements. Arxiv 1443, arXiv:14433578534543697987related:QygubTRfTsgJ. [Google Scholar]
- Lahiri, S.; Sohl-Dickstein, J.; Ganguli, S. A universal tradeoff between power, precision and speed in physical communication. Arxiv 2016, arXiv:1603.07758. [Google Scholar]
- Bo, S.; Giudice, M.D.; Celani, A. Thermodynamic limits to information harvesting by sensory systems. J. Stat. Mech. 2015, P01014. [Google Scholar] [CrossRef]
- Ouldridge, T.E. The importance of thermodynamics for molecular systems, and the importance of molecular systems for thermodynamics. Nat. Comput. 2018, 17, 3–29. [Google Scholar] [CrossRef]
- Stephens, D.W. Variance and the value of information. Am. Nat. 1989, 134, 128–140. [Google Scholar] [CrossRef]
- Haccou, P.; Iwasa, Y. Optimal mixed strategies in stochastic environments. Theor. Populat. Biol. 1995, 47, 212–243. [Google Scholar] [CrossRef]
- Shannon information and biological fitness. In Proceedings of the Information Theory Workshop, San Antonio, TX, USA, 24–29 October 2004.
- Kussell, E.; Leibler, S. Phenotypic diversity, population growth, and information in fluctuating environments. Science 2005, 309, 2075–2078. [Google Scholar] [CrossRef]
- Donaldson-Matasci, M.C.; Bergstrom, C.T.; Lachmann, M. The fitness value of information. Oikos 2010, 119, 219–230. [Google Scholar] [CrossRef]
- Rivoire, O.; Leibler, S. The value of information for populations in varying environments. J. Stat. Phys. 2011, 142, 1124–1166. [Google Scholar] [CrossRef]
- Pugatch, R.; Barkai, N.; Tlusty, T. Asymptotic Cellular Growth Rate as the Effective Information Utilization Rate. Arxiv 2013, arXiv:1308.0623v3. [Google Scholar]
- Rivoire, O.; Leibler, S. A model for the generation and transmission of variations in evolution. Proc. Natl. Acad. Sci. USA 2014, 111, E1940-9. [Google Scholar] [CrossRef] [PubMed]
- Rivoire, O. Informations in Models of Evolutionary Dynamics. J. Stat. Phys. 2015, 162, 1324–1352. [Google Scholar] [CrossRef]
- Kobayashi, T.J.; Sughiyama, Y. Fluctuation Relations of Fitness and Information in Population Dynamics. Phys. Rev. Lett. 2015, 115, 238102-5. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, T.J.; Sughiyama, Y. Stochastic and Information-thermodynamic Structures of Population Dynamics in Fluctuating Environment. Arxiv 1703, arXiv:1703.00125. [Google Scholar]
- Leibler, S.; Kussell, E. Individual histories and selection in heterogeneous populations. Proc. Natl. Acad. Sci. USA 2010, 107, 13183–13188. [Google Scholar] [CrossRef]
- Sughiyama, Y.; Kobayashi, T.J.; Tsumura, K.; Aihara, K. Pathwise thermodynamic structure in population dynamics. Phys. Rev. E 2015, 91, 032120. [Google Scholar] [CrossRef]
- Kramer, G. Directed Information for Channels with Feedback. Ph.D. Thesis, Swiss federal institute of technology, Zurich, Switzerland, 1998. [Google Scholar]
- Permuter, H.H.; Kim, Y.-H.; Weissman, T. Interpretations of Directed Information in Portfolio Theory, Data Compression, and Hypothesis Testing. IEEE Trans. Inform. Theory 2011, 57, 3248–3259. [Google Scholar] [CrossRef]
- Baldi, P. Autoencoders, Unsupervised Learning, and Deep Architectures. JMLR Workshop Conf. Proc. 2012, 27, 37–50. [Google Scholar]
- Sagawa, T. Thermodynamics of Information Processing in Small Systems; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Sagawa, T.; Ueda, M. Nonequilibrium thermodynamics of feedback control. Phys. Rev. E 2012, 85, 021104-16. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Aviyente, S. The relationship between transfer entropy and directed information. In Proceedings of the IEEE Statistical Signal Processing Workshop (SSP), Ann Arbor, MI, USA, 5–8 August 2012; pp. 73–76. [Google Scholar]
- Govern, C.C.; Wolde, P.R. Optimal resource allocation in cellular sensing systems. Proc. Natl. Acad. Sci. USA 2014, 111, 17486–17491. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kobayashi, T.J.; Sughiyama, Y. Fitness Gain of Individually Sensed Information by Cells. Entropy 2019, 21, 1002. https://doi.org/10.3390/e21101002
Kobayashi TJ, Sughiyama Y. Fitness Gain of Individually Sensed Information by Cells. Entropy. 2019; 21(10):1002. https://doi.org/10.3390/e21101002
Chicago/Turabian StyleKobayashi, Tetsuya J., and Yuki Sughiyama. 2019. "Fitness Gain of Individually Sensed Information by Cells" Entropy 21, no. 10: 1002. https://doi.org/10.3390/e21101002
APA StyleKobayashi, T. J., & Sughiyama, Y. (2019). Fitness Gain of Individually Sensed Information by Cells. Entropy, 21(10), 1002. https://doi.org/10.3390/e21101002




