A New Efficient Expression for the Conditional Expectation of the Blind Adaptive Deconvolution Problem Valid for the Entire Range ofSignal-to-Noise Ratio
Abstract
1. Introduction
2. System Description
- The source signal is given bywhere and are the real and imaginary parts of , respectively. It is assumed that and are independent and thatwhere stands for the expectation operation.
- The unknown channel is possibly a non-minimum phase linear time-invariant filter in which the transfer function has no “deep zeros”.
- The filter is a tap-delay line.
- The channel noise is an additive Gaussian white noise with variance where and are the variances of the real and imaginary parts of , respectively.
- The function is a memoryless nonlinear function that satisfies the additivity condition:where , are the real and imaginary parts of the equalized output, respectively.
3. The New Proposed Expression for the Conditional Expectation
- The convolutional noise is a zero mean, white Gaussian process with variance
- The source signal is an independent non-Gaussian signal with known variance and higher moments.
- The convolutional noise and the source signal are independent.
- The convolutional noise power is sufficiently low.
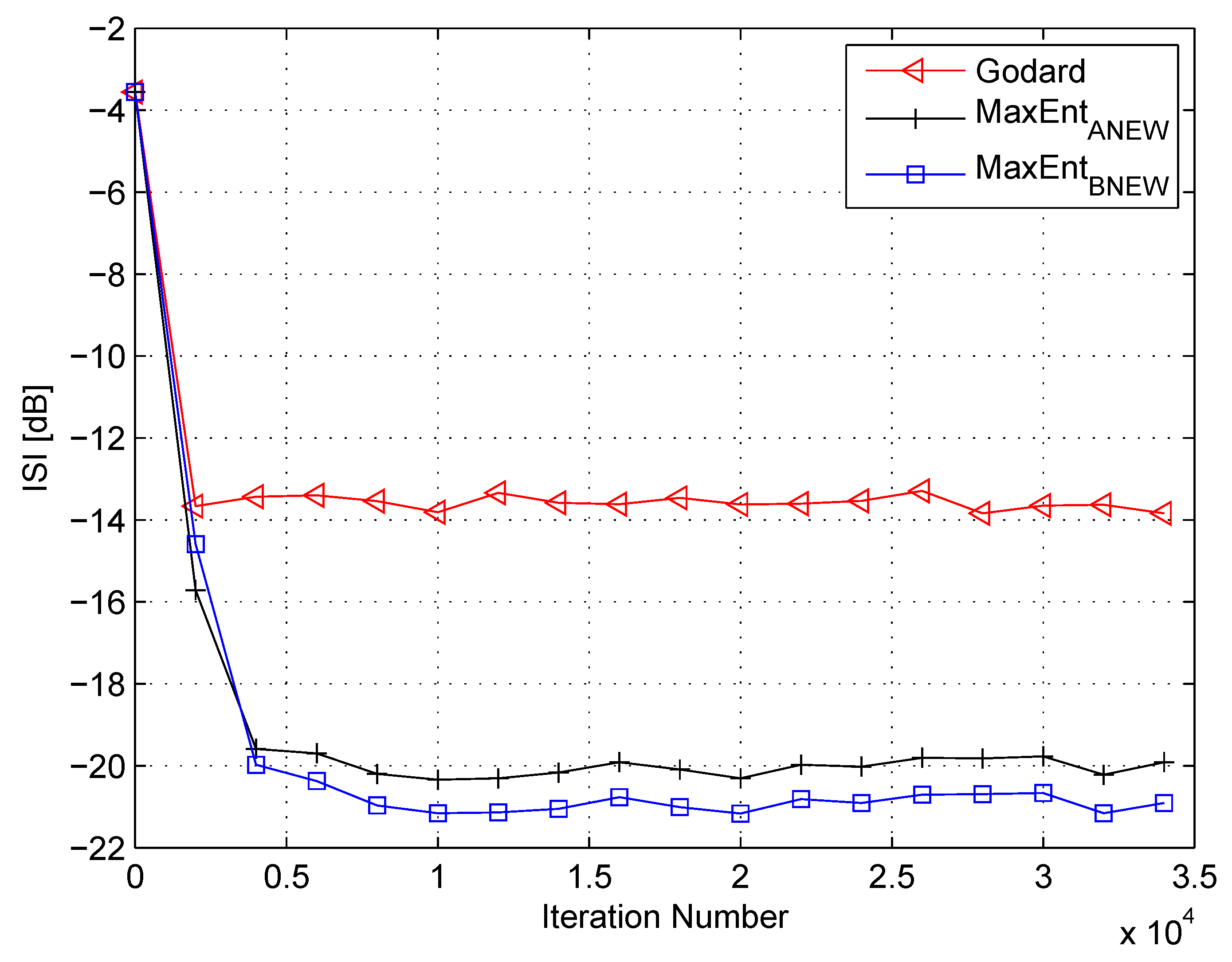
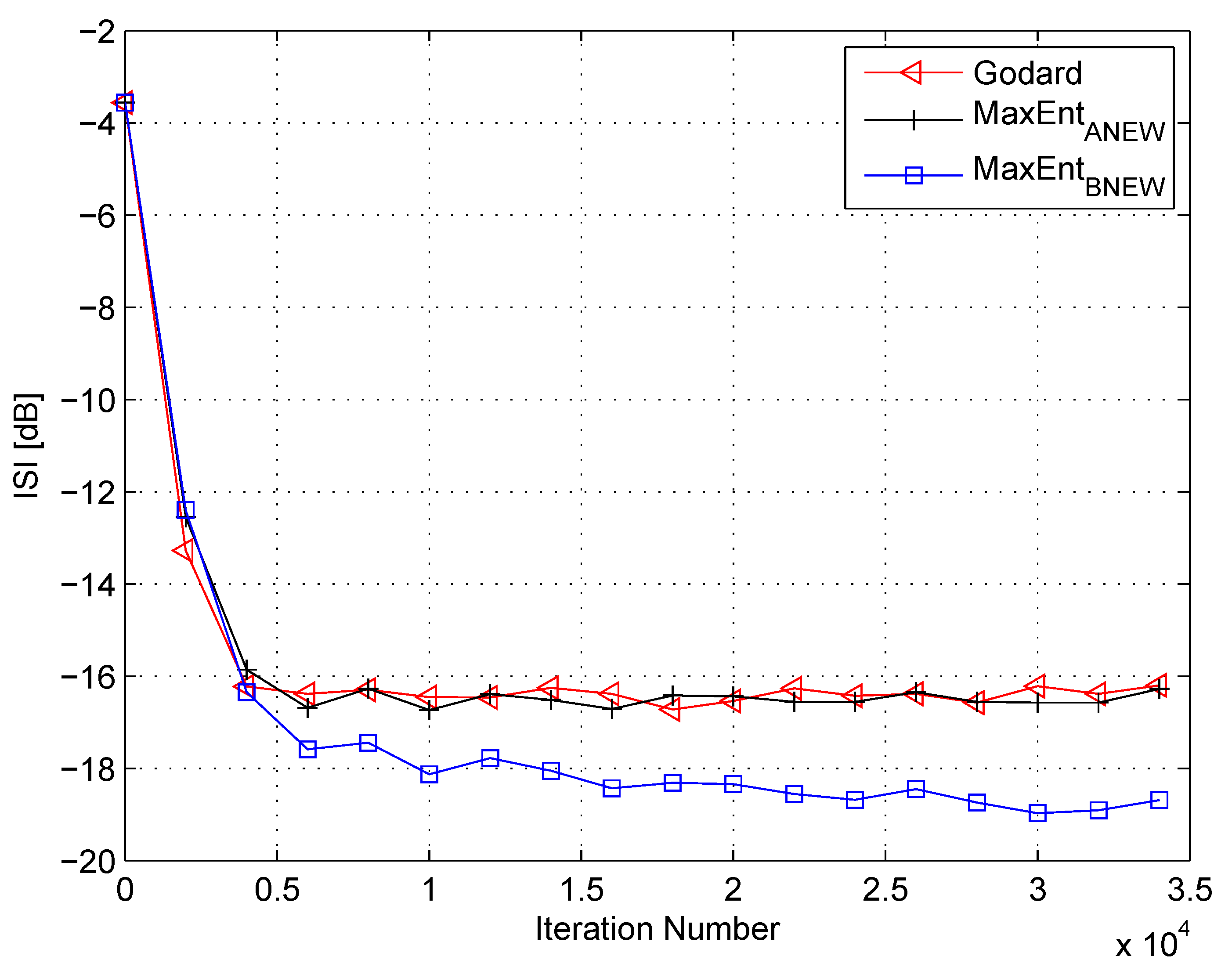
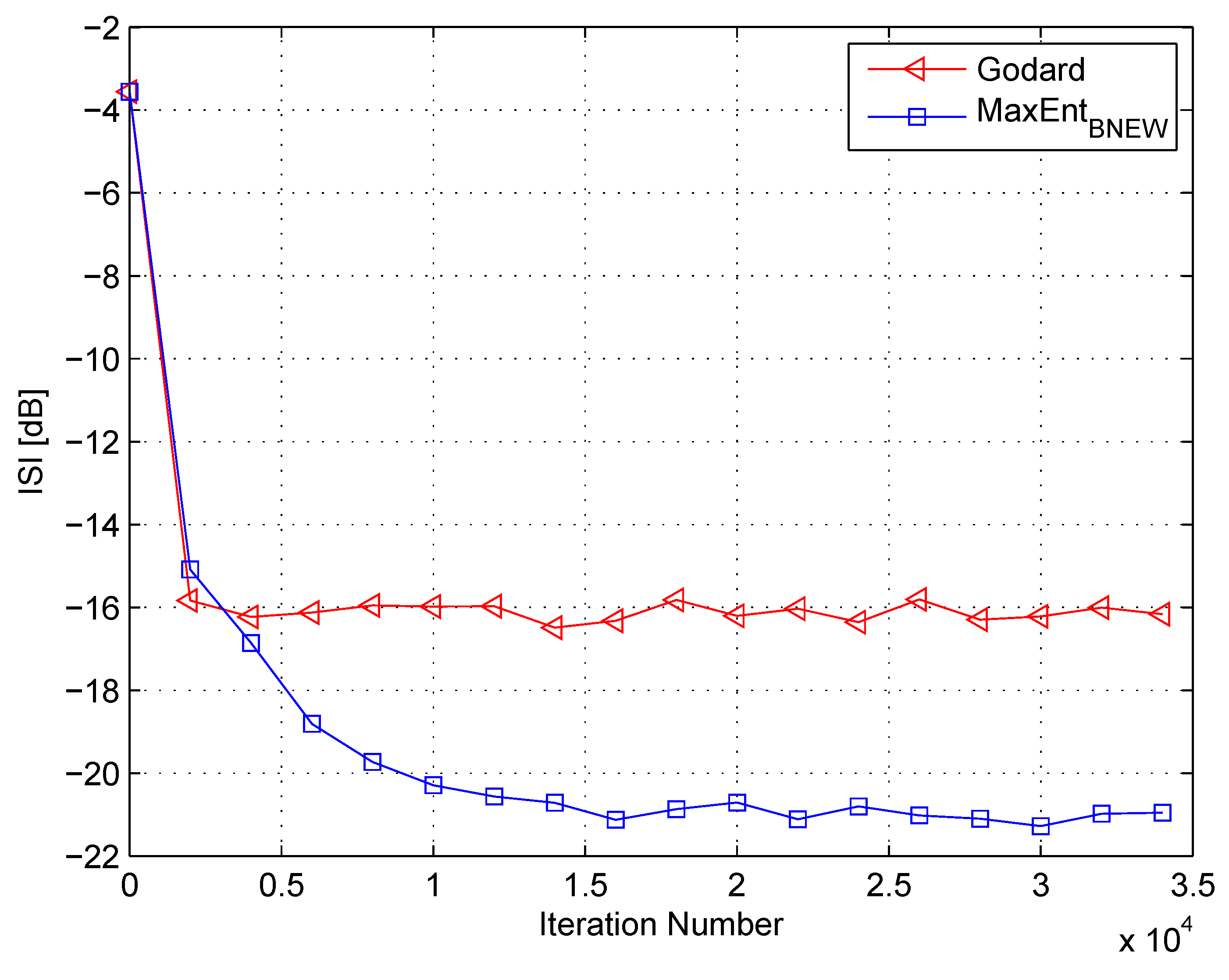
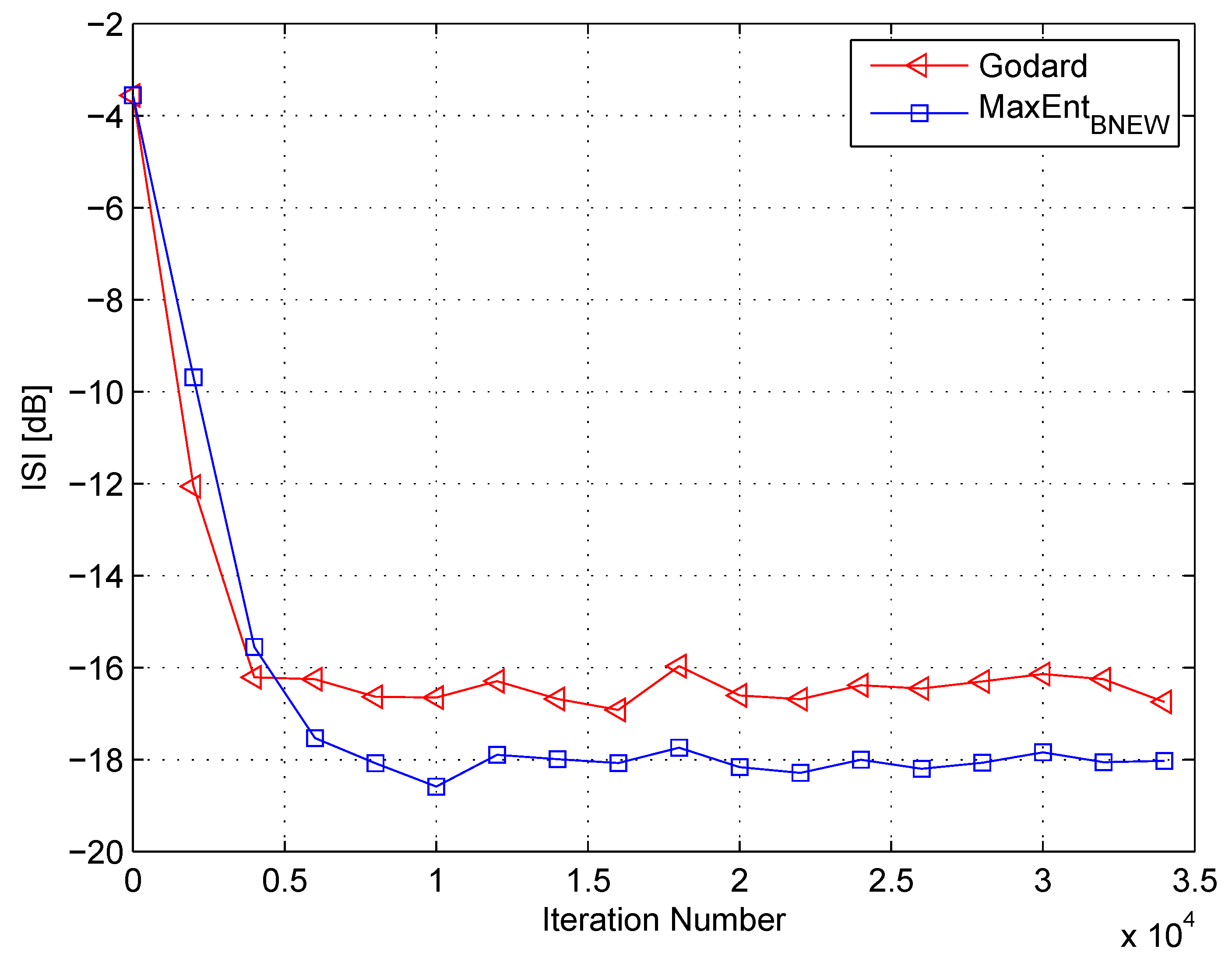
4. Simulation
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Shalvi, O.; Weinstein, E. New criteria for blind deconvolution of non-minimum phase systems (channels). IEEE Trans. Inf. Theory 1990, 36, 312–321. [Google Scholar] [CrossRef]
- Johnson, R.C.; Schniter, P.; Endres, T.J.; Behm, J.D.; Brown, D.R.; Casas, R.A. Blind Equalization Using the Constant Modulus Criterion: A Review. Proc. IEEE 1998, 86, 1927–1950. [Google Scholar] [CrossRef]
- Wiggins, R.A. Minimum entropy deconvolution. Geoexploration 1978, 16, 21–35. [Google Scholar] [CrossRef]
- Kazemi, N.; Sacchi, M.D. Sparse multichannel blind deconvolution. Geophysics 2014, 79, V143–V152. [Google Scholar] [CrossRef]
- Guitton, A.; Claerbout, J. Nonminimum phase deconvolution in the log domain: A sparse inversion approach. Geophysics 2015, 80, WD11–WD18. [Google Scholar] [CrossRef]
- Silva, M.T.M.; Arenas-Garcia, J. A Soft-Switching Blind Equalization Scheme via Convex Combination of Adaptive Filters. IEEE Trans. Signal Process. 2013, 61, 1171–1182. [Google Scholar] [CrossRef]
- Mitra, R.; Singh, S.; Mishra, A. Improved multi-stage clustering-based blind equalisation. IET Commun. 2011, 5, 1255–1261. [Google Scholar] [CrossRef]
- Gul, M.M.U.; Sheikh, S.A. Design and implementation of a blind adaptive equalizer using Frequency Domain Square Contour Algorithm. Digit. Signal Process. 2010, 20, 1697–1710. [Google Scholar]
- Sheikh, S.A.; Fan, P. New Blind Equalization techniques based on improved square contour algorithm. Digit. Signal Process. 2008, 18, 680–693. [Google Scholar] [CrossRef]
- Thaiupathump, T.; He, L.; Kassam, S.A. Square contour algorithm for blind equalization of QAM signals. Signal Process. 2006, 86, 3357–3370. [Google Scholar] [CrossRef]
- Sharma, V.; Raj, V.N. Convergence and performance analysis of Godard family and multimodulus algorithms for blind equalization. IEEE Trans. Signal Process. 2005, 53, 1520–1533. [Google Scholar] [CrossRef]
- Yuan, J.T.; Lin, T.C. Equalization and Carrier Phase Recovery of CMA and MMA in BlindAdaptive Receivers. IEEE Trans. Signal Process. 2010, 58, 3206–3217. [Google Scholar] [CrossRef]
- Yuan, J.T.; Tsai, K.D. Analysis of the multimodulus blind equalization algorithm in QAM communication systems. IEEE Trans. Commun. 2005, 53, 1427–1431. [Google Scholar] [CrossRef]
- Wu, H.C.; Wu, Y.; Principe, J.C.; Wang, X. Robust switching blind equalizer for wireless cognitive receivers. IEEE Trans. Wirel. Commun. 2008, 7, 1461–1465. [Google Scholar]
- Kundur, D.; Hatzinakos, D. A novel blind deconvolution scheme for image restoration using recursive filtering. IEEE Trans. Signal Process. 1998, 46, 375–390. [Google Scholar] [CrossRef]
- Likas, C.L.; Galatsanos, N.P. A variational approach for Bayesian blind image deconvolution. IEEE Trans. Signal Process. 2004, 52, 2222–2233. [Google Scholar] [CrossRef]
- Li, D.; Mersereau, R.M.; Simske, S. Blind Image Deconvolution Through Support Vector Regression. IEEE Trans. Neural Netw. 2007, 18, 931–935. [Google Scholar] [CrossRef] [PubMed]
- Amizic, B.; Spinoulas, L.; Molina, R.; Katsaggelos, A.K. Compressive Blind Image Deconvolution. IEEE Trans. Image Process. 2013, 22, 3994–4006. [Google Scholar] [CrossRef] [PubMed]
- Tzikas, D.G.; Likas, C.L.; Galatsanos, N.P. Variational Bayesian Sparse Kernel-Based Blind Image Deconvolution With Student’s-t Priors. IEEE Trans. Image Process. 2009, 18, 753–764. [Google Scholar] [CrossRef]
- Pinchas, M.; Bobrovsky, B.Z. A Maximum Entropy approach for blind deconvolution. Signal Process. 2006, 86, 2913–2931. [Google Scholar] [CrossRef]
- Feng, C.; Chi, C. Performance of cumulant based inverse filters for blind deconvolution. IEEE Trans. Signal Process. 1999, 47, 1922–1935. [Google Scholar] [CrossRef]
- Abrar, S.; Nandi, A.S. Blind Equalization of Square-QAM Signals: A Multimodulus Approach. IEEE Trans. Commun. 2010, 58, 1674–1685. [Google Scholar] [CrossRef]
- Vanka, R.N.; Murty, S.B.; Mouli, B.C. Performance comparison of supervised and unsupervised/blind equalization algorithms for QAM transmitted constellations. In Proceedings of the 2014 International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 20–21 February 2014. [Google Scholar]
- Ram Babu, T.; Kumar, P.R. Blind Channel Equalization Using CMA Algorithm. In Proceedings of the 2009 International Conference on Advances in Recent Technologies in Communication and Computing (ARTCom 09), Kottayam, India, 27–28 October 2009. [Google Scholar]
- Qin, Q.; Huahua, L.; Tingyao, J. A new study on VCMA-based blind equalization for underwater acoustic communications. In Proceedings of the 2013 International Conference on Mechatronic Sciences, Electric Engineering and Computer (MEC), Shengyang, China, 20–22 December 2013. [Google Scholar]
- Wang, J.; Huang, H.; Zhang, C.; Guan, J. A Study of the Blind Equalization in the Underwater Communication. In Proceedings of the WRI Global Congress on Intelligent Systems, GCIS ’09, Xiamen, China, 19–21 May 2009. [Google Scholar]
- Miranda, M.D.; Silva, M.T.M.; Nascimento, V.H. Avoiding Divergence in the Shalvi Weinstein Algorithm. IEEE Trans. Signal Process. 2008, 56, 5403–5413. [Google Scholar] [CrossRef]
- Samarasinghe, P.D.; Kennedy, R.A. Minimum Kurtosis CMA Deconvolution for Blind Image Restoration. In Proceedings of the 4th International Conference on Information and Automation for Sustainability, ICIAFS 2008, Colombo, Sri Lanka, 12–14 December 2008. [Google Scholar]
- Zhao, L.; Li, H. Application of the Sato blind deconvolution algorithm for correction of the gravimeter signal distortion. In Proceedings of the 2013 Third International Conference on Instrumentation, Measurement, Computer, Communication and Control, Shenyang, China, 21–23 September 2013; pp. 1413–1417. [Google Scholar]
- Fiori, S. Blind deconvolution by a Newton method on the non-unitary hypersphere. Int. J. Adapt. Control Signal Process. 2013, 27, 488–518. [Google Scholar] [CrossRef]
- Freiman, A.; Pinchas, M. A Maximum Entropy inspired model for the convolutional noise PDF. Digit. Signal Process. 2015, 39, 35–49. [Google Scholar] [CrossRef]
- Shevach, R.; Pinchas, M. A Closed-form Approximated Expression for the Residual ISI Obtained by Blind Adaptive Equalizers Applicable for the Non-Square QAM Constellation Input and Noisy Case. In Proceedings of the PECCS 2015, Angers, France, 11–13 February 2015; pp. 217–223. [Google Scholar]
- Abrar, S.; Ali, A.; Zerguine, A.; Nandi, A.K. Tracking Performance of Two Constant Modulus Equalizers. IEEE Commun. Lett. 2013, 17, 830–833. [Google Scholar] [CrossRef]
- Azim, A.W.; Abrar, S.; Zerguine, A.; Nandi, A.K. Steady-state performance of multimodulus blind equalizers. Signal Process. 2015, 108, 509–520. [Google Scholar] [CrossRef]
- Azim, A.W.; Abrar, S.; Zerguine, A.; Nandi, A.K. Performance analysis of a family of adaptive blind equalization algorithms for square-QAM. Digit. Signal Process. 2016, 48, 163–177. [Google Scholar] [CrossRef]
- Pinchas, M. Residual ISI Obtained by Nonblind Adaptive Equalizers and Fractional Noise. Math. Probl. Eng. 2013. [Google Scholar] [CrossRef]
- Pinchas, M. Two Blind Adaptive Equalizers Connected in Series for Equalization Performance Improvement. J. Signal Inf. Process. 2013, 4, 64–71. [Google Scholar] [CrossRef]
- Reuter, M.; Zeidler, J.R. Nonlinear Effects in LMS Adaptive Equalizers. IEEE Trans. Signal Process. 1999, 47, 1570–1579. [Google Scholar] [CrossRef]
- Makki, A.H.I.; Dey, A.K.; Khan, M.A. Comparative study on LMS and CMA channel equalization. In Proceedings of the 2010 International Conference on Information Society (i-Society), London, UK, 28–30 June 2010; pp. 487–489. [Google Scholar]
- Tugcu, E.; Çakir, F.; Özen, A. A New Step Size Control Technique for Blind and Non-Blind Equalization Algorithms. Radioengineering 2013, 22, 44. [Google Scholar]
- Ali, A.; Abrar, S.; Zerguine, A.; Nandi, A.K. Newton-like minimum entropy equalization algorithm for APSK systems. Signal Process. 2014, 101, 74–86. [Google Scholar] [CrossRef]
- Pinchas, M. The Whole Story behind Blind Adaptive Equalizers/Blind Deconvolution; e-Books Publications Department, Bentham Science Publishers: Sharjah, UAE, 2012. [Google Scholar]
- Haykin, S. Adaptive Filter Theory. In Blind Deconvolution; Haykin, S., Ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Bellini, S. Bussgang techniques for blind equalization. In Proceedings of the IEEE Global Telecommunication Conference Records, Houston, TX, USA, 1–4 December 1986. [Google Scholar]
- Bellini, S. Blind Equalization. Alta Freq. 1988, 57, 445–450. [Google Scholar]
- Fiori, S. A contribution to (neuromorphic) blind deconvolution by flexible approximated Bayesian estimation. Signal Process. 2001, 81, 2131–2153. [Google Scholar] [CrossRef]
- Pinchas, M. 16QAM Blind Equalization Method via Maximum Entropy Density Approximation Technique. In Proceedings of the IEEE 2011 International Conference on Signal and Information Processing (CSIP2011), Shanghai, China, 28–30 October 2011. [Google Scholar]
- Pinchas, M.; Bobrovsky, B.Z. A Novel HOS Approach for Blind Channel Equalization. IEEE Trans. Wirel. Commun. 2007, 6, 875–886. [Google Scholar] [CrossRef]
- Pinchas, M. New Lagrange Multipliers for the Blind Adaptive Deconvolution Problem Applicable for the Noisy Case. Entropy 2016, 18, 65. [Google Scholar] [CrossRef]
- Nikias, C.L.; Petropulu, A.P. (Eds.) Higher-Order Spectra Analysis a Nonlinear Signal Processing Framework; Prentice-Hall: Enlewood Cliffs, NJ, USA, 1993; pp. 419–425. [Google Scholar]
- Nandi, A.K. (Ed.) Blind Estimation Using Higher-Order Statistics; Kluwer Academic: Boston, MA, USA, 1999. [Google Scholar]
- Pinchas, M. A novel expression for the achievable MSE performance obtained by blind adaptive equalizers. Signal Image Video Process. 2013, 7, 67–74. [Google Scholar] [CrossRef]
- Godard, D.N. Self recovering equalization and carrier tracking in two-dimenional data communication system. IEEE Trans. Commun. 1980, 28, 1867–1875. [Google Scholar] [CrossRef]


© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinchas, M. A New Efficient Expression for the Conditional Expectation of the Blind Adaptive Deconvolution Problem Valid for the Entire Range ofSignal-to-Noise Ratio. Entropy 2019, 21, 72. https://doi.org/10.3390/e21010072
Pinchas M. A New Efficient Expression for the Conditional Expectation of the Blind Adaptive Deconvolution Problem Valid for the Entire Range ofSignal-to-Noise Ratio. Entropy. 2019; 21(1):72. https://doi.org/10.3390/e21010072
Chicago/Turabian StylePinchas, Monika. 2019. "A New Efficient Expression for the Conditional Expectation of the Blind Adaptive Deconvolution Problem Valid for the Entire Range ofSignal-to-Noise Ratio" Entropy 21, no. 1: 72. https://doi.org/10.3390/e21010072
APA StylePinchas, M. (2019). A New Efficient Expression for the Conditional Expectation of the Blind Adaptive Deconvolution Problem Valid for the Entire Range ofSignal-to-Noise Ratio. Entropy, 21(1), 72. https://doi.org/10.3390/e21010072



