Improving the Robustness of Entangled States by Basis Transformation
Abstract
1. Introduction
2. Robustness of Cat-Like States and Its Enhancement Method
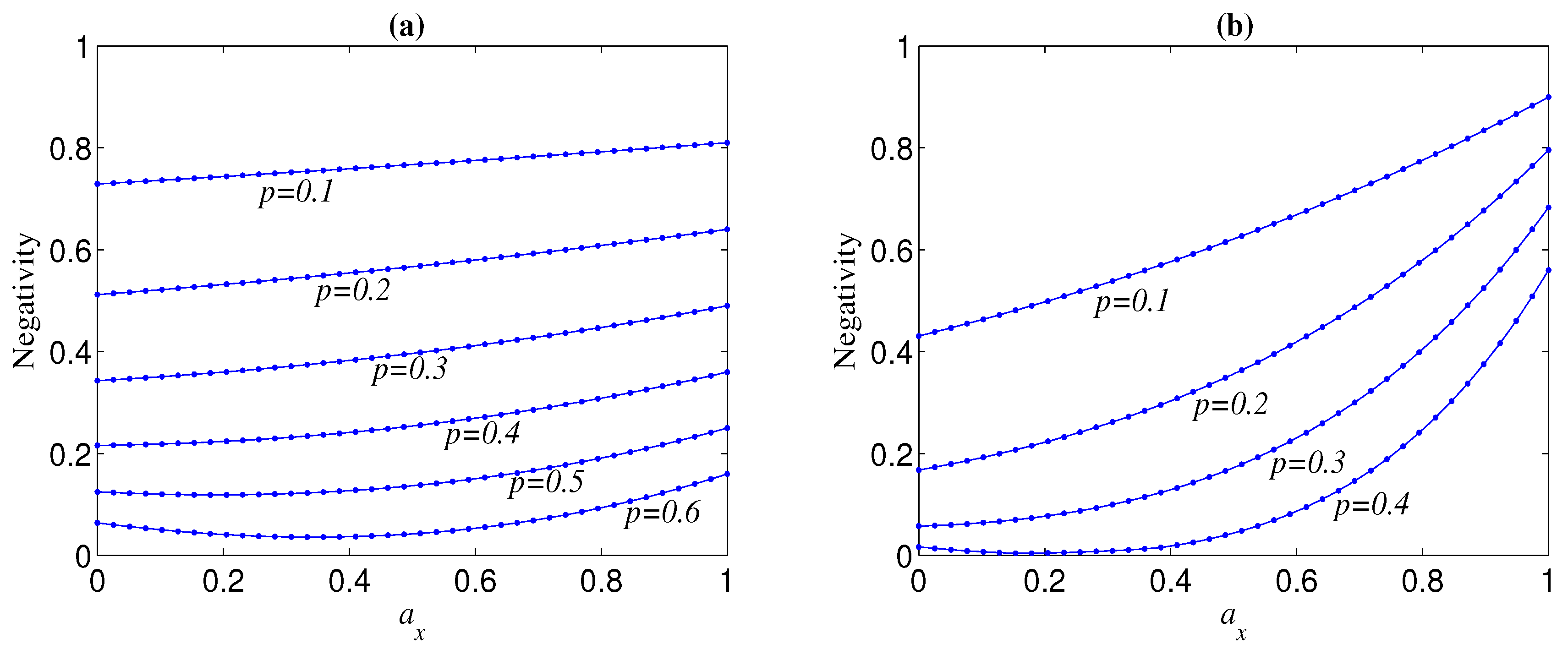
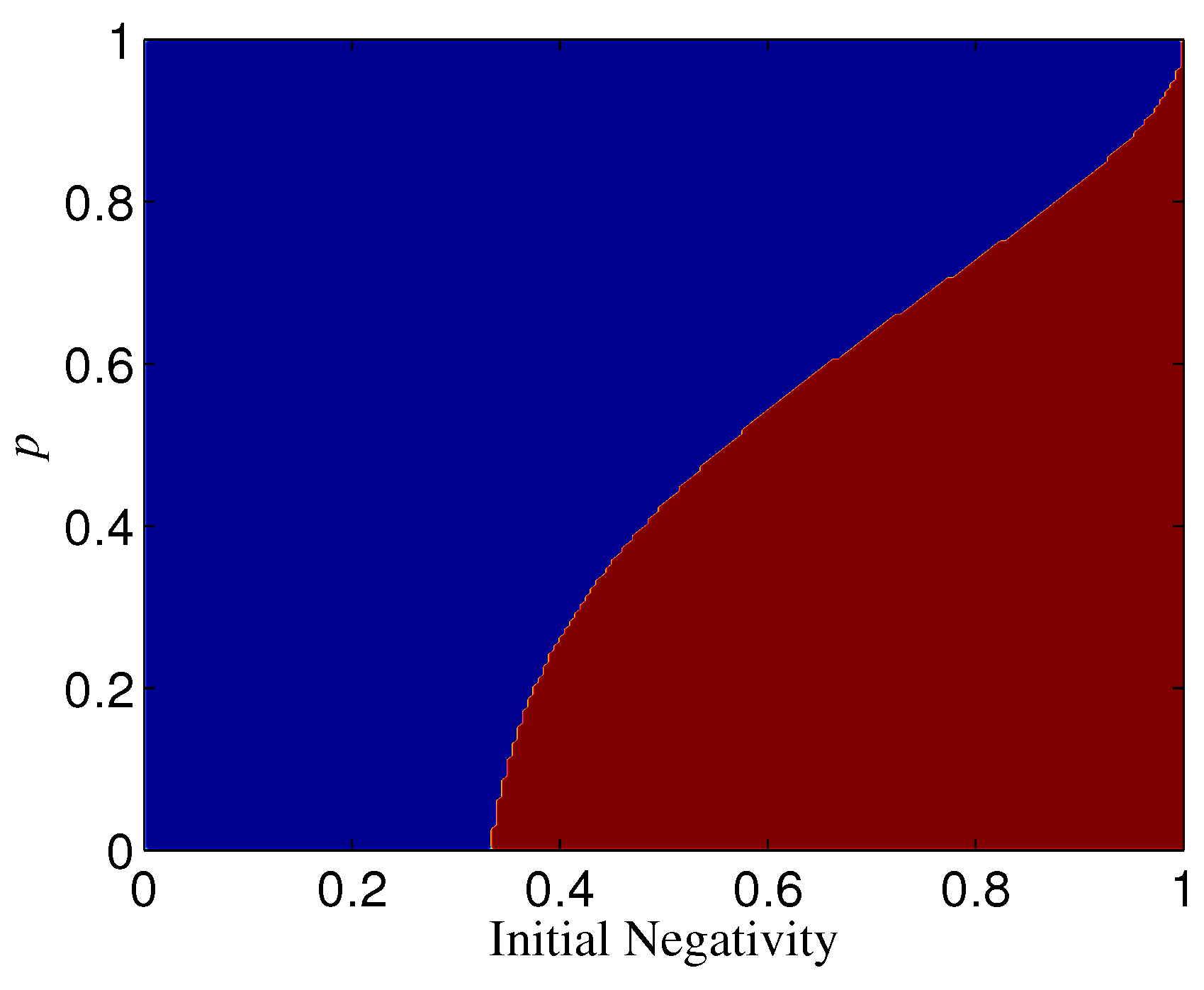
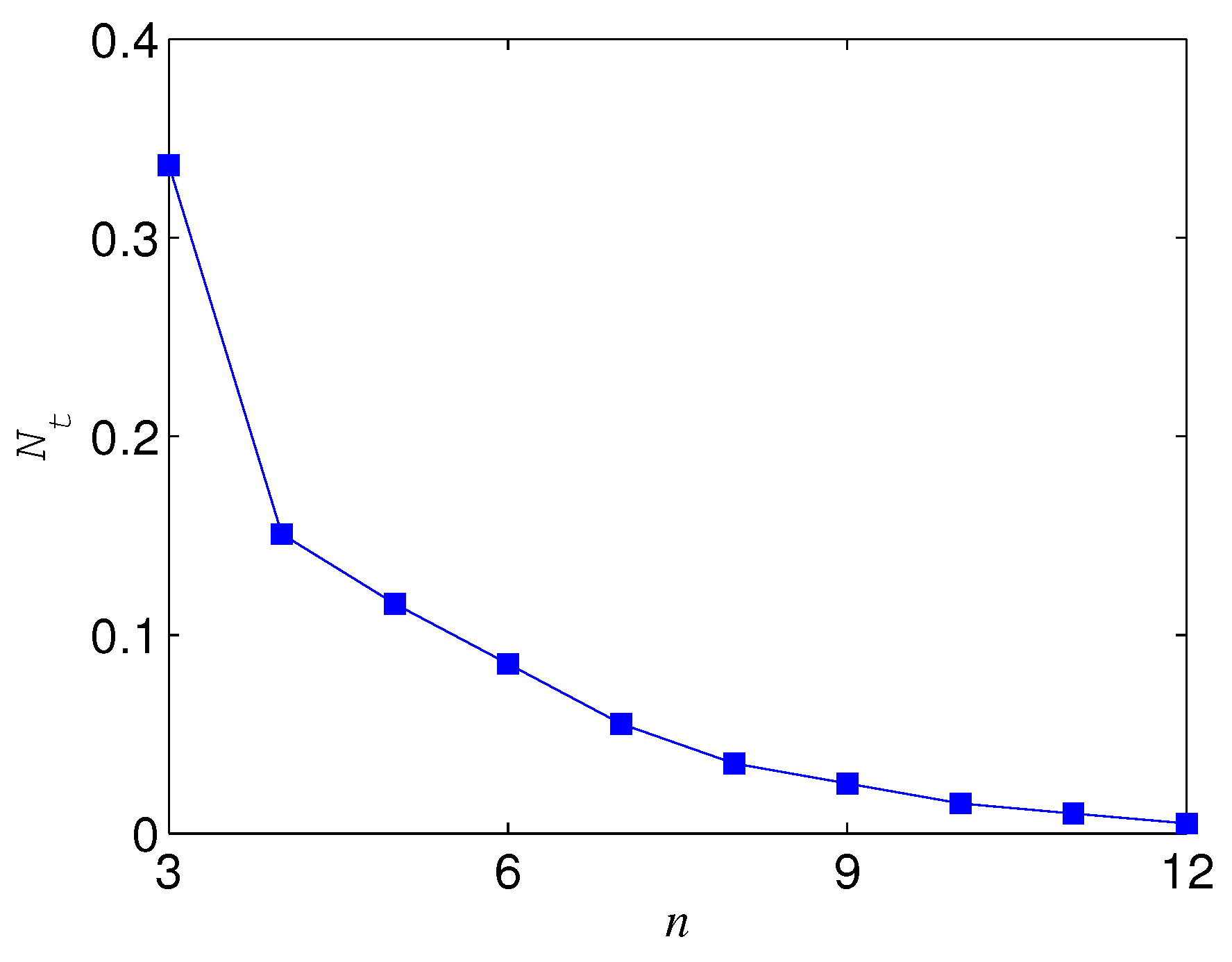
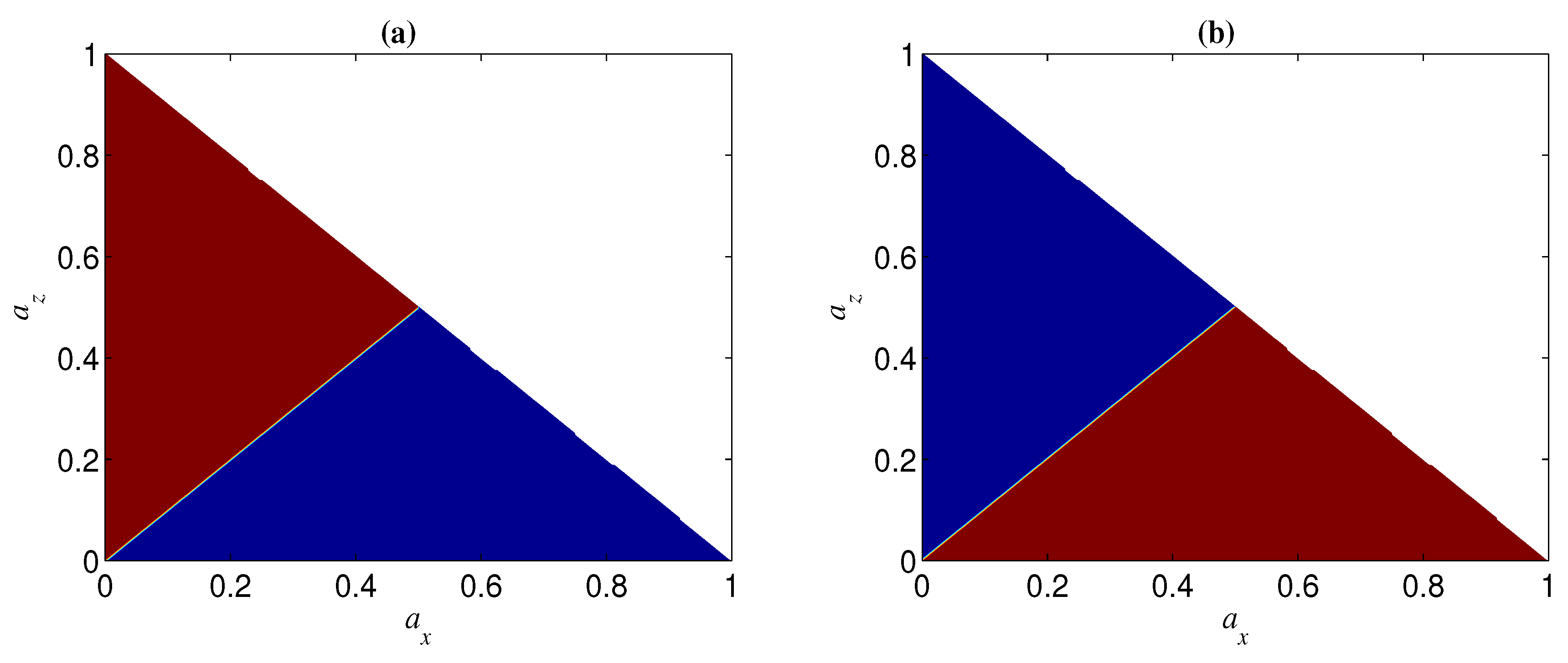
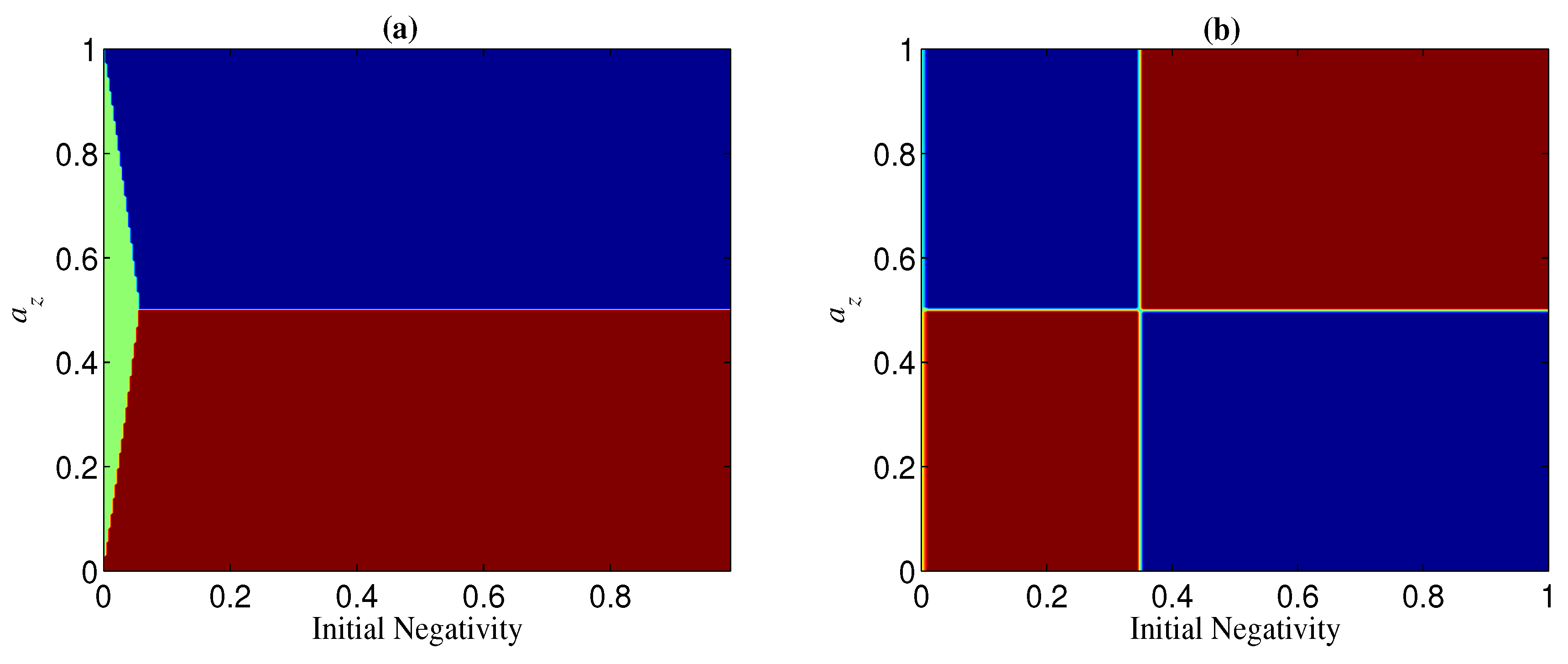
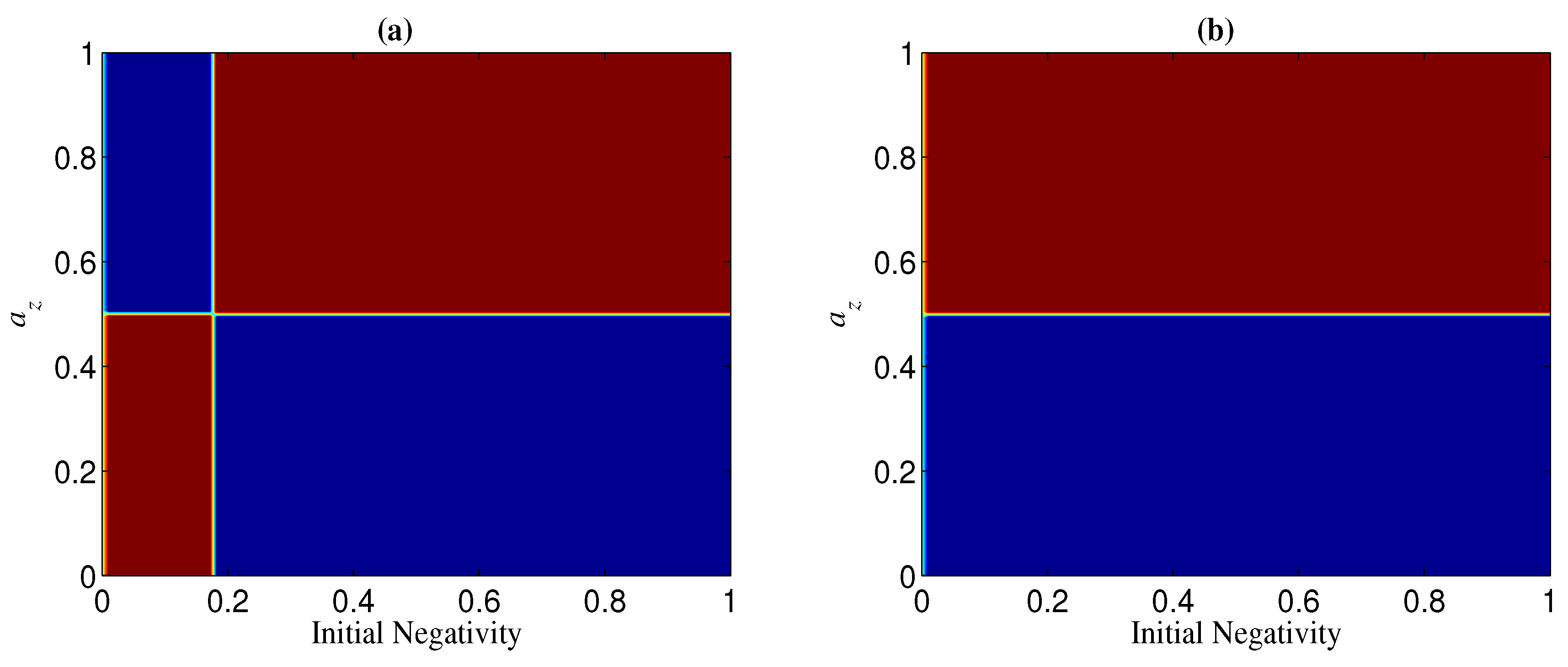
2.1. Robustness of Cat-Like States in the Computational Basis
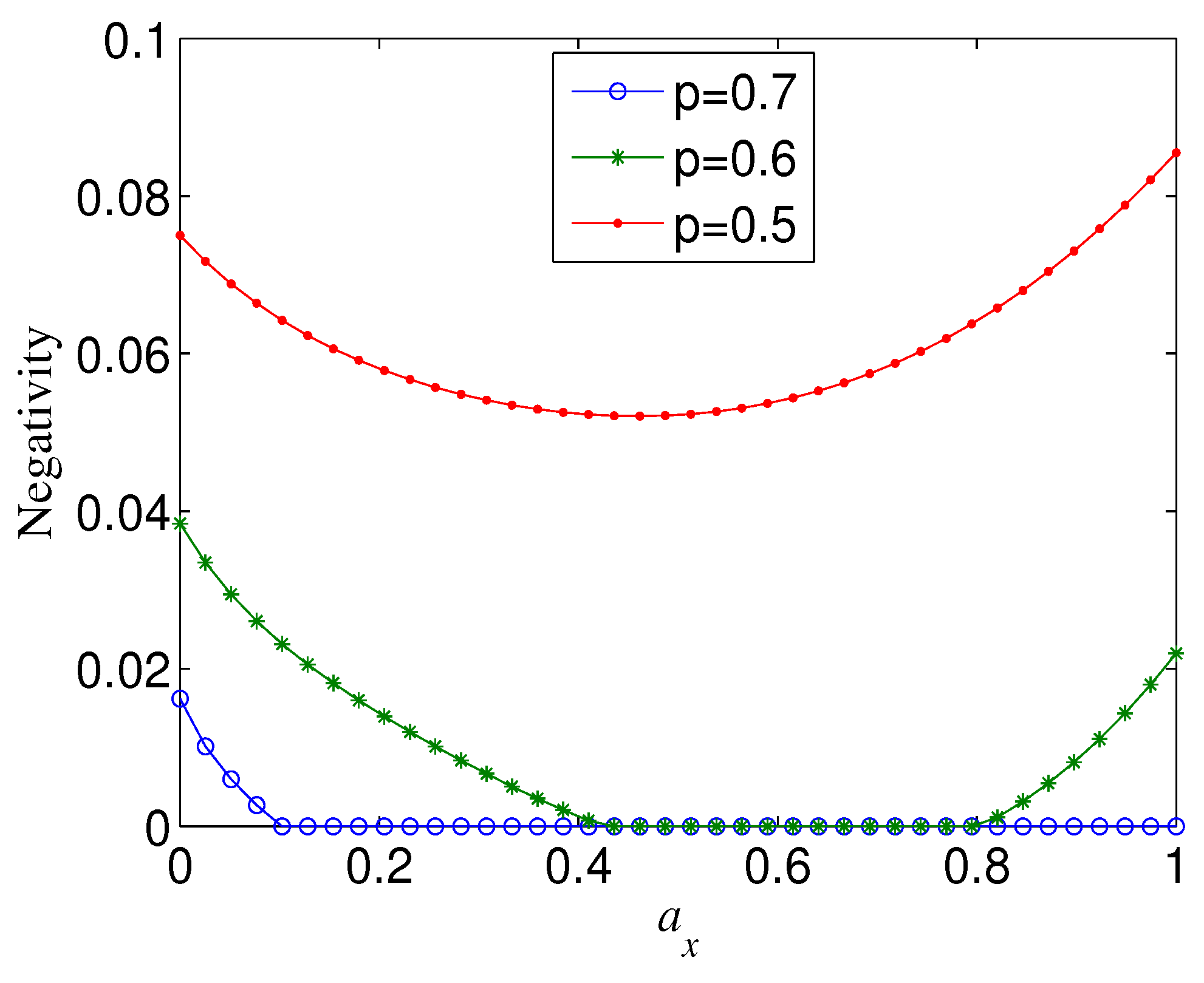
2.2. Robustness of Cat-Like States in the Transversal Basis
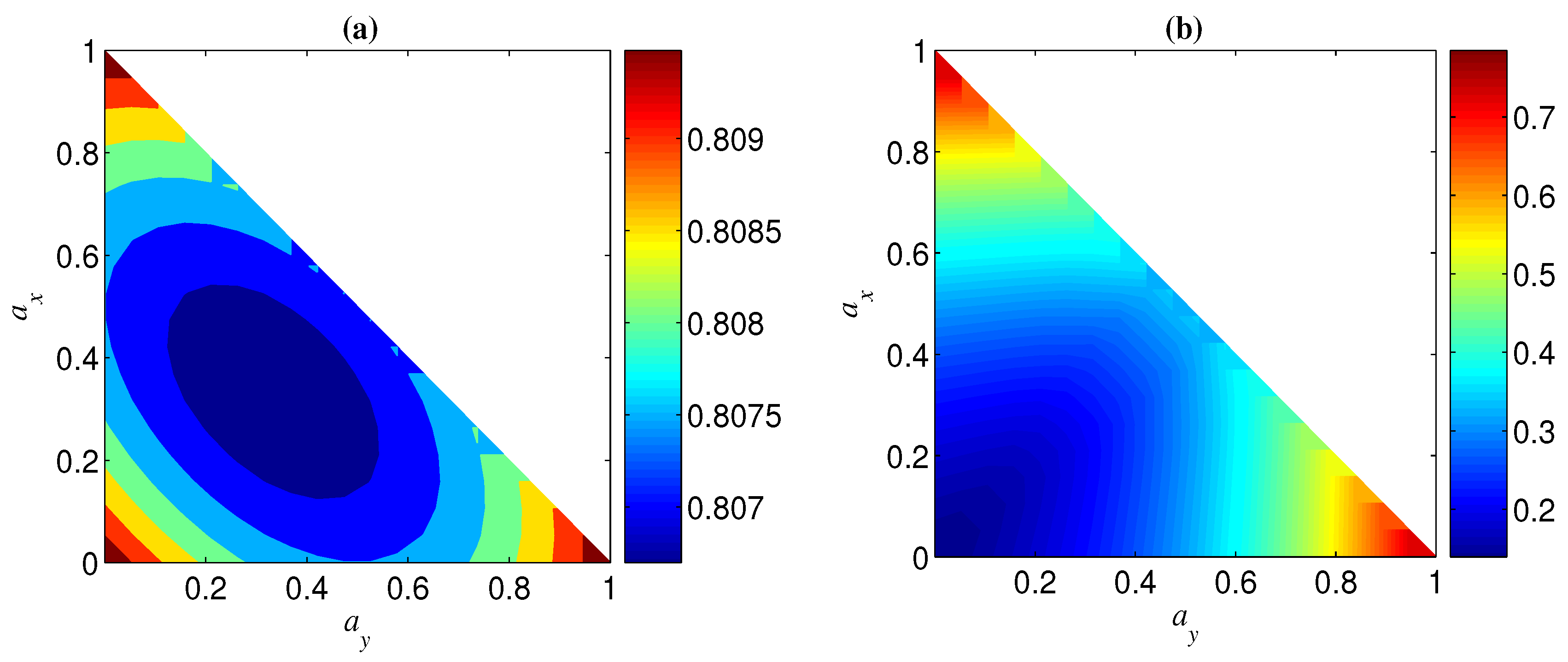
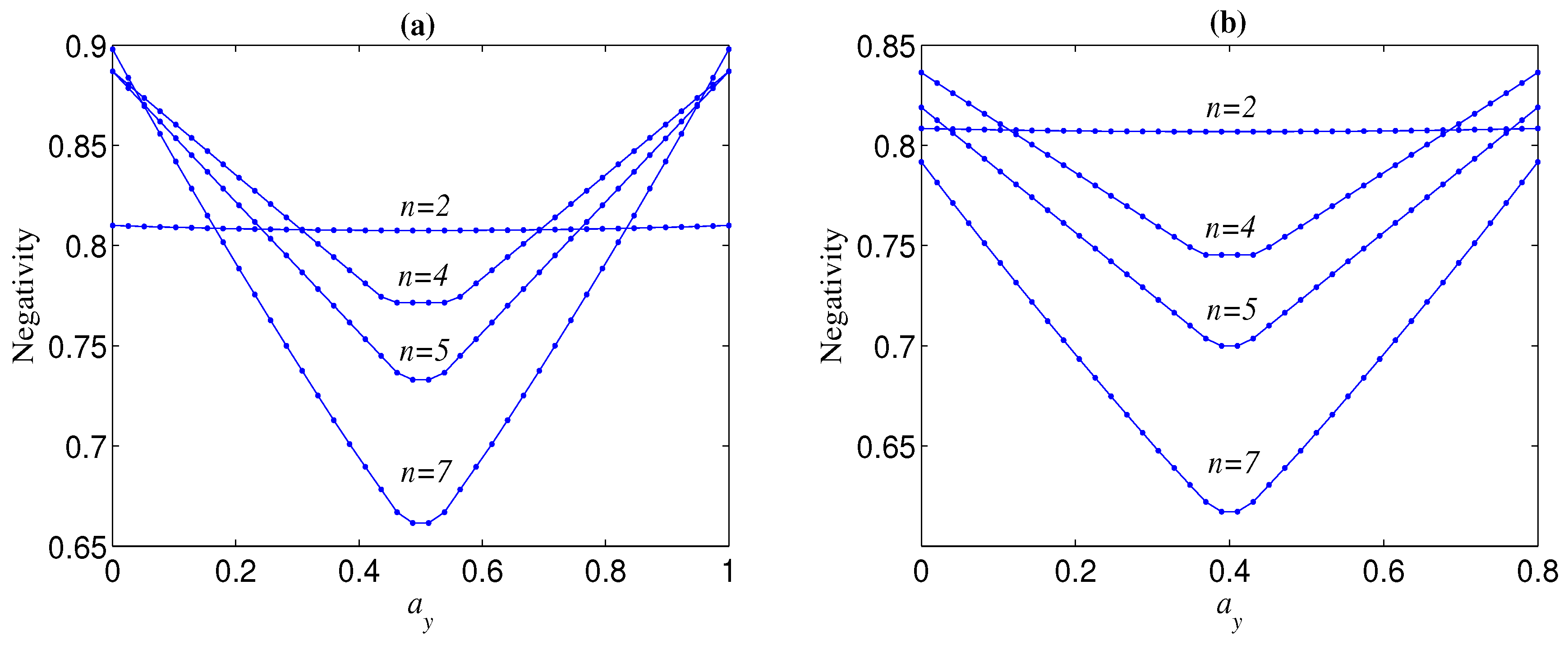
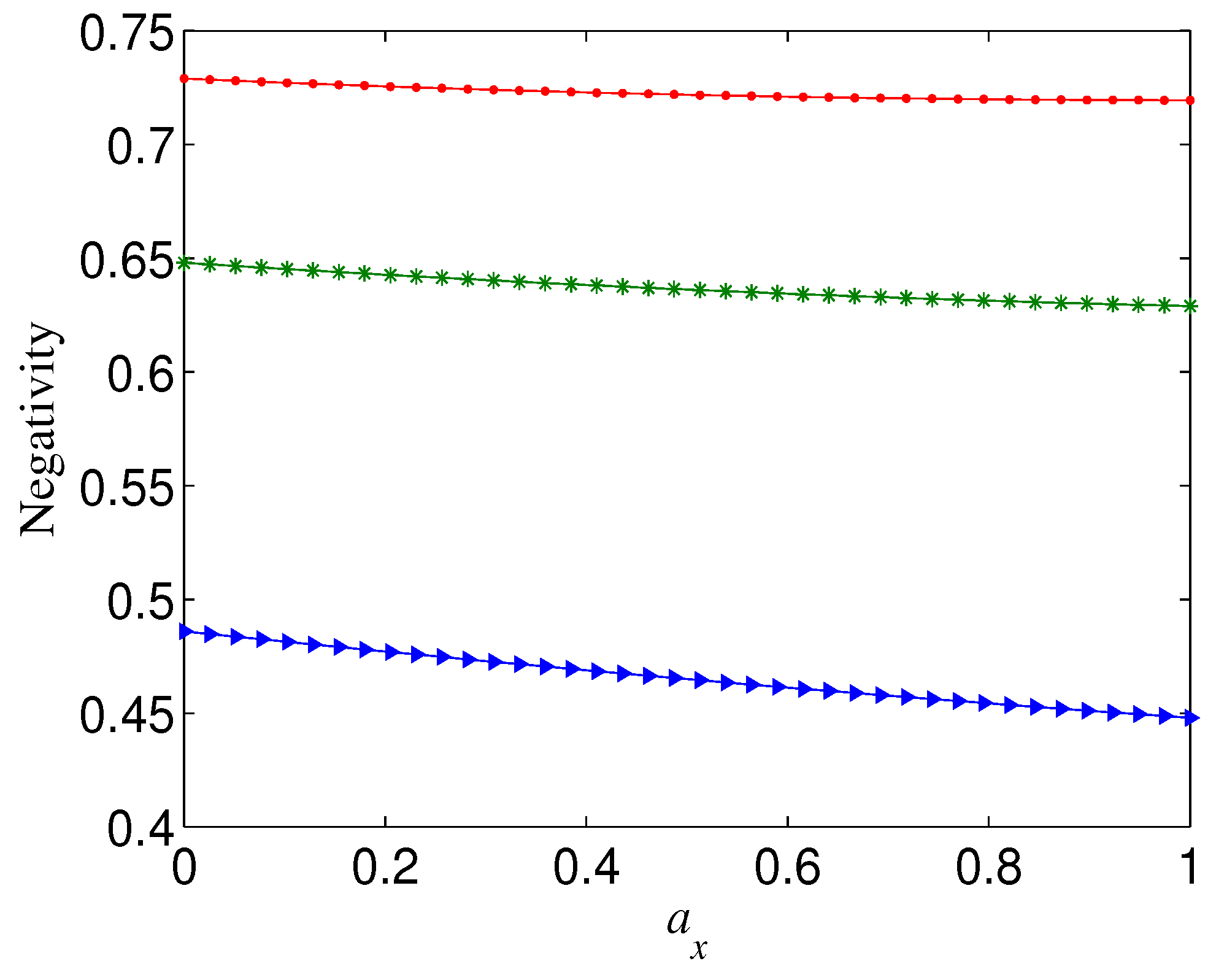
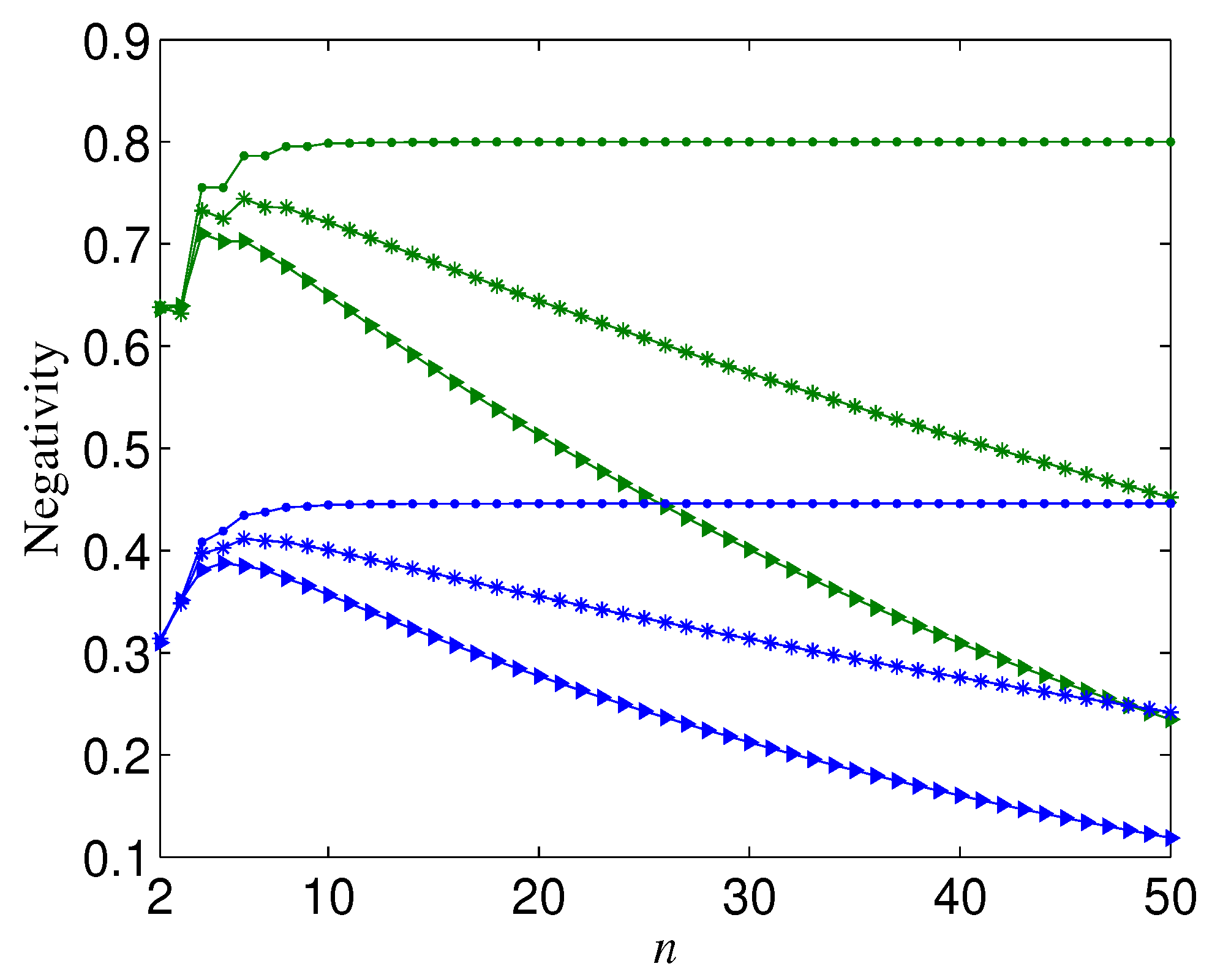
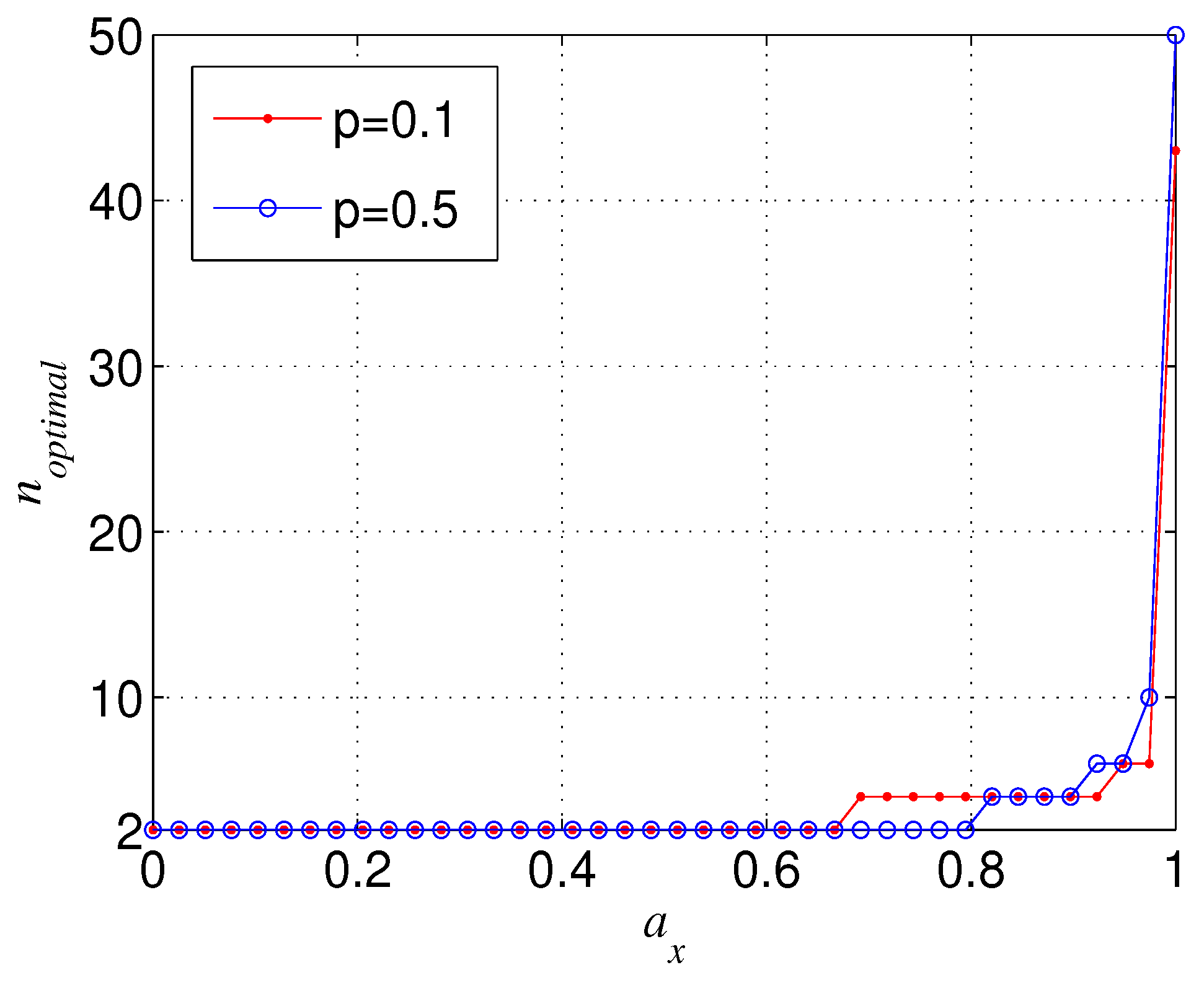
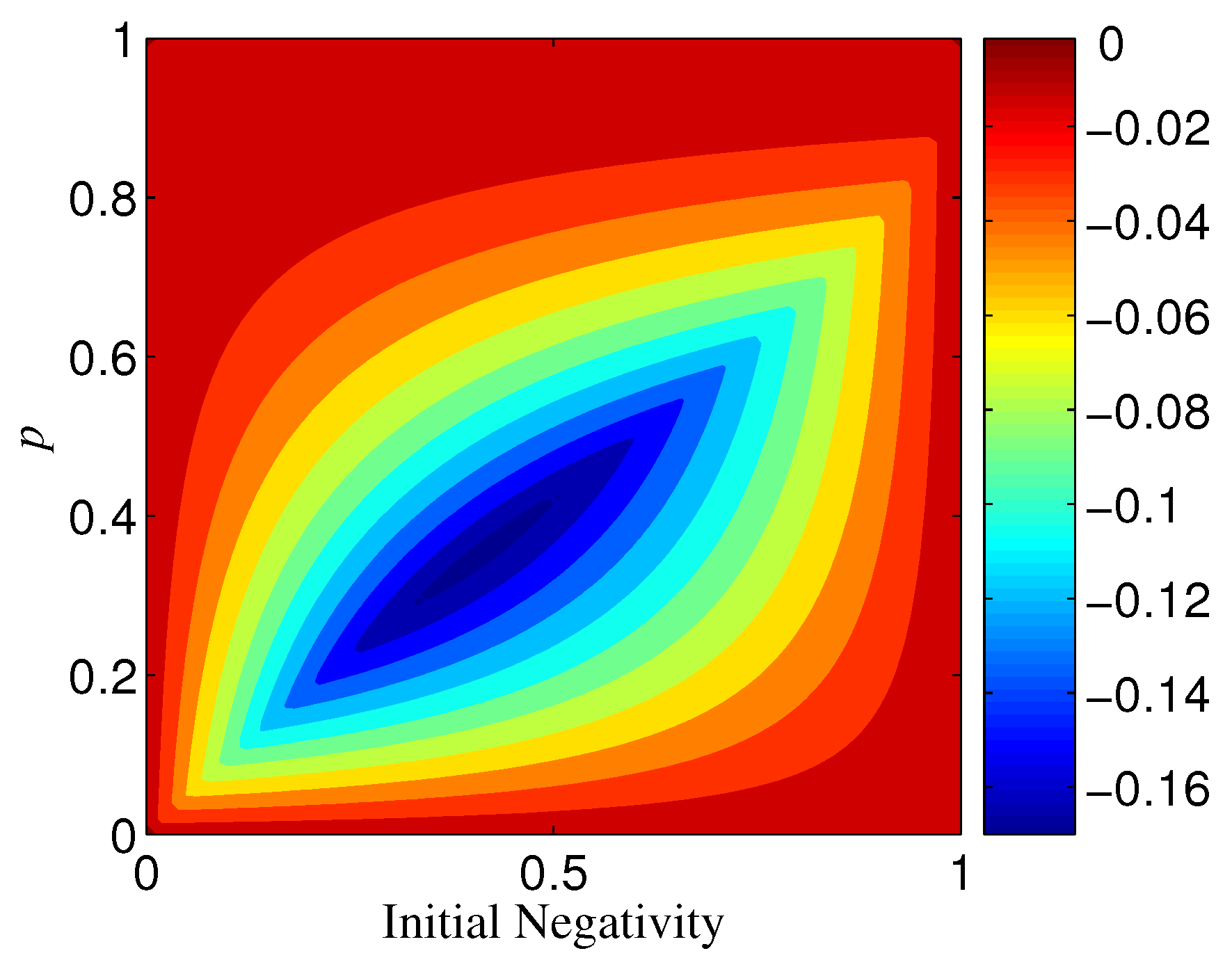
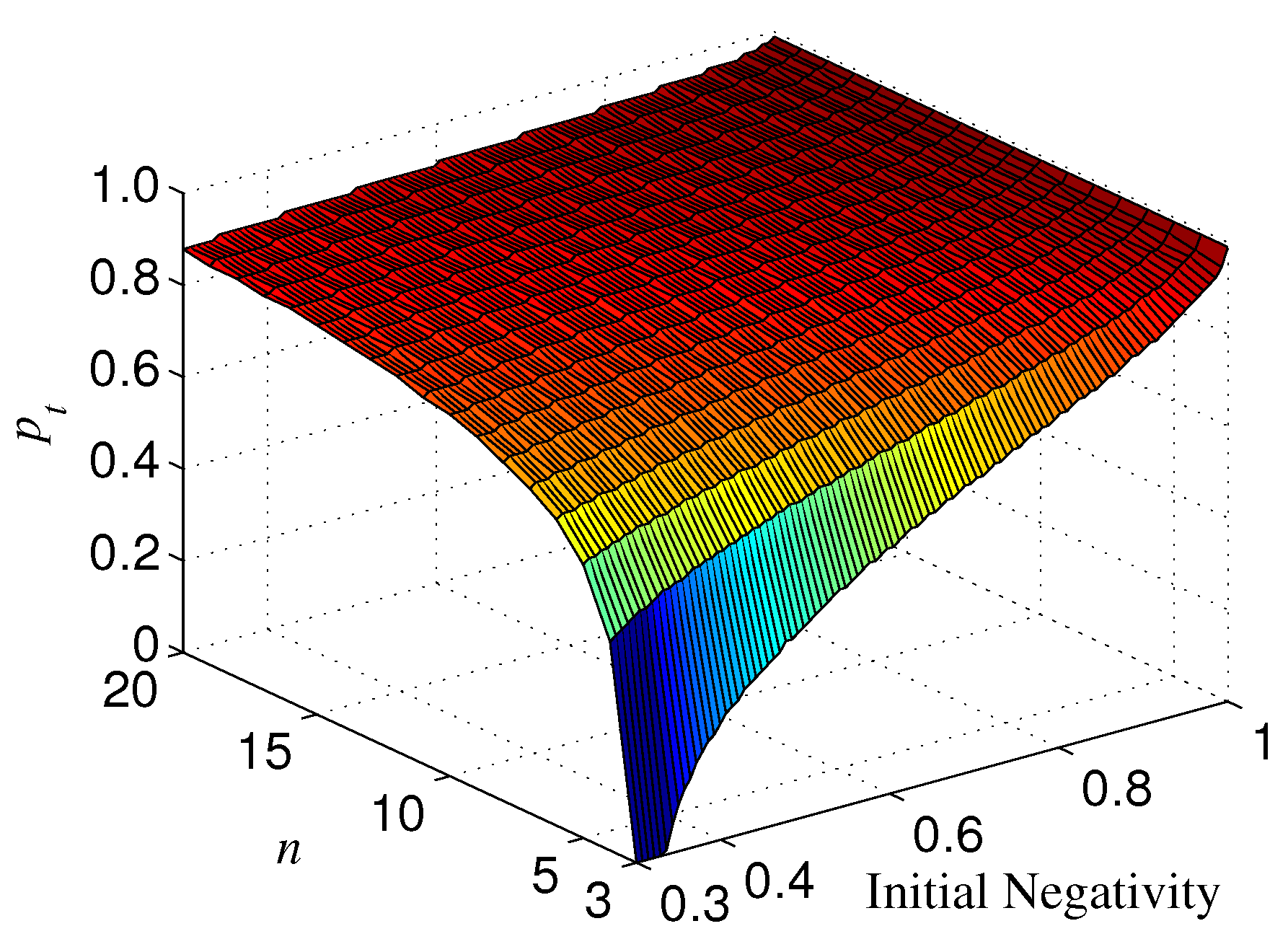
2.3. Enhancing the Robustness of Cat-Like States by Basis Transformation
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Brunner, N.; Cavalcanti, D.; Pironio, S.; Scarani, V.; Wehner, S. Bell nonlocality. Rev. Mod. Phys. 2014, 86, 419–478. [Google Scholar] [CrossRef]
- Vedral, V. Quantum entanglement. Nat. Phys. 2014, 10, 256–258. [Google Scholar] [CrossRef]
- Lo Franco, R.; Compagno, G. Quantum entanglement of identical particles by standard information-theoretic notions. Sci. Rep. 2016, 6, 20603. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.W.; Chen, Z.B.; Lu, C.Y.; et al. Multiphoton entanglement and interferometry. Rev. Mod. Phys. 2012, 84, 777–838. [Google Scholar] [CrossRef]
- Lo Franco, R.; Compagno, G. Indistinguishability of Elementary Systems as a Resource for Quantum Information Processing. Phys. Rev. Lett. 2018, 120, 240403. [Google Scholar] [CrossRef] [PubMed]
- Rab, A.S.; Polino, E.; Man, Z.X.; An, N.B.; Xia, Y.-J.; Spagnolo, N.; Franco, R.L.; Sciarrino, F. Entanglement of photons in their dual wave-particle nature. Nat. Commun. 2017, 8, 915. [Google Scholar] [CrossRef] [PubMed]
- Gardiner, C.W.; Zoller, P. Quantum Noise, 3rd ed.; Springer: Berlin, Germany, 2004. [Google Scholar]
- Aolita, L.; de Melo, F.; Davidovich, L. Open-system dynamics of entanglement: A key issues review. Rep. Prog. Phys. 2015, 78, 042001. [Google Scholar] [CrossRef]
- Knoll, L.T.; Schmiegelow, C.T.; Larotonda, M.A. Noisy quantum teleportation: An experimental study on the influence of local environments. Phys. Rev. A 2014, 90, 042332. [Google Scholar] [CrossRef]
- Cavalcanti, D.; Skrzypczyk, P.; Šupić, I. All Entangled States can Demonstrate Nonclassical Teleportation. Phys. Rev. Lett. 2017, 119, 110501. [Google Scholar] [CrossRef]
- Chaves, R.; Brask, J.B.; Markiewicz, M.; Kołodyński, J.; Acín, A. Noisy Metrology beyond the Standard Quantum Limit. Phys. Rev. Lett. 2013, 111, 120401. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef]
- Duan, L.M.; Monroe, C. Quantum networks with trapped ions. Rev. Mod. Phys. 2010, 82, 1209–1224. [Google Scholar] [CrossRef]
- Carvalho, A.R.R.; Santos, M.F. Distant entanglement protected through artificially increased local temperature. New J. Phys. 2011, 13, 013010. [Google Scholar] [CrossRef]
- Mascarenhas, E.; Cavalcanti, D.; Vedral, V.; Santos, M.F. Physically realizable entanglement by local continuous measurements. Phys. Rev. A 2011, 83, 022311. [Google Scholar] [CrossRef]
- Hartmann, L.; Dür, W.; Briegel, H.J. Steady-state entanglement in open and noisy quantum systems. Phys. Rev. A 2006, 74, 052304. [Google Scholar] [CrossRef]
- Carvalho, A.R.R.; Reid, A.J.S.; Hope, J.J. Controlling entanglement by direct quantum feedback. Phys. Rev. A 2008, 78, 012334. [Google Scholar] [CrossRef]
- Platzer, F.; Mintert, F.; Buchleitner, A. Optimal dynamical control of many-body entanglement. Phys. Rev. Lett. 2010, 105, 020501. [Google Scholar] [CrossRef]
- Sun, Q.; Al-Amri, M.; Davidovich, L.; Zubairy, M. Reversing entanglement change by a weak measurement. Phys. Rev. A 2010, 82, 052323. [Google Scholar] [CrossRef]
- Kim, Y.S.; Lee, J.C.; Kwon, O.; Kim, Y.H. Protecting entanglement from decoherence using weak measurement and quantum measurement reversal. Nat. Phys. 2012, 8, 117–120. [Google Scholar] [CrossRef]
- Xu, J.S.; Sun, K.; Li, C.F.; Xu, X.; Guo, G.; Andersson, E.; Franco, R.L.; Compagno, G. Experimental recovery of quantum correlations in absence of system–environment back-action. Nat. Commun. 2013, 4, 2851. [Google Scholar] [CrossRef]
- Lo Franco, R.; D’Arrigo, A.; Falci, G.; Compagno, G.; Paladino, E. Preserving entanglement and nonlocality in solid-state qubits by dynamical decoupling. Phys. Rev. B 2014, 90, 054304. [Google Scholar] [CrossRef]
- D’Arrigo, A.; Lo Franco, R.; Benenti, G.; Paladino, E.; Falci, G. Recovering entanglement by local operations. Ann. Phys. 2014, 350, 211–224. [Google Scholar] [CrossRef]
- Terhal, B.M. Quantum error correction for quantum memories. Rev. Mod. Phys. 2015, 87, 307–346. [Google Scholar] [CrossRef]
- Orieux, A.; D’Arrigo, A.; Ferranti, G.; Paladino, E.; Falci, G.; Sciarrino, F.; Mataloni, P. Experimental on-demand recovery of entanglement by local operations within non-Markovian dynamics. Sci. Rep. 2015, 5, 8575. [Google Scholar] [CrossRef] [PubMed]
- D’Arrigo, A.; Benenti, G.; Lo Franco, R.; Falci, G.; Paladino, E. Hidden entanglement, system–environment information flow and non-Markovianity. Int. J. Quantum Inf. 2014, 12, 1461005. [Google Scholar] [CrossRef]
- Man, Z.X.; Xia, Y.J.; Lo Franco, R. Cavity-based architecture to preserve quantum coherence and entanglement. Sci. Rep. 2015, 5, 13843. [Google Scholar] [CrossRef] [PubMed]
- Ong, E.T.S.; Chew, L.Y. The Effect of Spin Squeezing on the Entanglement Entropy of Kicked Tops. Entropy 2016, 18, 116. [Google Scholar] [CrossRef]
- Lo Franco, R. Nonlocality threshold for entanglement under general dephasing evolutions: A case study. Quantum Inf. Process. 2016, 15, 2393–2404. [Google Scholar] [CrossRef]
- Mortezapour, A.; Naeimi, G.; Lo Franco, R. Coherence and entanglement dynamics of vibrating qubits. Opt. Commun. 2018, 424, 26–31. [Google Scholar] [CrossRef]
- Mortezapour, A.; Lo Franco, R. Protecting quantum resources via frequency modulation of qubits in leaky cavities. Sci. Rep. 2018, 8, 14304. [Google Scholar] [CrossRef]
- Bennett, C.H.; DiVincenzo, D.P.; Smolin, J.A.; Wootters, W.K. Mixed state entanglement and quantum error correction. Phys. Rev. A 1996, 54, 3824–3851. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Brassard, G.; Popescu, S.; Smolin, J.A.; Wootters, W.K. Purification of Noisy Entanglement and Faithful Teleportation via Noisy Channels. Phys. Rev. Lett. 1996, 76, 722–725. [Google Scholar] [CrossRef] [PubMed]
- Murao, M.; Plenio, M.B.; Popescu, S.; Vedral, V.; Knight, P.L. Multiparticle entanglement purification protocols. Phys. Rev. A 1998, 57, R4075–R4078. [Google Scholar] [CrossRef]
- Aschauer, H.; Dür, W.; Briegel, H.J. Multiparticle entanglement purification for two-colorable graph states. Phys. Rev. A 2005, 71, 012319. [Google Scholar] [CrossRef]
- Czechlewski, M.; Grudka, A.; Ishizaka, S.; Wójcik, A. Entanglement purification protocol for amixture of a pure entangled state and a pure product state. Phys. Rev. A 2009, 80, 014303. [Google Scholar] [CrossRef]
- Wang, X.W.; Tang, S.Q.; Yuan, J.B.; Zhang, D.Y. Distilling perfect GHZ states from two copies of non-GHZ-diagonal mixed states. Opt. Commun. 2017, 392, 185–189. [Google Scholar] [CrossRef]
- Yuan, J.; Tang, S.; Wang, X.; Zhang, D. One-step distillation of local-unitary-equivalent GHZ-type states. Quantum Inf. Process. 2018, 17, 259. [Google Scholar] [CrossRef]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Inseparable two spin-1/2 density matrices can be distilled to a singlet form. Phys. Rev. Lett. 1997, 78, 574–577. [Google Scholar] [CrossRef]
- Kwiat, P.G.; Barraza-Lopez, S.; Stefanov, A.; Gisin, N. Experimental entanglement distillation and ‘hidden’ non-locality. Nature 2001, 409, 1014–1017. [Google Scholar] [CrossRef]
- Wang, X.W.; Yu, S.; Zhang, D.Y.; Oh, C.H. Effect of weak measurement on entanglement distribution over noisy channels. Sci. Rep. 2016, 6, 22408. [Google Scholar] [CrossRef]
- Fröwis, F.; Dür, W. Stability of encoded macroscopic quantum superpositions. Phys. Rev. A 2012, 85, 052329. [Google Scholar] [CrossRef]
- Filippov, S.N.; Frizen, V.V.; Kolobova, D.V. Ultimate entanglement robustness of two-qubit states against general local noises. Phys. Rev. A 2018, 97, 012322. [Google Scholar] [CrossRef]
- Mintert, F. Robust entangled states. J. Phys. A Math. Theor. 2010, 43, 245303. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Evolution from entanglement to decoherence of bipartite mixed “X” states. Quantum Inf. Comput. 2007, 7, 459–468. [Google Scholar]
- Chaves, R.; Aolita, L.; Acín, A. Robust multipartite quantum correlations without complex encodings. Phys. Rev. A 2012, 86, 020301(R). [Google Scholar] [CrossRef]
- Ali, M.; Gühne, O. Robustness of multiparticle entanglement: Specific entanglement classes and random states. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 055503. [Google Scholar] [CrossRef]
- Arthur, T.T.; Martin, T.; Fai, L.C. Disentanglement and quantum states transitions dynamics in spin-qutrit systems: Dephasing random telegraph noise and the relevance of the initial state. Quantum Inf. Process. 2018, 17, 37. [Google Scholar] [CrossRef]
- Aolita, L.; Cavalcanti, D.; Chaves, R.; Dhara, C.; Davidovich, L.; Acin, A. Noisy evolution of graph-state entanglement. Phys. Rev. A 2010, 82, 032317. [Google Scholar] [CrossRef]
- Shen, L.T.; Shi, Z.C.; Wu, H.Z.; Yang, Z.B. Dynamics of Entanglement in JaynesCCummings Nodes with Nonidentical Qubit-Field Coupling Strengths. Entropy 2017, 19, 331. [Google Scholar] [CrossRef]
- Borras, A.; Majtey, A.P.; Plastino, A.R. Robustness of highly entangled multiqubit states under decoherence. Phys. Rev. A 2009, 79, 022108. [Google Scholar] [CrossRef]
- Kesting, F.; Fröwis, F.; Dür, W. Effective noise channels for encoded quantum systems. Phys. Rev. A 2013, 88, 042305. [Google Scholar] [CrossRef]
- Vidal, G.; Werner, R.F. Computable measure of entanglement. Phys. Rev. A 2002, 65, 032314. [Google Scholar] [CrossRef]
- Życzkowski, K.; Horodecki, P.; Sanpera, A.; Lewenstein, M. Volume of the set of separable states. Phys. Rev. A 1998, 58, 883–892. [Google Scholar] [CrossRef]
- Hashemi Rafsanjani, S.M.; Huber, M.; Broadbent, C.J.; Eberly, J.H. Genuinely multipartite concurrence of N-qubit X matrices. Phys. Rev. A 2012, 86, 062303. [Google Scholar] [CrossRef]
- Streltsov, A.; Adesso, G.; Plenio, M.B. Quantum coherence as a resource. Rev. Mod. Phys. 2017, 89, 041003. [Google Scholar] [CrossRef]
- Bromley, T.R.; Cianciaruso, M.; Adesso, G. Frozen Quantum Coherence. Phys. Rev. Lett. 2015, 114, 210401. [Google Scholar] [CrossRef] [PubMed]
- Silva, I.A.; Souza, A.M.; Bromley, T.R.; Cianciaruso, M.; Marx, R.; Sarthour, R.S.; Oliveira, I.S.; Franco, R.L.; Glaser, S.J.; deAzevedo, E.R.; et al. Observation of Time-Invariant Coherence in a Nuclear Magnetic Resonance Quantum Simulator. Phys. Rev. Lett. 2016, 117, 160402. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.-W.; Tang, S.-Q.; Liu, Y.; Yuan, J.-B. Improving the Robustness of Entangled States by Basis Transformation. Entropy 2019, 21, 59. https://doi.org/10.3390/e21010059
Wang X-W, Tang S-Q, Liu Y, Yuan J-B. Improving the Robustness of Entangled States by Basis Transformation. Entropy. 2019; 21(1):59. https://doi.org/10.3390/e21010059
Chicago/Turabian StyleWang, Xin-Wen, Shi-Qing Tang, Yan Liu, and Ji-Bing Yuan. 2019. "Improving the Robustness of Entangled States by Basis Transformation" Entropy 21, no. 1: 59. https://doi.org/10.3390/e21010059
APA StyleWang, X.-W., Tang, S.-Q., Liu, Y., & Yuan, J.-B. (2019). Improving the Robustness of Entangled States by Basis Transformation. Entropy, 21(1), 59. https://doi.org/10.3390/e21010059



