Rolling Element Bearing Fault Diagnosis under Impulsive Noise Environment Based on Cyclic Correntropy Spectrum
Abstract
1. Introduction
- A cyclostationary analysis method based on the correntropy function is introduced into the fault diagnosis of the rolling element bearing under an impulsive noise environment.
- The kernel size of the correntropy function is investigated to find out its influence on the rolling element bearing fault diagnosis.
- The diagnosis performance of the proposed method is compared with the Fast Kurtogram method using train axle bearing data to verify its suitability.
2. Fundamentals of Correntropy Function and Cyclic Spectral Analysis
2.1. Correntropy Function
2.2. Cyclic Spectral Analysis
3. Cyclostationary Analysis Based on Correntropy Function
3.1. Fundamental of CCE Function and CCE Spectrum
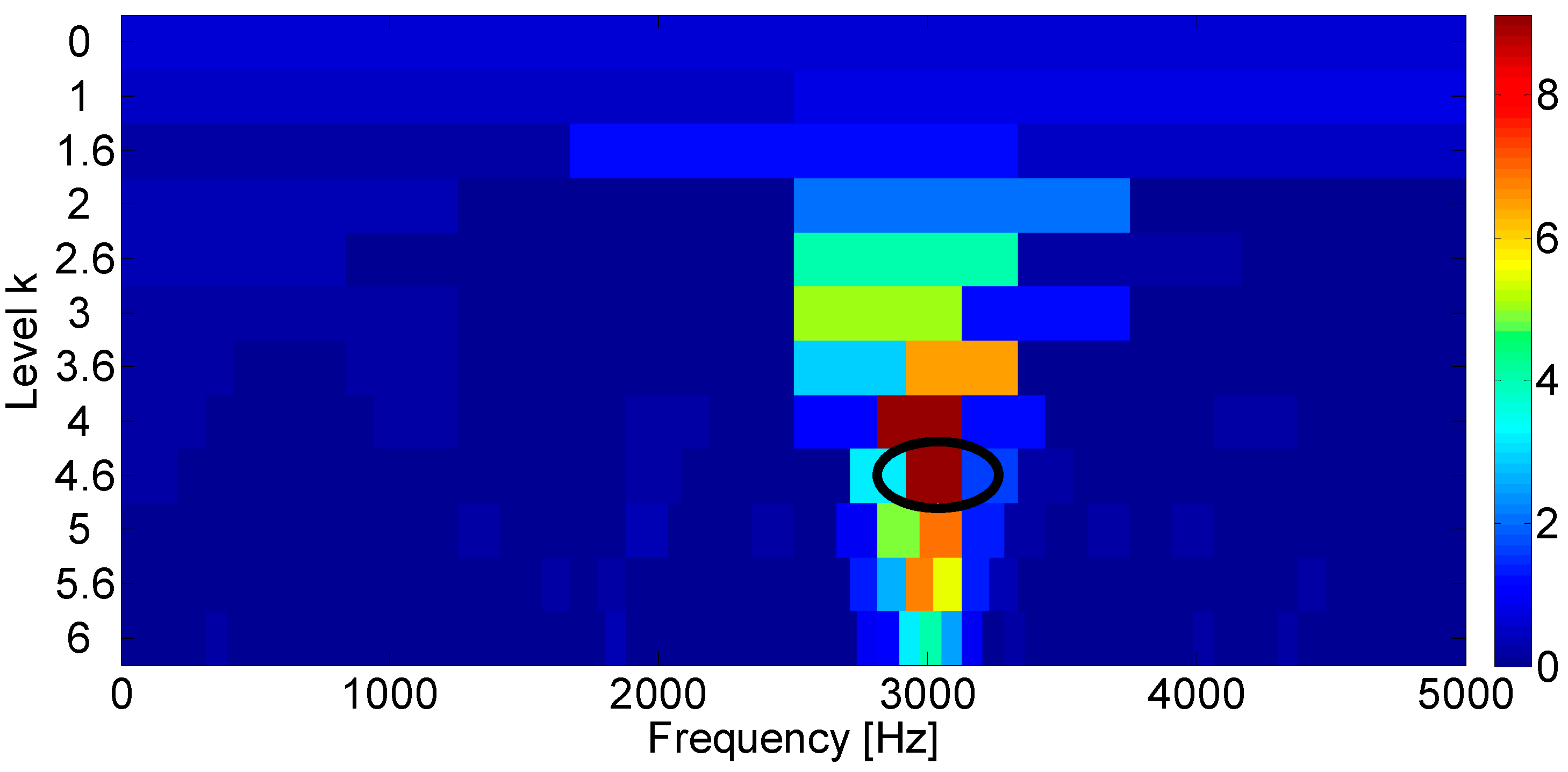
3.2. Kernel Size Selection of the CCE Function
3.3. Estimation of CCES
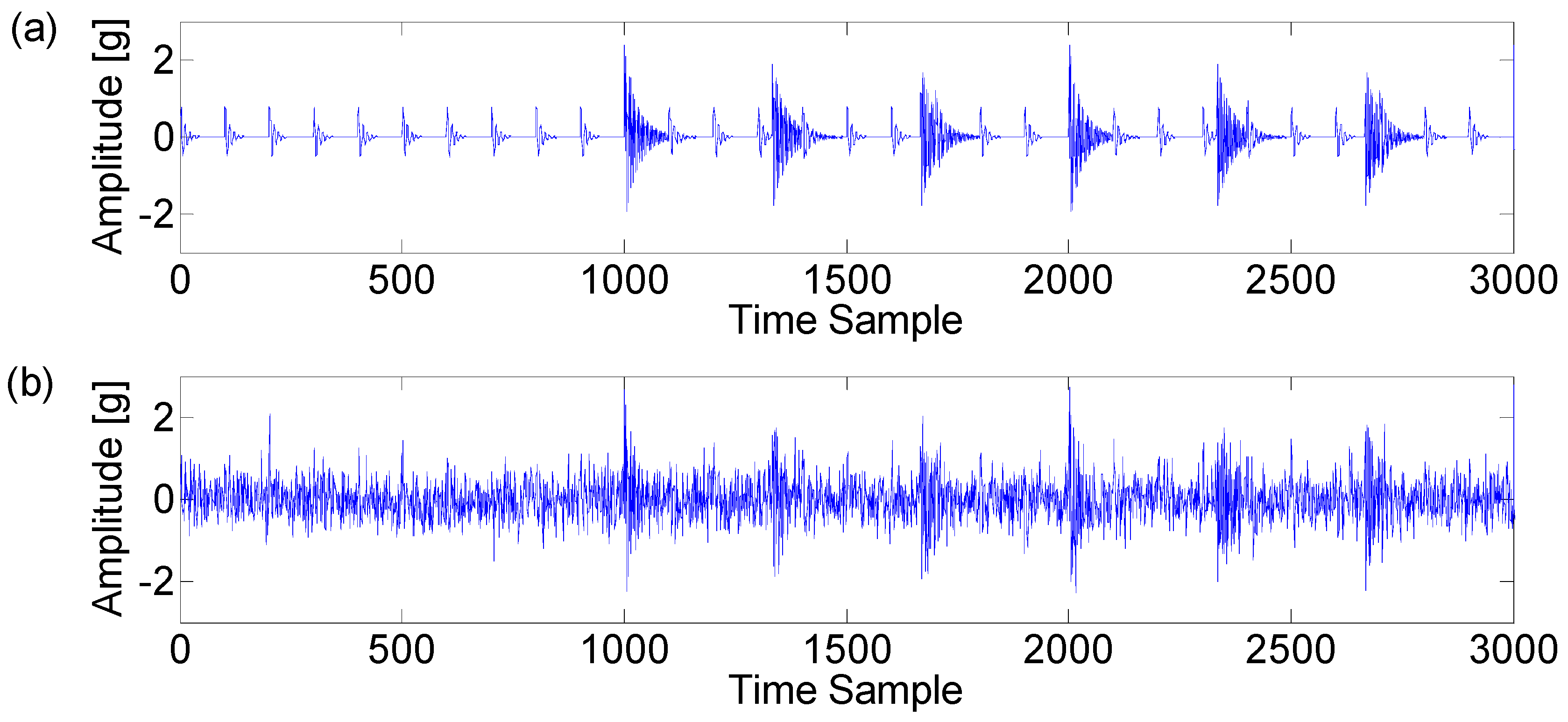
4. Validation of CCES on Bearing Fault Diagnosis
4.1. Estimation of CCES
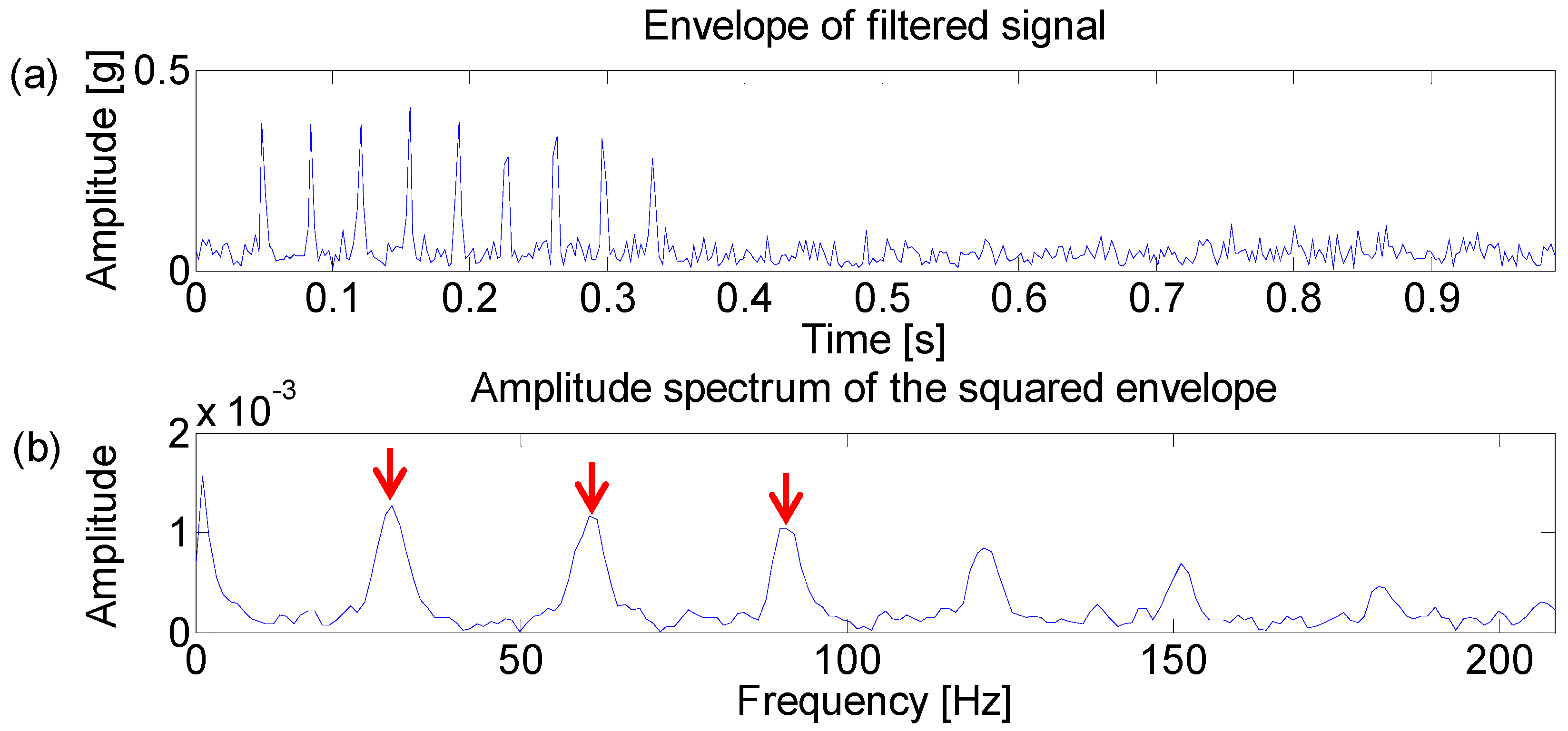
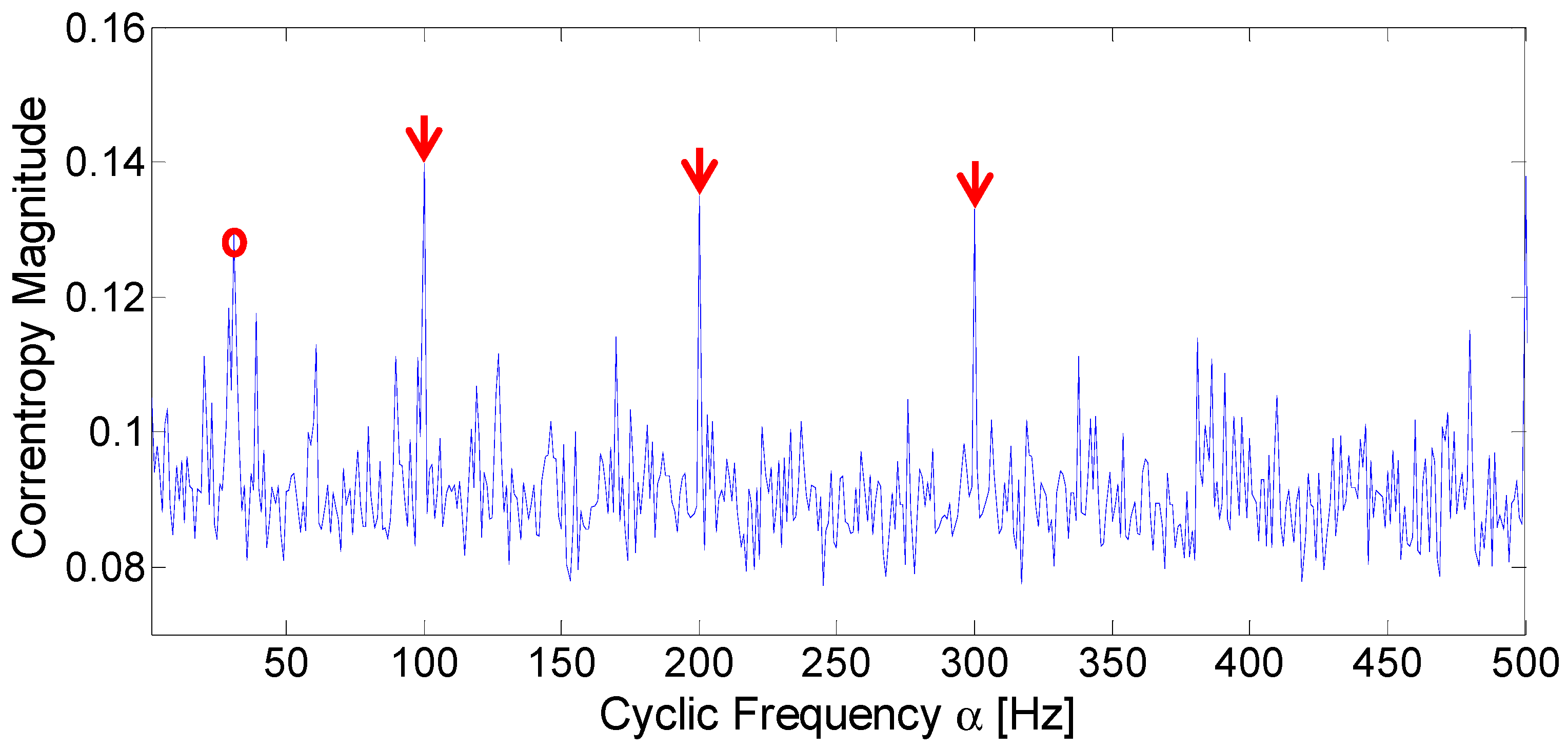
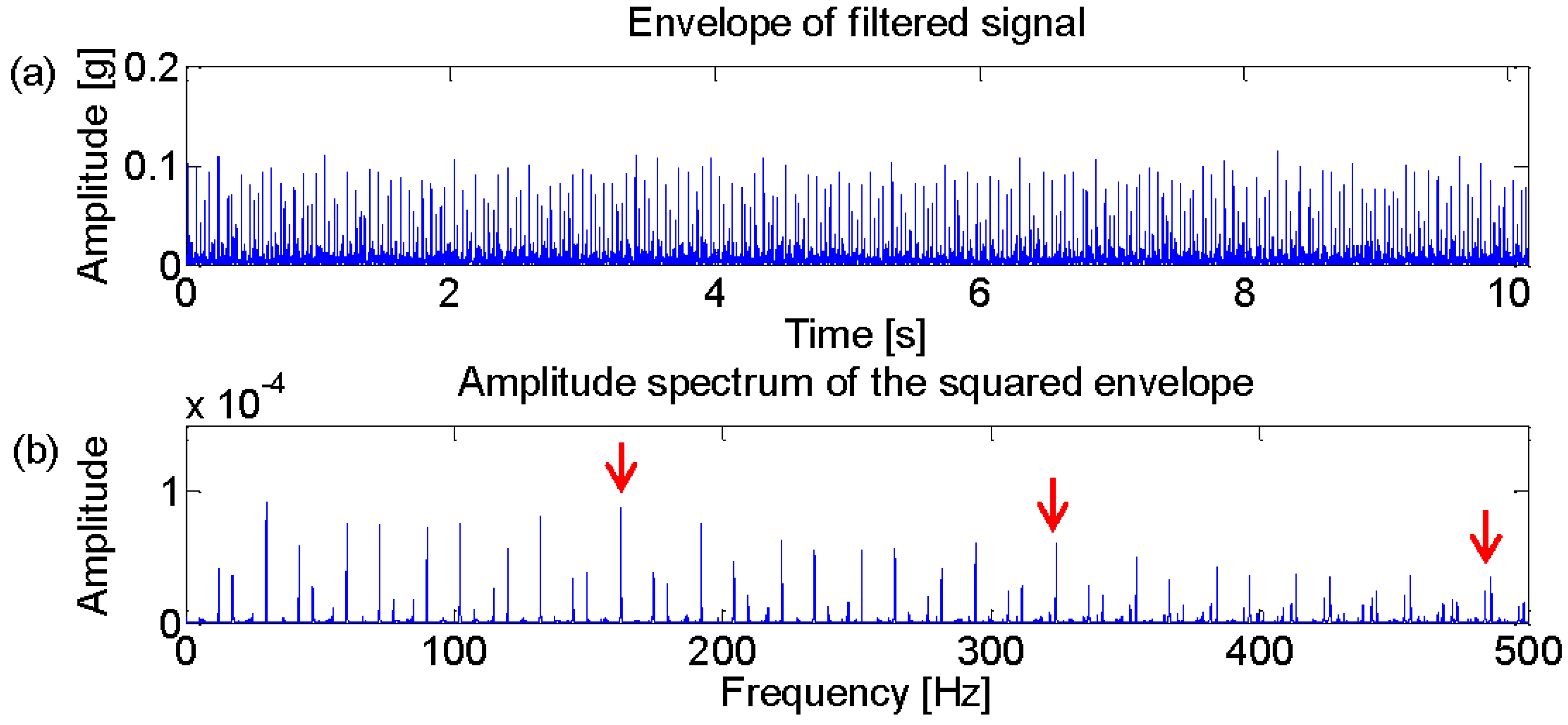
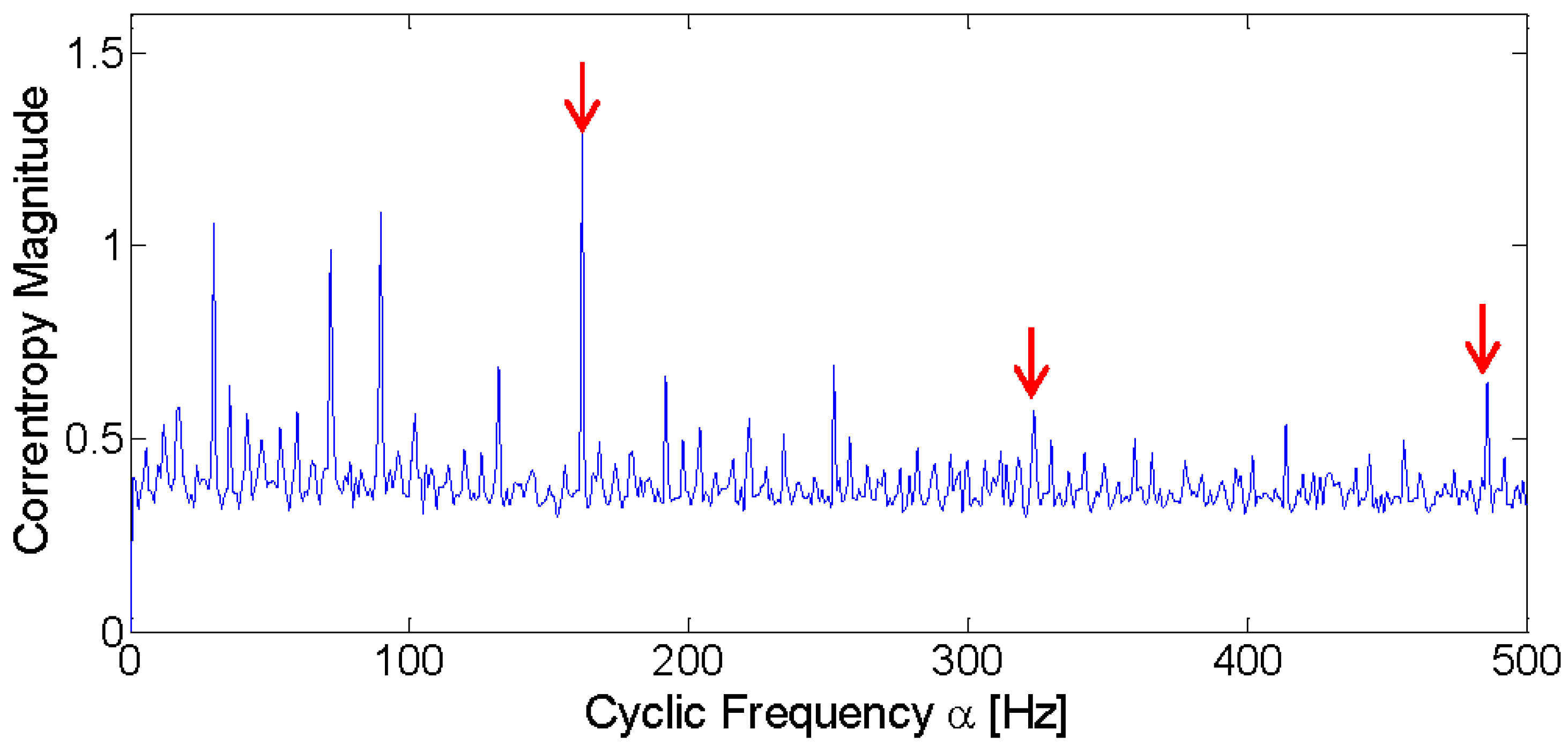
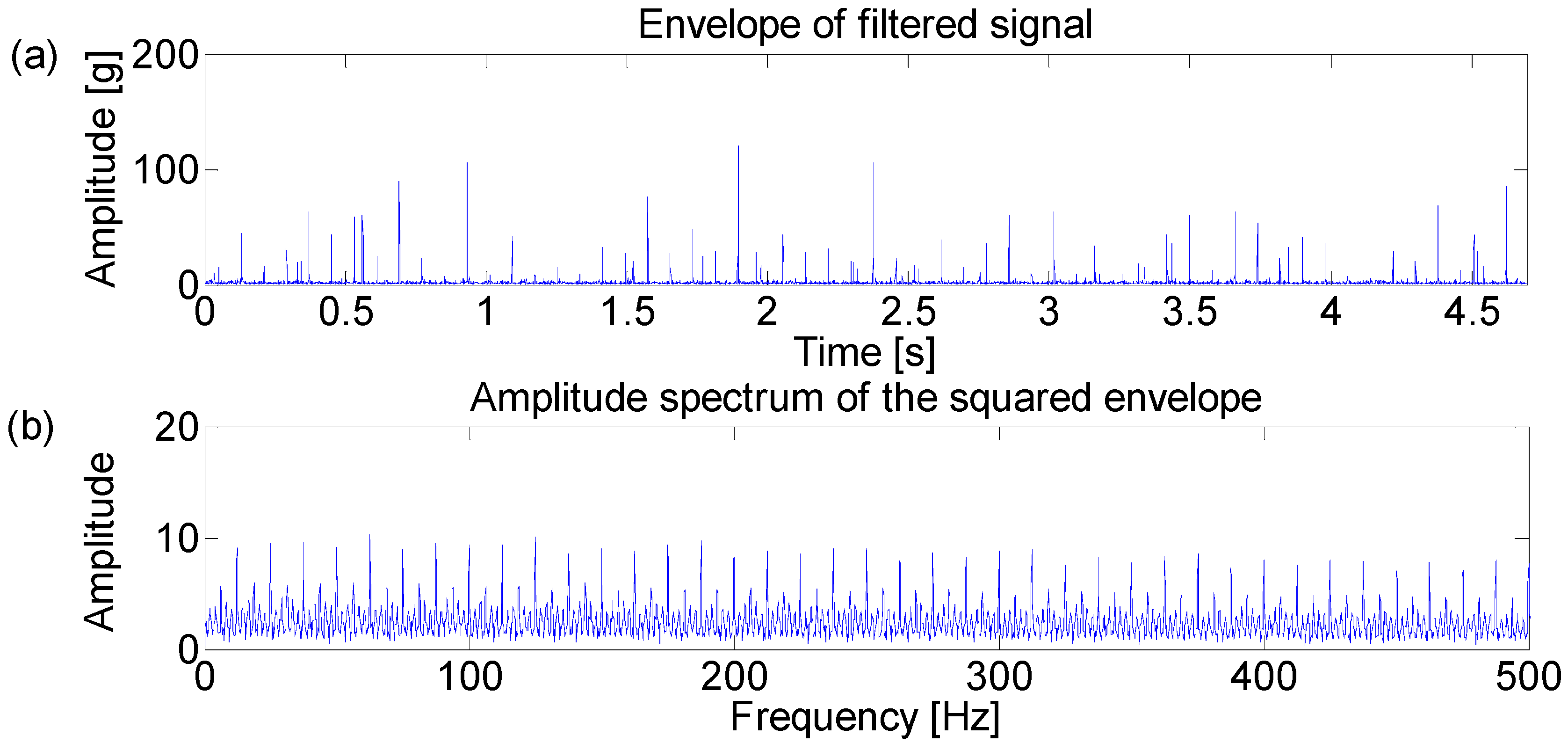
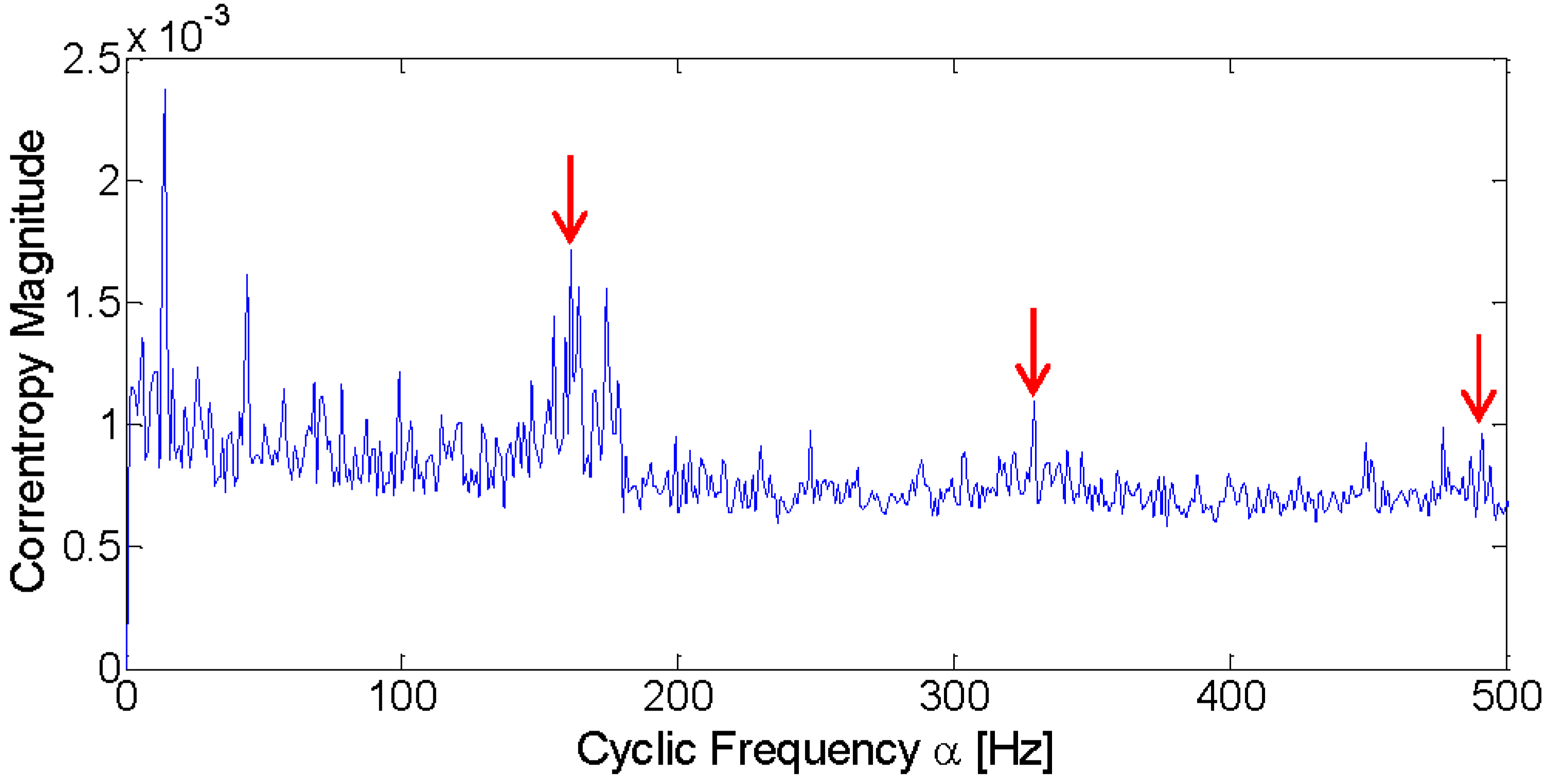
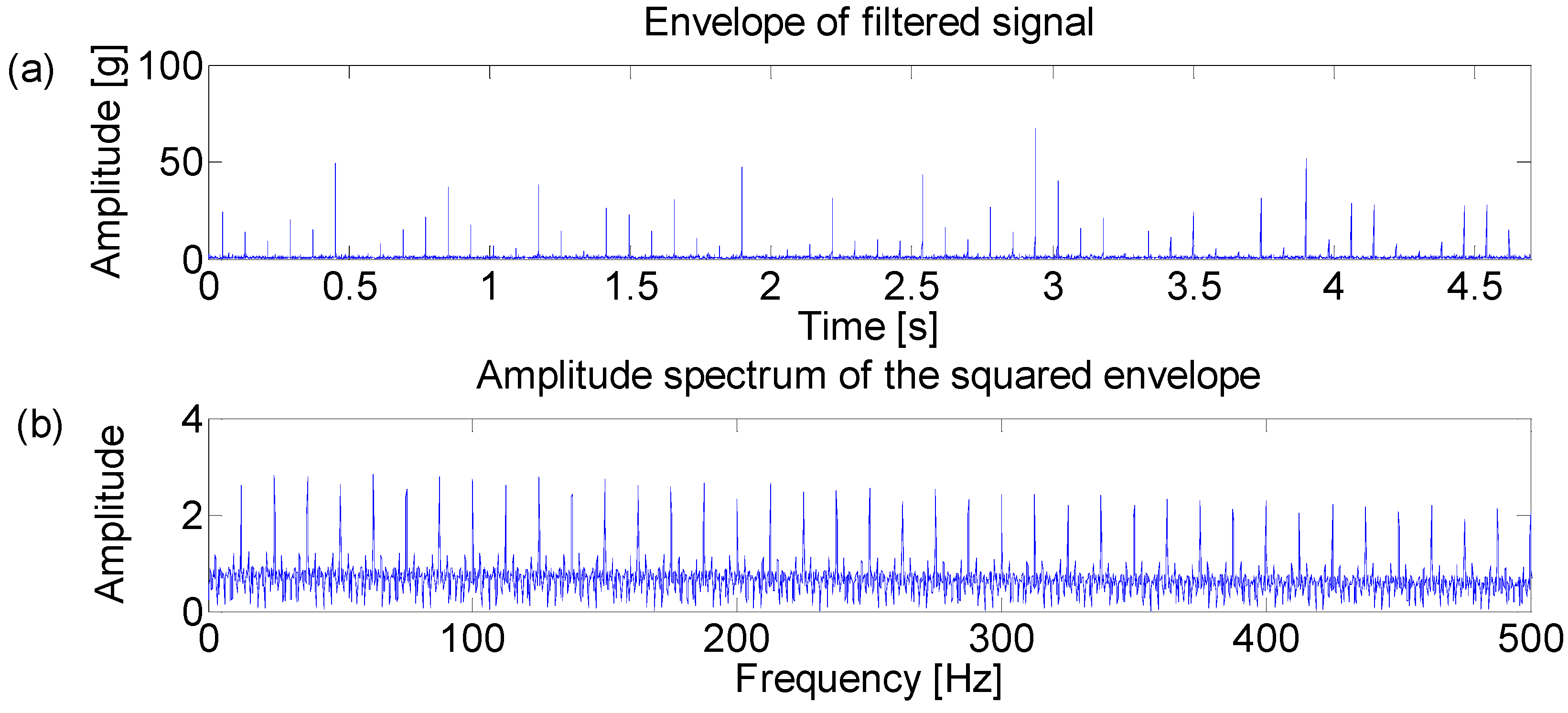
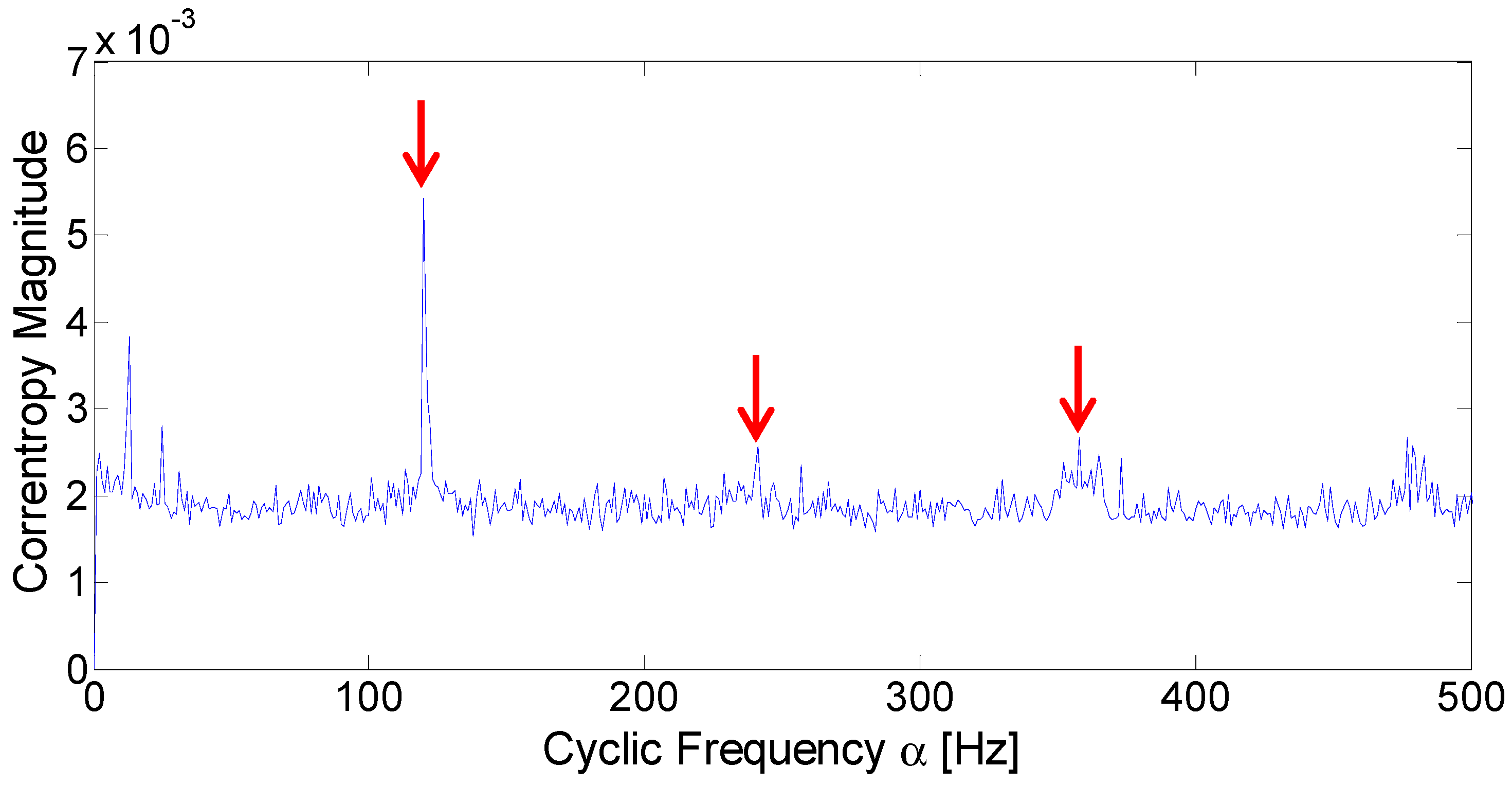
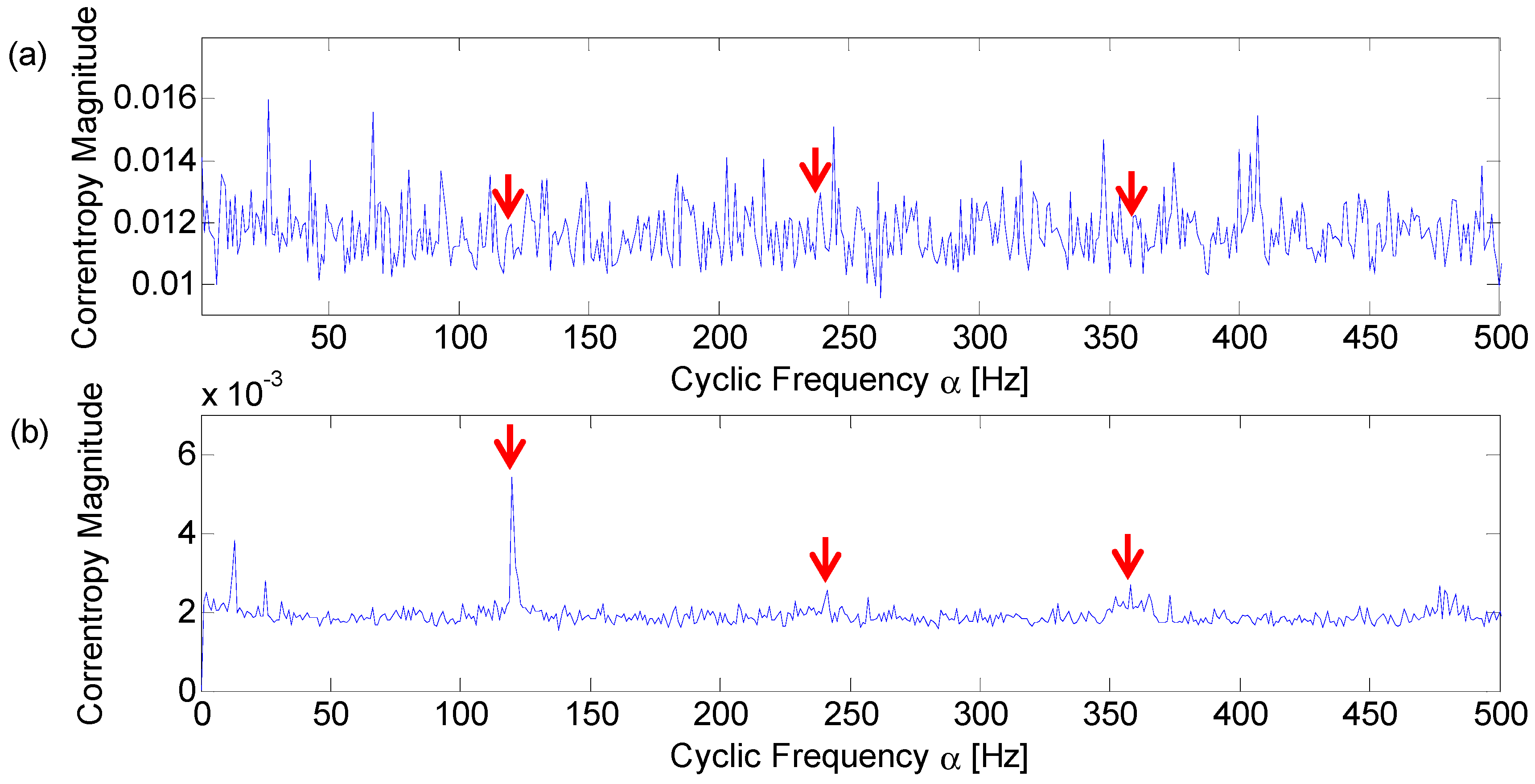
4.2. Case Study 1
4.3. Case Study 2
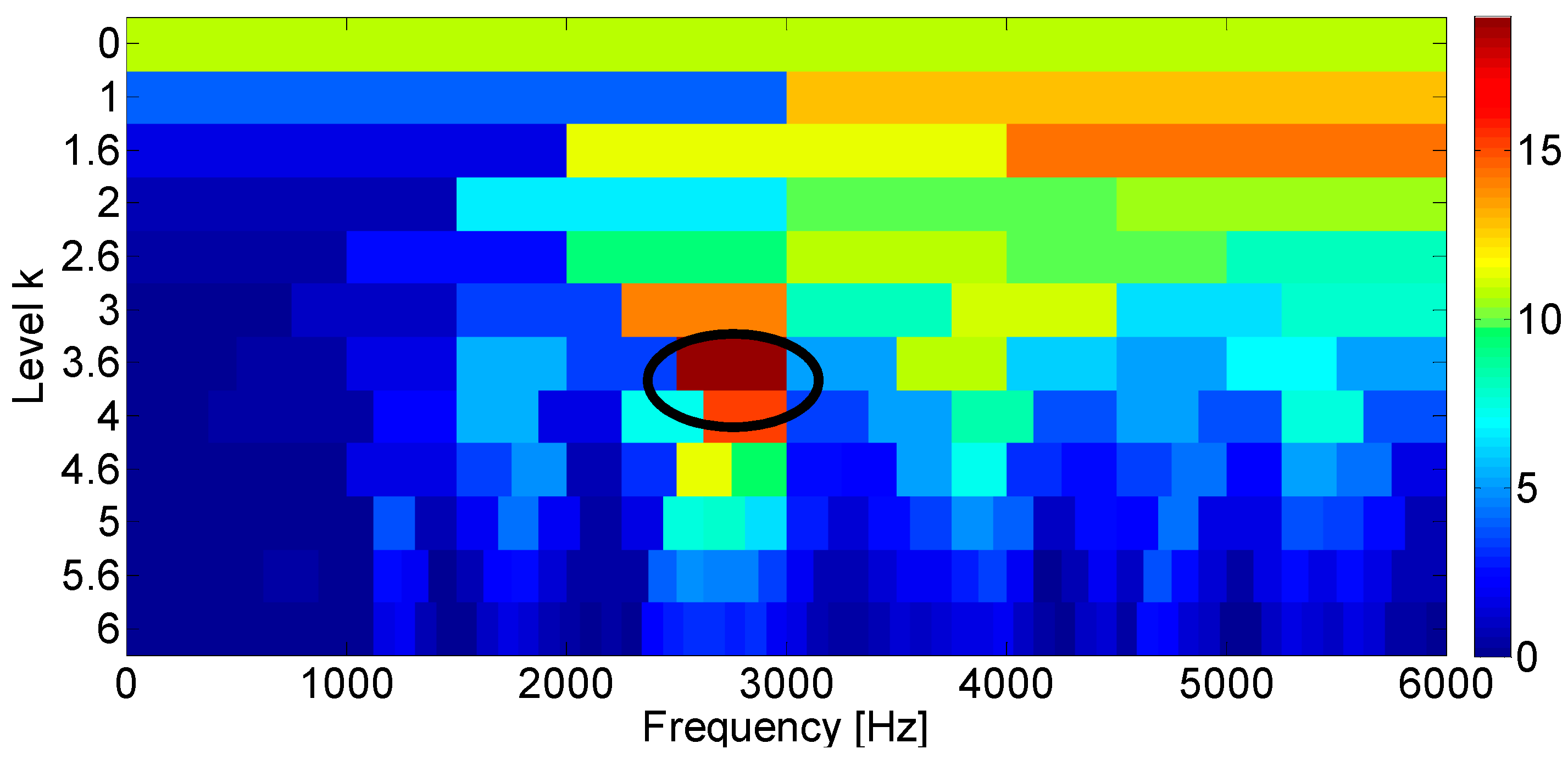
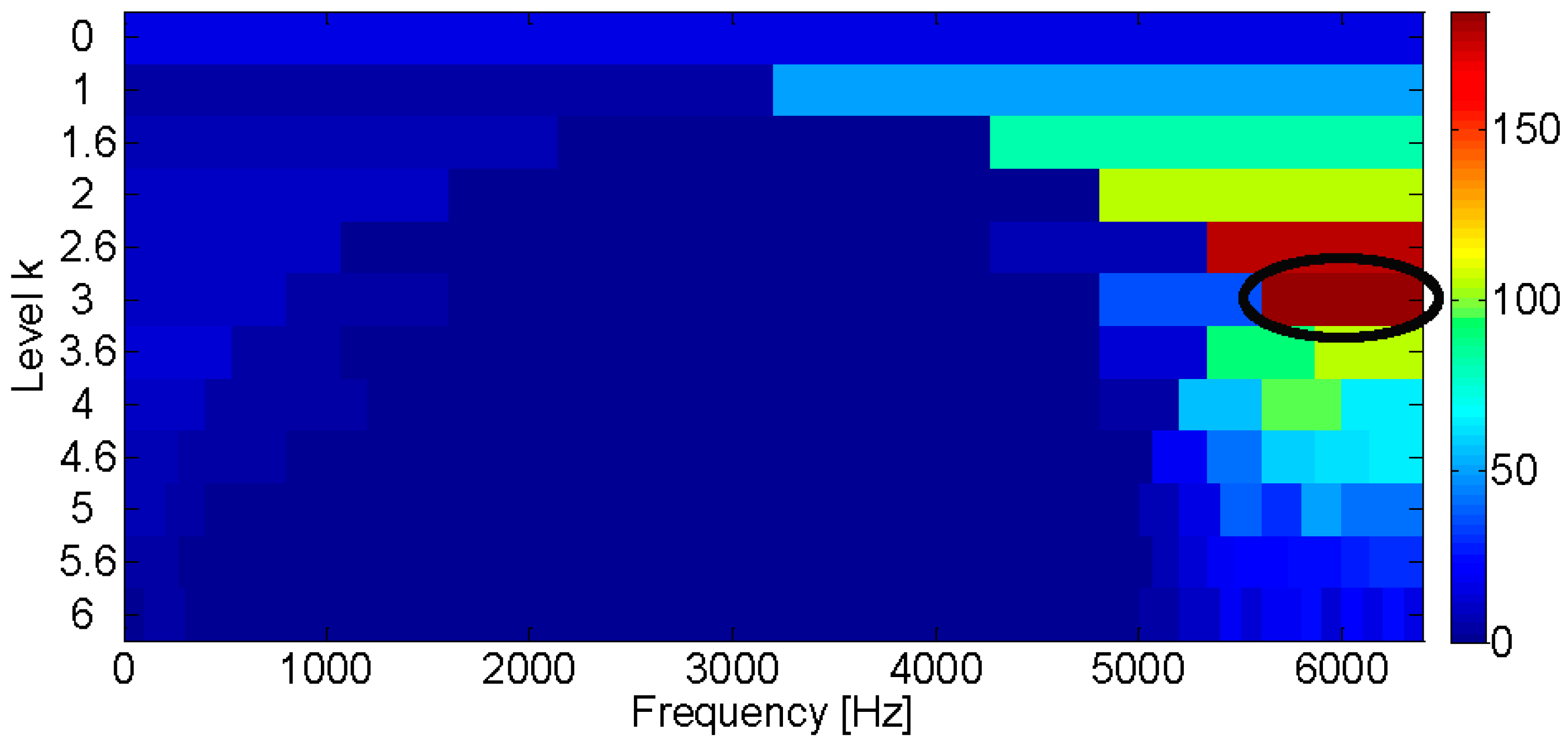
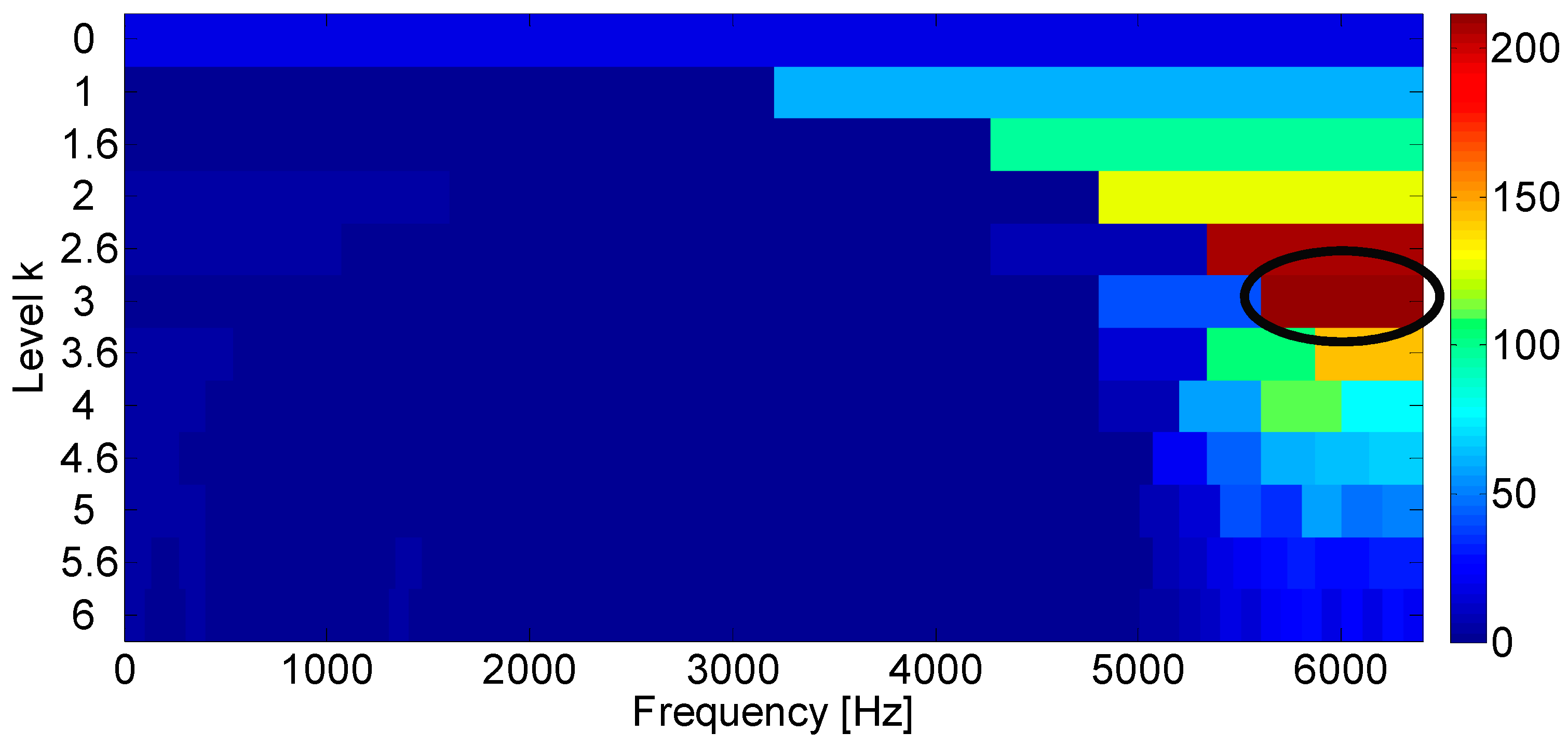
4.4. Influence of Kernel Size on the Diagnosis Performance
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, D.; Tsui, K.-L.; Miao, Q. Prognostics and health management: A review of vibration based bearing and gear health indicators. IEEE Access 2018, 6, 665–676. [Google Scholar] [CrossRef]
- Feng, Z.; Liang, M.; Chu, F. Recent advances in time–frequency analysis methods for machinery fault diagnosis: A review with application examples. Mech. Syst. Signal Process. 2013, 38, 165–205. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Z.; Zhang, Z.; Jia, L.; Qin, Y. A Semi-Supervised Approach to Bearing Fault Diagnosis under Variable Conditions towards Imbalanced Unlabeled Data. Sensors 2018, 18, 2097. [Google Scholar] [CrossRef] [PubMed]
- Ho, D.; Randall, R. Optimisation of bearing diagnostic techniques using simulated and actual bearing fault signals. Mech. Syst. Signal Process. 2000, 14, 763–788. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Antoni, J.; Randall, R. The spectral kurtosis: Application to the vibratory surveillance and diagnostics of rotating machines. Mech. Syst. Signal Process. 2006, 20, 308–331. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Peter, W.T.; Wang, D. The design of a new sparsogram for fast bearing fault diagnosis: Part 1 of the two related manuscripts that have a joint title as “Two automatic vibration-based fault diagnostic methods using the novel sparsity measurement–Parts 1 and 2”. Mech. Syst. Signal Process. 2013, 40, 499–519. [Google Scholar] [CrossRef]
- He, D.; Wang, X.; Li, S.; Lin, J.; Zhao, M. Identification of multiple faults in rotating machinery based on minimum entropy deconvolution combined with spectral kurtosis. Mech. Syst. Signal Process. 2016, 81, 235–249. [Google Scholar] [CrossRef]
- Wang, Y.; Xiang, J.; Markert, R.; Liang, M. Spectral kurtosis for fault detection, diagnosis and prognostics of rotating machines: A review with applications. Mech. Syst. Signal Process. 2016, 66, 679–698. [Google Scholar] [CrossRef]
- Smith, W.A.; Fan, Z.; Peng, Z.; Li, H.; Randall, R.B. Optimised Spectral Kurtosis for bearing diagnostics under electromagnetic interference. Mech. Syst. Signal Process. 2016, 75, 371–394. [Google Scholar] [CrossRef]
- Bozchalooi, I.S.; Liang, M. A smoothness index-guided approach to wavelet parameter selection in signal de-noising and fault detection. J. Sound Vib. 2007, 308, 246–267. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J. Improvement of kurtosis-guided-grams via Gini index for bearing fault feature identification. Meas. Sci. Technol. 2017, 28, 125001. [Google Scholar] [CrossRef]
- Barszcz, T.; JabŁoński, A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kurtogram. Mech. Syst. Signal Process. 2011, 25, 431–451. [Google Scholar] [CrossRef]
- Antoni, J. The infogram: Entropic evidence of the signature of repetitive transients. Mech. Syst. Signal Process. 2016, 74, 73–94. [Google Scholar] [CrossRef]
- Antoni, J.; Bonnardot, F.; Raad, A.; El Badaoui, M. Cyclostationary modelling of rotating machine vibration signals. Mech. Syst. Signal Process. 2004, 18, 1285–1314. [Google Scholar] [CrossRef]
- Antoni, J. Cyclic spectral analysis in practice. Mech. Syst. Signal Process. 2007, 21, 597–630. [Google Scholar] [CrossRef]
- Antoni, J. Cyclostationarity by examples. Mech. Syst. Signal Process. 2009, 23, 987–1036. [Google Scholar] [CrossRef]
- Antoni, J.; Hanson, D. Detection of surface ships from interception of cyclostationary signature with the cyclic modulation coherence. IEEE J. Ocean. Eng. 2012, 37, 478–493. [Google Scholar] [CrossRef]
- Antoni, J.; Xin, G.; Hamzaoui, N. Fast computation of the spectral correlation. Mech. Syst. Signal Process. 2017, 92, 248–277. [Google Scholar] [CrossRef]
- Luan, S.; Qiu, T.; Zhu, Y.; Yu, L. Cyclic correntropy and its spectrum in frequency estimation in the presence of impulsive noise. Signal Process. 2016, 120, 503–508. [Google Scholar] [CrossRef]
- Liu, T.; Qiu, T.; Luan, S. Cyclic Correntropy: Foundations and Theories. IEEE Access 2018, 6, 34659–34669. [Google Scholar] [CrossRef]
- Fontes, A.I.; Rego, J.B.; Martins, A.d.M.; Silveira, L.F.; Príncipe, J.C. Cyclostationary correntropy: Definition and applications. Expert Syst. Appl. 2017, 69, 110–117. [Google Scholar] [CrossRef]
- Santamaría, I.; Pokharel, P.P.; Principe, J.C. Generalized correlation function: Definition, properties, and application to blind equalization. IEEE Trans. Signal Process. 2006, 54, 2187–2197. [Google Scholar] [CrossRef]
- Parzen, E. Statistical Methods on Time Series by Hilbert Space Methods; Applied Mathematics and Statistics Laboratory, Stanford University: Stanford, CA, USA, 1959; Volume 23. [Google Scholar]
- Chen, B.; Xing, L.; Zhao, H.; Zheng, N.; Prı, J.C. Generalized correntropy for robust adaptive filtering. IEEE Trans. Signal Process. 2016, 64, 3376–3387. [Google Scholar] [CrossRef]
- Liu, W.; Pokharel, P.P.; Príncipe, J.C. Correntropy: Properties and applications in non-Gaussian signal processing. IEEE Trans. Signal Process. 2007, 55, 5286–5298. [Google Scholar] [CrossRef]
- Gunduz, A.; Principe, J.C. Correntropy as a novel measure for nonlinearity tests. Signal Process. 2009, 89, 14–23. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, Y.Y.; Li, L. Correntropy matching pursuit with application to robust digit and face recognition. IEEE Trans. Cybern. 2017, 47, 1354–1366. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Shi, J.; Zhang, X.; Ma, W.; Chen, B.; Senior Member, I. Kernel recursive maximum correntropy. Signal Process. 2015, 117, 11–16. [Google Scholar] [CrossRef]
- Erdogmus, D.; Principe, J.C. An error-entropy minimization algorithm for supervised training of nonlinear adaptive systems. IEEE Trans. Signal Process. 2002, 50, 1780–1786. [Google Scholar] [CrossRef]
- Xu, J.-W.; Paiva, A.R.; Park, I.; Príncipe, J.C. A Reproducing Kernel Hilbert Space Framework for Information-Theoretic Learning. IEEE Trans. Signal Process. 2008, 56, 5891–5902. [Google Scholar]
- Jenssen, R.; Erdogmus, D.; Principe, J.C.; Eltoft, T. Towards a unification of information theoretic learning and kernel methods. In Machine Learning for Signal Processing, 2004, Proceedings of the 2004 14th IEEE Signal Processing Society Workshop, Sao Luis, Brazil, 29 September–1 October 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 93–102. [Google Scholar]
- Zhao, S.; Chen, B.; Principe, J.C. An adaptive kernel width update for correntropy. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, Australia, 10–15 June 2012; pp. 1–5. [Google Scholar]
- Bowman, A.W. An alternative method of cross-validation for the smoothing of density estimates. Biometrika 1984, 71, 353–360. [Google Scholar] [CrossRef]
- Sheather, S.J. Density estimation. Stat. Sci. 2004, 19, 588–597. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman & Hall: London, UK, 1986; ISBN 0-412-24620-1. [Google Scholar]
- Antoni, J.; Randall, R. A stochastic model for simulation and diagnostics of rolling element bearings with localized faults. J. Vib. Acoust. 2003, 125, 282–289. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center Website. Available online: http://csegroups.case.edu/bearingdatacenter/home (accessed on 18 January 2018).
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Smith, W.A.; Randall, R.B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process. 2015, 64, 100–131. [Google Scholar] [CrossRef]
- Zhao, X.; Qin, Y.; Kou, L.; Liu, Z. Understanding real faults of axle box bearings based on vibration data using decision tree. In Proceedings of the 2018 IEEE International Conference on Prognostics and Health Management (ICPHM), Seattle, WA, USA, 11–13 June 2018; pp. 1–5. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Qin, Y.; He, C.; Jia, L.; Kou, L. Rolling Element Bearing Fault Diagnosis under Impulsive Noise Environment Based on Cyclic Correntropy Spectrum. Entropy 2019, 21, 50. https://doi.org/10.3390/e21010050
Zhao X, Qin Y, He C, Jia L, Kou L. Rolling Element Bearing Fault Diagnosis under Impulsive Noise Environment Based on Cyclic Correntropy Spectrum. Entropy. 2019; 21(1):50. https://doi.org/10.3390/e21010050
Chicago/Turabian StyleZhao, Xuejun, Yong Qin, Changbo He, Limin Jia, and Linlin Kou. 2019. "Rolling Element Bearing Fault Diagnosis under Impulsive Noise Environment Based on Cyclic Correntropy Spectrum" Entropy 21, no. 1: 50. https://doi.org/10.3390/e21010050
APA StyleZhao, X., Qin, Y., He, C., Jia, L., & Kou, L. (2019). Rolling Element Bearing Fault Diagnosis under Impulsive Noise Environment Based on Cyclic Correntropy Spectrum. Entropy, 21(1), 50. https://doi.org/10.3390/e21010050




