Optimization of Thurston’s Core Entropy Algorithm for Polynomials with a Critical Point of Maximal Order
Abstract
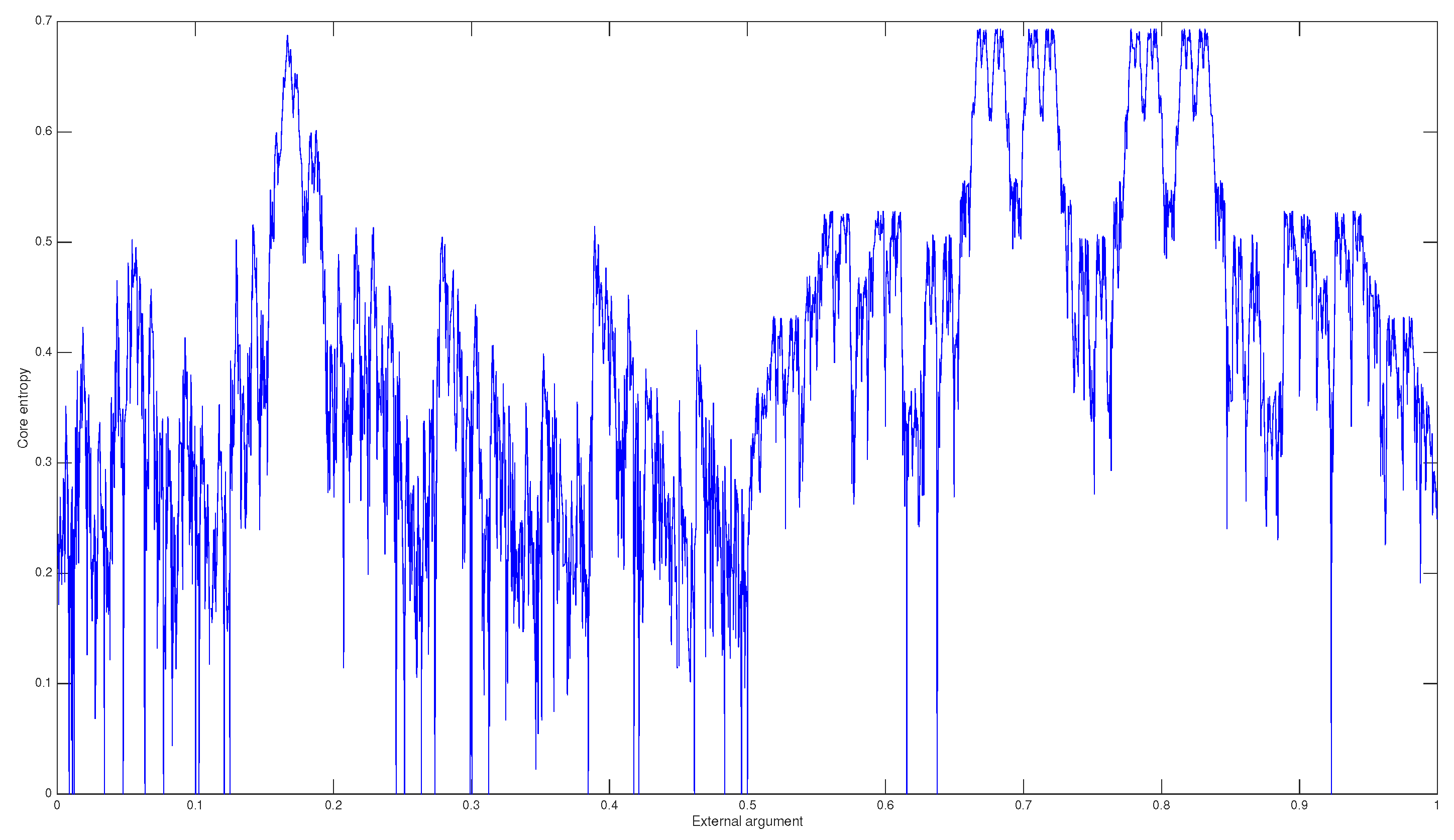
:1. Introduction
2. Thurston’s Algorithm
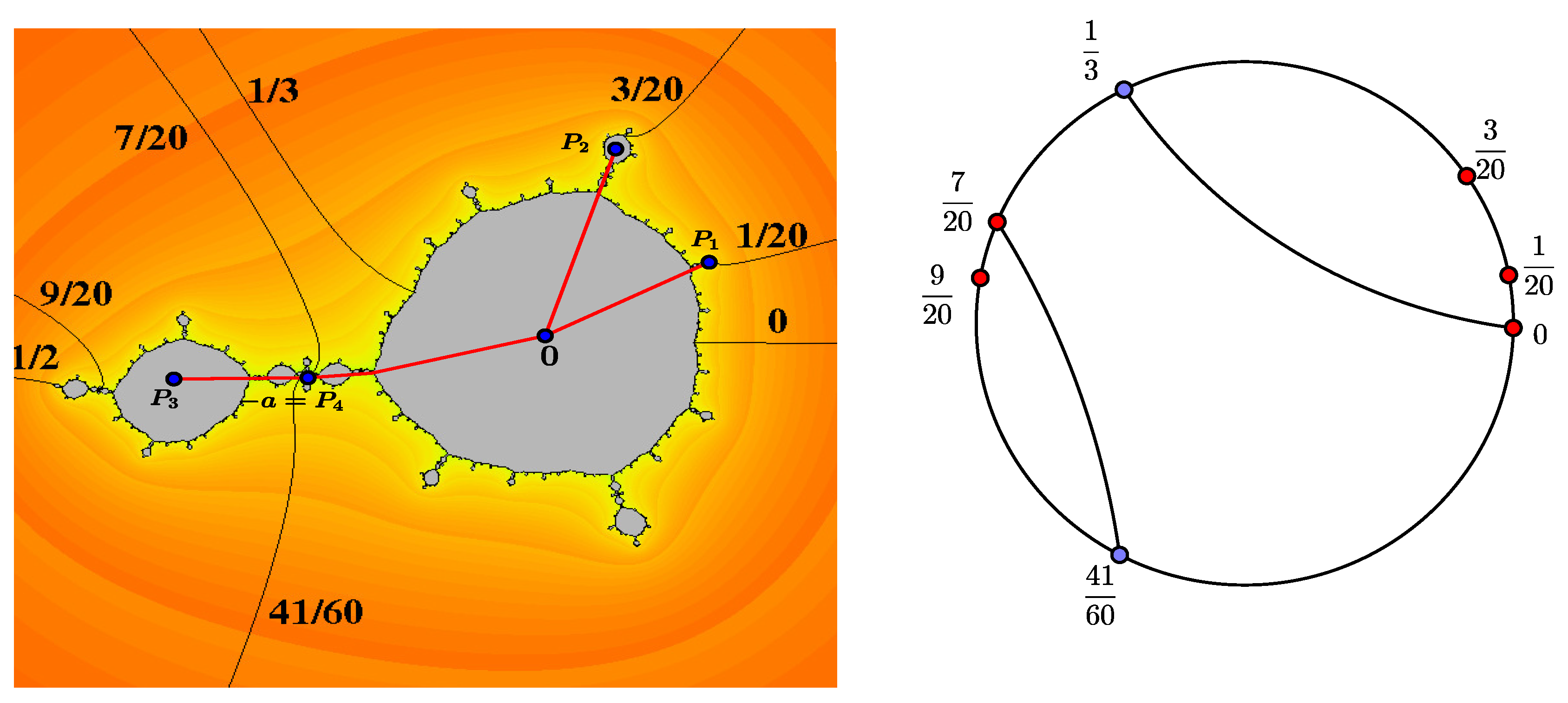
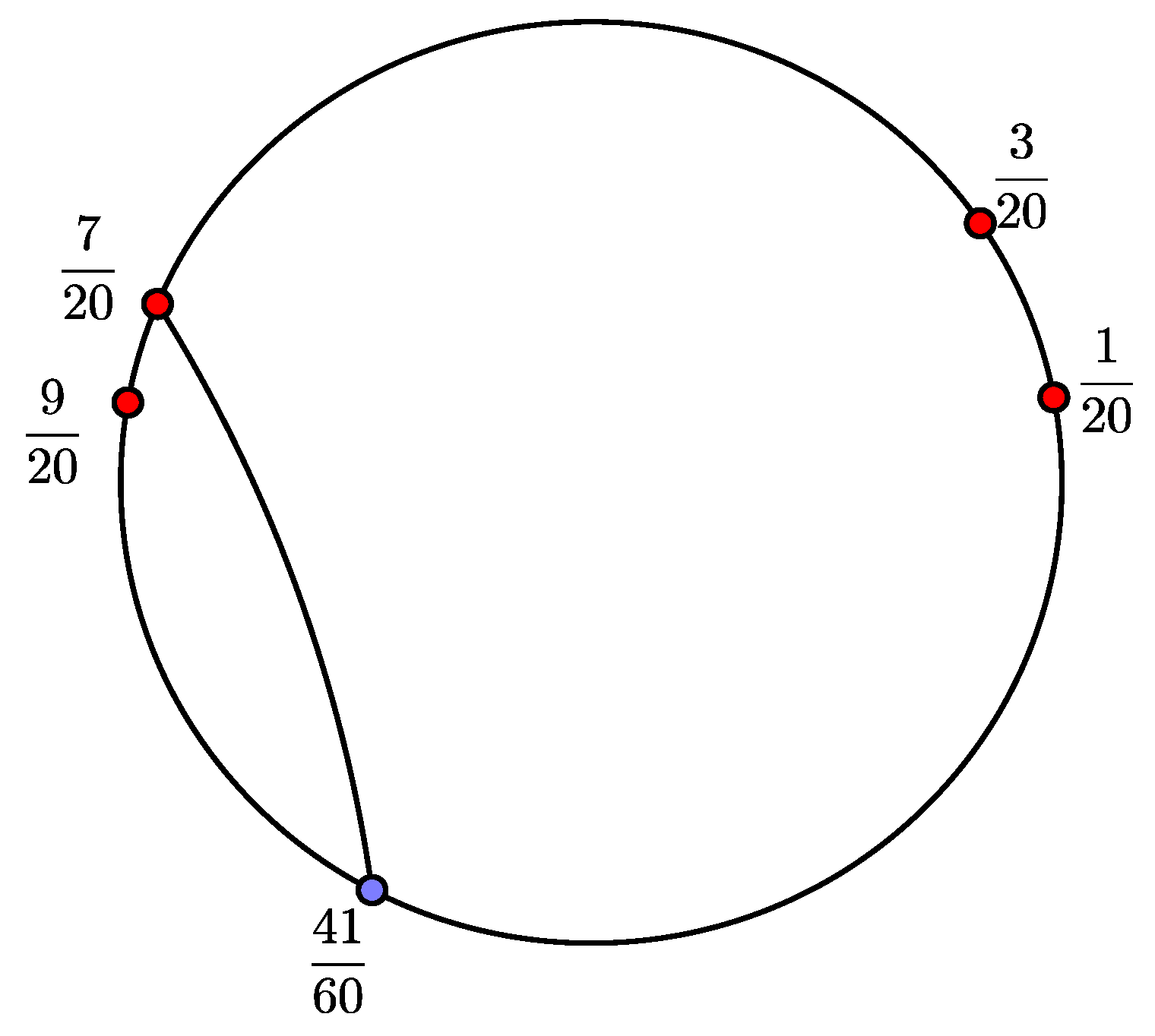
2.1. The Algorithm of Thurston for Polynomials of Degree d
- (1)
- The ray lands on a point q at the boundary of U.
- (2)
- There exists a sector based at q, delimited by and the internal ray of U that lands at q, such that the sector does not contain any other external ray that lands on q.
- (1)
- If U is periodic with orbitwe build for all in this orbit simultaneously.
- (2)
- If the Fatou component U is strictly preperiodic, take n as the smallest number for which is a critical Fatou component. Let be such that , where is the point where lands on and . Consider a ray that supports component U which contains z. Define as the set of the arguments of the supporting rays of U that, under , go to .
- Each , consists of a unique angle.
- The convex hulls of and in the unit disk intersect each other in, at most, one point of , for any in the set .
- For each i, and .
| Algorithm 1 Thurston’s Algorithm |
|
2.2. Thurston’s Algorithm in the Polynomial Family (1)
| Algorithm 2 The Adapted Thurston’s Algorithm |
|
- (1)
- If , in this case, the core entropy is zero, and we show that in the restricted algorithm. The spectral radius of matrix is 1.
- (2)
- If , we show that transformation can be built without considering the line of separation of the critical point (0).
- (1)
- If is the center of a capture component, then the orbit of eventually contains the zero angle, which is a fixed angle. In this case, the postcritical set of is . Hence, .
- (2)
- If eventually goes to , with a fixed p, then the orbit of contains the zero angle; thus, as above, .
- (3)
- In any other case, the orbits of and are disjoint. Hence, the postcritical set iswhere with .
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Douady, A. Topological Entropy of Unimodal Maps: Monotonicity for Quadratic Polynomials; Springer: Berlin, Germany, 1993; pp. 65–87. [Google Scholar]
- Milnor, J.; Thurston, W. On Iterated Maps of the Interval, in Dynamical Systems; Springer: Berlin, Germany, 1988; pp. 465–563. [Google Scholar]
- Milnor, J.; Tresser, C. On entropy and monotonicity for real cubic maps, with an appendix by Adrien Douady and Pierrette Sentenac. Commun. Math. Phys. 2000, 209, 123–178. [Google Scholar] [CrossRef]
- Radulescu, A. The connected isentropes conjecture in a space of quartic polynomials. Discrete Contin. Dyn. Syst. 2007, 19, 139–175. [Google Scholar] [CrossRef]
- Bruin, H.; van Strien, S. Monotonicity of entropy for real multimodal maps. J. Am. Math. Soc. 2015, 28, 1–61. [Google Scholar] [CrossRef]
- Li, T. A Monotonicity Conjecture for the Entropy of Hubbard Trees. Ph.D. Thesis, State University of New York at Stony Brook, Stony Brook, NY, USA, August 2007. [Google Scholar]
- Poirier, A. Hubbard trees. Fund. Math. 2010, 208, 193–248. [Google Scholar] [CrossRef]
- Thurston, W.P. Geometry and dynamics of iterated Rational Maps. In Complex Dynamics; Schleicher, D., Selinger, N., Eds.; AK Peters/CRC Press: Wellesley, MA, USA, 2009; pp. 3–137. [Google Scholar]
- Gao, Y. On Thurston’s core entropy algorithm. arXiv, 2015; arXiv:1511.06513v2. [Google Scholar]
- Tiozzo, G. Entropy, Dimension and Combinatorial Moduli for One-Dimensional Dynamical Systems. Ph.D. Thesis, Harvard University, Ann Arbor, MI, USA, April 2013. [Google Scholar]
- Tiozzo, G. Continuity of core entropy of quadratic polynomials. Invent. Math. 2016, 203, 891–921. [Google Scholar] [CrossRef]
- Gao, Y.; Tiozzo, G. The core entropy for polynomials of higher degree. arXiv, 2017; arXiv:1703.08703. [Google Scholar]
- Roesch, P. Hyperbolic components of polynomials with a fixed critical point of maximal order, (English, French summary). Ann. Sci. École Norm. Super. 2007, 40, 901–949. [Google Scholar] [CrossRef]
- Milnor, J. Periodic Orbits, External Rays and the Mandelbrot Set: An Expository Account; Geometrie Complexe et Systemes Dynamiques, Astérisque; American Mathematical Society: Providence, RI, USA, 2000; Volume 261, pp. 277–333. [Google Scholar]
- Milnor, J. Cubic polynomial maps with periodic critical orbit, Part I. In Complex Dynamics: Families and Friends; Schleicher, D., Peters, A.K., Eds.; CRC Press: Boca Raton, FL, USA, 2009; pp. 333–411. [Google Scholar]
- Pole, D. Linear Algebra, a Modern Introduction, 2nd ed.; Thomson: Belmont, CA, USA, 2006. [Google Scholar]
- Block, L.B.; Coppel, W.A. Dynamics in One Dimension; Lecture Notes in Mathematics; Springer: Berlin, Germany, 1992; p. 1513. [Google Scholar]
- Carleson, L.; Gamelin, T.W. Complex Dynamics; Universitext: Tracts in Mathematics; Springer: New York, NY, USA, 1993. [Google Scholar]
- Douady, A. Algorithms for computing angles in the Mandelbort set. In Chaotic Dynamics and Fractals; Academic Press: Cambridge, MA, USA, 1986; pp. 155–168. [Google Scholar]
- Zakeri, S. Biaccessibility in quadratic Julia Sets. Ergod. Theory Dyn. Syst. 2000, 20, 1859–1883. [Google Scholar] [CrossRef]
- Douady, A.; Hubbard, J.H. Étude dynamique des polynômes complexes. In Publications Mathématiques d’Orsay; Mathematical Publications of Orsay; Université de Paris-Sud, Département de Mathématiques: Orsay, France, 1984. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blé, G.; González, D. Optimization of Thurston’s Core Entropy Algorithm for Polynomials with a Critical Point of Maximal Order. Entropy 2018, 20, 695. https://doi.org/10.3390/e20090695
Blé G, González D. Optimization of Thurston’s Core Entropy Algorithm for Polynomials with a Critical Point of Maximal Order. Entropy. 2018; 20(9):695. https://doi.org/10.3390/e20090695
Chicago/Turabian StyleBlé, Gamaliel, and Domingo González. 2018. "Optimization of Thurston’s Core Entropy Algorithm for Polynomials with a Critical Point of Maximal Order" Entropy 20, no. 9: 695. https://doi.org/10.3390/e20090695
APA StyleBlé, G., & González, D. (2018). Optimization of Thurston’s Core Entropy Algorithm for Polynomials with a Critical Point of Maximal Order. Entropy, 20(9), 695. https://doi.org/10.3390/e20090695




