Study on a Novel Fault Damage Degree Identification Method Using High-Order Differential Mathematical Morphology Gradient Spectrum Entropy
Abstract
:1. Introduction
2. Basic Methods
2.1. Mathematical Morphology
2.2. MultiScale Mathematical Morphology
2.3. Mathematical Morphology Gradient Spectrum
2.4. Mathematicall Morphology Gradient Spectrum Entropy (MMGSE)
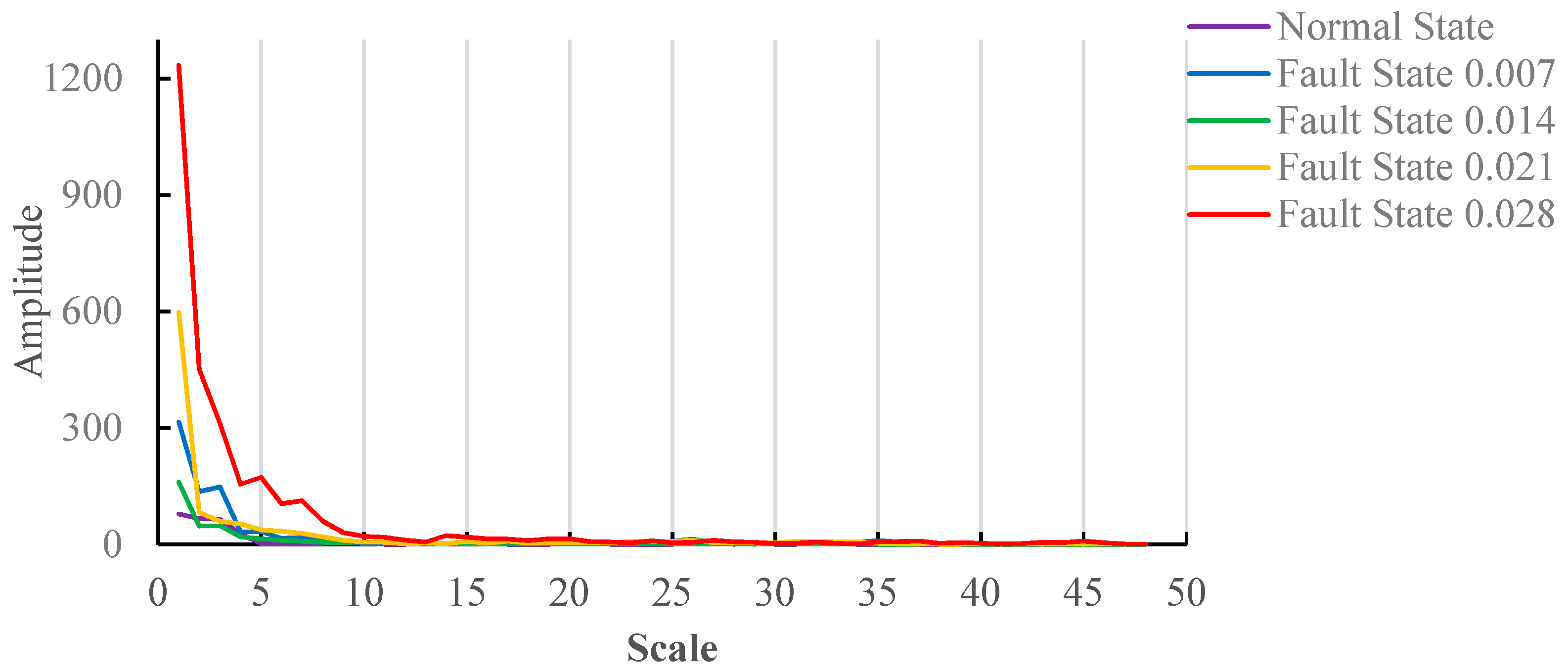
3. High-Order Differential Mathematical Morphological Gradient Spectrum Entropy
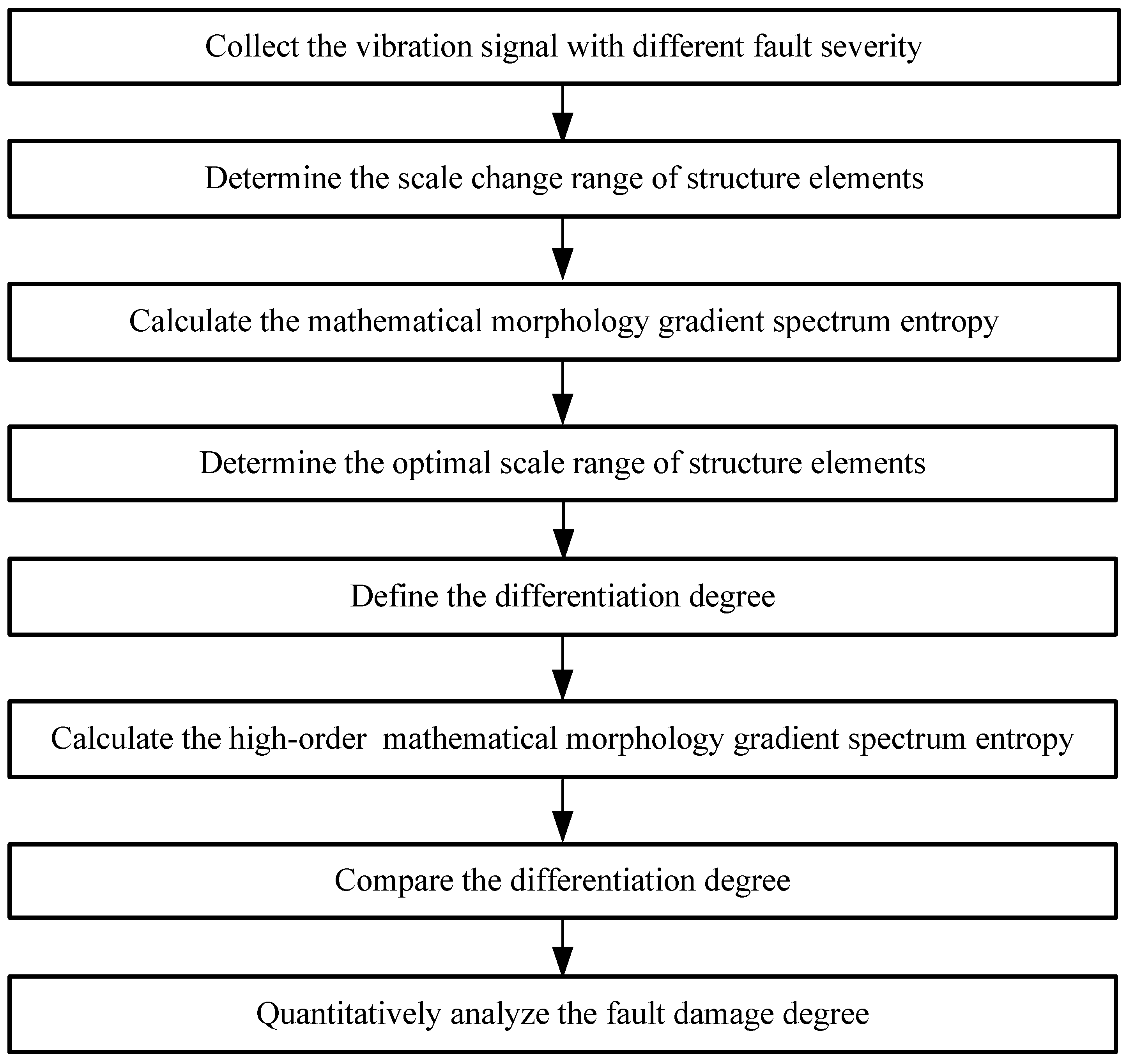
4. A Novel Fault Damage Degree Identification Method
5. Data Sources and Experimental Environment
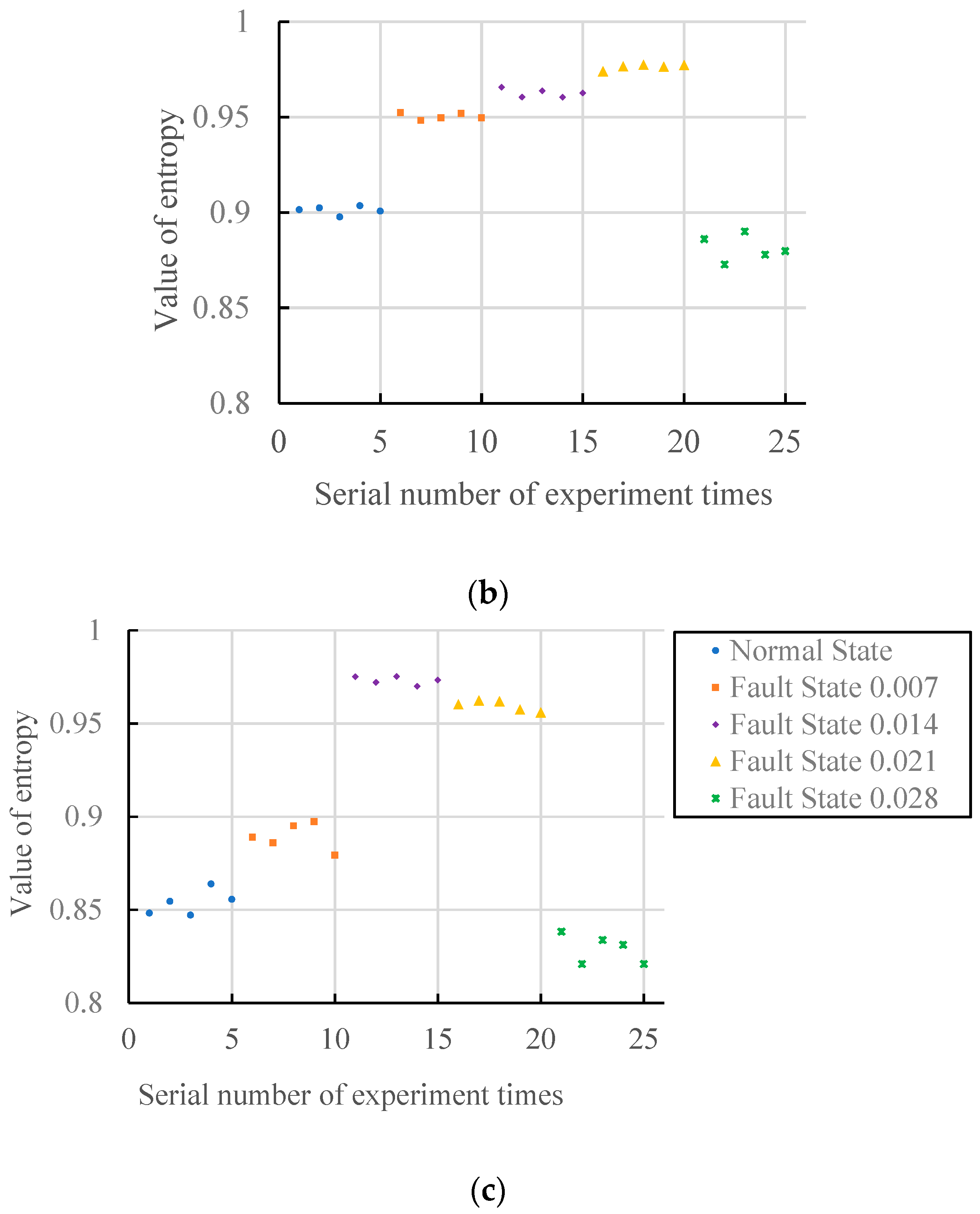
6. Analysis of the Influence of Damage Degree Identification of Bearing Fault under a Changing Scale
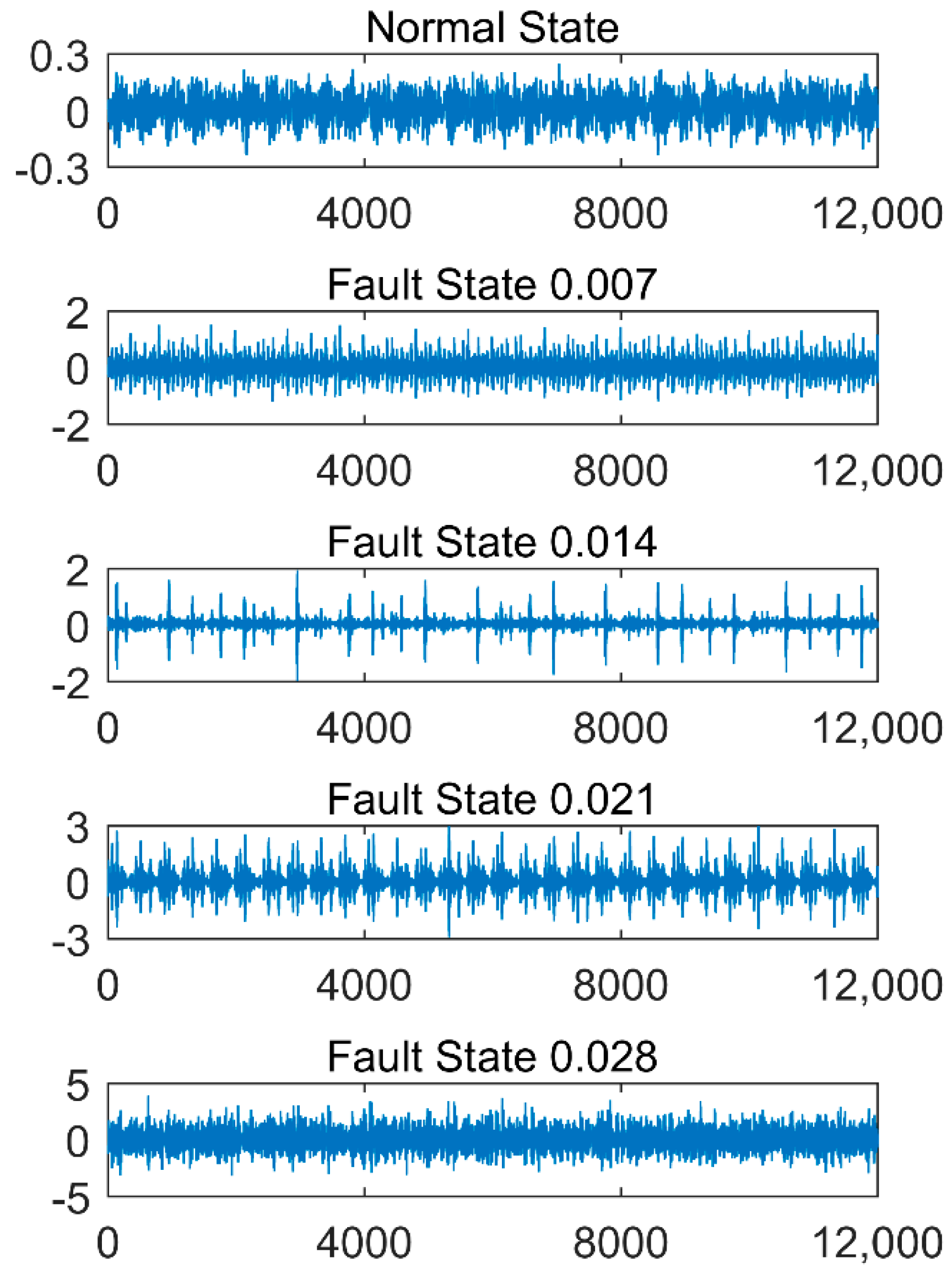
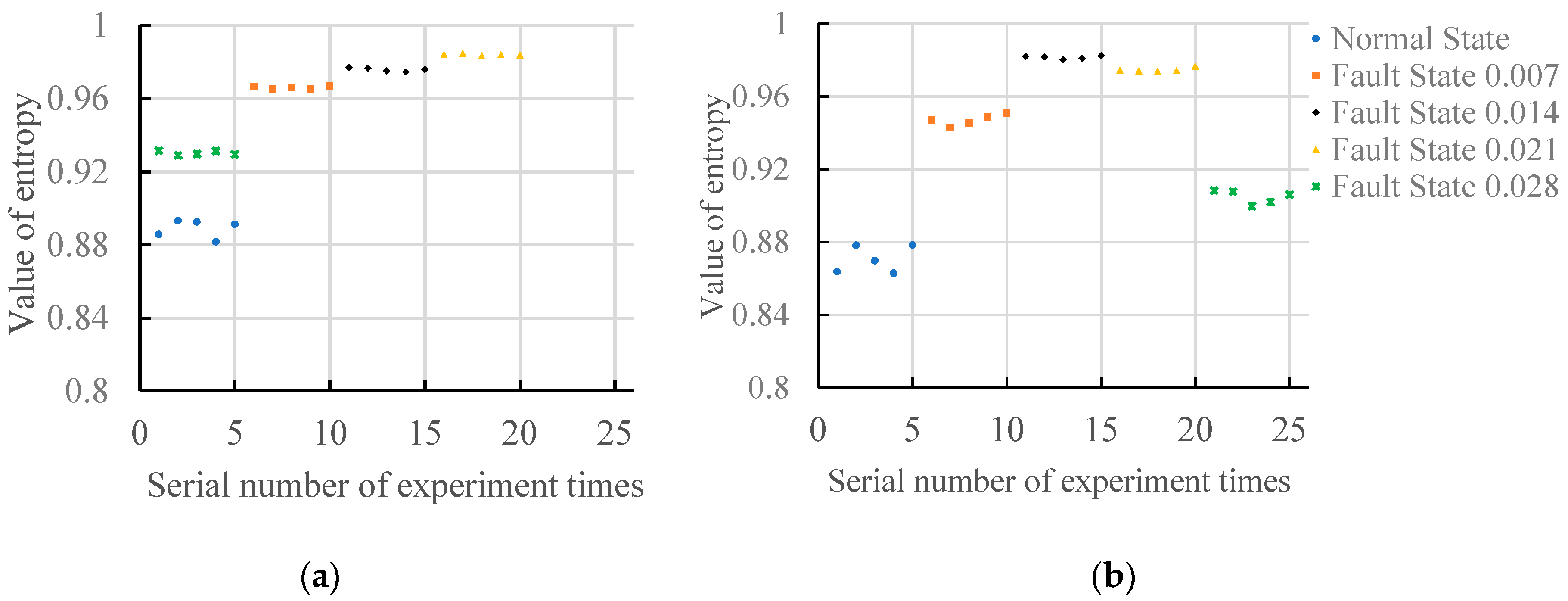
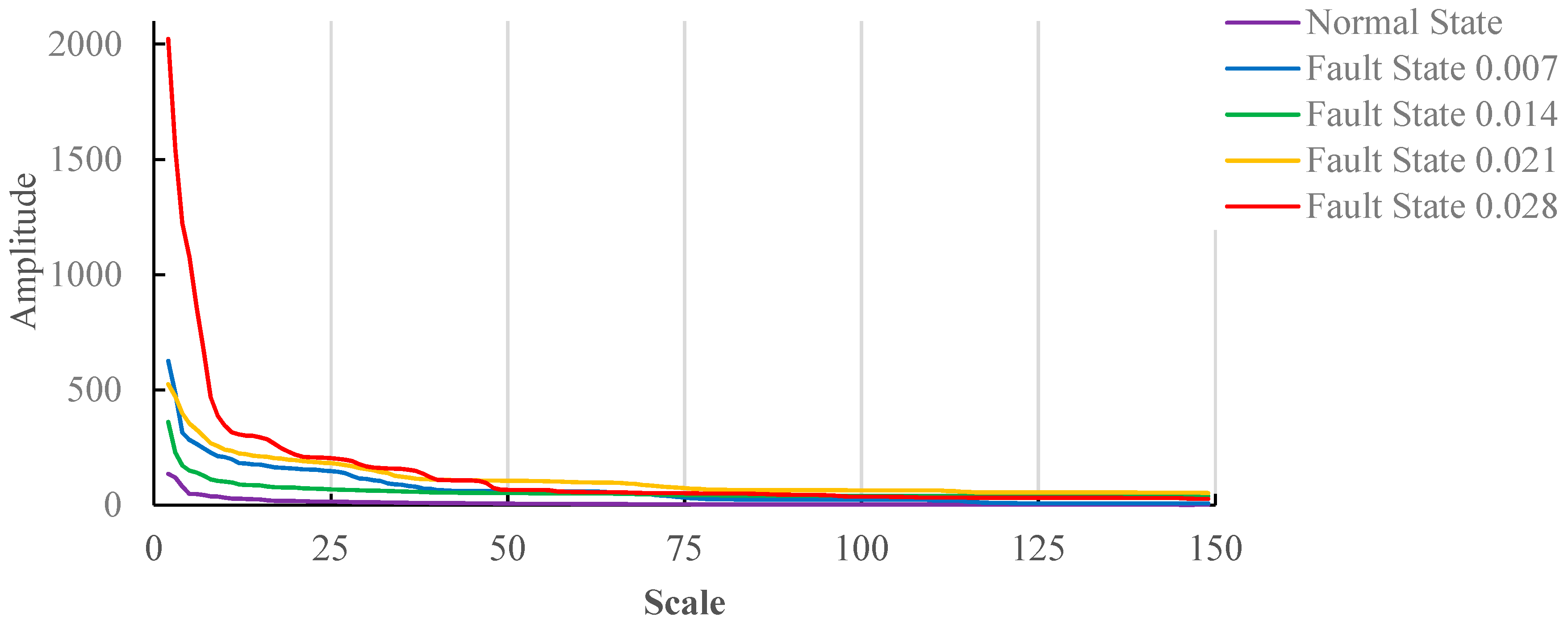
6.1. Analysis of Vibration Signals of Motors with No-Load
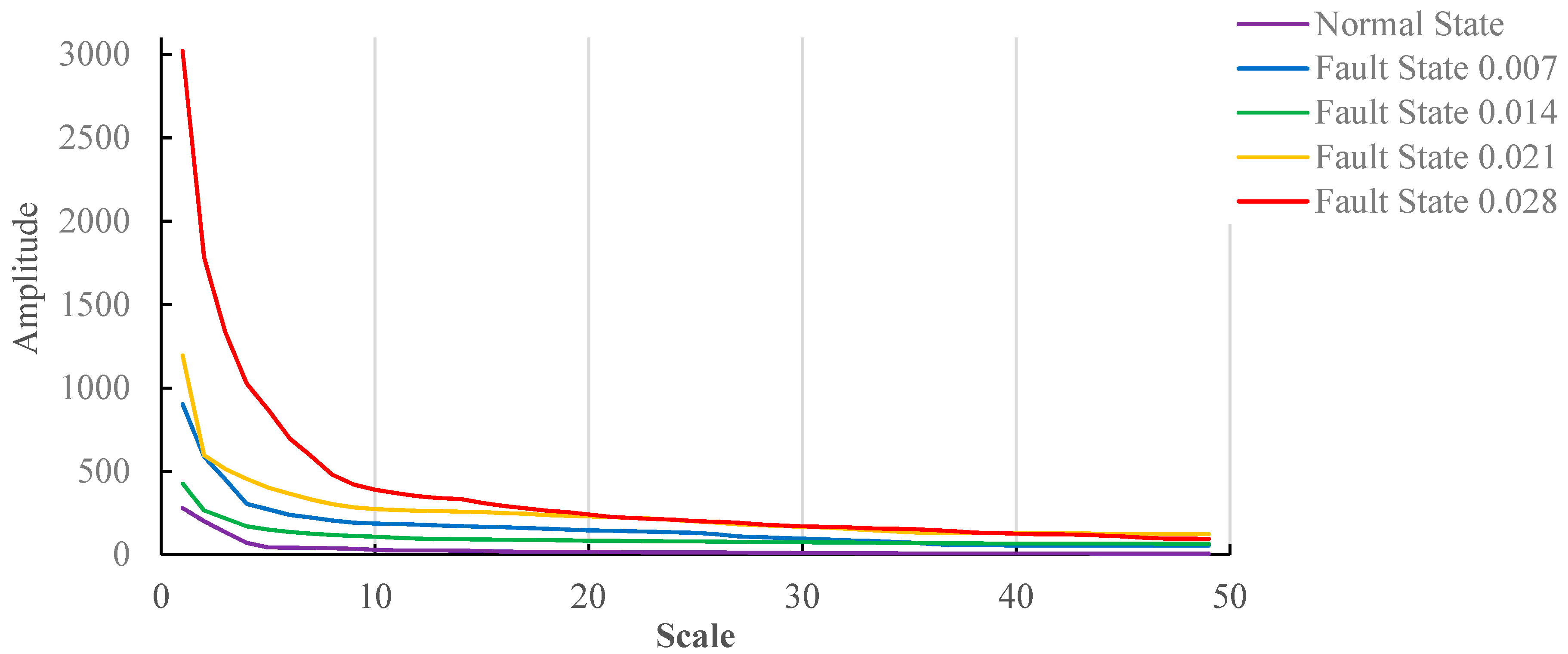
- (1)
- There is a non-negative lower bound in a whole monotone decreasing sequence.
- (2)
- The front value of the gradient spectrum varies greatly, and the back value of the gradient spectrum varies a little (up to zero).
- (3)
- The gradient spectrum is discrete.
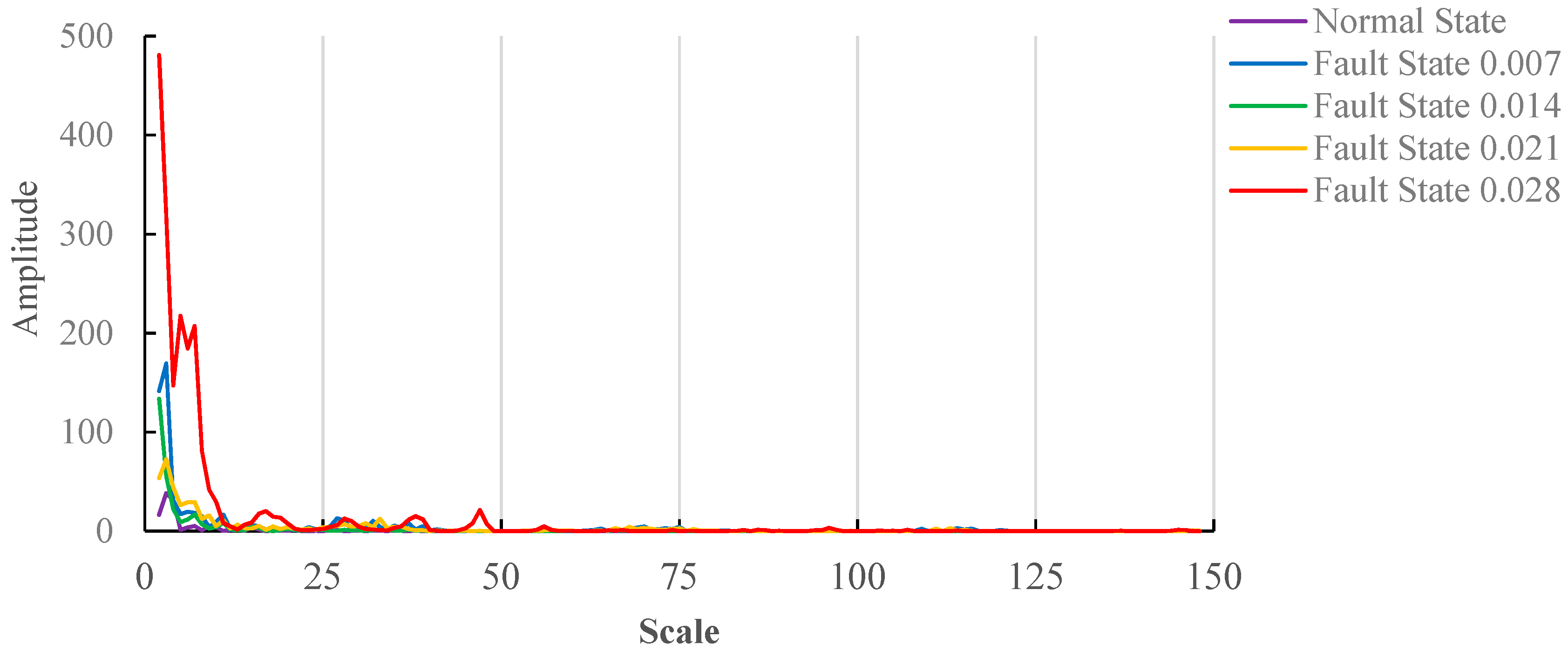
6.2. Analysis of Vibration Signals of Motors with Load(3HP)
6.3. Comprehensive Analysis of Experimental Results
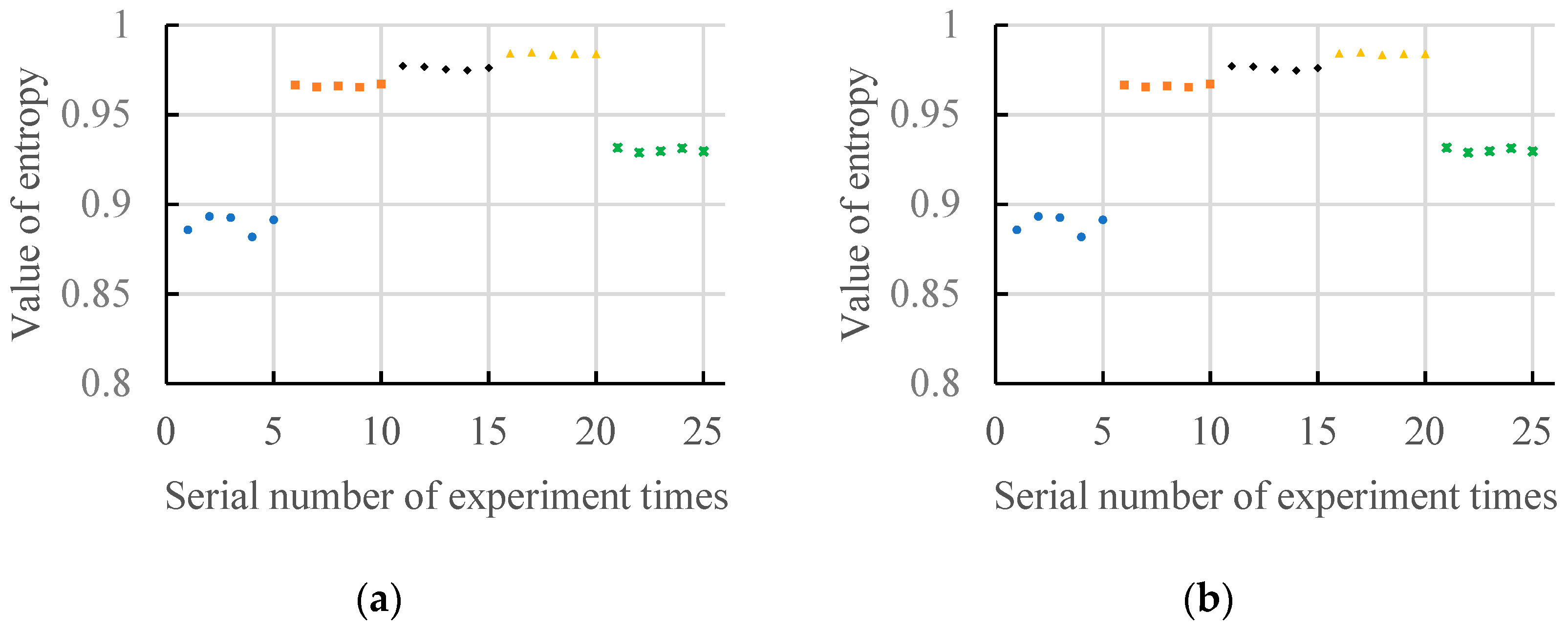
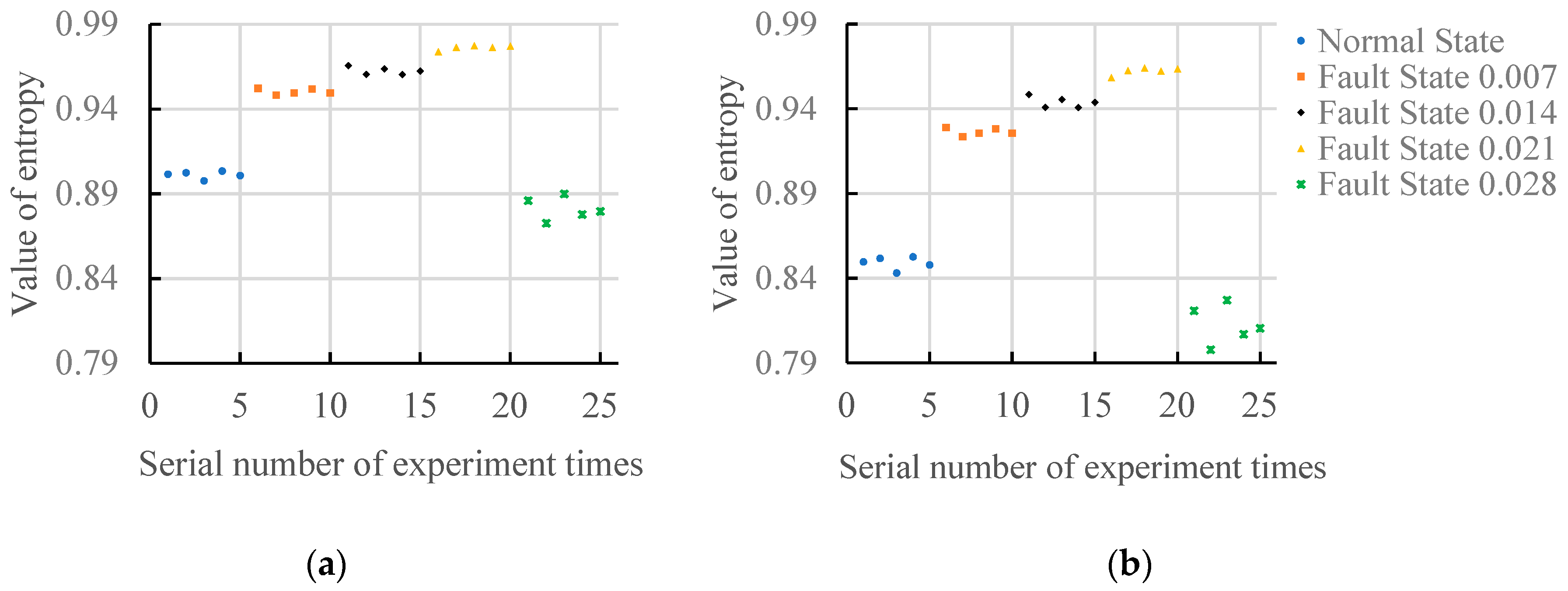
7. Application Case Analysis
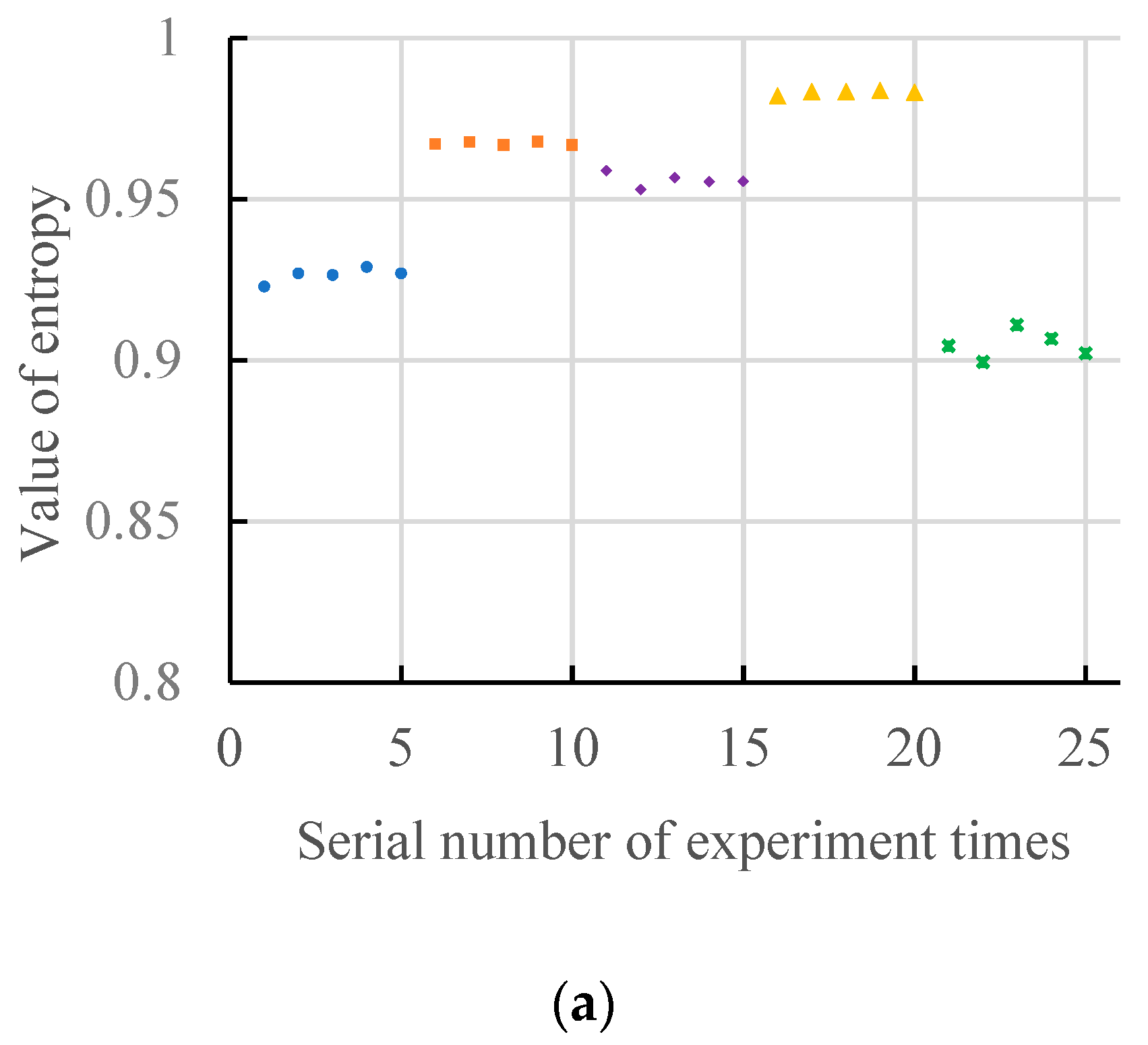
7.1. Analysis of Motors with No-Load State
7.2. Analysis of Motors with the Load(3HP) State
7.3. Comprehensive Analysis of Experimental Results
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Basaran, C.; Yan, C.Y. A Thermodynamic framework for damage mechanics of solder joints. J. Electron. Packag. 1998, 120, 379–384. [Google Scholar] [CrossRef]
- Frosini, L.; Bassi, E. Stator current and motor efficiency as indicators for different types of bearing faults in induction motors. IEEE Trans. Ind. Electron. 2010, 57, 244–251. [Google Scholar] [CrossRef]
- Begg, S.E.; Fowkes, N.; Stemler, T. Fault detection in vibration systems: Identifying damaged moorings. Ocean Eng. 2018, 164, 577–589. [Google Scholar] [CrossRef]
- Miraskari, M.; Hemmati, F.; Alqaradawi, M.Y. Linear stability analysis of finite length journal bearings in laminar and turbulent regimes. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 231, 1254–1267. [Google Scholar] [CrossRef]
- Frosini, L.; Harlisca, C.; Szabo, L. Induction machine bearing fault detection by means of statistical processing of the stray flux measurement. IEEE Trans. Ind. Electron. 2015, 62, 1846–1854. [Google Scholar] [CrossRef]
- Zhang, J.; Ragab, T.; Basaran, C. Influence of vacancy defects on the damage mechanics of graphene nanoribbons. Int. J. Damage Mech. 2017, 26, 28–48. [Google Scholar] [CrossRef]
- Szabo, L.; Ruba, M.; Szasz, C. Fault tolerant bio-inspired system controlled modular switched reluctance machine. Automatika 2014, 55, 53–63. [Google Scholar] [CrossRef]
- Temfack, T.; Basaran, C. Experimental verification of thermodynamic fatigue life prediction model using entropy as damage metric. Mater. Sci. Technol. 2015, 31, 1627–1632. [Google Scholar] [CrossRef]
- Hemmati, F.; Alqaradawi, M.; Gadala, M.S. Rolling element bearing fault diagnostics using acoustic emission technique and advanced signal processing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 64–77. [Google Scholar] [CrossRef]
- Miraskari, M.; Hemmati, F.; Jalali, A. A robust modification to the universal cavitation algorithm in journal bearings. J. Tribol.-Trans. ASME 2017, 139, 031703. [Google Scholar] [CrossRef]
- Jalan, A.K.; Mohanty, A.R. Model based fault diagnosis of a rotor-bearing system for misalignment and unbalance under steady-state condition. J. Sound Vib. 2009, 327, 604–622. [Google Scholar] [CrossRef]
- Sudhaker, G.N.D.S.; Sekhar, A.S. Identification of unbalance in a rotor system. J. Sound Vib. 2011, 330, 2299–2313. [Google Scholar] [CrossRef]
- Lal, M.; Tiwari, R. Multi-fault identification in simple rotor-bearing-coupling systems based on forced response measurements. Mech. Mach. Theory 2012, 51, 87–109. [Google Scholar] [CrossRef]
- Cui, L.; Zhang, Y.; Zhang, F.; Zhang, J.; Lee, S. Vibration response mechanism of faulty outer race rolling element bearings for quantitative analysis. J. Sound Vib. 2016, 364, 67–76. [Google Scholar] [CrossRef]
- Zhao, S.F.; Lin, L.; Xu, G.H.; Wang, J.; Zhang, W.M. Quantitative diagnosis of a spall-like fault of a rolling element bearing by empirical mode decomposition and the approximate entropy method. Mech. Syst. Signal Process. 2013, 40, 154–177. [Google Scholar] [CrossRef]
- Jü, H.; Shen, C.Q.; Huang, W.G.; Li, S.; Zhu, Z.K. Quantitative diagnosis of bearing fault based on support vector regression. J. Vib. Meas. Diagn. 2014, 34, 767–771. (In Chinese) [Google Scholar]
- Zhang, D.J.; Wu, Q.H.; Zhang, J.F. Accurate fault location based on transients extraction using mathematical morphology. Electron. Lett. 2002, 38, 1583–1585. [Google Scholar] [CrossRef]
- Zhang, L.J.; Xu, J.W.; Yang, H.H. Multiscale morphology analysis and its application to fault diagnosis. Mech. Syst. Signal Process. 2008, 22, 597–610. [Google Scholar] [CrossRef]
- Luo, J.S.; Yu, D.J.; Liang, M. Gear fault detection under time-varying rotating speed via joint application of multiscale chirplet path pursuit and multiscale morphology analysis. Struct. Health Monit. 2012, 11, 526–537. [Google Scholar] [CrossRef]
- Li, C.; Liang, M. Continuous-scale mathematical morphology-based optimal scale band demodulation of impulsive feature for bearing defect diagnosis. J. Sound Vib. 2012, 331, 5864–5879. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, Z.W.; Sun, W. A new structuring element for multi-scale morphology analysis and its application in rolling element bearing fault diagnosis. J. Vib. Control 2015, 21, 765–789. [Google Scholar] [CrossRef]
- Wang, S.T.; Zhang, J.L.; Li, Y.Y. Rotating machinery fault diagnosis based on mathematical morphology and fuzzy clustering. Chin. J. Sci. Instrum. 2012, 33, 1054–1061. [Google Scholar]
- Gong, T.K.; Yuan, Y.B.; Yuan, X.H. Application of optimized multiscale mathematical morphology for bearing fault diagnosis. Meas. Sci. Technol. 2017, 28, 045401. [Google Scholar] [CrossRef]
- Li, Y.B.; Xu, M.Q.; Liang, X.H. Application of bandwidth EMD and adaptive multiscale morphology analysis for incipient fault diagnosis of rolling bearings. IEEE Trans. Ind. Electron. 2017, 64, 6506–6517. [Google Scholar] [CrossRef]
- Deng, F.Y.; Yang, S.P.; Tang, G.J. Self adaptive multi-scale morphology AVG-Hat filter and its application to fault feature extraction for wheel bearing. Meas. Sci. Technol. 2017, 28, 045011. [Google Scholar] [CrossRef]
- Xu, T.L.; Yin, Z.J.; Cai, D.Y. Fault diagnosis for rotating machinery based on Local Mean Decomposition morphology filtering and Least Square Support Vector Machine. J. Intell. Fuzzy Syst. 2017, 32, 2061–2070. [Google Scholar] [CrossRef]
- Liu, P.; Li, H.R.; Xu, B.H. A performance degradation feature extraction method and its application based on mathematical morphological gradient spectrum entropy. J. Vib. Shock 2016, 35, 86–90. [Google Scholar]
- Qu, D.F.; Tveranger, J.; Fachri, M. Influence of deformation-band fault damage zone on reservoir performance. Interpretation 2017, 5, SP41–SP56. [Google Scholar] [CrossRef]
- Chen, Y.H.; Peng, G.L.; Xie, C.H. ACDIN: Bridging the gap between artificial and real bearing damages for bearing fault diagnosis. Neurocomputing 2018, 294, 61–71. [Google Scholar] [CrossRef]
- Li, G.Y.; Liang, X.H.; Li, F.Y. Model-based analysis and fault diagnosis of a compound planetary gear set with damaged sun gear. J. Mech. Sci. Technol. 2018, 32, 3081–3096. [Google Scholar] [CrossRef]
- Yao, W.; Basaran, C. Damage mechanics of electromigration and thermomigration in lead-free solder alloys under alternating current: An experimental study. Int. J. Damage Mech. 2014, 23, 203–221. [Google Scholar] [CrossRef]
- Deng, W.; Yao, R.; Zhao, H.M.; Yang, X.H.; Li, G.Y. A novel intelligent diagnosis method using optimal LS-SVM with improved PSO algorithm. Soft Comput. 2017. [Google Scholar] [CrossRef]
- Basaran, C.; Nie, S. An irreversible thermodynamics theory for damage mechanics of solids. Int. J. Damage Mech. 2004, 13, 205–223. [Google Scholar] [CrossRef]
- Deng, W.; Zhao, H.M.; Zou, L.; Li, G.Y.; Yang, X.H.; Wu, D.Q. A novel collaborative optimization algorithm in solving complex optimization problems. Soft Comput. 2017, 21, 4387–4398. [Google Scholar] [CrossRef]
- Sosnovskiy, L.; Sherbakov, S. A model of mechanothermodynamic entropy in tribology. Entropy 2017, 19, 115. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, S.J.; Zhao, H.M.; Yang, X.H. A novel fault diagnosis method based on integrating empirical wavelet transform and fuzzy entropy for motor bearing. IEEE Access 2018. [Google Scholar] [CrossRef]
- Hemmati, F.; Alqaradawi, M.; Gadala, M.S. Optimized statistical parameters of acoustic emission signals for monitoring of rolling element bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 897–906. [Google Scholar] [CrossRef]
- Deng, W.; Zhao, H.M.; Yang, X.H.; Xiong, J.X.; Sun, M.; Li, B. Study on an improved adaptive PSO algorithm for solving multi-objective gate assignment. Appl. Soft Comput. 2017, 59, 288–302. [Google Scholar] [CrossRef]
- Yao, W.; Basaran, C. Computational damage mechanics of electromigration and thermomigration. J. Appl. Phys. 2013, 114, 103708. [Google Scholar] [CrossRef]
- Zhao, H.M.; Sun, M.; Deng, W.; Yang, X.H. A new feature extraction method based on EEMD and multi-scale fuzzy entropy for motor bearing. Entropy 2017, 19, 14. [Google Scholar] [CrossRef]
- Hemmati, F.; Orfali, W.; Gadala, M.S. Roller bearing acoustic signature extraction by wavelet packet transform, applications in fault detection and size estimation. Appl. Acoust. 2016, 104, 101–118. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Matheron, G.; Serra, J. The birth of mathematical morphology. In Proceedings of the 6th International Symposium on Mathematical Morphology, Sydney, Australia, 3–5 April 2002; Csiro Publishing: Clayton, Australia, 2002. [Google Scholar]
- Bai, X.Z.; Zhou, F.G.; Xue, B.D. Discrimination ability improvement of invariant moment based on multi-scale mathematical morphology. Optik 2013, 124, 1314–1319. [Google Scholar] [CrossRef]
- Bearing Data Center. Available online: http://csegroups.case.edu/bearingdatacenter/home (accessed on 6 July 2016).
| Fault Damage Degree | Mean Value | Discrimination | ||
|---|---|---|---|---|
| Normal state | 0.8352 | 0.8889 | / | / |
| Fault damage degree 0.007 | 0.9442 | 0.9660 | 0.1090 | 0.0771 |
| Fault damage degree 0.014 | 0.9552 | 0.9759 | 0.0110 | 0.0099 |
| Fault damage degree 0.021 | 0.9677 | 0.9840 | 0.0125 | 0.0081 |
| Fault damage degree 0.028 | 0.8626 | 0.9302 | −0.1051 | −0.0538 |
| Fault Damage Degree | Mean Value | Discrimination | ||
|---|---|---|---|---|
| Normal state | 0.8221 | 0.9011 | / | / |
| Fault damage degree 0.007 | 0.9100 | 0.9503 | 0.0879 | 0.0492 |
| Fault damage degree 0.014 | 0.9387 | 0.9626 | 0.0287 | 0.0123 |
| Fault damage degree 0.021 | 0.9543 | 0.9763 | 0.0156 | 0.0137 |
| Fault damage degree 0.028 | 0.7831 | 0.8813 | −0.1712 | −0.0950 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Yao, R.; Xu, L.; Yuan, Y.; Li, G.; Deng, W. Study on a Novel Fault Damage Degree Identification Method Using High-Order Differential Mathematical Morphology Gradient Spectrum Entropy. Entropy 2018, 20, 682. https://doi.org/10.3390/e20090682
Zhao H, Yao R, Xu L, Yuan Y, Li G, Deng W. Study on a Novel Fault Damage Degree Identification Method Using High-Order Differential Mathematical Morphology Gradient Spectrum Entropy. Entropy. 2018; 20(9):682. https://doi.org/10.3390/e20090682
Chicago/Turabian StyleZhao, Huimin, Rui Yao, Ling Xu, Yu Yuan, Guangyu Li, and Wu Deng. 2018. "Study on a Novel Fault Damage Degree Identification Method Using High-Order Differential Mathematical Morphology Gradient Spectrum Entropy" Entropy 20, no. 9: 682. https://doi.org/10.3390/e20090682
APA StyleZhao, H., Yao, R., Xu, L., Yuan, Y., Li, G., & Deng, W. (2018). Study on a Novel Fault Damage Degree Identification Method Using High-Order Differential Mathematical Morphology Gradient Spectrum Entropy. Entropy, 20(9), 682. https://doi.org/10.3390/e20090682





