Assessing Time Series Reversibility through Permutation Patterns
Abstract
1. Introduction
2. Assessing Time Series Reversibility
2.1. Permutation Patterns
2.2. Time Reversibility of Permutation Patterns
2.3. Directed Horizontal Visibility Graphs
2.4. Markov Chain Approach
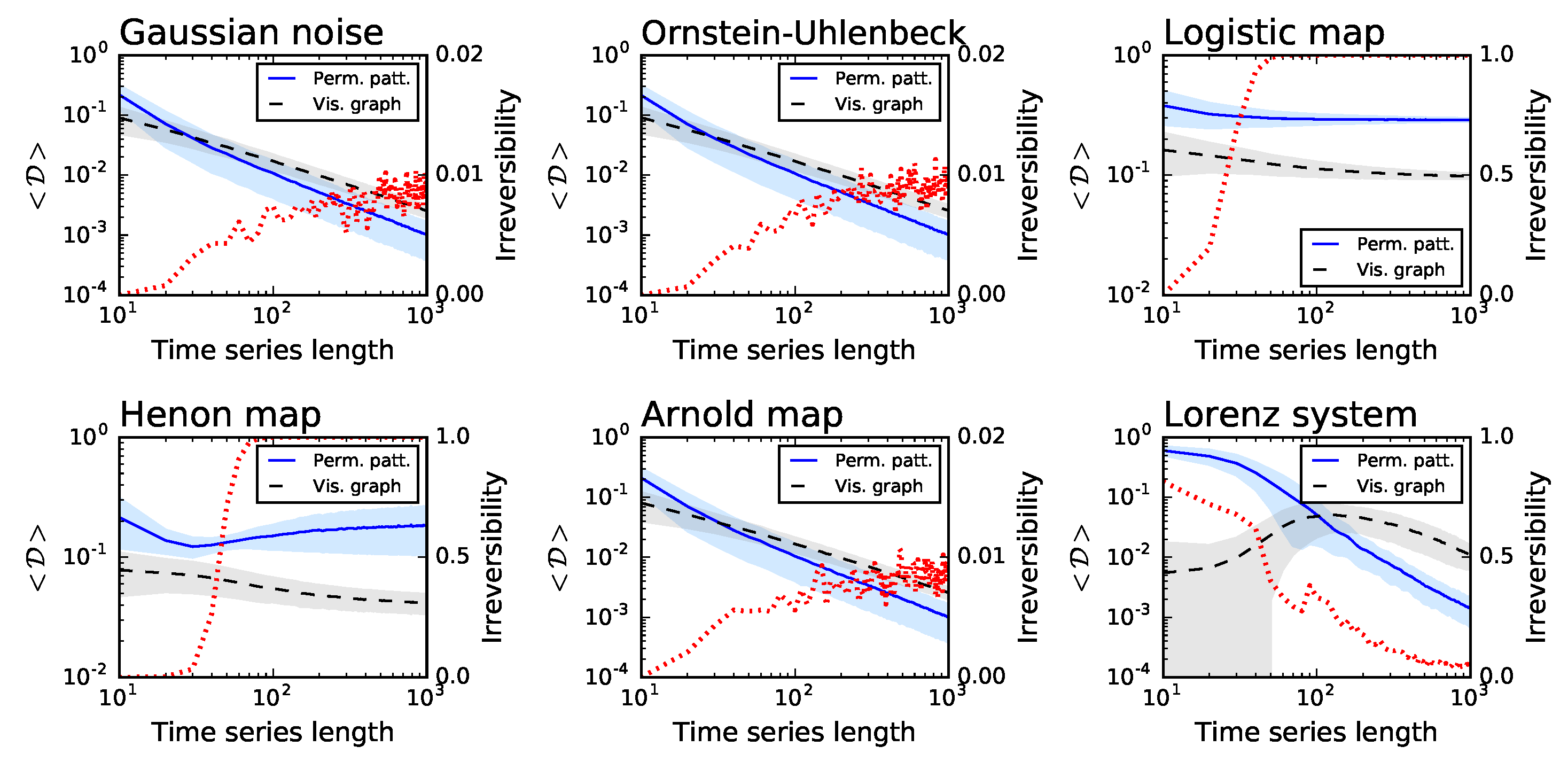
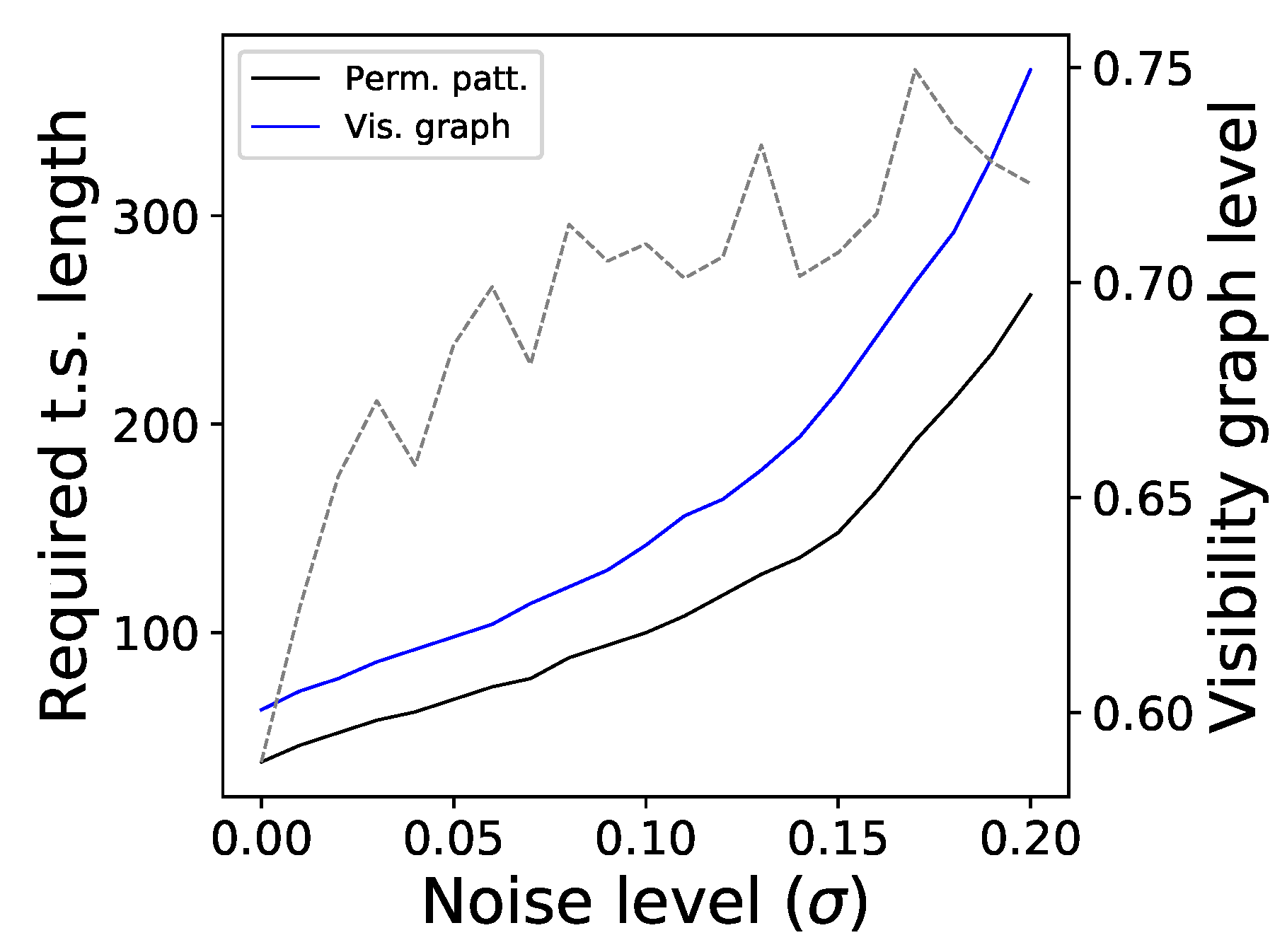
3. Validation with Synthetic Time Series
- Two reversible stochastic processes, namely a time series of values drawn from a Gaussian distribution , and an Ornstein–Uhlenbeck process, a mean-reverting linear Gaussian process T [41].
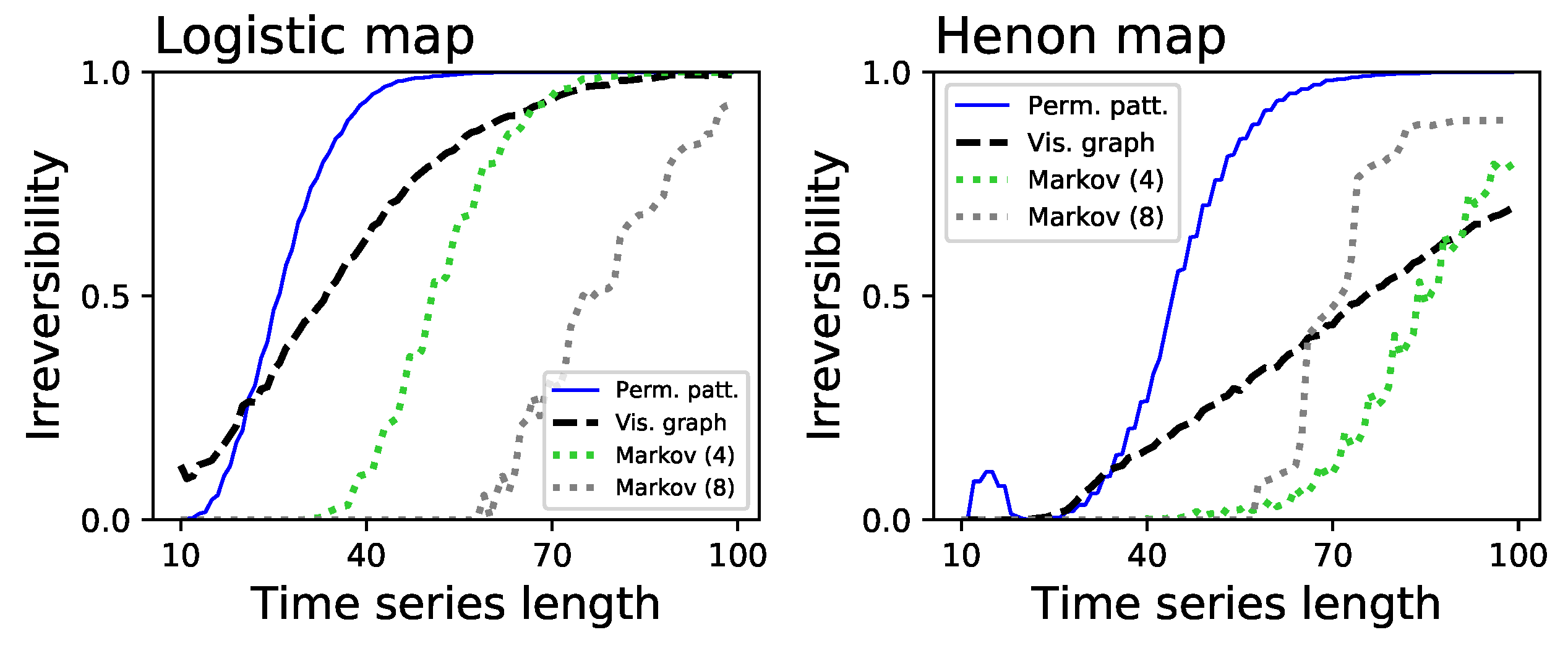
- Two dissipative chaotic maps, respectively, a logistic map (defined as , with ) and a Henon map (, , with and ). Dissipative systems are by definition irreversible [42].
- The Arnold Cat map, and example of a conservative chaotic map (. The analysed time series corresponds to the evolution of the x variable.
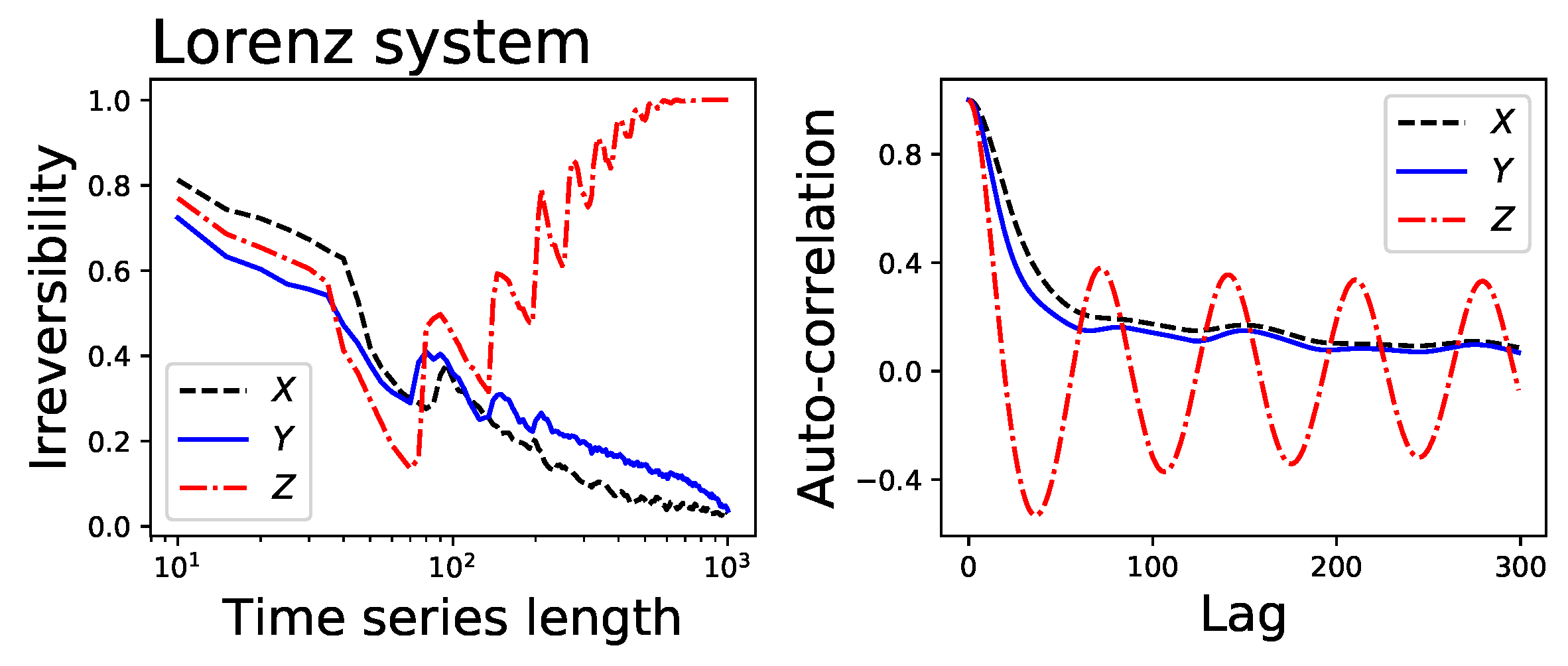
- The Lorenz chaotic system, defined as , , and (with , and , integration step of ). Unless otherwise stated, the analysed time series corresponds to the evolution of the x variable.
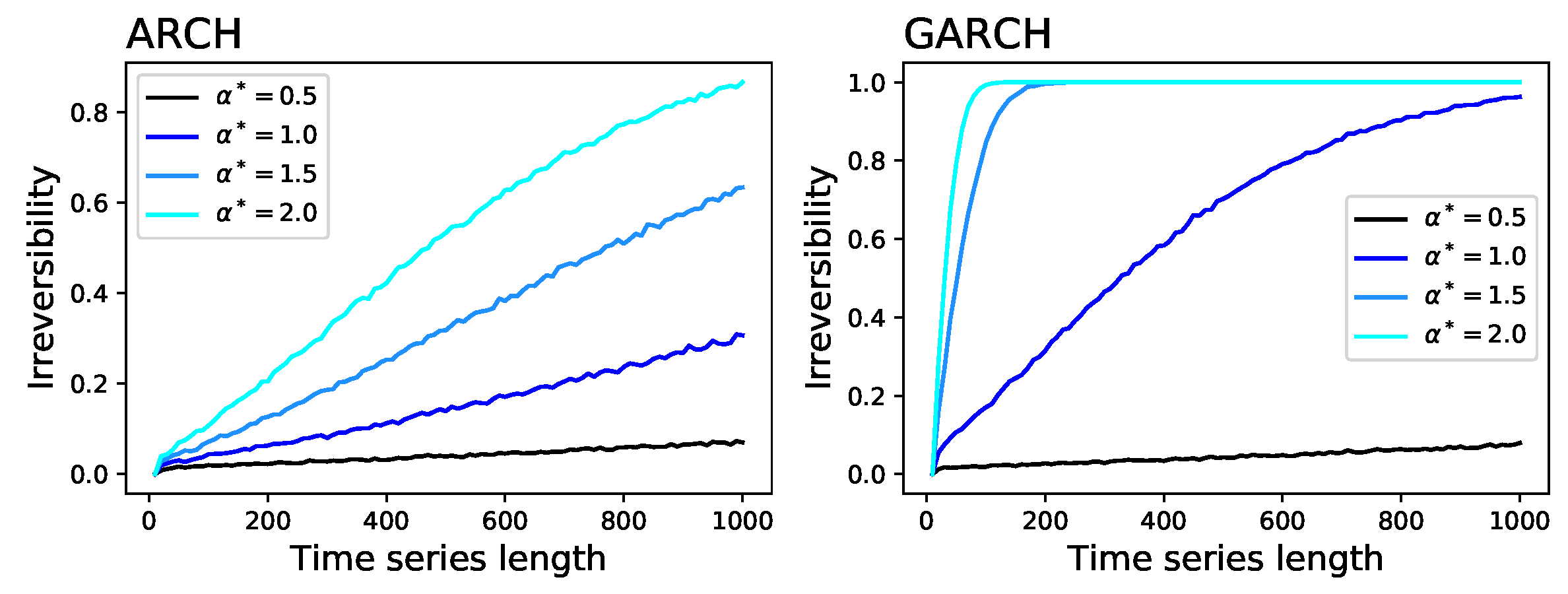
- Time series generated through an Autoregressive Conditional Heteroskedasticity (ARCH) model [43] defined as , with and being independent random numbers drawn from an uniform distribution . Note that is a parameter controlling the strength of the time dependence between present and past values of x, and hence its irreversibility.
- Time series generated through a Generalised Autoregressive Conditional Heteroskedasticity (GARCH) model [44] defined as , with and being independent random numbers drawn from an uniform distribution . Note that the difference with respect to the ARCH model resides in the fact that here depends directly on its past. As in the previous case, is controlling the time irreversibility of the model.
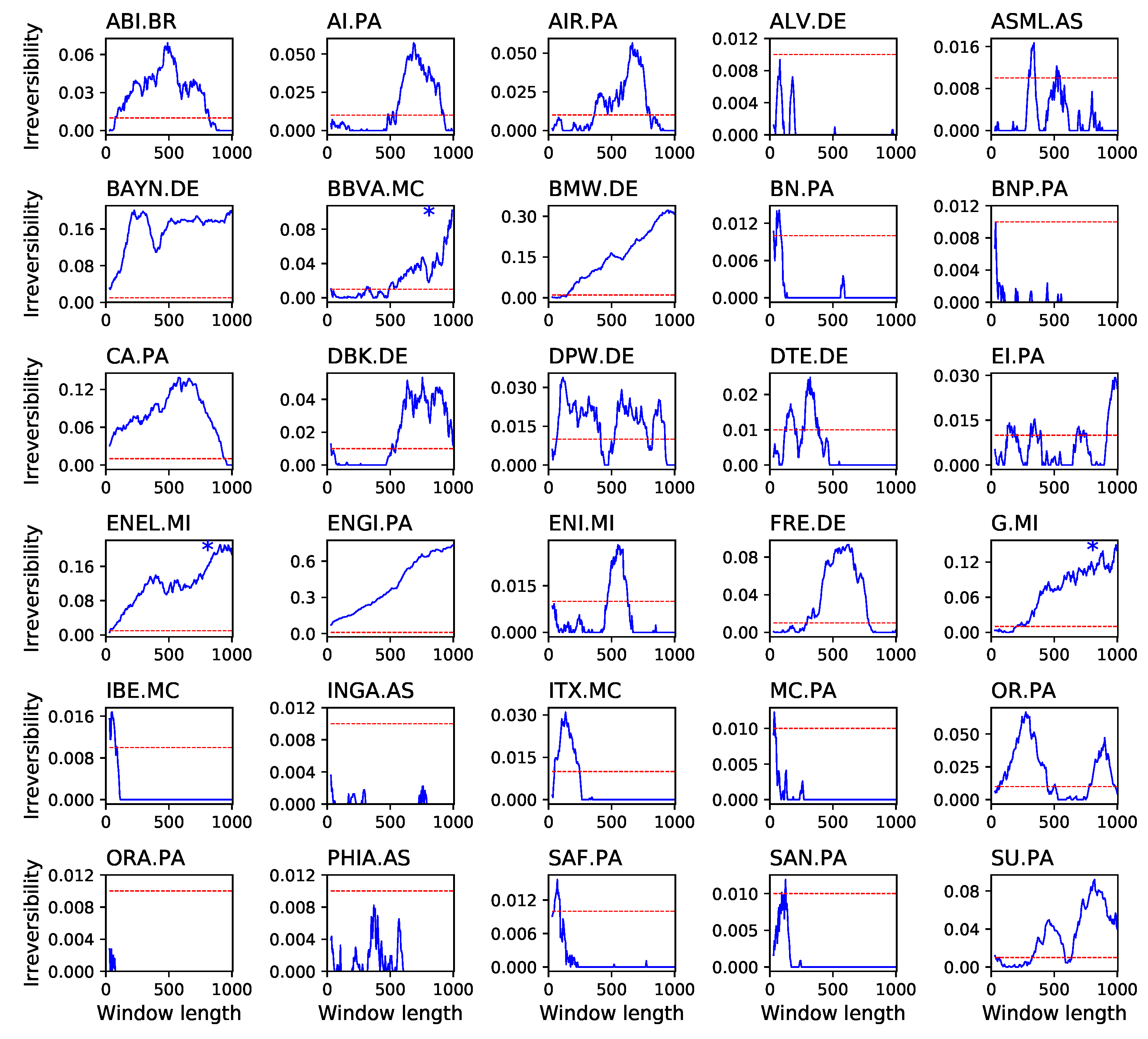
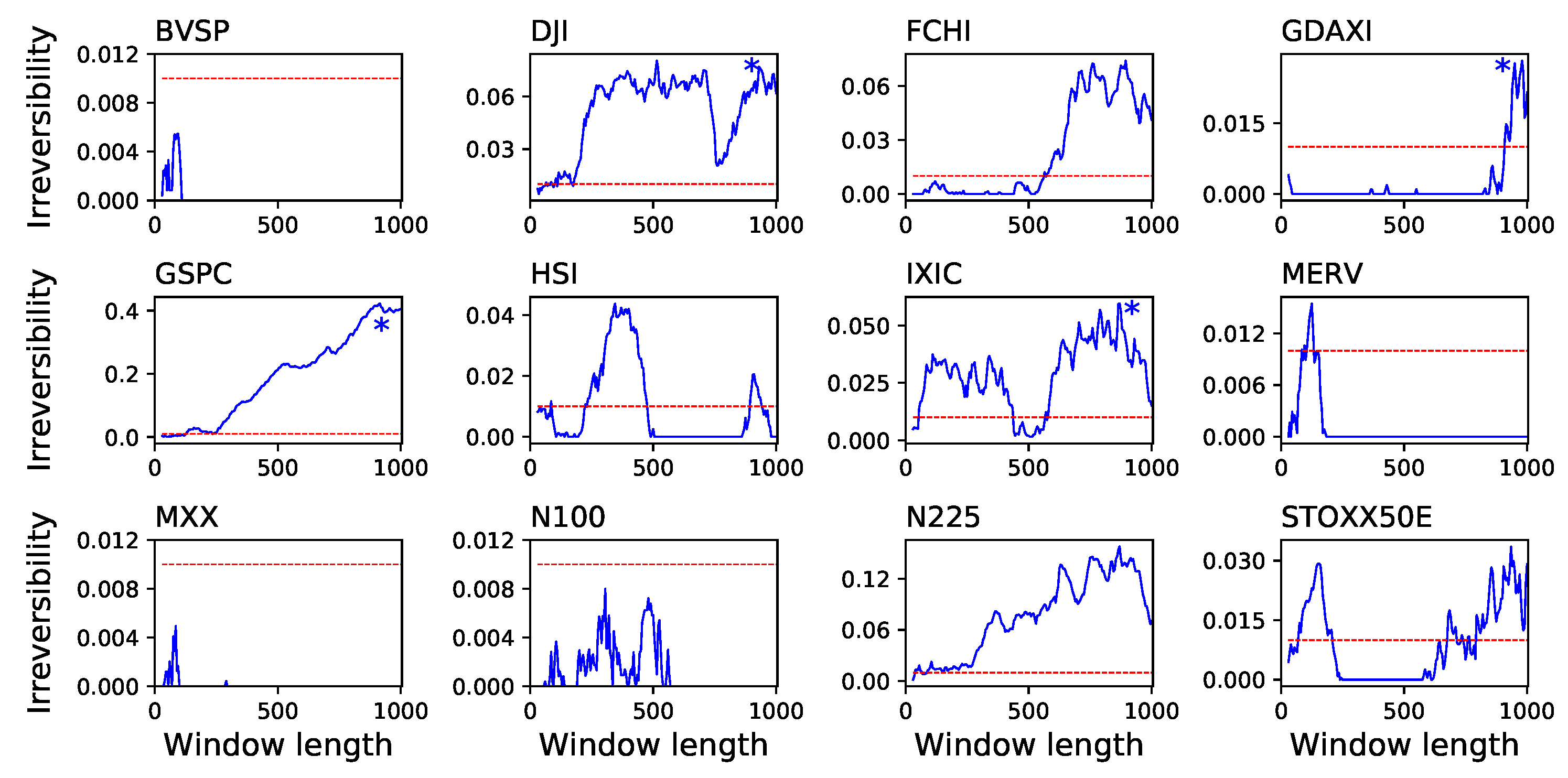
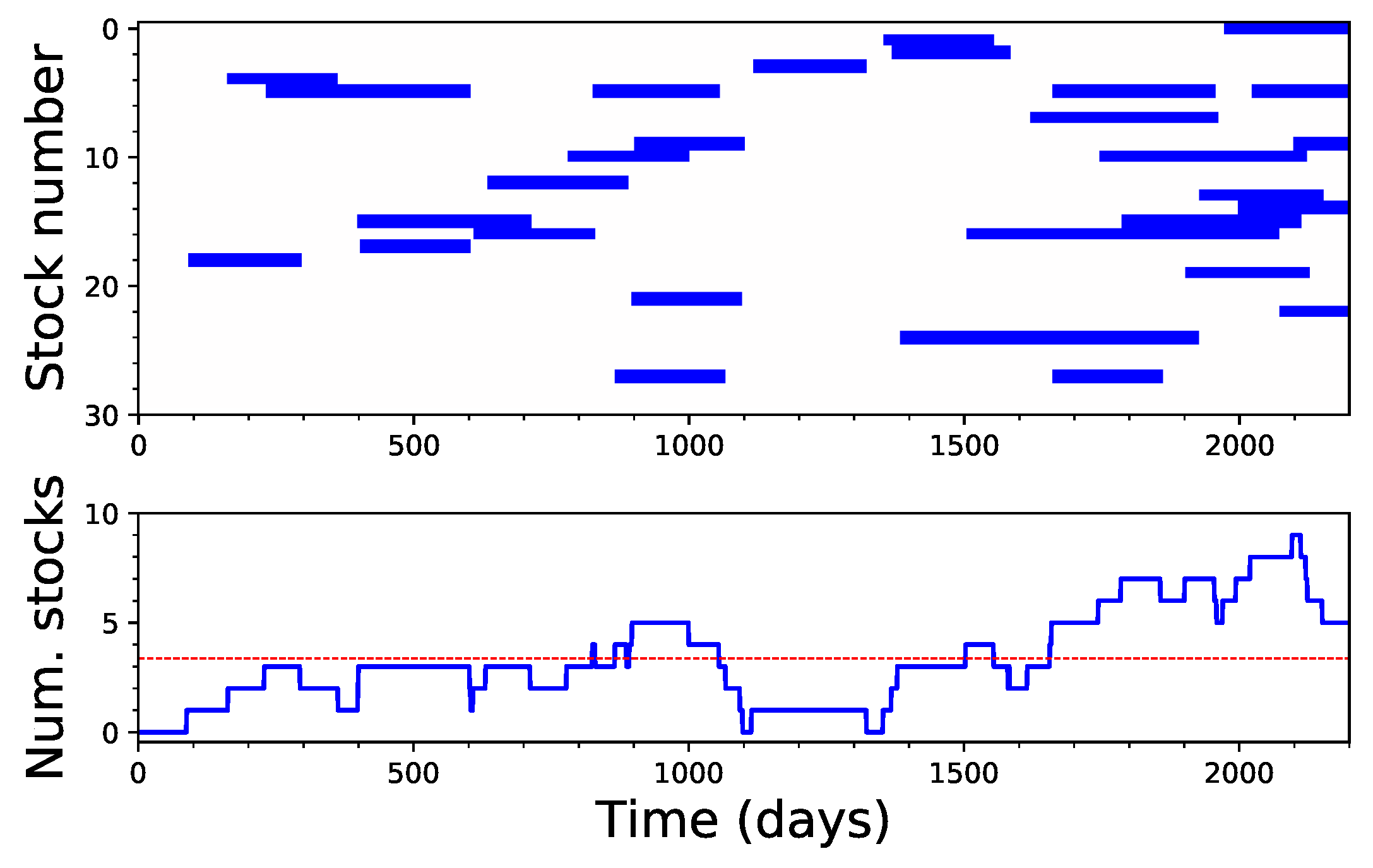
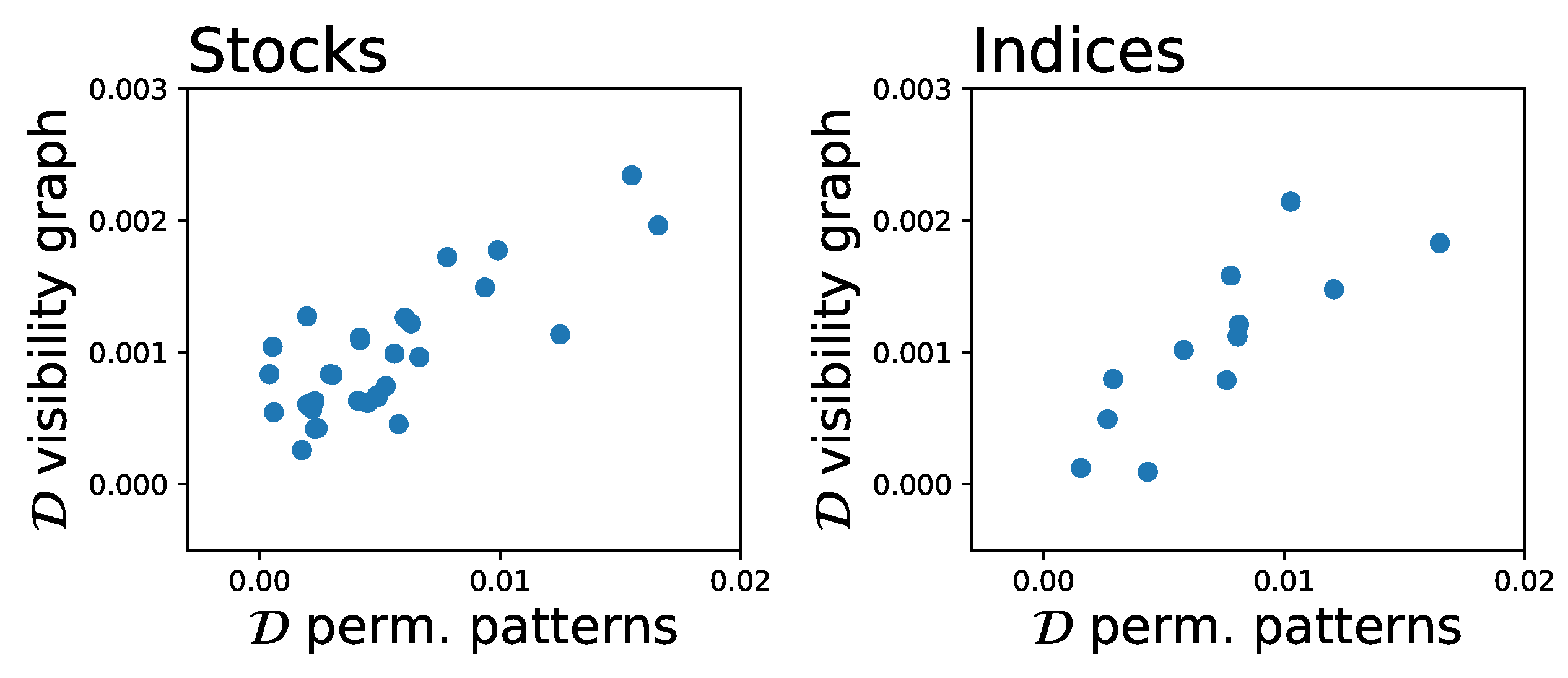
4. Application to Financial Time Series
5. Discussion and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Puglisi, A.; Villamaina, D. Irreversible effects of memory. Europhys. Lett. 2009, 88, 30004. [Google Scholar] [CrossRef]
- Xia, J.; Shang, P.; Wang, J.; Shi, W. Classifying of financial time series based on multiscale entropy and multiscale time irreversibility. Phys. A Stat. Mech. Appl. 2014, 400, 151–158. [Google Scholar] [CrossRef]
- Lawrance, A. Directionality and reversibility in time series. Int. Stat. Rev. 1991, 59, 67–79. [Google Scholar] [CrossRef]
- Stone, L.; Landan, G.; May, R.M. Detecting time’s arrow: A method for identifying nonlinearity and deterministic chaos in time-series data. Proc. R. Soc. Lond. B 1996, 263, 1509–1513. [Google Scholar] [CrossRef]
- Cox, D.R.; Hand, D.; Herzberg, A. Foundations of Statistical Inference, Theoretical Statistics, Time Series and Stochastic Processes; Cambridge University Press: London, UK, 2005. [Google Scholar]
- Roldán, É.; Parrondo, J.M. Estimating dissipation from single stationary trajectories. Phys. Rev. Lett. 2010, 105, 150607. [Google Scholar] [CrossRef] [PubMed]
- Daw, C.; Finney, C.; Kennel, M. Symbolic approach for measuring temporal “irreversibility”. Phys. Rev. E 2000, 62, 1912–1921. [Google Scholar] [CrossRef]
- Kennel, M.B. Testing time symmetry in time series using data compression dictionaries. Phys. Rev. E 2004, 69, 056208. [Google Scholar] [CrossRef] [PubMed]
- Lacasa, L.; Nunez, A.; Roldán, É.; Parrondo, J.M.; Luque, B. Time series irreversibility: A visibility graph approach. Eur. Phys. J. B 2012, 85, 217. [Google Scholar] [CrossRef]
- Donges, J.F.; Donner, R.V.; Kurths, J. Testing time series irreversibility using complex network methods. Europhys. Lett. 2013, 102, 10004. [Google Scholar] [CrossRef]
- Flanagan, R.; Lacasa, L. Irreversibility of financial time series: A graph-theoretical approach. Phys. Lett. A 2016, 380, 1689–1697. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Broken asymmetry of the human heartbeat: loss of time irreversibility in aging and disease. Phys. Rev. Lett. 2005, 95, 198102. [Google Scholar] [CrossRef] [PubMed]
- Squartini, F.; Arndt, P.F. Quantifying the stationarity and time reversibility of the nucleotide substitution process. Mol. Biol. Evol. 2008, 25, 2525–2535. [Google Scholar] [CrossRef] [PubMed]
- Ramsey, J.B.; Rothman, P. Time irreversibility and business cycle asymmetry. J. Money Credit Bank. 1996, 28, 1–21. [Google Scholar] [CrossRef]
- Chen, Y.T.; Chou, R.Y.; Kuan, C.M. Testing time reversibility without moment restrictions. J. Econometrics 2000, 95, 199–218. [Google Scholar] [CrossRef]
- Belaire-Franch, J.; Contreras, D. Tests for time reversibility: A complementarity analysis. Econ. Lett. 2003, 81, 187–195. [Google Scholar] [CrossRef]
- Chen, Y.T. Testing serial independence against time irreversibility. Stud. Nonlinear Dyn. Econ. 2003, 7, 1–30. [Google Scholar] [CrossRef]
- Racine, J.S.; Maasoumi, E. A versatile and robust metric entropy test of time-reversibility, and other hypotheses. J. Econom. 2007, 138, 547–567. [Google Scholar] [CrossRef]
- Sharifdoost, M.; Mahmoodi, S.; Pasha, E. A statistical test for time reversibility of stationary finite state Markov chains. Appl. Math. Sci. 2009, 52, 2563–2574. [Google Scholar]
- Zumbach, G. Time reversal invariance in finance. Quant. Financ. 2009, 9, 505–515. [Google Scholar] [CrossRef]
- De Sousa, A.M.Y.R.; Takayasu, H.; Takayasu, M. Detection of statistical asymmetries in non-stationary sign time series: Analysis of foreign exchange data. PLoS ONE 2017, 12, e0177652. [Google Scholar]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation entropy and its main biomedical and econophysics applications: A review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Fama, E.F. Efficient capital markets: A review of theory and empirical work. J. Financ. 1970, 25, 383–417. [Google Scholar] [CrossRef]
- Eom, C.; Oh, G.; Jung, W.S. Relationship between efficiency and predictability in stock price change. Phys. A Stat. Mech. Appl. 2008, 387, 5511–5517. [Google Scholar] [CrossRef]
- Campbell, J.Y.; Lo, A.W.C.; MacKinlay, A.C. The Econometrics of Financial Markets, 2nd ed.; Princeton University press: Princeton, NJ, USA, 1997. [Google Scholar]
- Lim, K.P. Ranking market efficiency for stock markets: A nonlinear perspective. Phys. A Stat. Mech. Appl. 2007, 376, 445–454. [Google Scholar] [CrossRef]
- Cajueiro, D.O.; Tabak, B.M. The Hurst exponent over time: Testing the assertion that emerging markets are becoming more efficient. Phys. A Stat. Mech. Appl. 2004, 336, 521–537. [Google Scholar] [CrossRef]
- Barunik, J.; Kristoufek, L. On Hurst exponent estimation under heavy-tailed distributions. Phys. A Stat. Mech. Appl. 2010, 389, 3844–3855. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Gu, R.; Cao, J.; Wang, H. Analysis of market efficiency for the Shanghai stock market over time. Phys. A: Stat. Mech. Appl. 2010, 389, 1635–1642. [Google Scholar] [CrossRef]
- Fong, W.M. Time reversibility tests of volume–volatility dynamics for stock returns. Econ. Lett. 2003, 81, 39–45. [Google Scholar] [CrossRef]
- Jiang, C.; Shang, P.; Shi, W. Multiscale multifractal time irreversibility analysis of stock markets. Phys. A Stat. Mech. Appl. 2016, 462, 492–507. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Fuglede, B.; Topsoe, F. Jensen-Shannon divergence and Hilbert space embedding. In Proceedings of the 2004 IEEE International Symposium on Information Theory, Chicago, IL, USA, 27 June–2 July 2004; p. 31. [Google Scholar]
- Lacasa, L.; Flanagan, R. Time reversibility from visibility graphs of nonstationary processes. Phys. Rev. E 2015, 92, 022817. [Google Scholar] [CrossRef] [PubMed]
- Lacasa, L.; Luque, B.; Ballesteros, F.; Luque, J.; Nuno, J.C. From time series to complex networks: The visibility graph. Proc. Nat. Acad. Sci. USA 2008, 105, 4972–4975. [Google Scholar] [CrossRef] [PubMed]
- Luque, B.; Lacasa, L.; Ballesteros, F.; Luque, J. Horizontal visibility graphs: Exact results for random time series. Phys. Rev. E 2009, 80, 046103. [Google Scholar] [CrossRef] [PubMed]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef] [PubMed]
- Costa, L.d.F.; Rodrigues, F.A.; Travieso, G.; Villas Boas, P.R. Characterization of complex networks: A survey of measurements. Adv. Phys. 2007, 56, 167–242. [Google Scholar] [CrossRef]
- Norris, J.R. Markov Chains, 2nd ed.; Cambridge University Press: London, UK, 1998. [Google Scholar]
- Weiss, G. Time-reversibility of linear stochastic processes. J. Appl. Probab. 1975, 12, 831–836. [Google Scholar] [CrossRef]
- Mori, H.; Kuramoto, Y. Dissipative Structures and Chaos; Springer: Berlin, Germany, 2013. [Google Scholar]
- Hamilton, J.D.; Susmel, R. Autoregressive conditional heteroskedasticity and changes in regime. J. Econom. 1994, 64, 307–333. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- MacKinnon, J.G. Approximate asymptotic distribution functions for unit-root and cointegration tests. J. Bus. Econ. Stat. 1994, 12, 167–176. [Google Scholar]
- Bian, C.; Qin, C.; Ma, Q.D.; Shen, Q. Modified permutation-entropy analysis of heartbeat dynamics. Phys. Rev. E 2012, 85, 021906. [Google Scholar] [CrossRef] [PubMed]
- Amigó, J.M.; Zambrano, S.; Sanjuán, M.A. True and false forbidden patterns in deterministic and random dynamics. Europhys. Lett. 2007, 79, 50001. [Google Scholar] [CrossRef]
| Stock Code | Name | Country | Capitalisation |
|---|---|---|---|
| ABI.BR | Anheuser Busch Inbev NV | Belgium | 182.039 B€ |
| AI.PA | Air Liquide | France | 46.635 B€ |
| AIR.PA | Airbus SE | France | 72.22 B€ |
| ALV.DE | Allianz SE | Germany | 91.67 B€ |
| ASML.AS | ASML Holding N.V. | Netherlands | 71.596 B€ |
| BAYN.DE | Bayer AG | Germany | 87.425 B€ |
| BBVA.MC | Banco Bilbao Vizcaya Argentaria, S.A. | Spain | 49.919 B€ |
| BMW.DE | Bayerische Motoren Werke AG | Germany | 62.545 B€ |
| BN.PA | Danone SA | France | 44.386 B€ |
| BNP.PA | BNP Paribas SA | France | 84.307 B€ |
| CA.PA | Carrefour SA | France | 14.13 B€ |
| DBK.DE | Deutsche Bank AG | Germany | 32.651 B€ |
| DPW.DE | Deutsche Post AG | Germany | 48.763 B€ |
| DTE.DE | Deutsche Telekom AG | Germany | 69.937 B€ |
| EI.PA | Essilor International SA | France | 24.22 B€ |
| ENEL.MI | Enel SpA | Italy | 53.528 B€ |
| ENGI.PA | ENGIE SA | France | 34.648 B€ |
| ENI.MI | Eni S.p.A. | Italy | 53.801 B€ |
| FRE.DE | Fresenius SE & Co. KGaA | Germany | 37.235 B€ |
| G.MI | Assicurazioni Generali S.p.A. | Italy | 25.281 B€ |
| IBE.MC | Iberdrola, S.A. | Spain | 42.207 B€ |
| INGA.AS | ING Groep N.V. | Netherlands | 64.689 B€ |
| ITX.MC | Industria de Diseño Textil, S.A. | Spain | 89.425 B€ |
| MC.PA | LVMH Moët Hennessy Louis Vuitton S.E. | France | 121.994 B€ |
| OR.PA | L’Oréal S.A. | France | 102.244 B€ |
| ORA.PA | Orange S.A. | France | 39.275 B€ |
| PHIA.AS | Koninklijke Philips N.V. | Netherlands | 31.07 B€ |
| SAF.PA | Safran SA | France | 37.748 B€ |
| SAN.PA | Sanofi SA | France | 87.918 B€ |
| SU.PA | Schneider Electric S.E. | France | 42.25 B€ |
| Index Code | Name | Country |
|---|---|---|
| BVSP | IBOVESPA | Brasil |
| DJI | Dow Jones Industrial Average | USA |
| FCHI | CAC 40 | France |
| GDAXI | DAX | Germany |
| GSPC | S&P 500 | USA |
| HSI | Hang Seng Index | Hong Kong |
| IXIC | NASDAQ Composite | USA |
| MERV | MERVAL Buenos Aires | Argentina |
| MXX | IPC Mexico | Mexico |
| N100 | EURONEXT 100 | Europe |
| N225 | Nikkei 225 | Japan |
| STOXX50E | EURO STOXX 50 | Europe |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zanin, M.; Rodríguez-González, A.; Menasalvas Ruiz, E.; Papo, D. Assessing Time Series Reversibility through Permutation Patterns. Entropy 2018, 20, 665. https://doi.org/10.3390/e20090665
Zanin M, Rodríguez-González A, Menasalvas Ruiz E, Papo D. Assessing Time Series Reversibility through Permutation Patterns. Entropy. 2018; 20(9):665. https://doi.org/10.3390/e20090665
Chicago/Turabian StyleZanin, Massimiliano, Alejandro Rodríguez-González, Ernestina Menasalvas Ruiz, and David Papo. 2018. "Assessing Time Series Reversibility through Permutation Patterns" Entropy 20, no. 9: 665. https://doi.org/10.3390/e20090665
APA StyleZanin, M., Rodríguez-González, A., Menasalvas Ruiz, E., & Papo, D. (2018). Assessing Time Series Reversibility through Permutation Patterns. Entropy, 20(9), 665. https://doi.org/10.3390/e20090665








