Cross-Sectoral Information Transfer in the Chinese Stock Market around Its Crash in 2015
Abstract
1. Introduction
2. Methodology
2.1. Transfer Entropy
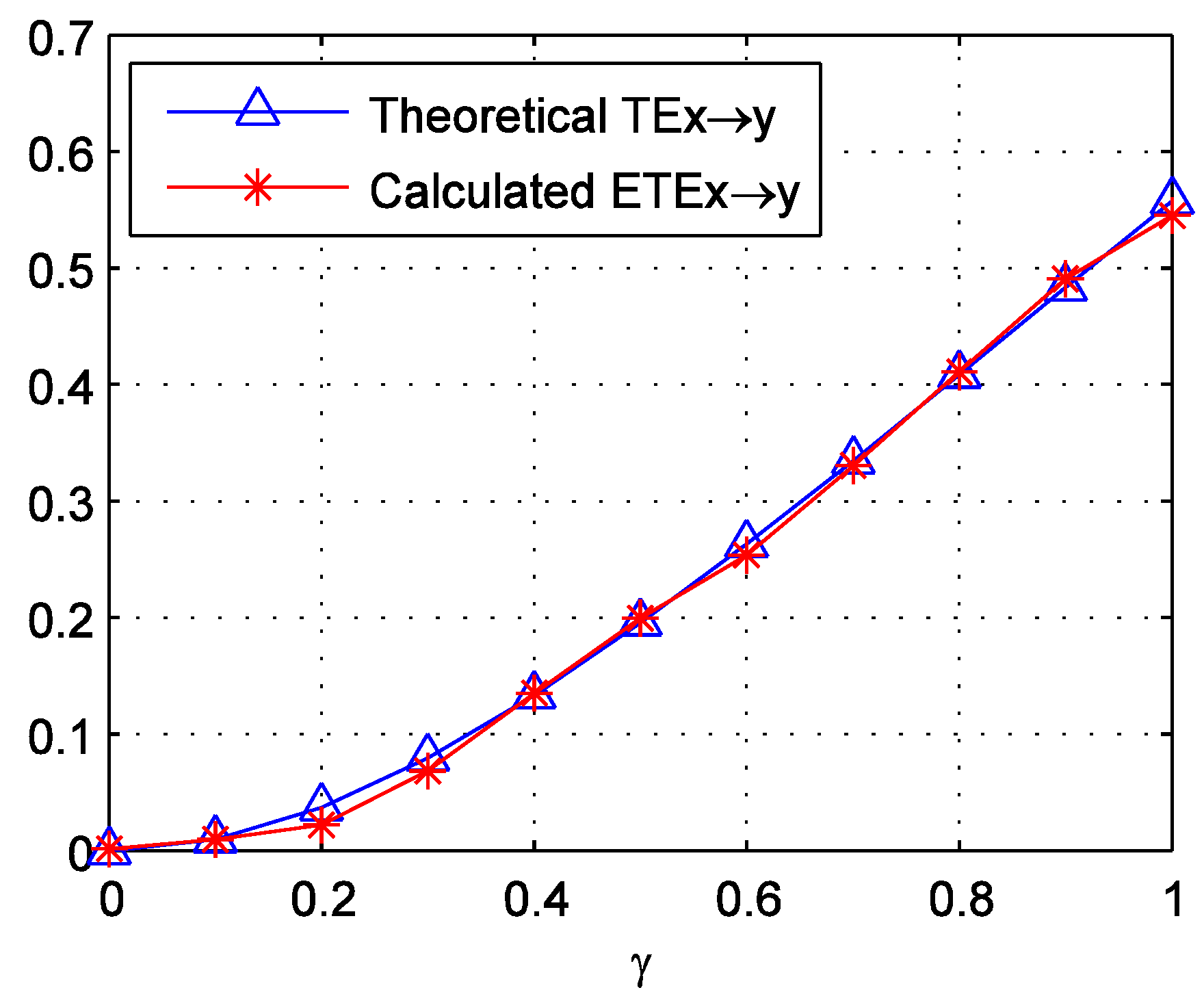
2.2. Effective Transfer Entropy
2.3. Kernel Density Estimation
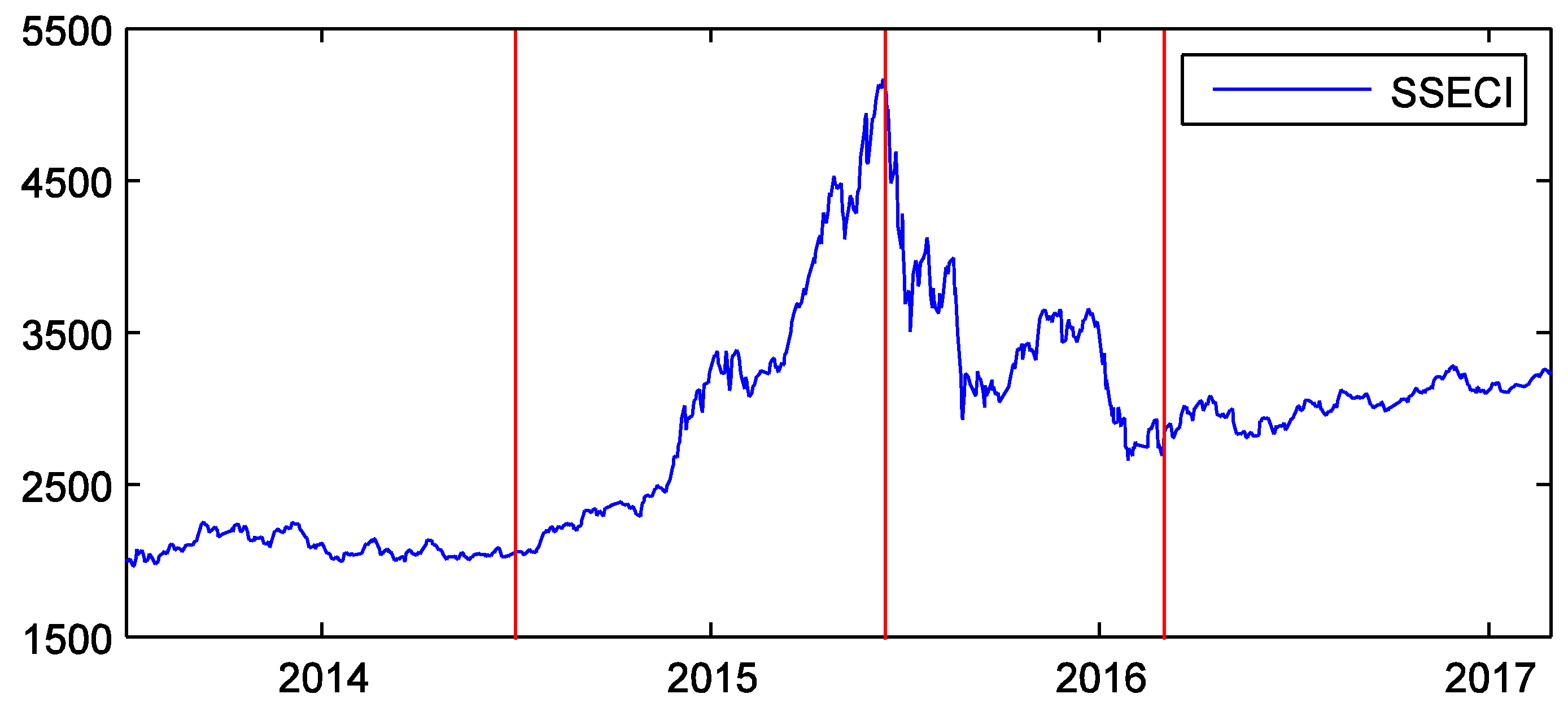
3. Data
4. Results and Discussion
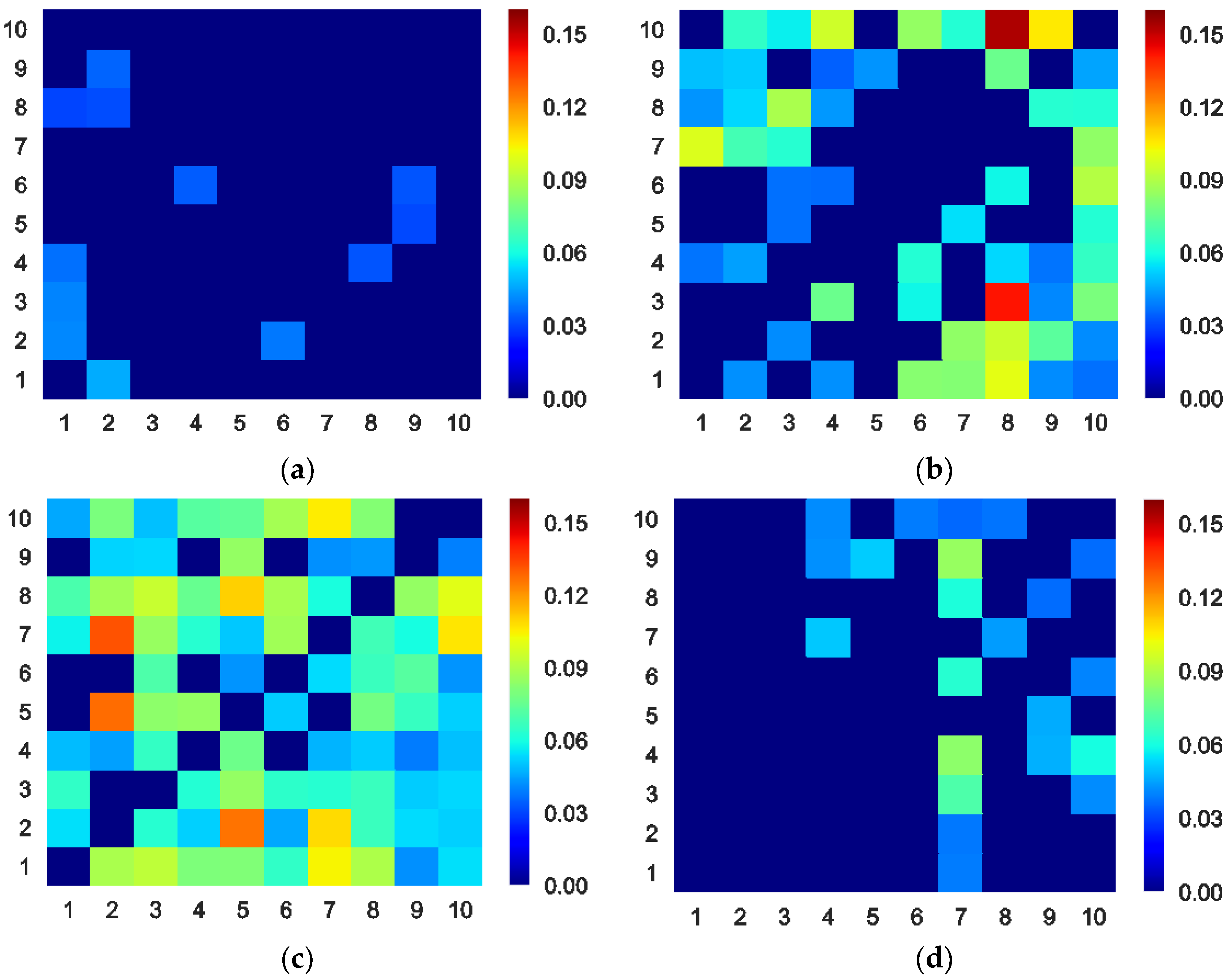
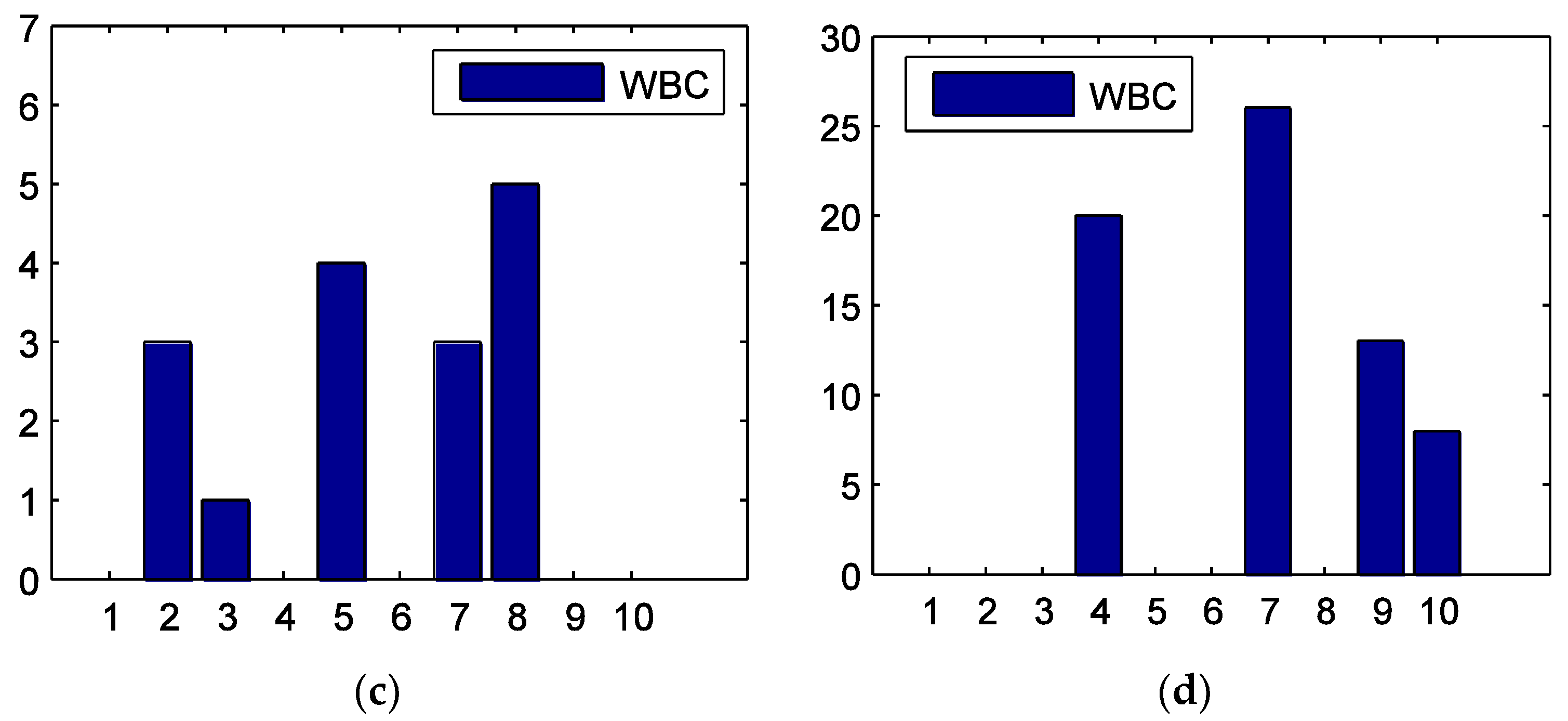
4.1. ETE between Sectors
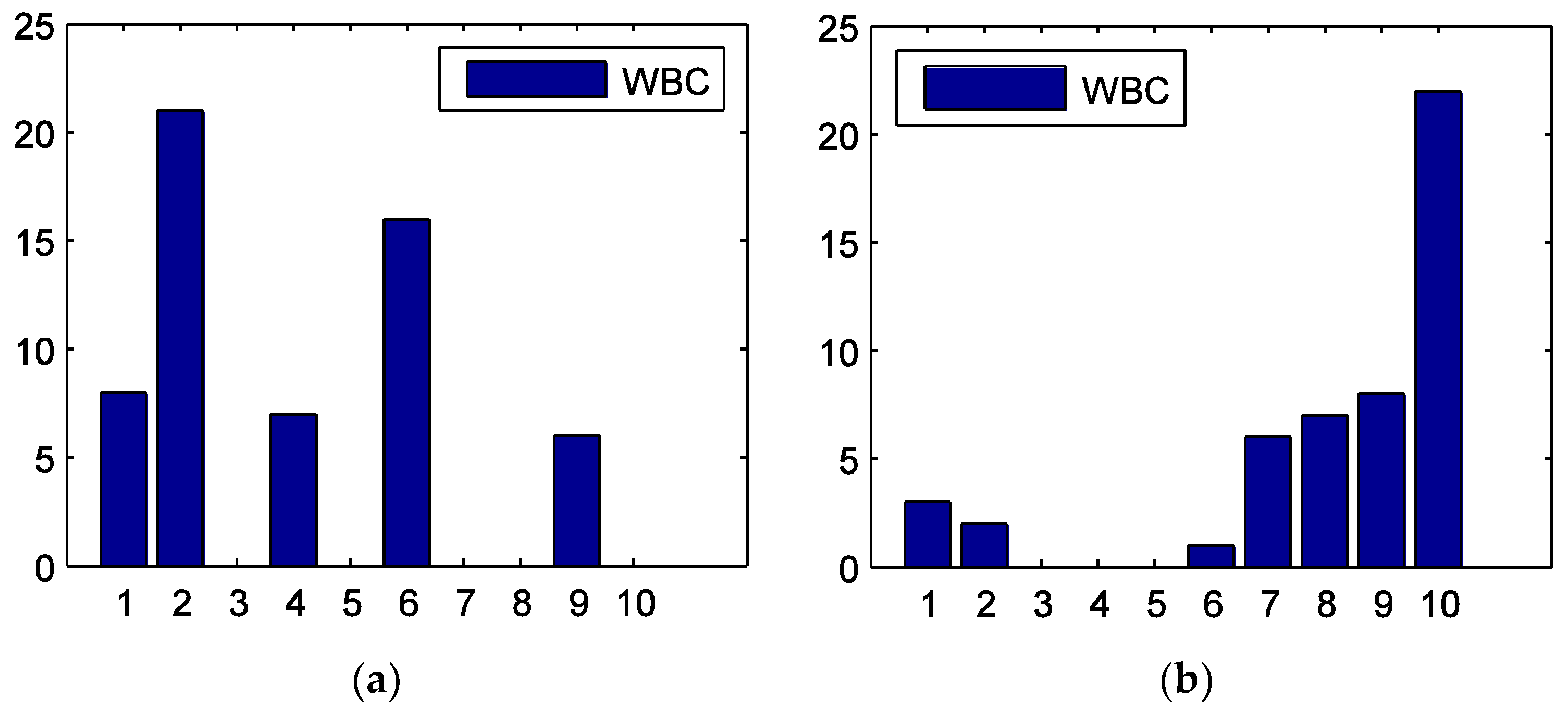
4.2. Centrality of Sectors
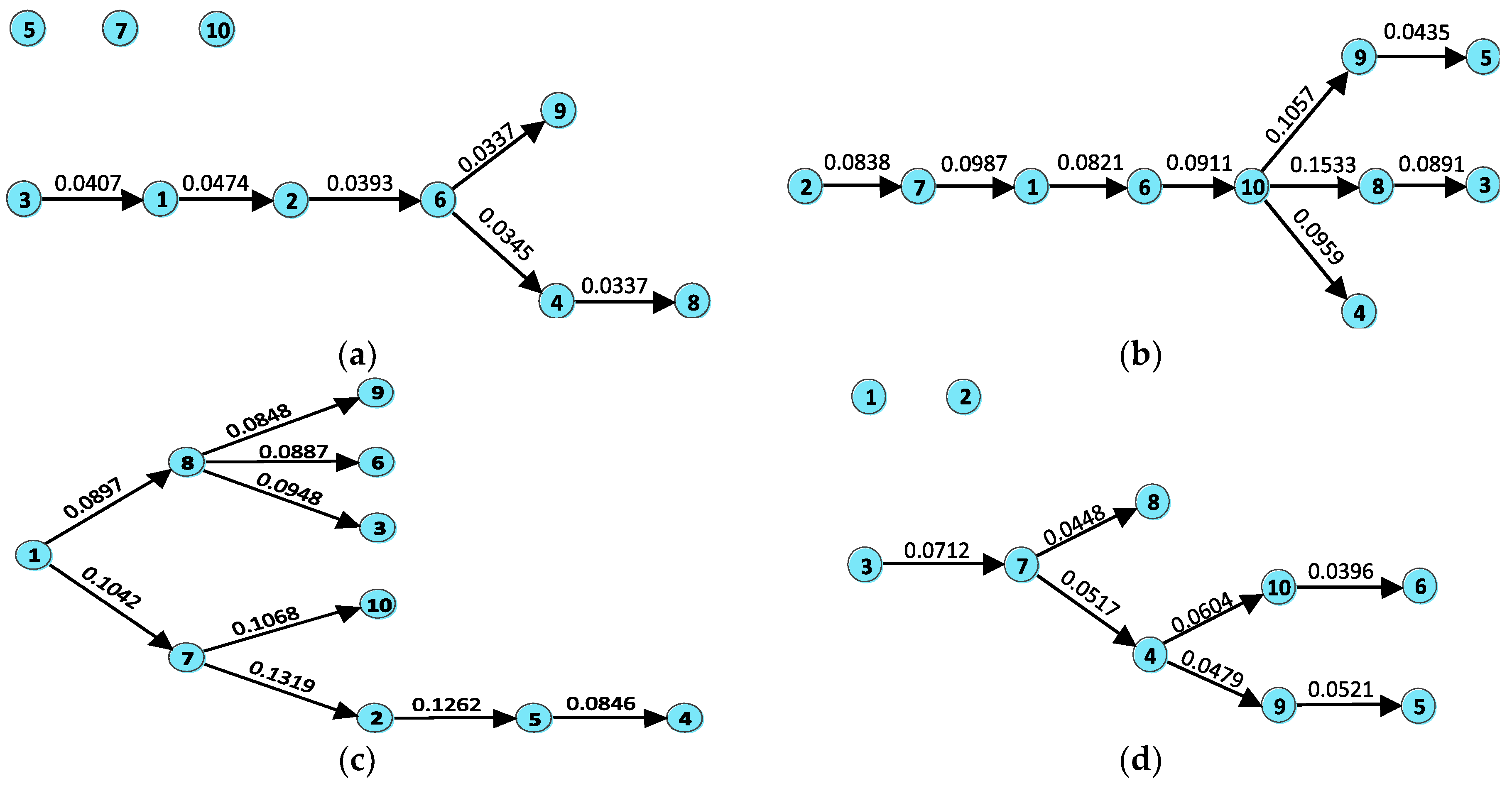
4.3. Directed Maximum Spanning Tree
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Qian, J. The 2015 Stock Panic of China: A Narrative. 2016. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2795543 (accessed on 21 September 2017).
- Song, G. The Drivers of the Great Bull Stock Market of 2015 in China: Evidence and Policy Implications. 2015. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2643051 (accessed on 21 September 2017).
- Zeng, F.; Huang, W.-C.; Hueng, J. On Chinese Government’s Stock Market Rescue Efforts in 2015. Mod. Econ. 2016, 07, 411–418. [Google Scholar] [CrossRef]
- Liu, D.; Gu, H.; Xing, T. The meltdown of the Chinese equity market in the summer of 2015. Int. Rev. Econ. Financ. 2016, 45, 504–517. [Google Scholar] [CrossRef]
- Hou, Y.; Liu, F.; Gao, J.; Cheng, C.; Song, C. Characterizing Complexity Changes in Chinese Stock Markets by Permutation Entropy. Entropy 2017, 19, 514. [Google Scholar] [CrossRef]
- Lu, L.; Lu, L. Unveiling China’s Stock Market Bubble: Margin Financing, the Leveraged Bull and Governmental Responses. J. Int. Bank. Law Rugul. 2017, 32, 145–159. [Google Scholar]
- Honey, C.J.; Kotter, R.; Breakspear, M.; Sporns, O. Network structure of cerebral cortex shapes functional connectivity on multiple time scales. Proc. Natl. Acad. Sci. USA 2007, 104, 10240–10245. [Google Scholar] [CrossRef] [PubMed]
- Wibral, M.; Rahm, B.; Rieder, M.; Lindner, M.; Vicente, R.; Kaiser, J. Transfer entropy in magnetoencephalographic data: Quantifying information flow in cortical and cerebellar networks. Prog. Biophys. Mol. Biophys. 2011, 105, 80–97. [Google Scholar] [CrossRef] [PubMed]
- Murari, A.; Peluso, E.; Gelfusa, M.; Garzotti, L.; Frigione, D.; Lungaroni, M.; Pisano, F.; Gaudio, P. Application of transfer entropy to causality detection and synchronization experiments in tokamaks. Nucl. Fusion 2016, 56, 026006. [Google Scholar] [CrossRef]
- Van Milligen, B.P.; Hoefel, U.; Nicolau, J.H.; Hirsch, M.; García, L.; Carreras, B.A.; Hidalgo, C. Study of radial heat transport in W7-X using the transfer entropy. Nucl. Fusion 2018, 58, 076002. [Google Scholar] [CrossRef]
- Bhaskar, A.; Ramesh, D.S.; Vichare, G.; Koganti, T.; Gurubaran, S. Quantitative assessment of drivers of recent global temperature variability: An information theoretic approach. Clim. Dyn. 2017, 49, 3877–3886. [Google Scholar] [CrossRef]
- Oh, M.; Kim, S.; Lim, K.; Kim, S.Y. Time series analysis of the Antarctic Circumpolar Wave via symbolic transfer entropy. Physica A 2018, 499, 233–240. [Google Scholar] [CrossRef]
- Hu, F.; Nie, L.-J.; Fu, S.-J. Information Dynamics in the Interaction between a Prey and a Predator Fish. Entropy 2015, 17, 7230–7241. [Google Scholar] [CrossRef]
- Orange, N.; Abaid, N. A transfer entropy analysis of leader-follower interactions in flying bats. Eur. Phys. J.-Spec. Top. 2015, 224, 3279–3293. [Google Scholar] [CrossRef]
- Kwon, O.; Yang, J.S. Information flow between stock indices. EPL-Europhys. Lett. 2008, 82, 68003. [Google Scholar] [CrossRef]
- Yang, C.; Tang, M.; Cao, Y.; Chen, Y.; Deng, Q. The study on variation of influential regions in China from a perspective of asymmetry economic information flow. Physica A 2015, 436, 180–187. [Google Scholar] [CrossRef]
- Dimpfl, T.; Peter, F.J. The impact of the financial crisis on transatlantic information flows: An intraday analysis. J. Int. Financ. Mark. Inst. Money 2014, 31, 1–13. [Google Scholar] [CrossRef]
- Sandoval, L. Structure of a Global Network of Financial Companies Based on Transfer Entropy. Entropy 2014, 16, 4443–4482. [Google Scholar] [CrossRef]
- Sensoy, A.; Sobaci, C.; Sensoy, S.; Alali, F. Effective transfer entropy approach to information flow between exchange rates and stock markets. Chaos Soliton Fractals 2014, 68, 180–185. [Google Scholar] [CrossRef]
- Bekiros, S.; Nguyen, D.K.; Sandoval Junior, L.; Uddin, G.S. Information diffusion, cluster formation and entropy-based network dynamics in equity and commodity markets. Eur. J. Oper. Res. 2017, 256, 945–961. [Google Scholar] [CrossRef]
- Kim, J.; Kim, G.; An, S.; Kwon, Y.K.; Yoon, S. Entropy-based analysis and bioinformatics-inspired integration of global economic information transfer. PLoS ONE 2013, 8, e51986. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer entropy—A model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci. 2011, 30, 45–67. [Google Scholar] [CrossRef] [PubMed]
- Marschinski, R.; Kantz, H. Analysing the information flow between financial time series. Eur. Phys. J. B 2002, 30, 275–281. [Google Scholar] [CrossRef]
- Lungarella, M.; Ishiguro, K.; Kuniyoshi, Y.; Otsu, N. Methods for quantifying the causal structure of bivariate time series. Int. J. Bifurc. Chaos 2007, 17, 903–921. [Google Scholar] [CrossRef]
- Khan, S.; Bandyopadhyay, S.; Ganguly, A.R.; Saigal, S.; Erickson, D.J., 3rd; Protopopescu, V.; Ostrouchov, G. Relative performance of mutual information estimation methods for quantifying the dependence among short and noisy data. Phys. Rev. E 2007, 76, 026209. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Nemati, S.; Silva, I.; Edwards, B.A.; Butler, J.P.; Malhotra, A. Transfer entropy estimation and directional coupling change detection in biomedical time series. Biomed. Eng. Online 2012, 11, 19. [Google Scholar] [CrossRef] [PubMed]
- Gibbons, A. Spanning-trees, branchings and connectivity. In Algorithmic Graph Theory; Cambridge University Press: London, UK, 1985; pp. 42–49. ISBN 0-521-24659-8. [Google Scholar]
- Bellingeri, M.; Bodini, A. Food web’s backbones and energy delivery in ecosystems. Oikos 2016, 125, 586–594. [Google Scholar] [CrossRef]
- Chen, B.; Wang, J.; Zhao, H.; Principe, J. Insights into Entropy as a Measure of Multivariate Variability. Entropy 2016, 18, 196. [Google Scholar] [CrossRef]
- Chávez, M.; Martinerie, J.; Le Van Quyen, M. Statistical assessment of nonlinear causality: Application to epileptic EEG signals. J. Neurosci. Methods 2003, 124, 113–128. [Google Scholar]
- Kaiser, A.; Schreiber, T. Information transfer in continuous processes. Physica D 2002, 166, 43–62. [Google Scholar] [CrossRef]
- Ruddell, B.L.; Kumar, P. Ecohydrologic process networks: 1. Identification. Water Resour. Res. 2009, 45, 1–22. [Google Scholar] [CrossRef]
- Lizier, J.T.; Prokopenko, M. Differentiating information transfer and causal effect. Eur. Phys. J. B 2010, 73, 605–615. [Google Scholar] [CrossRef]
- Qi, Y.; Im, W. Quantification of Drive-Response Relationships between Residues during Protein Folding. J. Chem. Theory Comput. 2013, 9, 3799–3805. [Google Scholar] [CrossRef] [PubMed]
- Moon, Y.-I.; Rajagopalan, B.; Lall, U. Estimation of mutual information using kernel density estimators. Phys. Rev. E 1995, 52, 2318–2321. [Google Scholar] [CrossRef]
- Ahmad, I.; Lin, P.E. A nonparametric estimation of the entropy for absolutely continuous distributions. IEEE T. Inform. Theory 1976, 22, 372–375. [Google Scholar] [CrossRef]
- Le Caillec, J.M.; Itani, A.; Gueriot, D.; Rakotondratsimba, Y. Stock Picking by Probability–Possibility Approaches. IEEE Trans. Fuzzy Syst. 2017, 25, 333–349. [Google Scholar] [CrossRef]
- Gao, Y.-C.; Tang, H.-L.; Cai, S.-M.; Gao, J.-J.; Stanley, H.E. The impact of margin trading on share price evolution: A cascading failure model investigation. Physica A 2018, 505, 69–76. [Google Scholar] [CrossRef]
- Zhai, P.; Ma, R. An Analysis on the Structural Breaks in Dynamic Conditional Correlations among Equity Markets Based on the ICSS Algorithm: The Case from 2015–2016 Chinese Stock Market Turmoil. 2017. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2959830 (accessed on 11 October 2017).
- Roni, B.; Abbas, G.; Wang, S. Return and Volatility Spillovers Effects: Study of Asian Emerging Stock Markets. J. Syst. Sci. Inform. 2018, 6, 97–119. [Google Scholar] [CrossRef]
- Albano, A.M.; Muench, J.; Schwartz, C.; Mees, A.I.; Rapp, P.E. Singular-value decomposition and the Grassberger-Procaccia algorithm. Phys. Rev. A 1988, 38, 3017–3026. [Google Scholar] [CrossRef]
- Shang, P.; Li, X.; Kamae, S. Chaotic analysis of traffic time series. Chaos Soliton Fractals 2005, 25, 121–128. [Google Scholar] [CrossRef]
- Yook, S.-H.; Chae, H.; Kim, J.; Kim, Y. Finding modules and hierarchy in weighted financial network using transfer entropy. Physica A 2016, 447, 493–501. [Google Scholar] [CrossRef]
- Daugherty, M.S.; Jithendranathan, T. A study of linkages between frontier markets and the U.S. equity markets using multivariate GARCH and transfer entropy. J. Mult. Financ. Manag. 2015, 32–33, 95–115. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, W.; Shen, J.; Mo, Z.; Peng, Y. Smart city with Chinese characteristics against the background of big data: Idea, action and risk. J. Clean. Prod. 2018, 173, 60–66. [Google Scholar] [CrossRef]
- Yuan, J.; Shen, J.; Pan, L.; Zhao, C.; Kang, J. Smart grids in China. Renew. Sustain. Energy Rev. 2014, 37, 896–906. [Google Scholar] [CrossRef]
- Li, L. China’s manufacturing locus in 2025: With a comparison of “Made-in-China 2025” and “Industry 4.0”. Technol. Forecast. Soc. Chang. 2017, in press. [Google Scholar] [CrossRef]
- Xie, H.; Wang, S.; Chen, X.; Wu, J. Bibliometric analysis of “Internet-plus”. Inform. Learn. Sci. 2017, 118, 583–595. [Google Scholar] [CrossRef]
- Cohen, L.; Frazzini, A. Economic links and predictable returns. J. Financ. 2008, 63, 1977–2011. [Google Scholar] [CrossRef]
- Andersen, T.G. Return volatility and trading volume: An information flow interpretation of stochastic volatility. J. Financ. 1996, 51, 169–204. [Google Scholar] [CrossRef]
- Abhyankar, A.H. Return and volatility dynamics in the FT-SE 100 stock index and stock index futures markets. J. Futures Mark. 1995, 15, 457–488. [Google Scholar] [CrossRef]
- Judge, A.; Reancharoen, T. An empirical examination of the lead–lag relationship between spot and futures markets: Evidence from Thailand. Pac-Basin Financ. J. 2014, 29, 335–358. [Google Scholar] [CrossRef]
- Hou, K.; Moskowitz, T.J. Market Frictions, Price Delay, and the Cross-Section of Expected Returns. Rev. Financ. Stud. 2005, 18, 981–1020. [Google Scholar] [CrossRef]
- Menzly, L.; Ozbas, O. Market segmentation and cross-predictability of returns. J. Financ. 2010, 65, 1555–1580. [Google Scholar] [CrossRef]
- Chordia, T.; Roll, R.; Subrahmanyam, A. Liquidity and market efficiency. J. Financ. Econ. 2008, 87, 249–268. [Google Scholar] [CrossRef]
- Zhang, Y.C. Toward a theory of marginally efficient markets. Physica A 1999, 269, 30–44. [Google Scholar] [CrossRef]
- Zunino, L.; Zanin, M.; Tabak, B.M.; Pérez, D.G.; Rosso, O.A. Complexity-entropy causality plane: A useful approach to quantify the stock market inefficiency. Physica A 2010, 389, 1891–1901. [Google Scholar] [CrossRef]
- Junior, L.S.; Mullokandov, A.; Kenett, D.Y. Dependency relations among international stock market indices. J. Risk Financ. Manag. 2015, 8, 227–265. [Google Scholar] [CrossRef]
- Shahrur, H.; Becker, Y.L.; Rosenfeld, D. Return predictability along the supply chain: The international evidence. Financ. Anal. J. 2010, 66, 60–77. [Google Scholar] [CrossRef]
- Zheng, D.; Li, H.; Chiang, T.C. Herding within industries: Evidence from Asian stock markets. Int. Rev. Econ. Financ. 2017, 51, 487–509. [Google Scholar] [CrossRef]
- Lü, L.; Chen, D.; Ren, X.-L.; Zhang, Q.-M.; Zhang, Y.-C.; Zhou, T. Vital nodes identification in complex networks. Phys. Rep. 2016, 650, 1–63. [Google Scholar] [CrossRef]
- Kwapien, J.; Oswiecimka, P.; Forczek, M.; Drozdz, S. Minimum spanning tree filtering of correlations for varying time scales and size of fluctuations. Phys. Rev. E 2017, 95, 052313. [Google Scholar] [CrossRef] [PubMed]
| No. | Index Name | No. | Index Name |
|---|---|---|---|
| 1 | CSI Energy | 6 | CSI Health Care |
| 2 | CSI Materials | 7 | CSI Financials |
| 3 | CSI Industrials | 8 | CSI Information Technology |
| 4 | CSI Consumer Discretionary | 9 | CSI Telecommunication Services |
| 5 | CSI Consumer Staples | 10 | CSI Utilities |
| No. | ADF Statistic | Jarque-Bera Statistic | No. | ADF Statistic | Jarque-Bera Statistic |
|---|---|---|---|---|---|
| 1 | −28.6154 *** | 765.3783 *** | 6 | −28.4199 *** | 902.8109 *** |
| 2 | −28.2453 *** | 823.1612 *** | 7 | −28.7902 *** | 953.3962 *** |
| 3 | −26.7147 *** | 783.1250 *** | 8 | −27.1013 *** | 351.2834 *** |
| 4 | −27.7279 *** | 753.9022 *** | 9 | −27.6364 *** | 548.0041 *** |
| 5 | −23.0576 *** | 867.0495 *** | 10 | −27.9620 *** | 970.4217 *** |
| Tranquil | Bull | Crash | Post-crash | |
|---|---|---|---|---|
| Average ETE | 0.0049 | 0.0384 | 0.0619 | 0.0123 |
| No. | Sector Name | Pre-Bull | Bull | Crash | Post-Crash |
|---|---|---|---|---|---|
| 1 | Energy | 0.0474 | 0.4301 | 0.7006 | 0.0396 |
| 2 | Materials | 0.0811 | 0.3366 | 0.6279 | 0.0392 |
| 3 | Industrials | 0.0407 | 0.3985 | 0.5149 | 0.1133 |
| 4 | Consumer Discretionary | 0.0714 | 0.3055 | 0.4283 | 0.1918 |
| 5 | Consumer Staples | 0.0316 | 0.1557 | 0.5451 | 0.0471 |
| 6 | Health Care | 0.0682 | 0.2251 | 0.3525 | 0.1048 |
| 7 | Financials | 0 | 0.3147 | 0.7130 | 0.0965 |
| 8 | Information Technology | 0.0628 | 0.3573 | 0.7729 | 0.0989 |
| 9 | Telecommunication Services | 0.0361 | 0.3045 | 0.3194 | 0.2176 |
| 10 | Utilities | 0 | 0.6259 | 0.5983 | 0.1565 |
| No. | Sector Name | Pre-Bull | Bull | Crash | Post-Crash |
|---|---|---|---|---|---|
| 1 | Energy | 0.1509 | 0.2314 | 0.3450 | 0 |
| 2 | Materials | 0.1156 | 0.3289 | 0.6136 | 0 |
| 3 | Industrials | 0 | 0.3278 | 0.6609 | 0 |
| 4 | Consumer Discretionary | 0.0345 | 0.3319 | 0.4932 | 0.1367 |
| 5 | Consumer Staples | 0 | 0.0435 | 0.7335 | 0.0521 |
| 6 | Health Care | 0.0393 | 0.2888 | 0.4924 | 0.0396 |
| 7 | Financials | 0 | 0.2835 | 0.5885 | 0.4808 |
| 8 | Information Technology | 0.0337 | 0.6807 | 0.6157 | 0.0832 |
| 9 | Telecommunication Services | 0.0653 | 0.3646 | 0.4743 | 0.1325 |
| 10 | Utilities | 0 | 0.5725 | 0.5558 | 0.1806 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Hui, X. Cross-Sectoral Information Transfer in the Chinese Stock Market around Its Crash in 2015. Entropy 2018, 20, 663. https://doi.org/10.3390/e20090663
Wang X, Hui X. Cross-Sectoral Information Transfer in the Chinese Stock Market around Its Crash in 2015. Entropy. 2018; 20(9):663. https://doi.org/10.3390/e20090663
Chicago/Turabian StyleWang, Xudong, and Xiaofeng Hui. 2018. "Cross-Sectoral Information Transfer in the Chinese Stock Market around Its Crash in 2015" Entropy 20, no. 9: 663. https://doi.org/10.3390/e20090663
APA StyleWang, X., & Hui, X. (2018). Cross-Sectoral Information Transfer in the Chinese Stock Market around Its Crash in 2015. Entropy, 20(9), 663. https://doi.org/10.3390/e20090663




