3.1. AR Uses and Performance as Described by Kritzman et al.
Kritzman et al. [
5] discuss the need to develop tools that can detect systemic risk. The hope is that these proposed tools can help portfolio managers avoid the typical loses during contractions, as returns often become highly correlated during bear markets.
Additionally, Kritzman et al. [
5] noted the occurrence of large regime changes between low volatility expansions and high volatility financial downturns over the financial cycles.
Kritzman et al. found:
“…1. Most significant U.S. stock market drawdowns were preceded by spikes in the absorption ratio.
2. Stock prices, on average, depreciated significantly following spikes in the absorption ratio and, on average, appreciated significantly in the wake of sharp declines in the absorption ratio.
3. The absorption ratio was a leading indicator of the U.S. housing market bubble.
4. The absorption ratio systematically rose in advance of market turbulence.
5. Important milestones throughout the global financial crisis coincided with shifts in the absorption ratio…”.
Kritzman et al. [
5], p. 113
In the following discussion, an analysis of R/C will produce similar results as Kritzman found for AR. In addition, it will be shown that R/C provides additional information about the complete financial cycle not available with AR. Ultimately the different perspectives and strengths of these two measures could be combined to reduce systemic and regime change induced risk.
3.2. R/C and Polycyclic Portfolio Rebalancing
Systematic shocks have different effects on two the broad classes of assets dubbed procyclical and counter cyclical assets. Procyclical assets tend to rise in value when the economy is expanding and fall with the advent of a recession. Countercyclical assets are instead negatively correlated with the state of the economy. Despite the use of optimization methods, hedging, and ad hoc rebalancing techniques, most portfolios are procyclical in behavior and tend to lose value as the economy slows and equity markets fall due to systematic shocks. In this paper, a new portfolio rebalancing technique is introduced, which has the potential to favorably and systematically pivot a portfolio between pro and counter cyclical strategies before regime changes in the economy. This “polycyclic” approach offers potential portfolio returns well above those of traditional methods. This technique can be implemented independently or in conjunction with other portfolio optimization methods. (To be truly polycyclic, the R/C rebalancing would be between long and short positions and/or procyclical and countercyclical assets.)
Traditional strategic asset allocation methods can result in large portfolio value losses from the inevitable changes in economic conditions over time. To better deal with these challenges, regime-based strategies attempt to adjust the portfolio’s risk profile to the current state of the economy. In regime-based asset allocation, the evolution of the economy is described by typically 2–4 regimes that are detected by means of hidden markov models. Regime-based models have been shown to have superior out-of-sample profitability when compared to more rigid investment structures. This article introduces the concept of dynamic asset allocation and portfolio rebalancing via an economy’s relative information processing ratio. This new information theory-based investment method offers advantages over both traditional and regime-based asset allocation methods.
Theoretical and Practical Limitations of Traditional Regime Based Strategies
One of the most popular regime models in current use are hidden markov switching models (HMSM). These methods assume that only the current data set is useful in predicting the current state of the economy. In contrast, R/C makes use of the current and past evolution of the economy as evidenced by R/C to determine the current economic state.
Determining the proper number of regimes to include in (HMSM) models is an important but unsolved problem, as per Kasashara and Shimotsu [
9]. Too few or too many regimes and the data series cannot be properly modeled; Cavicchioli [
10]. “In practice the state dimension of the Markov chain is sometimes dictated by the actual application or it is determined in an informal manner…” Cavicchioli [
10]. More formal mathematical methods such as the likelihood ratio test statistic fail for reasons such as “unidentifiable parameters, the true parameter being on the boundary of the parameter space, and the degeneracy of the Fisher information matrix…” Kasashara and Shimotsu [
9]. Additionally, there is no explicit justification to assume that the number of regimes is constant as the data series evolves.
3.3. The R/C Model and Polycyclic Portfolio Rebalancing (PPR)
Polycyclic Portfolio Rebalancing (PPR) was developed based on ideas from information theory. Parker [
6,
11] started with the assumption that a hypothetical variable R indicates the amount of information that the economy as a whole is attempting to process and that C is the capacity of the economy to process that information. The ratio R/C is then defined as the economy’s relative information processing ratio. Using an alternative derivation of the yield curve, Parker [
6] demonstrated how to derive an estimate of R/C using actual daily yield rates. This allows one to quickly derive a valuable unlagged snapshot of the state of the economy each day at the close of business.
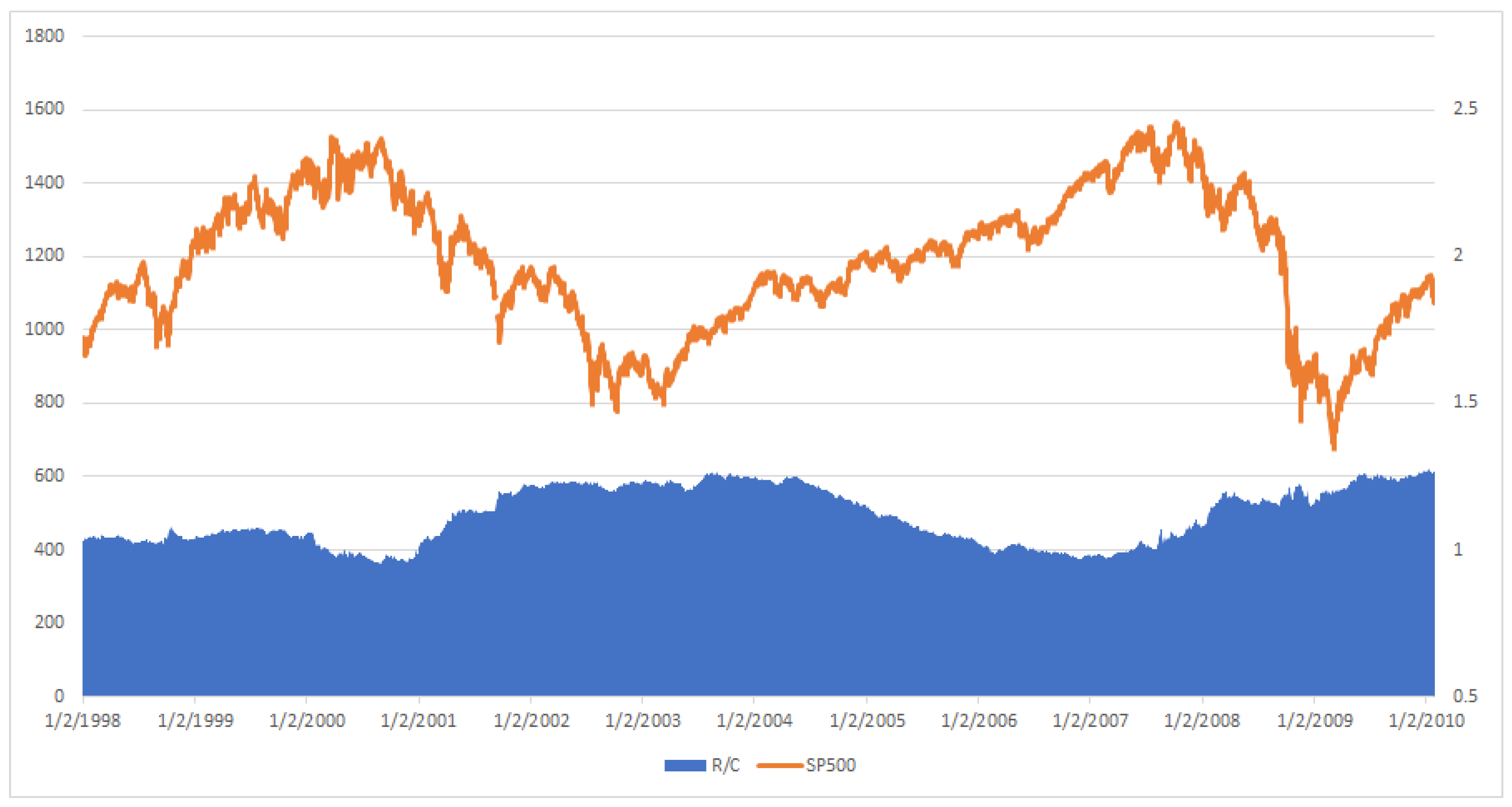
Parker [
11] examined the time evolution of R/C during bull and bear markets. As seen in
Figure 2 and in detail in Parker [
11], R/C rises, reaches a maximum, and then falls in a cyclical pattern with stable maximum and minimum values. The evolution of this information process provides a new and intuitive explanation of the boom and bust financial cycles, as seen from an information theoretic perspective. Parker argued that this new variable reveals a new causal factor in the evolution of financial and business cycles; see Parker [
6,
11].
3.4. Polycyclic Portfolio Rebalancing (PPR) using R/C and the Variance of R/C over Financial Cycles
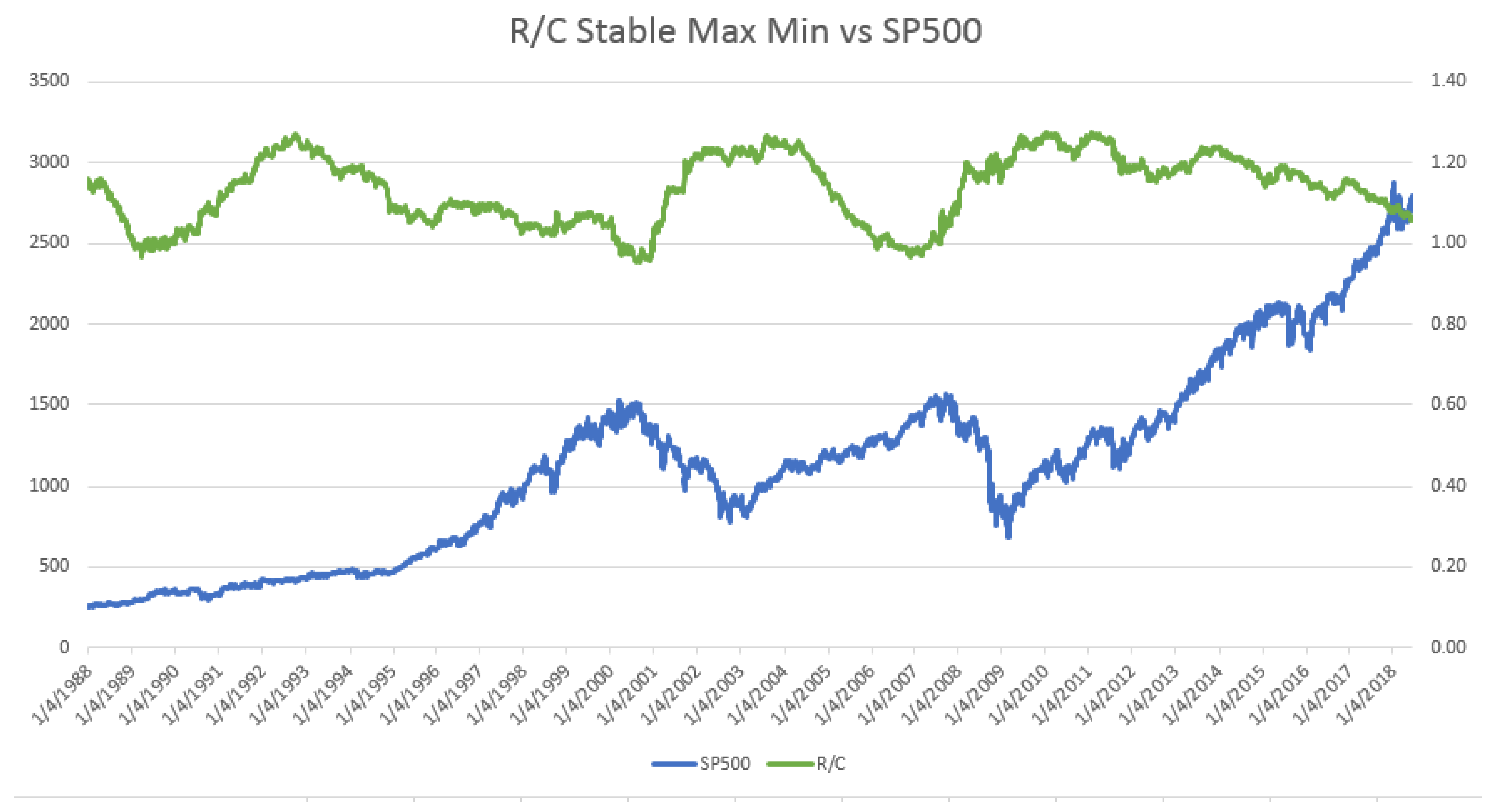
One difficulty portfolio managers face is the fact that market contractions and expansions last for irregular time intervals. Additionally, financial market peaks and troughs are also of non-constant magnitude or amplitude over time. Various techniques have largely unsuccessfully attempted to determine financial cycle lengths. Instead of trying to determine the length of a financial cycle, this paper demonstrates how to use the recurring characteristics of the evolution of R/C to indicate periods of a high probability of regime change.
There are a couple of important characteristics of the evolution of R/C over the business cycle. Similar to the equity markets, R/C experiences well-defined long-term upward and downward movements over time. Secondly in contrast to the equity market price cycles, R/C has a stable amplitude (or stable maximum and minimum values over the cycle), as seen in
Figure 2. Since the stable turning points of R/C coincide (or slightly precede those of the equity markets) R/C provides a means of measuring the market’s distance from a turning point.
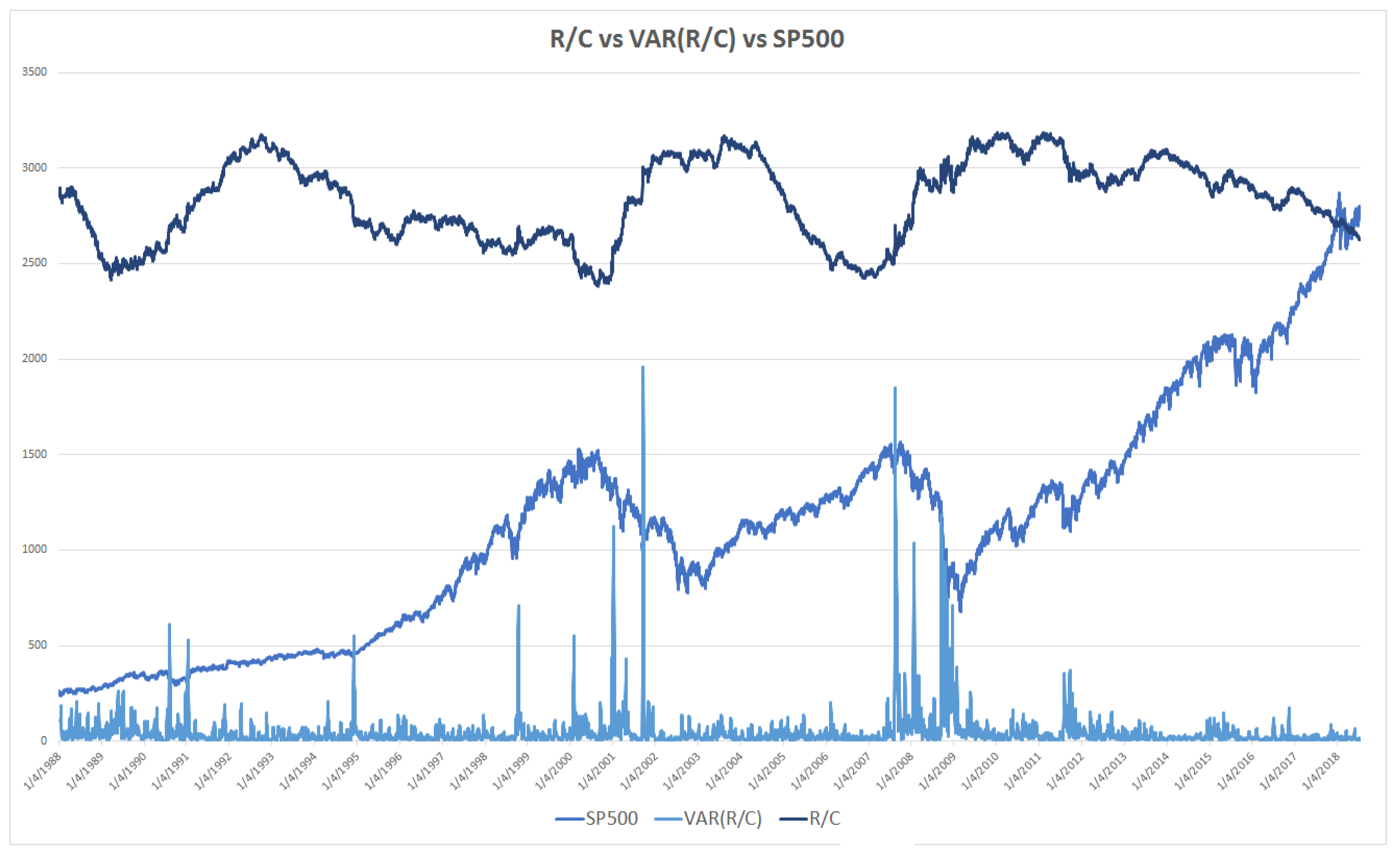
Additionally, the combination of different levels of R/C and its variance can be used to provide a range of early warnings of market turns. Parker [
6,
11] found an inverse relationship between the level of R/C and the variance of R/C. Thus, when R/C nears its minimum, the variance of R/C peaks. The meaning and consequences of the spike in the variance of R/C were explored by Parker [
6,
11]. Basically, extreme changes in the variance of R/C reflect the explosive loss of information in individual markets and the economy as a whole. The variance of R/C is added to R/C and the SP500 in
Figure 3.
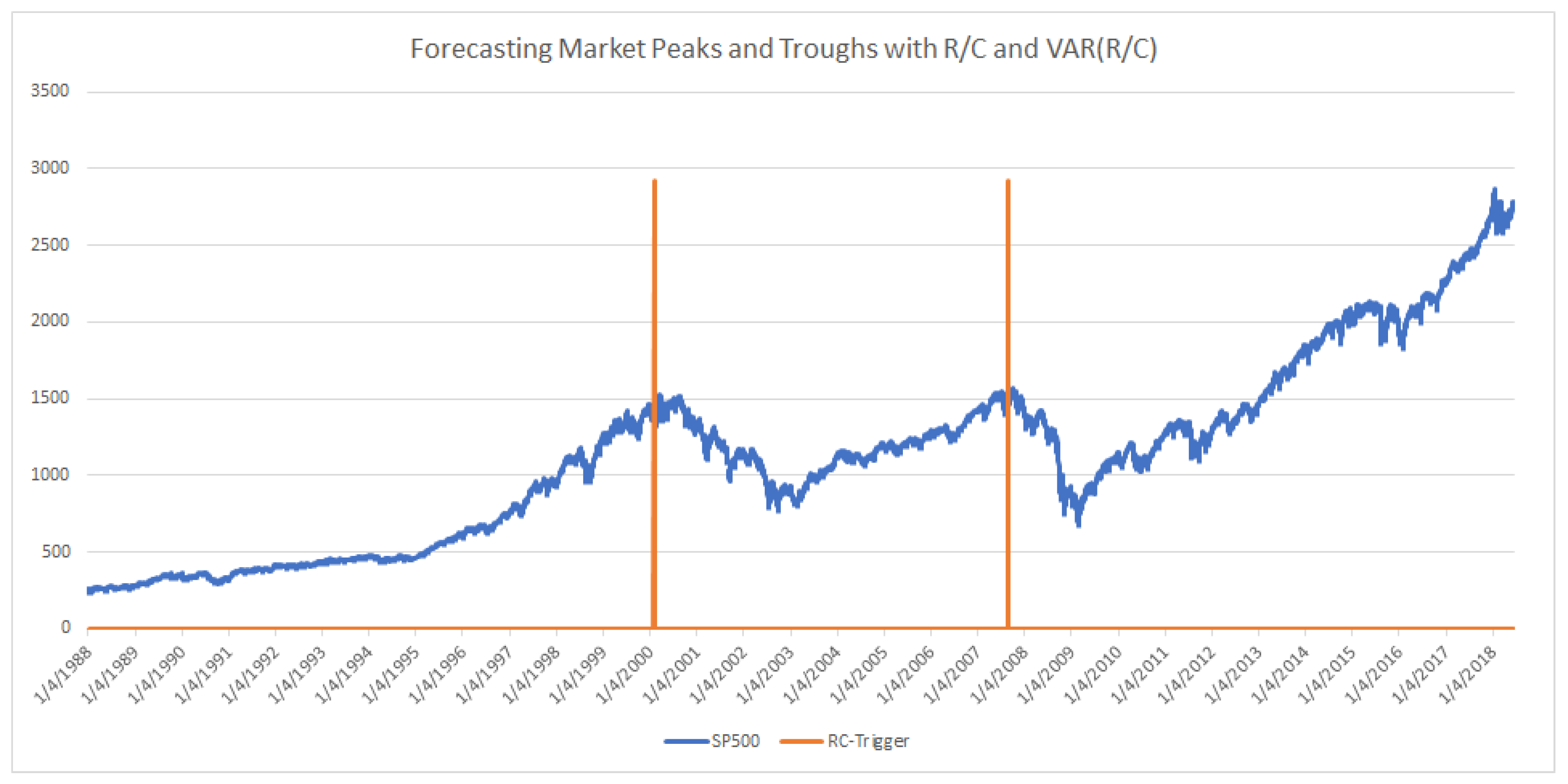
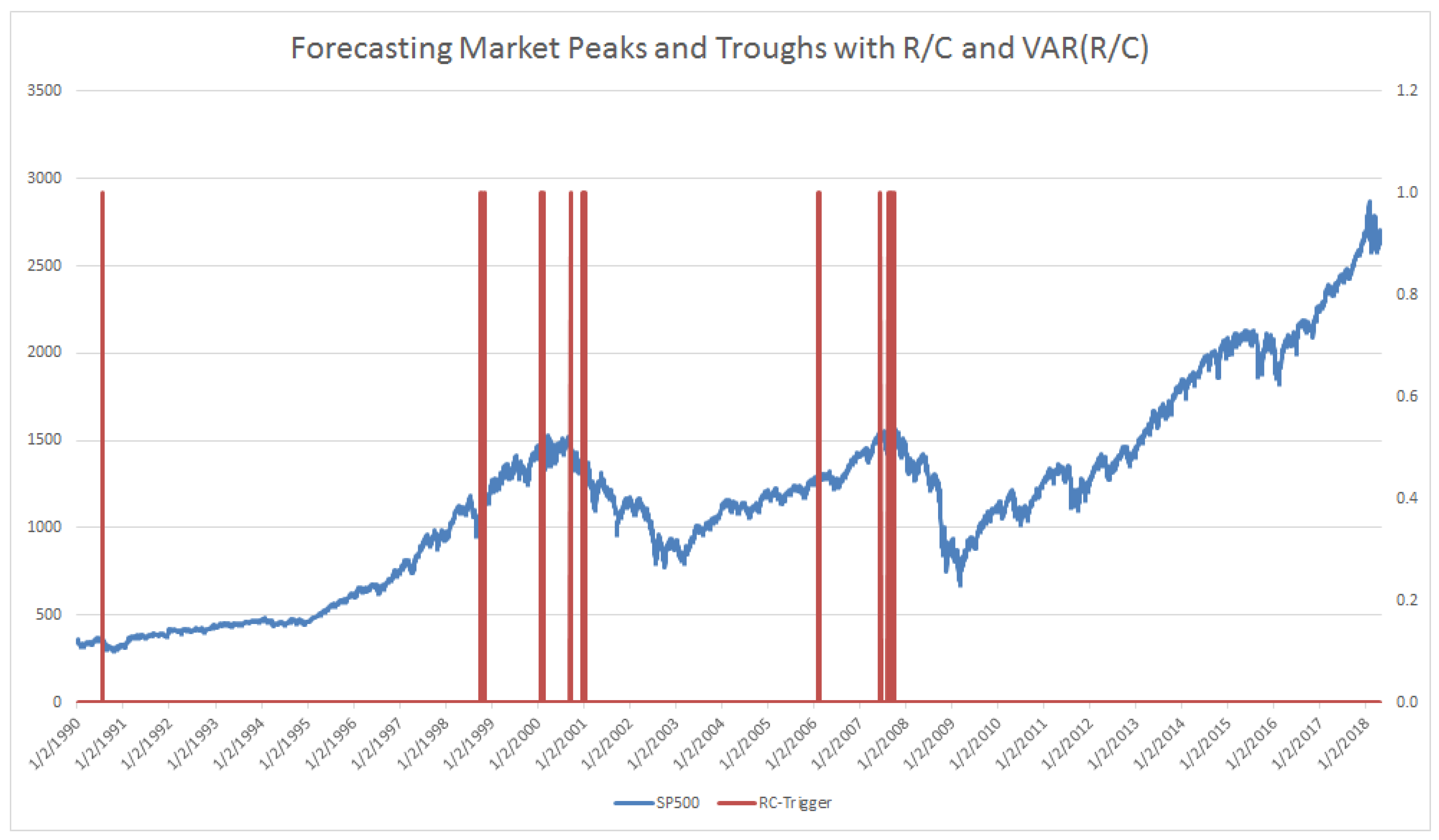
When the level of R/C falls to near 1.0 and the variance of R/C spikes dramatically, the probability that the market (SP500 in this case) is near its peak nears 100%. In
Figure 4 below, there only two periods that fit the above criteria in over 7600 trading-days of data. Specifically, these data points are generated when R/C <1.02 and VAR(R/C) > 11 times the average variance of R/C in a 10-day window. The indicator alerts below at 50 and 43 days before the 3/24/2000 and 10/9/2007 market peaks, respectively (and nearly as important there are no false alerts over the 7600 trading-day period). (The empirical behavior of R/C and the variance of R/C are consistent with the mathematical theory originally presented in Parker [
12]. In that paper, the author hypothesized that when R/C (ratio there is described as CC
A/CC
L) approaches 1.00, the behavior of the information processing variable R/C transitions from a normally distributed variable to a Cauchy distributed variable. This would imply that as R/C approaches 1.00, the variance of R/C should also experience a transition to more extreme values.) Just as Kritzman [
5] cautioned for AR, R/C triggers should be seen as more of a “near necessary condition for a significant drawdown, just not a sufficient condition”. The R/C measure indicates the high probability and not the certainty of a market decline, despite the impressive performance indicated in
Figure 4.
By adjusting portfolios to take into account the evolving R/C level and variance, the portfolios will automatically be dynamically optimized to the systematic risk generated by the long run evolution of the business cycle. Unlike current methods such as hidden markov models, this new method uses the present day’s data to determine the current state and all past R/C data to indicate the economy’s trajectory along the R/C cycle. Hidden markov models assume that only the last period of data is relevant and only look to determine the current state of the economy and not future evolution.
The portfolio management process is facilitated using rebalancing triggers, which activate at predetermined combinations of the levels and variance of R/C. In the simple example that follows, the triggers can be viewed as long, medium, and short-term indicators of the distance to or probability of a near term market turning point. Portfolios can be adjusted in a systematic and intuitive fashion at the activation of these triggers.
3.5. Simple Example Using the R/C-Cycle Systematic Risk Triggers (Bear Market Emergence)
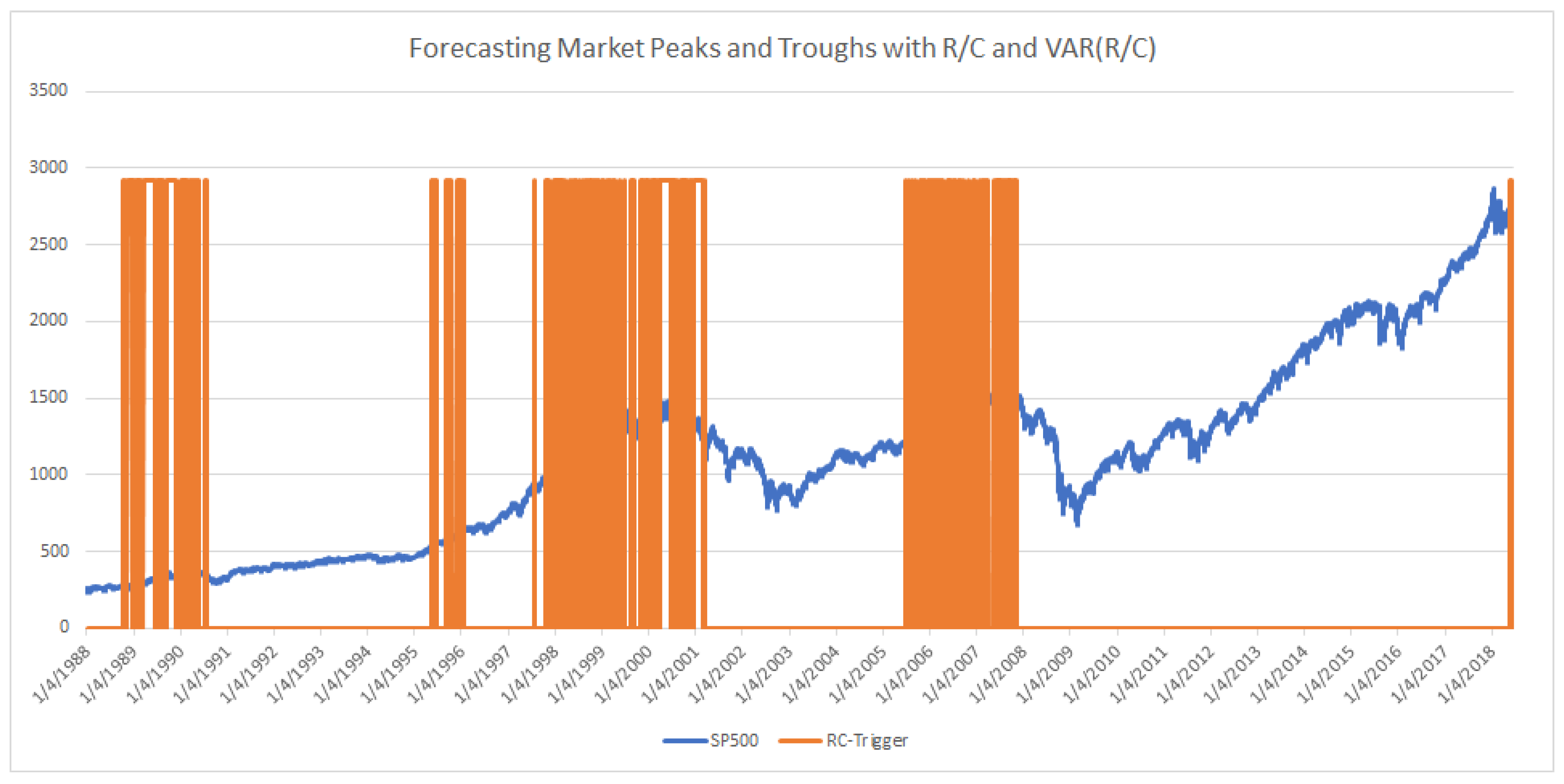
One proposed use of triggers for portfolio adjustment is illustrated below, composed of three risk levels to the onset of a bear market (20% or larger market decline). Levels 1, 2, and 3 correspond to long range (very conservative), medium range (less conservative), and shortest range (least conservative) portfolio adjustment criteria, respectively. Note that there are other arrangements and adjustment methods possible, dependent on a particular portfolio manger’s desired risk levels and adjustment criteria. (For example, the current level and rate of change of R/C could be used to determine an estimate of the time till the emergence of a bear market (at R/C ≈ 1.00). This estimated time span could then be inputted into standard probability of loss measures to proactively adjust the portfolio over the R/C cycle. Visit the author’s website
www.entropicfinance.com for other such examples.) Once a desired level such as Level 1 has been detected, as seen in
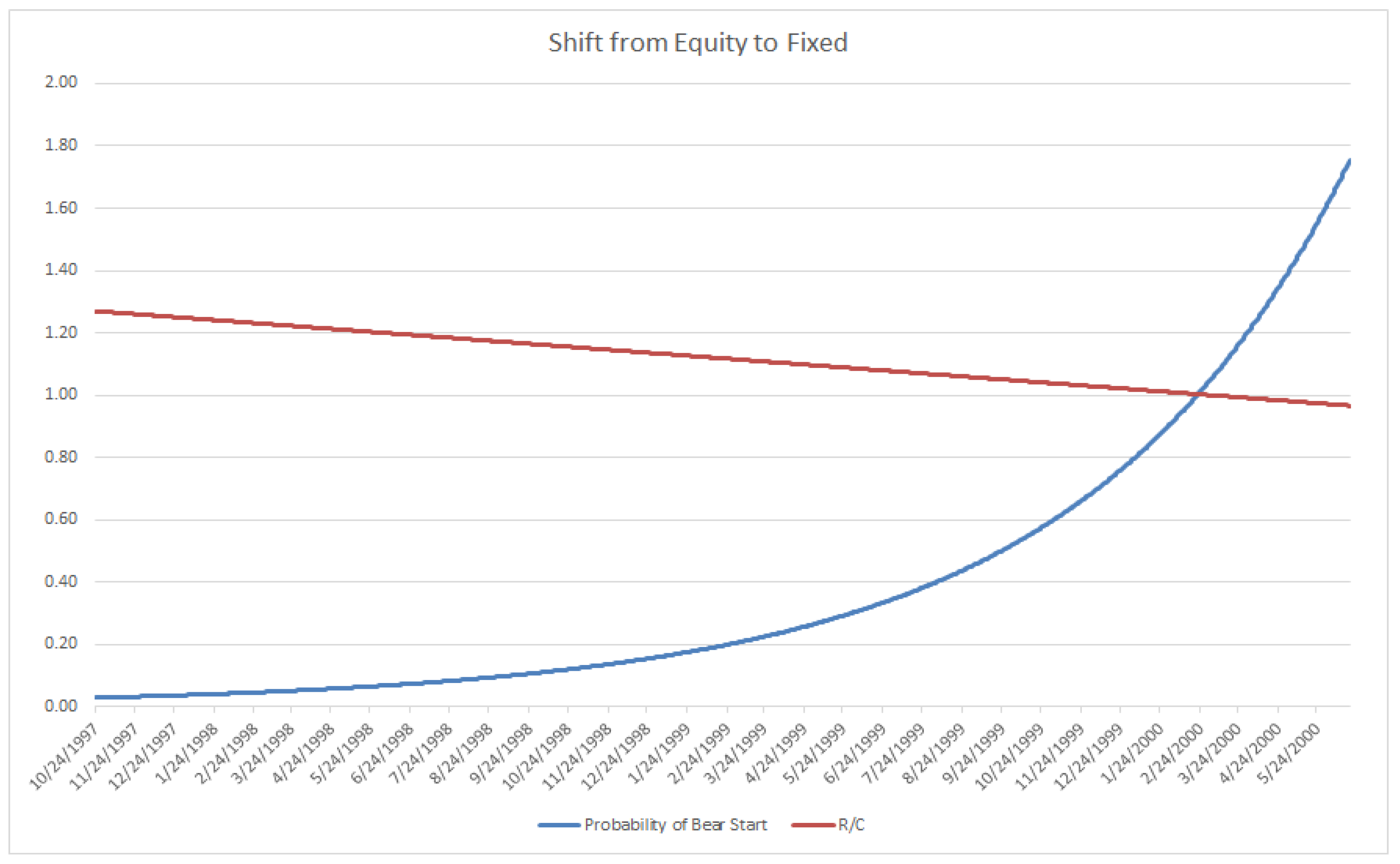
Figure 5, long range systematic portfolio adjustment can be initiated. Given that the probability of an immediate downturn is low but increasing, an exponential type of adjustment from equities to fixed may be desired, as demonstrated in
Figure 6. Initially the risk of an imminent bear market start is negligible, which would indicate 1% to fixed or other safer investments and 99% to equities. Over time, as R/C falls, the portfolio would increasingly shift to fixed at an increasing rate approaching 100% fixed as R/C reaches 1.00. Note, if the level 1 trigger was not sustained, as seen in
Figure 5, the portfolio would be reset to 100% equities awaiting the next trigger alert. The exponentially increasing shift would reduce false trigger loses that turned out not to be sustained long run movements to a bear market. This sort of strategy could be combined with other tactical or systemic risk reduction measures. Interestingly, in the middle of 2018, a level 1 trigger signal was detected using this criterion, as seen at the very end of the sample period in
Figure 4.
Trigger Level 1: (Bear Market Emergence Signals: 1/4/1988 through 6/18/2018).
After trigger begin exponentially increasing shift of portfolio from Equity to Fixed (Most of shift occurs in later periods).
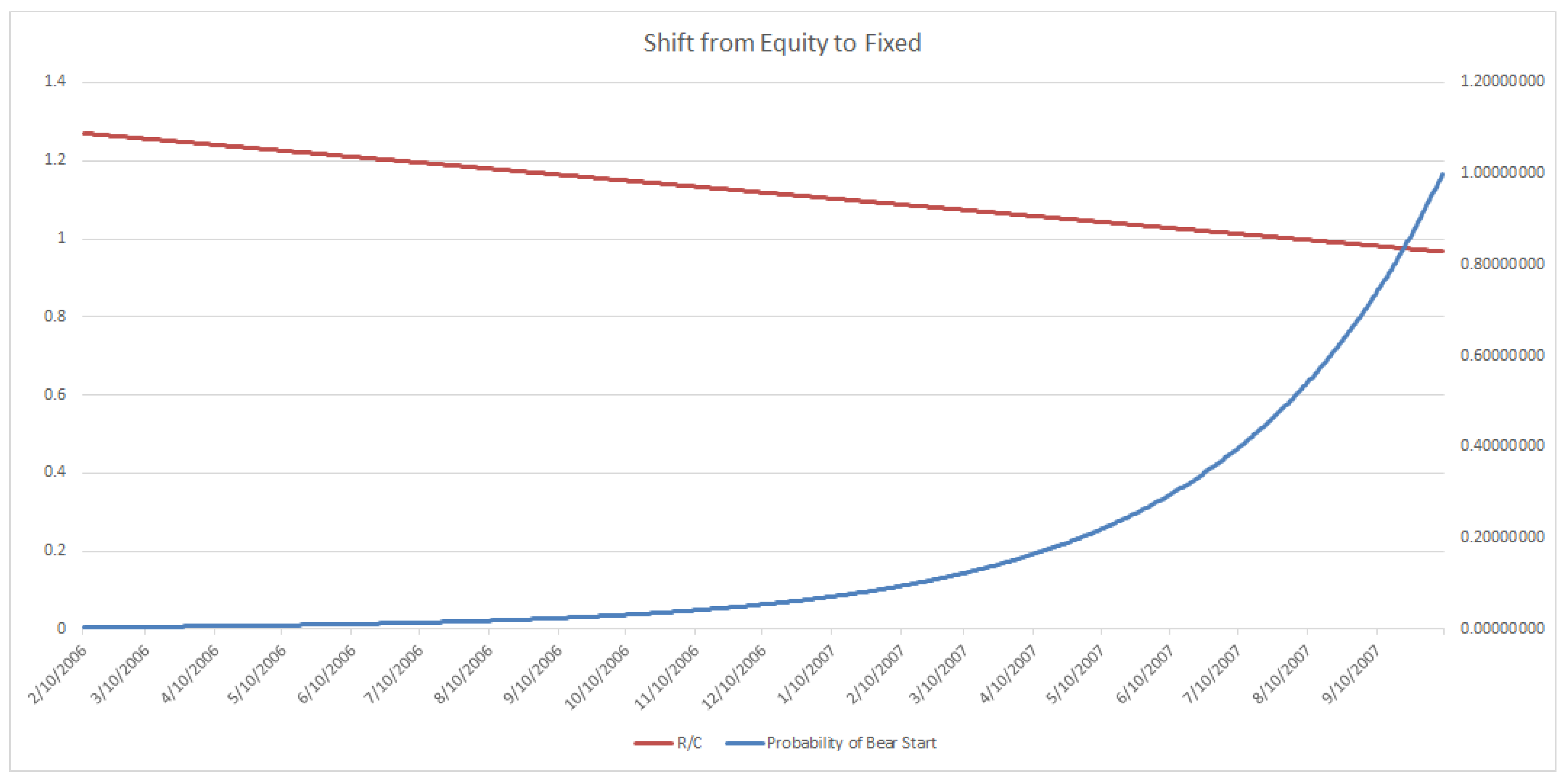
A similar reasoning can be used for portfolio managers wishing to utilize the less conservative trigger level 2, which would have activated as seen in
Figure 7. The suggested exponential shifting would then have begun, as demonstrated in
Figure 8. Finally, when the level 3 riskiest alert, as seen previously in
Figure 4, is detected, an immediate shift to 100% fixed or safer portfolio assets is indicated. As mentioned in previously a true “polycyclic” portfolio would take a short position on procyclical assets and or a long position on countercyclical assets at the trigger. Note that this type of R/C-cycle analysis and portfolio adjustment could similarly be done for the emergence of a bull market, as studied by Parker [
11].
3.6. Summary of the Tradeoffs between the Example Triggers
Trigger Level 1: This is for most risk averse portfolio managers and clients who wish to begin adjusting their portfolio well before the onset of a bear market. This level of user will sacrifice a larger portion of potential gains as the market climbs to its maximum before the onset of a bear market. The user will also have the least risk of suffering losses on missing the onset of a bear market.
Trigger Level 2: This is for less risk averse portfolio managers and clients who wish to begin adjusting their portfolio later than Level 1 users before the onset of a bear market. This level of user will sacrifice less potential gains than a Level 1 user as the market climbs to its maximum before the onset of a bear market. The user will also have less risk of suffering losses on missing the onset of a bear market than Level 3 but more than Level 1.
Trigger Level 3: This is for least risk averse portfolio managers and clients who wish to begin adjusting their portfolio immediately before the onset of a bear market. This level of user will sacrifice a very little of the potential gains as the market climbs to its maximum before the onset of a bear market. This user will also base their turning point on very few days of trigger activation. This level, while accurate over the last 2 cycles over 30 years, also had the fewest trigger points—only 3 activation points beginning 50 days before the 3/24/2000 peak and 1 activation point 43 days before the 10/9/2007 peak. Note that there were zero false positives of these 4 trading days out of over 7600 trading days, and the results conform to the mathematical theory proposed in [
12]. In addition to those who wish to shift their portfolio to a conservative stance at the latest possible date as indicated by R/C, this level may be attractive to those who wish to take a large short position before the bear market begins.