Tensile Behavior and Evolution of the Phases in the Al10Co25Cr8Fe15Ni36Ti6 Compositionally Complex/High Entropy Alloy
Abstract
1. Introduction
2. Materials and Methods
2.1. Alloy Preparation
2.2. Microstructural Observations
2.3. Mechanical Tests
3. Results and Discussion
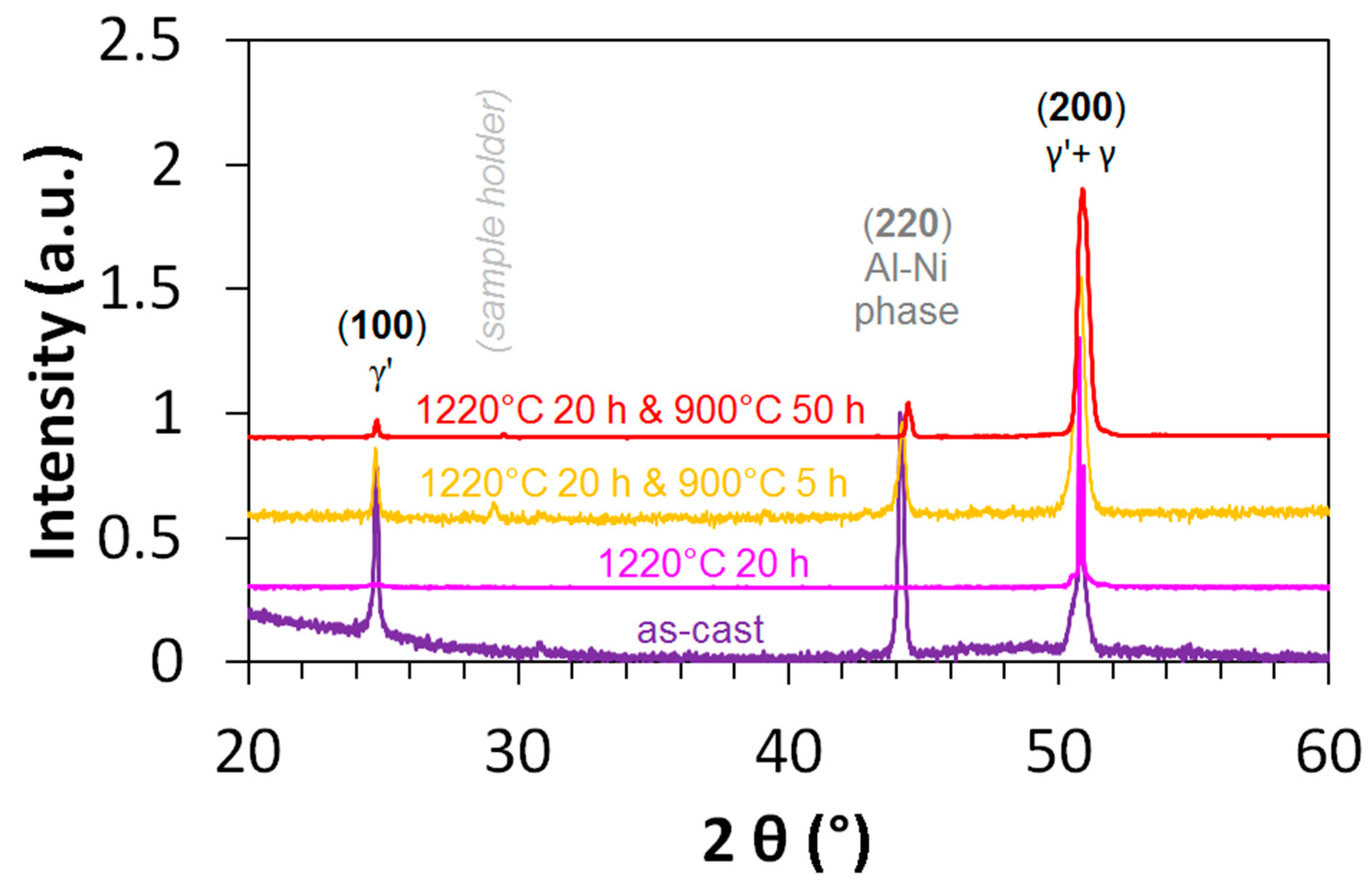
3.1. Morphological Evolution
3.1.1. Al-Ni Rich Needles
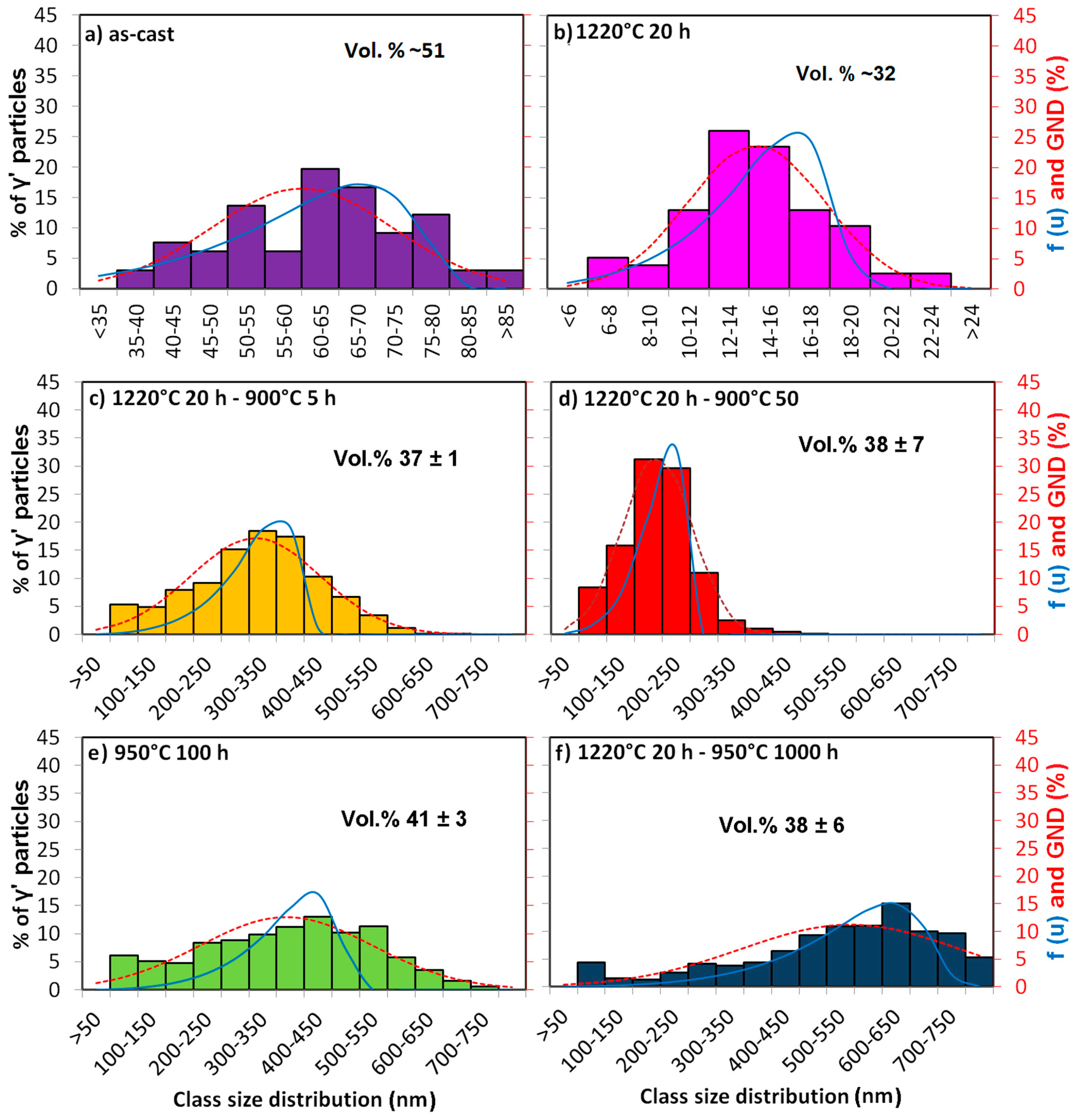
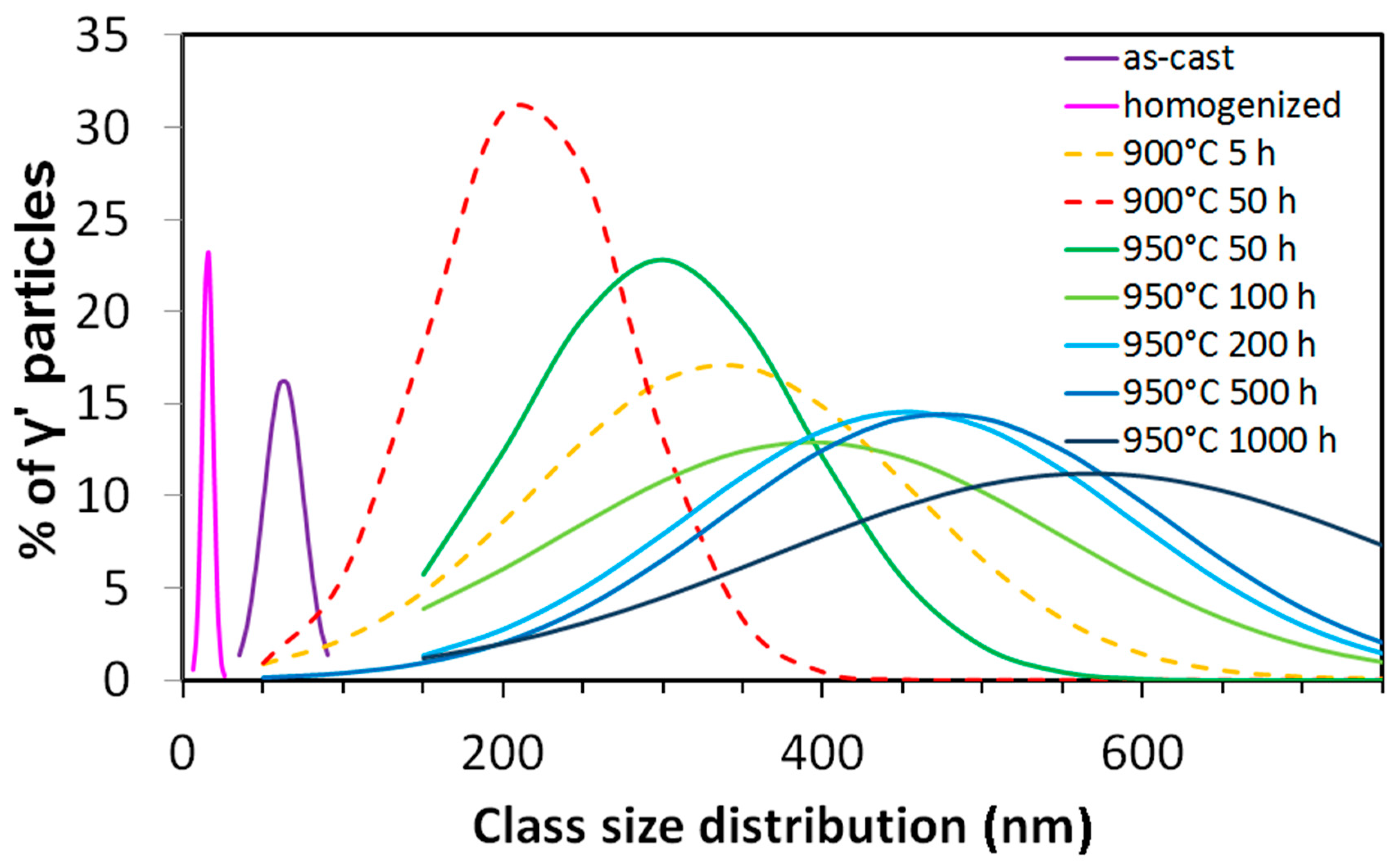
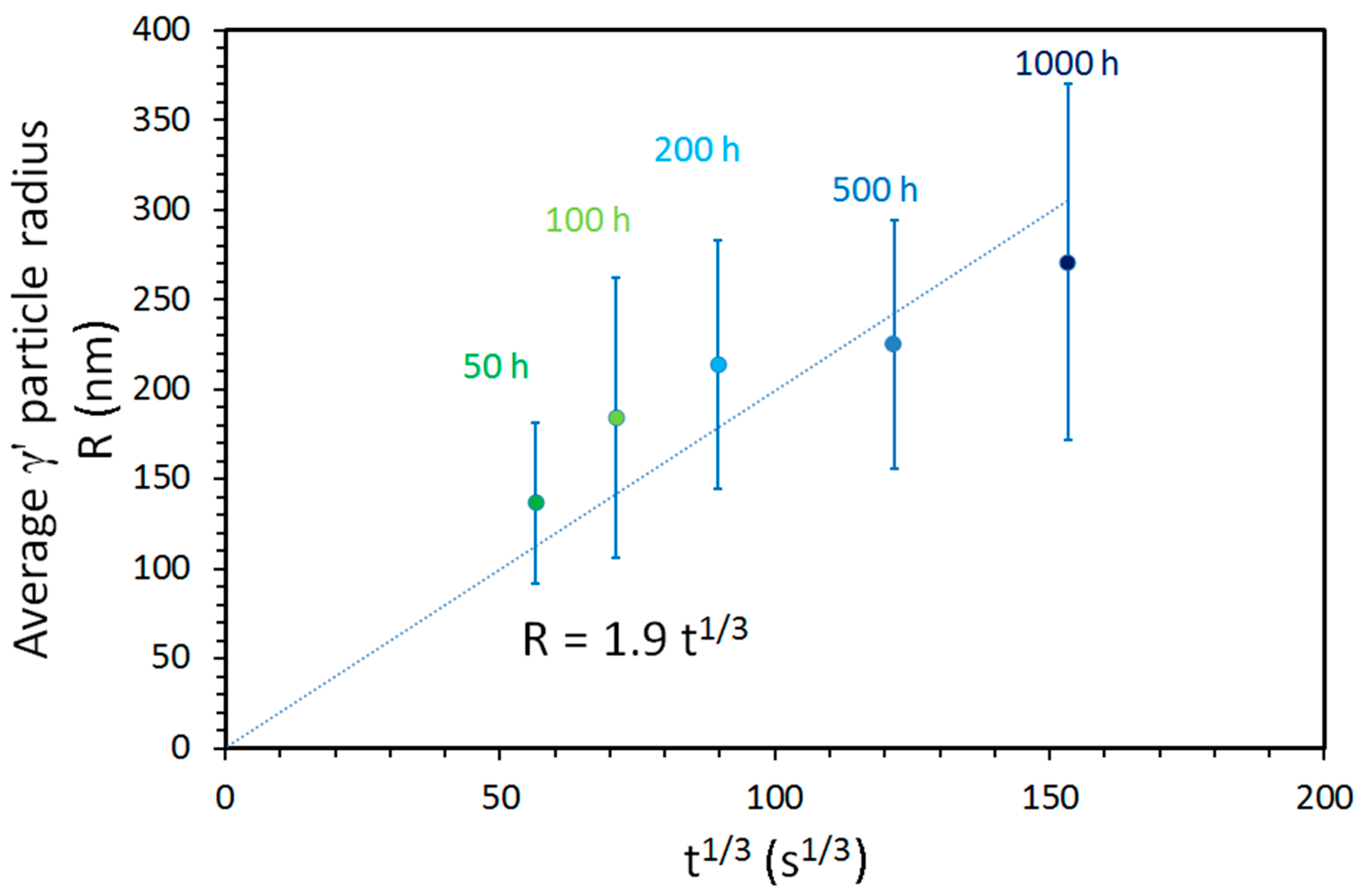
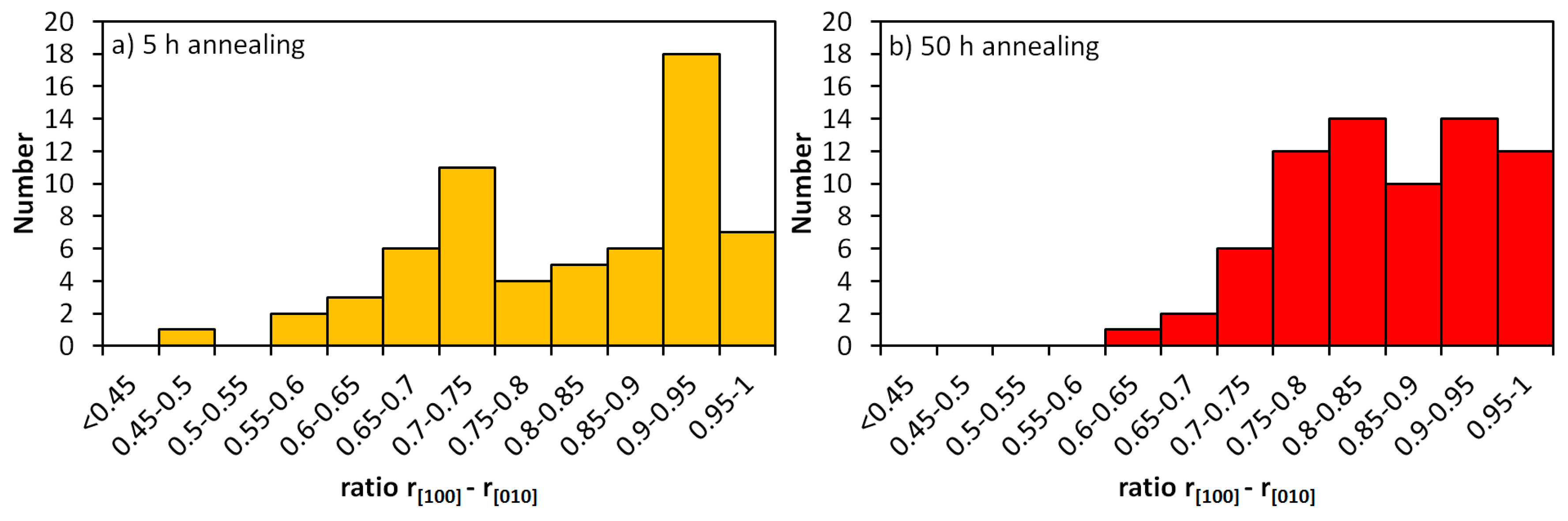
3.1.2. The γ-γ’ Morphology in Detail
3.2. Mechanical Observations
3.2.1. Tensile Tests
- The deformation temperature and the implied softening of the material
- The abundance of the Al-Ni rich needles
- The state of the γ’ precipitates
- 1.
- The deformation temperature is the most important factor. The heating from RT to 800 °C implies a softening of the material and allows for a more ductile tensile behavior. The fracture micrographs of the samples deformed at RT, shown in Figure 9a,e, show little (900 °C 50 h state, Figure 9a) or no (950 °C 100 h state, Figure 9e) necking behavior and thus a quite brittle fracture. The samples deformed at 800 °C (Figure 9c,g) display an important necking and thus a ductile fracture.
- 2.
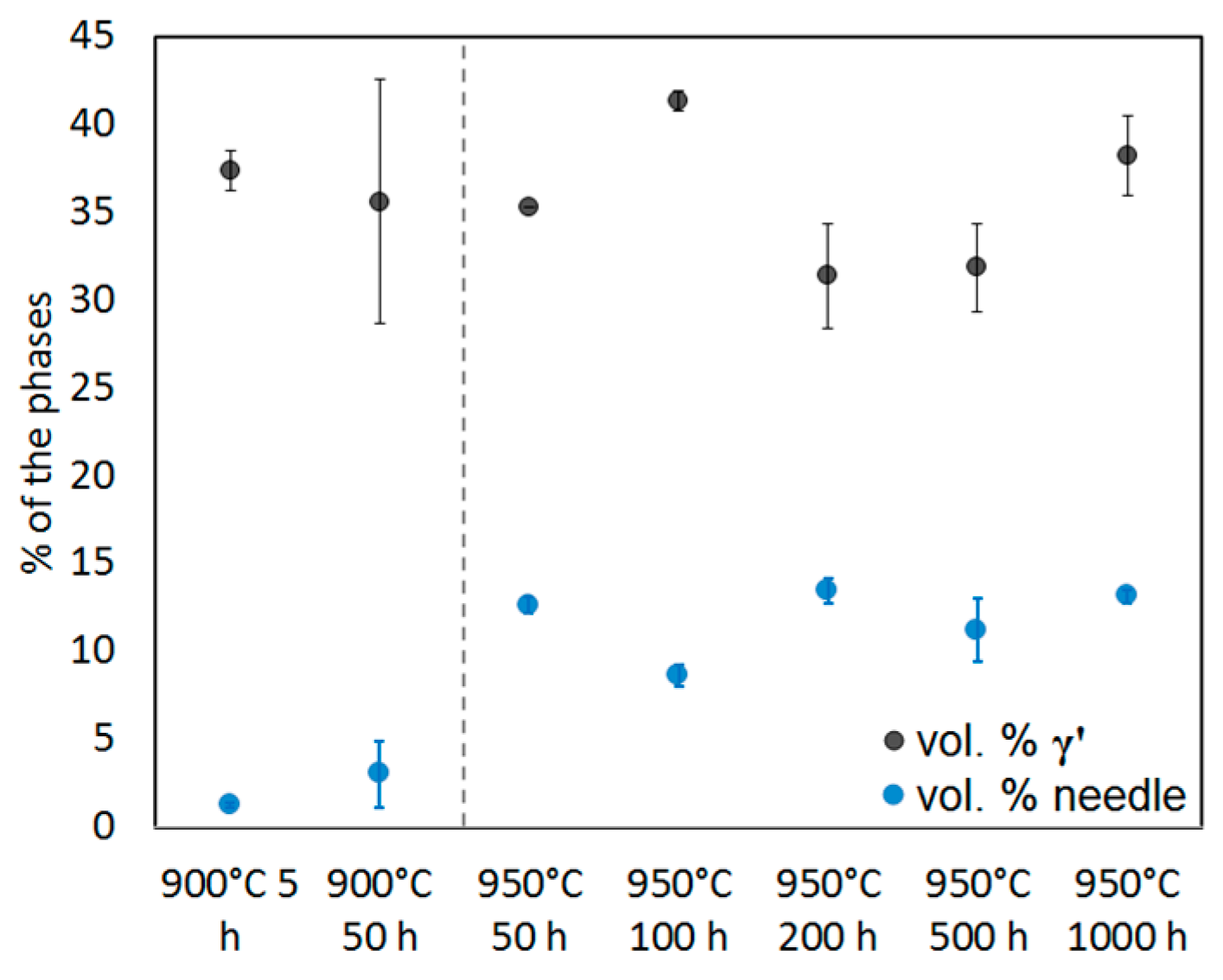
- The amount of needles is lowest in the 900 °C 5 h annealed alloy (about 1%) and highest in the 950 °C 100 h annealed alloy (about 13%). Both the longer annealing times and the higher annealing temperature increase the amount of needles, but the temperature has the stronger influence. In all five states annealed at 950 °C, the volume fraction of needles is up to ten times higher than in the 900 °C annealed states.
- 3.
- The γ-γ’ morphology at room temperature has been analyzed in detail (see Section 3.1.2) and is responsible for the difference in behavior between the 900 °C 5 h and the 900 °C 50 h state. As stated above, after 900 °C 5 h annealing, the γ’ precipitates have not yet established their optimum cuboidal shape. After 900 °C 50 h annealing, however, with the cuboids sides parallel to the tensile load direction and thus a higher geometrical ordering, the dislocation movement is more difficult. This effect is in accordance with the order hardening mechanism, which is often observed in Ni-based alloys [33,34].
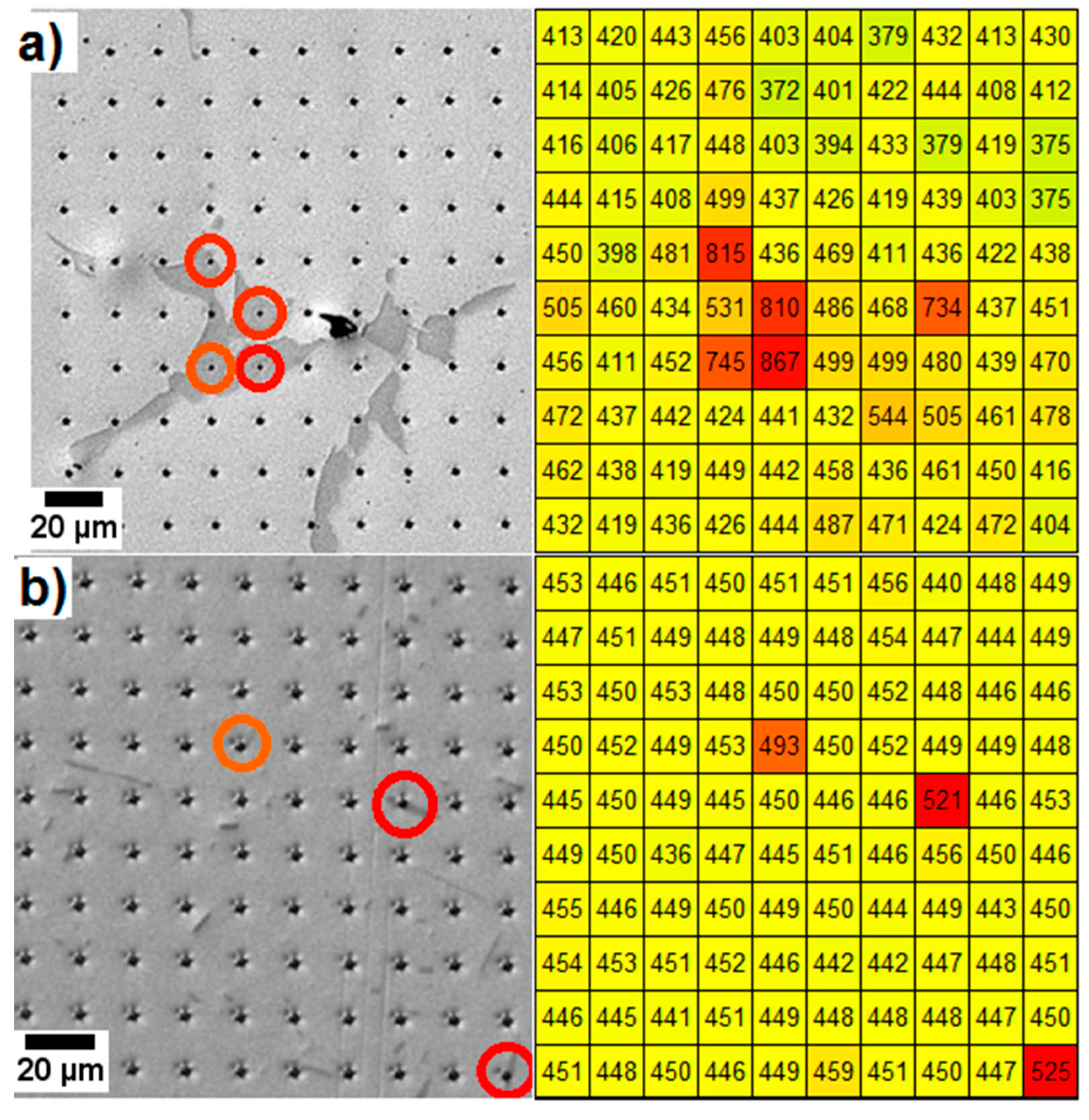
3.2.2. Micro- and Nanohardness
3.3. Comparison with Other Alloys
- -
- High entropy alloys Al10Co25Cr8Fe15Ni36Ti6, Co20Cr20Fe20Mn20Ni20, Al8Cr17Co17Cu8Fe17Ni33
- -
- Ni-based Alloy 800H and Inconel 617, Alloy 800, and Inconel 706 single crystal Ni-based CMSX-4
- -
- Co-based Co-9Al-9W-2Ta-0.02B
- -
- Co-Ni based Co-30Ni-10Al-5Mo-2Ta and TMW-4M3-1.
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Di Martino, S.F.; Faulkner, R.G.; Hogg, S.C.; Vujic, S.; Tassa, O. Characterisation of microstructure and creep properties of alloy 617 for high-temperature applications. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2014, 619, 77–86. [Google Scholar] [CrossRef]
- Zhang, W.R.; Liaw, P.K.; Zhang, Y. Science and technology in high-entropy alloys. Sci. China Mater. 2018, 61, 2–22. [Google Scholar] [CrossRef]
- Klimova, M.; Stepanov, N.; Shaysultanov, D.; Chernichenko, R.; Yurchenko, N.; Sanin, V.; Zherebtsov, S. Microstructure and mechanical properties evolution of the al, c-containing cocrfenimn-type high-entropy alloy during cold rolling. Materials 2018, 11, 53. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.Y.; Yin, H.; Xu, Y. Microstructure, Mechanical and tribological properties of oxide dispersion strengthened high-entropy alloys. Materials 2017, 10, 1312. [Google Scholar] [CrossRef] [PubMed]
- Nam, S.; Kim, M.J.; Hwang, J.Y.; Choi, H. Strengthening of Al0.15CoCrCuFeNiTix–C (x = 0, 1, 2) high-entropy alloys by grain refinement and using nanoscale carbides via powder metallurgical route. J. Alloys Compd. 2018, 762, 29–37. [Google Scholar] [CrossRef]
- Manzoni, A.M.; Glatzel, U. New multiphase compositionally complex alloys driven by the high entropy alloy approach. Mater. Charact. 2018, in press. [Google Scholar] [CrossRef]
- Durand-Charre, M. The Microstructure of Superalloys; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA; Washington, DC, USA, 1997; p. 124. [Google Scholar]
- Singh, S.; Wanderka, N.; Kiefer, K.; Siemensmeyer, K.; Banhart, J. Effect of decomposition of the Cr–Fe–Co rich phase of AlCoCrCuFeNi high entropy alloy on magnetic properties. Ultramicroscopy 2011, 111, 619–622. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Wanderka, N.; Murty, B.S.; Glatzel, U.; Banhart, J. Decomposition in multi-component AlCoCrCuFeNi high-entropy alloy. Acta Mater. 2011, 59, 182–190. [Google Scholar] [CrossRef]
- Tong, C.J.; Chen, M.R.; Chen, S.K.; Yeh, J.W.; Shun, T.T.; Lin, S.J.; Chang, S.Y. Mechanical performance of the Al x CoCrCuFeNi high-entropy alloy system with multiprincipal elements. Metall. Mater. Trans. A 2005, 36, 1263–1271. [Google Scholar] [CrossRef]
- Tong, C.J.; Chen, Y.L.; Chen, S.K.; Yeh, J.W.; Shun, T.T.; Tsau, C.H.; Lin, S.J.; Chang, S.Y. Microstructure characterization of Al x CoCrCuFeNi high-entropy alloy system with multiprincipal elements. Metall. Mater. Trans. A 2005, 36, 881–893. [Google Scholar] [CrossRef]
- Daoud, H.M.; Manzoni, A.; Völkl, R.; Wanderka, N.; Glatzel, U. Microstructure and tensile behavior of Al8Co17Cr17Cu8Fe17Ni33 (at.%) high-entropy alloy. JOM 2013, 65, 1805–1814. [Google Scholar] [CrossRef]
- Manzoni, A.; Daoud, H.; Völkl, R.; Glatzel, U.; Wanderka, N. Phase separation in equiatomic AlCoCrFeNi high-entropy alloy. Ultramicroscopy 2013, 132, 212–215. [Google Scholar] [CrossRef] [PubMed]
- Manzoni, A.; Daoud, H.; Mondal, S.; van Smaalen, S.; Völkl, R.; Glatzel, U.; Wanderka, N. Investigation of phases in Al23Co15Cr23Cu8Fe15Ni16 and Al8Co17Cr17Cu8Fe17Ni33 high entropy alloys and comparison with equilibrium phases predicted by Thermo-Calc. J. Alloys Compd. 2013, 552, 430–436. [Google Scholar] [CrossRef]
- Manzoni, A.M.; Daoud, H.M.; Voelkl, R.; Glatzel, U.; Wanderka, N. Influence of W, Mo and Ti trace elements on the phase separation in Al8Co17Cr17Cu8Fe17Ni33 based high entropy alloy. Ultramicroscopy 2015, 159, 265–271. [Google Scholar] [CrossRef] [PubMed]
- Daoud, H.M.; Manzoni, A.M.; Völkl, R.; Wanderka, N.; Glatzel, U. Oxidation Behavior of Al8Co17Cr17Cu8Fe17Ni33, Al23Co15Cr23Cu8Fe15Ni15, and Al17Co17Cr17Cu17Fe17Ni17 Compositionally Complex Alloys (High-Entropy Alloys) at Elevated Temperatures in Air. Adv. Eng. Mater. 2015, 17, 1134–1141. [Google Scholar] [CrossRef]
- Jien-Wei, Y. Recent progress in high entropy alloys. Ann. Chim. Sci. Mat. 2006, 31, 633–648. [Google Scholar]
- The Version Tccr; Thermocalc Software AB: Stockholm, Sweden. Available online: http://www.Thermocalc.Com (accessed on 15 June 2016).
- Thermotech Ni-Based Superalloys Database, TTNi7, 7.0, Thermo-Calc Software AB: Stockholm, Sweden, 2006.
- Daoud, H.M.; Manzoni, A.M.; Wanderka, N.; Glatzel, U. High-temperature tensile strength of Al10Co25Cr8Fe15Ni36Ti6 compositionally complex alloy (high-entropy alloy). JOM 2015, 67, 2271–2277. [Google Scholar] [CrossRef]
- Otto, F.; Dlouhy, A.; Somsen, C.; Bei, H.; Eggeler, G.; George, E.P. The influences of temperature and microstructure on the tensile properties of a CoCrFeMnNi high-entropy alloy. Acta Mater. 2013, 61, 5743–5755. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Shaysultanov, D.G.; Stepanov, N.D.; Salishchev, G.A.; Senkov, O.N. Tensile properties of an AlCrCuNiFeCo high-entropy alloy in as-cast and wrought conditions. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2012, 533, 107–118. [Google Scholar] [CrossRef]
- Arganda-Carreras, I.; Kaynig, V.; Rueden, C.; Eliceiri, K.W.; Schindelin, J.; Cardona, A.; Seung, H.S. Trainable weka segmentation: A machine learning tool for microscopy pixel classification. Bioinformatics 2017, 33, 2424–2426. [Google Scholar] [CrossRef] [PubMed]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676. [Google Scholar] [CrossRef] [PubMed]
- Rueden, C.T.; Schindelin, J.; Hiner, M.C.; DeZonia, B.E.; Walter, A.E.; Arena, E.T.; Eliceiri, K.W. ImageJ2: ImageJ for the next generation of scientific image data. BMC Bioinform. 2017, 18, 529. [Google Scholar] [CrossRef] [PubMed]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. Nih image to imagej: 25 years of image analysis. Nat. Methods 2012, 9, 671. [Google Scholar] [CrossRef] [PubMed]
- Wagner, C. Theorie der Alterung von Niederschlägen durch Umlösen (Ostwald-Reifung). Z. Elektrochem Ber. Bunsenges. Phys. Chem. 1961, 65, 581–591. [Google Scholar]
- Lifshitz, I.M.; Slyozov, V.V. The kinetics of precipitation from supersaturated solid solutions. J. Phys. Chem. Solids 1961, 19, 35–50. [Google Scholar] [CrossRef]
- Kahlweit, M. Ostwald ripening of precipitates. Adv. Colloid Interface Sci. 1975, 5, 1–35. [Google Scholar] [CrossRef]
- Baldan, A. Review progress in Ostwald ripening theories and their applications to nickel-base superalloys Part I: Ostwald ripening theories. J. Mater. Sci. 2002, 37, 2171–2202. [Google Scholar] [CrossRef]
- Sudbrack, C.K.; Yoon, K.E.; Mao, Z.; Noebe, R.D.; Isheim, D.; Seidman, D.N. Temporal Evolution of Nanostructures in a Model Nickel-Base Superalloy: Experiments and Simulations; Minerals, Metals & Materials Soc.: Warrendale, PA, USA, 2003; pp. 43–50. [Google Scholar]
- Gleiter, H. Microstructure. In Physical Metallurgy; Cahn, R.W., Hassen, P., Eds.; North-Holland Physics Publishing: Amsterdam, The Netherlands; Oxford, UK; New York, NY, USA; Tokyo, Japan, 1983; Volume 1, p. 1973. [Google Scholar]
- Sengupta, A.; Putatunda, S.K.; Bartosiewicz, L.; Hangas, J.; Nailos, P.J.; Peputapeck, M.; Alberts, F.E. Tensile behavior of a new single-crystal nickel-based superalloy (CMSX-4) at room and elevated temperatures. J. Mater. Eng. Perform. 1994, 3, 73–81. [Google Scholar] [CrossRef]
- Müller, L.; Glatzel, U.; Feller-Kniepmeier, M. Calculation of the internal stresses and strains in the microstructure of a single crystal nickel-base superalloy during creep. Acta Metall. Mater. 1993, 41, 3401–3411. [Google Scholar] [CrossRef]
- Reed, R.C. The Superalloys. Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Wu, Q.Y.; Song, H.J.; Swindeman, R.W.; Shingledecker, J.P.; Vasudevan, V.K. Microstructure of long-term aged in617 Ni-base superalloy. Metal. Mater. Trans. A Phys. Met. Mater. Sci. 2008, 39, 2569–2585. [Google Scholar] [CrossRef]
- Inconel Alloy 617. Available online: http://www.Specialmetals.Com/documents/inconel%20alloy%20617.Pdf (accessed on 3 December 2015).
- Wanderka, N.; Naundorf, V.; Banhart, J.; Mukherji, D.; Genovesse, D.D.; Rosler, J. Microstructural characterization of Inconel 706 alloy. Surf. Interface Anal. 2004, 36, 546–551. [Google Scholar] [CrossRef]
- Alloy 800. Available online: http://www.Sandmeyersteel.Com/images/alloy-800-spec-sheet.Pdf (accessed on 3 December 2015).
- Coppola, R.; Fiorentin, S.R. Study of γ′-precipitation kinetics in alloy 800 at 575 °C by small angle neutron scattering. Nucl. Instr. Meth. Phys. Res. Sect. B Beam Interact. Mater. Atoms 1987, 22, 564–572. [Google Scholar] [CrossRef]
- Vittori, M. Gamma particle coarsening and yield in alloy 800. J. Mater. Sci. 1981, 16, 3461–3469. [Google Scholar] [CrossRef]
- Nilsson, J.O.; Thorvaldsson, T. Low cycle fatigue behavior of alloy 800 h at 600–800 °C—Effect of grain size and gamma particle dispersion. Fatigue Fracture Eng. Mater. Struct. 1985, 8, 373–384. [Google Scholar] [CrossRef]
- Zhong, F.; Li, S.S.; Sha, J.B. Tensile behaviour of Co–Al–W–Ta–B–Mo alloys with a coherent γ/γ′ microstructure at room and high temperatures. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2015, 637, 175–182. [Google Scholar] [CrossRef]
- Feng, G.; Li, H.; Li, S.S.; Sha, J.B. Effect of Mo additions on microstructure and tensile behavior of a Co–Al–W–Ta–B alloy at room temperature. Scripta Mater. 2012, 67, 499–502. [Google Scholar] [CrossRef]
- Makineni, S.K.; Samanta, A.; Rojhirunsakool, T.; Alam, T.; Nithin, B.; Singh, A.K.; Banerjee, R.; Chattopadhyay, K. A new class of high strength high temperature cobalt based γ–γ′ Co–Mo–Al alloys stabilized with Ta addition. Acta. Mater. 2015, 97, 29–40. [Google Scholar] [CrossRef]
- Gu, Y.; Zhong, Z.; Yuan, Y.; Osada, T.; Cui, C.; Yokokawa, T.; Harada, H. An advanced cast-and-wrought superalloy (TMW-4M3) for turbine disk applications beyond 700 C. In Proceedings of the International Symposium on Superalloys, Champion, PA, USA, 10 September 2012; Volume 903, pp. 903–910. [Google Scholar]
- Osada, T.; Gu, Y.F.; Nagashima, N.; Yuan, Y.; Yokokawa, T.; Harada, H. Optimum microstructure combination for maximizing tensile strength in a polycrystalline superalloy with a two-phase structure. Acta Mater. 2013, 61, 1820–1829. [Google Scholar] [CrossRef]




| Phase | Composition (at.%) | |||||
|---|---|---|---|---|---|---|
| Al | Co | Cr | Fe | Ni | Ti | |
| Nominal | 10 | 25 | 8 | 15 | 36 | 6 |
| As-cast | ||||||
| De -γ matrix | 8.8 ± 2.2 | 29.5 ± 1.8 | 7.7 ± 1.2 | 20.0 ± 4.2 | 30.7 ± 4.3 | 3.2 ± 1.7 |
| De -γ’ precipitate | 12.1 ± 1.4 | 22.3 ± 1.9 | 3.1 ± 1.1 | 7.7 ± 1.7 | 45.5 ± 2.9 | 9.3 ± 1.2 |
| ID core | 20.6 ± 2.5 | 23.3 ± 1.4 | 3.6 ± 0.9 | 9.1 ± 1.2 | 34.3 ± 2.2 | 9.1 ± 0.5 |
| Homogenized 1220 °C 20 h | ||||||
| γ Matrix | 9.3 ± 1.6 | 26.1 ± 0.8 | 7.2 ± 0.5 | 14.8 ± 1.0 | 37.1 ± 0.8 | 5.5 ± 0.5 |
| γ’ precipitate | ||||||
| Annealed 1220 °C 20 h—900 °C 5 h | ||||||
| γ matrix | 8.9 ± 1.7 | 28.1 ± 1.2 | 9.4 ± 0.7 | 18.8 ± 0.9 | 31.1 ± 1.1 | 3.6 ± 0.4 |
| Primary γ’ precipitate | 14.0 ± 1.0 | 21.4 ± 0.8 | 3.6 ± 0.4 | 8.2 ± 0.6 | 44.4 ± 1.1 | 8.3 ± 0.8 |
| Al-Ni needle | 24.7 ± 1.9 | 20.8 ± 0.7 | 2.9 ± 0.2 | 9.4 ± 0.1 | 36.2 ± 1.1 | 6.0 ± 0.2 |
| Annealed 1220 °C 20 h—900 °C 50 h | ||||||
| γ matrix | 6.9 ± 0.6 | 29.5 ± 0.5 | 9.3 ± 0.4 | 20.4 ± 0.6 | 30.4 ± 1.0 | 3.5 ± 0.4 |
| Primary γ’ precipitate | 11.4 ± 0.6 | 22.5 ± 0.6 | 3.5 ± 0.4 | 8.8 ± 0.7 | 45.0± 1.5 | 8.7 ± 0.5 |
| Al-Ni needle | 24.4 ± 1.3 | 21.9 ± 1.7 | 3.6 ± 0.2 | 10.7 ± 0.4 | 33.9 ± 0.6 | 5.6 ± 0.2 |
| PropertyState | As-Cast | Homogenized 1220 °C-20 h | Annealed 1220 °C-20 h/900 °C-5 h | Annealed 1220 °C-20 h/900 °C-50 h | Annealed 1220 °C-20 h/950 °C-100 h | |
|---|---|---|---|---|---|---|
| Morphological data | Size of primary γ’ precipitates (nm) | 60 ± 12 | 14 ± 3 | 368 ± 92 | 315 ± 62 | 388 ± 132 |
| Volume fraction of primary γ’ precipitates | ~57 | ~32 | ~45 | ~40 | ~45 | |
| Volume fraction of the (needle-like) Al-Ni phase | ~5 | 0 | ~1 | ~4 | ~9 | |
| Mechanical data | Micro HV50/20 | 343 ± 22 (DE) | 341 ± 12 | 345 ± 14 | 345 ± 17 | 373 ± 11 |
| Nano HV0.025/20 γ-γ’ | 433 ± 32 (DE) | 457 ± 5 | 448 ± 7 | 451 ± 5 | 454 ± 91 | |
| Nano HV0.025/20 Al-Ni phase | 736 ± 87 (ID) | - | 569 ± 61 | 560 ± 148 | 647 ± 72 | |
| Ultimate tensile strength σTS at RT (MPa) | - | - | 786 from [20] | 1197 ± 6 | 758 ± 40 | |
| Yield strength at RT (MPa) | - | - | 568 from [20] | 648 ± 1 | 473 ± 38 | |
| Elongation at RT (%) | 12 from [20] | 26 ± 1 | 5 ± 1 | |||
| Young’s modulus at RT (GPa) | - | - | 90 ± 18 | 99 ± 37 | 118 ± 32 | |
| Ultimate tensile strength σTS at 800 °C (MPa) | - | - | 672 from [20] | 575 ± 7 | 493 ± 40 | |
| Yield strength at 800 °C (MPa) | - | - | 535 from [20] | 450 | 310 ± 15 | |
| Elongation to fracture at 800 °C (%) | - | - | 27 from [20] | 20 ± 4 | 14 ± 5 | |
| Young’s modulus at 800 °C (GPa) | - | - | 52 ± 6 | 54 ± 4 | 51 ± 10 |
| Alloy | Size of the Primary γ’ Precipitates (after Optimum Heat Treatment) | Volume Fraction of the Primary γ’ Precipitates (after Optimum Heat Treatment) | Additional Phases (except γ Matrix) | Ultimate Tensile Strength at 800 °C (MPa) | Ref. | |
|---|---|---|---|---|---|---|
| HEAS | Al8Cr17Co17Cu8Fe17Ni33 | 20 nm | 20% | L12 at grain boundaries | Not known | [14,15] |
| Al10Co25Cr8Fe15Ni36Ti6 | 191 nm | 36% | Al-Ni rich needles | 565 | this work | |
| Co20Cr20Fe20Mn20Ni20 | - | - | - | ~170 | [21] | |
| Al17Co17 Cr17Cu17Fe17Ni17 | - | - | A2, B2, fcc1, fcc2, L12 | 180 | [22] | |
| Ni-based alloys | CMSX-4 | 500 nm | 70% | - | ~1100 | [33,35] |
| Inconel 617 | 80 nm | 5% | Ni2(Cr,Mo); MC; M23C6; M6C | ~500 | [36,37] | |
| Inconel 706 | 10–100 nm | <25% | γ″, η, carbides, nitrides, (Ni3Nb) | Not known | [38] | |
| Alloy 800 | <10 nm | 1% | Cr23C6, TiC | ~180 | [39,40,41] | |
| Alloy 800H | <100 nm | small | Cr23C6, TiC | ~200 | [39,42] | |
| Co-based alloy | Co-9Al-9W-2Ta-0.02B | ~200 nm | ~70% | - | ~580 | [43,44] |
| Co-Ni based alloys | Co-30Ni-10-A-5Mo-2Ta | 30–50 nm | ~74% | - | >600 | [45] |
| TMW-4M3-1 | <2.5 μm | 17% | Secondary & tertiary γ’, σ, η | below 1122 | [46,47] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manzoni, A.M.; Haas, S.; Daoud, H.; Glatzel, U.; Förster, C.; Wanderka, N. Tensile Behavior and Evolution of the Phases in the Al10Co25Cr8Fe15Ni36Ti6 Compositionally Complex/High Entropy Alloy. Entropy 2018, 20, 646. https://doi.org/10.3390/e20090646
Manzoni AM, Haas S, Daoud H, Glatzel U, Förster C, Wanderka N. Tensile Behavior and Evolution of the Phases in the Al10Co25Cr8Fe15Ni36Ti6 Compositionally Complex/High Entropy Alloy. Entropy. 2018; 20(9):646. https://doi.org/10.3390/e20090646
Chicago/Turabian StyleManzoni, Anna Maria, Sebastian Haas, Haneen Daoud, Uwe Glatzel, Christiane Förster, and Nelia Wanderka. 2018. "Tensile Behavior and Evolution of the Phases in the Al10Co25Cr8Fe15Ni36Ti6 Compositionally Complex/High Entropy Alloy" Entropy 20, no. 9: 646. https://doi.org/10.3390/e20090646
APA StyleManzoni, A. M., Haas, S., Daoud, H., Glatzel, U., Förster, C., & Wanderka, N. (2018). Tensile Behavior and Evolution of the Phases in the Al10Co25Cr8Fe15Ni36Ti6 Compositionally Complex/High Entropy Alloy. Entropy, 20(9), 646. https://doi.org/10.3390/e20090646





