New Binary Locally Repairable Codes with Locality 2 and Uneven Availabilities for Hot Data
Abstract
:1. Introduction
2. Preliminaries
2.1. Notations and Definitions
2.2. Locally Repairable Codes
2.3. Bounds for Optimality of LRCs
3. A New Family of BLRCs
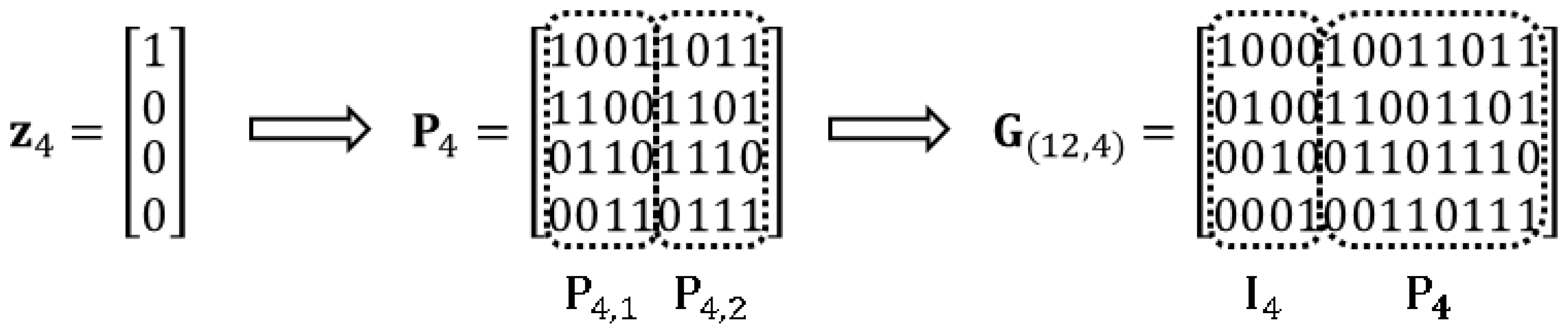
3.1. Construction of New BLRCs
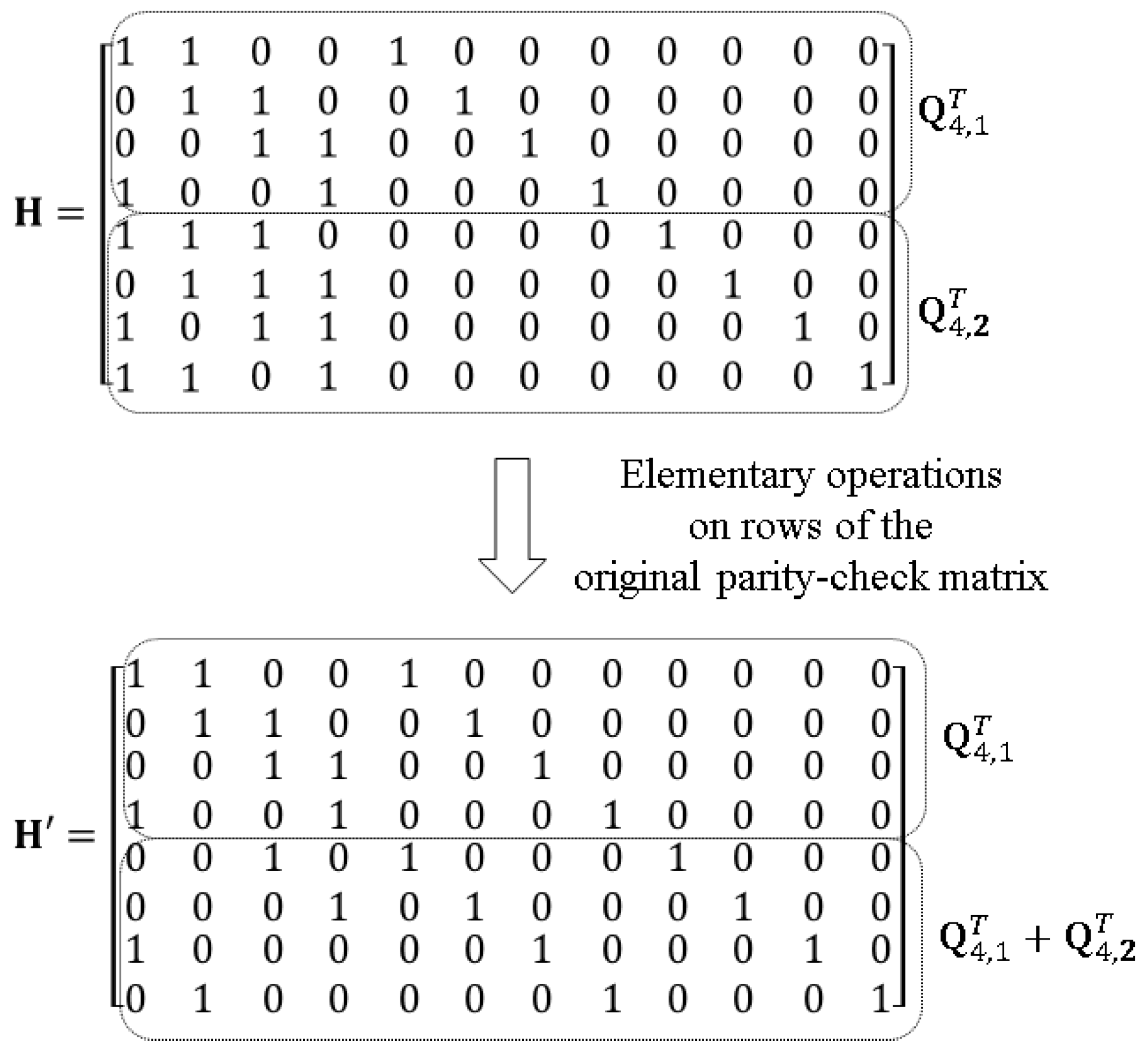
3.2. Locality and Availability of the Proposed BLRCs
3.3. Optimality of the Proposed BLRCs
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kim, S.-H.; Lee, I.-Y. Block access token renewal scheme based on secret sharing in Apache Hadoop. Entropy 2014, 16, 4185–4198. [Google Scholar] [CrossRef]
- Tamura, Y.; Yamada, S. Reliability analysis based on a jump diffusion model with two Wiener processes for cloud computing with big data. Entropy 2015, 17, 4533–4546. [Google Scholar] [CrossRef]
- Weatherspoon, H.; Kubiatowicz, J. Erasure coding vs. replication: A quantitative comparison. In Proceedings of the 1st International Workshop on Peer-to-Peer Systems, Cambridge, MA, USA, 7–8 March 2002; pp. 328–337. [Google Scholar]
- Dimakis, A.G.; Godfrey, P.B.; Wu, Y.; Wainwright, M.J.; Ramchandran, K. Network coding for distributed storage systems. IEEE Trans. Inf. Theory 2010, 56, 4539–4551. [Google Scholar] [CrossRef]
- Rouayheb, S.E.; Ramchandran, K. Fractional repetition codes for repair in distributed storage systems. In Proceedings of the 48th Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 29 September–1 October 2010; pp. 1510–1517. [Google Scholar]
- Park, H.; Kim, Y.-S. Construction of fractional repetition codes with variable parameters for distributed storage systems. Entropy 2016, 18, 441. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Park, H.; No, J.-S. Construction of new fractional repetition codes from relative difference sets with λ=1. Entropy 2017, 19, 563. [Google Scholar] [CrossRef]
- Gopalan, P.; Huang, C.; Simitci, H.; Yekhanin, S. On the locality of codeword symbols. IEEE Trans. Inf. Theory 2012, 58, 6925–6934. [Google Scholar] [CrossRef]
- Pamies-Juarez, L.; Hollmann, H.D.L.; Oggier, F. Locally Repairable Codes with Multiple Repair Alternatives. 2013. Available online: https://arxiv.org/abs/1302.5518 (accessed on 22 August 2018).
- Kralevska, K.; Gligoroski, D.; Øverby, H. Balanced locally repairable codes. In Proceedings of the 9th International Symposium on Turbo Codes and Iterative Information Processing, Brest, France, 5–9 September 2016; pp. 280–284. [Google Scholar]
- Wang, A.; Zhang, Z.; Liu, M. Achieving arbitrary locality and availability in binary codes. In Proceedings of the IEEE International Symposium on Information Theory, Hong Kong, China, 14–19 June 2015; pp. 1866–1870. [Google Scholar]
- Rawat, A.; Papailiopoulos, D.S.; Dimakis, A.G.; Vishwanath, S. Locality and availability in distributed storage. IEEE Trans. Inf. Theory 2016, 62, 4481–4493. [Google Scholar] [CrossRef]
- Tamo, I.; Barg, A. A family of optimal locally recoverable codes. IEEE Trans. Inf. Theory 2014, 60, 4661–4676. [Google Scholar] [CrossRef]
- Shahabinejad, M.; Khabbazian, M.; Ardakani, M. A class of binary locally repairable codes. IEEE Trans. Commun. 2016, 64, 3182–3193. [Google Scholar] [CrossRef]
- Nam, M.-Y.; Song, H.-Y. Binary locally repairable codes with minimum distance at least six based on partial t-spreads. IEEE Commun. Lett. 2017, 21, 1683–1686. [Google Scholar] [CrossRef]
- Cadambe, V.R.; Mazumdar, A. Bounds on the size of locally recoverable codes. IEEE Trans. Inf. Theory 2015, 61, 5787–5794. [Google Scholar] [CrossRef]
- Silberstein, N.; Zeh, A. Optimal binary locally repairable codes via anticodes. In Proceedings of the IEEE International Symposium on Information Theory, Hong Kong, China, 14–19 June 2015; pp. 1247–1251. [Google Scholar]
- Kadhe, S.; Sprintson, A. Codes with unequal locality. In Proceedings of the IEEE International Symposium on Information Theory, Barcelona, Spain, 10–15 July 2016; pp. 435–439. [Google Scholar]
- Zeh, A.; Yaakobi, E. Bounds and constructions of codes with multiple localities. In Proceedings of the IEEE International Symposium on Information Theory, Barcelona, Spain, 10–15 July 2016; pp. 640–644. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, K.-S.; Park, H.; No, J.-S. New Binary Locally Repairable Codes with Locality 2 and Uneven Availabilities for Hot Data. Entropy 2018, 20, 636. https://doi.org/10.3390/e20090636
Lee K-S, Park H, No J-S. New Binary Locally Repairable Codes with Locality 2 and Uneven Availabilities for Hot Data. Entropy. 2018; 20(9):636. https://doi.org/10.3390/e20090636
Chicago/Turabian StyleLee, Kang-Seok, Hosung Park, and Jong-Seon No. 2018. "New Binary Locally Repairable Codes with Locality 2 and Uneven Availabilities for Hot Data" Entropy 20, no. 9: 636. https://doi.org/10.3390/e20090636
APA StyleLee, K.-S., Park, H., & No, J.-S. (2018). New Binary Locally Repairable Codes with Locality 2 and Uneven Availabilities for Hot Data. Entropy, 20(9), 636. https://doi.org/10.3390/e20090636







