1. Introduction
The discovery of different fluctuation theorems (FTs) over the last two decades constitutes a major progress in nonequilibrium physics [
1,
2,
3,
4,
5,
6]. These relations are exact constraints that some fluctuating quantities satisfy arbitrarily far from equilibrium. They have been verified experimentally in many different contexts, ranging from biophysics to electronic circuits [
7]. However, they come in different forms: detailed fluctuation theorems (DFTs) or integral fluctuation theorems (IFTs), and concern various types of quantities. Understanding how they are related and to what extent they involve mathematical quantities or interesting physical observables can be challenging.
The aim of this paper is to provide a simple yet elegant method to identify a class of finite-time DFTs for time-inhomogeneous Markovian jump processes. The method is based on splitting the entropy production (EP) in three contributions by introducing a reference probability mass function (PMF). The latter is parametrized by the time-dependent driving protocol, which renders the dynamics time-inhomogeneous. The first contribution quantifies the EP as if the system were in the reference PMF, the second the extent to which the reference PMF changes with the driving protocol, and the last the mismatch between the actual and the reference PMF. We show that when the system is initially prepared in the reference PMF, the joint probability distribution for the first two terms always satisfies a DFT. We then show that various known DFTs can be immediately recovered as special cases. We emphasize at which level our results make contact with physics and also clarify the nontrivial connection between DFTs and EP fluctuations. Our EP splitting is also shown to be connected to information theory. Indeed, it can be used to derive a generalized Landauer principle identifying the minimal cost needed to move the actual PMF away from the reference PMF. While unifying, we emphasize that our approach by no means encompasses all previously derived FTs and that other FT generalizations have been made (e.g., [
5,
8,
9,
10,
11]).
The plan of this paper is as follows. Time-inhomogeneous Markov jump processes are introduced in
Section 2. Our main results are presented in
Section 3: We first introduce the EP as a quantifier of detailed balance breaking, and we then show that by choosing a reference PMF, a splitting of the EP ensues. This enables us to identify the fluctuating quantities satisfying a DFT and an IFT when the system is initially prepared in the reference PMF. While IFTs hold for arbitrary reference PMFs, DFTs require reference PMFs to be solely determined by the driving protocol encoding the time dependence of the rates. The EP decomposition is also shown to lead to a generalized Landauer principle. The remaining sections are devoted to selecting specific reference PMFs and showing that they give rise to interesting mathematics or physics: In
Section 4 the steady-state PMF of the Markov jump process is chosen, giving rise to the adiabatic–nonadiabatic split of the EP [
12]. In
Section 5 the equilibrium PMF of a spanning tree of the graph defined by the Markov jump process is chosen, and gives rise to a cycle–cocycle decomposition of the EP [
13]. Physics is introduced in
Section 6, and the properties that the Markov jump process must satisfy to describe the thermodynamics of an open system are described. In
Section 7 the microcanonical distribution is chosen as the reference PMF, leading to the splitting of the EP into system and reservoir entropy change. Finally, in
Section 8, the generalized Gibbs equilibrium PMF is chosen as a reference and leads to a conservative–nonconservative splitting of the EP [
14]. Conclusions are finally drawn, and some technical proofs are discussed in the appendices.
2. Markov Jump Process
We introduce time-inhomogeneous Markovian jump processes and set the notation.
We consider an externally driven open system described by a finite number of states, which we label by
n. Allowed transitions between pairs of states are identified by directed edges,
where the label
indexes different transitions between the same pair of states (e.g., transitions due to different reservoirs). The evolution in time of the probability of finding the system in the state
n,
, is ruled by the
master equation (ME):
where the elements of the
rate matrix are represented as
The latter is written in terms of stochastic transition rates,
, and the functions
which map each transition to the state from which it originates (origin) and to which it leads (target), respectively. The off-diagonal entries of the rate matrix (the first term in brackets) give the probability per unit time to transition from
m to
n. The diagonal ones (second term in brackets) are the escape rates denoting the probability per unit time of leaving the state
m. For thermodynamic consistency, we assume that each transition
is reversible, namely if
is finite, the corresponding backward transition
is allowed and additionally has a finite rate
. For simplicity, we also assume that the rate matrix is irreducible at all times, so that the stochastic dynamics is ensured to be ergodic. The Markov jump process is said to be
time-inhomogeneous when the transition rates depend on time. The driving
protocol value determines the values of all rates at time
t,
.
The ME (
2) can be rewritten as a continuity equation:
where we introduced the averaged transition
probability fluxes,
and the
incidence matrix D,
which couples each transition to the pair of states that it connects, and hence encodes the
network topology. On the graph identified by the vertices
and the edges
, it can be viewed as a (negative) divergence operator when acting on edge-space vectors—as in the ME (
5)—or as a gradient operator when acting on vertex-space vectors. It satisfies the symmetry
.
Example
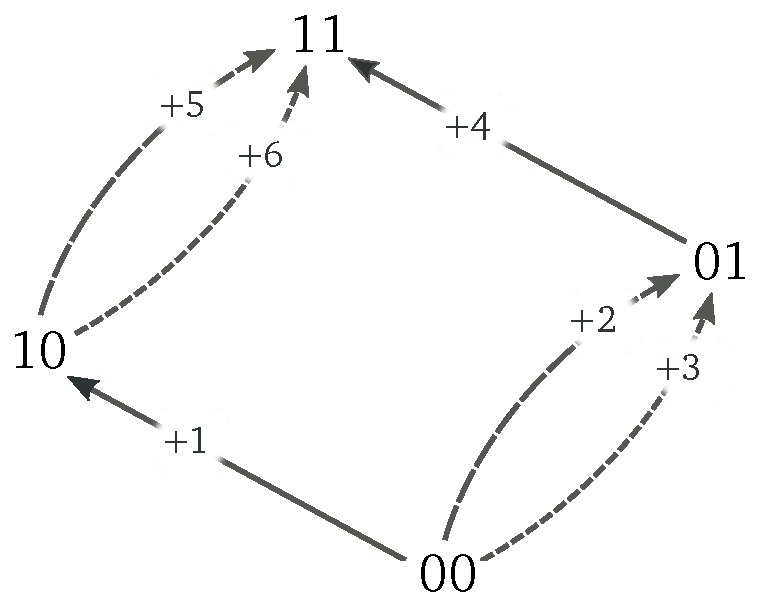
Let us consider the Markov jump process on the network in
Figure 1, in which only the six forward transitions are depicted. It is characterized by four states, {00,01,10,11}, connected by transitions as described by the incidence matrix:
Backward transitions are obtained from .
Notation
From now on, upper–lower indices and Einstein summation notation will be used: repeated upper–lower indices implies the summation over all the allowed values for those indices. Time derivatives are denoted by “” or “”, whereas the overdot “” is reserved for rates of change of quantities that are not exact time derivatives of state functions. We also take the Boltzmann constant equal to 1.
4. Adiabatic–Nonadiabatic Decomposition
We now provide a first instance of reference PMF based on the fixed point of the Markov jump process.
The Perron–Frobenius theorem ensures that the ME (
5) has, at all times, a unique instantaneous
steady-state PMFWhen using this PMF as the reference,
=
, we recover the
adiabatic–nonadiabatic EP rate decomposition [
12,
16,
21,
22,
23,
24]. More specifically, the nonconservative term gives the
adiabatic contribution which is zero only if the steady state satisfies detailed balance, and the conservative term gives the
nonadiabatic contribution which characterizes transient and driving effects. A specific feature of this decomposition is that both terms are non-negative, as proved in
Appendix C:
and
. In turn, the nonadiabatic contribution decomposes into a relative entropy term and a driving one.
Provided that the forward and backward processes start in the steady state corresponding to the initial value of the respective protocol, the general DFT and IFT derived in Equation (
32) and Equation (
34) hold for the adiabatic and driving contributions of the adiabatic–nonadiabatic EP decomposition [
12,
21].
In detailed-balanced systems, the adiabatic contribution is vanishing,
, and we obtain a FT for the sole driving contribution:
The celebrated Crooks’ DFT [
25,
26,
27] and Jarzynski’s IFT [
28] are of this type.
Additional FTs
Due to the particular mathematical properties of the steady-state PMF, additional FTs for the adiabatic and driving terms ensue. These are not covered by our main DFT, Equation (
32), and their proofs are discussed in
Appendix D.
For the former, the forward process is produced by the original dynamics initially prepared in an arbitrary PMF. The backward process instead has the same initial PMF and the same driving protocol as the forward process, but the dynamics is governed by the rates
At any time, the following DFT relates the two processes,
where
is the probability of observing
adiabatic EP during the backward process. The Speck–Seifert IFT for the housekeeping heat is the IFT version of this DFT [
29].
For the driving term, the forward process is again produced by the original dynamics, but now initially prepared in a steady state. The backward process is instead produced by the rates (
45) with time-reversed driving protocol and the system must initially be prepared in a steady state. Under these conditions, one has
where
is the probability of observing
driving EP during the backward process. The Hatano–Sasa IFT [
30] is the IFT version of this DFT.
5. Cycle–Cocycle Decomposition
We proceed by providing a second instance of reference PMF based on the equilibrium PMF for a spanning tree of the graph defined by the incidence matrix of the Markov jump process.
We partition the edges of the graph into two disjoint subsets:
and
. The former identifies a
spanning tree, namely a minimal subset of paired edges,
, that connects all states. These edges are called
cochords. All the other edges form
, and are called
chords. Equivalently,
is a maximal subset of edges that does not enclose any cycle—the trivial loops composed by forward and backward transitions,
, are not regarded as cycles. The graph obtained by combining
and
identifies one and only one cycle, denoted by
, for
. Algebraically, cycles are characterized as:
where
, for
, represent the vectors in the edge space whose entries are all zero except for those corresponding to the edges of the cycle, which are equal to one.
We now note that if
were the sole allowed transitions, the PMF defined as follows would be an equilibrium steady state [
15]:
where
is a normalization factor, and
denotes the spanning tree
rooted in
n, namely the set of edges of
that are oriented towards the state
n. Indeed,
would satisfy the property of detailed balance, Equation (
9):
We now pick this equilibrium PMF as a reference for our EP decomposition,
. However, in order to derive the specific expressions for
and
, the following result is necessary: the edge probability fluxes can be decomposed as
where
denotes the canonical basis of the edge vector space:
[
31]. Algebraically, this decomposition hinges on the fact that the set
is a basis of the edge vector space [
13]. Note that for
, the only nonvanishing contribution in Equation (
51) comes from the cycle identified by
e, and hence
. The coefficients
are called
cocycle fluxes for the cochords,
, and
cycle fluxes for the chords,
. They can be understood as follows [
13]: removing a pair of edges,
e and
, from the spanning tree (
) disconnects two blocks of states. The cocycle flux
of that edge is the probability flowing from the block identified by the origin of
e,
, to that identified by the target of
e,
. Instead, the cycle flux
of an edge,
, quantifies the probability flowing along the cycle formed by adding that edge to the spanning tree. Graphical illustrations of cocycle and cycle
currents,
, can be found in Reference [
13].
We can now proceed with our main task. Using Equations (
48) and (
49), we verify that
where
is the cycle affinity related to
. It follows that
from which the nonconservative contribution readily follows:
In the last equality, we used the property of cycle fluxes discussed after Equation (
51). Hence, the nonconservative contribution accounts for the dissipation along network cycles. In turn, combining Equation (
16) with Equations (
51) and (
52), one obtains the conservative contribution
which accounts for the dissipation along cocycles. Using these last two results, the EP decomposition (
14) becomes the
cycle–cocycle decomposition found in Reference [
13]:
As for all decompositions, the conservative contribution—here the cocycle one—vanishes at steady state in the absence of driving. The cycle contribution instead disappears in detailed-balanced systems, when all the cycle affinities vanish. This statement is indeed the
Kolmogorov criterion for detailed balance [
32,
33].
The fluxes decomposition Equation (
51) is also valid at the trajectory level, where the cycle and cocycle fluxes become fluctuating instantaneous fluxes,
. Obviously, the same holds true for the cycle–cocycle EP decomposition. Therefore, if the system is in an equilibrium PMF of type (
49) at the beginning of the forward and the backward process, a DFT and an IFT hold by applying Equations (
32) and (
34). Note that the fluctuating quantity appearing in the DFT,
, can be interpreted as the EP of the extended process in which, at time
t, the driving is stopped, all transitions in
are shut down, and the system is allowed to relax to equilibrium—which is the initial PMF of the backward process.
It is worth mentioning that one can easily extend the formulation of our DFT by considering the joint probability distribution for each subcontribution of
and
antisymmetrical under time reversal. This can be shown using either the proof in
Appendix B [
16], or that in
Appendix A [
14]. In the case of the cycle–cocycle decomposition, it would lead to
which is a generalization of the DFT derived in Reference [
34] to time-inhomogeneous systems. In turn, the latter is a generalization of the steady-state DFT derived by Andrieux and Gaspard in Reference [
35] to finite times.
Example
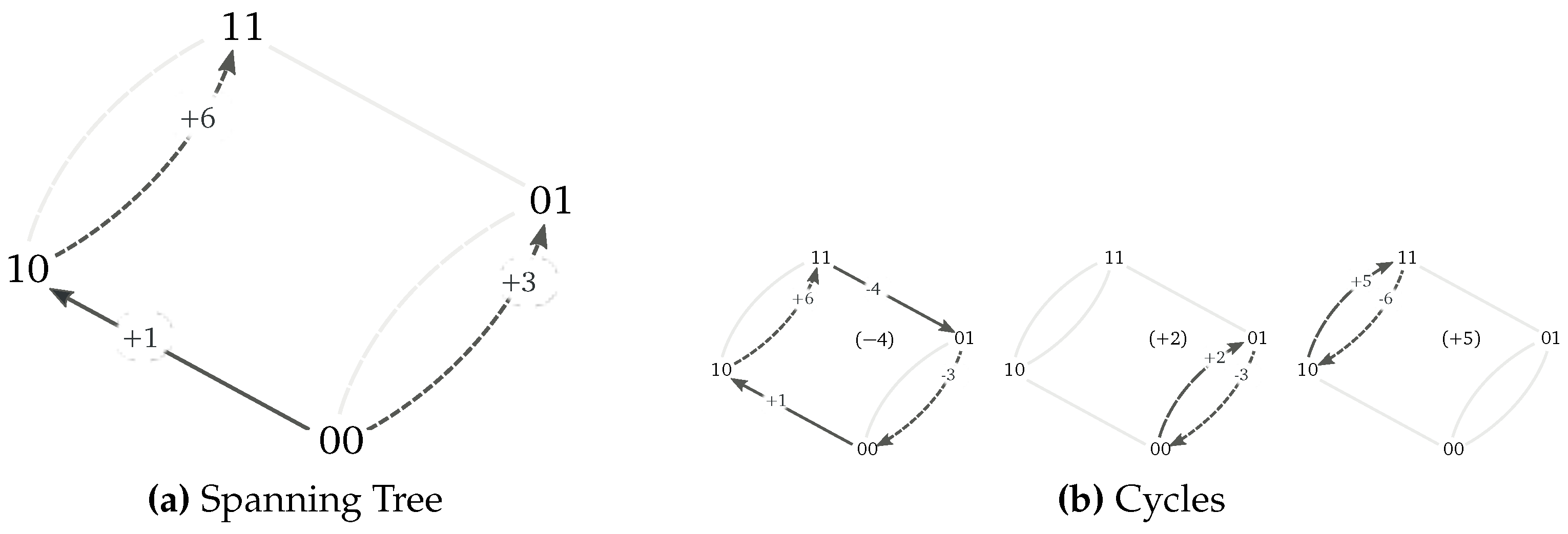
A spanning tree for the network in
Figure 1 is depicted in
Figure 3a. The cycles defined by the corresponding chords are depicted in
Figure 3b. Algebraically, these cycles are represented as
where the negative entries must be regarded as transitions performed in the backward direction. The corresponding affinities, which determine the nonconservative contribution (
55), hence read:
The affinities corresponding to the cycles taken in the backward direction follow from
. Regarding the expression of the cocycle fluxes, it can be checked that they are equal to
by expanding Equation (
57) into Equation (
10).
6. Stochastic Thermodynamics
The results obtained until this point are mathematical and have a priori no connection to physics. We now specify the conditions under which a Markov jump process describes the dynamics of an open physical system in contact with multiple reservoirs. This will enable us to introduce physically motivated decompositions and derive DFTs with a clear thermodynamic interpretation.
Each system state,
n, is now characterized by given values of some
system quantities,
, for
, which include the internal energy,
, and possibly additional ones (see
Table 2 for some examples). These must be regarded as globally
conserved quantities, as their change in the system is always balanced by an opposite change in the reservoirs. When labeling the reservoirs with
, for
, the
balance equation for
along the transition
e can be written as:
The lhs is the overall change in the system, whereas
denotes the changes due to internal transformations (e.g., chemical reactions [
36,
37]), and
quantifies the amount of
supplied by the reservoir
r to the system along the transition
e. For the purposes of our discussion, we introduce the index
—i.e.,
the conserved quantity exchanged with the reservoir r—and define the matrix
whose entries are
. All indices used in the following discussion are summarized in
Table 3. Microscopic reversibility requires that
. Note that more than one reservoir may be involved in each transition (see
Figure 4).
In addition to the trivial set of conserved quantities
, the system may be characterized by some additional ones, which are
specific for each system. We now sketch the systematic procedure to identify these quantities and the corresponding conservation laws [
14,
38]. Algebraically, conservation laws can be identified as a maximal set of independent vectors in the
y-space,
, for
, such that
Indeed, the quantities
, for
, are combinations of exchange contributions
, for
, which vanish along all cycles. They must therefore identify some state variables,
, for
, in the same way curl-free vector fields are conservative and identify scalar potentials:
This equation can be regarded as the balance equation for the conserved quantities. In the absence of internal transformations,
, trivial conservation laws correspond to
, so that the balance Equations (
62) are recovered. Notice that each
is defined up to a reference value.
Each reservoir
r is characterized by a set of
entropic intensive fields conjugated to the exchange of the system quantities
,
for
(e.g., [
39] § 2–3). A short list of
–
conjugated pairs is reported in
Table 2. The thermodynamic consistency of the stochastic dynamics is ensured by the
local detailed balance,
It relates the log ratio of the forward and backward transition rates to the entropy change in the reservoirs resulting from the transfer of system quantities during that transition. This entropy change is evaluated using equilibrium thermodynamics (in the reservoirs), and reads
. The second term on the rhs is the internal entropy change occurring during the transition, as
quantifies the internal entropy of the state
n. This term can be seen as the outcome of a coarse-graining procedure over a finer description in which multiple states with the same system quantities are collected in one single
n [
40]. Using Equation (
65), the affinities, Equation (
11), can be rewritten as:
This relation shows that the affinity is the entropy change in all reservoirs plus the system entropy change. In other words, while Equation (
64) characterizes the balance of the conserved quantities along the transitions, Equation (
66) characterizes the corresponding lack of balance for entropy, namely the second law.
As for the transition rates, the changes in time of the internal entropy S, the conserved quantities (hence ), and their conjugated fields , are all encoded in the protocol function . Physically, this modeling describes the two possible ways of controlling a system: either through or S which characterize the system states, or through which characterize the properties of the reservoirs.
Example
We illustrate the role of system-specific conservation laws by considering the double quantum dot (QD) depicted in
Figure 5a [
41,
42,
43], whose network of transition and energy landscape are drawn in
Figure 1 and
Figure 5b, respectively. Electrons can enter empty dots from the reservoirs, but cannot jump from one dot to the other. When the two dots are occupied, an interaction energy,
u, arises. Energy,
, and total number of electrons,
, characterize each state of the system:
where the first entry in
n refers to the occupancy of the upper dot, and the second to the lower.
The entries of the matrix
for the forward transitions are:
(see
Figure 1), whereas the entries related to backward transition follow from
. For instance, along the first transition the system gains
energy and 1 electron from the reservoir 1. The vector of entropic intensive fields is given by
Since the QDs and the electrons have no internal entropy,
for all
n, the local detailed balance property, Equation (
65), can be easily recovered from the product
. From a stochastic dynamics perspective, this property arises when considering fermionic transition rates, namely
and
for electrons entering and leaving the dot.
A maximal set of independent vectors in
y-space satisfying Equation (
63) is composed of
The first vector identifies the energy state variable,
:
The other two instead give the occupancy of the upper and lower dots,
and
:
A posteriori, we see that these conservation laws arise from the fact that no electron transfer from one dot to the other is allowed. The total occupancy of the system, , is recovered from the sum of the last two vectors.
Now that a nonequilibrium thermodynamics has been built on top of the Markov jump process, we can proceed by considering two physical relevant .
7. System–Reservoirs Decomposition
We start by considering a microcanonical PMF as reference:
where
is the
Boltzmann’s equilibrium entropy. With this choice, the reference affinities become sums of entropy changes in the reservoirs
and hence the nonconservative contribution becomes the rate of entropy change in all reservoirs
For the conservative contribution, one instead obtains:
Using Equation (
17), it can be rewritten in terms of the Gibbs–Shannon entropy,
and the Boltzmann entropy. Indeed,
and
so that
The conservative contribution thus contains changes in the system entropy caused by the dynamics and the external drive.
The EP decomposition (
14) with Equations (
76) and (
81) is thus the well-known
system–reservoir decomposition (i.e., the traditional
entropy balance). Since the same decomposition holds at the trajectory level, if the initial PMF of the forward and backward processes are microcanonical, the DFT and IFT hold by applying Equations (
32) and (
34). When the driving does not affect the internal entropy of the system states
, the DFT and IFT hold for the reservoir entropy alone. Finally, the fluctuating quantity appearing in the DFT,
, can be interpreted as the EP of the extended process in which, at time
t, the driving is stopped, all temperatures are raised to infinity,
, and the system is allowed to relax to equilibrium—the initial PMF of the backward process.
8. Conservative–Nonconservative Decomposition
We now turn to a reference PMF which accounts for conservation laws: the generalized Gibbs PMF.
To characterize this PMFs, we observe that since
are linearly independent (otherwise we would have linearly dependent conserved quantities), one can always identify a set of
y’s, denoted by
, such that the matrix whose rows are
, for
, is nonsingular. We denote by
for
, the columns of the inverse matrix. All other
y’s are denoted by
. Using the splitting
–
and the properties of
, in combination with the balance equation for conserved quantities, Equation (
64), the local detailed balance (
65) can be decomposed as
where
are the system-specific intensive fields conjugated to the conserved quantities, and
are differences of intensive fields called nonconservative
fundamental forces. Indeed, these nonconservative forces are responsible for breaking detailed balance. When they all vanish,
for all
, the system is indeed detailed balanced and the PMF
with
, satisfies the detailed balance property (
9). The potential corresponding to Equation (
85),
, is minus the
Massieu potential which is constructed by using all conservation laws (e.g., [
39] §§ 5-4 and 19-1, [
44] § 3.13). Choosing the PMF (
85) as a reference,
, the reference affinity straightforwardly ensues from Equation (
82),
Hence,
where
are the fundamental currents conjugated to the forces. For the conservative contribution, one obtains
When written as in Equation (
17), its two contributions are:
which relates the equilibrium Massieu potential to its averaged nonequilibrium counterpart; and
which quantifies the dissipation due to external manipulations of
, the fields
, and the conserved quantities
. We emphasize that since
encompasses all conserved quantities,
captures all dissipative contributions due to conservative forces. Hence,
consists of a minimal number,
, of purely nonconservative contributions. The EP decomposition Equation (
14) with Equations (
87) and (
89) is the
conservative–nonconservative decomposition of the EP obtained in Reference [
14].
The conservative–nonconservative splitting of the EP can also be made at the trajectory level. Hence, if the initial condition of the forward and backward process is of the form (
85), the DFT and IFT given by Equations (
32) and (
34) hold.
Here too, the fluctuating quantity appearing in the DFT,
, can be interpreted as the EP of an extended process including relaxation, but for nonisothermal processes the procedure can be significantly more involved. The details of this discussion can be found in Reference [
14].
Example
We now provide the expressions of
and
for the double QD discussed in the previous example (
Figure 5). Therefore, we split the set
in
and
, which is valid since the matrix whose entries are
is an identity matrix (see Equation (
70)). The fields conjugated with the complete set of conservation laws, Equation (
83), are:
from which the reference potential of the state
n, Equation (
85), follows
Instead, the fundamental forces, Equation (
84), are given by
from which the reference affinities follow (Equation (
86)). The first two forces drive the energy flowing into the first reservoir from the second and third ones, respectively, whereas the third force drives the electrons flowing from the third to the second reservoir.
9. Conclusions
In this paper, we presented a general method to construct DFTs for Markov jump processes. The strategy to identify the fluctuating quantities which satisfy the DFT consists of splitting the EP in two by making use of a reference PMF. The choice of the reference PMF is arbitrary for IFTs, but must solely depend on the driving protocol for DFTs. Out of the infinite number of FTs that can be considered, we tried to select those that have interesting mathematical properties or that can be expressed in terms of physical quantities when the Markov jump process is complemented with a thermodynamic structure.
Table 1 summarizes the terms of to the EP for each of our choices. We also emphasized that the EP always satisfies an IFT but generically not a DFT. Connections to information theory were also made by formulating a generalized Landauer principle.
We do not claim to have been exhaustive, and many other reference PMFs may be interesting. We can mention at least two more interesting cases. By considering the steady-state PMF which is obtained when removing some edges from the graph (but not all chords as in
Section 5), the marginal thermodynamic theory presented in References [
45,
46] emerges. One can also consider a reference PMF in between the microcanonical PMF, which takes no conserved quantity into account, and the generalized Gibbs one, which takes them all into account. This happens for instance when only the obvious conserved quantities are accounted for,
, as discussed in Reference [
47]. In this case, one uses the fields of a given reservoir to define the reference equilibrium potential
where
is determined by the normalization. The number of nonconservative forces appearing in
will be
. However, in case additional conservation laws are present (
), some of these forces are dependent on others and their number will be larger than the minimal,
.