Factor analysis is a statistical method for extracting simple structures to explain inter-relations between manifest and latent variables. The origin dates back to the works of [
1], and the single factor model was extended to the multiple factor model [
2]. These days, factor analysis is widely applied in behavioral sciences [
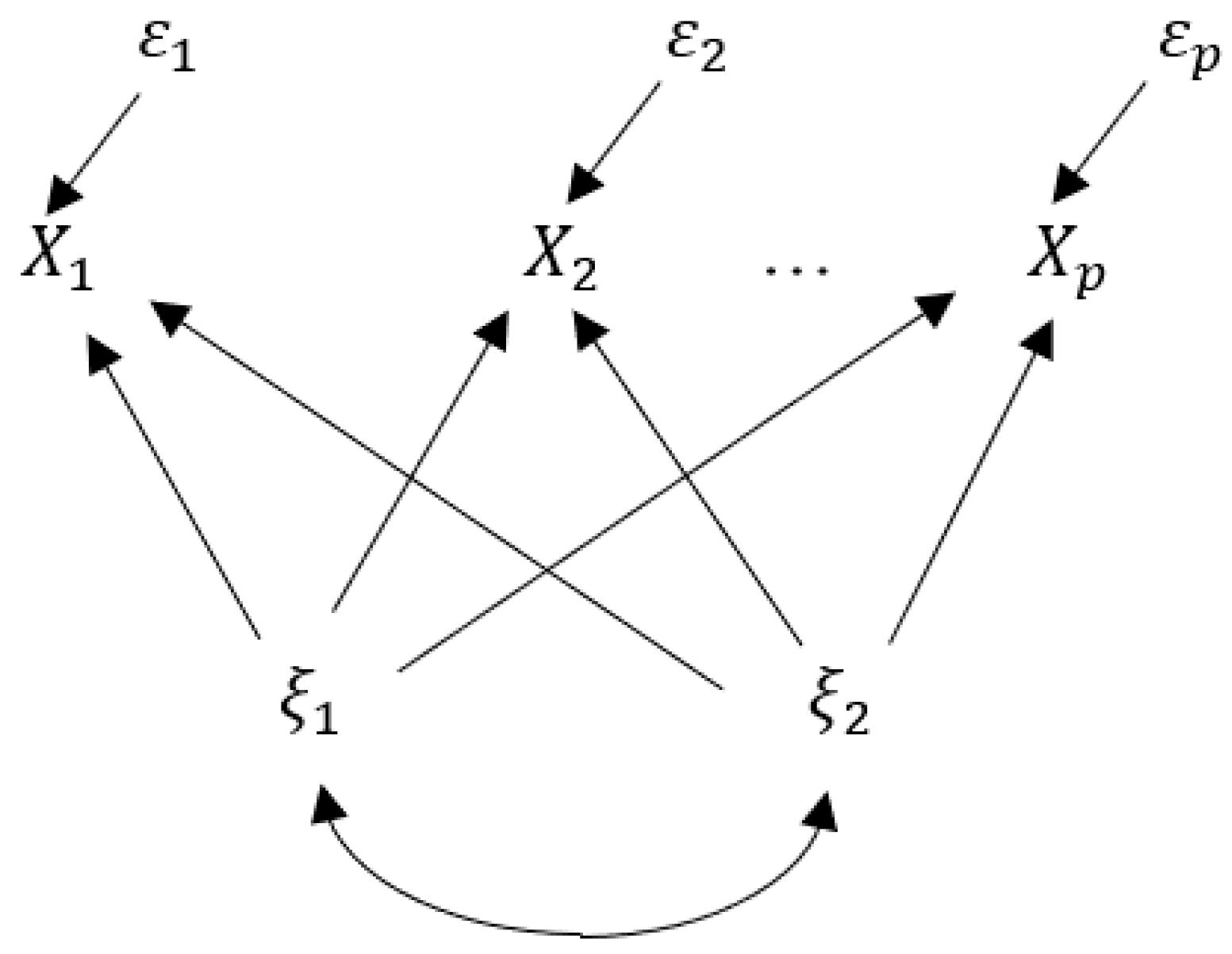
3]; hence, it is important to interpret the extracted factors and is critical to explain how such factors influence manifest variables, that is, measurement of factor contribution. Let
be manifest variables;
latent variables (common factors);
unique factors related to
; and let
be factor loadings that are weights of factors
to explain
. Then, the factor analysis model is given as follows:
where
For the simplicity of discussion, common factors
are assumed to be mutually independent in this section, that is, we first consider an orthogonal factor analysis model. In the conventional approach, the contribution of factor
to all manifest variables
,
, is defined as follows:
The above definition of factor contributions is based on the following decomposition of the total of variances of the observed variables
[
4] (p. 59):
What physical meaning does the above quantity have? Applying it to the manifest variables observed, however, such a decomposition leads to scale-variant results. For this reason, factor contribution is usually considered on the standardized versions of manifest variables
. What does it mean to measure factor contributions by (2)? For standardized manifest variables
, we have
Then, (2) is the sum of the coefficients of determination for all standardized manifest variables
with respect to a single latent variable
. The squared correlation coefficients (3), that is,
, are the ratios of explained variances of a manifest variable
, and in this sense, they can be interpreted as the contributions (effects) of factors
to the manifest variable
. Although, what does the sum of these with respect to all manifest variables
, that is, (2), mean? The conventional method may be intuitively reasonable for measuring factor contributions; however, we think it is sensible to propose a method measuring factor contributions as the effects of factors on the manifest variable vector
, which are interpretable and have a theoretical basis. There is no research on this topic as far as we have searched. The present paper provides an entropy-based solution to the problem. Entropy is a useful concept to measure the uncertainty in the systems of random variables and sample spaces [
5] and it can be applied to measure multivariate dependences of random variables [
6,
7].
This paper proposes an entropy-based method for measuring factor contributions of
to the manifest variable vector
concerned, which can treat not only orthogonal factors, but also oblique cases. The present paper has five sections in addition to this section. In
Section 2, the conventional method for measuring factor contributions is reviewed.
Section 3 considers the factor analysis model in view of entropy and makes a preliminary discussion on measurement of factor contribution. In
Section 4, an entropy-based path analysis is applied as a tool to measure factor contributions. Contributions of factors
are defined by the total effects of the factors on the manifest variable vector, and the contributions are decomposed into those to manifest variables and subsets of manifest variables.
Section 5 illustrates the present method using a numerical example. Finally, in
Section 6, some conclusions are provided.