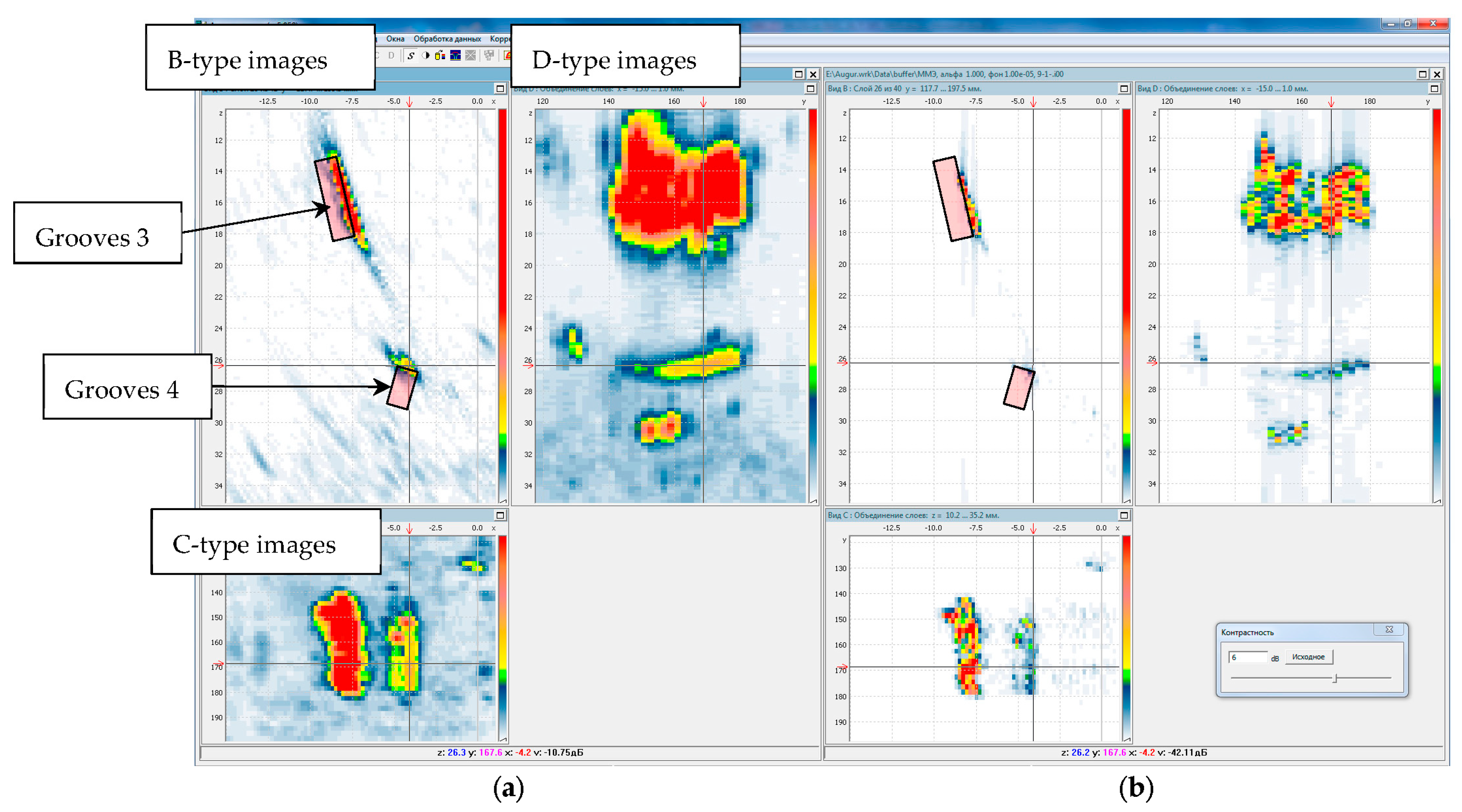
1. Introduction
At present, in the practice of ultrasonic testing (UT), flaw detectors using antenna arrays are widely used. Two technologies are used to visualize the internal volume of objects: phased antenna array (PAA) technology [
1], which is by far the most widely used technology and digital focusing with an antenna (DFA) technology [
2,
3]. In the paper [
4] devoted to the comparison of the capabilities of PAA and DFA flaw detectors, it was concluded that DFA technology is more promising from an algorithmic point of view, and therefore the paper is devoted to the processing of echoes measured by DFA flaw detectors. One can afford such an analogy: PAA technology can be compared with dough, from which one can quickly bake only bread, and DFA technology is flour, salt and other ingredients that will allow one to knead the dough for any bakery or confectionery, but in this case, one need more time to get the final result.
With single-sided access, typical for ultrasonic inspection practice, it is effective to use two antenna arrays of
Ne elements mounted on prisms and placed on the left (N–side) and on the right (P–side) from the welded joint to obtain a high-quality image of the reflectors. At the first stage of the application of the DFA-technology, echo signals are measured during the emission and reception by all combinations of pairs of elements of the antenna array [
5]. In the paper [
6], this mode of echo recording is called the dual scan mode, and in [
7] the full matrix capture (FMC) mode. Echoes, radiated by one element and accepted by all elements, are called a shot. The equipment should support work on the N–(arrow with a blue fill in
Figure 1), P–(arrow with a green fill) and NP–(arrows with a yellow fill) acoustic channels. The acquisition of echoes by an antenna array operating in the dual scan mode when it is mechanically moved is called a triple scan mode [
6], or the migration of the antenna array [
8]. Joint coherent processing of echoes by the C–SAFT method for different positions of the antenna array allows obtaining a high-quality image of the reflectors, which fundamentally distinguishes the algorithmic capabilities of DFA–flaw detectors from PAA-flaw detectors [
4]. For echoes measured in triple-scan mode, it is possible to obtain focused images beyond the near-range of the antenna array, which is especially important for objects with a thickness of more than 70 mm and for objects with high structural noise.
In the second stage, the image of the reflectors
is reconstructed by the Combined Synthetic Aperture Focusing Technique (C–SAFT) [
5,
8], based on the measured echoes, which can be modified to take into account the multipath propagation of ultrasound in the object with uneven boundaries and the presence of regions with different acoustic properties [
9,
10]. Sometimes the C–SAFT algorithm is called the Total Focusing Method (TFM) [
7]. In the Born approximation, the measured echo signals
can be represented as a system of linear Equations [
7]:
where
is the matrix which describes the propagation of the ultrasonic pulse,
—the additive noise of the measurements. Note that the vector
and
can be lexically formed from the matrices, and vice versa.
A fragment of the image having a maximum amplitude in the region of a sharp measurement of the acoustic properties of the monitoring object, for example, the boundary of the discontinuity, is called an indication. A false indication is an indication that does not correspond to the discontinuity boundary and is formed due to the limitations of the acoustic path model.
The higher the resolution of the reflector image and the lower the noise level, thus the number of reflectors, their sizes and type can be determined more accurately. This increases the reliability of the UT. The maximum entropy method, which is a nonlinear method, should increase the resolution and reduce the image noise level. The paper considers several options of the ME method application for obtaining high-quality image of reflectors and for increasing the speed of echo signal acquisition.
Section 2 summarizes the principles of reflectors image reconstruction from measured echoes.
Section 3 describes a model experiment in which the possibility of increasing the signal-to-noise ratio of reflectors in materials with high attenuation when compressing complex signals by the ME method is demonstrated. In
Section 4 a modification of the ME method for the case of a variable waveform measured in the TOFD mode is considered.
Section 5.1 describes the results of a model experiment for obtaining a super-resolution image for a set of point-type reflectors and for a pipeline fragment of 800 mm diameter with fracture models.
Section 5.2 presents the results of a model experiment to improve the image quality of flat-bottomed holes with a diameter of 1 mm.
Section 5.3 demonstrates the effectiveness of the ME method to produce an image of side drilled holes in a composite weld with a high level of structural noise.
Section 6 is devoted to improving the speed of echo acquisition in FMC mode using CDMA technology and the ME method.
3. Increasing the Signal-To-Noise Ratio of the Image Due to Deconvolution of Complex Signals
To increase the signal/noise ratio in objects with high absorption, complex signals can be emitted [
36] if the radiating electronics of the flaw detector support this mode. After the compression procedure, which can be performed using matched filtering, the longitudinal resolution of the image will be about the same as using simple signals of minimal duration, but the signal ratio increases many times over. The compression of the echo signals using a matched filter can result in “side lobes”. In the paper [
37], it was proposed to use the ME method for the compression of complex signals to achieve the effect of superresolution. Practical application of the ME method for compression of signals is impossible without a demonstration of its stability to the influence of noise.
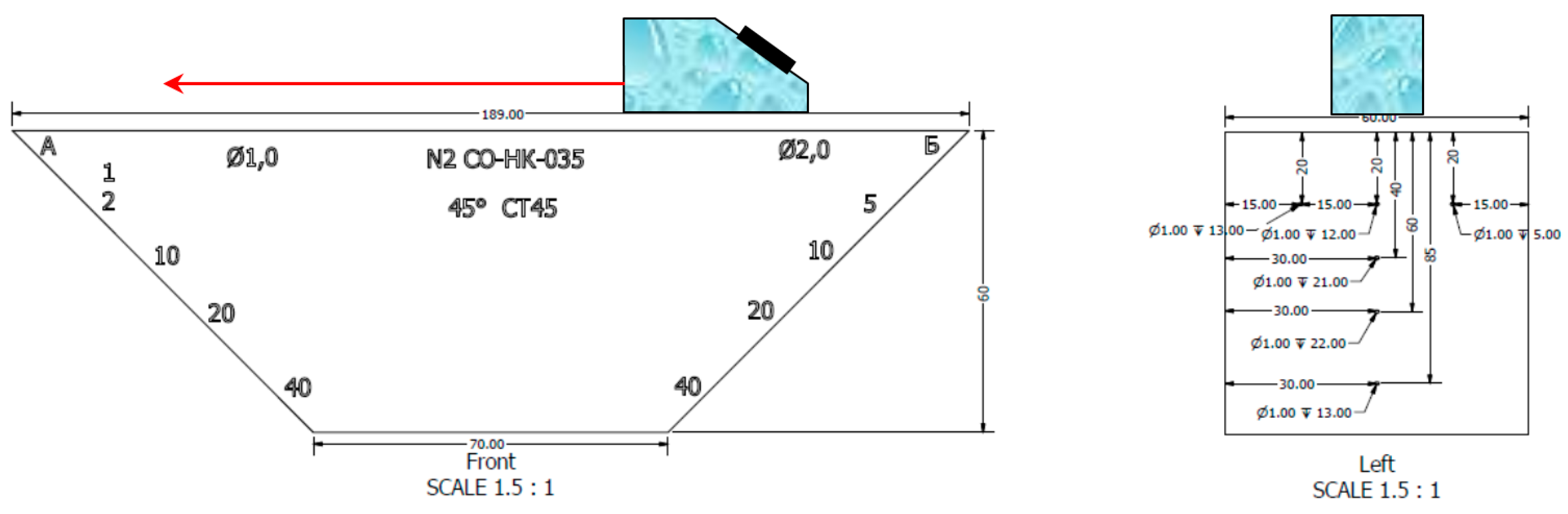
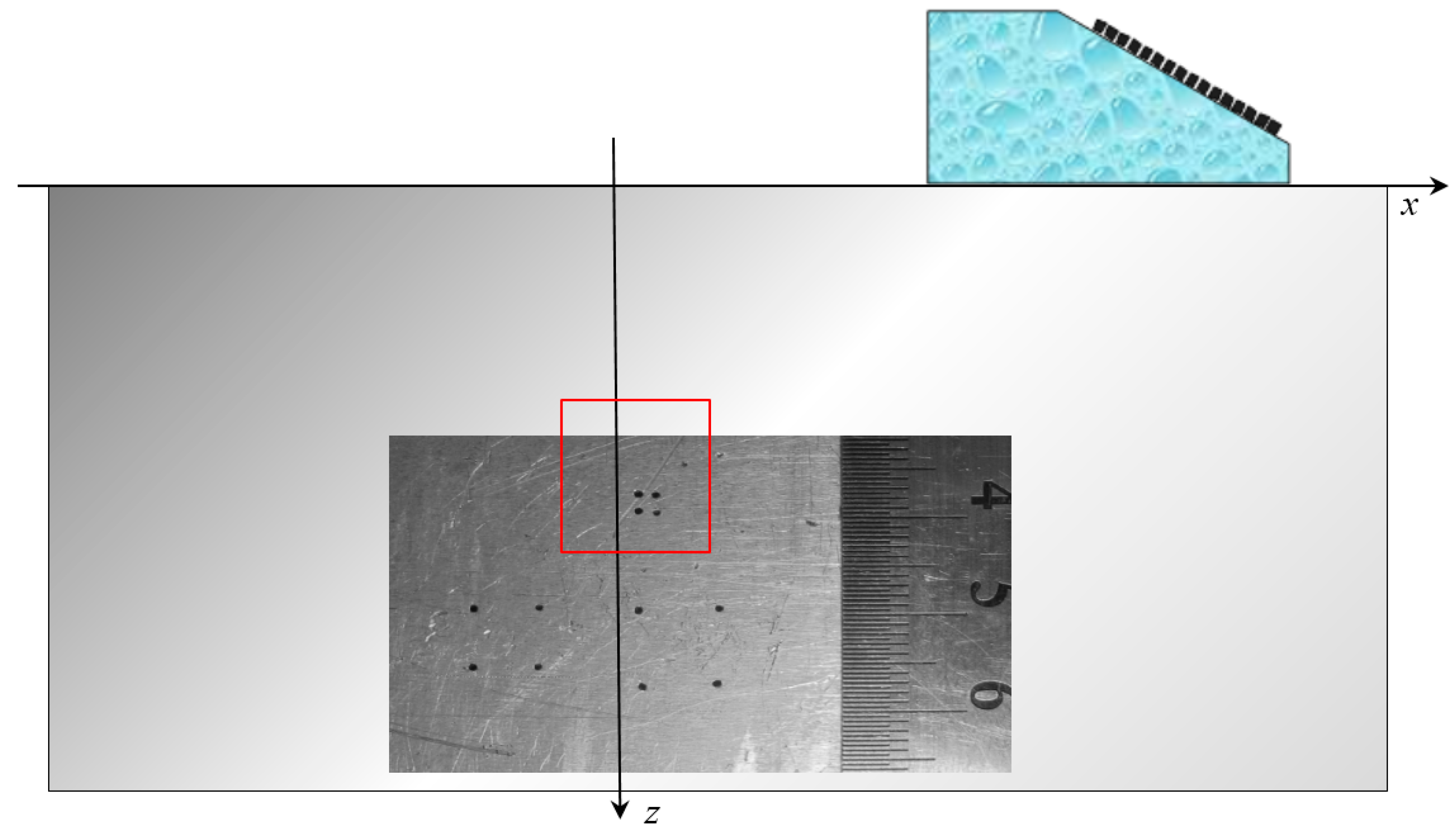
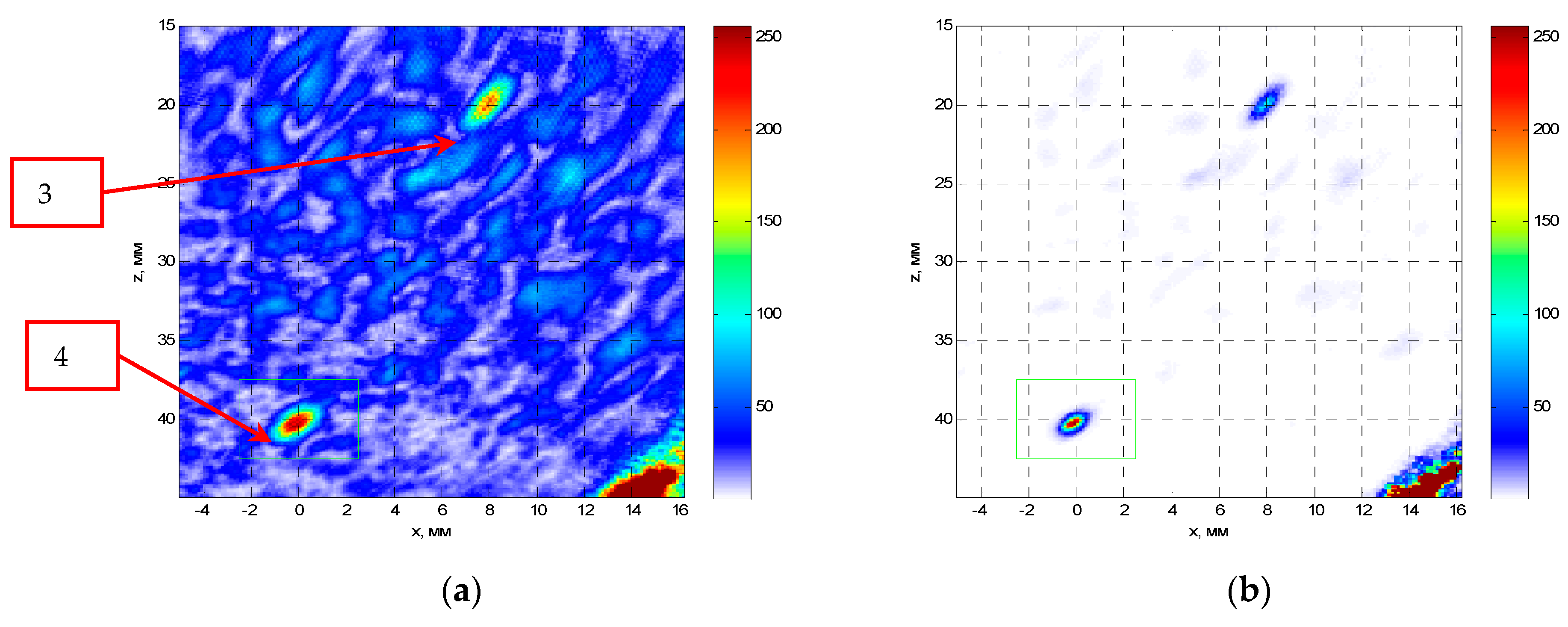
In the model experiment, the piezoelectric transducer (resonance frequency of 4.0 MHz, input angle of 40 degrees, half the opening angle of 20 degrees) moved along the scanning line, which is shown by the red arrow at
Figure 2. Echo signals reflected from a 1.0 mm diameter flat-bottomed hole with a 45-degree slope at a depth of 40.0 mm were recorded (
Figure 2 and
Figure 3). The phase-manipulated signal according to the Barker code with a length of 13 was used as a probing signal.
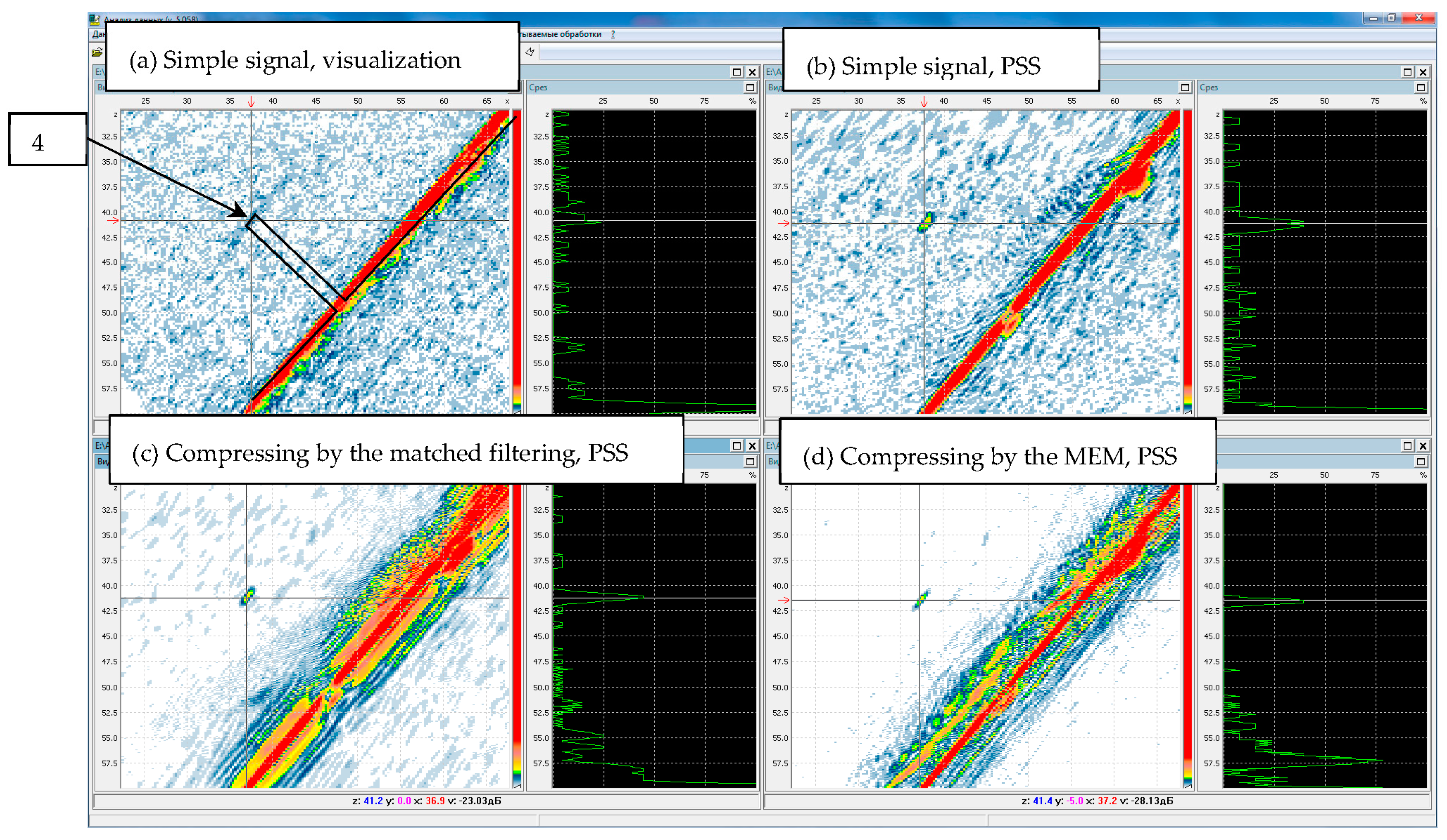
Figure 4a shows the result of visualization of the image of a flat-bottomed hole when a simple pulse is emitted. Visualization means finding the echo envelope and displaying it without spatial processing along the central beam of the transducer for all points of the spatial aperture. On the picture, the lines of black outline the boundaries of the hole and the sample. It can be seen that the indication from the hole, the center of which is indicated by a cross-shaped marker, is barely detected because of the noise level comparable with its amplitude.
Figure 4b shows the result of the reconstruction of the image by these echo signals by the method of projection in spectral space (PSS or FT–SAFT) [
38]. The signal-to-noise image obtained by the PSS increased by more than 12 dB in comparison with the visualization, and the front resolution decreased from 15 mm to 1 mm.
Figure 4c shows the image of the bottom of the hole recovered by the method of PSS in the signals, compressed by the matched filtering, and
Figure 4d—signals, compressed by the method of ME according to the Formula (8). The use of a complex signal resulted in an additional increase in the SNR of more than 12 dB. After the compression of the complex signal by the ME method, the noise level decreased by at least 20 dB, and the beam resolution decreased from 0.7 mm to 0.2 mm. Since the Barker code was used, the level of «side lobes» is insignificant after the compression of the echo signals by the matched filtration.
Thus, the use of complex signals and their compression by the ME method can increase the signal-to-noise ratio by more than 40 dB. This is a very large margin of sensitivity for ultrasonic testing in materials with high absorption.
4. Reconstruction of the Image by Tofd-Echoes
In the practice of ultrasonic nondestructive testing, the time-of-flight diffraction (TOFD) [
39] method is widely used, when pulsing and receiving transducers with a wide beam spread pattern move along the welded joint along an axis
perpendicular to the plane of
Figure 5. The measured echo signals
are informative and allow to detect cracks quite effectively, since the diffraction echo signals from the upper and lower edges of the crack differ in phase by about 180 degrees. The small size of acquired echo signals data set allows monitoring at a very high speed.
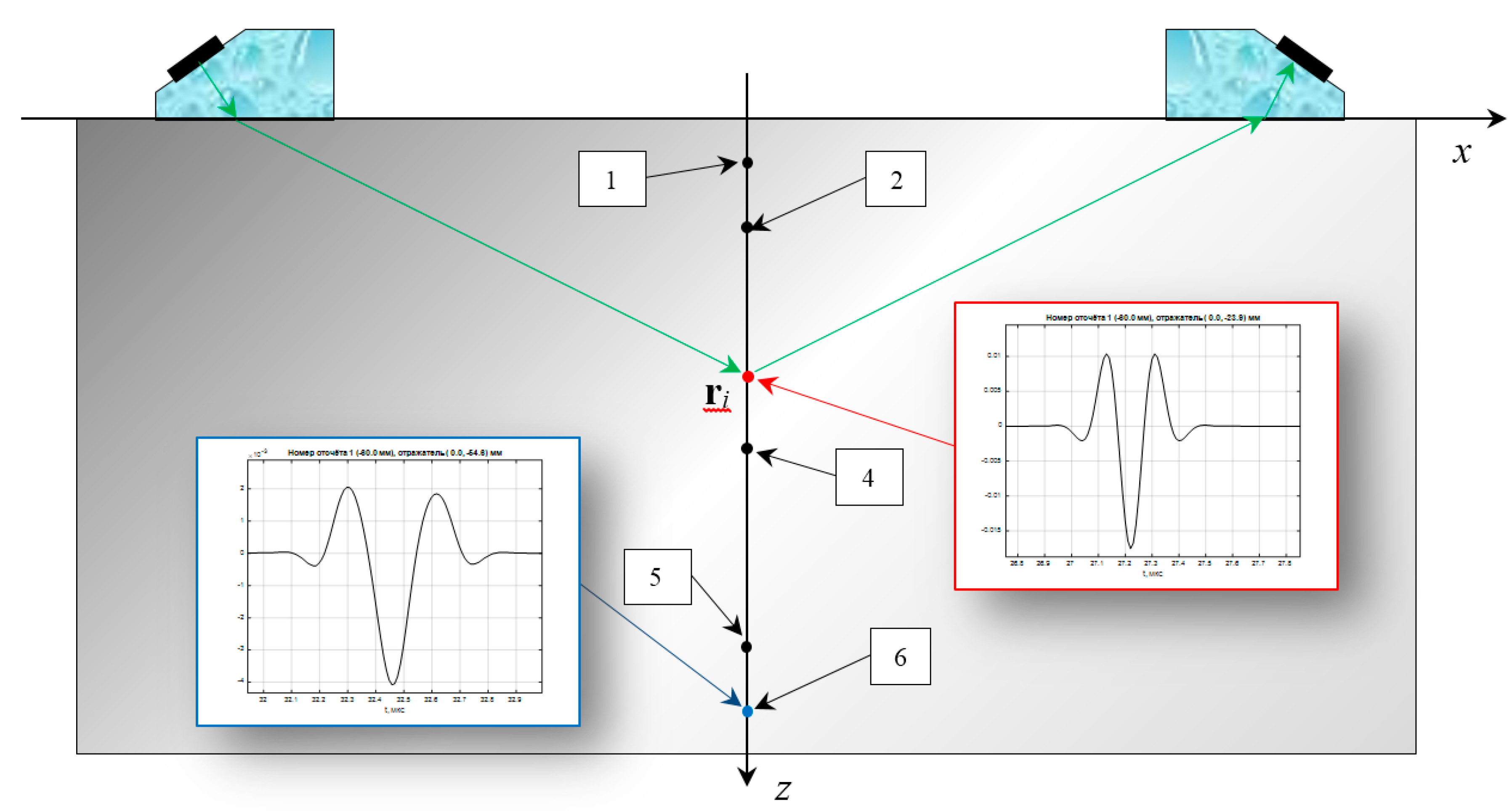
In
Figure 5, the green arrows schematically show the trajectory of the propagation of the longitudinal wave pulse from the fragment of the radiating piezo crystal to the fragment of the receiving piezo crystal. The point-type reflector at the point
is shown in red
. To calculate the received echo signal, it is necessary to calculate the delay time and amplitude for all the rays when the pulse is emitted when an electric pulse
with a central frequency of 5 MHz is applied to the piezo crystal and to integrate on the surface of the piezo crystal, which will allow calculating the pulse
at the point
. A set of trajectories from the reflector to the surface of the receiving piezo crystal can be used to estimate the echo signal
measured by the receiver. The finite dimensions of the piezo crystal lead to the fact that the shape of the measured echo signal will change. The pulse from the reflector (depth 25 mm) at the intersection of the acoustic axes of the transducers practically the same as the probe pulse and is shown in
Figure 5 by the balloon with the red border. The echo signal from the point-type reflector at a depth of 45 mm is shown in
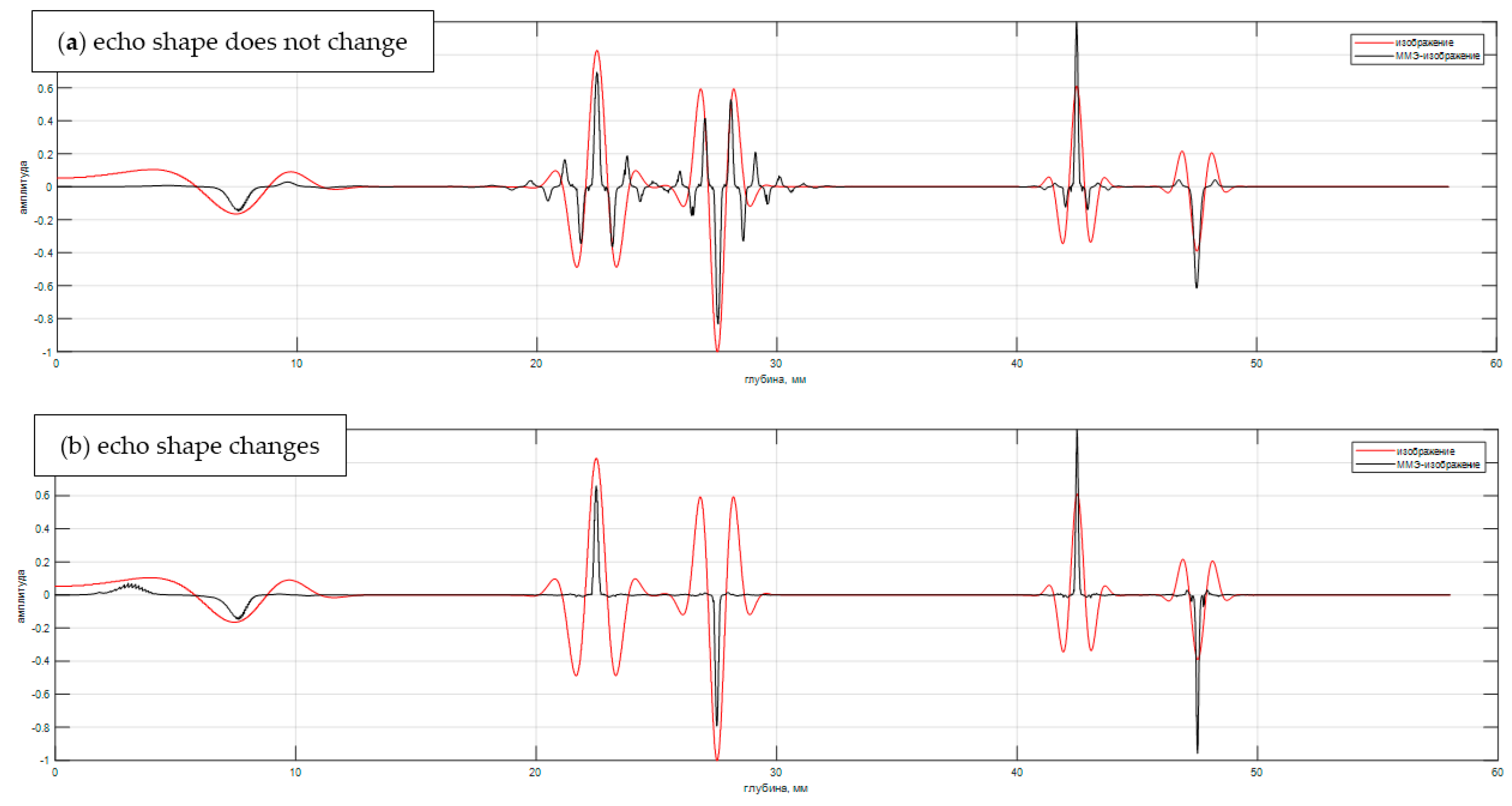
Figure 5 by the blue balloon. The scale of both graphs is the same along the time axis and is equal to 1 µs, and the amplitudes are equalized. It can be seen that when the distance from the acoustic axis of the echo shape changes significantly.
Thus, after calculating , it is possible to construct a matrix and to reduce the problem of estimation along the axis by the measured echo signal using the Equations (8) and (10). If the propagation time of the pulse is calculated from the centers of the of piezo crystal as a function of the depth of the point reflector, then the form can be estimated from the formula . This formula can be considered as a degenerate version of the C–SAFT method.
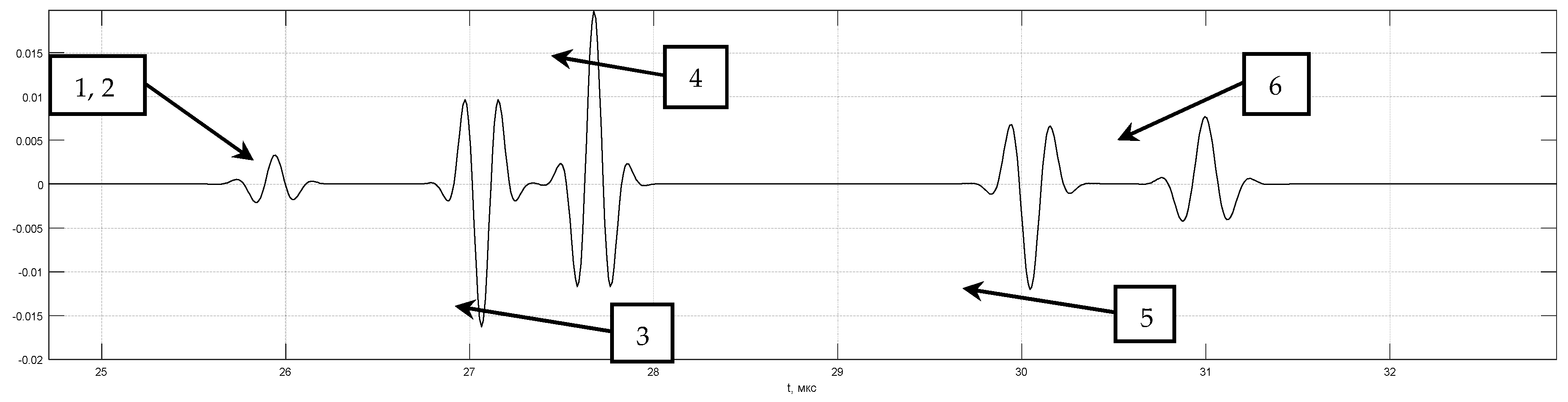
Figure 6 shows the calculated echo signal
from the six point-type reflectors for a distance between the front faces of the transducers is 120 mm. The first pair of reflectors with coordinates 2.5 mm and 7.5 mm, the reflection coefficients 1 and −1 simulates a crack with a height of 5 mm, similarly, the second pair has coordinates 22.5 and 27.5 mm, and the third one 42.5 and 47.5 mm. The pulse of the head wave and one reflected from the object bottom of the sample were not calculated. Echoes from the second and third pairs are resolved and have a phase shift of 180 degrees. Echo signals from the first pair of reflectors will not be resolved, so at low depths
changes weakly. The amplitude and shape of pulses from the reflectors are different due to the divergence of the ultrasonic beam and the finite size of the piezoelectric plates.
Figure 7a shows the result of the evaluation of
(black graph) and
(red graph) when the matrix
is formed taking into account the echo shape
calculated for the depth of 45 mm. This led to the fact that the images of the third pair (reflectors 5 and 6) have the form of a
–function, and the image of the reflectors of the second pair has «side lobes» of the order of 40%. Under ideal reconstruction of the values of the reflection coefficient
in this example must be equal to 1 or −1.
Figure 7b shows the result of the evaluation of
and
at the calculation of the matrix
of echo shape
for all depths. The
has no difference from the shape
p(
t) except for the nonlinear scale transformation according to the dependency
, but the
has a resolution of more than five times higher than for
, which allows one to resolve reflectors 1 and 2. The amplitude of the reflector is 1 small since the calculation of
did not take into account the feature of calculating the refractive index near the first critical angle [
40]. It is clear that such a convincing result (
Figure 7b) obtained in the absence of measurement noise and operator noise. To obtain better images of reflectors 1 and 2, it is necessary to bring together the emitting and receiving converters.
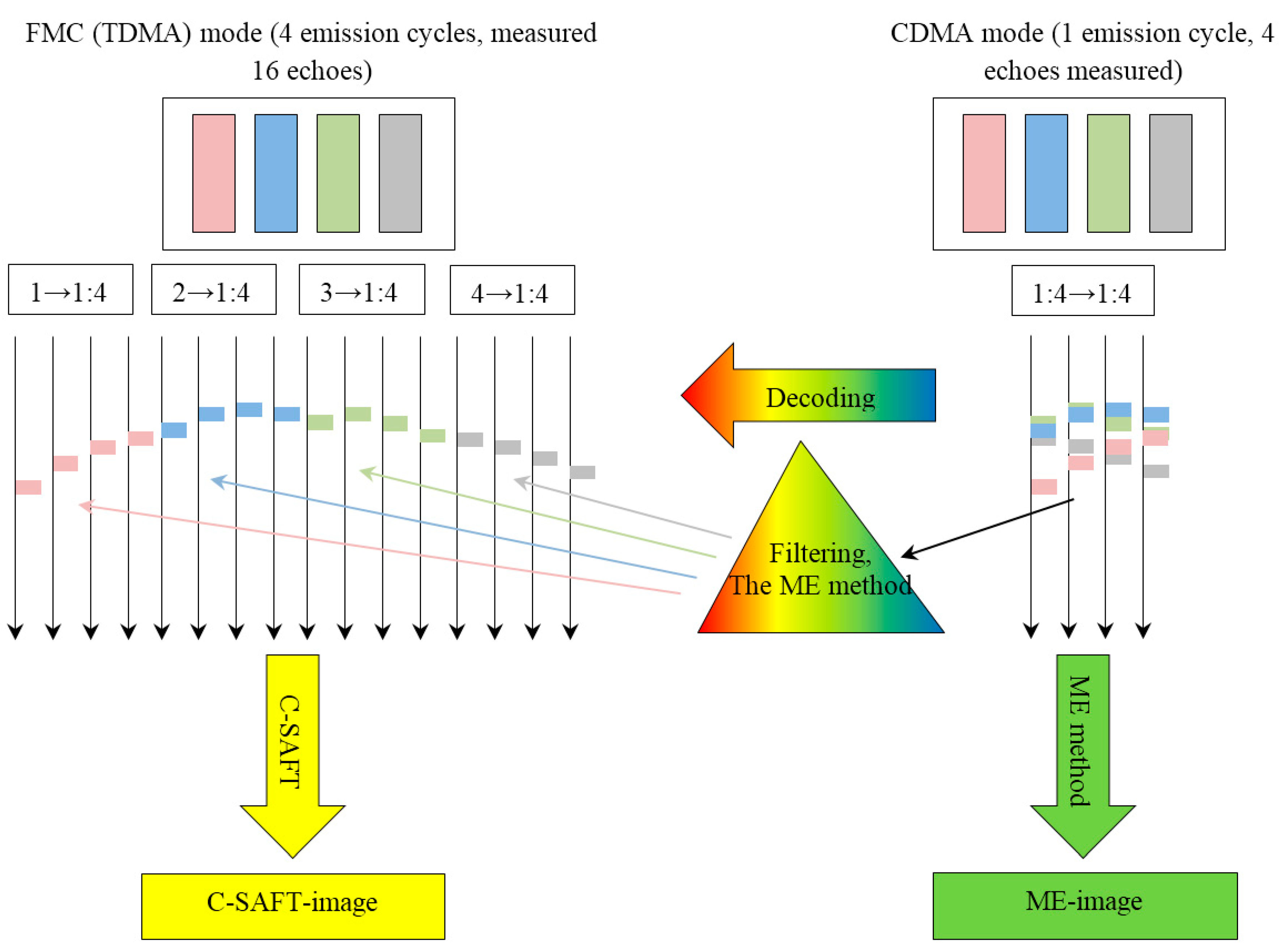
6. Increasing of Echoes Acquisition Rate
The disadvantage of acquiring echoes by double scanning is a large amount of measured data. With an increase in the number of elements of the antenna array, the number of echoes increases as a square. Therefore, in spite of the fact that the echoes are measured in cycles of the probing signal, the transfer of a large volume of echoes from the measurement unit to the computer for image reconstruction may take a long time.
From the point of view of the theory of multichannel communication, the dual scan mode is similar to the situation where users send a message in turn which is received by all users. The consistent nature of the radiation of the probe pulse allows us to answer the question: “Who is the source of the message?” This communication mode, when each pair of receiver-transmitter is allocated the whole spectrum or most of it for a selected period of time, is called time-division multiple access (TDMA) [
43]. If all users could send their messages at the same time, and at the reception, it would be possible to select all the messages and understand: “Who sent the message?”—it would essentially increase the rate of echo signal acquisition and decease their amount. To solve this problem in the theory of multichannel communication, when the transmission channels have a common frequency band but different code modulation, a code division multiple access technology has been developed, which is called code division multiple access (CDMA) [
43]. For its implementation, all elements of the antenna array are simultaneously excited, each with its unique probing pulse
, and echoes are simultaneously received by all elements of the antenna array. Schematically, echoes measured in CDMA mode
are shown in
Figure 16 on the right and they can be represented by the expression:
The first way to use this approach is to decode the echo signals
so that the
m-th subscriber can make an evaluation of the echo signal
from the subscriber with the number
n. For effective decoding of echo signals, the correlation function
of a set of coding signals
intended for excitation of elements of the antenna array must have the following property:
where
is the Kronecker symbol. The set of signals having the property (18) is called orthogonal. Signals for practical use with this property are not known, but several sets of coding signals
sn(
t) have been developed, which to some extent approach the ideal set with the property (18). Sets of such signals are called pseudo-orthogonal. These include phase-manipulated signals encoded by a sequence of length
. The law of change of the chip phase can be determined by the Kasami codes [
44], Gold [
45], de Brain [
46], in which the phase of each chip can take values 0 or 180 degrees. It is possible to use Zadov–Chu sequences with arbitrary phase for each chip [
47]. A set of sequences with a random phase can also be considered as pseudo-orthogonal. Each chip can determine the phase of one period at the carrier frequency
, but the option of random frequency measurement
from chip to chip is possible. For the emitting of such signals to the arbitrary pulse generator of the flaw detector, higher requirements are imposed, in comparison with the usual shock excitation generator.
The first way to restore the image is as follows. After selecting a set of code signals
, their simultaneous pulsing and reception in one cycle, the measured echoes
must be decoded to evaluate the signals
p(
t), as if measurements were made in the FMC mode. By decoded echoes
using the C–SAFT method, one can restore the image (arrow and rectangle with a yellow fill in
Figure 16). In
Figure 16 the decoding procedure is likened to the passage of a beam of light through a prism. If we use the color analogy in
Figure 16, the decoding with the correct selection of signals
will allow the signals
from the total set
to be “colored” only in one color. Considering the circumstance that pulses of “different colors” can be very close to each other, the algorithm of decoding should provide a high resolution in time domain.
A common method of decoding complex signals
is matched filtering with a code signal
. Given that matched filtering in the time domain is equivalent to convolution [
43], the decoding operation can be written as:
This algorithm for compression of complex signals has a high speed and allows one to obtain images with a frequency of more than 10 Hz, but it does not allow to obtain a low level of interchannel noise and achieve the effect of super-resolution. For decoding of echoes by Equation (19), the level of interchannel noise, i.e., the average value of the cross-correlation function of signals in the set , can be estimated as the value of .
A more complex method of decoding simple or complex signals is based on the use of the maximum entropy method [
37] and was considered in the section Processing of echo signals presented in a complex form. To obtain the estimation of echo signals by the ME method by measured
for each
from a set of coding signals
, it is necessary to form a matrix
. The time of decoding of echoes
by the ME method is much longer than by the Formula (19), which will lead to decreasing the frequency of image formation. But for an automated system with post-processing, such a speed limit is not essential.
The second way to obtain the image is to get the image of the reflectors immediately using the ME method without decoding
, as described in section Restoring the image of reflectors. This method in
Figure 16 corresponds to an arrow and a rectangle with a green fill.
The efficiency of the algorithms for decoding echoes depends on the type of reflectors being reconstructed and their quantity, since this depends on how close to each other the echoes are located. That is, the quality of the decoding of echoes from a single point reflector can be very good [
48], but when processing echoes from many reflectors, the reconstructed image may end up with an unacceptably high level of inter-channel interference. Ideally, the use of CDMA technology will allow to measure for an antenna array of 128 elements only in one cycle instead of 128, and decrease the number of echoes from 16,348 to 128.
The model experiment was carried out on the sample described in
Section 4 with drilled holes in the rescattering test, but using the electronic unit of the AUGUR-ART system, which allows pulsing complex signals. As a set of complex signals, 32 (
) phase-manipulated signals according to the Kasami code were used with length
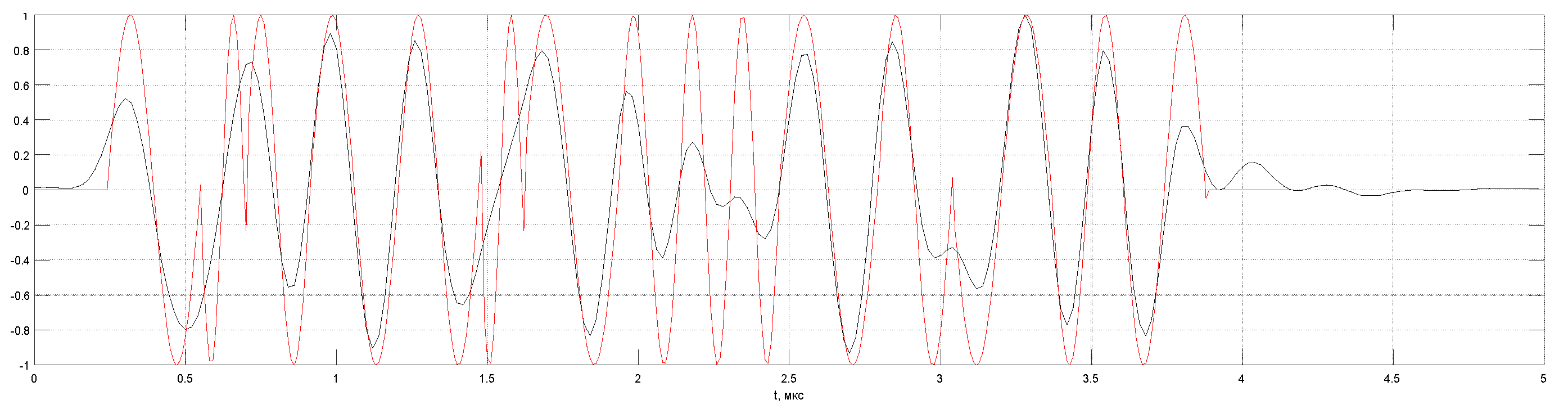
. Each period had a frequency randomly distributed in the [5 ± 2] MHz band. To acquire echoes, an antenna array was used (5 MHz, 32 elements, crystal size 0.9 × 10 mm, 0.1 mm pitch) on a rexolite prism with a slope angle of 35 degrees.
Figure 17 shows an example of one complex probing signal (red graph) prepared for study and emitted and received by the equipment used (black graph). One can see that the limited bandwidth of the antenna array distorts the ideal shape of the probing signal: in the received echo signal, sharp phase jumps are actually lost when the chip changes and the signal amplitude changes from chip to chip.
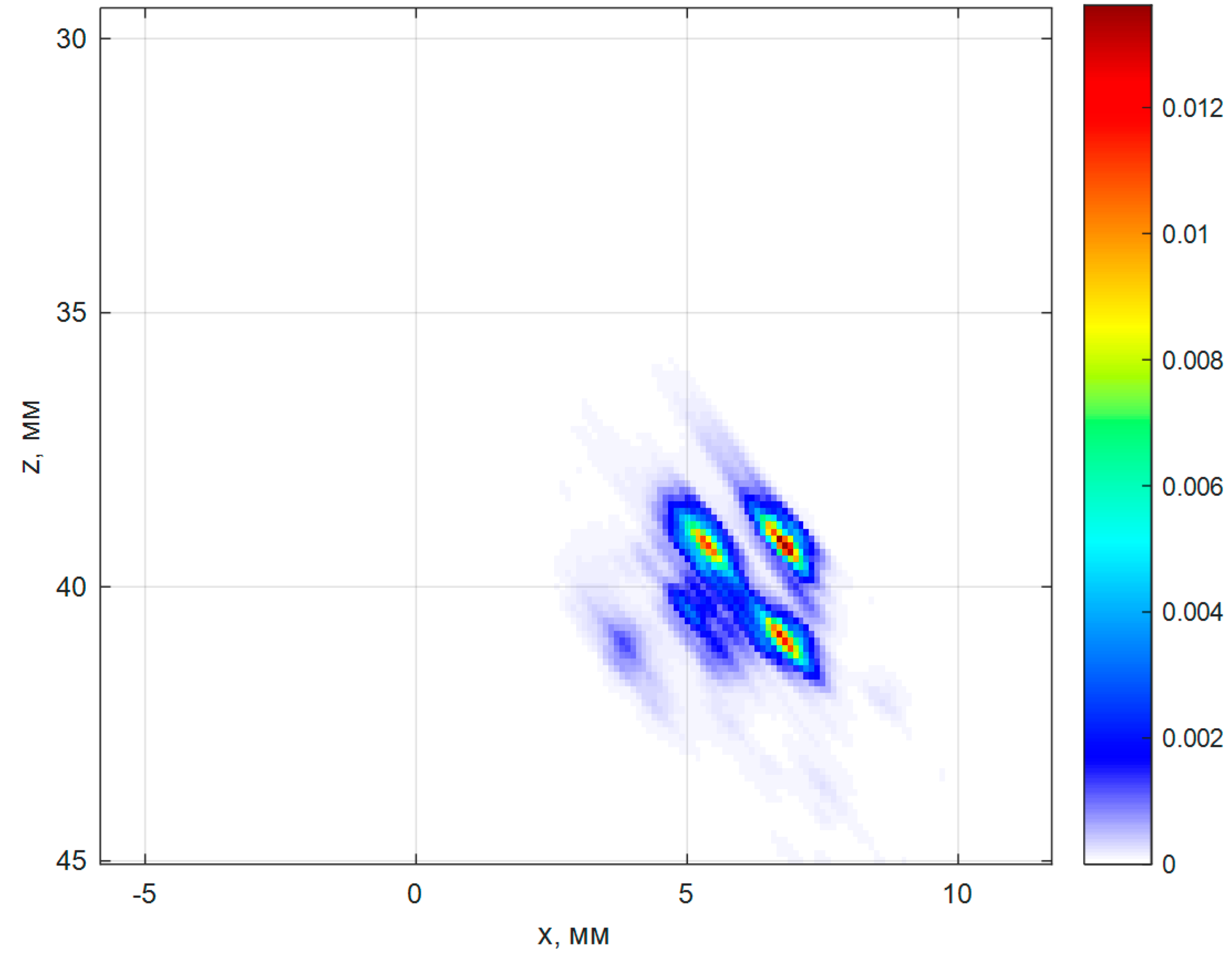
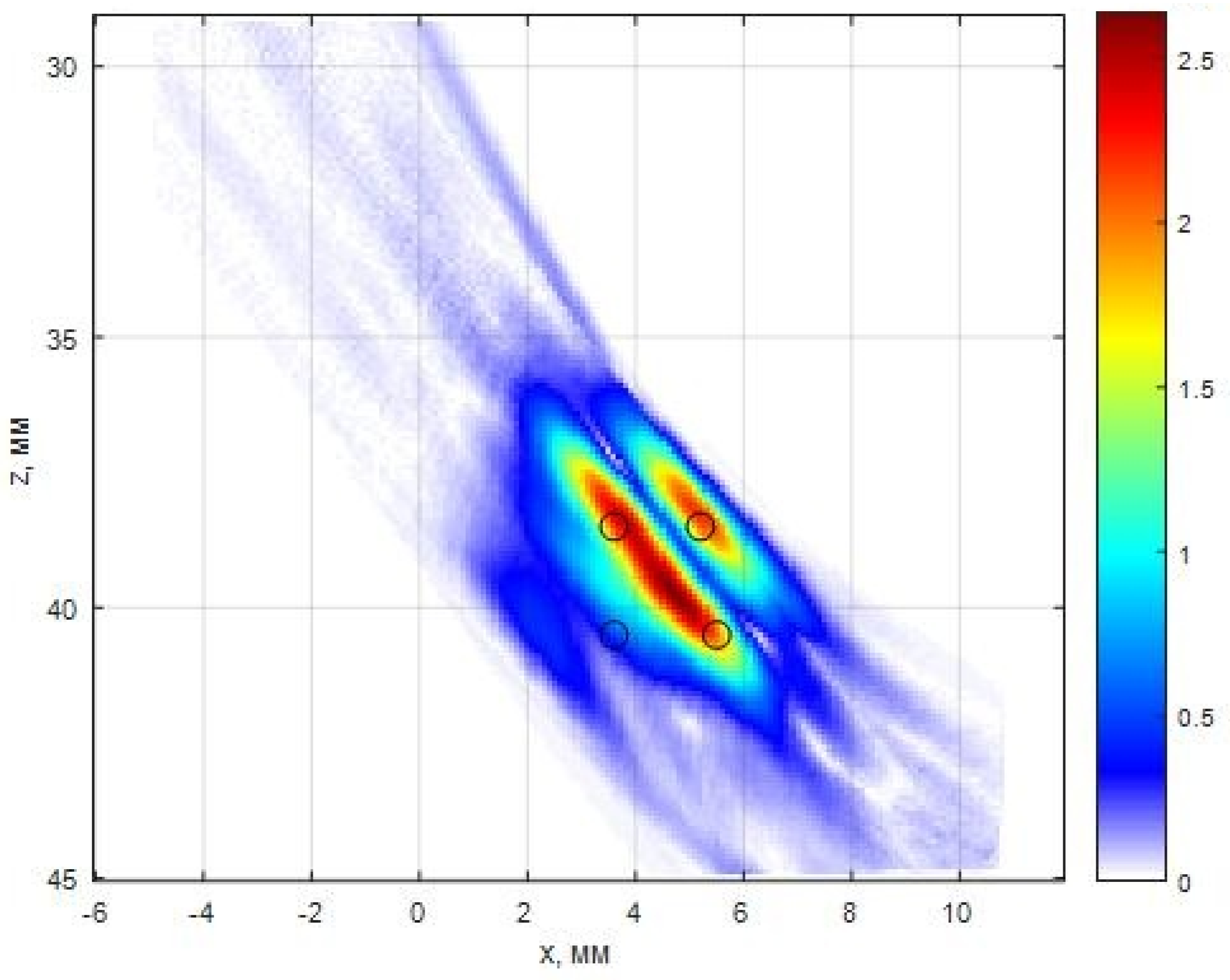
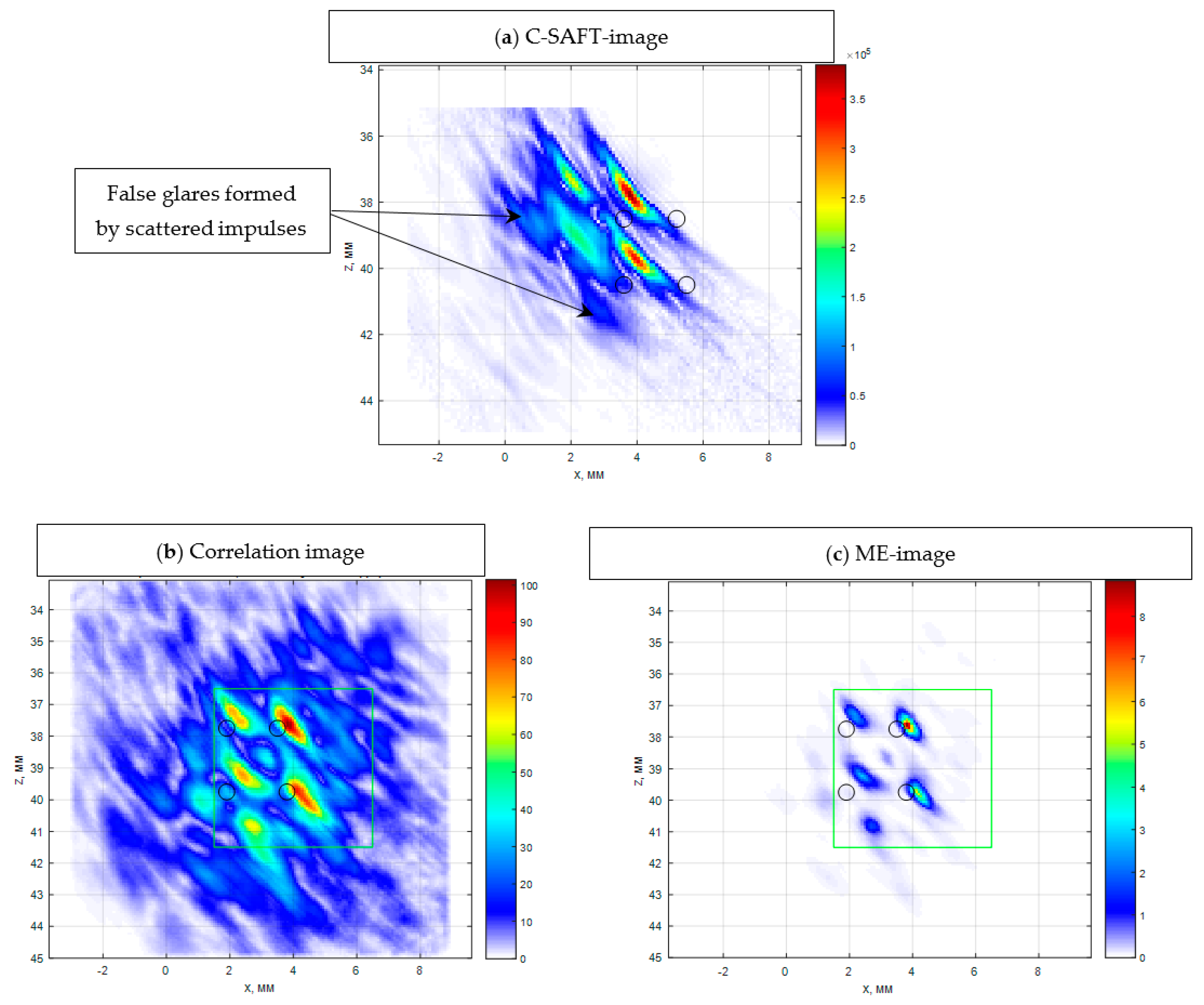
Figure 18a shows the image of the four side drilled holes reconstructed by the C–SAFT method in the set of echoes measured during the emission of a simple signal in the FMC mode. There are three indications corresponding to the boundaries of the three holes, which are accurately resolved since the reconstruction made for transverse wave. But apart from them, the pulses scattered between the holes formed several false indications, which do not allow us to determine not just the type of reflectors, but also their quantity. The signal-to-noise ratio of the image can be estimated as 28 dB.
Figure 18b shows the image reconstructed by the correlation method according to Equation (6) during decoding by matched filtering. Due to the high level of inter-channel interference, the image quality due to a low signal-to-noise ratio of 12 dB has an unacceptably low quality.
Figure 18c shows the result of the reconstruction of the image of the reflectors with 32 echoes
by the ME method according to Equation (8) (
,
). The longitudinal and frontal resolution of the image increased more than twofold in comparison with the image of
Figure 18a. On the ME image, the indications of the four holes are clearly visible, and one false indication with a commensurate amplitude. It should be recalled that the acquisition time of echoes
is in
times shorter than the measurement time in FMC mode. The data set of the measured echo signals is as much smaller.
7. Conclusions
The use of the maximum entropy method allows one to improve the quality of the reconstructed image of the reflectors and thereby increase the reliability of ultrasonic non-destructive testing. The use of the ME method in the model experiments increased the resolution of the image by a factor of three in comparison with the linear reconstruction methods. This made it possible to more accurately determine the type and number of reflectors.
Compression of complex signals by the ME method made it possible to increase the signal-to-noise ratio more than by 20 dB for the imaging in materials with a high attenuation, which made it possible to detect reflectors at a great depth with superresolution. The ME method is equivalent to reducing the duration of echo signals length, and this should reduce the level of structural noise. In the model experiment, it was possible to reduce the level of structural noise of the reflector image by 12 dB.
Since when processing echoes measured in TOFD mode, the shape of the echoes depends on the depth of the reflectors, a variant of the ME method, taking this into account, was proposed. In a numerical experiment, the effectiveness of this approach is shown.
The possibility of using the ME method for obtaining a 2.5D-image of the reflectors in a reference block made from 800 mm diameter pipe. Application of the ME method together with CDMA technology allowed to reduce the echoes acquisition time by FMC and obtain an image with superresolution. In the model experiment it was possible to increase the rate of echo signal registration for the 32-element elemental array by 32 times. With the increase in the number of elements of the antenna array, the proposed approach further increases the rate of registration of echoes. This can be very important for ultrasound medical diagnosis.