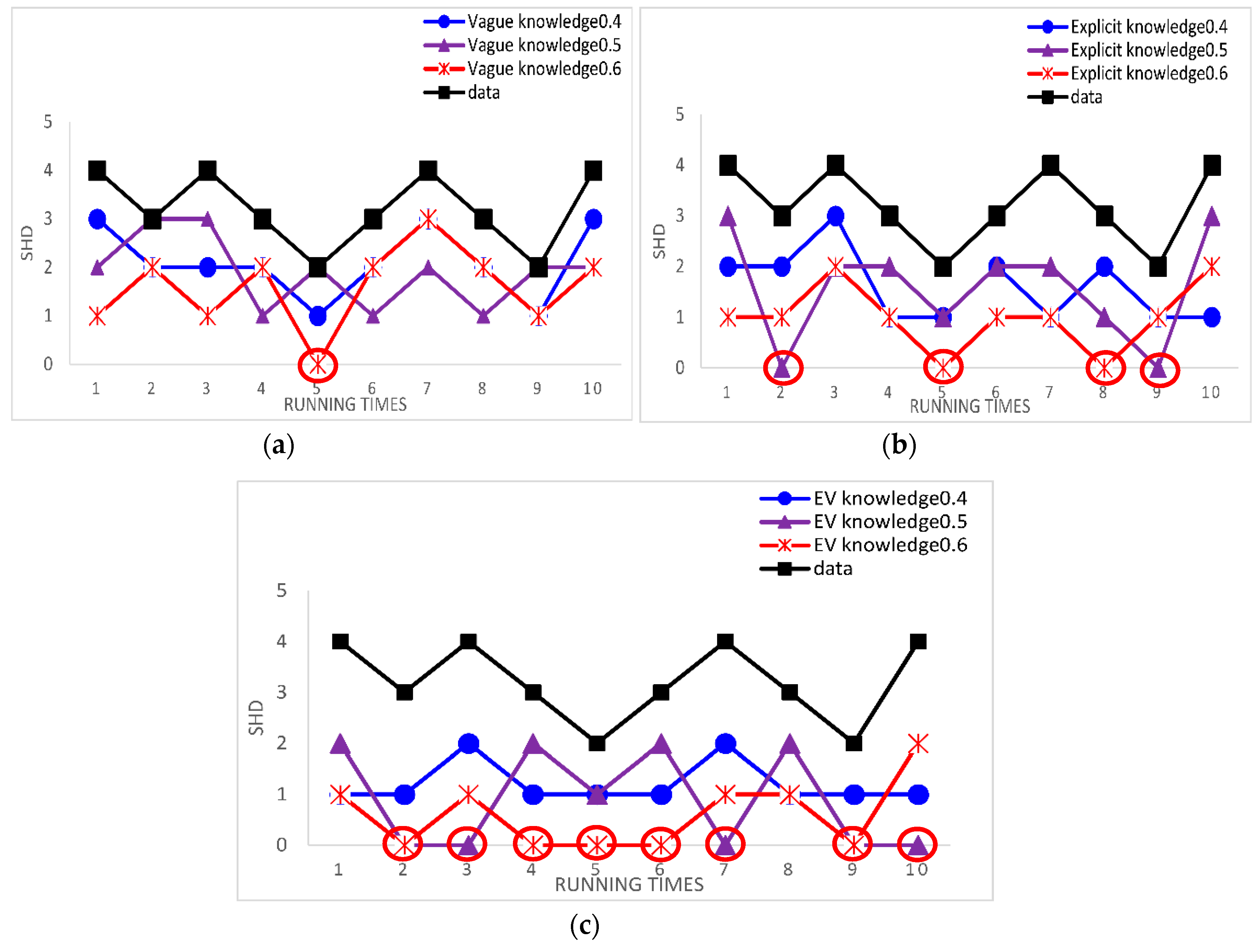
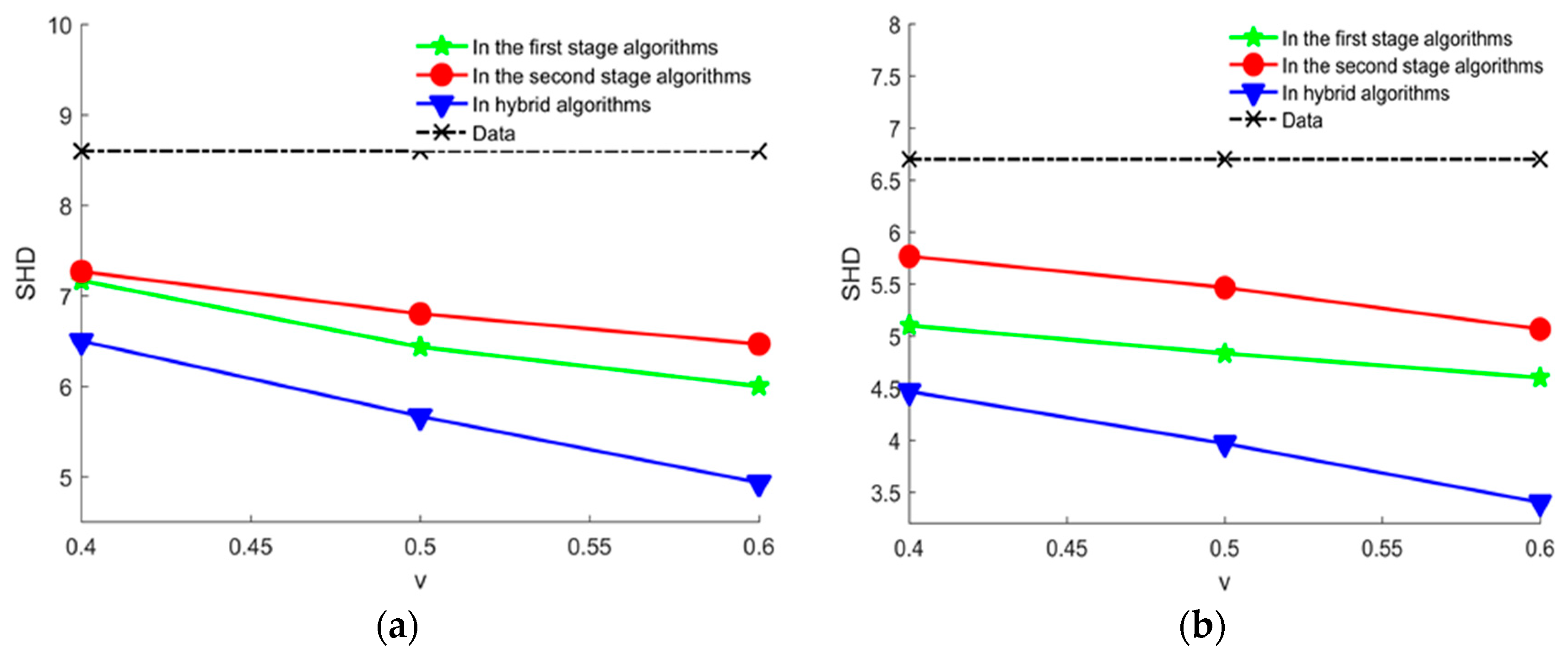
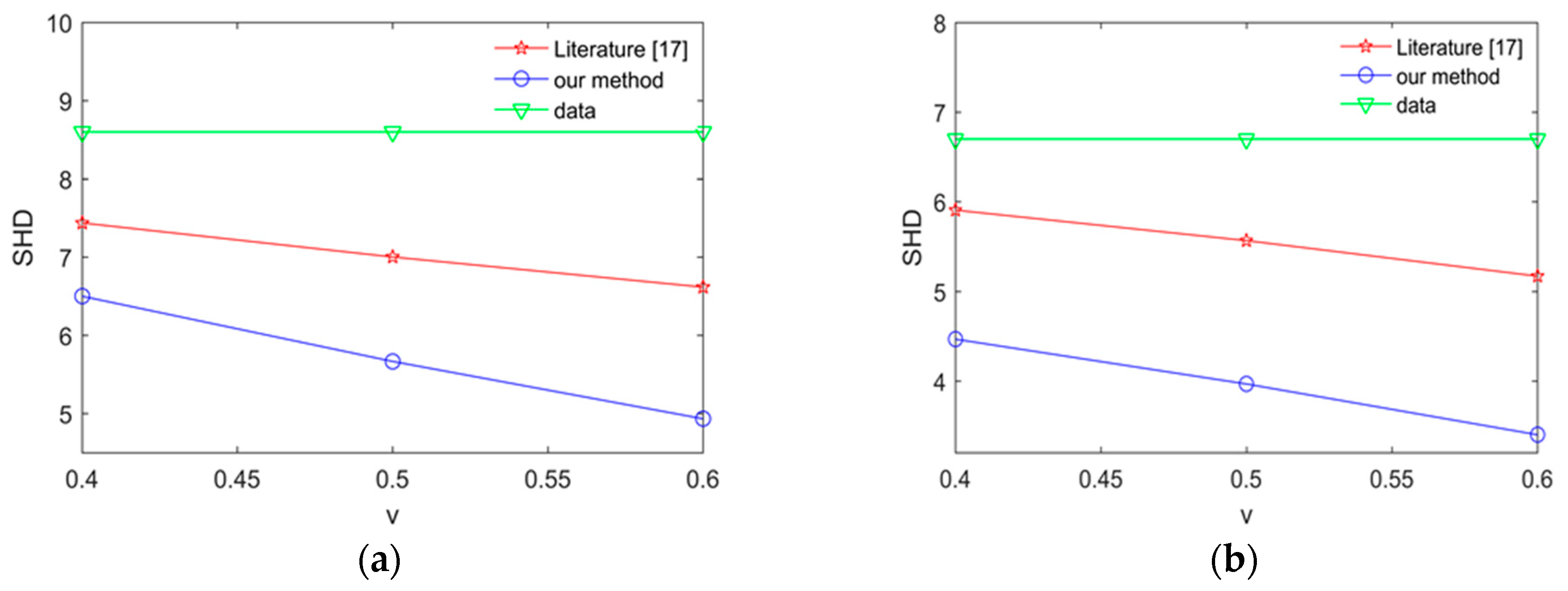
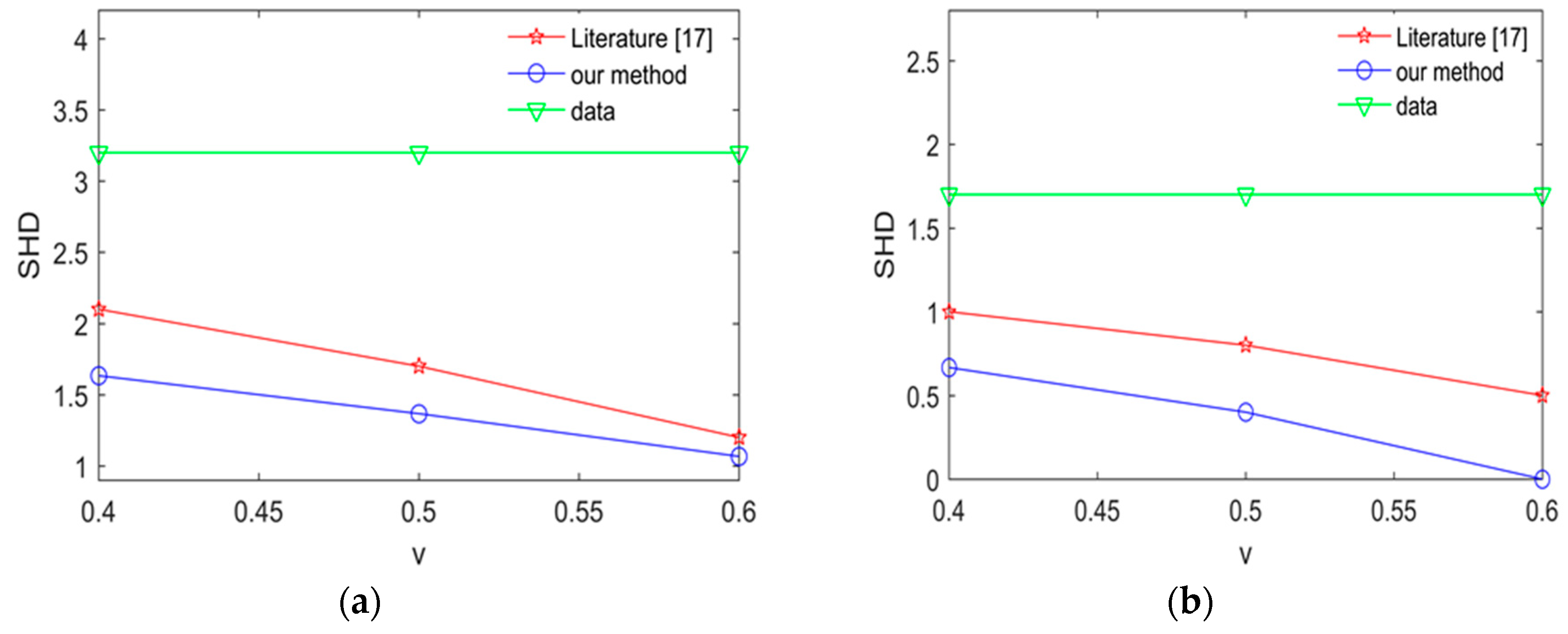
In order to improve the learning performance and utilization of knowledge, this paper applies knowledge to two stage algorithm of hybrid algorithms respectively.
3.1. Using Different Types of Experts’ Knowledge with the First Stage Structure Learning Algorithm
In order to guide the search of the second stage structure learning algorithms better, we need to determine a better initial network structure in the first stage structure learning algorithms. In this paper, we formulate rules for adding and deleting edges of different types of experts’ knowledge to modify the initial network structure in order to improve the accuracy of the initial network structure and improve the overall performance of the algorithm. Firstly, the credibility of experts’ knowledge is determined according to the accuracy parameters of experts. In addition, the different experts’ knowledge is fused based on the credibility of experts’ knowledge. The purpose of these two steps is to fuse different experts’ knowledge on the same set of nodes based on credibility. Finally, by formulating rules for adding and deleting edges of different types of experts’ knowledge, the fusion of experts’ knowledge is modified the initial network structure based on credibility. It can be divided into the following three steps.
(1) To determine the credibility of experts’ knowledge
The credibility of experts’ knowledge is the probability that experts’ knowledge is true. Different kinds of experts’ knowledge have different credibility. The credibility of experts’ knowledge is determined according to the accuracy parameters of experts.
represents the credibility that the experts’ knowledge is the l-th kind and the expert is the i-th. Take the i-th expert as an example to explain the credibility of different kinds of expert knowledge .
The i-th expert’ explicit knowledge which indicates the existence edge between the node pair includes . The two kinds of knowledge don’t essentially differ and the credibility is the same, and credibility of two kinds of knowledge can be written as .
The i-th expert’ explicit knowledge which indicates the absent edge between the node pair includes , and credibility of this kind of knowledge can be written as .
The i-th expert’ vague knowledge which indicates the existence edge between the node pair includes , and credibility of this kind of knowledge can be written as .
The i-th expert’ vague knowledge which indicates the absent edge between the node pair includes . The two kinds of knowledge don’t essentially differ and the credibility is the same, and credibility of two kinds of knowledge can be written as .
(2) The different experts’ knowledge fusion based on the credibility of experts’ knowledge
As mentioned earlier, the i-th expert’s knowledge of j-th node pair takes values in the domain . For a specific node pair, the experts’ knowledge may not be inconsistent. We take the following four steps to fuse different experts’ knowledge for the j-th node pair:
- (a)
Divide the experts for the j-th node pair into six sets including and (Define as a set of experts for the j-th node pair with the same kind lth of knowledge).
- (b)
Sum and normalize the credibility of the six kinds of knowledge for the
j-th node pair:
- (c)
Divide the close interval into six subintervals including , , , , and . For a which is a random number [0,1], if where is the k-th subinterval as previously described, choose the l-th kind of experts’ knowledge where as the result of knowledge fusion for j-th node pair. These six kinds of knowledge are not mutually exclusive, so we cannot simply choose the knowledge with higher . We divide the close interval [0,1] into six subintervals whose length are , , , , , which is the same with roulette. And we use a random number located in [0,1] which trends to choose the knowledge with higher . Put the result into the set of C′ or .
- (d)
Calculate the credibility
of the result of knowledge fusion for the
j-th node pair:
where
is a function that returns the number of elements in the set
. Put the
into the set of credibility
B. The experts’ knowledge set
and
and the corresponding credibility set
B after fusion will be used as inputs to the following rule.
(3) Modify the process of generating the initial network structure by rules for adding and deleting edges of different types of experts’ knowledge
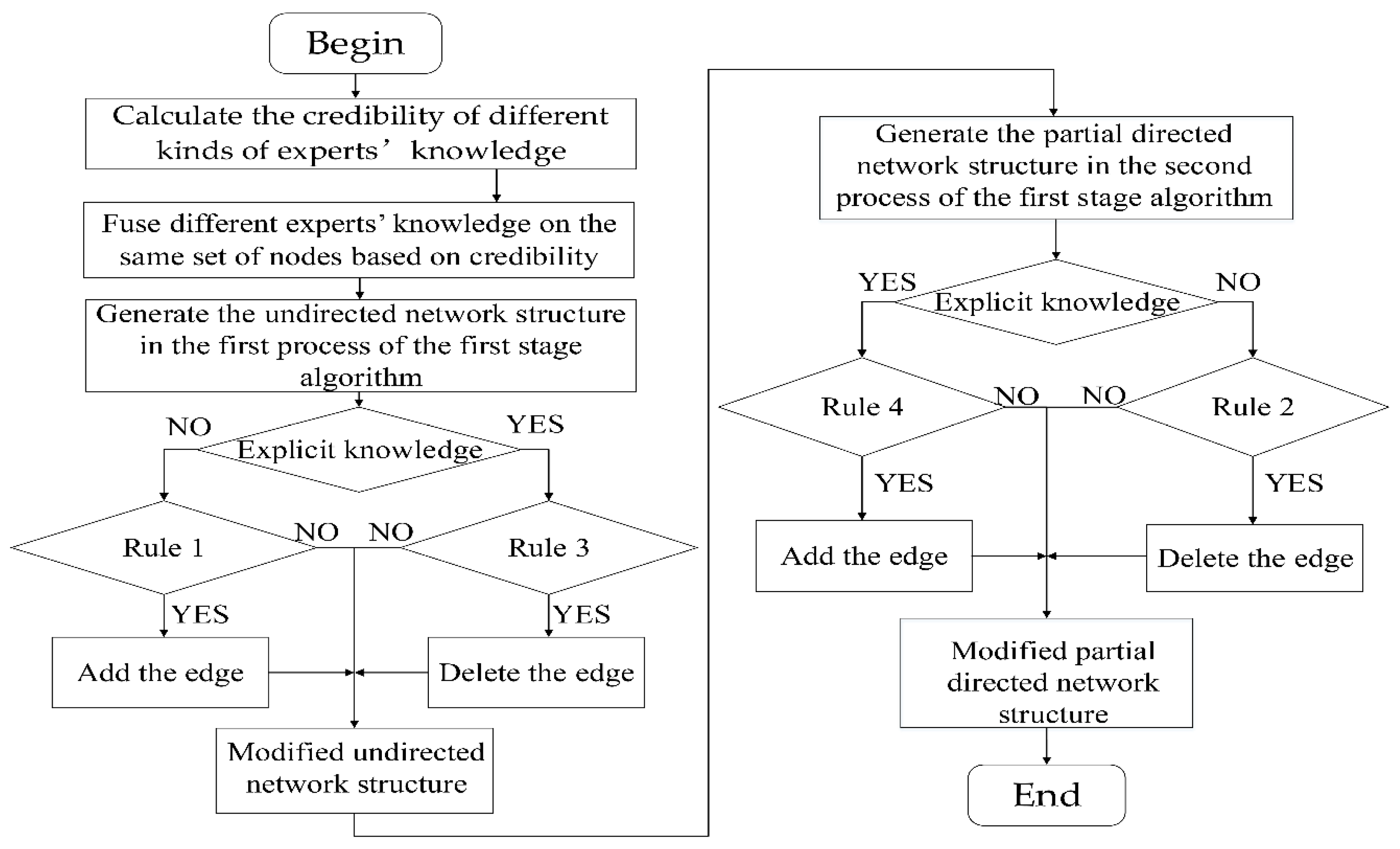
In this paper, we use the rule-based method to formulate the rules for adding and deleting edges of different types of experts’ knowledge. Based on the rules, we modify the undirected network structure that is determined by the first process in the first stage structure learning and the partial directed network structure that is determined by the second process in the first stage structure learning. The rules for adding and deleting edges of different types of experts’ knowledge are described below.
Rules for adding and deleting edges of vague knowledge include the rule for adding the edge in the undirected network structure and the rule for deleting the edge in the partial directed network structure.
Rule 1. (The rule for adding the edge in the undirected network structure)
represents the undirected network structure after adding the edge, andrepresents the undirected network structure before adding the edge. For, including, the credibility of knowledge is, if,.
Rule 2. (The rule for deleting the edge in the partial network structure)
represents the partial network structure after deleting the edge, andrepresents the partial network structure before deleting the edge. For, including, the credibility of knowledge is, with l = 5 or 6, if,.
Rules for adding and deleting edges of explicit knowledge include the rule for deleting the edge in the undirected network structure and the rule for adding the edge in the partial directed network structure.
Rule 3. (The rule for deleting the edge in the undirected network structure)
represents the undirected network structure after deleting the edge, andrepresents the undirected network structure before deleting the edge. For, including, the credibility of knowledge is, if,.
Rule 4. (The rule for adding the edge in the partial network structure)
represents the partial network structure after adding the edge, andrepresents the partial network structure before adding the edge. For, including, the credibility of knowledge is, with l = 1 or 2, if.
The schematic diagram of using different types of experts’ knowledge with the first stage structure learning algorithm is shown in
Figure 2.
3.2. Using Different Types of Experts’ Knowledge with the Second Stage Structure Learning Algorithm
The second stage structure learning algorithms use a search strategy to select the structure with the highest score of a scoring function. The key to select the “optimal” structure is the scoring function.
Explicit-accuracy-based scoring function is proposed by [
17]. First, [
17] sets up three various problem models. Then, [
17] derives some independence statements from three models using the principle of d-separation. Last, scoring function is derived with simplification of independence statements derived above. And this scoring function is given as:
This scoring function is composed of two parts:
and
. The first part is the marginal likelihood part of BDeu scoring function [
18].
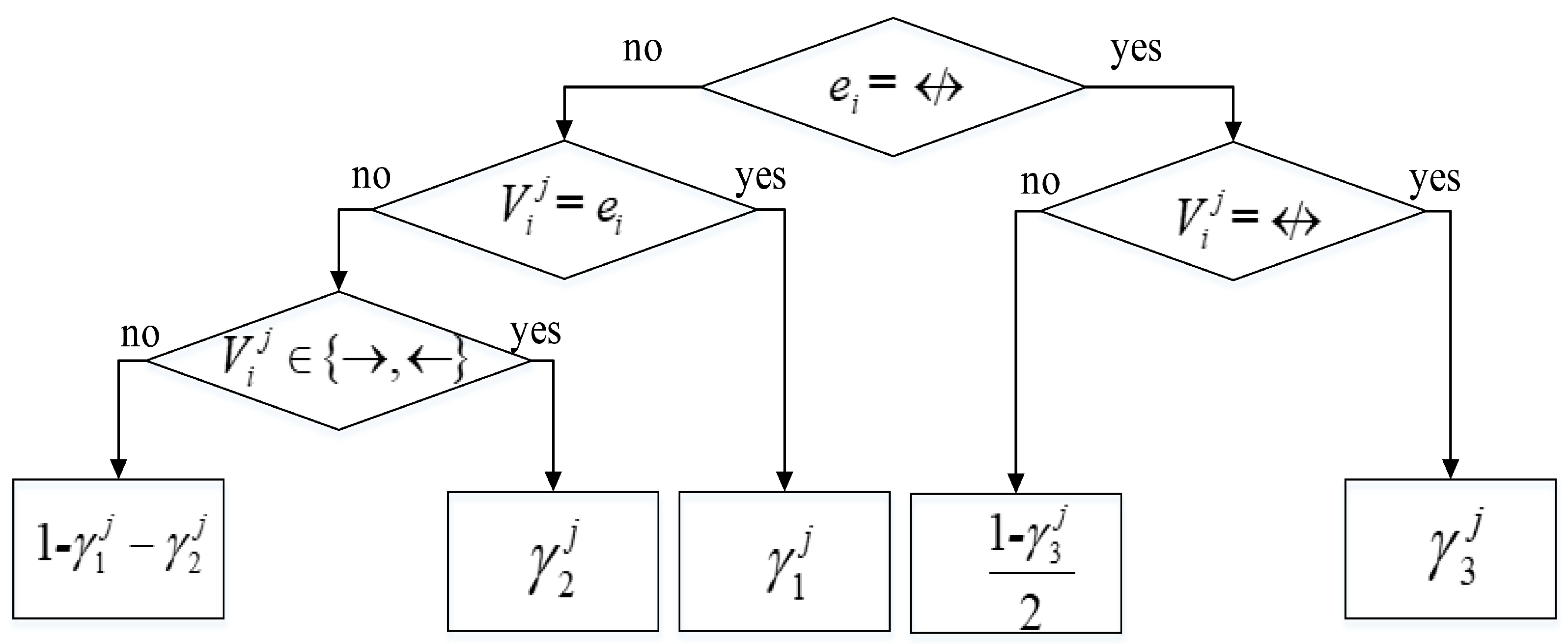
in the second part indicates the probability of
given
and is computed using the decision tree shown in
Figure 3.
We can comprehend this scoring function in this way. The first part of Explicit-accuracy-based scoring function means the scoring function which measures the goodness of network to data. The second part of Explicit-accuracy-based scoring function means a penalization which measures the difference between experts’ knowledge with network. Experts’ knowledge here only refers to the explicit knowledge. Based on this, in this paper, the Explicit-Vague-BIC (EVBIC) scoring function is proposed and given as:
where
is the number of node pairs with explicit knowledge, and
is the number of node pairs with vague knowledge.
is the three kinds of explicit knowledge and
is the three kinds of vague knowledge. The EVBIC scoring function is composed of three parts. In the first part, we use the BIC scoring function as the scoring function which measures the goodness of network to data. The second and third part represent penalizations which measure the difference between experts’ knowledge with network. The second part represents the penalization which measures the difference between explicit knowledge and network. The third part represent the penalization which measures the difference between vague knowledge and network. In the same case, the vague knowledge is more ambiguous and weaker for building network structure than explicit knowledge. Therefore, we consider using a coefficient
to weigh the contribution of explicit knowledge and vague knowledge. Considering each vague knowledge corresponds to two kinds of relationship between nodes in BN structure, in this paper, we take
.
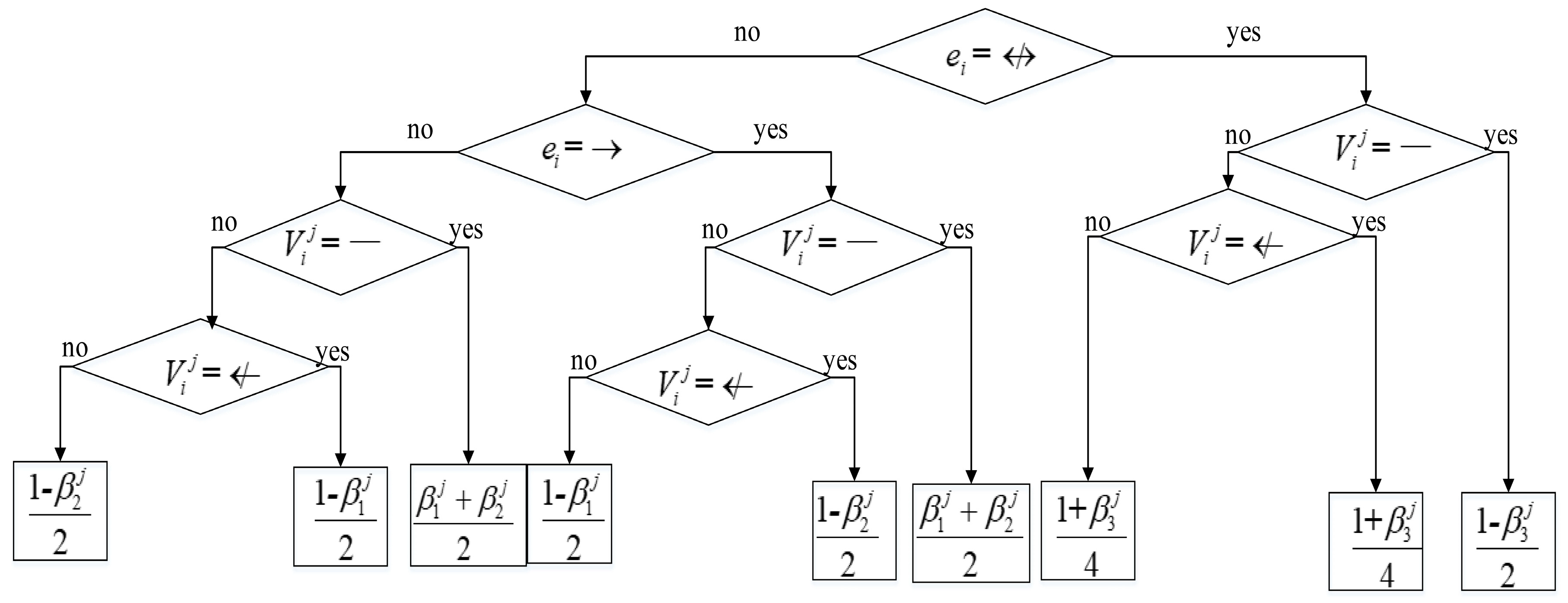
The term
in the second part in Equation (9) is calculated as the decision tree shown in
Figure 3. The calculation of the term
in the third part in Equation (9) is same as
Figure 3, as shown in
Figure 4.