1. Introduction
In recent years, robots working in teams have been replacing complex single robots in both civilian and military applications. Such multi-robot systems can bring extraordinary benefits. When some robots do not work well, the problem may be fixed by simply replacing them with new ones. In this way, complex tasks are decomposed into multiple subtasks with relatively low complexity [
1]. Therefore, the tasks can be accomplished with a lower cost. In military scenarios, autonomous robots are designed to cooperatively accomplish surveillance tasks [
2] or spy on targets in adversarial regions. In civilian fields, automatic driving techniques may be helpful in intelligent transportation systems.
Formation control is a crucial technique for multi-robot systems. When executing a designated task, robots typically coordinate by maintaining sequential formations. For instance, when robots are required to move a large object, it is necessary for them to work in a certain formation [
3]. In these situations, errors in the achieved formations may affect the tasks undertaken, which should be constrained in a reasonable range. Therefore, it is essential to estimate the formation error in system design. On the other hand, information theory has gained great success in estimation, which is a suitable choice to solve this problem.
There has been much work on multi-robot formation control. According to [
4], existing results can mainly be categorized into position-, displacement- and distance-based control.
In position-based control, the absolute positions are measured by sensors with respect to a global coordinate system. According to the measurements, robots adjust their own positions to stand in a formation. To enhance the system robustness, interactions among robots were introduced to the controller. Furthermore, the strategy of feedback coordination was proposed in [
5] to improve the stability.
In displacement-based control, robots sense neighboring companions and estimate their relative positions with respect to the global coordinate system. In this way, robots need to find their own orientation with respect to the desired formation. The global coordinate system itself and the absolute positions in it do not need to be explicitly known. Regarding this type of controller, the single-integrator modeled scenarios [
6,
7], the double-integrator modeled scenarios, the general linear agent scenarios [
8] and the nonholonomic agent scenarios [
9] were discussed recently in existing works.
In distance-based control, robots adjust distances between them to achieve the desired formation. In this process, each robot needs to sense neighboring companions and measure its relative positions with respect to its own coordinate system. The orientations of these local coordinate systems do not have to be unified. The distance-based control includes directed and undirected control. For undirected control, where the robot interaction graph is undirected, rigidity [
10] was proposed as a requirement for the interaction graph. For directed control with directed interaction graphs, the notion of persistence was introduced to characterize the interaction graph [
11]. Based on the basic feasibility requirements, problems of stabilization [
12] and n-dimensional control [
13] were further investigated.
The attitude control of robots is a supplement to position control in multi-robot systems. In [
14], a general framework was presented to analyze the attitude tracking control for a rigid body. Furthermore, the attitude control for spacecraft [
15,
16] and leader-follower cooperative attitude control [
17] were also investigated.
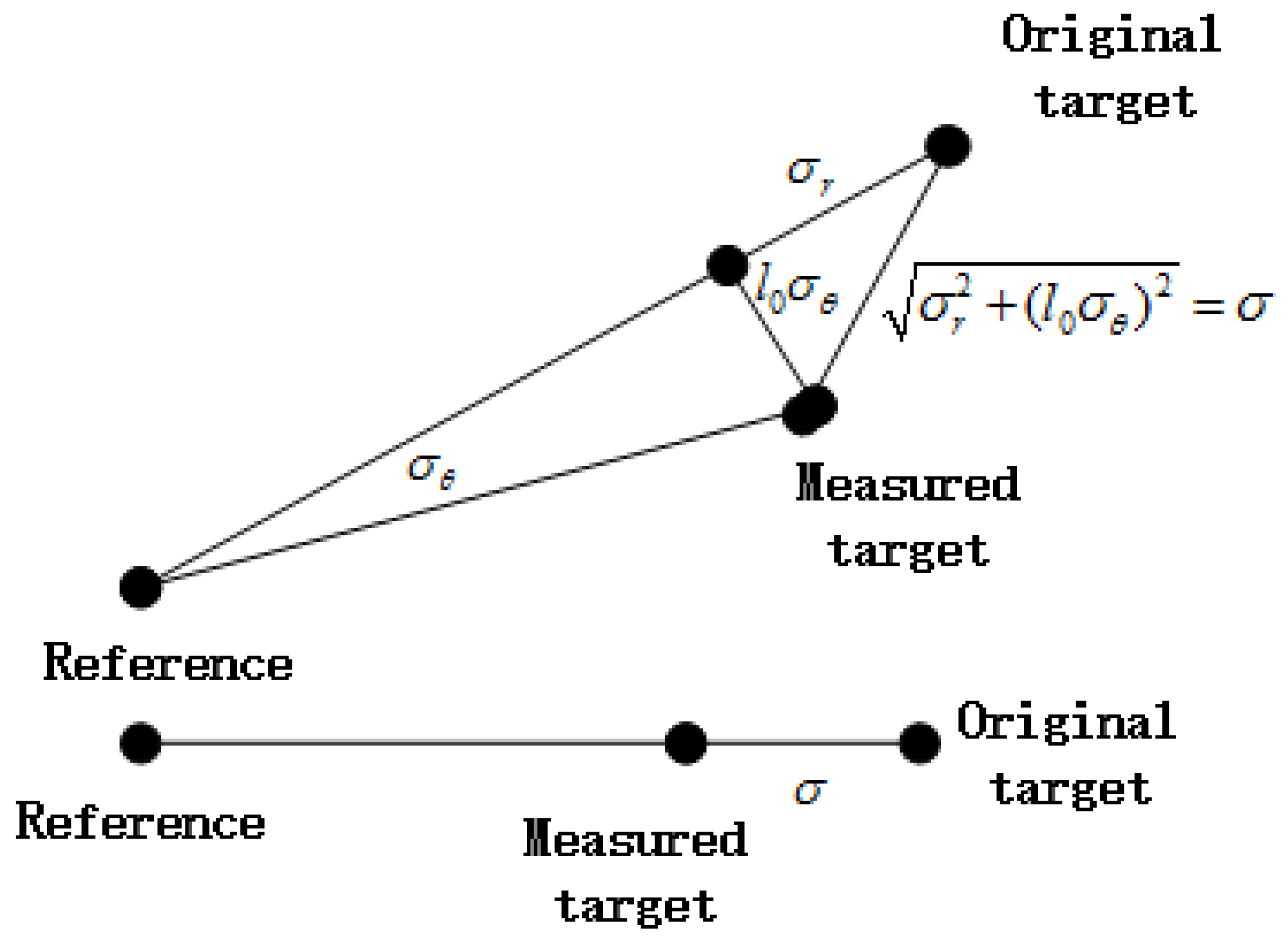
However, formation error analysis is still an open problem in theory. In multi-robot systems, formation error has to be constrained so that the tasks undertaken are not affected. Therefore, in system design, the error needs to be estimated for the adjustment of the system parameters. In the communication field, information theory has gained great success in error control. In multi-robot systems, it is also an appropriate choice to solve the estimation problem. In this paper, the formation error is defined in the form of distance. The Bayes risk representing formation error is estimated by calculating the mutual information between the measured value and the desired value. The results are further developed, and a lower bound of formation error is derived.
In this paper, our main focus is on leader-follower control scenarios, where each robot has a reference and follows it until the robot arrives at its desired position. Note that the leader traditionally refers to a leading robot followed by all other ones. However, in this paper, each robot is allowed to have a different reference as its leader. If the reference is chosen as other robots, it is a displacement-based control. If the reference is a fixed place, it is regarded as a position-based control. Each robot measures its reference with sensors and reaches the desired position by controllers. In this process, the sensors and controllers both result in errors. By introducing the notions of information theory, we derive a lower bound of formation error with respect to the precision of sensors and controllers. This newly-developed theoretical result can assist the design of a multi-robot formation system according to the application requirements. Finally, simulations are carried out to check our theoretical results.
For simplicity, the contributions in this paper are summarized as follows: (1) setting up a model to describe the errors of sensors and controllers in formation control; (2) applying information theory to estimate the formation error and deriving a lower bound with respect to system parameters; (3) testing the estimation results with a quasi-static control model in multi-robot systems.
The rest of the paper is organized as follows: In
Section 2, the problem statement is provided. In
Section 3, a problem model is set up. In
Section 4, the issue is fit into a distributed estimation problem in information theory. The estimated error lower bound and its proof are provided in
Section 5. Afterwards, the simulations are displayed to check the theoretical results in
Section 6. Finally, the conclusion is given in
Section 7.
5. Proof of Lower Bound
In this section, a proof of the lower bound in Theorem 1 is provided. In [
20], the authors proposed theorems to estimate the lower bound of Bayes risk by information theory. The theorems are introduced as lemmas to analyze the formation error.
Lemma 1 ([
20] (Theorem 3))
. For any arbitrary norm and any , the parameter of interest and W is distributed in on each dimension. X are samples of parameter W. The Bayes risk on estimation of W with respect to the distortion function satisfies:where is the volume of the unit ball in (, ) and is the gamma function. When a real-valued W is estimated with respect to , (13) is simplified as:Considering the unconditional version, there is a simpler form: In fact, (
15) is an unconditional version of Lemma 1, which gives a lower bound of
. This is for the case
. If the range of the distribution is
, (
15) is supposed to be multiplied by
. Besides,
W and
X are unconditional on
U. Therefore, the unconditional version is taken for estimation.
Lemma 2 ([
20] (Theorem 4))
. In decentralized estimation with a single processor, for any choice of and ,where C is the Shannon capacity of the noisy channel and represents the properties of the channel. In this problem, there is no process across the noisy channel. Then:
is defined as follows. Given a channel with conditional distribution K whose input alphabet is X and output alphabet is Y, the reference input distribution on X is . is the K-L divergence. For a constant and any other input distribution on X, if , K satisfies strong data processing inequalities (SDPI) at .
The SDPI constant of
K at input distribution
is defined as:
The SDPI constant of
K is defined as:
With Lemma 2, an upper bound of is derived with respect to the system parameters. Lemma 1 gives a lower bound of Bayes risk with respect to . Therefore, the combination of Lemmas 1 and 2 leads to a final estimation of the lower bound.
In this problem, the channel loss in information theory is not considered, for there is no process across the channel. That is, the channel capacity
C is infinite. In (
16), the upper bound of
is the minimum value of three elements. Among them,
is related to
C. Therefore, it is supposed to be ignored. Then, the upper bound (
16) is simplified as:
In formation error analysis,
denotes
n measurements of parameter
W. Each of its element
satisfies
.
is a continuous random variable. After the quantization with rate
b, there will be loss of information. Therefore,
is larger than
b. That is,
Then, the upper bound (
20) is further simplified as (
22).
Then, the following step is to estimate and separately.
Clarke [
21] showed that:
where
represents the differential entropy of
W.
is the Fisher information matrix.
From (
4), the probability distribution density of
W is
.
Then, the differential entropy of
W is:
The Fisher information is:
From (
6),
is a joint Gaussian distribution of
n independent samples. Then:
Substituting (
26) into (
25),
In this system, since
,
. By (
23) and (
24), the estimation of
is:
As for the estimation of
, the critical step is to estimate
. Here, a lemma in [
20] is introduced to achieve it.
Lemma 3 ([
20] (Lemma 5))
. For a joint distribution , suppose there is a constant such that the forward channel satisfies:for all and .Then, the SDPI constants of the forward channel and the backward channel satisfy:and: The measurement of parameter
W is
. Then,
is replaced with
. From (
19),
Then, together with (
31),
Therefore, the critical step is to estimate .
From (
6),
is a joint Gaussian distribution, with
w as its mean. Then:
From (
29),
is the minimum value of (
34). As each element in
is independent of each other, the problem is equivalent to minimizing
. Let:
where
and
. (
35) is transformed as:
When
, (
36) increases with
x. Therefore, (
36) is minimized at
. Then:
As
,
Similarly, when
, (
36) decreases as
x increases. Therefore, (
36) is minimized at
. Then:
To derive the minimum point, (
36) is transformed as follows:
Equation (
40) is a quadratic function of
and
. Then, the minimum value is reached at
. That is:
Equation (
41) is a quadratic function of
w. The minimum point of (
41) is
. Therefore:
Together with (
38) and (
42),
Then:
Together with (
34),
That is (see (
29)):
Finally, from Lemma 3 and (
33),
With the estimated value of
and
, the conclusion is:
In (
15),
is supposed to be replaced with
, for
W is estimated by
V here. The lower bound in (
15) is multiplied by parameter
. According to the upper bound given in (
48), the final lower bound of the Bayes risk is derived as:
Therefore, the proof of Theorem 1 is accomplished.
6. Simulations
To test the formation error analysis result, the leader-follower mode to achieve a formation is first realized in MATLAB.
In leader-follower mode, there are plenty of controllers with different operation precisions. The controllers may use operations with complex techniques to control the acceleration of movements. In fact, the moving speed can be viewed as a constant during a short time interval. Therefore, the single-integrator controller in (
50) is applied to represent other controllers in a quasi-static model. Note that in this control model, each movement represents the average movements in a time slot. In this way, the controller is simplified, and the simulation concentrates on testing the formation error analysis with respect to system parameters.
In (
50),
is the control input and
is the position.
is the differential derivative of
.
is the maximum speed of robots. The direction of
is not restricted. That is, robots are supposed to be omnidirectional. In simulations, the continuous control operation is replaced by the discrete control model. Time is discrete, and the refreshment of speed input is also discrete. In the quasi-static model, robots are supposed to update the speed instantaneously. In each time slot, each robot will move a grid towards its target. Then, after several time slots, each robot will reach its target grid, and the system will reach a stable state, which ends the whole process. The grids mentioned above are shown in
Figure 3. The controllers are set to ensure precision in discrete grids. If the robot discovers that there are any other robot in its target grid or heading towards the grid, it will wait a time slot until the grid is clear to move in it. In this way, collisions are avoided in the process.
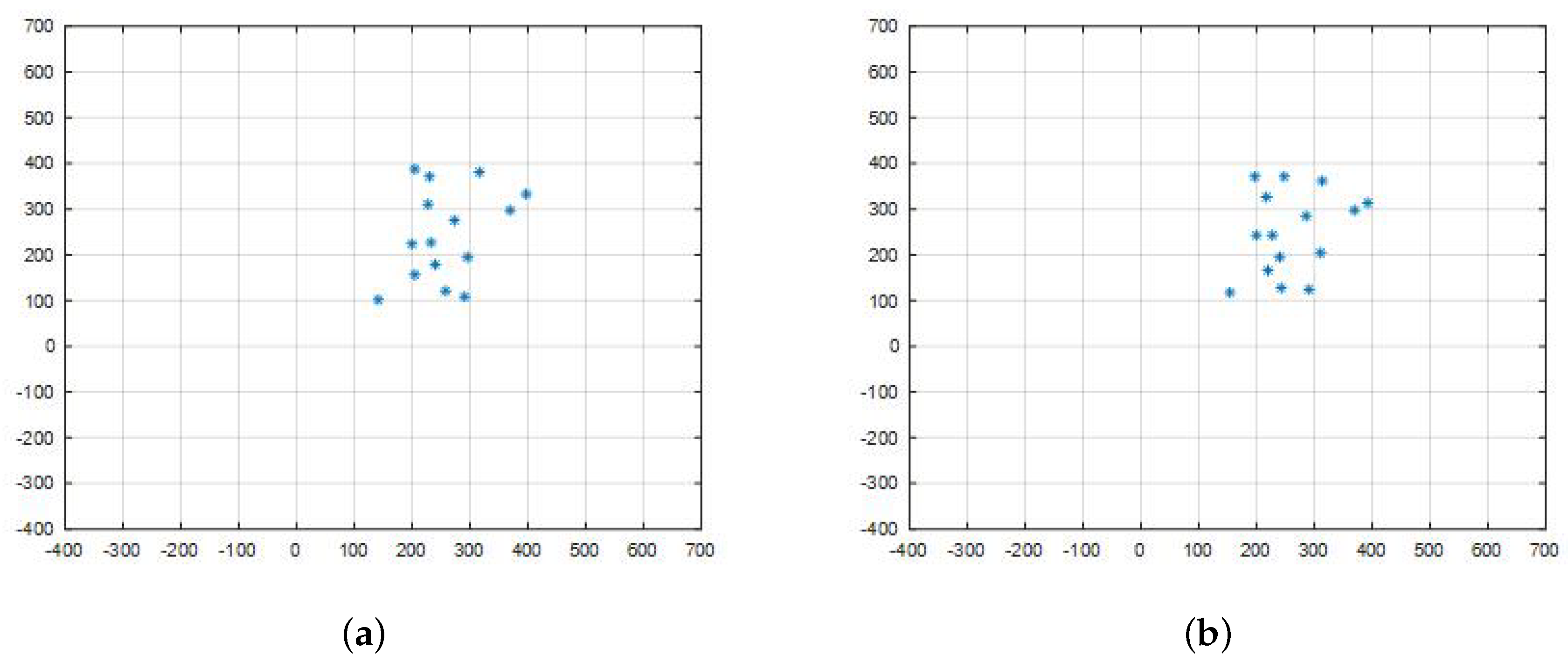
6.1. Formation Illustration
In simulations, the working space is a square area with size
. There are 15 robots, and the initial positions are generated randomly. The controlling range
is set as 300, and the quantification rate is
. That is, the operation error of the controller is within
. The maximum speed
is five, and the measuring variance is
. As shown in
Figure 5, robots in random initial positions are required to reach a square formation under the quasi-static control mode.
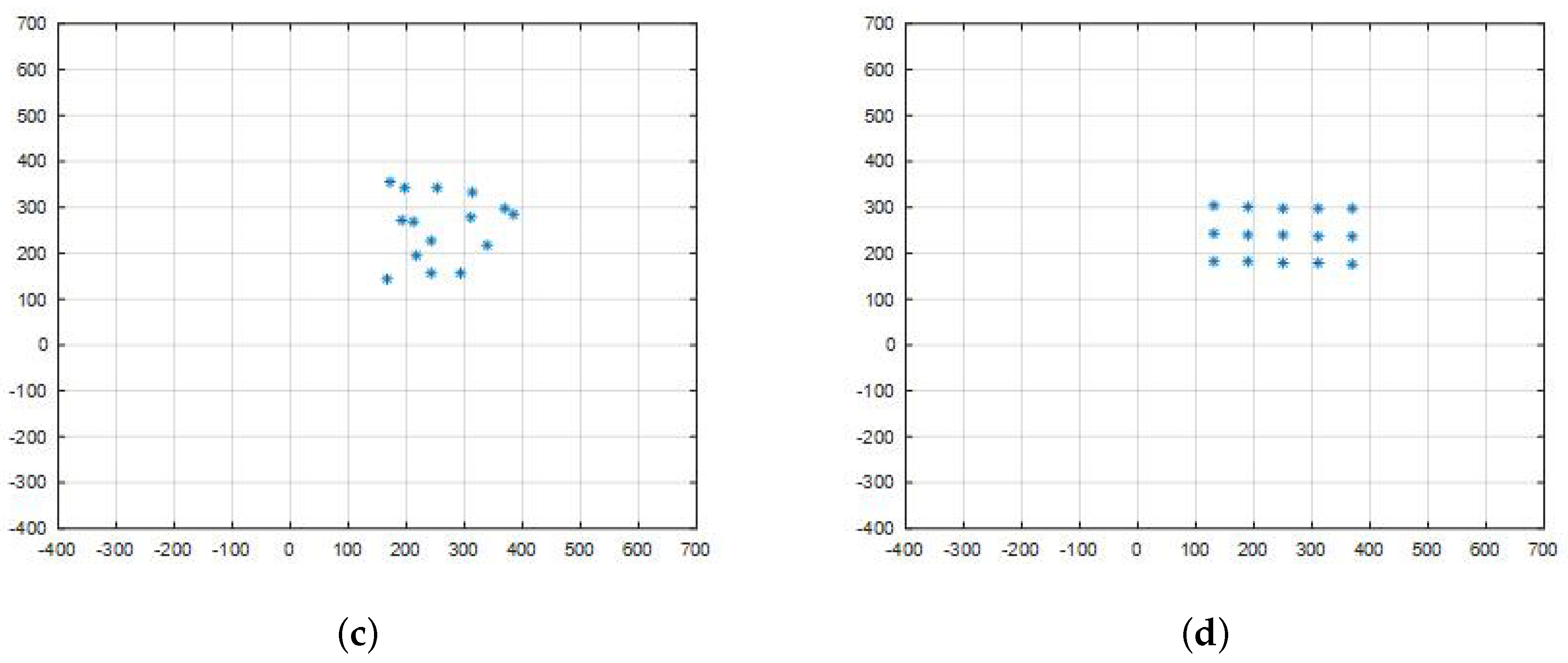
6.2. Formation Error Analysis
To investigate the offsets of the theoretical lower bound on formation error, we carry out simulations to check the errors of achieved formations with respect to the system parameters. The experimental data are fit with the least squares method. The calculated lower bound is also shown for comparison.
In each simulation, the conditioning parameter is adjusted in a previously set range. For each parameter value, 20 experiments are carried out. Robots are in random initial positions. They achieve the circle formation shown in
Figure 6. The formation error for each experiment is recorded.
6.2.1. Measuring Times n
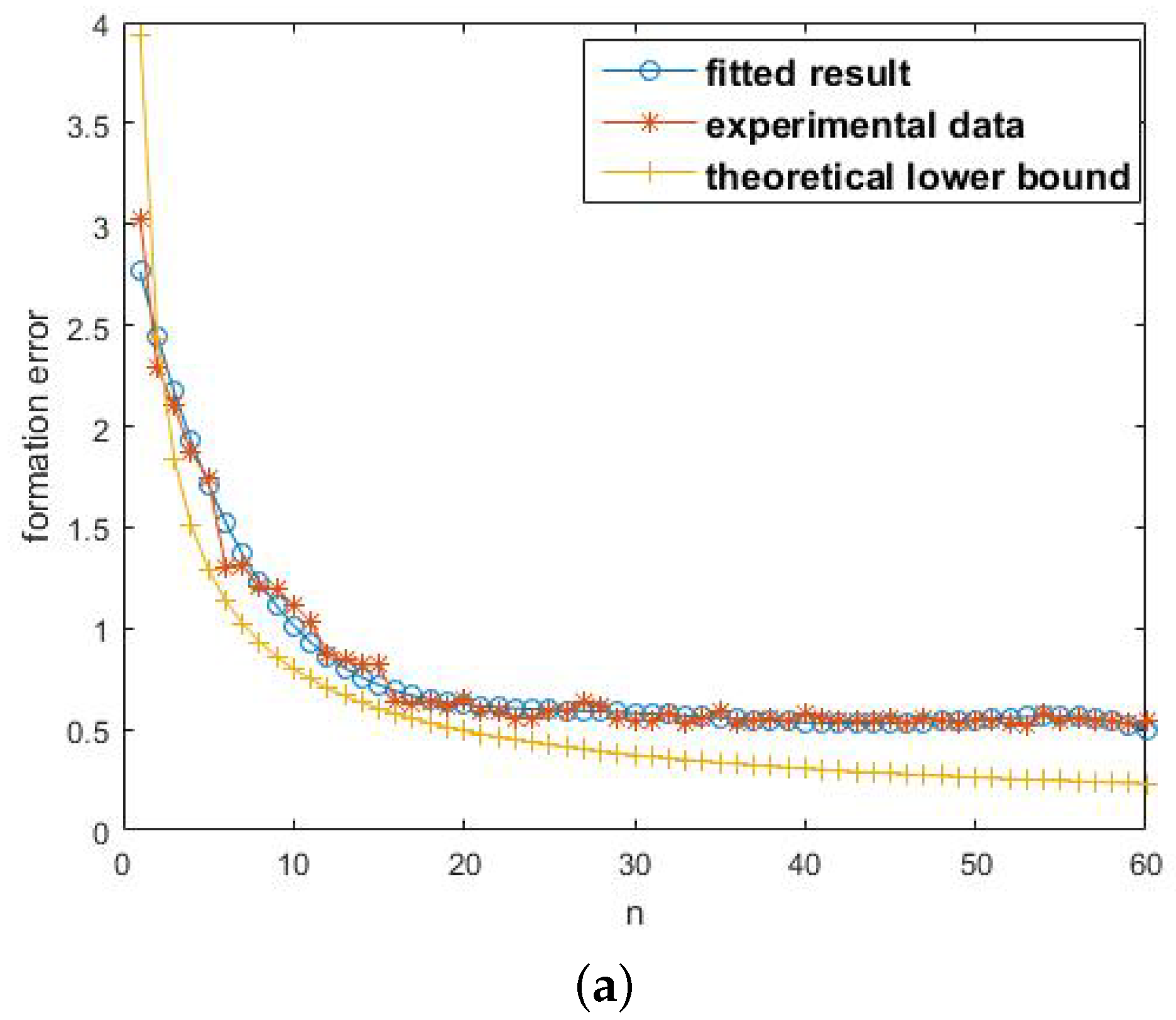
As discussed above, each robot measures the desired position n times to get its final target. There are 15 robots. The one-dimensional measuring variance is set to be two, and . The controlling range is 200. The distance is partitioned into 200 sections within which the precision of control operation is ensured. Converting it into the quantization rate, it is . The maximum speed is five. n ranges from 1–60. In the theoretical analysis, the distance empirical ranging threshold is .
Figure 7a shows the formation error with respect to
n. All curves decrease as
n increases. As a matter of common sense, when
n is small, increasing
n apparently reduces the formation error. When
n is large enough, increasing
n does not obtain obvious evolution. The tendency of curves is consistent with common sense. The curve marked by “*” represents the experimental data, and the curve marked by “o” is the fitting result with the least squares method. The curve marked by “+” is the calculated lower bound by Theorem 1. At the beginning, the theoretical result is a little larger than the experimental data. This is due to less statistics performed. Note that in the remaining majority part, the lower bound is below the experimental data, and the tendency is the same.
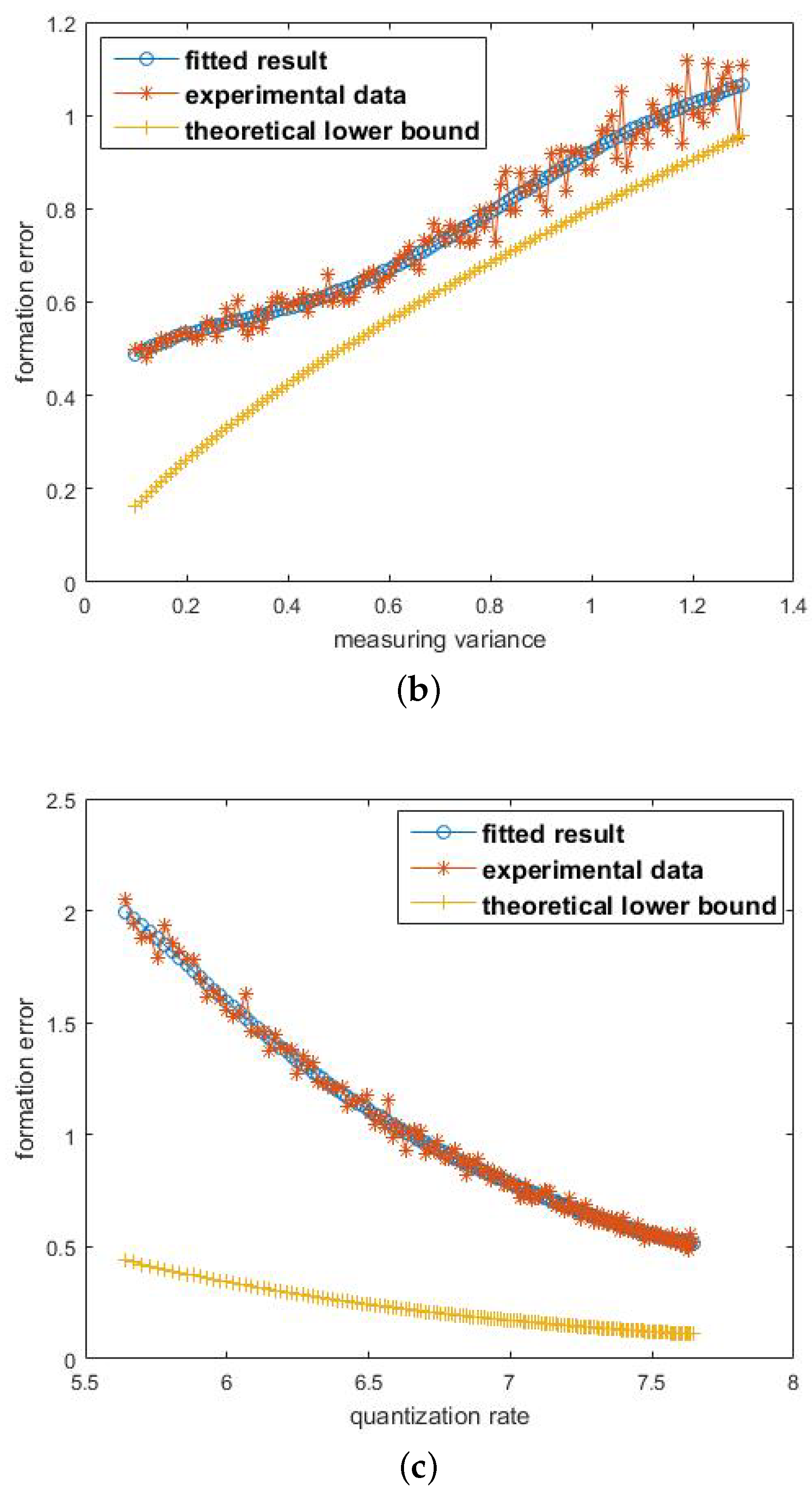
6.2.2. Measuring Variance
There are 15 robots each of which measures the distance 10 times. The controlling range is 200. The distance is partitioned into 200 sections within which the precision of control operation is ensured. Converting it into the quantization rate, it is . The maximum speed is five. The one-dimensional variance ranges from 0.1–1.3, and . In the theoretical analysis, the distance empirical ranging threshold is .
Figure 7b shows the tendency of formation error with respect to measuring variance
. In general, all curves increase with
. As a matter of common sense, when the measuring variance increases, the measuring error increases and therefore results in the increase of formation errors. The tendency of curves is consistent with the common intuition. The theoretical lower bound is below the experimental data, and their tendencies are the same.
6.2.3. Quantification Rate b
There are 15 robots each of which measures the distance 10 times. The controlling range is 200, and the maximum speed is five. The one-dimensional measuring variance of each robot is and . The whole range is partitioned into grids within which the precision of control operation is ensured. The quantization rate b satisfies . In the theoretical analysis, the distance empirical ranging threshold is .
Figure 7c shows the tendency of formation error with respect to the quantization rate
b. All curves decrease as
b increases. As a matter of common sense, when
b increases, the operation precision of the controller increases, resulting in the decrease of formation errors. When
b is large enough, the decreasing tendency slows down. The tendency of curves is consistent with the common intuition. The lower bound is below the experimental data. Though there is a gap between them, their tendencies are similar.