Quantum Quantifiers for an Atom System Interacting with a Quantum Field Based on Pseudoharmonic Oscillator States
Abstract
1. Introduction
2. Physics Model and Dynamics
3. Quantum Quantifiers
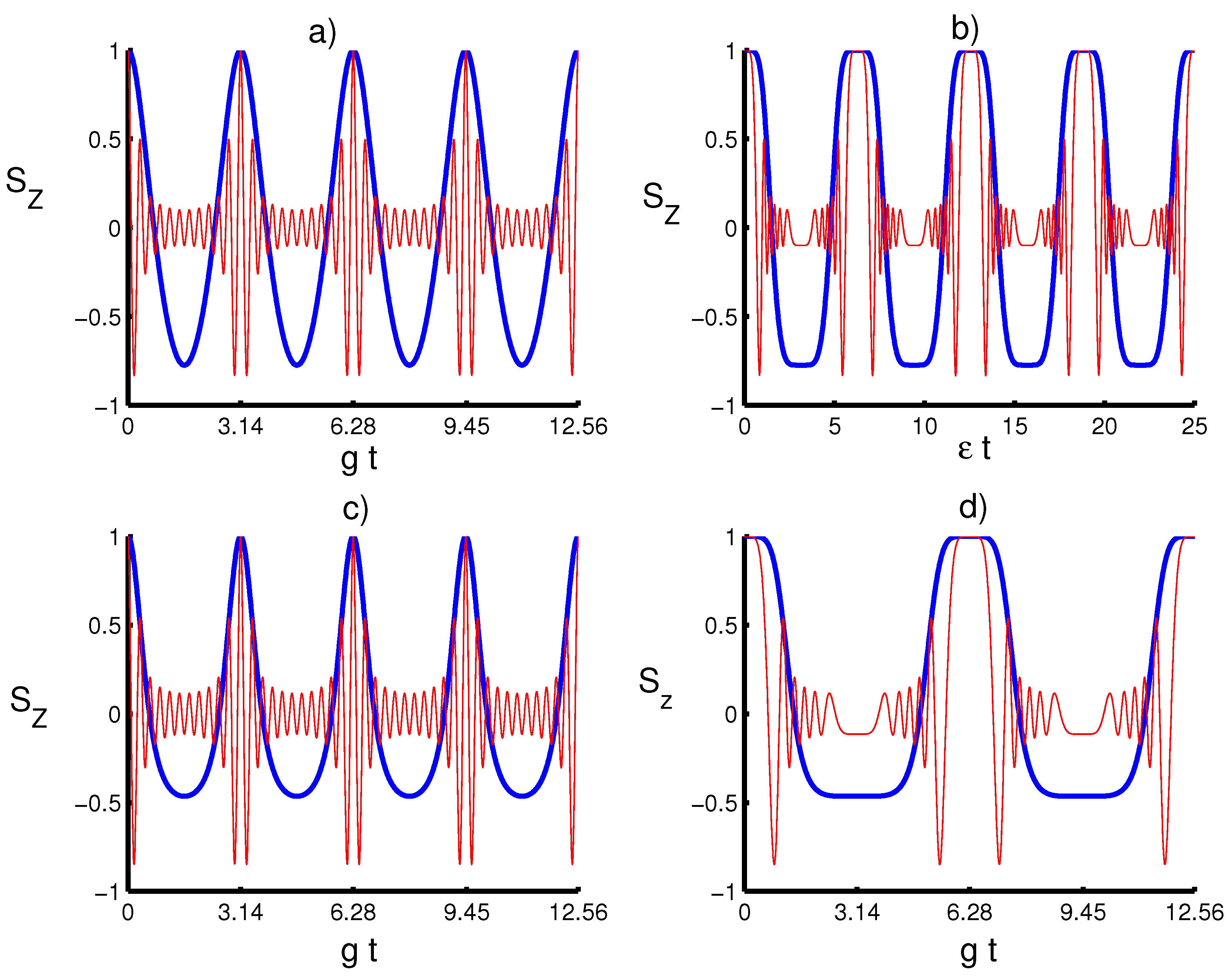
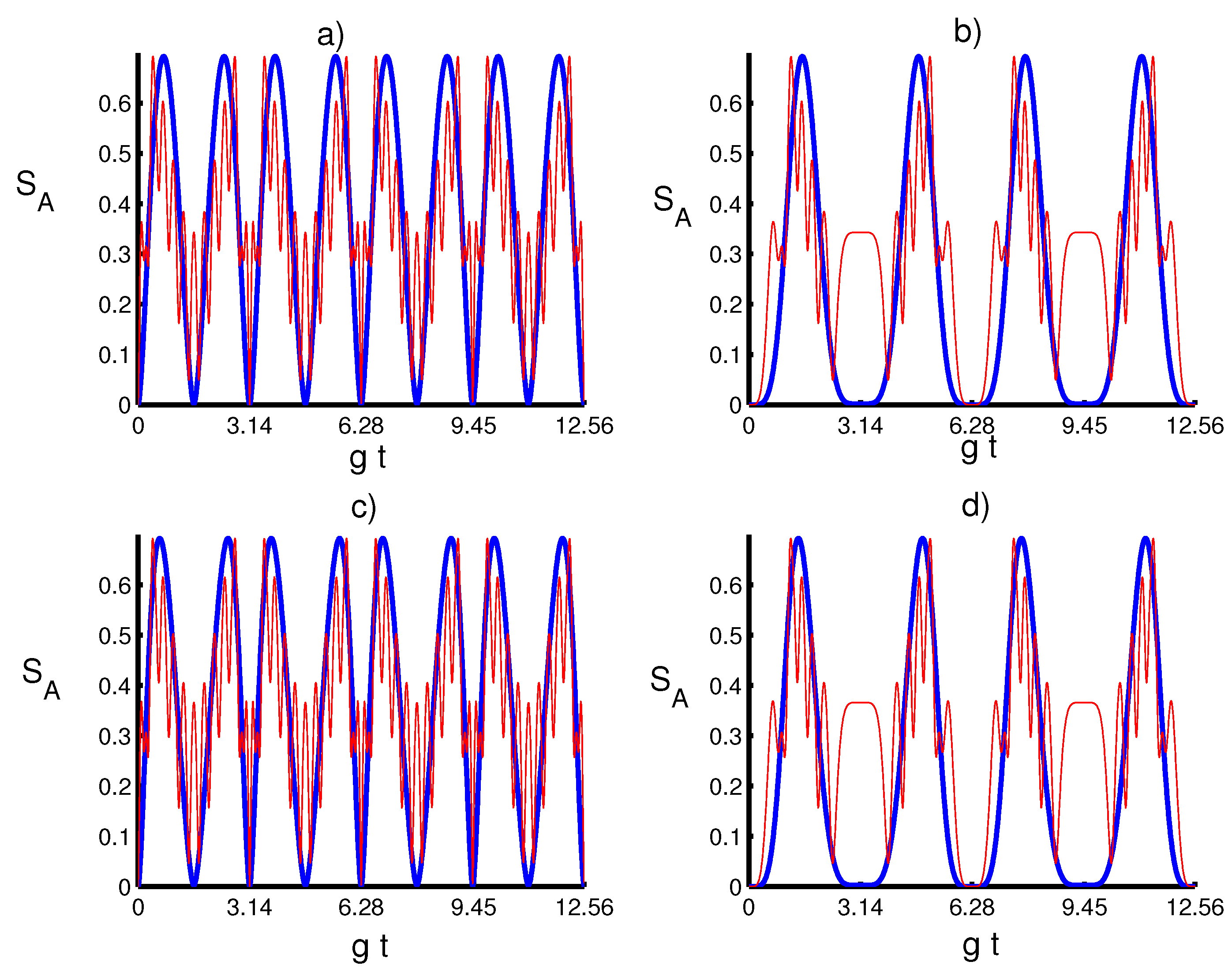
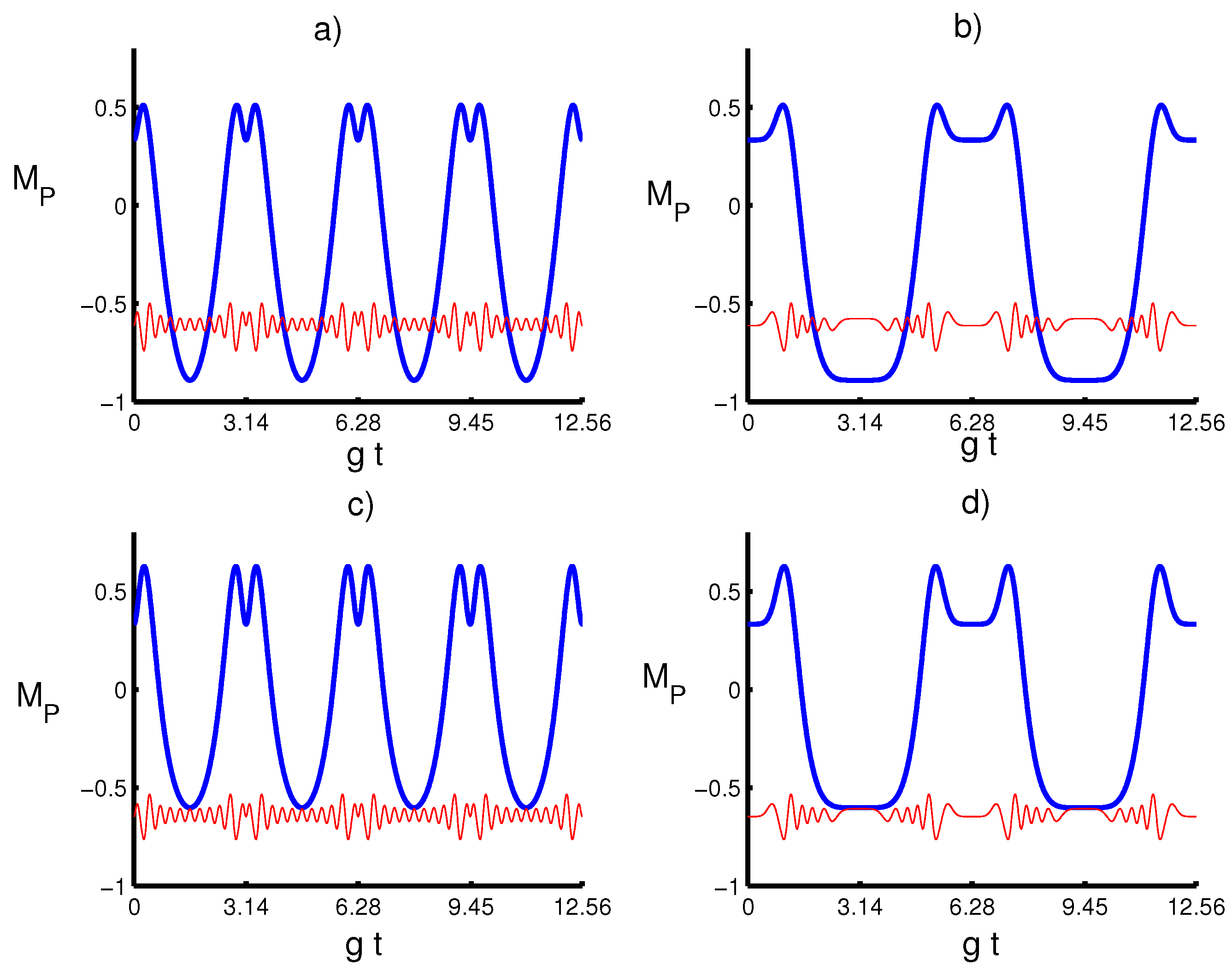
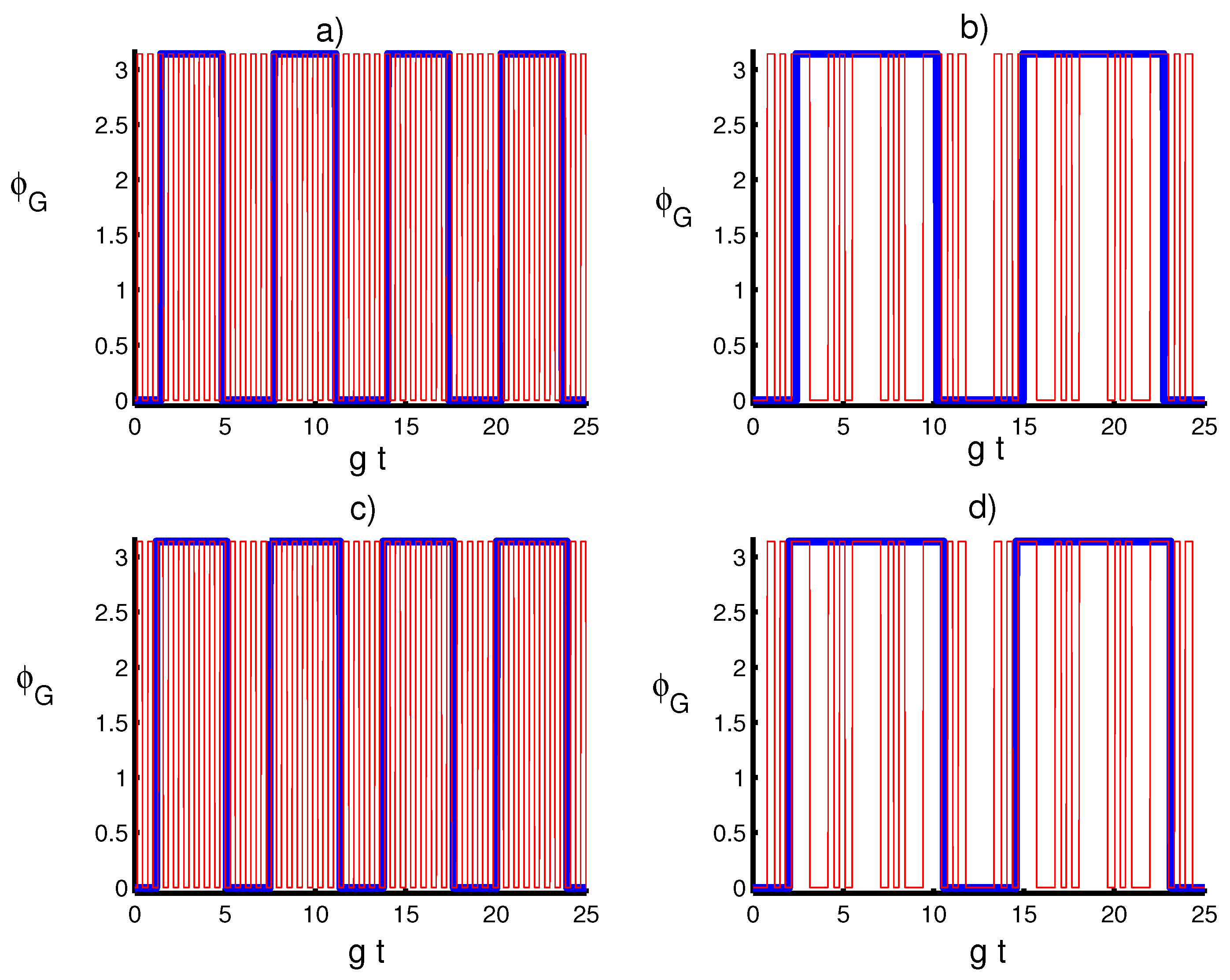
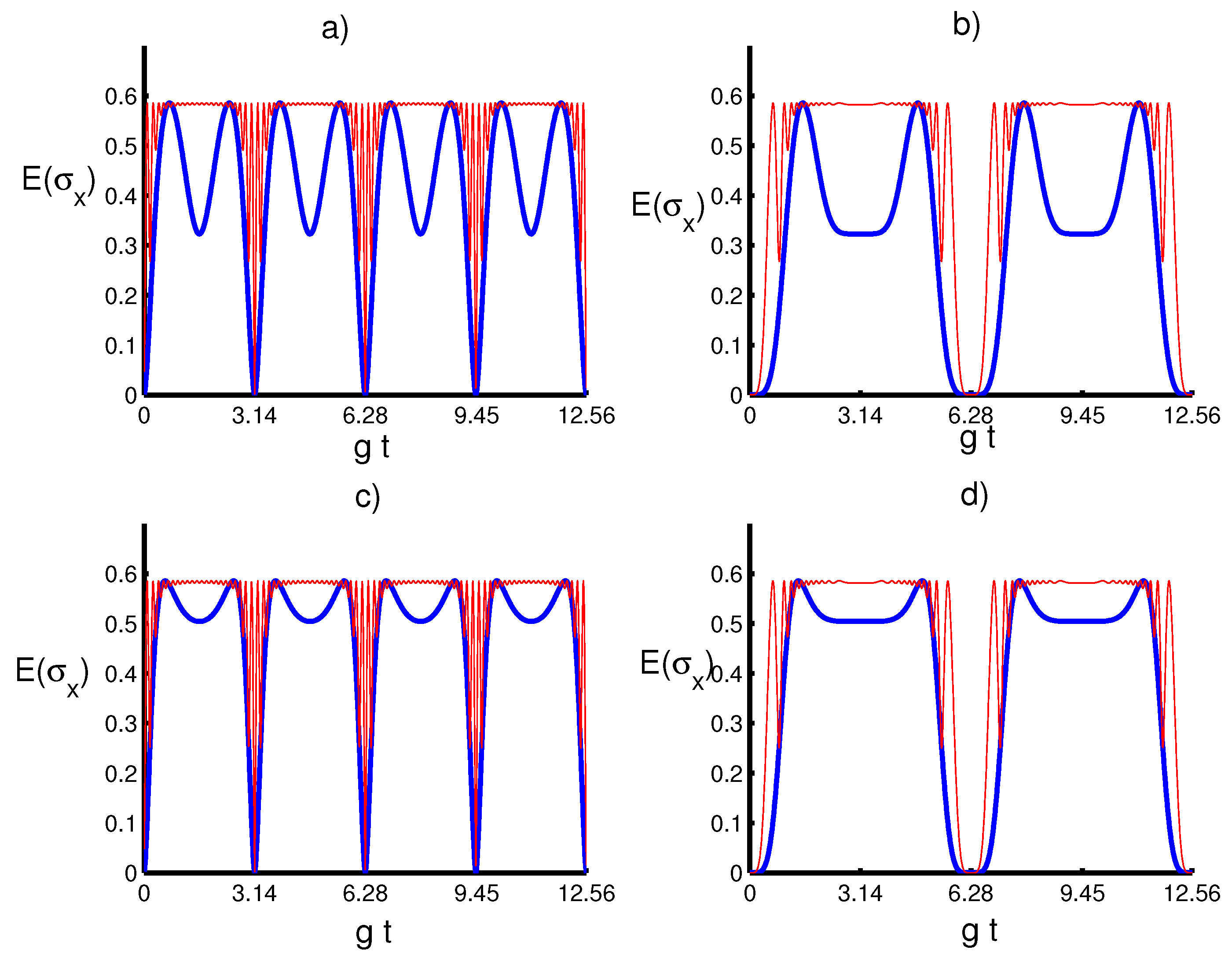
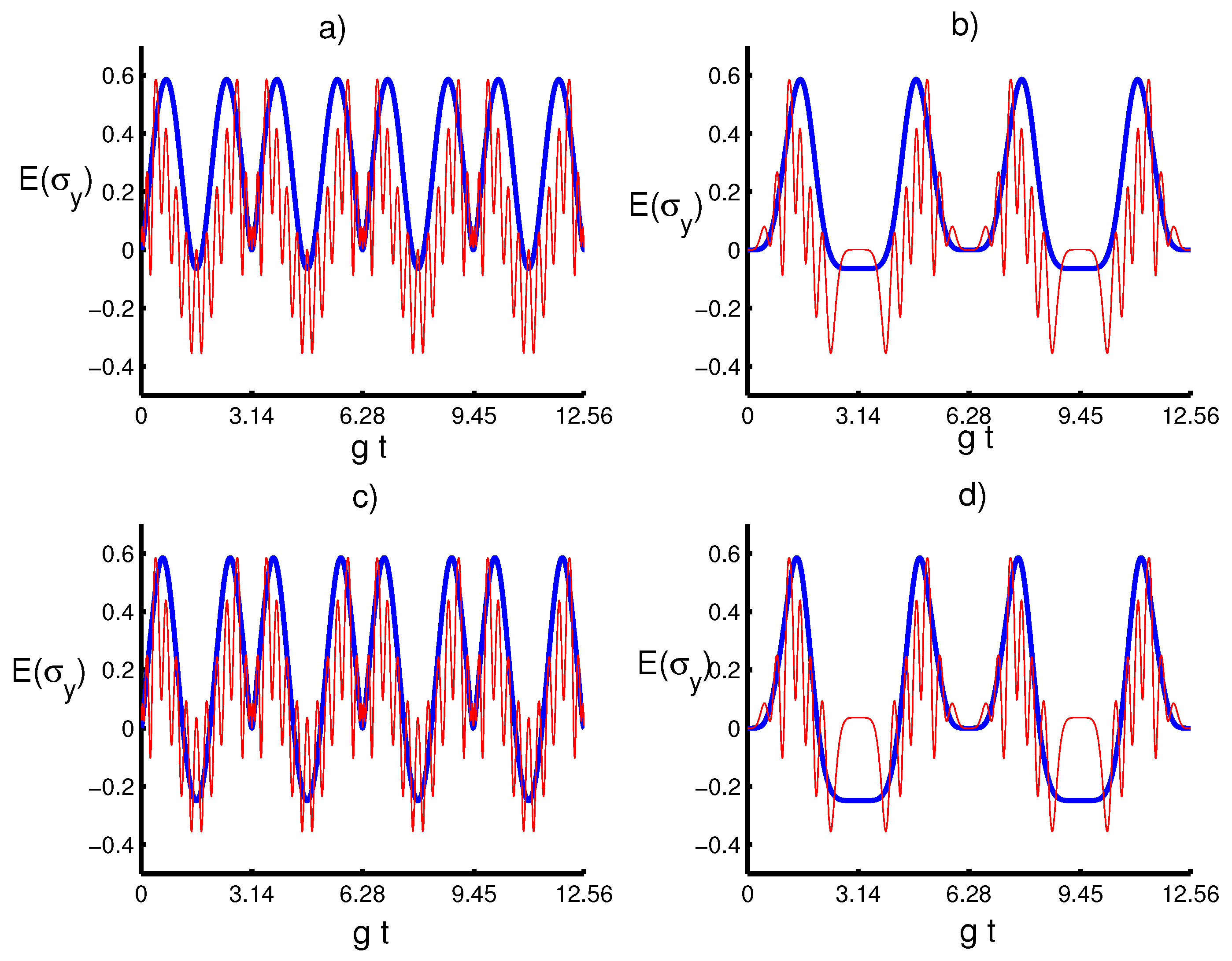
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Alber, G.; Beth, T.; Horodecki, M.; Horodecki, P.; Horodecki, R.; Rötteler, M.; Weinfurter, H.; Zeilinger, R.A. Quantum Information; Springer: Berlin, Germany, 2001; Chapter 5. [Google Scholar]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef]
- Joo, J.; Munro, W.J.; Spiller, T.P. Quantum metrology with entangled coherent states. Phys. Rev. Lett. 2011, 107, 083601. [Google Scholar] [CrossRef] [PubMed]
- Amico, L.; Fazio, R.; Osterloh, A.; Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 2008, 80, 517–576. [Google Scholar] [CrossRef]
- Gershenfeld, N.A.; Chuang, I.L. Bulk spin-resonance quantum computation. Science 1997, 275, 350–356. [Google Scholar] [CrossRef] [PubMed]
- Tóth, G.; Simon, C.; Cirac, J.I. Entanglement detection based on interference and particle counting. Phys. Rev. A 2003, 68, 062310. [Google Scholar] [CrossRef]
- Sete, E.A.; Eleuch, H.; Ooi, C.R. Light-to-matter entanglement transfer in optomechanics. JOSA B 2014, 31, 2821–2828. [Google Scholar] [CrossRef]
- Zheng, S.B.; Guo, G.C. Efficient scheme for two-atom entanglement and quantum information processing in cavity QED. Phys. Rev. Lett. 2000, 85, 2392–2395. [Google Scholar] [CrossRef] [PubMed]
- Blinov, B.B.; Moehring, D.L.; Duan, L.M.; Monroe, C. Observation of entanglement between a single trapped atom and a single photon. Nature 2004, 428, 153–157. [Google Scholar] [CrossRef] [PubMed]
- Togan, E.; Chu, Y.; Trifonov, A.S.; Jiang, L.; Maze, J.; Childress, L.; Dutt, M.G.; Sørensen, A.S.; Hemmer, P.R.; Zibrov, A.S.; et al. Quantum entanglement between an optical photon and a solid-state spin qubit. Nature 2010, 466, 730–734. [Google Scholar] [CrossRef] [PubMed]
- Wilk, T.; Webster, S.C.; Kuhn, A.; Rempe, G. Single-atom single-photon quantum interface. Science 2007, 317, 488–490. [Google Scholar] [CrossRef] [PubMed]
- Olmschenk, S.; Matsukevich, D.N.; Maunz, P.; Hayes, D.; Duan, L.M.; Monroe, C. Quantum teleportation between distant matter qubits. Science 2009, 323, 486–489. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.S.; Chen, Y.A.; Zhao, B.; Chen, S.; Schmiedmayer, J.; Pan, J.W. Experimental demonstration of a BDCZ quantum repeater node. Nature 2008, 454, 1098–1101. [Google Scholar] [CrossRef] [PubMed]
- Ritter, S.; Nölleke, C.; Hahn, C.; Reiserer, A.; Neuzner, A.; Uphoff, M.; Mücke, M.; Figueroa, E.; Bochmann, J.; Rempe, G. An elementary quantum network of single atoms in optical cavities. Nature 2012, 484, 195–200. [Google Scholar] [CrossRef] [PubMed]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 1984, 392, 45–57. [Google Scholar] [CrossRef]
- Aharonov, Y.; Anandan, J. Phase change during a cyclic quantum evolution. Phys. Rev. Lett. 1987, 58, 1593–1596. [Google Scholar] [CrossRef] [PubMed]
- Simon, B. Holonomy, the quantum adiabatic theorem, and Berry’s phase. Phys. Rev. Lett. 1983, 51, 2167–2170. [Google Scholar] [CrossRef]
- Anandan, J.; Stodolsky, L. Some geometrical considerations of Berry’s phase. Phys. Rev. D 1987, 35, 2597–2600. [Google Scholar] [CrossRef]
- Samuel, J.; Bhandari, R. General setting for Berry’s phase. Phys. Rev. Lett. 1988, 60, 2339–2342. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Cao, X.Z.; Su, Q.P.; Xiong, S.J.; Yang, C.P. Multi-target-qubit unconventional geometric phase gate in a multi-cavity system. Sci. Rep. 2016, 6, 21562. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.L.; Wang, Z.; Wu, C.; Kwek, L.C.; Lai, C.H.; Oh, C.H. Scheme for unconventional geometric quantum computation in cavity QED. Phys. Rev. A 2007, 75, 052312. [Google Scholar] [CrossRef]
- Xiang-Bin, W.; Keiji, M. Nonadiabatic conditional geometric phase shift with NMR. Phys. Rev. Lett. 2001, 87, 097901. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.L.; Wang, Z.D. Implementation of universal quantum gates based on nonadiabatic geometric phases. Phys. Rev. Lett. 2002, 96, 289901. [Google Scholar] [CrossRef]
- Falci, G.; Fazio, R.; Palma, G.M.; Siewert, J.; Vedral, V. Detection of geometric phases in superconducting nanocircuits. Nature 2000, 407, 355–358. [Google Scholar] [CrossRef] [PubMed]
- Drummond, P.D.; Ficek, Z. Quantum Squeezing; Springer: Berlin, Germany, 2004. [Google Scholar]
- Wodkiewicz, K. Reduced quantum fluctuations in the Josephson junction. Phys. Rev. B 1985, 32, 4750. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Puri, R.R. Cooperative behavior of atoms irradiated by broadband squeezed light. Phys. Rev. A 1990, 41, 3782–3791. [Google Scholar] [CrossRef] [PubMed]
- Ashraf, M.M.; Razmi, M.S.K. Atomic-dipole squeezing and emission spectra of the nondegenerate two-photon Jaynes-Cummings model. Phys. Rev. A 1992, 45, 8121–8128. [Google Scholar] [CrossRef] [PubMed]
- Kitagawa, M.; Ueda, M. Squeezed spin states. Phys. Rev. A 1993, 47, 5138. [Google Scholar] [CrossRef] [PubMed]
- Civitarese, O.; Reboiro, M. Atomic squeezing in three level atoms. Phys. Lett. A 2006, 357, 224–228. [Google Scholar] [CrossRef]
- Civitarese, O.; Reboiro, M.; Rebón, L.; Tielas, D. Atomic squeezing in three-level atoms with effective dipole–dipole atomic interaction. Phys. Lett. A 2010, 374, 2117–2121. [Google Scholar] [CrossRef]
- Poulsen, U.V.; Mølmer, K. Squeezed light from spin-squeezed atoms. Phys. Rev. Lett. 2001, 87, 123601. [Google Scholar] [CrossRef] [PubMed]
- Yukalov, V.I.; Yukalova, E.P. Atomic squeezing under collective emission. Phys. Rev. A 2004, 70, 053828. [Google Scholar] [CrossRef]
- Wang, X. Spin squeezing in nonlinear spin-coherent states. J. Opt. B Quantum Semiclass. Opt. 2001, 3, 93–96. [Google Scholar] [CrossRef]
- Rojo, A.G. Optimally squeezed spin states. Phys. Rev. A 2003, 68, 013807. [Google Scholar] [CrossRef]
- Wang, X.; Sanders, B.C. Relations between bosonic quadrature squeezing and atomic spin squeezing. Phys. Rev. A 2003, 68, 033821. [Google Scholar] [CrossRef]
- Dicke, R.H. Coherence in spontaneous radiation processes. Phys. Rev. 1954, 93, 99–110. [Google Scholar] [CrossRef]
- El-Orany, F.A.; Wahiddin, M.R.B.; Obada, A.S. Single-atom entropy squeezing for two two-level atoms interacting with a single-mode radiation field. Opt. Commun. 2008, 281, 2854–2863. [Google Scholar] [CrossRef]
- Barnett, S.M.; Knight, P.L. Dissipation in a fundamental model of quantum optical resonance. Phys. Rev. A 1986, 33, 2444–2448. [Google Scholar] [CrossRef]
- Puri, R.R.; Agarwal, G.S. Finite-Q cavity electrodynamics: Dynamical and statistical aspects. Phys. Rev. A 1987, 35, 3433–3449. [Google Scholar] [CrossRef]
- Eiselt, J.; Risken, H. Quasiprobability distributions for the Jaynes-Cummings model with cavity damping. Phys. Rev. A 1991, 43, 346–360. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Khalek, S.; Obada, A.S. New features of Wehrl entropy and Wehrl PD of a single Cooper-pair box placed inside a dissipative cavity. Ann. Phys. 2010, 325, 2542–2549. [Google Scholar] [CrossRef]
- Klauder, J.R.; Skagerstam, B.S. Coherent States-Applications in Physics and Mathematical Physics; World Scientific: Singapore, 1985. [Google Scholar]
- Zhang, W.M.; Gilmore, R. Coherent states: Theory and some applications. Rev. Mod. Phys. 1990, 62, 867–927. [Google Scholar] [CrossRef]
- Glauber, R.J. The quantum theory of optical coherence. Phys. Rev. 1963, 130, 2529–2539. [Google Scholar] [CrossRef]
- Walls, D.F. Squeezed states of light. Nature 1983, 306, 141–146. [Google Scholar] [CrossRef]
- Loudon, R.; Knight, P.L. Squeezed light. J. Mod. Opt. 1987, 34, 709–759. [Google Scholar] [CrossRef]
- Popov, D. Barut-Girardello coherent states of the pseudoharmonic oscillator. J. Phys. A Math. Gen. 2001, 34, 5283. [Google Scholar]
- Popov, D.; Sajfert, V.; Zaharie, I. Pseudoharmonic oscillator and their associated Gazeau–Klauder coherent states. Phys. A Stat. Mech. Appl. 2008, 387, 4459–4474. [Google Scholar] [CrossRef]
- Sage, M.; Goodisman, J. Improving on the conventional presentation of molecular vibrations: Advantages of the pseudoharmonic potential and the direct construction of potential energy curves. Am. J. Phys. 1985, 53, 350–355. [Google Scholar] [CrossRef]
- Gazeau, J.P.; Klauder, J.R. Coherent states for systems with discrete and continuous spectrum. J. Phys. A Math. Gen. 1999, 32, 123–132. [Google Scholar] [CrossRef]
- Klauder, J.R.; Penson, K.A.; Sixdeniers, J.M. Constructing coherent states through solutions of Stieltjes and Hausdorff moment problems. Phys. Rev. A 2001, 64, 013817. [Google Scholar] [CrossRef]
- Gol’dman, I.I.; Krivchenko, V.D.; Kogan, V.I.; Galitskiy, V.M. Problems in Quantum Mechanics; Infosearch: London, UK, 1960. [Google Scholar]
- Roy, B.; Roy, P. Gazeau–Klauder coherent state for the Morse potential and some of its properties. Phys. Lett. A 2002, 296, 187–191. [Google Scholar] [CrossRef]
- Fakhri, H.; Chenaghlou, A. Barut–Girardello coherent states for the Morse potential. Phys. Lett. A 2003, 310, 1–8. [Google Scholar] [CrossRef]
- Popov, D. Gazeau–Klauder quasi-coherent states for the Morse oscillator. Phys. Lett. A 2003, 316, 369–381. [Google Scholar] [CrossRef]
- Popov, D.; Davidovic, D.M.; Arsenovic, D.; Saifert, V. P-function of the pseudo harmonic oscillator in terms of Klauder-Perelomov coherent states. Acta Phys. Slovaca 2006, 56, 445–453. [Google Scholar]
- Walls, D.F.; Milburn, G.J. Quantum Optics; Springer: Berlin, Germany, 1994. [Google Scholar]
- Wang, X.; Sanders, B.C.; Pan, S.H. Entangled coherent states for systems with SU (2) and SU (1, 1) symmetries. J. Phys. A Math. Gen. 2000, 33, 7451–7467. [Google Scholar] [CrossRef]
- Popov, D.; Pop, N.; Luminosu, I.; Chiriţoiu, V. Density matrix approach of the excitation on coherent states of the pseudoharmonic oscillator. EPL Europhys. Lett. 2009, 87, 44003. [Google Scholar] [CrossRef]
- Mojaveri, B.; Dehghani, A. Generalized su (1, 1) coherent states for pseudo harmonic oscillator and their nonclassical properties. Eur. Phys. J. D 2013, 67, 179. [Google Scholar] [CrossRef]
- Perelomov, A.M. Coherent states for arbitrary Lie group. Commun. Math. Phys. 1972, 26, 222–236. [Google Scholar] [CrossRef]
- Wodkiewicz, K.; Eberly, J.H. Coherent states, squeezed fluctuations, and the SU (2) am SU (1, 1) groups in quantum-optics applications. JOSA B 1985, 2, 458–466. [Google Scholar] [CrossRef]
- Popov, D.; Pop, N.; Sajfert, V. Excitation on the Coherent States of Pseudoharmonic Oscillator. AIP Conf. Proc. 2009, 1131, 61–66. [Google Scholar]
- Perelomov, A.M. Generalized Coherent States and Their Applications; Springer: Berlin, Germany, 1986. [Google Scholar]
- Gerry, C.C.; Silverman, S. Path integral for coherent states of the dynamical group SU (1, 1). J. Math. Phys. 1982, 23, 1995–2003. [Google Scholar] [CrossRef]
- Janes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Phoenix, S.J.; Knight, P.L. Comment on “Collapse and revival of the state vector in the Jaynes-Cummings model: An example of state preparation by a quantum apparatus”. Phys. Rev. Lett. 1991, 66, 2833. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, B.; Herschbach, D. Alignment and trapping of molecules in intense laser fields. Phys. Rev. Lett. 1995, 74, 4623–4626. [Google Scholar] [CrossRef] [PubMed]
- Rempe, G.; Walther, H.; Klein, N. Observation of quantum collapse and revival in a one-atom maser. Phys. Rev. Lett. 1987, 58, 353–356. [Google Scholar] [CrossRef] [PubMed]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Berrada, K.; El Baz, M.; Hassouni, Y. On the construction of generalized su (1, 1) coherent states. Rep. Math. Phys. 2011, 68, 23–35. [Google Scholar] [CrossRef]
- Abdel-Khalek, S.; Berrada, K.; Ooi, C.R. Beam splitter entangler for nonlinear bosonic fields. Laser Phys. 2012, 22, 1449–1454. [Google Scholar] [CrossRef]
- Pancharatnam, S. The adiabatic phase and pancharatnam’s phase for polarized light. Proc. Indian Acad. Sci. 1956, 44, 247–262. [Google Scholar]
- Fang, M.F.; Zhou, P.; Swain, S. Entropy squeezing for a two-level atom. J. Mod. Opt. 2000, 47, 1043–1053. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raffah, B.M.; Berrada, K. Quantum Quantifiers for an Atom System Interacting with a Quantum Field Based on Pseudoharmonic Oscillator States. Entropy 2018, 20, 607. https://doi.org/10.3390/e20080607
Raffah BM, Berrada K. Quantum Quantifiers for an Atom System Interacting with a Quantum Field Based on Pseudoharmonic Oscillator States. Entropy. 2018; 20(8):607. https://doi.org/10.3390/e20080607
Chicago/Turabian StyleRaffah, Bahaaudin Mohammadnoor, and Kamal Berrada. 2018. "Quantum Quantifiers for an Atom System Interacting with a Quantum Field Based on Pseudoharmonic Oscillator States" Entropy 20, no. 8: 607. https://doi.org/10.3390/e20080607
APA StyleRaffah, B. M., & Berrada, K. (2018). Quantum Quantifiers for an Atom System Interacting with a Quantum Field Based on Pseudoharmonic Oscillator States. Entropy, 20(8), 607. https://doi.org/10.3390/e20080607



