Identity Vector Extraction by Perceptual Wavelet Packet Entropy and Convolutional Neural Network for Voice Authentication
Abstract
:1. Introduction
- (1)
- Design a PWPT according to the human auditory model named Greenwood scale function.
- (2)
- Utilize the PWPT to convert speech utterance into wavelet entropy feature vectors.
- (3)
- Design a CNN according to the phonetic DNN.
- (4)
- Utilize the CNN to estimate frame posteriors of feature vector from i-vector extraction.
2. Wavelet Entropy Feature Extraction
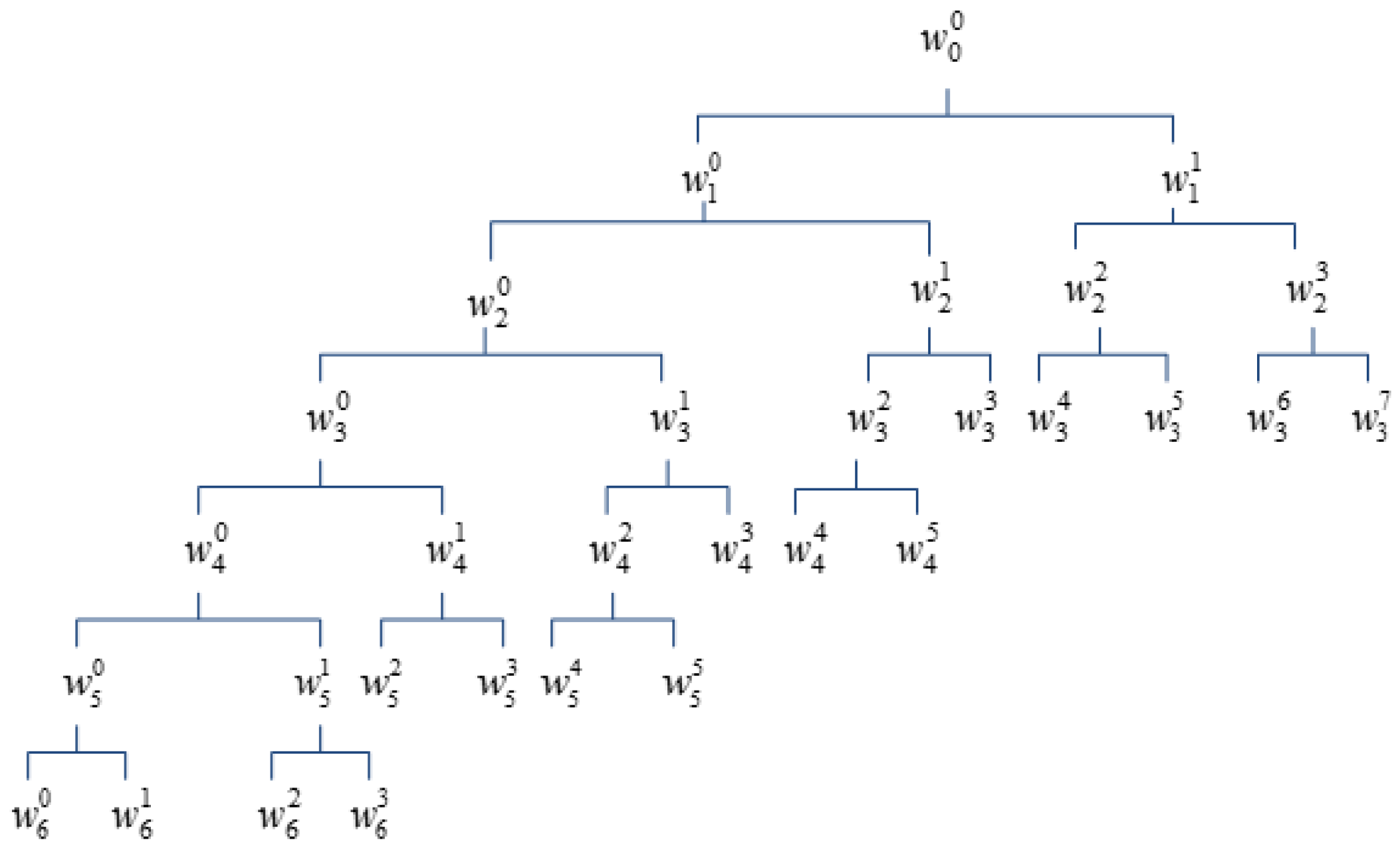
2.1. Wavelet Packet Transform
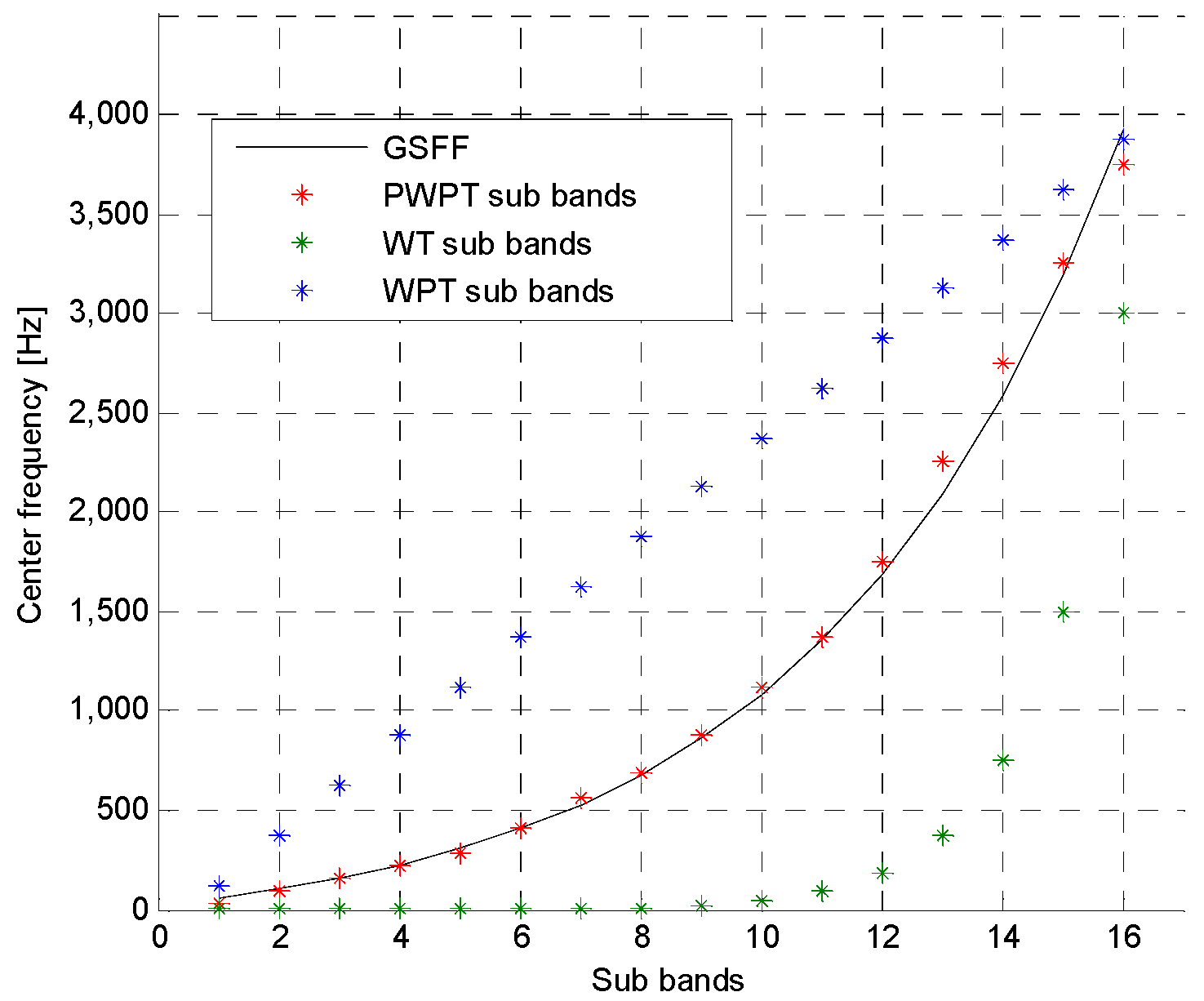
2.2. Perceptual Wavelet Packet Transform
2.3. PWPT-Based Wavelet Entropy Feature
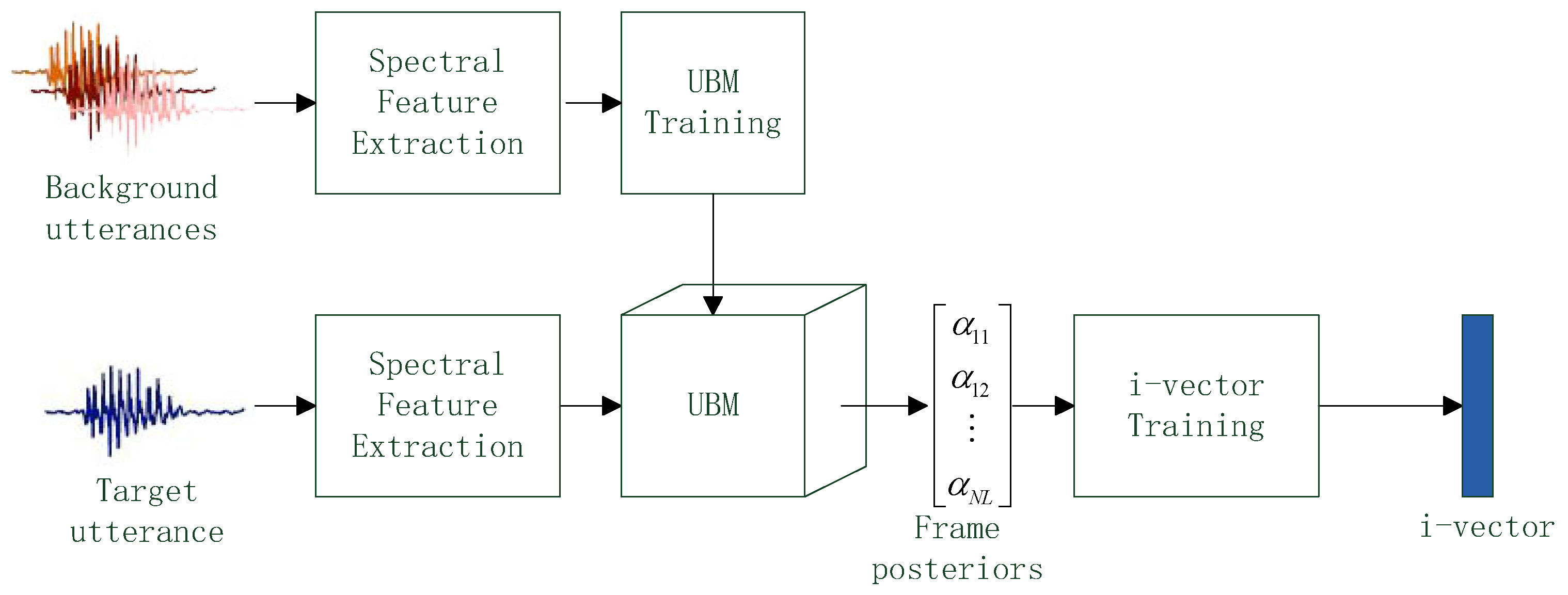
3. i-Vector Extraction
3.1. i-Vector Definition and Extraction Framwork
3.2. Typical i-Vector Extraction
3.3. i-Vector Extraction with CNN
4. Voice Authentication
5. Results and Discussion
5.1. Database and Experimental Platform and Performance Standards
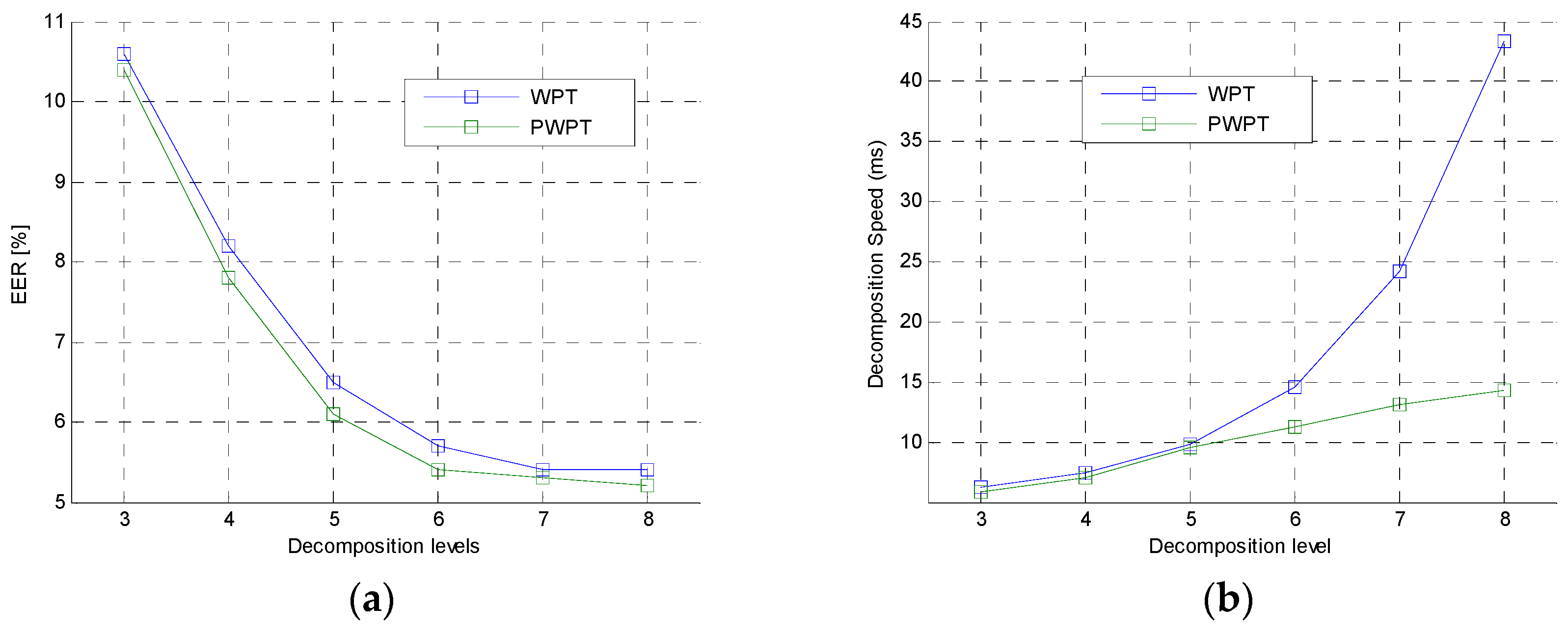
5.2. Mother Wavelet Selelction
5.3. Evaluation of Different Spectral Featrures
5.4. Evaluationof Different UBMs
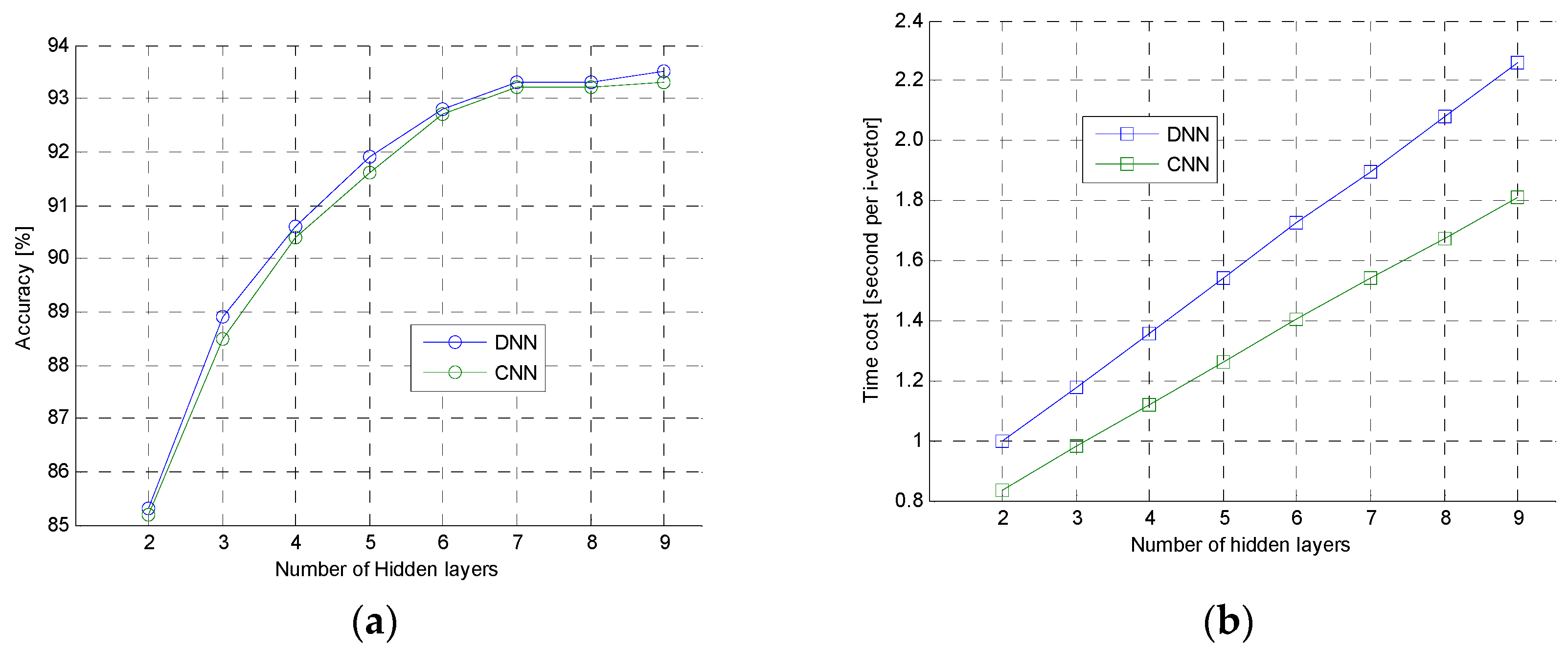
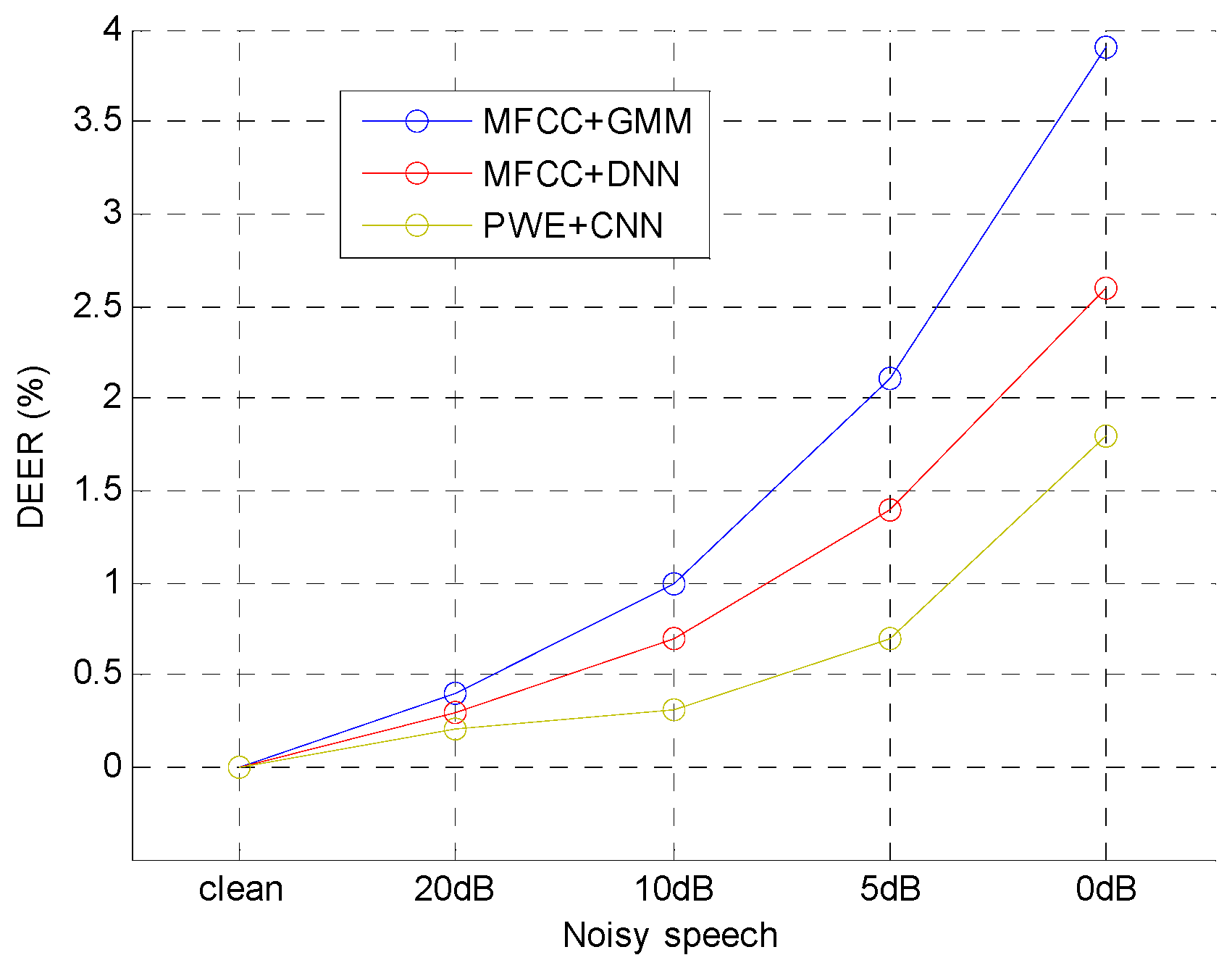
5.5. Comparison of Different i-Vector Extraction Methods
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kenny, P.; Puellet, P.; Dehak, N. A study of inter-speaker variability in speaker verification. Audio Speech Lang. Process. 2008, 16, 980–988. [Google Scholar] [CrossRef]
- Sizov, A.; Khoury, E.; Kinnunen, T. Joint speaker verification and antispoofing in the i-vector space. IEEE Trans. Inf. Forensics Secur. 2016, 10, 821–832. [Google Scholar] [CrossRef]
- Yu, C.; Zhang, C.; Kelly, F.; Sangwan, A.; Hansen, J.H. Text-available speaker recognition system for forensic applications. In Proceedings of the Interspeech, San Francisco, CA, USA, 8–12 September 2016; pp. 1844–1847. [Google Scholar]
- Daqrouq, K.; Azzawi, K.A. Average framing linear prediction coding with wavelet transform for text-independent speaker identification system. Comput. Electr. Eng. 2012, 38, 1467–1479. [Google Scholar] [CrossRef]
- Srivastava, S.; Bhardwaj, S.; Bhandari, A.; Gupta, K.; Bahl, H.; Gupta, J.R.P. Wavelet packet based Mel frequency cepstral coefficient features for text independent speaker identification. Intell. Inf. 2013, 182, 237–247. [Google Scholar]
- Wu, X.Q.; Wang, K.Q.; Zhang, D. Wavelet Energy Feature Extraction and Matching for Palm print Recognition. J. Comput. Sci. Technol. 2005, 20, 411–418. [Google Scholar] [CrossRef]
- Jiao, M.; Lou, L.; Geng, X. Speech enhancement based on the wiener filter and wavelet entropy. In Proceedings of the International Conference on Fuzzy Systems and knowledge Discovery, Zhangjiajie, China, 15–17 August 2015; pp. 1956–1960. [Google Scholar]
- Besbes, S.; Lachiri, Z. Wavelet packet energy and entropy features for classification of stressed speech. In Proceedings of the 17th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering, Sousse, Tunisia, 19–21 December 2017; pp. 98–103. [Google Scholar]
- Daqrouq, K.; Sweidan, H.; Balamesh, A.; Ajour, M.N. Off-line handwritten signature recognition by wavelet entropy and neural network. Entropy 2017, 6, 252. [Google Scholar] [CrossRef]
- Dachasilaruk, S.; Bleeck, S.; White, P. Improving speech intelligibility in perceptual wavelet packet-based speech coding for cochlear implants. In Proceedings of the International Conference on Biomedical Engineering and Informatics, Dalian, China, 14–16 October 2014; pp. 323–328. [Google Scholar]
- Chen, F.; Li, C.; An, Q.; Liang, F.; Qi, F.; Li, S.; Wang, J. Noise suppression in 94 GHz Radar-detected speech based on perceptual wavelet packet. Entropy 2016, 7, 265. [Google Scholar] [CrossRef]
- Dehak, N.; Kenny, P.J.; Dehak, R. Front-end factor analysis for speaekr verification. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 788–798. [Google Scholar] [CrossRef]
- Lei, Y.; Scheffer, N.; Ferer, L.; McLaren, M. A novel scheme for speaker recognition using a phonetically-aware deep neural network. In Proceedings of the IEEE International Conference on Acoustic, Speech and Signal Processing, Florence, Italy, 4–9 May 2014; pp. 1695–1699. [Google Scholar]
- Liu, Y.; Qian, Y.; Chen, N. Deep feature for text-dependent speaker verification. Speech Commun. 2015, 73, 1–13. [Google Scholar] [CrossRef]
- Li, N.; Mak, M.; Chien, J. Deep neural network driven mixture of PLDA for robust i-vector speaker verification. In Proceedings of the IEEE Spoken Language Technology Workshop, San Diego, CA, USA, 13–16 December 2017; pp. 186–191. [Google Scholar]
- Mitra, V.; Franco, H. Time-frequency convolutional networks for robust speech recognition. In Proceedings of the 2015 IEEE Workshop on Automatic Speech Recognition and Understanding (ASRU), Scottsdale, AZ, USA, 13–17 December 2015; pp. 317–323. [Google Scholar]
- Zhang, Y.; Pezeshki, M.; Brakel, P.; Zhang, S.; Bengio, C.L.Y.; Courville, A. Towards end-to-end speech recognition with deep convolutional neural network. In Proceedings of the Interspeech, San Francisco, CA, USA, 8–12 September 2016; pp. 410–415. [Google Scholar]
- Greenwood, D.D. Critical bandwidth and the frequency coordinates of the basilar membrane. Acout. Soc. Am. 1961, 33, 1344–1356. [Google Scholar] [CrossRef]
- Lepage, E. The mammalian cochlear map is optimally warped. J. Acoust. Soc. Am. 2003, 114, 896–906. [Google Scholar] [CrossRef] [PubMed]
- Carnero, B.; Drygajlo, A. Perceptual speech coding and enhancement Using frame-synchronized fast wavelet packet transform algorithm. Trans. Signal Process. 1999, 47, 1622–1636. [Google Scholar] [CrossRef]
- Almaadeed, N.; Aggoun, A.; Amira, A. Speaker identification using multimodal neural network and wavelet analysis. Biometrics 2014, 4, 2047–4938. [Google Scholar] [CrossRef]
- Kenny, P.; Boulianne, G.; Dumouchel, P. Eigenvoice Modeling with Sparse Trainning Data. IEEE Trans. Speech Audio Process. 2005, 13, 345–354. [Google Scholar] [CrossRef]
- Wamg, S.; Qian, Y.; Yu, K. What does the speaker embedding encode? In Proceedings of the Interspeech, Stockholm, Sweden, 20–24 August 2017; pp. 1497–1501. [Google Scholar]
- George, K.K.; Kumar, C.S.; Ramachandran, K.I.; Ashish, P. Cosine Distance Features for Robust Speaker Verification. In Proceedings of the Interspeech, Dresden, Germany, 6–10 September 2015; pp. 234–238. [Google Scholar]
- Klosowski, P.; Dustor, A.; Lzydorczyk, J. Speaker verification performance evaluation based on open source speech processing software and TIMIT speech corpus. Comput. Netw. 2015, 522, 400–409. [Google Scholar]
- Nagrani, A.; Chung, J.S.; Zisserman, A. VoxCeleb: A large-scale speaker identification dataset. In Proceedings of the Interspeech, Stockholm, Sweden, 20–24 August 2017; pp. 2616–2620. [Google Scholar]
- Daubechies, I. Orthonormal basis of compactly supported wavelet. Comput. Pure Appl. Math. 1988, 41, 909–996. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, J. Multi-level wavelet Shannon entropy-based method for signal-sensor sault location. Entropy 2015, 17, 7101–7117. [Google Scholar] [CrossRef]
- Daqrouq, K. Wavelet entropy and neural network for text-independent speaker identification. Eng. Appl. Artif. Intell. 2011, 24, 769–802. [Google Scholar] [CrossRef]
- Abdel-Hamid, O.; Mohamed, A.; Jiang, H.; Penn, G. Applying convolutional neural network concepts to hybrid NN-HMM model for speech recognition. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing, Kyoto, Japan, 25–30 March 2012; pp. 4277–4280. [Google Scholar]
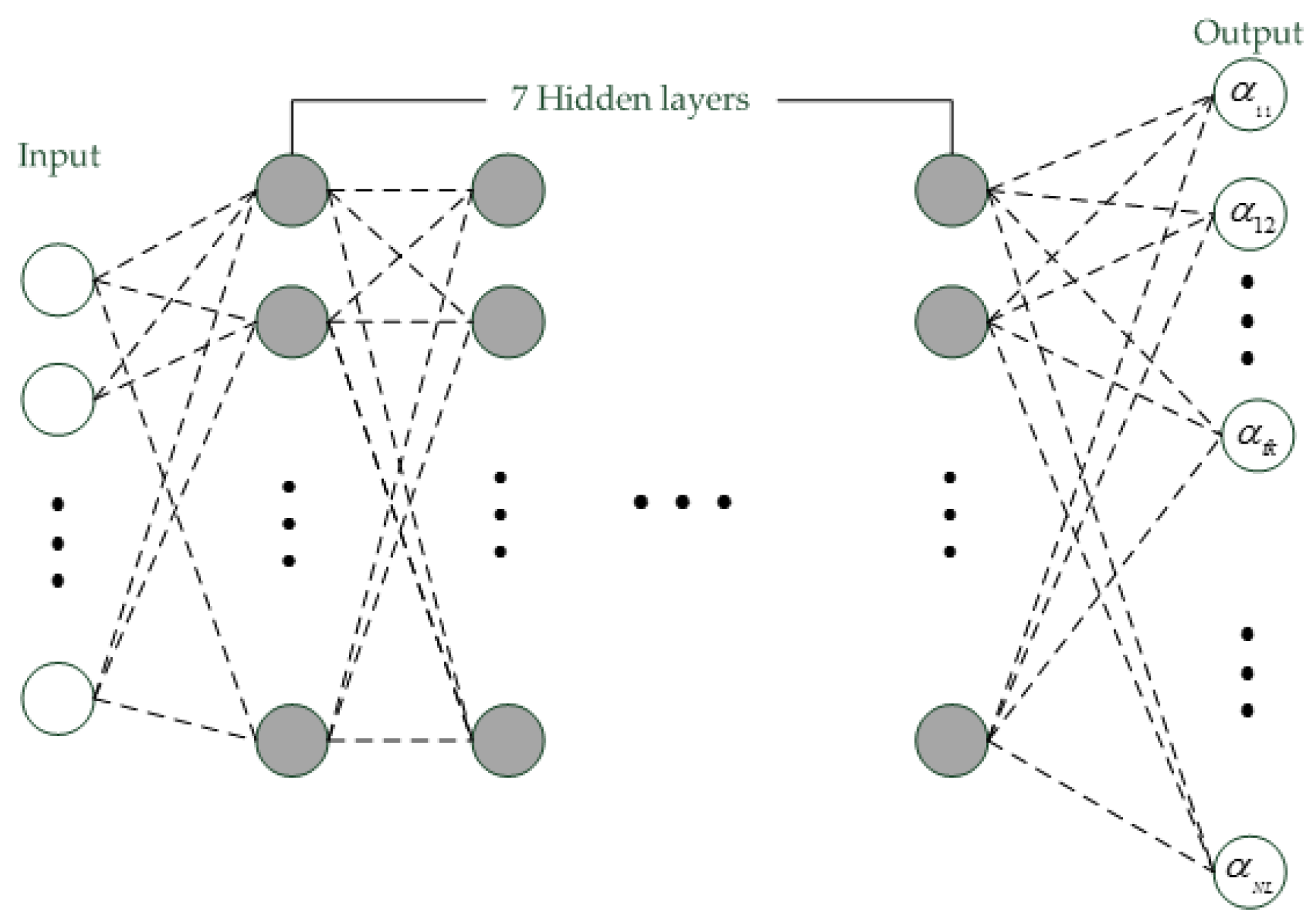
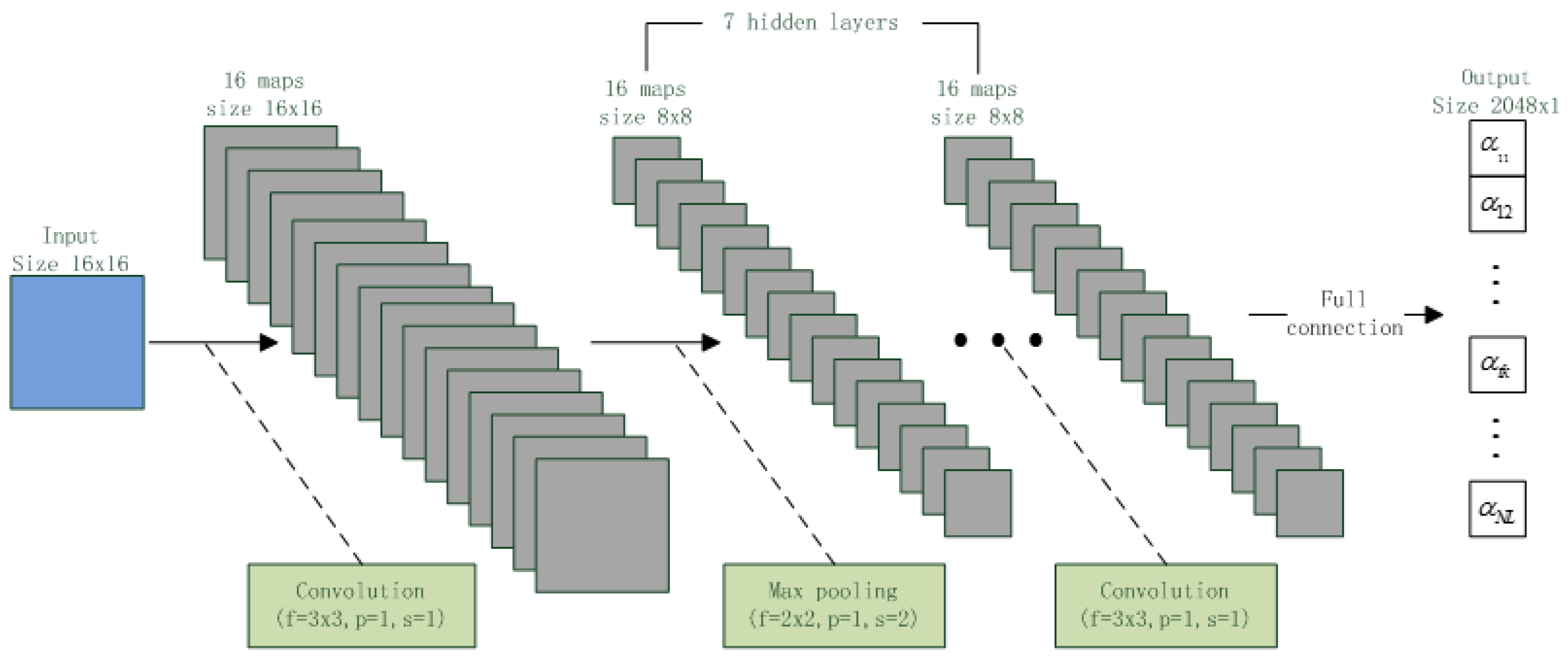

| Layer | Shape | Node Size | Parameter Size | |||
|---|---|---|---|---|---|---|
| DNN | CNN | DNN | CNN | DNN | CNN | |
| Input Layer | 256 × 1, 1 | 16 × 16, 1 | 256 | 256 | 226,144 | 272 |
| Hidden Layer 1~7 | 1024 × 1, 1 | 8 × 8, 16 | 1024 | 1024 | 1,048,576 | 160 |
| Output Layer | 2048 × 1, 1 | 2048 × 1, 1 | 2048 | 2048 | 131,072 | 131,072 |
| Wavelets | ESERs | Wavelets | ESERs | Wavelets | ESERs | Wavelets | ESERs |
|---|---|---|---|---|---|---|---|
| Db 1 | 888.37 | Db 6 | 896.53 | Sym 1 | 888.35 | Sym 6 | 908.39 |
| Db 2 | 890.32 | Db 7 | 891.69 | Sym 2 | 890.36 | Sym 7 | 902.44 |
| Db 3 | 897.44 | Db 8 | 890.84 | Sym 3 | 894.93 | Sym 8 | 898.37 |
| Db 4 | 907.45 | Db 9 | 888.21 | Sym 4 | 899.75 | Sym 9 | 896.35 |
| Db 5 | 901.41 | Db 10 | 884.50 | Sym 5 | 903.82 | Sym 10 | 891.34 |
| WT | WPT | PWPT | |
|---|---|---|---|
| ShE | 8.51 | 5.46 | 5.49 |
| NE | 8.57 | 5.53 | 5.51 |
| LE | 9.03 | 6.67 | 6.78 |
| SE | 8.91 | 6.23 | 6.27 |
| Spectral Features | EER (%) | Accuracy (%) | ||
|---|---|---|---|---|
| Noisy | Clean | Noisy | Clean | |
| PWPT-NE | 6.24 | 5.53 | 90.13 | 92.14 |
| WPT-NE | 7.11 | 5.51 | 89.47 | 92.48 |
| WT-NE | 10.27 | 8.43 | 86.39. | 90.12 |
| MFCC | 11.43 | 9.23 | 83.10 | 89.31 |
| LPCC | 11.77 | 9.31 | 83.24 | 88.97 |
| UBMs | EER (%) | Accuracy (%) | ||
|---|---|---|---|---|
| Noisy | Clean | Noisy | Clean | |
| GMM (1024) | 13.42 | 11.96 | 82.75 | 86.19 |
| GMM (2048) | 11.19 | 9.23 | 86.17 | 89.94 |
| GMM (3072) | 9.78 | 7.54 | 88.73 | 91.97 |
| DNN | 7.11 | 5.51 | 89.47 | 92.48 |
| CNN | 6.24 | 5.53 | 90.13 | 92.14 |
| Strategies | EER (%) | Accuracy (%) | ||
|---|---|---|---|---|
| Noisy | Clean | Noisy | Clean | |
| MFCC + GMM | 13.02 | 9.15 | 80.74 | 89.59 |
| WPE + GMM | 13.17 | 10.97. | 85.97 | 87.49 |
| MFCC + DNN | 10.15 | 5.68 | 85.6 | 91.91 |
| WPE + DNN | 8.76 | 6.87 | 90.17 | 92.87 |
| MFCC + CNN | 8.02 | 5.97 | 86.43 | 91.48. |
| WPE + CNN | 6.24 | 5.53 | 90.13 | 92.14 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, L.; She, K. Identity Vector Extraction by Perceptual Wavelet Packet Entropy and Convolutional Neural Network for Voice Authentication. Entropy 2018, 20, 600. https://doi.org/10.3390/e20080600
Lei L, She K. Identity Vector Extraction by Perceptual Wavelet Packet Entropy and Convolutional Neural Network for Voice Authentication. Entropy. 2018; 20(8):600. https://doi.org/10.3390/e20080600
Chicago/Turabian StyleLei, Lei, and Kun She. 2018. "Identity Vector Extraction by Perceptual Wavelet Packet Entropy and Convolutional Neural Network for Voice Authentication" Entropy 20, no. 8: 600. https://doi.org/10.3390/e20080600
APA StyleLei, L., & She, K. (2018). Identity Vector Extraction by Perceptual Wavelet Packet Entropy and Convolutional Neural Network for Voice Authentication. Entropy, 20(8), 600. https://doi.org/10.3390/e20080600






