Thermo-Fluid Characteristics of High Temperature Molten Salt Flowing in Single-Leaf Type Hollow Paddles
Abstract
:1. Introduction
2. Geometry Description
3. Numerical Model
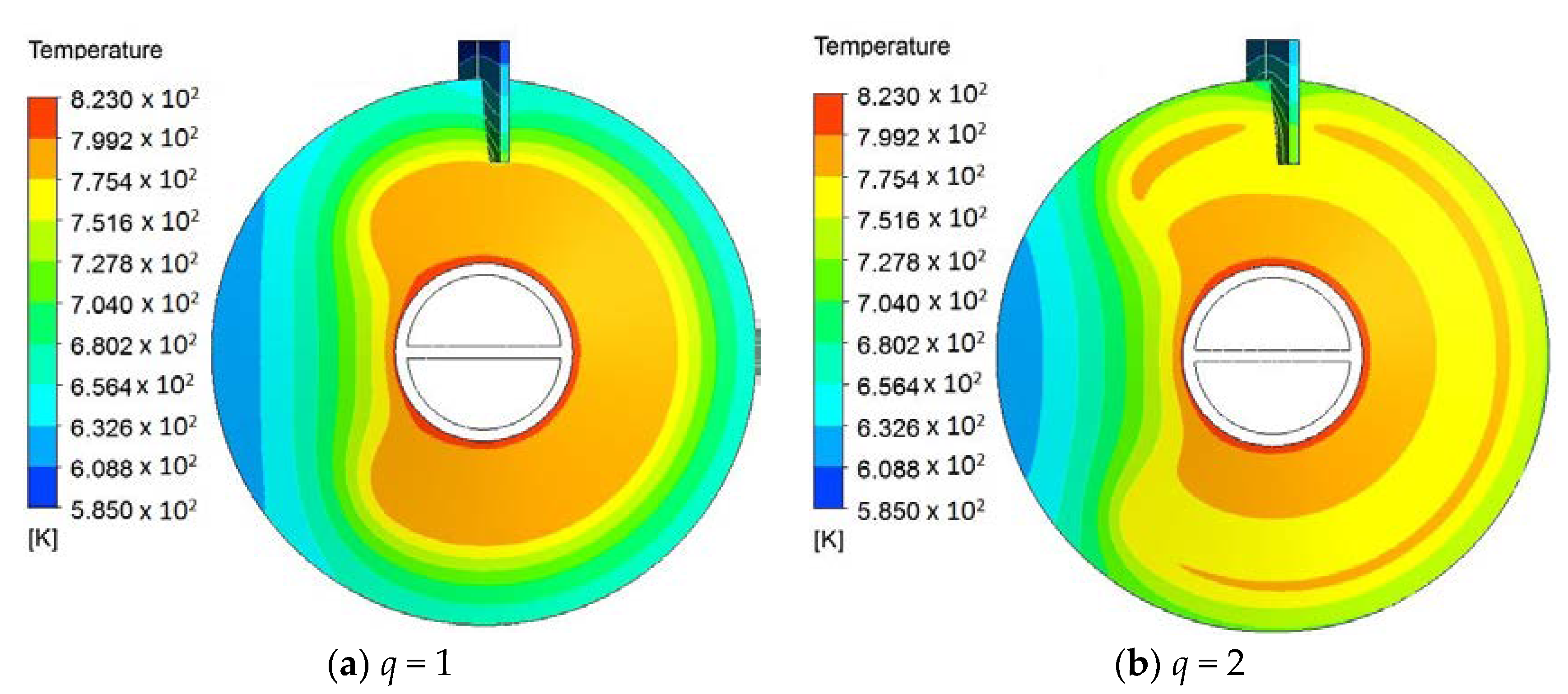
4. Results and Discussion
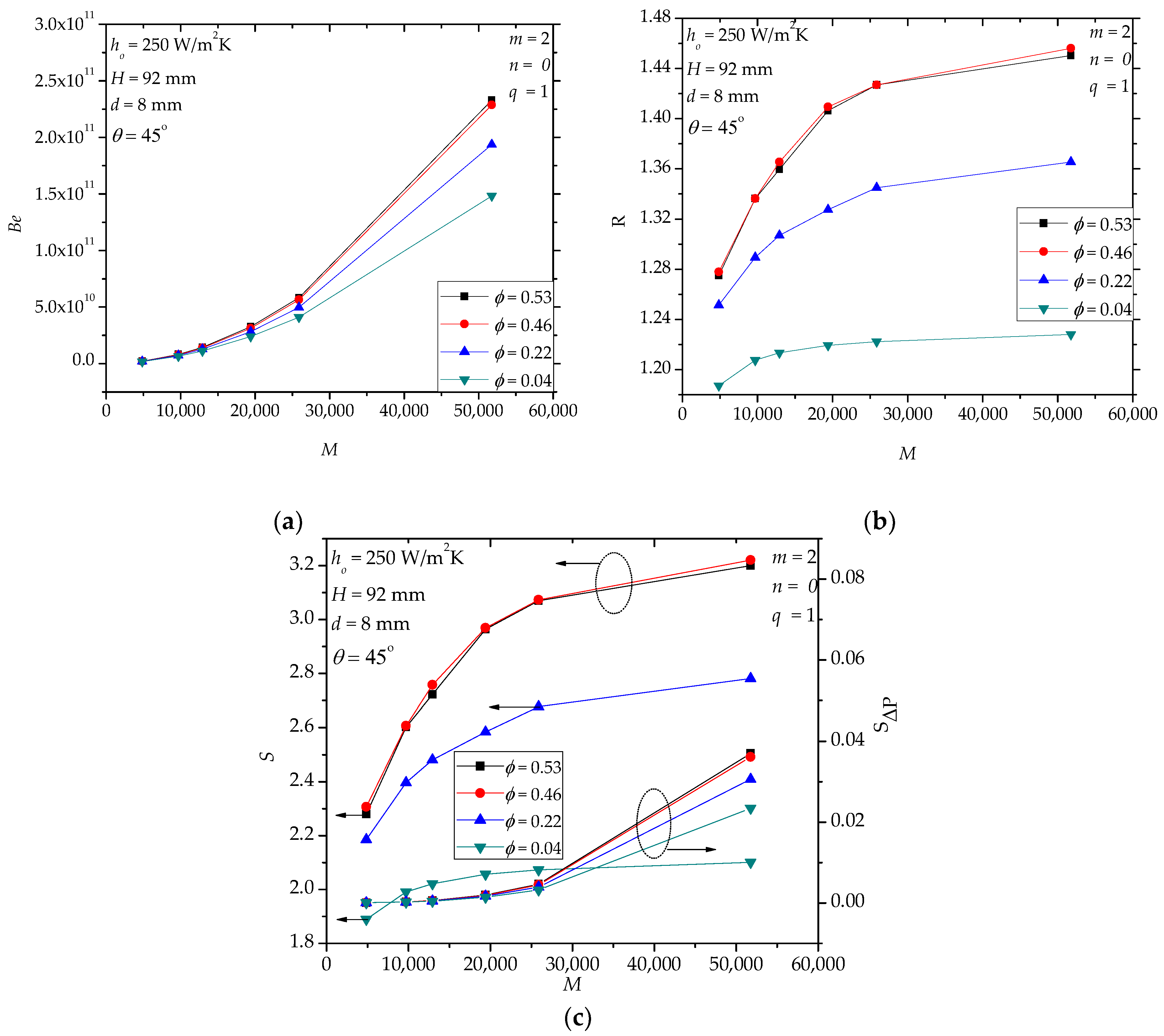
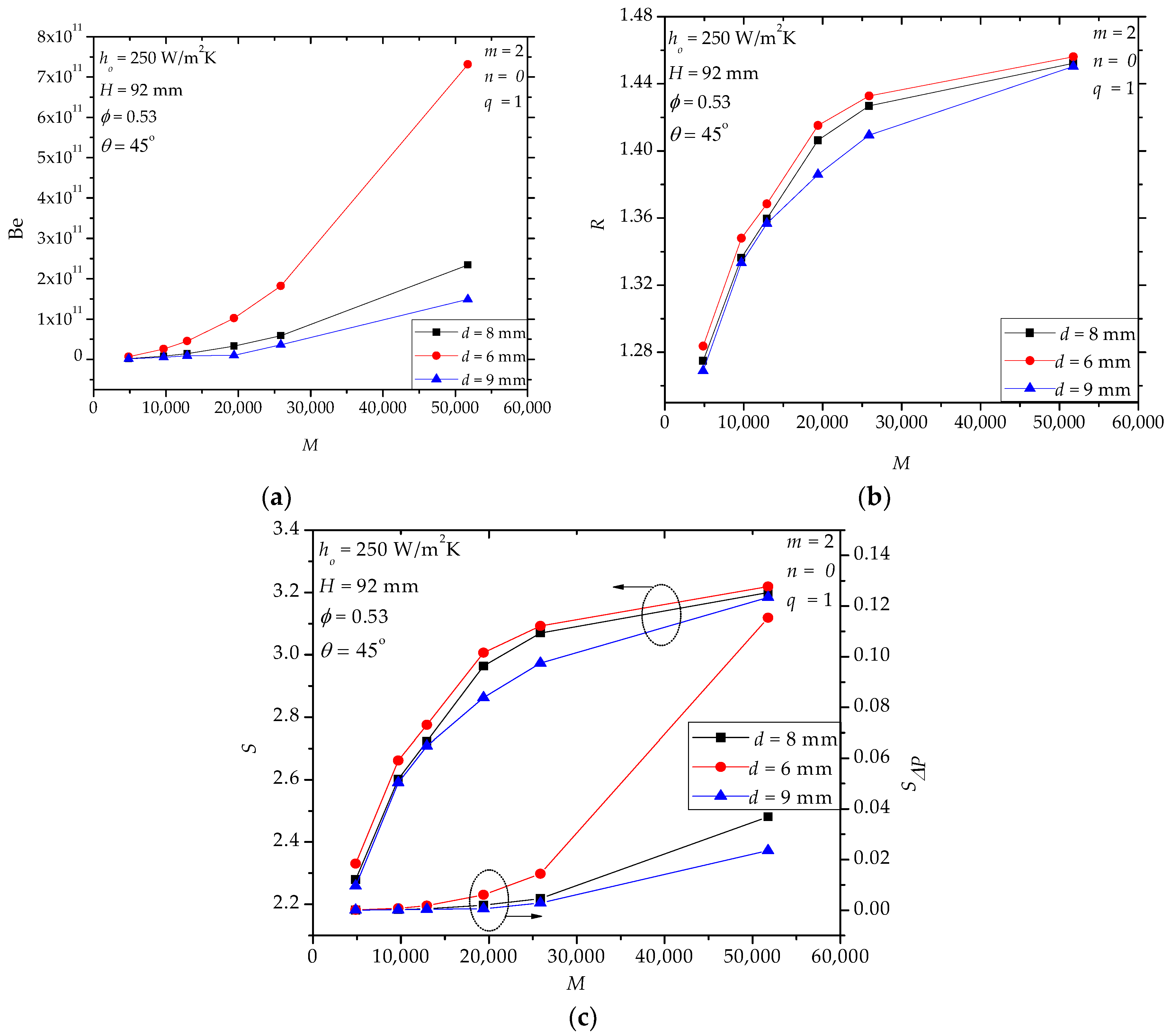
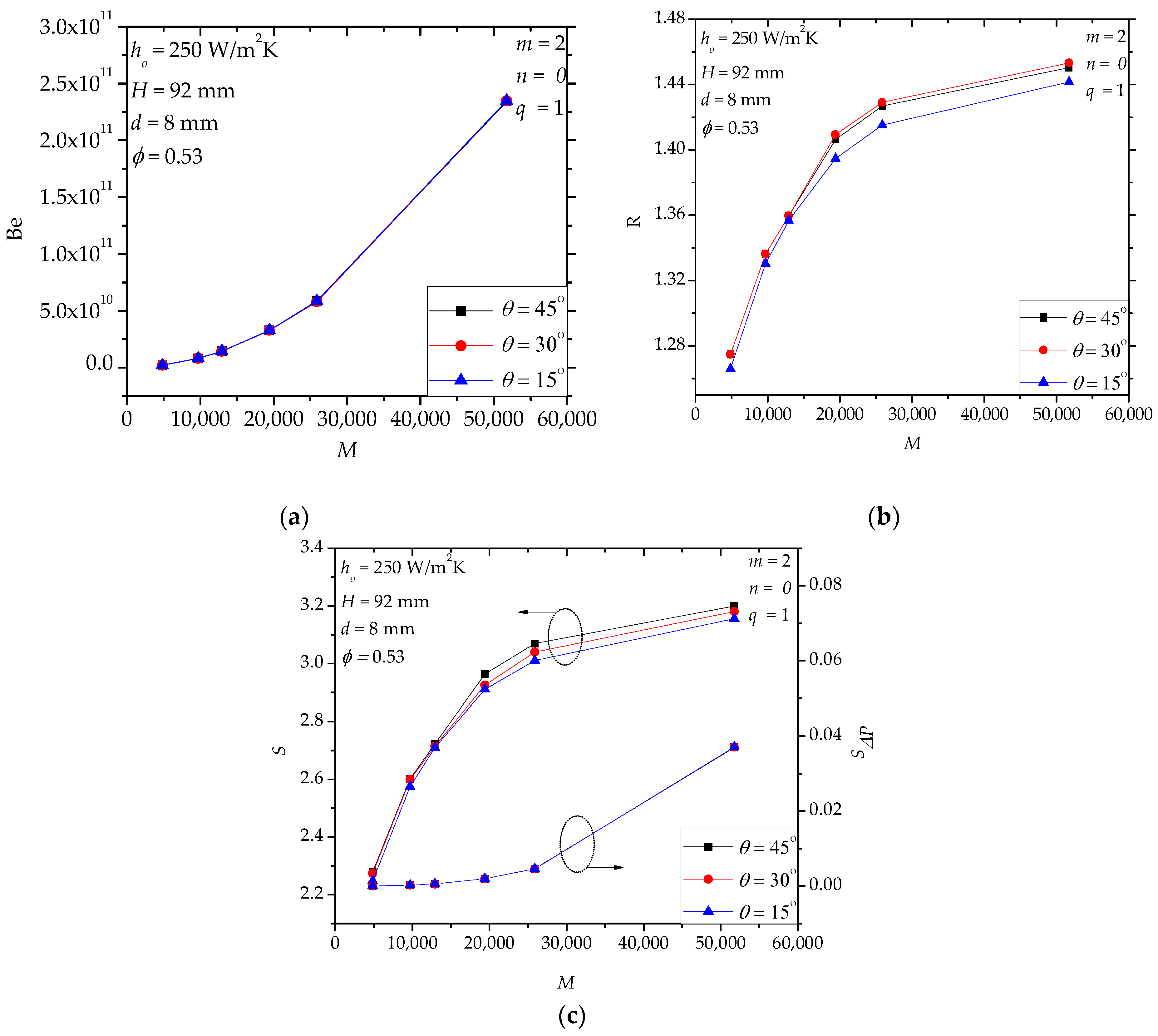
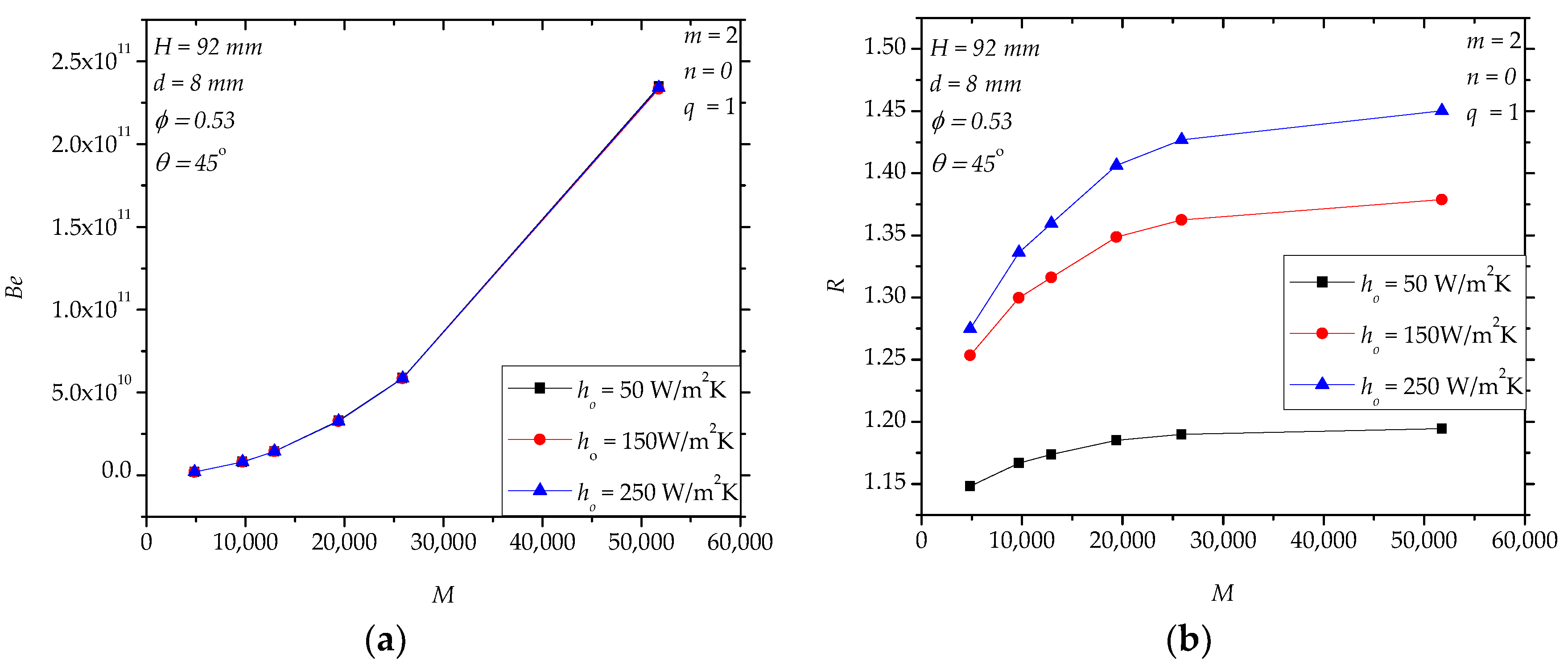
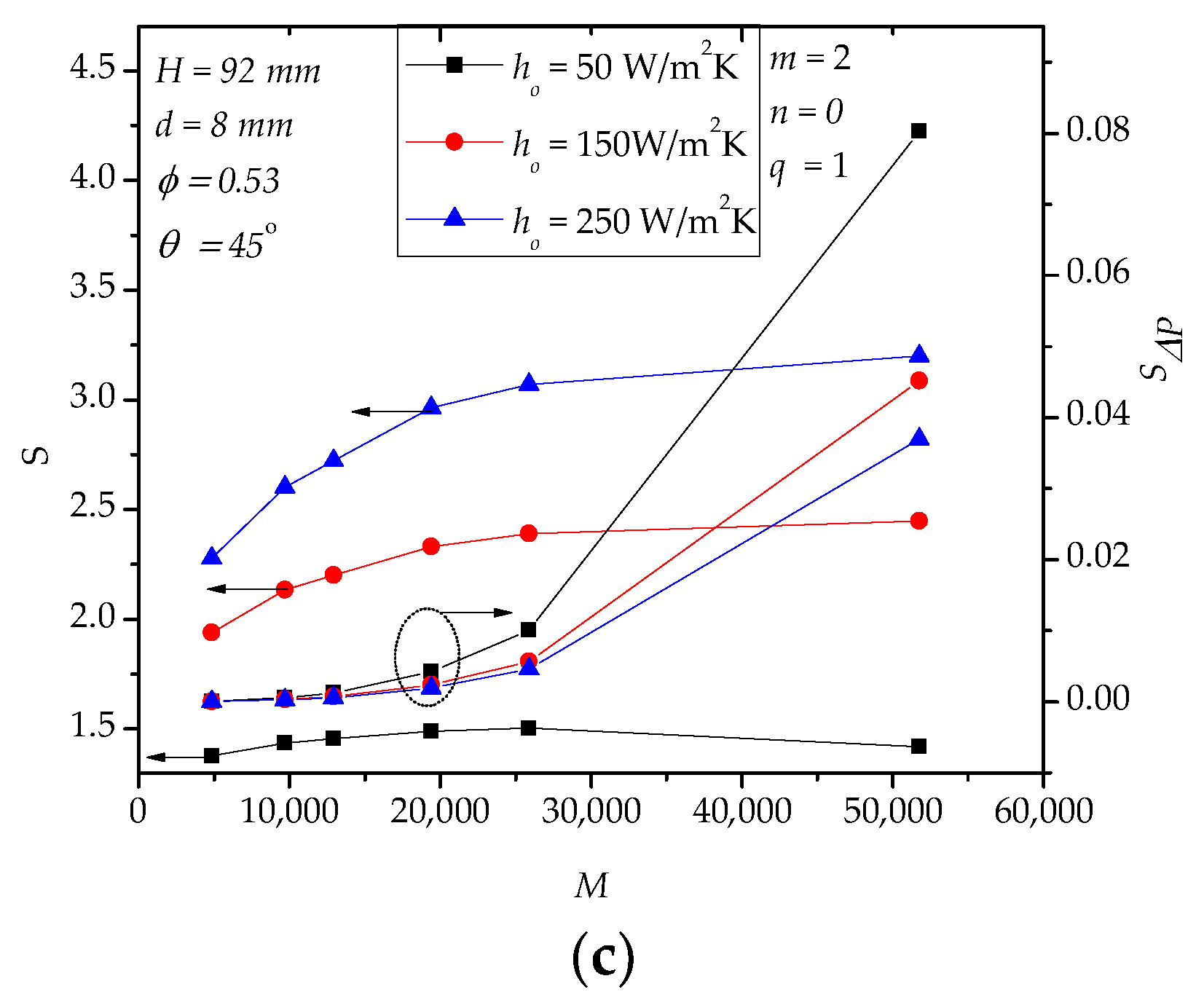
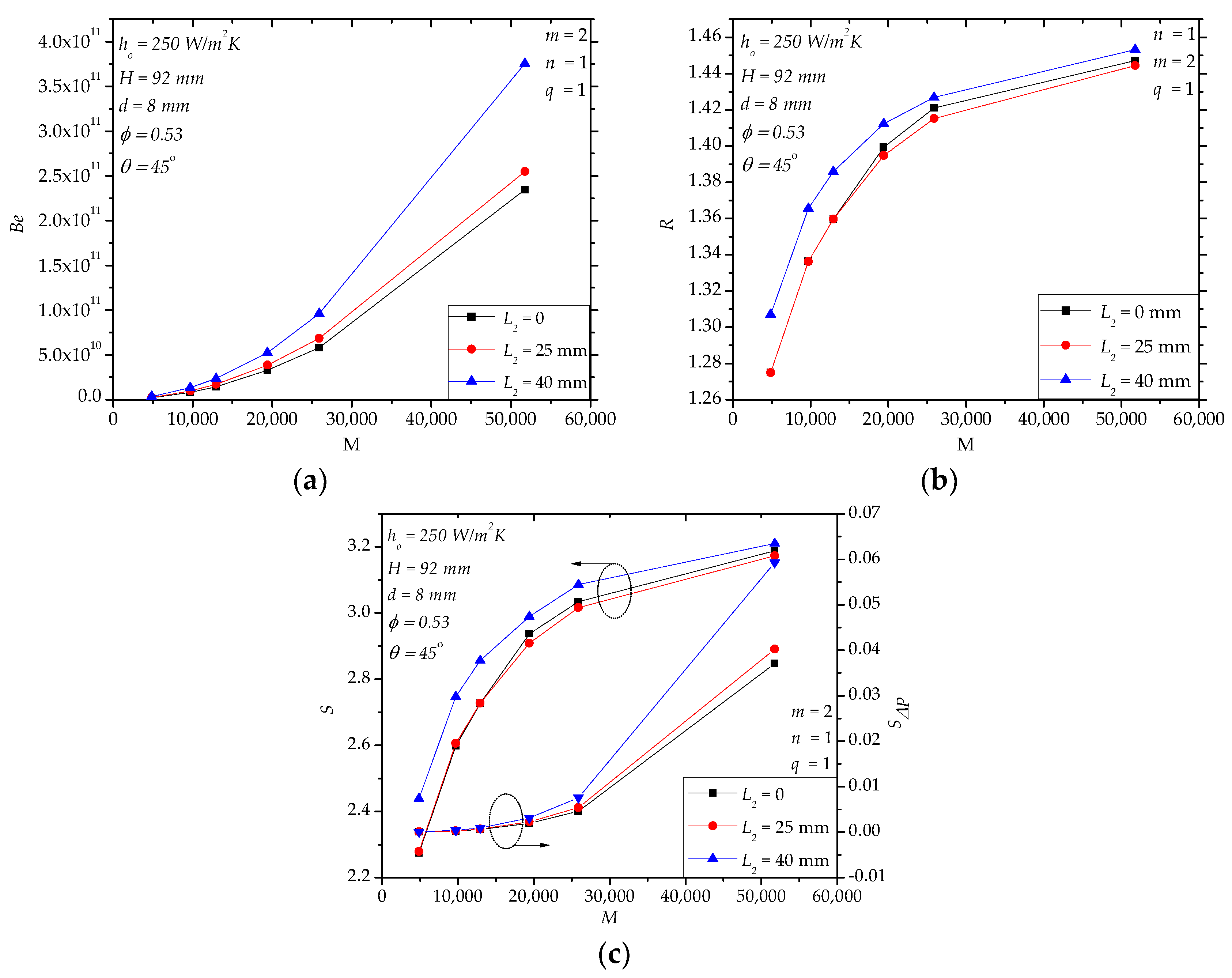
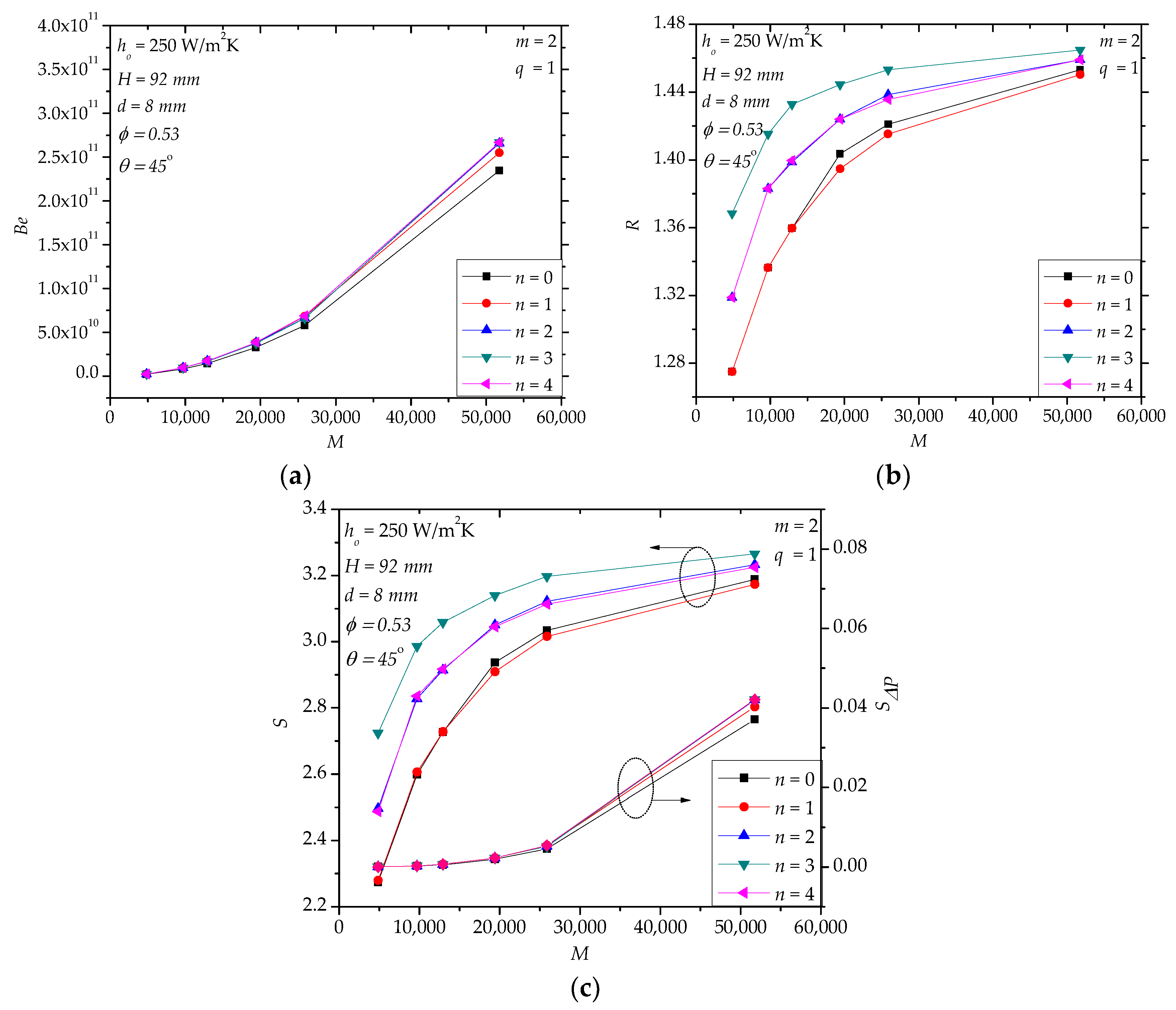
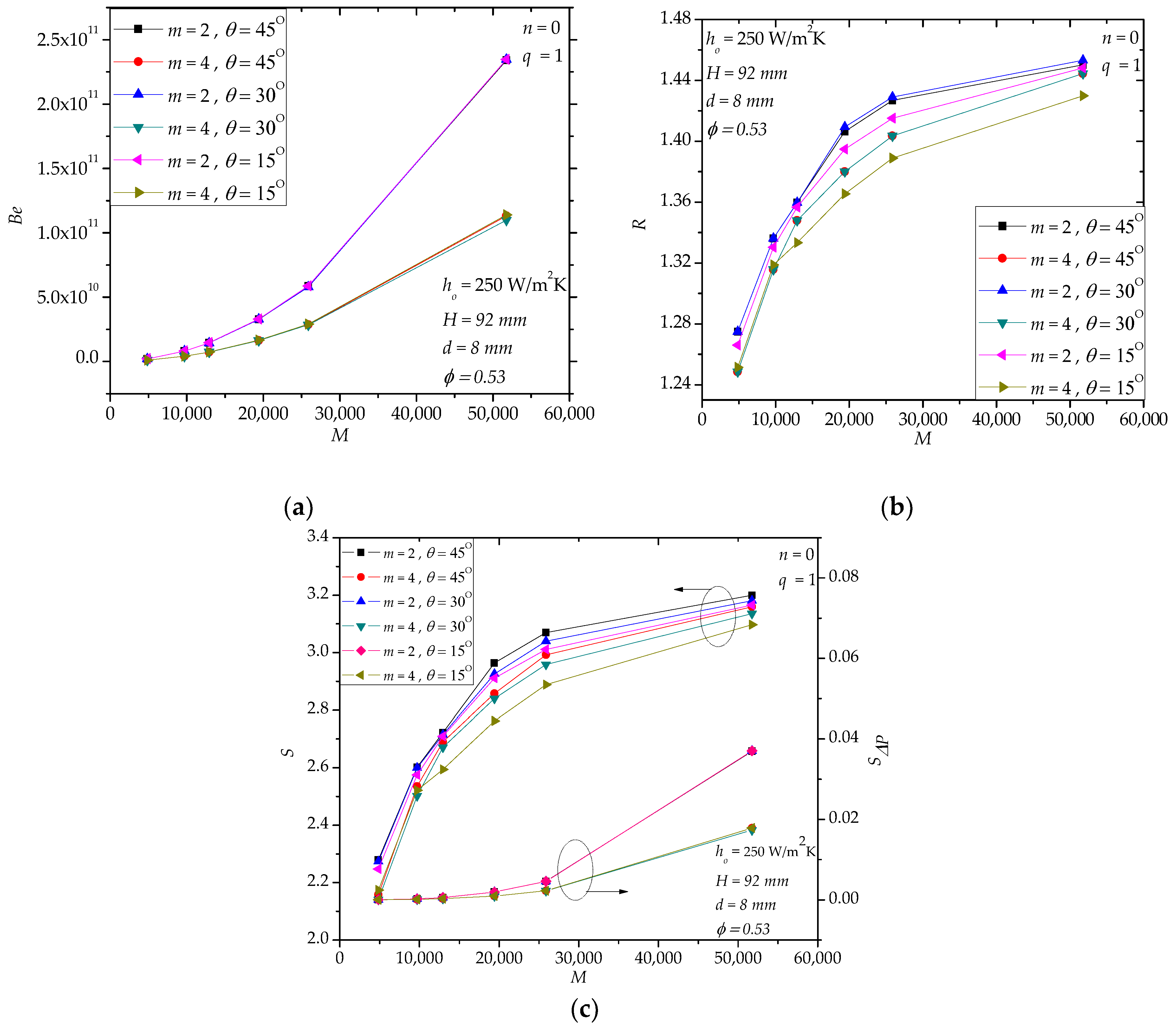
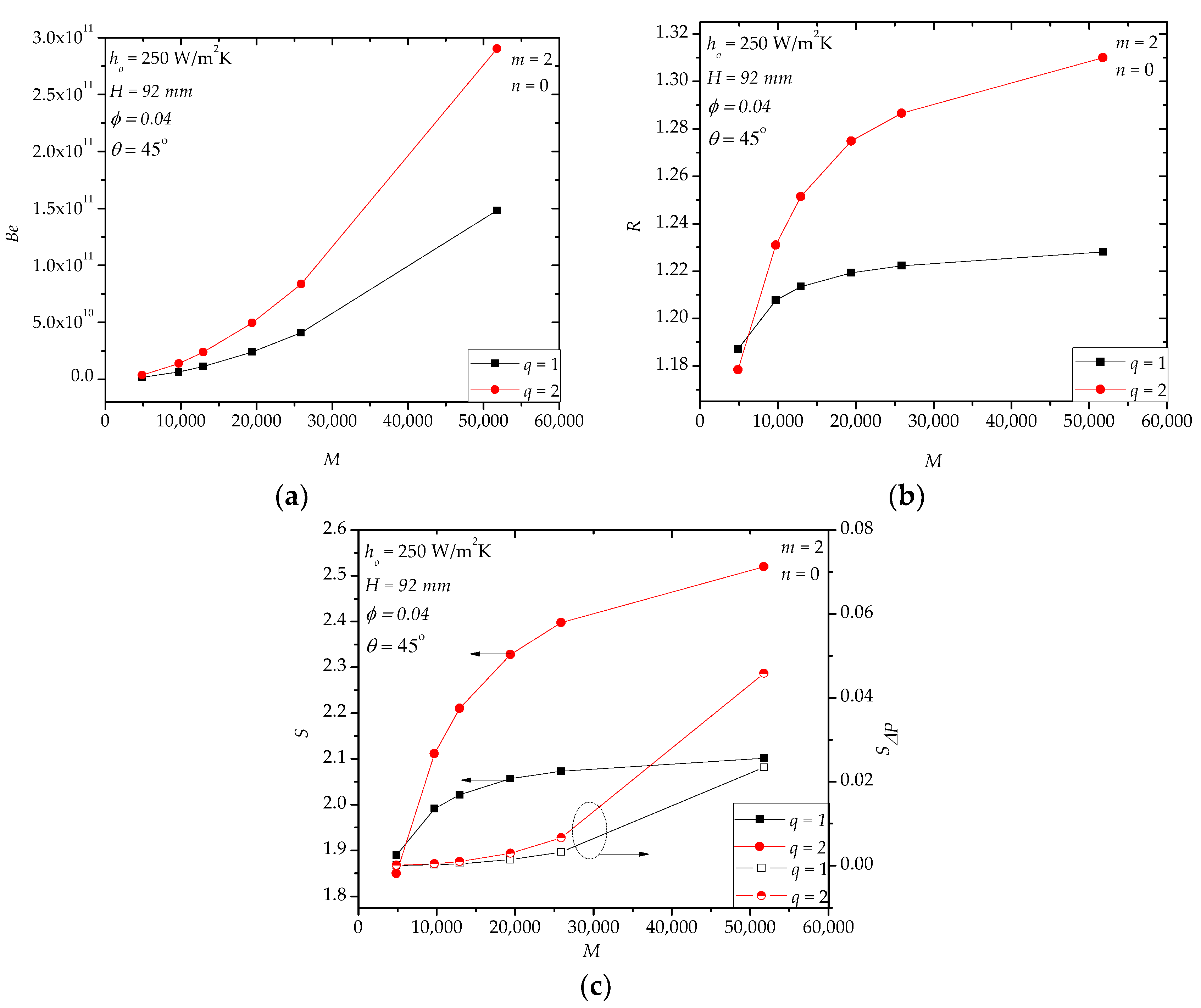
4.1. Case II
4.2. Case III
4.3. Case IV
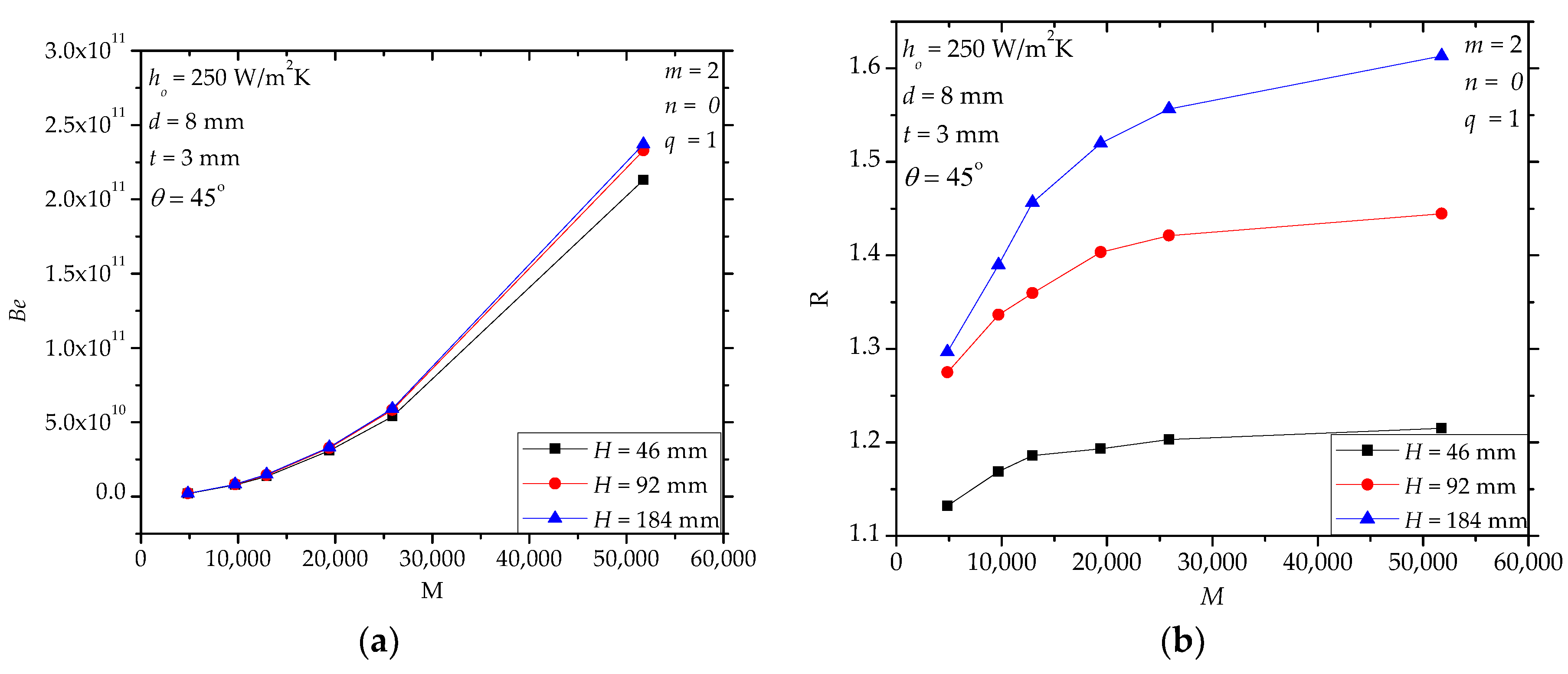
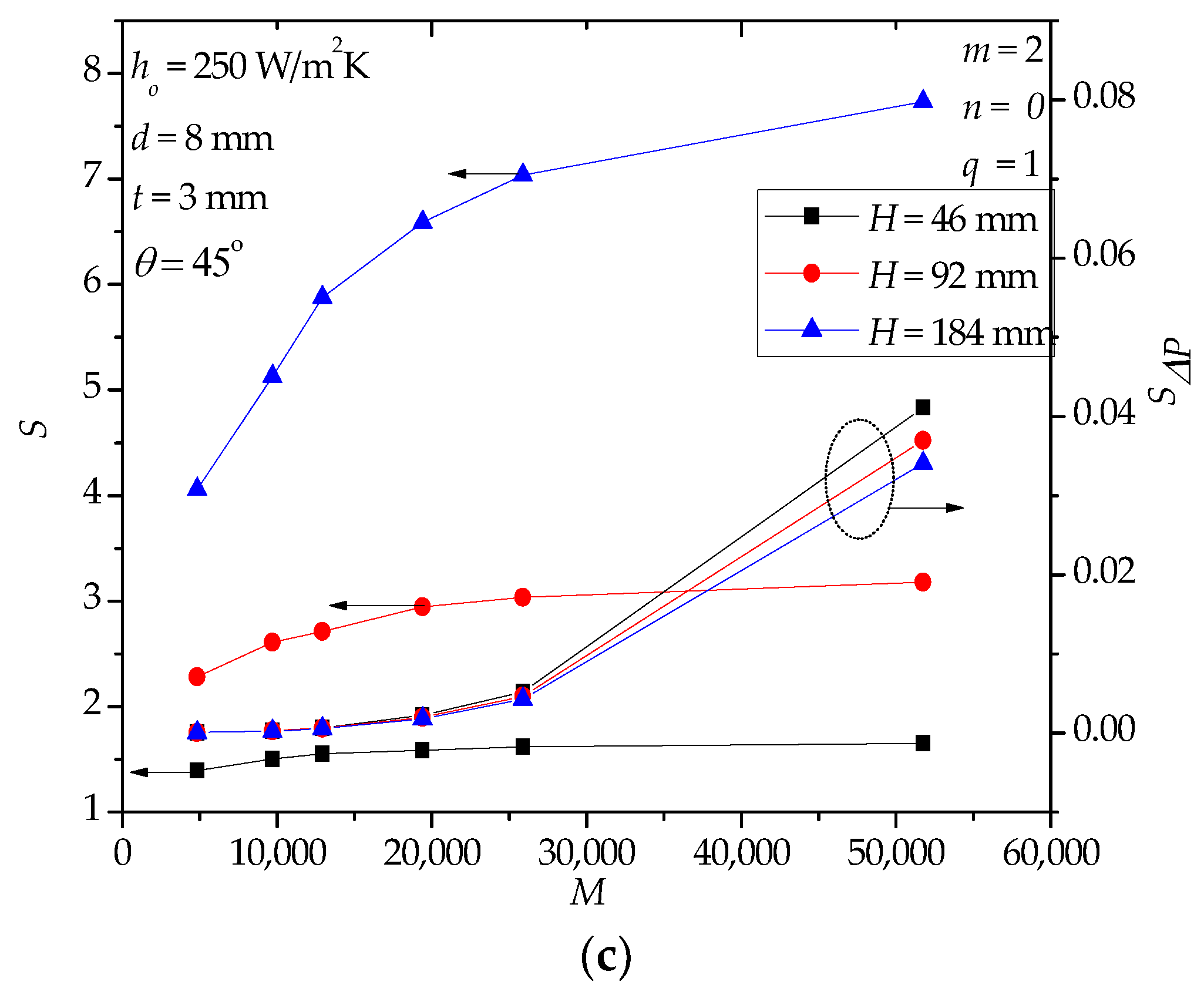
4.4. Further Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Be | Dimensionless pressure drop, i.e., Bejan number |
| cp | Specific heat at constant pressure, J/(kgK) |
| C1ε, C2ε, Cµ | Constants, Equations (7) and (8) |
| d | Diameter of flow holes, mm or m |
| e | Specific total energy, J/kg |
| E | Total energy, J |
| h | Enthalpy, J/kg |
| ho | Shell-side material convective heat transfer coefficient, W/(m2K) |
| H | Paddle height, mm or m |
| k | Turbulent kinetic energy, m2/s2 |
| L, L1, ..., L5 | Dimensions, mm or m, Figure 3 |
| m | Number of flow holes |
| Mass flow rate, kg/s | |
| M | Dimensionless mass flow rate |
| n | Number of baffles |
| P | Pressure, Pa |
| Prt | Turbulent Prandtl number |
| q | Number of channels |
| Heat transfer rate, W | |
| R | Dimensionless heat transfer rate |
| s | Specific entropy, J/(kgK) |
| S | Dimensionless entropy generation rate |
| Entropy generation rate, W/K | |
| t | Paddle thickness, mm or m |
| T | Temperature, K or |
| To | Shell-side material temperature, K or |
| u | Velocity component, m/s |
| Fluctuating velocity component, m/s | |
| v | Velocity, m/s |
| V | Volume of a paddle, m3 |
| Vf | Fluid volume in a paddle, m3 |
| x | Coordinate component, mm or m |
| Greek symbols | |
| α | Thermal diffusivity, m2/s |
| Thermal expansion coefficient, 1/K | |
| δij | Unit tensor |
| ΔP | Pressure drop, Pa |
| ε | Dissipation rate, m2/s3 |
| θ | Position angle of flow holes |
| λ | Thermal conductivity, W/(mK) |
| µ | Dynamic viscosity, kg/(ms) |
| µt | Turbulent viscosity, kg/(ms) |
| ρ | Density, kg/m3 |
| σk, σε | Constants in Equations (6) and (7) |
| τ | Time |
| Volume ratio, Equation (16) | |
| Subscripts | |
| i, j, l | Coordinate direction |
| in | Inlet |
| out | Outlet |
| s | Solid |
| w | Wall |
References
- Arlabosse, P.; Chavez, S.; Lecomte, D. Method for thermal design of paddle dryers: Application to municipal sewage sludge. Dry. Technol. 2004, 22, 2375–2393. [Google Scholar] [CrossRef]
- Arlabosse, P.; Chavez, S.; Prevot, C. Drying of municipal sewage sludge: From a laboratory scale batch indirect dryer to the paddle dryer. Braz. J. Chem. Eng. 2005, 22, 227–232. [Google Scholar] [CrossRef]
- Deng, W.Y.; Yan, J.H.; Li, X.D.; Wang, F.; Lu, S.Y.; Chi, Y.; Cen, K.F. Measurement and simulation of the contact drying of sewage sludge in a Nara-type paddle dryer. Chem. Eng. Sci. 2009, 64, 5117–5124. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, X.; Zhu, S.; Li, B. Sewage sludge flow and drying characteristics in paddle dryers. Defect Diffus. Forum 2013, 334–335, 365–368. [Google Scholar] [CrossRef]
- Charlou, C.; Milhé, M.; Sauceau, M.; Arlabosse, P. A new methodology for measurement of sludge residence time distribution in a paddle dryer using X-ray fluorescence analysis. Water Res. 2015, 69, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Milhé, M.; Charlou, C.; Sauceau, M.; Arlabosse, P. Modeling of sewage sludge flow in a continuous paddle dryer. Dry. Technol. 2015, 33, 1061–1067. [Google Scholar] [CrossRef]
- Milhé, M.; Sauceau, M.; Arlabosse, P. Influence of operating parameters on sewage sludge drying in a paddle dryer: Design of experiments for the determination of hold-up and water content profiles. Dry. Technol. 2015, 33, 1276–1285. [Google Scholar] [CrossRef]
- Milhé, M.; Sauceau, M.; Arlabosse, P. Modeling of a continuous sewage sludge paddle dryer by coupling Markov chains with penetration theory. Appl. Math. Model. 2016, 40, 8201–8216. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.T.; Chen, C.; Liu, B.; Ma, C.F. Investigation on forced convective in heat transfer of molten salts in circular tubes. Int. Commun. Heat Mass Transf. 2012, 39, 1550–1555. [Google Scholar] [CrossRef]
- Ferng, Y.M.; Lin, K.Y.; Chi, C.W. CFD investigating thermal-hydraulic characteristics of FLiNaK salt as a heat exchange fluid. Appl. Therm. Eng. 2012, 37, 235–240. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Vaidya, A.M.; Maheshwari, N.K.; Vijayan, P.K. Heat transfer and pressure drop characteristics of molten fluoride salt in circular pipe. Appl. Therm. Eng. 2013, 61, 198–205. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, X.; Chang, C.; Wang, Z.; Liu, H. An experimental study: Thermal performance of molten salt cavity receivers. Appl. Therm. Eng. 2013, 50, 334–341. [Google Scholar] [CrossRef]
- Du, B.C.; He, Y.L.; Wang, K.; Zhu, H.H. Convective heat transfer of molten salt in the shell-and-tube heat exchanger with segmental baffles. Int. Commun. Heat Mass Transf. 2017, 113, 456–465. [Google Scholar] [CrossRef]
- Du, B.C.; He, Y.L.; Qiu, Y.; Liang, Q.; Zhou, Y.P. Investigation on heat transfer characteristics of molten salt in a shell-and-tube heat exchanger. Int. Commun. Heat Mass Transf. 2018, 96, 61–68. [Google Scholar] [CrossRef]
- Lu, J.; He, S.; Ding, J.; Yang, J.; Liang, J. Convective heat transfer of high temperature molten salt in vertical annular duct with cooled wall. Appl. Therm. Eng. 2014, 73, 1519–1524. [Google Scholar] [CrossRef]
- Chen, Y.S.; Tian, J.; Fu, Y.; Tang, Z.F.; Zhu, H.H.; Wang, N.X. Experimental study of heat transfer enhancement for molten salt with transversely grooved tube heat exchanger in laminar-transition-turbulent regimes. Appl. Therm. Eng. 2018, 132, 95–101. [Google Scholar] [CrossRef]
- Carasik, L.B.; Shaver, D.R.; Haefner, J.B.; Hassan, Y.A. Steady RANS methodology for calculating pressure drop in an in-line molten salt compact cross flow heat exchanger. Prog. Nuclear Energy 2017, 101, 209–223. [Google Scholar] [CrossRef]
- Chen, X.; Wang, C.; Wu, Y.; Liu, B.; Ma, C. Characteristics of the mixed convection heat transfer of molten salts in horizontal square tubes. Sol. Energy 2017, 147, 248–256. [Google Scholar] [CrossRef]
- Fu, W.; Lin, H.; Liu, X.; Zhang, H. Constructal design of molten salt flow and heat transfer in horizontal hollow disc-shaped heaters. In Proceedings of the Constructal Law & Second Law Conference, Bucharest, Romania, 14–16 May 2017; Morega, A., Lorente, S., Eds.; The Publishing House of the Romanian Academy: Bucharest, Romania, 2017; pp. 171–187. [Google Scholar]
- Du, J.; Shao, F.; Du, W.; Zhang, H.; Liu, X. Review on high temperature molten salt heat exchangers and applications. Sol. Energy 2015, 8, 35–40, 55. (In Chinese) [Google Scholar]
- Bejan, A.; Lorente, S. Design with Constructal Theory, 1st ed.; Wiley & Sons Inc.: Hoboken, NJ, USA; New York, NY, USA, 2008; pp. 329–371. ISBN 978-0-471-99816-7. [Google Scholar]
- Zhang, K.; Du, J.; Liu, X.; Zhang, H. Molten salt flow and heat transfer in paddle heat exchangers. Int. J. Heat Technol. 2016, 34, 43–50. [Google Scholar] [CrossRef]
- Ji, L.; Liu, X.; Zhang, H. Steady and dynamic thermo-fluid performance of molten salt in paddle heat exchangers. Int. J. Fluid Mech. Res. 2016, 43, 472–488. [Google Scholar] [CrossRef]
- Du, J. Research on High Temperature Molten Salt in Paddle Heat Exchangers. Master’s Thesis, Nanjing University of Science and Technology, Nanjing, China, 2015. (In Chinese). [Google Scholar]
- Wang, W.; Zhang, H.; Liu, X. Research and application prospects of coal slime in paddle dryers. Ind. Boil. 2015, 149, 34–36. (In Chinese) [Google Scholar]
- Pope, S.B. Turbulent Flows, 1st ed.; Cambridge University Press & Beijing World Publishing Corporation: Cambridge, UK, 2010; pp. 14–18, 373–385. ISBN 978-7-5100-0573-2. [Google Scholar]
- Tufeu, R.; Petitet, J.P.; Denielou, L.; Le Neindre, B. Experimental determination of the thermal conductivity of molten pure salts and salt mixtures. Int. J. Thermophys. 1985, 6, 315–330. [Google Scholar] [CrossRef]
- ANSYS Fluent. User’s Manual; Version 14.5; Fluent Inc.: Canonsburg, PA, USA, 2012. [Google Scholar]
- Bejan, A. Entropy Generation Minimization, 1st ed.; CRC Press: Boca Raton, FL, USA, 1996; pp. 21–40. ISBN 0-8493-9651-4. [Google Scholar]
- Çengel, Y.A.; Boles, M.A. Thermodynamics: An Engineering Approach, 5th ed.; McGraw-Hill Education: New York, NY, USA, 2006; pp. 378–382, ISBN 0072884959, 9780072884951. [Google Scholar]
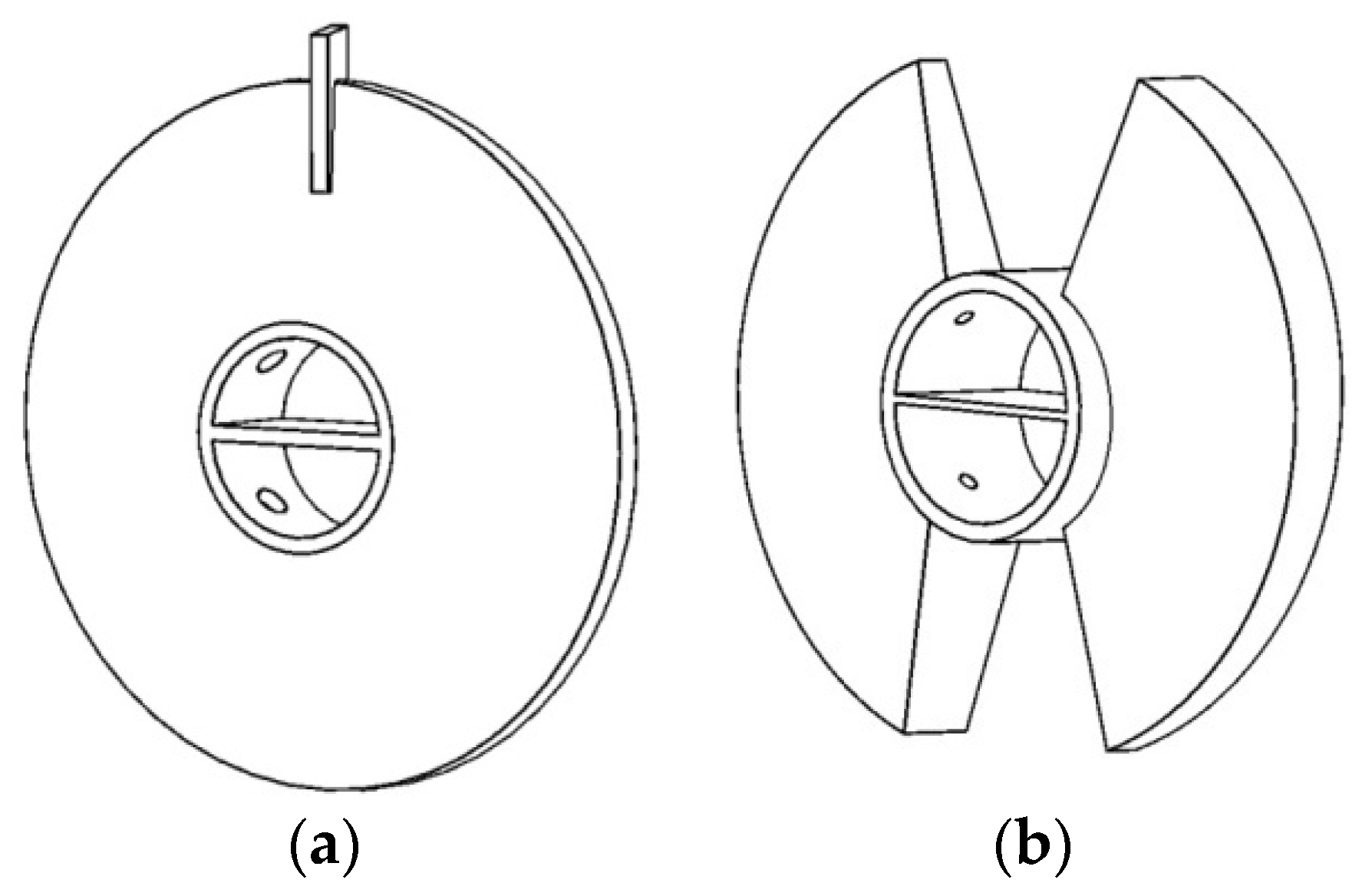
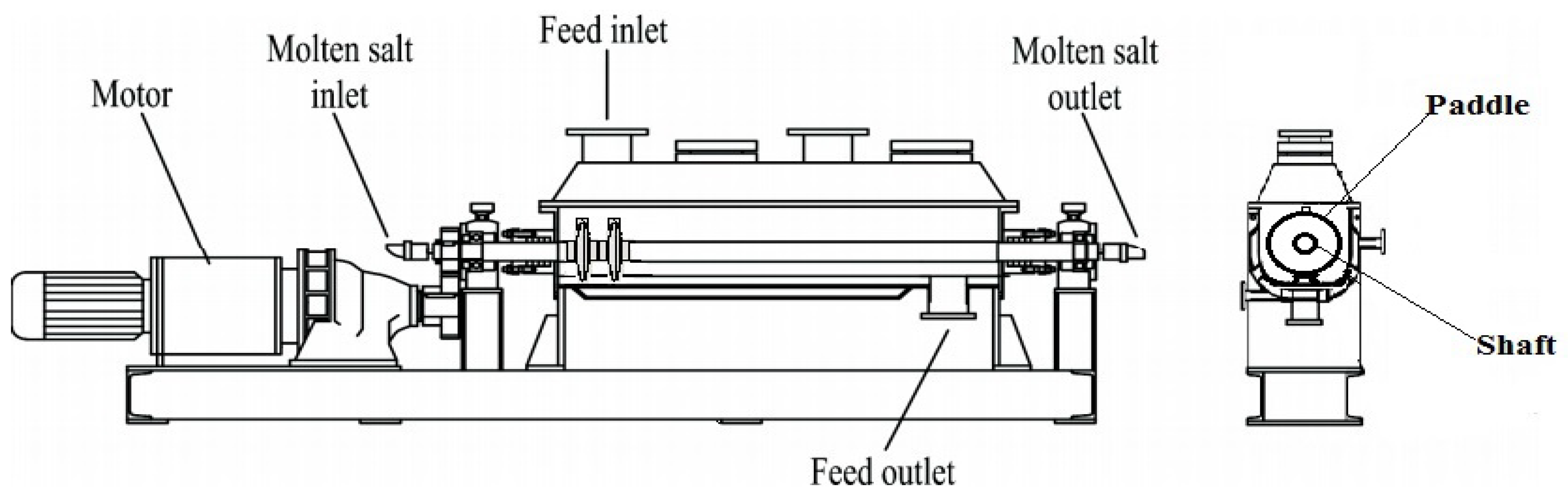
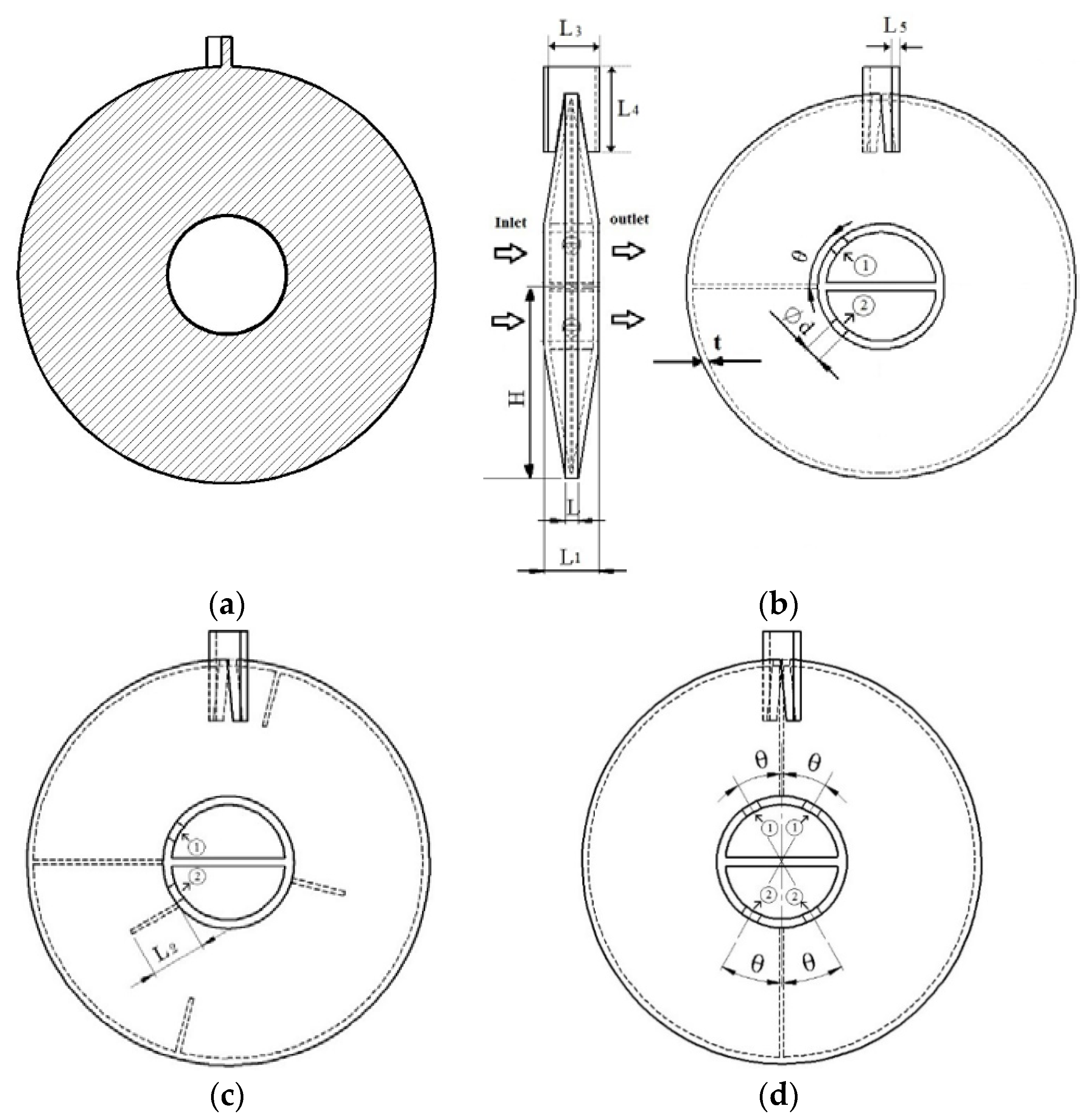

| Paddle Structure | Boundary Condition | |
|---|---|---|
| Fluid | Inlet | Tin = 550 °C |
| Outlet | Pout = 0 Pa | |
| Shell-side material | Shell-side material | To = 300 °C, ho = 250 W/(m2K) |
| Solid | Inside surfaces of shaft | Tw = 550 °C |
| End-wall surfaces of shaft | Adiabatic | |
| Property | ρ (kg/m3) | cp (J/(kg K)) | λ (W/(m K)) | μ (kg/(m s)) |
|---|---|---|---|---|
| Molten salt | 1944 | 1559.886 | 0.908 | 0.0012 |
| Stainless steel 316L | 8000 | 500 | 21.5 |
| Number of elements | 7,539,242 | 6,825,664 | 6,094,076 | 5,003,249 | 4,004,098 |
| Number of nodes | 1,866,142 | 1,731,115 | 1,566,281 | 1,318,141 | 1,063,456 |
| Pressure drop ΔP (Pa) | 30,997 | 30,922 | 31,131 | 31,430 | 28,020 |
| Heat transfer rate(W) | 2836 | 2841 | 2848 | 2848 | 2942 |
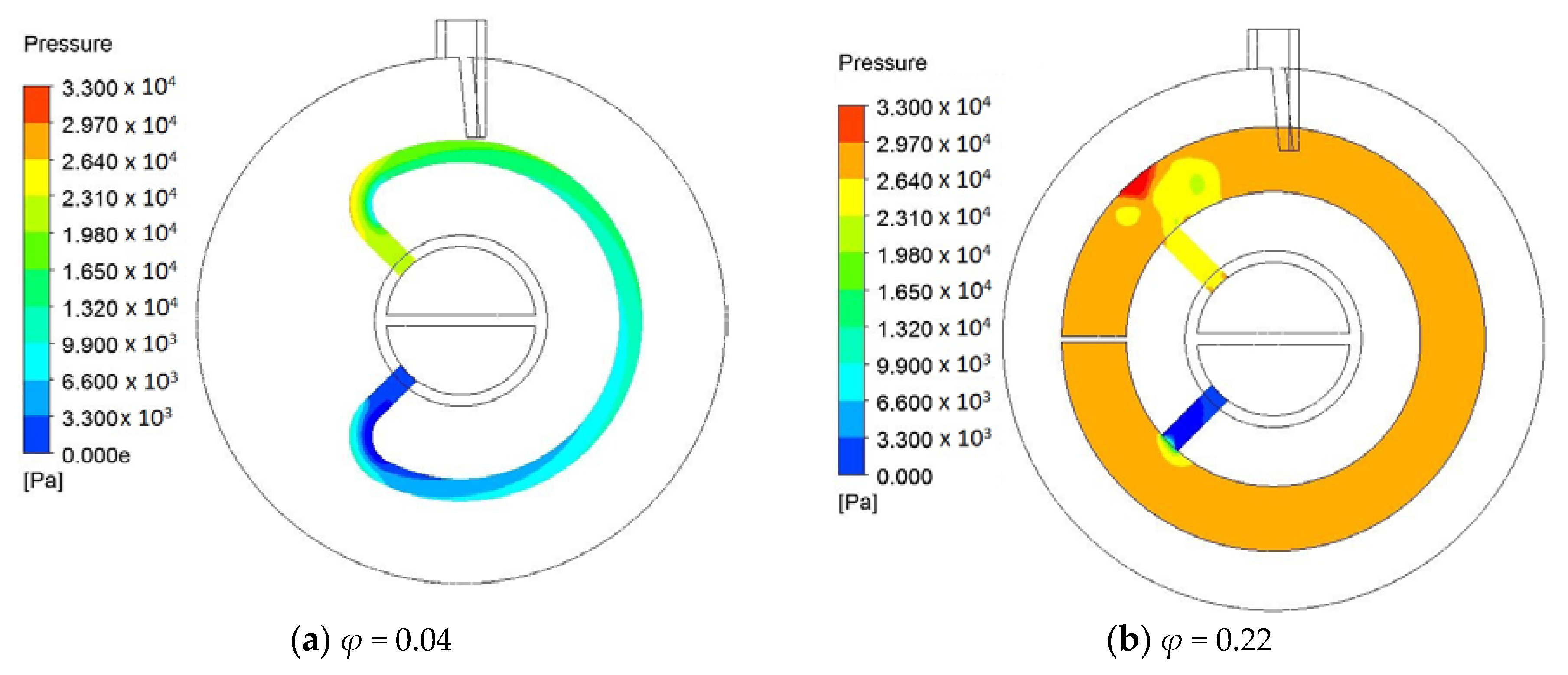
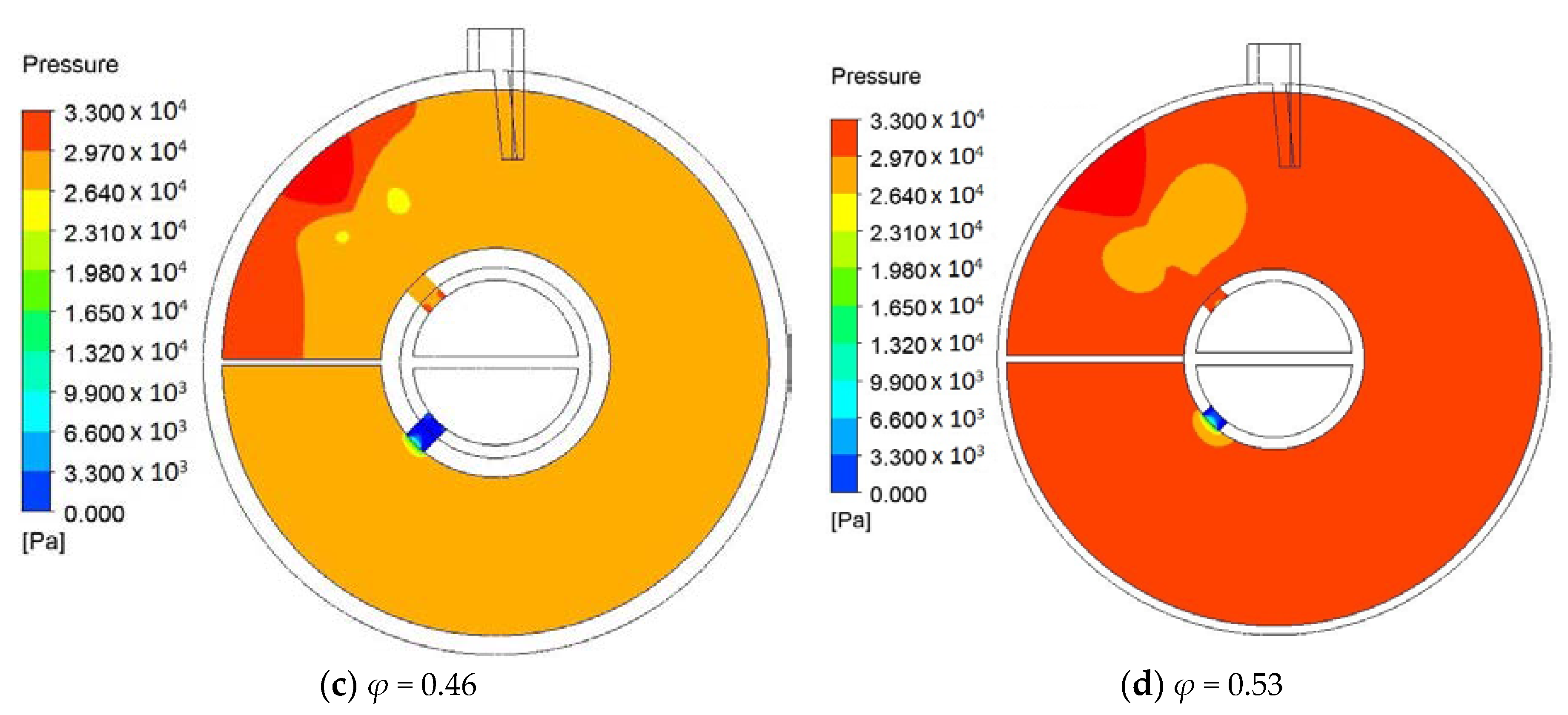
| φ | Paddle Type | Geometry Description |
|---|---|---|
| 0 | Solid | Reference: no fluid space in the paddle. |
| 0.04 | Hollow | The fluid space is a tube of 8 mm diameter in the paddle. |
| 0.22 | Hollow | t = 20 mm |
| 0.46 | Hollow | t = 6 mm |
| 0.53 | Hollow | t = 3 mm |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rajeh, T.; Tu, P.; Lin, H.; Zhang, H. Thermo-Fluid Characteristics of High Temperature Molten Salt Flowing in Single-Leaf Type Hollow Paddles. Entropy 2018, 20, 581. https://doi.org/10.3390/e20080581
Rajeh T, Tu P, Lin H, Zhang H. Thermo-Fluid Characteristics of High Temperature Molten Salt Flowing in Single-Leaf Type Hollow Paddles. Entropy. 2018; 20(8):581. https://doi.org/10.3390/e20080581
Chicago/Turabian StyleRajeh, Taha, Ping Tu, Hua Lin, and Houlei Zhang. 2018. "Thermo-Fluid Characteristics of High Temperature Molten Salt Flowing in Single-Leaf Type Hollow Paddles" Entropy 20, no. 8: 581. https://doi.org/10.3390/e20080581
APA StyleRajeh, T., Tu, P., Lin, H., & Zhang, H. (2018). Thermo-Fluid Characteristics of High Temperature Molten Salt Flowing in Single-Leaf Type Hollow Paddles. Entropy, 20(8), 581. https://doi.org/10.3390/e20080581




