Collective Motion of Repulsive Brownian Particles in Single-File Diffusion with and without Overtaking
Abstract
:1. Introduction
2. Formulation and Background
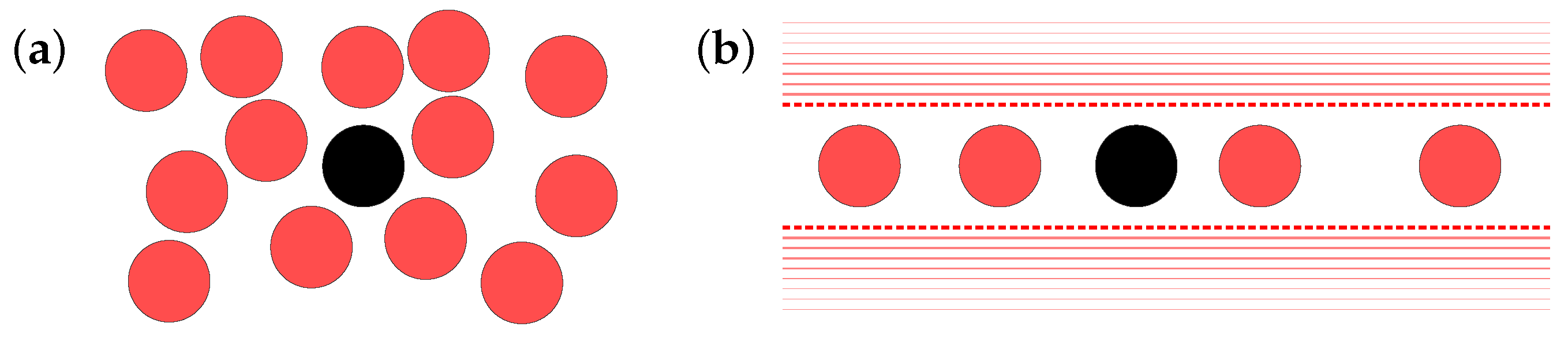
2.1. Specification of the System
2.2. Spatiotemporally Correlated Motion in SFD
2.3. Continuum Description
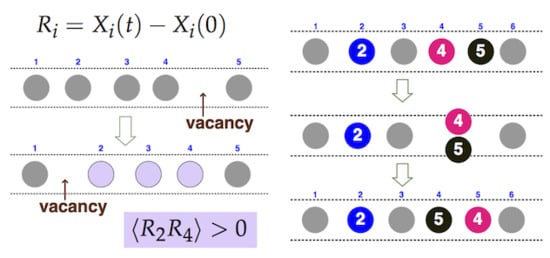
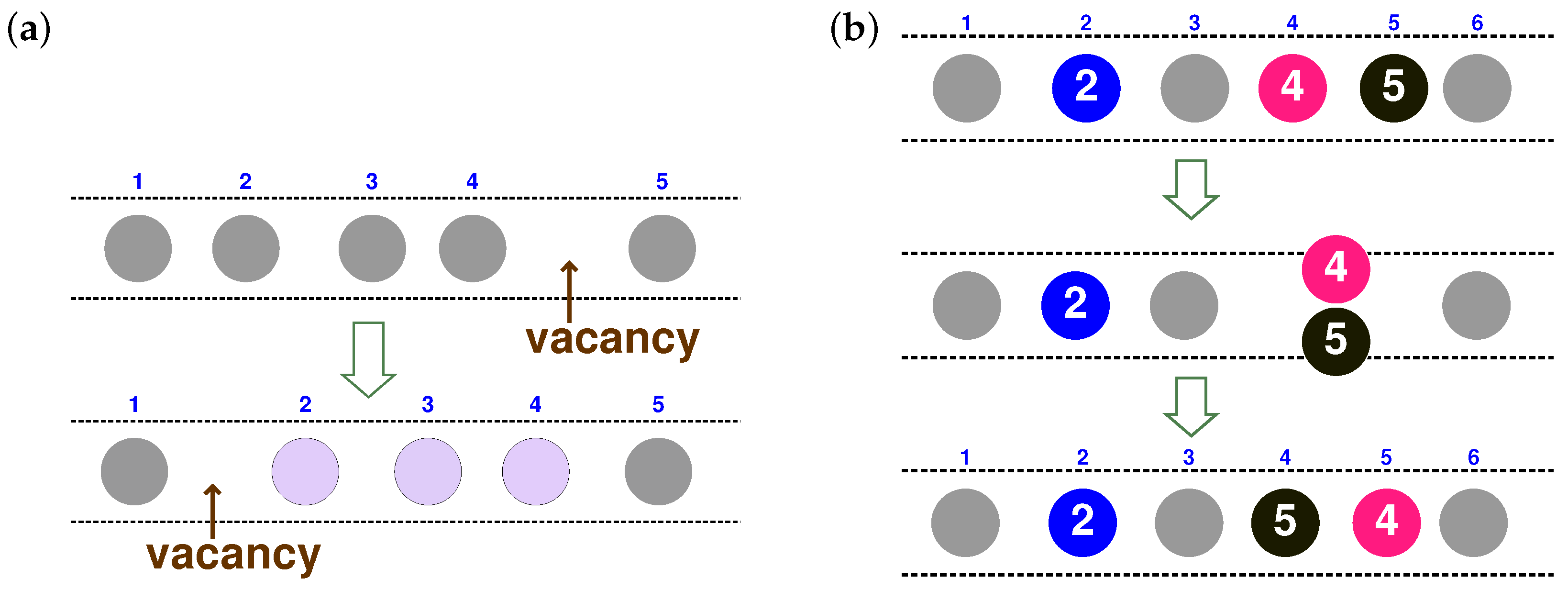
2.4. Label Variable
2.5. Kinematics of Overtaking Events
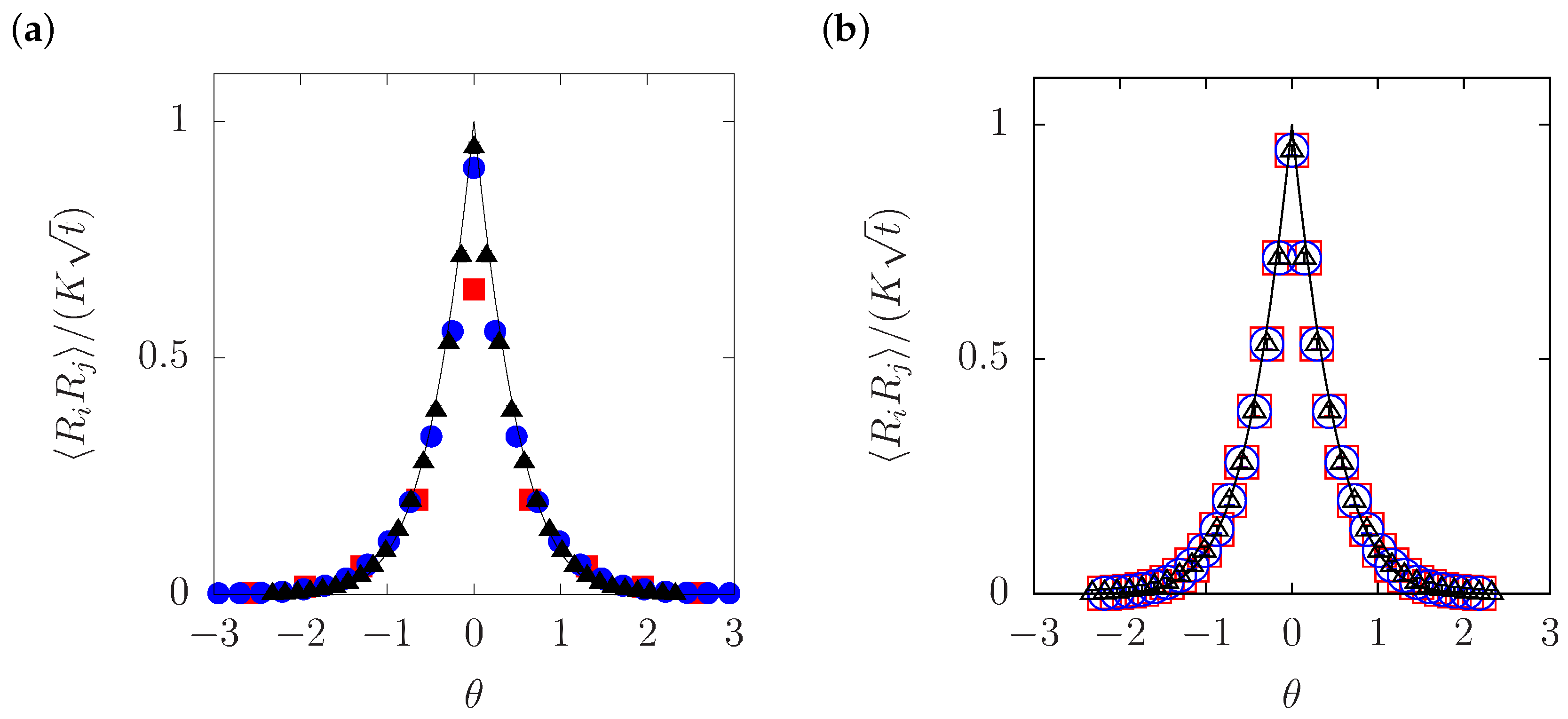
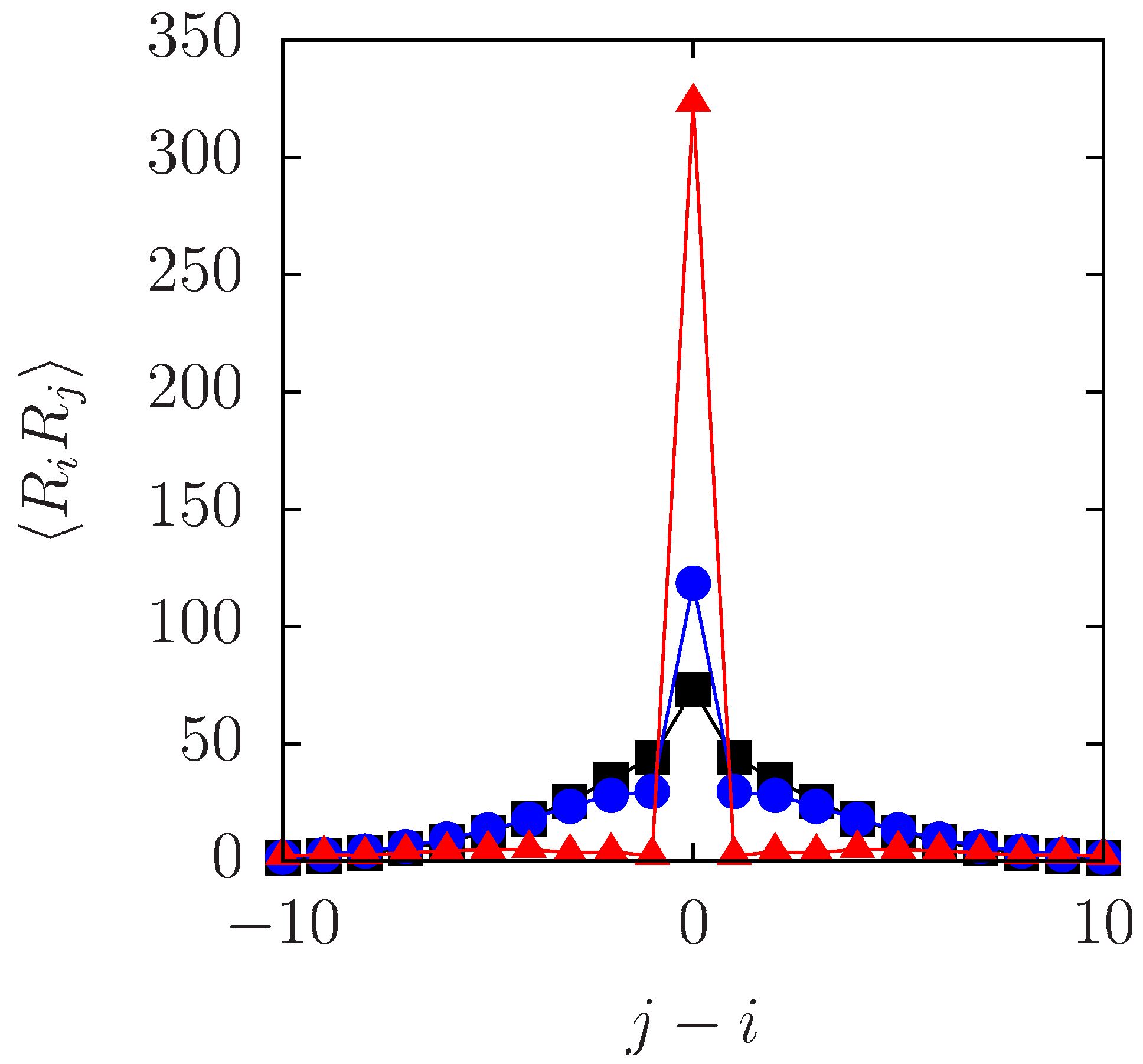
3. Displacement Correlation in SFD without Overtaking
3.1. Analytical Calculation of Displacement Correlation
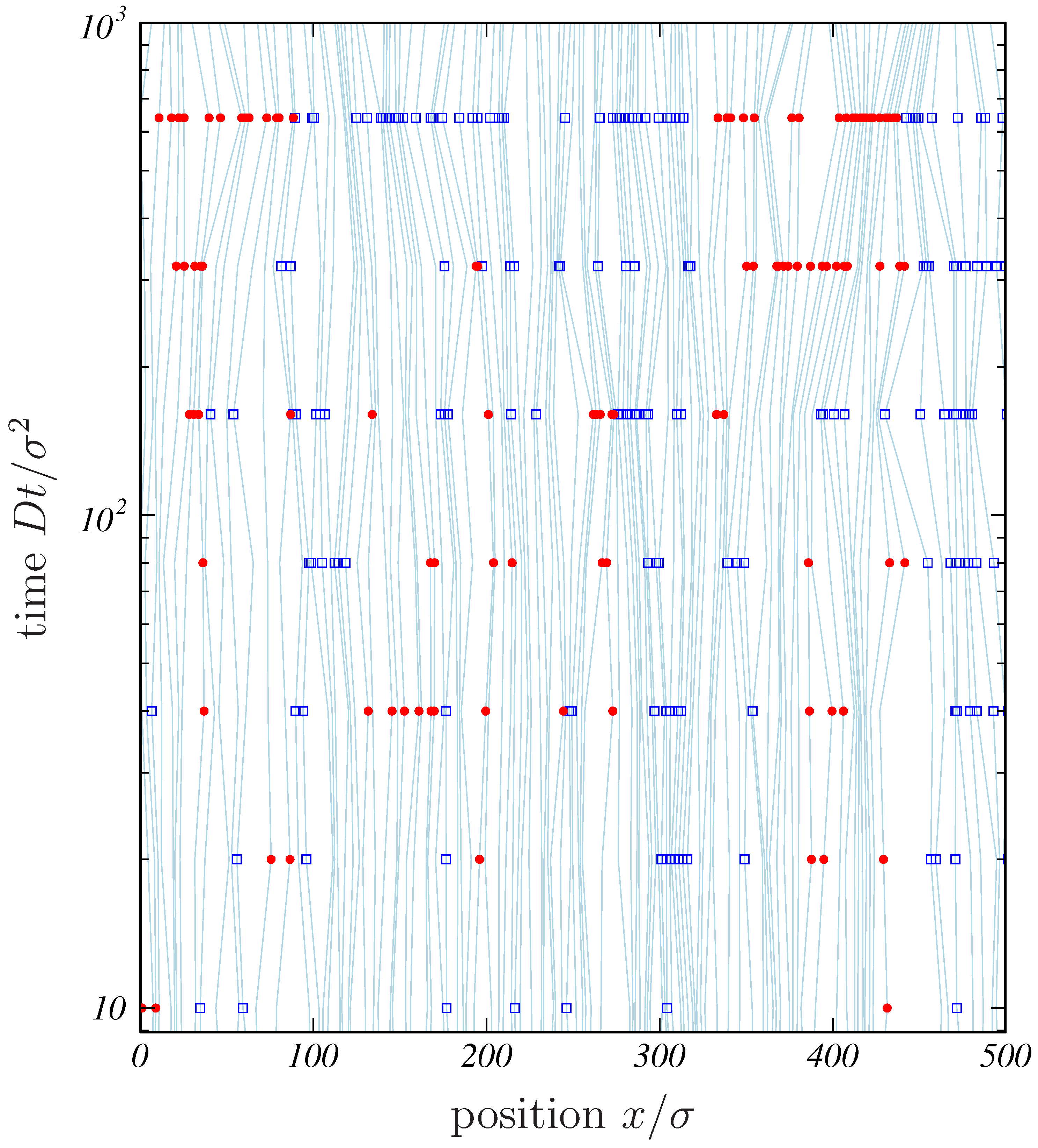
3.2. Particle Simulation in the Absence of Overtaking
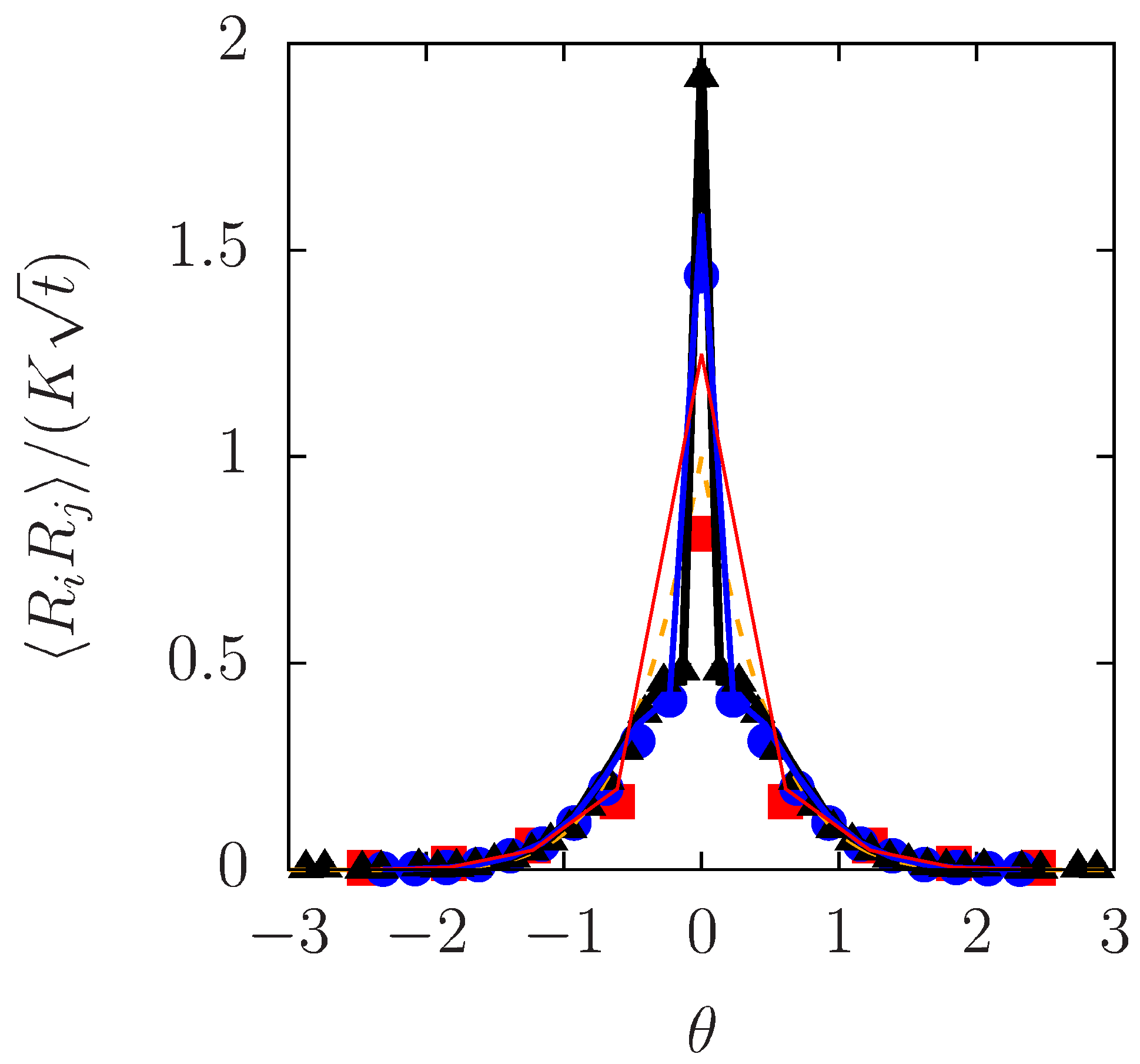
4. Effects of Overtaking on Displacement Correlation
4.1. Particle Simulation of SFD with Overtaking
4.2. Theory of Displacement Correlation in SFD with Overtaking
5. Discussion and Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| 1D | one-dimensional |
| 2D | two-dimensional |
| 3D | three-dimensional |
| MSD | mean square displacement |
| SFD | single-file diffusion |
Appendix A. Two-Body Propagator in the Amida-Kuji Process
Appendix B. Numerical Evaluation of the Hopping Rate
References
- Pusey, P.N.; van Megen, W. Observation of a glass transition in suspensions of spherical colloidal particles. Phys. Rev. Lett. 1987, 59, 2083. [Google Scholar] [CrossRef] [PubMed]
- Berthier, L.; Biroli, G. Theoretical perspective on the glass transition and amorphous materials. Rev. Mod. Phys. 2011, 83, 587–645. [Google Scholar] [CrossRef] [Green Version]
- Glotzer, S.C.; Novikov, V.N.; Schrøder, T.B. Time-dependent, four-point density correlation function description of dynamical heterogeneity and decoupling in supercooled liquids. J. Chem. Phys. 2000, 112, 509–512. [Google Scholar] [CrossRef]
- Ooshida, T.; Goto, S.; Matsumoto, T.; Nakahara, A.; Otsuki, M. Analytical calculation of four-point correlations for a simple model of cages involving numerous particles. Phys. Rev. E 2013, 88, 062108. [Google Scholar]
- Rallison, J.M. Brownian diffusion in concentrated suspensions of interacting particles. J. Fluid Mech. 1988, 186, 471–500. [Google Scholar] [CrossRef]
- Lefèvre, A.; Berthier, L.; Stinchcombe, R. Spatially heterogeneous dynamics in a model for granular compaction. Phys. Rev. E 2005, 72, 010301(R). [Google Scholar] [CrossRef] [PubMed]
- Pal, P.; O’Hern, C.S.; Blawzdziewicz, J.; Dufresne, E.R.; Stinchcombe, R. Minimal model for kinetic arrest. Phys. Rev. E 2008, 78, 011111. [Google Scholar] [CrossRef] [PubMed]
- Abel, S.M.; Tse, Y.L.S.; Andersen, H.C. Kinetic theories of dynamics and persistent caging in a one-dimensional lattice gas. Proc. Natl. Acad. Sci. USA 2009, 106, 15142–15147. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miyazaki, K. Garasu Ten’i to Môdo Ketsugô Riron (Glass Transition and Mode-Coupling Theory). Bussei Kenkyû 2007, 88, 621–720. (In Japanese) [Google Scholar]
- Ooshida, T.; Goto, S.; Matsumoto, T.; Otsuki, M. Insights from Single-File Diffusion into Cooperativity in Higher Dimensions. Biophys. Rev. Lett. 2016, 11, 9–38. [Google Scholar] [CrossRef]
- Harris, T.E. Diffusion with “collisions” between particles. J. Appl. Probab. 1965, 2, 323–338. [Google Scholar] [CrossRef]
- Alexander, S.; Pincus, P. Diffusion of labeled particles on one-dimensional chains. Phys. Rev. B 1978, 18, 2011. [Google Scholar] [CrossRef]
- Hahn, K.; Kärger, J. Propagator and mean-square displacement in single-file systems. J. Phys. A Math. Gen. 1995, 28, 3061–3070. [Google Scholar] [CrossRef]
- Kollmann, M. Single-file Diffusion of Atomic and Colloidal Systems: Asymptotic Laws. Phys. Rev. Lett. 2003, 90, 180602. [Google Scholar] [CrossRef] [PubMed]
- Illien, P.; Bénichou, O.; Mejía-Monasterio, C.; Oshanin, G.; Voituriez, R. Active Transport in Dense Diffusive Single-File Systems. Phys. Rev. Lett. 2013, 111, 038102. [Google Scholar] [CrossRef] [PubMed]
- Van Beijeren, H.; Kehr, K.W.; Kutner, R. Diffusion in concentrated lattice gases. III. Tracer diffusion on a one-dimensional lattice. Phys. Rev. B 1983, 28, 5711–5723. [Google Scholar] [CrossRef] [Green Version]
- Taloni, A.; Lomholt, M.A. Langevin formulation for single-file diffusion. Phys. Rev. E 2008, 78, 051116. [Google Scholar] [CrossRef] [PubMed]
- Taloni, A.; Marchesoni, F. Interacting single-file system: Fractional Langevin formulation versus diffusion-noise approach. Biophys. Rev. Lett. 2014, 9, 381–396. [Google Scholar] [CrossRef]
- Ooshida, T.; Goto, S.; Matsumoto, T.; Otsuki, M. Displacement correlation as an indicator of collective motion in one-dimensional and quasi-one-dimensional systems of repulsive Brownian particles. Mod. Phys. Lett. B 2015, 29, 1550221. [Google Scholar] [CrossRef]
- Majumdar, S.N.; Barma, M. Two-tag correlation functions in one-dimensional lattice gases. Physica A 1991, 177, 366–372. [Google Scholar] [CrossRef]
- Ooshida, T.; Goto, S.; Matsumoto, T.; Otsuki, M. Calculation of displacement correlation tensor indicating vortical cooperative motion in two-dimensional colloidal liquids. Phys. Rev. E 2016, 94, 022125. [Google Scholar] [CrossRef] [PubMed]
- Krapivsky, P.L.; Mallick, K.; Sadhu, T. Large Deviations in Single-File Diffusion. Phys. Rev. Lett. 2014, 113, 078101. [Google Scholar] [CrossRef] [PubMed]
- Hahn, K.; Kärger, J. Deviations from the normal time regime of single-file diffusion. J. Phys. Chem. B 1998, 102, 5766–5771. [Google Scholar] [CrossRef]
- Mon, K.; Percus, J. Self-diffusion of fluids in narrow cylindrical pores. J. Chem. Phys. 2002, 117, 2289–2292. [Google Scholar] [CrossRef]
- Lucena, D.; Tkachenko, D.; Nelissen, K.; Misko, V.R.; Ferreira, W.P.; Farias, G.A.; Peeters, F.M. Transition from single-file to two-dimensional diffusion of interacting particles in a quasi-one-dimensional channel. Phys. Rev. E 2012, 85, 031147. [Google Scholar] [CrossRef] [PubMed]
- Siems, U.; Kreuter, C.; Erbe, A.; Schwierz, N.; Sengupta, S.; Leiderer, P.; Nielaba, P. Non-monotonic crossover from single-file to regular diffusion in micro-channels. Sci. Rep. 2012, 2, 1015. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wanasundara, S.N.; Spiteri, R.J.; Bowles, R.K. A transition state theory for calculating hopping times and diffusion in highly confined fluids. J. Chem. Phys. 2014, 140, 024505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kutner, R.; van Beijeren, H.; Kehr, K.W. Diffusion in concentrated lattice gases. VI. Tracer diffusion on two coupled linear chains. Phys. Rev. B 1984, 30, 4382–4391. [Google Scholar] [CrossRef] [Green Version]
- Bénichou, O.; Illien, P.; Oshanin, G.; Sarracino, A.; Voituriez, R. Diffusion and Subdiffusion of Interacting Particles on Comblike Structures. Phys. Rev. Lett. 2015, 115, 220601. [Google Scholar] [CrossRef] [PubMed]
- Ooshida, T.; Goto, S.; Matsumoto, T.; Nakahara, A.; Otsuki, M. Continuum Theory of Single-File Diffusion in Terms of Label Variable. J. Phys. Soc. Jpn. 2011, 80, 074007. [Google Scholar] [Green Version]
- Berthier, L.; Witten, T.A. Compressing nearly hard sphere fluids increases glass fragility. Europhys. Lett. 2009, 86, 10001. [Google Scholar] [CrossRef] [Green Version]
- Dean, D.S. Langevin equation for the density of a system of interacting Langevin processes. J. Phys. A Math. Gen. 1996, 29, L613. [Google Scholar] [CrossRef]
- Kawasaki, K. Stochastic model of slow dynamics in supercooled liquids and dense colloidal suspensions. Phys. A 1994, 208, 35–64. [Google Scholar] [CrossRef]
- Kawasaki, K. Microscopic Analyses of the Dynamical Density Functional Equation of Dense Fluids. J. Stat. Phys. 1998, 93, 527–546. [Google Scholar] [CrossRef]
- Das, S.P. Statistical Physics of Liquids at Freezing and Beyond; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar]
- Das, S.P.; Yoshimori, A. Coarse-grained forms for equations describing the microscopic motion of particles in a fluid. Phys. Rev. E 2013, 88, 043008. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.; Kawasaki, K.; Jacquin, H.; van Wijland, F. Equilibrium dynamics of the Dean–Kawasaki equation: Mode-coupling theory and its extension. Phys. Rev. E 2014, 89, 012150. [Google Scholar] [CrossRef] [PubMed]
- Nägele, G. On the dynamics and structure of charge-stabilized suspensions. Phys. Rep. 1996, 272, 215–372. [Google Scholar] [CrossRef]
- Dhont, J.K.G. An Introduction to Dynamics of Colloids; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Lamb, H. Hydrodynamics, 6th ed.; Cambridge University Press: Cambridge, UK, 1932. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics. In Theoretical Physics; Butterworth-Heinemann: Oxford, UK, 1987; Volum 6. [Google Scholar]
- Toninelli, C.; Wyart, M.; Berthier, L.; Biroli, G.; Bouchaud, J.P. Dynamical susceptibility of glass formers: Contrasting the predictions of theoretical scenarios. Phys. Rev. E 2005, 71, 041505. [Google Scholar] [CrossRef] [PubMed]
- Flenner, E.; Szamel, G. Long-Range Spatial Correlations of Particle Displacements and the Emergence of Elasticity. Phys. Rev. Lett. 2015, 114, 025501. [Google Scholar] [CrossRef] [PubMed]
- Ooshida, T.; Otsuki, M. Effects of Cage-Breaking Events in Single-File Diffusion on Elongation Correlation. J. Phys. Soc. Jpn. 2017, 86, 113002. [Google Scholar] [CrossRef]
- Spohn, H. Nonlinear Fluctuating Hydrodynamics for Anharmonic Chains. J. Stat. Phys. 2014, 154, 1191–1227. [Google Scholar] [CrossRef] [Green Version]
- Kramers, H.A. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica 1940, 7, 284–304. [Google Scholar] [CrossRef]
- Sancho, J.M.; Miguel, M.S.; Dürr, D. Adiabatic Elimination for Systems of Brownian Particles with Nonconstant Damping Coefficients. J. Stat. Phys. 1982, 28, 291–305. [Google Scholar] [CrossRef]
- Sekimoto, K. Temporal Coarse Graining for Systems of Brownian Particles with Non-Constant Temperature. J. Phys. Soc. Jpn. 1999, 68, 1448–1449. [Google Scholar] [CrossRef]
- Inoue, Y. Statistical analysis on Amida-kuji. Phys. A Stat. Mech. Appl. 2006, 369, 867–876. [Google Scholar] [CrossRef]
- Yamanaka, K.; Nakano, S.I. Enumeration, Counting, and Random Generation of Ladder Lotteries. IEICE Trans. Inf. Syst. 2017, 100, 444–451. [Google Scholar] [CrossRef]
- Kitahara, K. Hi-heikô Kei no Kagaku II: Kanwa Katei no Tôkei Rikigaku [Science of Non-Equilibrium Systems II: Statistical Mechanics of Relaxation Processes]; Kôdansha: Tokyo, Japan, 1994. (In Japanese) [Google Scholar]
- Ahmadi, S.; Bowles, R.K. Diffusion in quasi-one-dimensional channels: A small system n, p, T transition state theory for hopping times. J. Chem. Phys. 2017, 146, 154505. [Google Scholar] [CrossRef] [PubMed]
- Oshanin, G.; Vasilyev, O.; Krapivsky, P.L.; Klafter, J. Survival of an evasive prey. Proc. Nat. Acad. Sci. USA 2009, 106, 13696–13701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Doliwa, B.; Heuer, A. Cooperativity and spatial correlations near the glass transition: Computer simulation results for hard spheres and disks. Phys. Rev. E 2000, 61, 6898–6908. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ooshida, T.; Goto, S.; Otsuki, M. Collective Motion of Repulsive Brownian Particles in Single-File Diffusion with and without Overtaking. Entropy 2018, 20, 565. https://doi.org/10.3390/e20080565
Ooshida T, Goto S, Otsuki M. Collective Motion of Repulsive Brownian Particles in Single-File Diffusion with and without Overtaking. Entropy. 2018; 20(8):565. https://doi.org/10.3390/e20080565
Chicago/Turabian StyleOoshida, Takeshi, Susumu Goto, and Michio Otsuki. 2018. "Collective Motion of Repulsive Brownian Particles in Single-File Diffusion with and without Overtaking" Entropy 20, no. 8: 565. https://doi.org/10.3390/e20080565
APA StyleOoshida, T., Goto, S., & Otsuki, M. (2018). Collective Motion of Repulsive Brownian Particles in Single-File Diffusion with and without Overtaking. Entropy, 20(8), 565. https://doi.org/10.3390/e20080565