Entropy Generation Due to the Heat Transfer for Evolving Spherical Objects
Abstract
1. Introduction
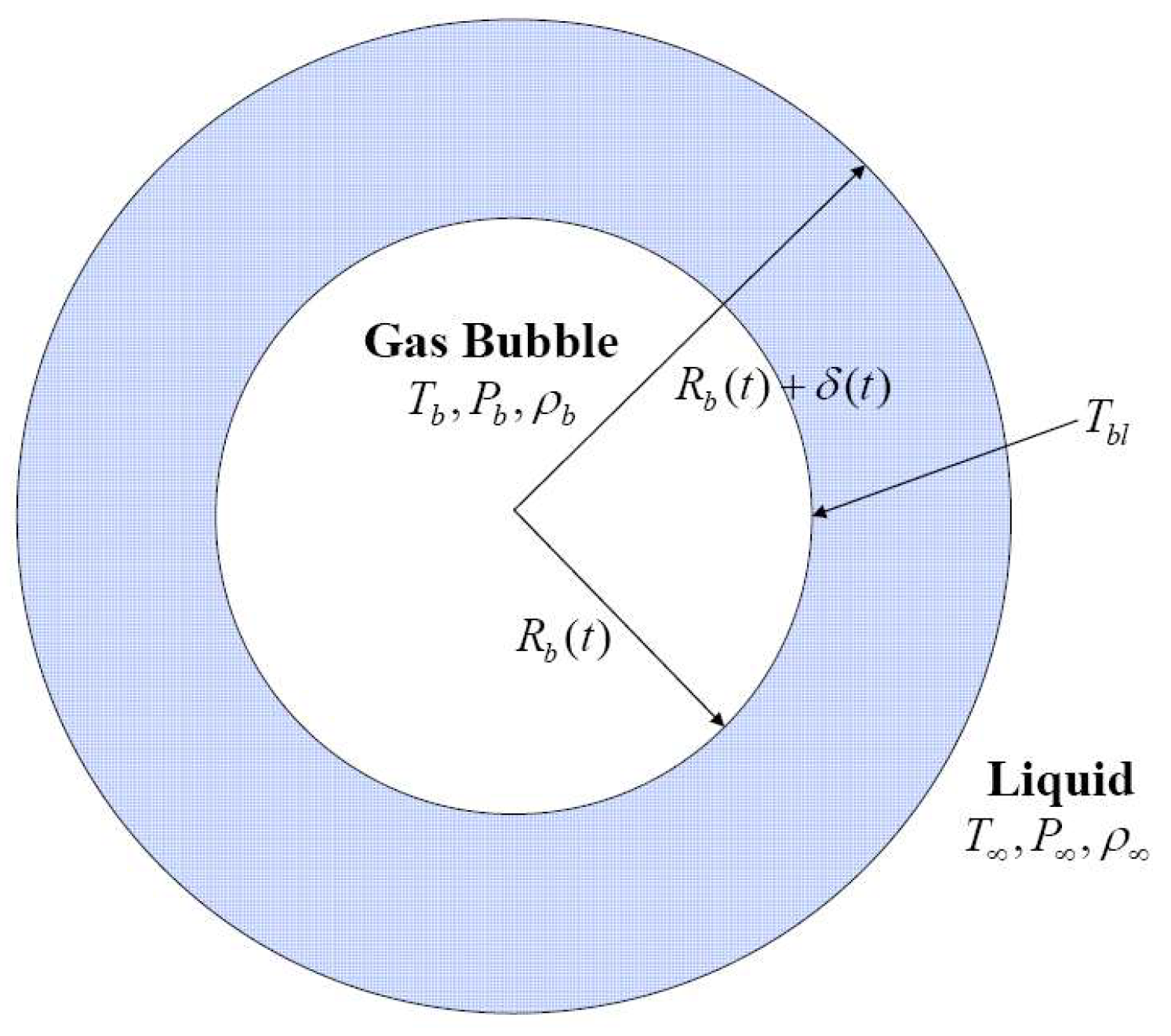
2. Bubble Evolution in Hot Liquid Medium
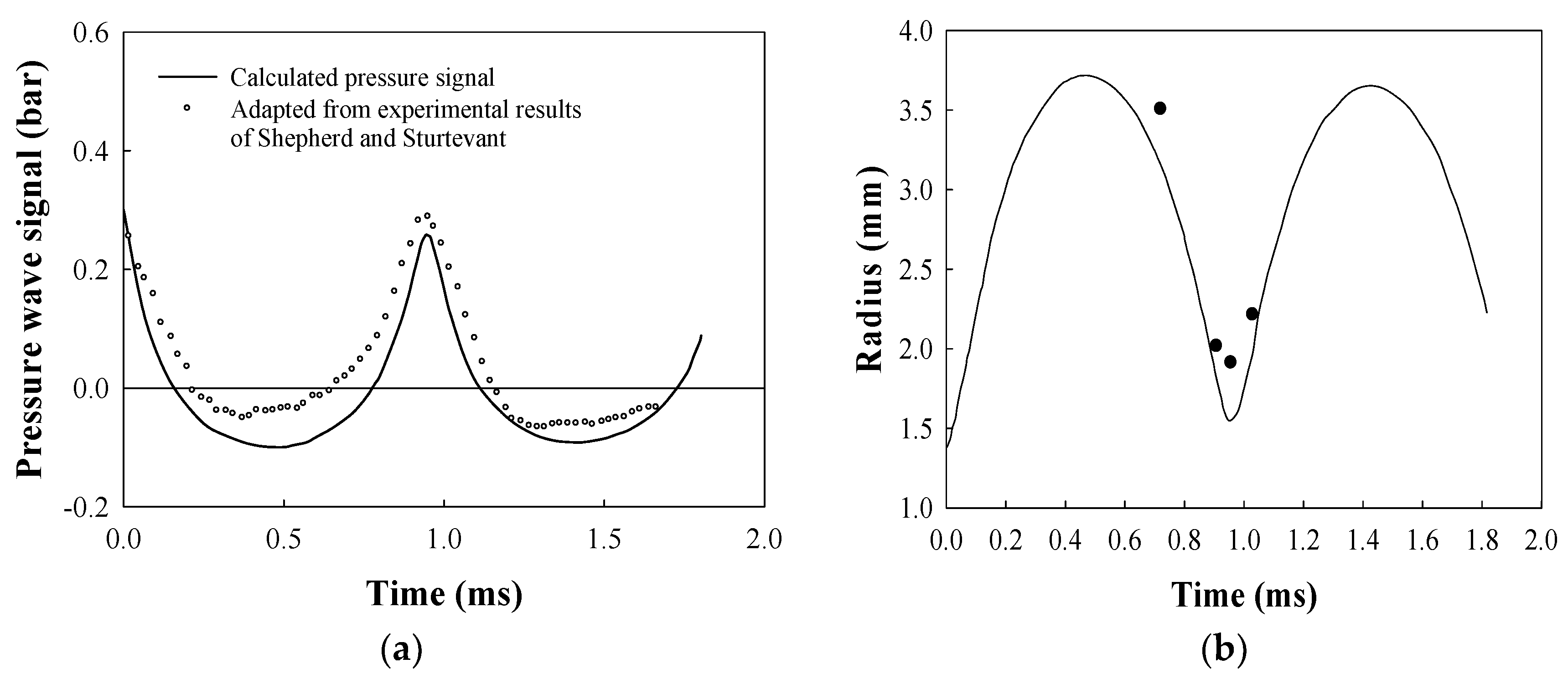
2.1. Evaporation of Liquid Droplet at Its Superheat Limit
2.2. Thermal Boundary Layer Adjacent to the Bubble Wall
2.3. Overall Energy Equation for a Bubble
2.4. Bubble Wall Motion
2.5. Energy Equation for the Liquid Adjacent to the Bubble Wall: The Thermal Boundary Layer
2.6. Entropy Generation during Bubble Evolution
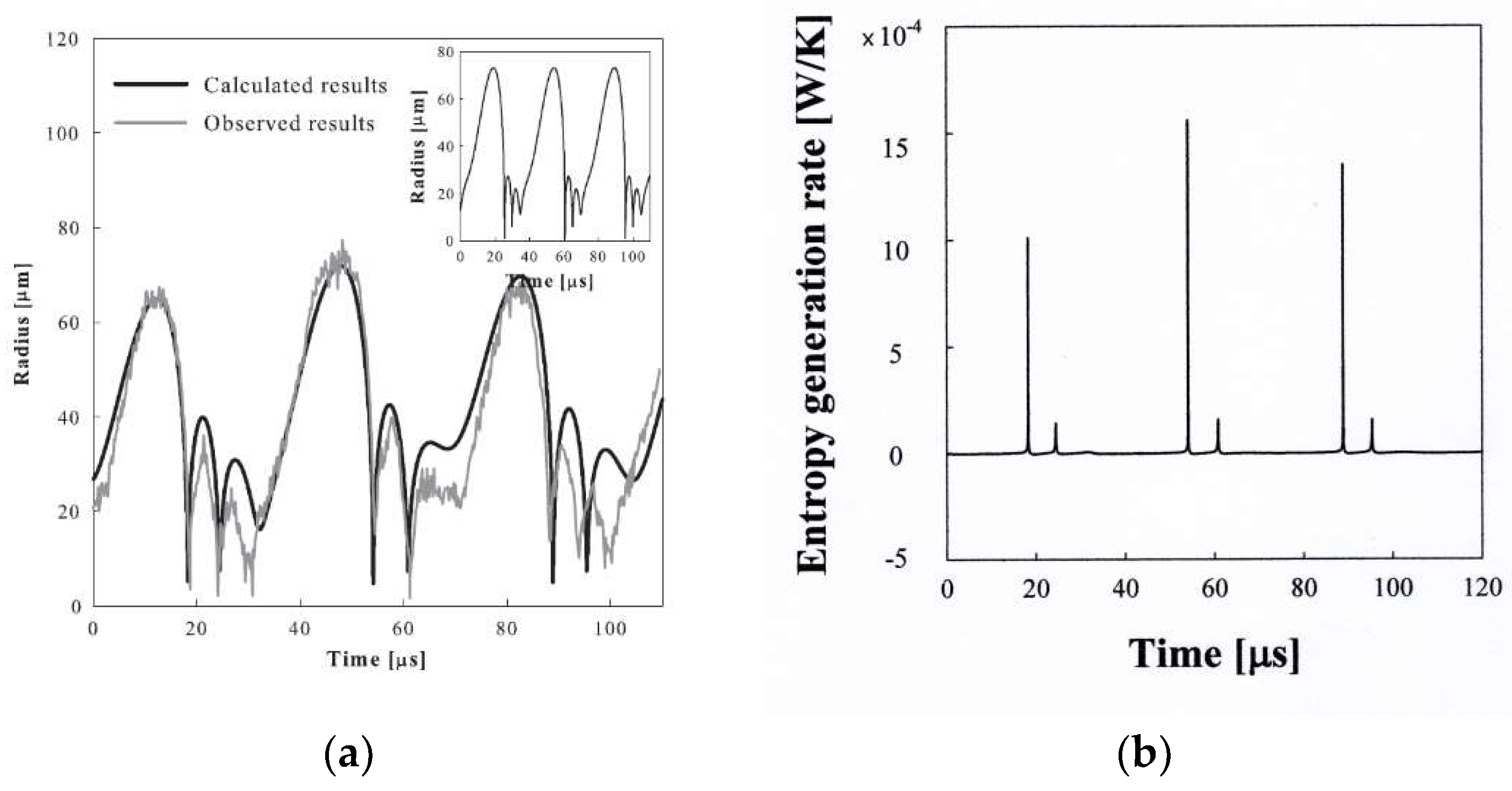
2.7. Evolution of a Bubble Formed from a Droplet at Its Superheat Limit in Hot Liquid Medium
3. Microbubble Behavior under an Ultrasonic Field
3.1. Mass, Momentum and Energy Conservations for Gas inside the Bubble
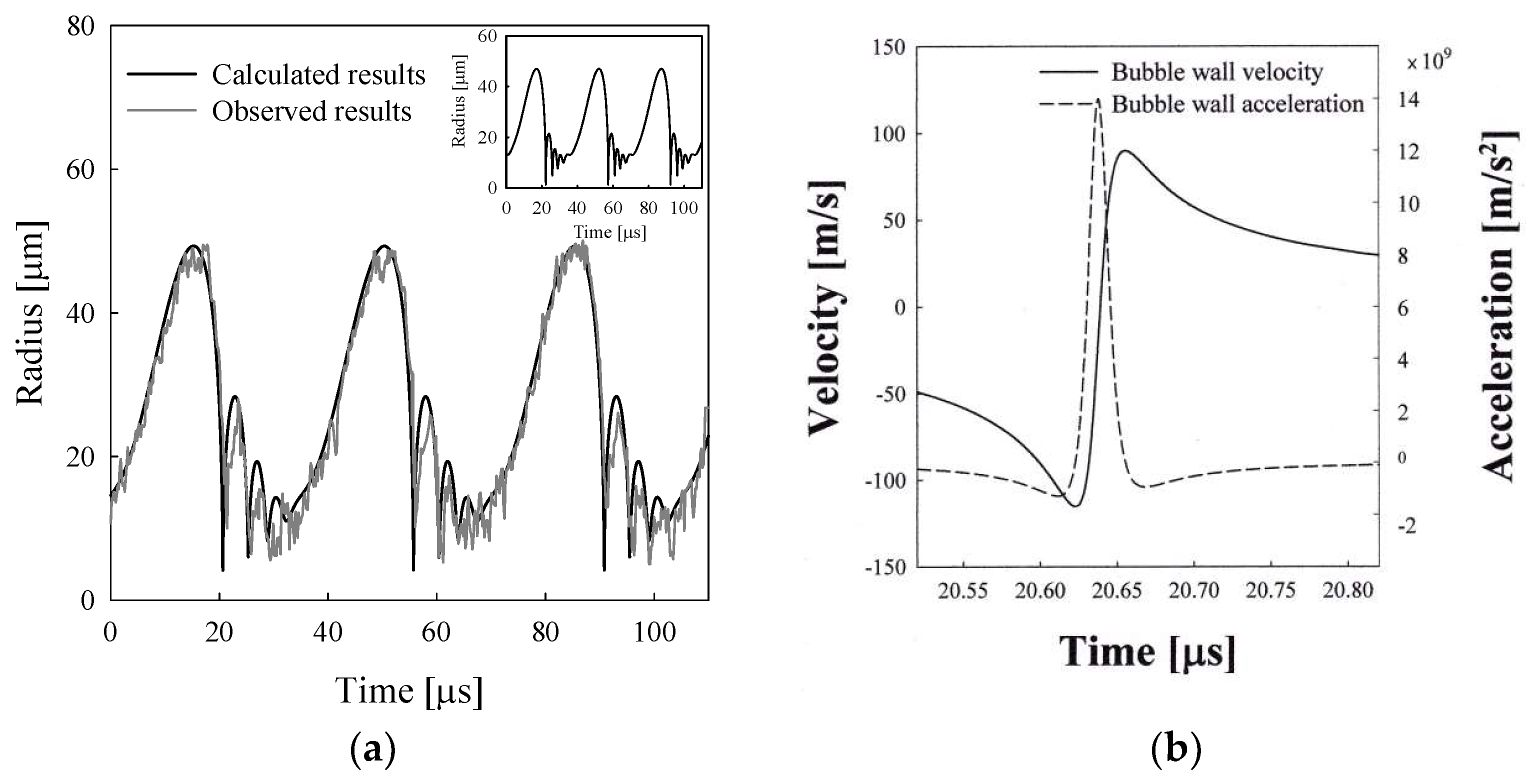
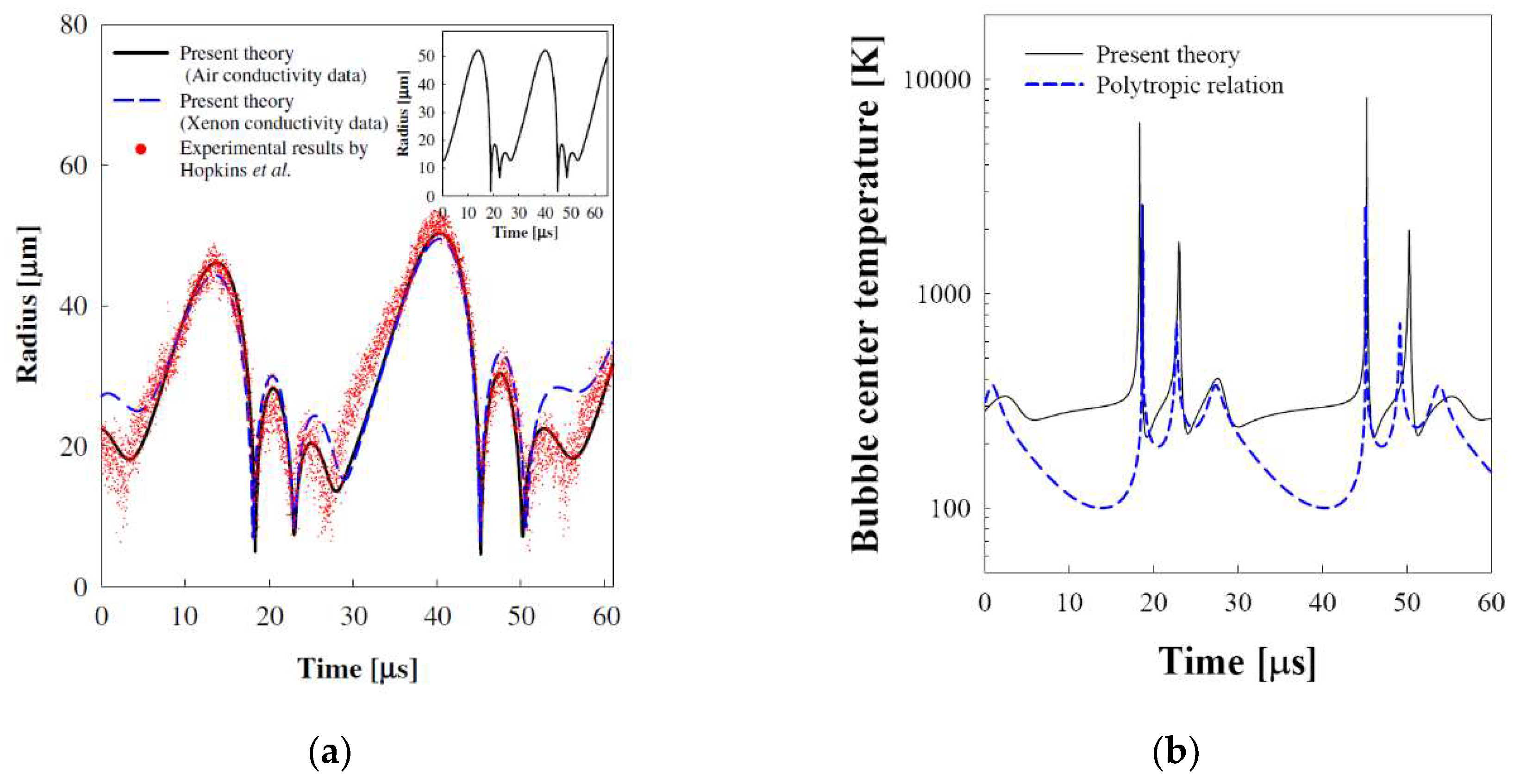
3.2. Bubble Wall Motion under an Ultrasonic Field
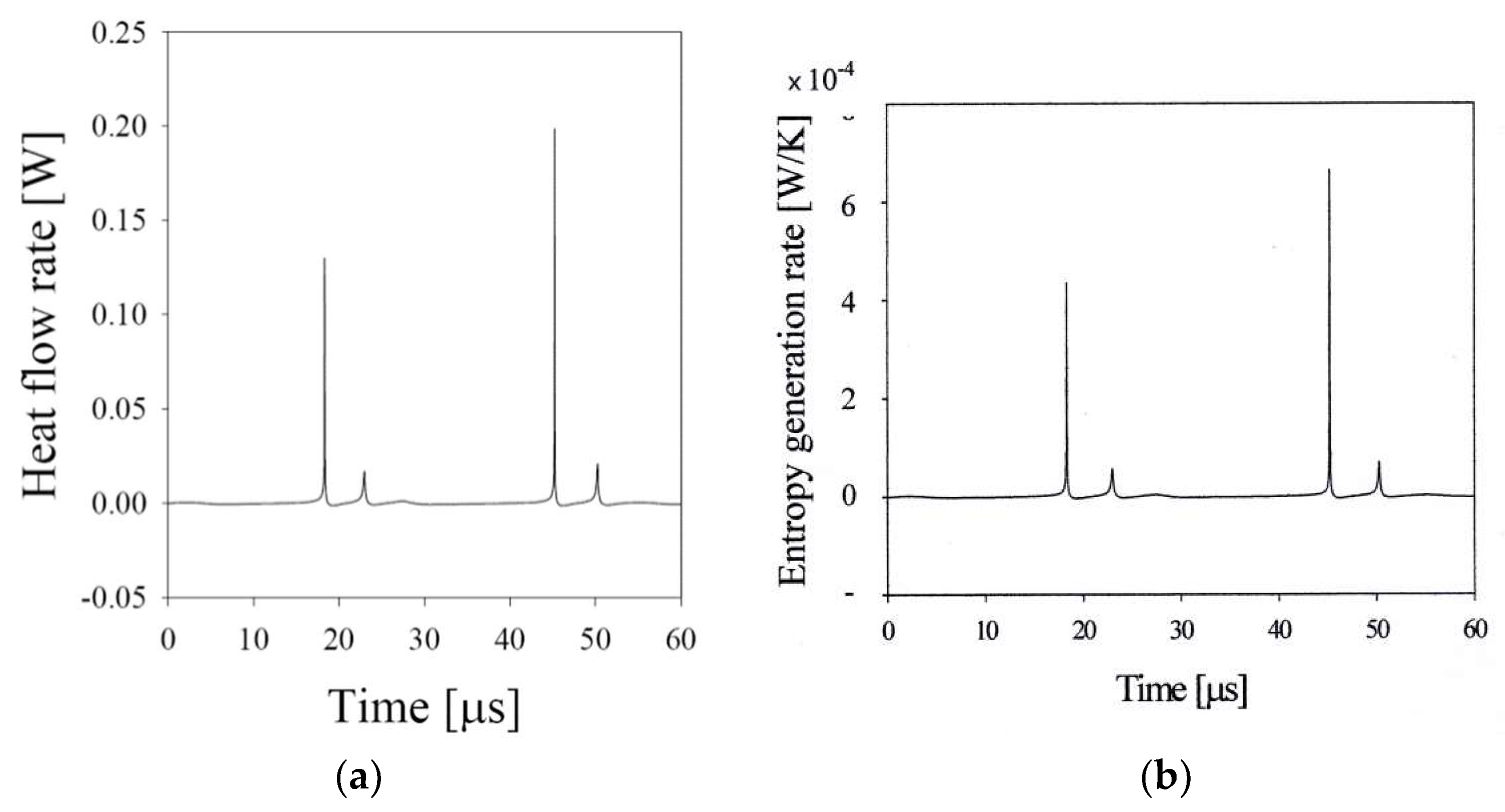
3.3. Sonoluminescing Bubble in Sulfuric Acid Solutions
4. Evolution of Stars
4.1. Hydrodynamics for the Stars
4.2. Core-Collapse Implosion: Early Supernova
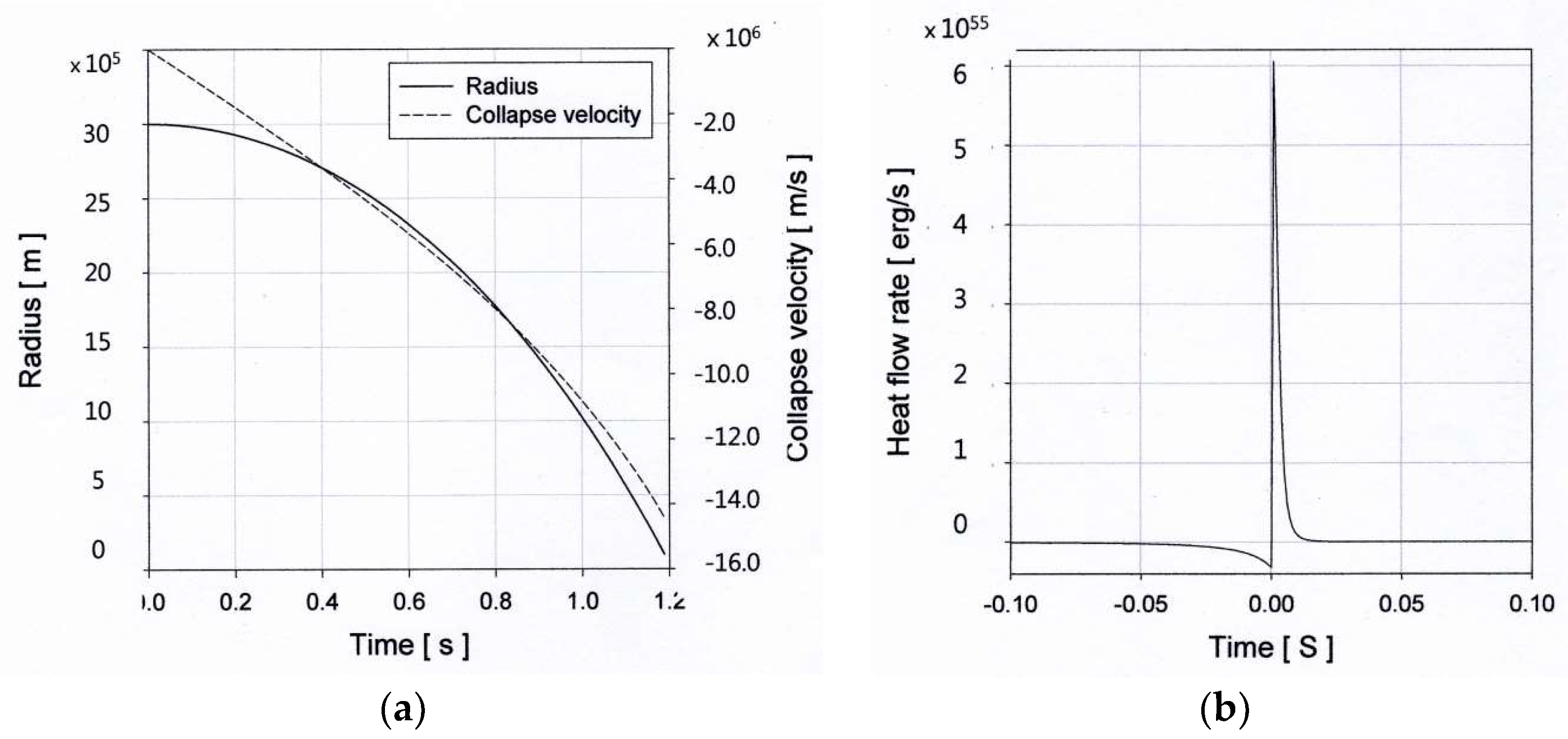
4.3. Supernova Explosions
4.4. Heat Transport Equation for the Core-Collapse Supernova Explosions
5. Conclusions
Funding
Conflicts of Interest
Nomenclature
| CB | sound speed at the bubble wall |
| Cp | heat capacity of star at constant pressure |
| Cp,b | heat capacity of gas at constant pressure |
| Cv | heat capacity of stat at constant volume |
| Cv,b | heat capacity of gas at constant volume |
| dm | average distance between molecules |
| dw | van der Waals’ diameter of liquid molecule |
| E | internal energy |
| fd | driving frequency of ultrasound |
| G | gravitational constant |
| kg | conductivity of gas |
| k1 | conductivity of liquid |
| mb | mass of bubble |
| M | mass of star |
| N | number density |
| n | polytropic index |
| P | pressure inside the star |
| PA | driving amplitude of ultrasound |
| Pb | pressure inside the bubble |
| Pbo | pressure at the bubble center |
| Ps | driving ultrasound pressure |
| Po | pressure at the center of star |
| P∞ | ambient pressure |
| Q | heat flow |
| qr | heat flux inside the bubble or star |
| rd | distance from the bubble center |
| R | radius of star |
| Ro | equilibrium radius of bubble |
| Rb | radius of bubble |
| Rg | gas constant |
| Rmin | minimum radius of star |
| Rmax | maximum radius of star |
| S | entropy |
| Sg | entropy generation |
| t | time |
| T | temperature of star |
| Tavg | average temperature of star |
| Tb | temperature of gas inside the bubble |
| Tbl | temperature at the bubble-liquid interface |
| Tbo | temperature at the bubble center |
| To | temperature at the center of star |
| T∞ | ambient temperature |
| Ub | velocity at the bubble wall |
| u | velocity inside the star |
| ug | gas velocity inside the bubble |
| V | volume of bubble |
| Vo | initial volume of fire-ball |
| Vm | effective volume of liquid molecule |
| W | potential for evolution of star |
| Z | coordination number |
Greek Letters
| α | thermal diffusivity of liquid |
| γ | specific heat ratio |
| δ | thermal boundary layer thickness |
| ε | energy of fire-ball or star |
| εm | energy needed to separate of pair of molecules |
| εo | potential parameter of London dispersion force |
| ρ | density of star |
| ρc | critical density of liquid |
| ρg | gas density inside the bubble |
| ρm | density of liquid |
| ρo | gas density at the center of bubble or star |
| ρ∞ | density of liquid medium |
| ϕ | gravitational potential |
| ω | angular frequency of ultrasound |
| μ | dynamic viscosity of liquid |
| σ | interfacial tension of liquid |
Subscripts
| b | bubble |
| o | center |
| ∞ | ambient liquid medium |
References
- Bejan, A. Advanced Engineering Thermodynamics; Wiley: New York, NY, USA, 1988; p. 606. [Google Scholar]
- Moody, F.J. Second law thinking–example application in reactor and containment technology. In Second Aspects of Thermal Design; Bejan, A., Reid, R.C., Eds.; American Society of Mechanical Engineers: New York, NY, USA, 1984; Volume HTD-33, pp. 1–9. [Google Scholar]
- Hopkins, S.D.; Putterman, S.J.; Kappus, B.A.; Suslick, K.S.; Camara, C.G. Dynamics of a sonoluminescing bubble in sulfuric acid. Phys. Rev. Lett. 2005, 95, 254301. [Google Scholar] [CrossRef] [PubMed]
- Prosperetti, A.; Crum, L.A.; Commander, K.W. Nonlinear bubble dynamics. J. Acoust. Soc. Am. 1988, 83, 502–514. [Google Scholar] [CrossRef]
- Jun, J.-H.; Kwak, H. Gravitational collapse of Newtonian stars. Int. J. Mod. Phys. D 2000, 9, 35–42. [Google Scholar] [CrossRef]
- Colgate, S.A.; White, R.H. The hydrodynamics behavior of supernova explosions. Astrophys. J. 1966, 143, 626–681. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology; John Wiley and Sons: New York, NY, USA, 1972. [Google Scholar]
- Oh, J.; Yoo, Y.; Seung, S.; Kwak, H. Laser-induced bubble formation on a micro gold particle levitated in water under ultrasonic field. Exp. Therm. Fluid Sci. 2018, 93, 285–291. [Google Scholar] [CrossRef]
- Blander, M.; Katz, J.L. Bubble nucleation in liquids. AIChE. J. 1975, 21, 833–848. [Google Scholar] [CrossRef]
- Shepherd, J.E.; Sturtevant, B. Rapid evaporation at the superheat limit. J. Fluid Mech. 1982, 121, 379–402. [Google Scholar] [CrossRef]
- Kwak, H.; Lee, S. Homogeneous bubble nucleation predicted by a molecular interaction model. J. Heat Trans. 1991, 113, 714–721. [Google Scholar] [CrossRef]
- Kwak, H.; Panton, R.L. Tensile strength of simple liquids predicted by a model of molecular interactions. J. Phys. D Appl. Phys. 1985, 18, 647–659. [Google Scholar] [CrossRef]
- Kwak, H.; Oh, S.; Park, C. Bubble dynamics on the evolving bubble formed from the droplet at the superheat limit. Int. J. Heat Mass Trans. 1995, 38, 1709–1718. [Google Scholar] [CrossRef]
- Theofanous, T.; Bias, L.; Isbin, H.S. A theoretical study on bubble growth in constant and time-dependent pressure fields. Chem. Eng. Sci. 1969, 24, 885–897. [Google Scholar] [CrossRef]
- Moody, F.J. Non-intuitive bubble effects in reactor and containment technology. In Fluids Engineering, Korea-U.S. Progress; Hemisphere: Washington, DC, USA, 1991; pp. 409–426. [Google Scholar]
- Vincenti, W.G.; Kruger, C.H. Infroduction to Physical Gas Dynamics; Robert E. Krieger Publishing Co: New York, NY, USA, 1965; pp. 407–412. [Google Scholar]
- Rayleigh, L. On the pressure developed in a liquid during the collapse of a spherical cavity. Phil. Mag. 1917, 34, 94–98. [Google Scholar] [CrossRef]
- Gaitan, D.F. An Experimental Investigation of Acoustic Cavitation in Gaseous Liquids. Ph.D. Thesis, The University of Mississippi, Oxford, MS, USA, 1990. [Google Scholar]
- Kwak, H.; Yang, H. An aspect of sonoluminescence from hydrodynamic theory. J. Phys. Soc. Jpn. 1995, 64, 1980–1992. [Google Scholar] [CrossRef]
- Lin, H.; Storey, B.D.; Szeri, A.J. Inertially driven inhomogeneities in violently collapsing bubbles: The validity of the Rayleigh-Plesset equation. J. Fluid Mech. 2002, 452, 145–162. [Google Scholar] [CrossRef]
- Kwak, H.; Na, J.H. Hydrodynamic solutions for a sonoluminescing gas bubble. Phys. Rev. Lett. 1996, 77, 4454–4457. [Google Scholar] [CrossRef] [PubMed]
- Kestin, J.; Knierim, K.; Masson, E.A.; Najafi, B.; Ro, S.T.; Waldman, M. Equilibrium and transport properties of the noble gases and their mixtures at low density. J. Phys. Chem. Ref. Data 1984, 13, 229–303. [Google Scholar] [CrossRef]
- Byun, K.-T.; Kim, K.Y.; Kwak, H. Sonoluminescence characteristics from micron and submicron bubbles. J. Korean Phys. Soc. 2005, 47, 1010–1022. [Google Scholar]
- Kim, K.Y.; Byun, K.-T.; Kwak, H. Characteristics of sonoluminescing bubbles in aqueous solutions of sulfuric acid. J. Phys. Soc. Jpn. 2006, 75, 114705. [Google Scholar]
- Delgadino, G.A.; Bonetto, F.J. Velocity interferometry technique used to measure the expansion and compression phases of a sonoluminecent bubble. Phys. Rev. E 1997, 56, R6248–R6251. [Google Scholar] [CrossRef]
- Keller, J.B.; Miksis, M. Bubble oscillations of large amplitude. J. Acoust. Soc. Am. 1980, 68, 628–633. [Google Scholar] [CrossRef]
- Kwak, H.; Na, J.H. Physical processes for single bubble sonoluminescence. J. Phys. Soc. Jpn. 1997, 66, 3074–3083. [Google Scholar] [CrossRef]
- Flannigan, D.J.; Hopkins, S.D.; Camara, C.G.; Putterman, S.J.; Suslick, K.S. Measurement of pressure and density inside a single sonoluminescing bubble. Phys. Rev. Lett. 2006, 96, 204301. [Google Scholar] [CrossRef] [PubMed]
- Jeon, J.; Lim, C.; Kwak, H. Measurement of pulse width of sonoluminescing gas bubble in sulfuric acid solution. J. Phys. Soc. Jpn. 2008, 77, 033703. [Google Scholar] [CrossRef]
- Gompf, B.; Gunther, R.; Nick, G.; Pecha, R.; Eisenmenger, W. Resolving sonoluminescence pulse width with time-correlated single photon counting. Phys. Rev. Lett. 1997, 79, 1405–1408. [Google Scholar] [CrossRef]
- Putterman, S.; Evans, P.G.; Vasquez, G.; Weninger, K. Cavitation science: Is there a simple theory of sonoluminescence? Nature 2001, 409, 782–783. [Google Scholar] [CrossRef] [PubMed]
- Hilgenfeldt, S.; Grossmann, S.; Lohse, D. Hilgenfeldt et al.’s reply. Nature 2001, 409, 783. [Google Scholar] [CrossRef]
- Kim, K.Y.; Kwak, H. Predictions of bubble behavior in sulfuric acid solutions by a set of solutions of Navier-Stokes equations. Chem. Eng. Sci. 2007, 62, 2880–2889. [Google Scholar]
- Jeans, J. The stability of a spherical nebula. J. Phil. Trans. Roy. Soc. 1902, 199, 1–53. [Google Scholar] [CrossRef]
- Rampp, M.; Janka, H.-T. Radiation hydrodynamics with neutrinos: Variable Eddington factor method for core-collapse supernova simulations. Astron. Asrophys. 2002, 396, 361–392. [Google Scholar] [CrossRef]
- Livne, E.; Burrows, A.; Walder, R.; Lichtenstadt, I.; Thompson, T.A. Two-dimensional, time-dependent, multigroup, multiangle radiation hydrodynamics test simulation in the core-collapse supernova context. Astrophys. J. 2004, 609, 277–287. [Google Scholar] [CrossRef]
- Buras, R.; Rampp, M.; Janka, H.-Th.; Kifonidis, K. Two-dimensional hydrodynamics core-collapse supernova simulations with spectral neutrino transport. I. Numerical method and results for a 15 M⊙ star. Astron. Asrophys. 2006, 447, 1049–1092. [Google Scholar] [CrossRef]
- Murphy, J.W.; Burrows, A. Criteria for core-collapse supernova explosions by the neutrino mechanism. Astrophys. J. 2008, 688, 1159–1175. [Google Scholar] [CrossRef]
- Kwak, H.; Jun, J.-H. Hydrodynamics and thermodynamics for Newtonian stars. Geophys. Astrophys. Fluid Dyn. 2003, 97, 45–58. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Snyder, H. On continued gravitational contraction. Phys. Rev. 1939, 56, 455–459. [Google Scholar] [CrossRef]
- Kwak, H. Core-collapse supernova explosions: An analytical one-dimensional analysis. Far East J. Appl. Math. 2015, 93, 247–248. [Google Scholar] [CrossRef]
- Burrows, A. Supernova explosions in the Universe. Nature 2000, 403, 727–733. [Google Scholar] [CrossRef] [PubMed]
- Burrows, A.; Hays, J.; Fryxell, B.A. On the nature of core-collapse supernova explosions. Astrophys. J. 1995, 450, 830–850. [Google Scholar] [CrossRef]
- Liebendoerfer, M.; Rampp, M.; Janka, H.-T.; Mezzacappa, A. Supernova simulations with Boltzmann neutrino transport: A comparison of methods. Astrophys. J. 2005, 620, 840–860. [Google Scholar] [CrossRef]
- Nordhaus, J.; Burrows, A.; Almgren, A.; Bell, J. Dimension as a key to the neutrino mechanism of core-collapse supernova explosions. Astrophys. J. 2010, 720, 694–703. [Google Scholar] [CrossRef]


© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwak, H.-Y. Entropy Generation Due to the Heat Transfer for Evolving Spherical Objects. Entropy 2018, 20, 562. https://doi.org/10.3390/e20080562
Kwak H-Y. Entropy Generation Due to the Heat Transfer for Evolving Spherical Objects. Entropy. 2018; 20(8):562. https://doi.org/10.3390/e20080562
Chicago/Turabian StyleKwak, Ho-Young. 2018. "Entropy Generation Due to the Heat Transfer for Evolving Spherical Objects" Entropy 20, no. 8: 562. https://doi.org/10.3390/e20080562
APA StyleKwak, H.-Y. (2018). Entropy Generation Due to the Heat Transfer for Evolving Spherical Objects. Entropy, 20(8), 562. https://doi.org/10.3390/e20080562



