A Measure of Information Available for Inference
Abstract
1. Introduction
2. Methods
2.1. Definition of a System
2.2. Information Stored in the Neural Network
2.3. Free-Energy Principle
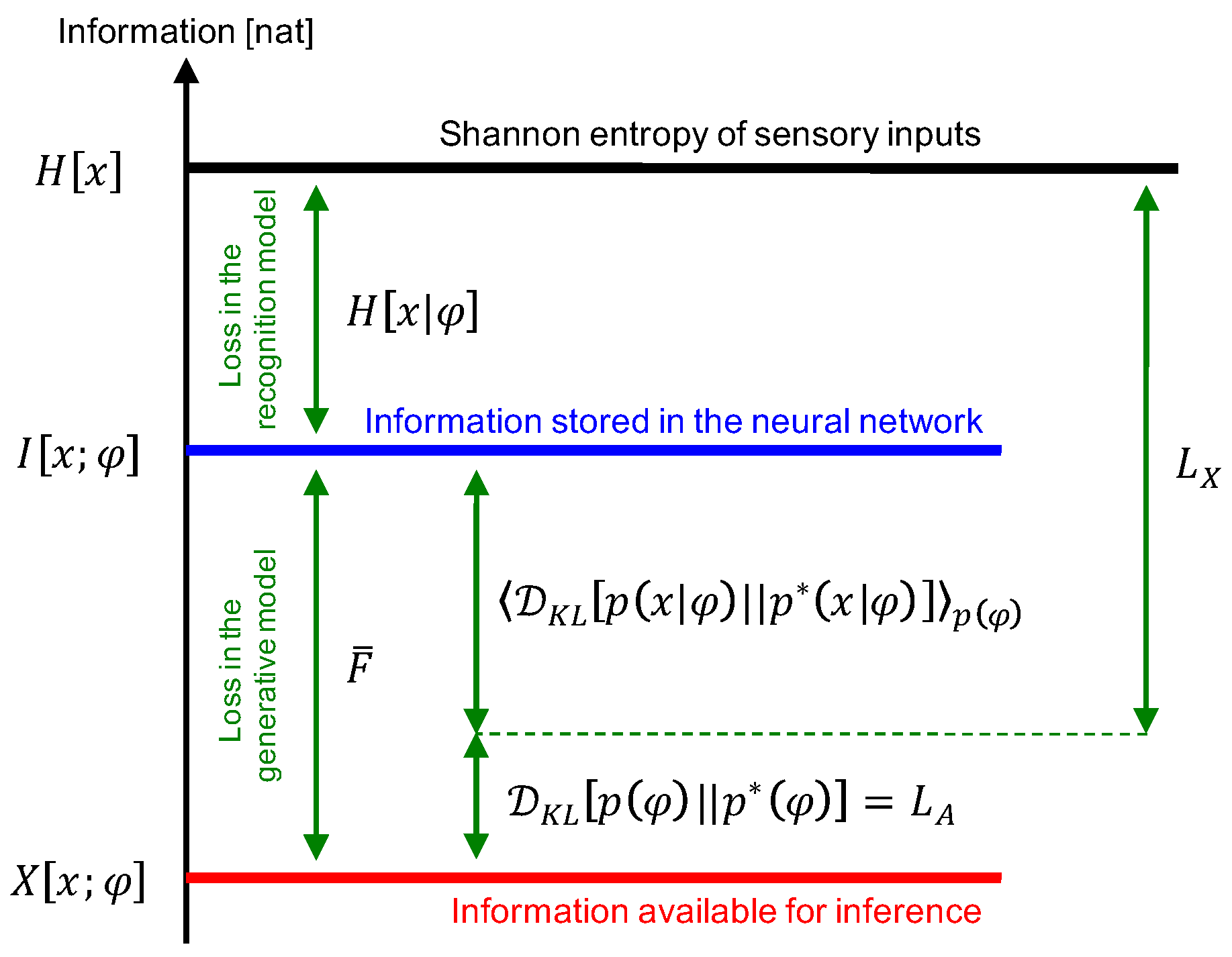
2.4. Information Available for Inference
3. Comparison between the Free-Energy Principle and Related Theories
3.1. Infomax Principle
3.2. Principal Component Analysis
3.3. Independent Component Analysis
4. Simulation and Results
5. Discussion
Acknowledgments
Conflicts of Interest
References
- DiCarlo, J.J.; Zoccolan, D.; Rust, N.C. How does the brain solve visual object recognition? Neuron 2012, 73, 415–434. [Google Scholar] [CrossRef] [PubMed]
- Bronkhorst, A.W. The cocktail party phenomenon: A review of research on speech intelligibility in multiple-talker conditions. Acta Acust. United Acust. 2000, 86, 117–128. [Google Scholar]
- Brown, G.D.; Yamada, S.; Sejnowski, T.J. Independent component analysis at the neural cocktail party. Trends Neurosci. 2001, 24, 54–63. [Google Scholar] [CrossRef]
- Haykin, S.; Chen, Z. The cocktail party problem. Neural Comput. 2005, 17, 1875–1902. [Google Scholar] [CrossRef] [PubMed]
- Narayan, R.; Best, V.; Ozmeral, E.; McClaine, E.; Dent, M.; Shinn-Cunningham, B.; Sen, K. Cortical interference effects in the cocktail party problem. Nat. Neurosci. 2007, 10, 1601–1607. [Google Scholar] [CrossRef] [PubMed]
- Mesgarani, N.; Chang, E.F. Selective cortical representation of attended speaker in multi-talker speech perception. Nature 2012, 485, 233–236. [Google Scholar] [CrossRef] [PubMed]
- Golumbic, E.M.Z.; Ding, N.; Bickel, S.; Lakatos, P.; Schevon, C.A.; McKhann, G.M.; Schroeder, C.E. Mechanisms underlying selective neuronal tracking of attended speech at a “cocktail party”. Neuron 2013, 77, 980–991. [Google Scholar]
- Dayan, P.; Abbott, L.F. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems; MIT Press: London, UK, 2001. [Google Scholar]
- Gerstner, W.; Kistler, W. Spiking Neuron Models: Single Neurons, Populations, Plasticity; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Von Helmholtz, H. Concerning the perceptions in general. In Treatise on Physiological Optics, 3rd ed.; Dover Publications: New York, NY, USA, 1962. [Google Scholar]
- Dayan, P.; Hinton, G.E.; Neal, R.M.; Zemel, R.S. The helmholtz machine. Neural Comput. 1995, 7, 889–904. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.; Kilner, J.; Harrison, L. A free energy principle for the brain. J. Physiol. Paris 2006, 100, 70–87. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J. Hierarchical model in the brain. PLoS Comput. Biol. 2008, 4, e1000211. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. The free-energy principle: A unified brain theory? Nat. Rev. Neurosci. 2010, 11, 127–138. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. A free energy principle for biological systems. Entropy 2012, 14, 2100–2121. [Google Scholar]
- Friston, K.; FitzGerald, T.; Rigoli, F.; Schwartenbeck, P.; Pezzulo, G. Active inference: A process theory. Neural Comput. 2017, 29, 1–49. [Google Scholar] [CrossRef] [PubMed]
- George, D.; Hawkins, J. Towards a mathematical theory of cortical micro-circuits. PLoS Comput. Biol. 2009, 5, e1000532. [Google Scholar] [CrossRef] [PubMed]
- Bastos, A.M.; Usrey, W.M.; Adams, R.A.; Mangun, G.R.; Fries, P.; Friston, K.J. Canonical microcircuits for predictive coding. Neuron 2012, 76, 695–711. [Google Scholar] [CrossRef] [PubMed]
- Rao, R.P.; Ballard, D.H. Predictive coding in the visual cortex: A functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 1999, 2, 79–87. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. A theory of cortical responses. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2005, 360, 815–836. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J.; Daunizeau, J.; Kiebel, S.J. Reinforcement learning or active inference? PLoS ONE 2009, 4, e6421. [Google Scholar] [CrossRef] [PubMed]
- Kilner, J.M.; Friston, K.J.; Frith, C.D. Predictive coding: An account of the mirror neuron system. Cognit. Process. 2007, 8, 159–166. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.; Mattout, J.; Kilner, J. Action understanding and active inference. Biol. Cybern. 2011, 104, 137–160. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J.; Frith, C.D. Active inference, communication and hermeneutics. Cortex 2015, 68, 129–143. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.; Frith, C. A duet for one. Conscious. Cognit. 2015, 36, 390–405. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, P.C.; Frith, C.D. Perceiving is believing: A Bayesian approach to explaining the positive symptoms of schizophrenia. Nat. Rev. Neurosci. 2009, 10, 48–58. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J.; Stephan, K.E.; Montague, R.; Dolan, R.J. Computational psychiatry: The brain as a phantastic organ. Lancet Psychiatry 2014, 1, 148–158. [Google Scholar] [CrossRef]
- Linsker, R. Self-organization in a perceptual network. Computer 1988, 21, 105–117. [Google Scholar] [CrossRef]
- Linsker, R. Local synaptic learning rules suffice to maximize mutual information in a linear network. Neural Comput. 1992, 4, 691–702. [Google Scholar] [CrossRef]
- Lee, T.W.; Girolami, M.; Bell, A.J.; Sejnowski, T.J. A unifying information-theoretic framework for independent component analysis. Comput. Math. Appl. 2000, 39, 1–21. [Google Scholar] [CrossRef]
- Simoncelli, E.P.; Olshausen, B.A. Natural image statistics and neural representation. Ann. Rev. Neurosci. 2001, 24, 1193–1216. [Google Scholar] [CrossRef] [PubMed]
- Belouchrani, A.; Abed-Meraim, K.; Cardoso, J.F.; Moulines, E. A blind source separation technique using second-order statistics. Signal Process. IEEE Trans. 1997, 45, 434–444. [Google Scholar] [CrossRef]
- Choi, S.; Cichocki, A.; Park, H.M.; Lee, S.Y. Blind source separation and independent component analysis: A review. Neural Inf. Process. Lett. Rev. 2005, 6, 1–57. [Google Scholar]
- Cichocki, A.; Zdunek, R.; Phan, A.H.; Amari, S.I. Nonnegative Matrix and Tensor Factorizations: Applications to Exploratory Multi-Way Data Analysis and Blind Source Separation; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Comon, P.; Jutten, C. Handbook of Blind Source Separation: Independent Component Analysis and Applications; Academic Press: Oxford, UK, 2010. [Google Scholar]
- Palmer, J.; Rao, B.D.; Wipf, D.P. Perspectives on sparse Bayesian learning. Adv. Neural Inf. Proc. Syst. 2004, 27, 249–256. [Google Scholar]
- Olshausen, B.A.; Field, D.J. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature 1996, 381, 607–609. [Google Scholar] [CrossRef] [PubMed]
- Olshausen, B.A.; Field, D.J. Sparse coding with an overcomplete basis set: A strategy employed by V1? Vis. Res. 1997, 37, 3311–3325. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: New York, NY, USA, 1991. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: San Fransisco, CA, USA, 1988. [Google Scholar]
- Friston, K.J. Life as we know it. J. R. Soc. Interface 2013, 10, 20130475. [Google Scholar] [CrossRef] [PubMed]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Arora, S.; Risteski, A. Provable benefits of representation learning. arXiv, 2017; arXiv:1706.04601. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Isomura, T.; Kotani, K.; Jimbo, Y. Cultured Cortical Neurons Can Perform Blind Source Separation According to the Free-Energy Principle. PLoS Comput. Biol. 2015, 11, e1004643. [Google Scholar] [CrossRef] [PubMed]
- Xu, L. Least mean square error reconstruction principle for self-organizing neural-nets. Neural Netw. 1993, 6, 627–648. [Google Scholar] [CrossRef]
- Amari, S.I.; Cichocki, A.; Yang, H.H. A new learning algorithm for blind signal separation. Adv. Neural Inf. Proc. Syst. 1996, 8, 757–763. [Google Scholar]
- Oja, E. Neural networks, principal components, and subspaces. Int. J. Neural Syst. 1989, 1, 61–68. [Google Scholar] [CrossRef]
- Bell, A.J.; Sejnowski, T.J. An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 1995, 7, 1129–1159. [Google Scholar] [CrossRef] [PubMed]
- Bell, A.J.; Sejnowski, T.J. The “independent components” of natural scenes are edge filters. Vis. Res. 1997, 37, 3327–3338. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Isomura, T.; Toyoizumi, T. Error-gated Hebbian rule: A local learning rule for principal and independent component analysis. Sci. Rep. 2018, 8, 1835. [Google Scholar] [CrossRef] [PubMed]
- Hyvärinen, A.; Pajunen, P. Nonlinear independent component analysis: Existence and uniqueness results. Neural Netw. 1999, 12, 429–439. [Google Scholar] [CrossRef]
- Yang, H.H.; Amari, S.I. Adaptive online learning algorithms for blind separation: Maximum entropy and minimum mutual information. Neural Comput. 1997, 9, 1457–1482. [Google Scholar] [CrossRef]
- Latham, P.E.; Nirenberg, S. Synergy, redundancy, and independence in population codes, revisited. J. Neurosci. 2005, 25, 5195–5206. [Google Scholar] [CrossRef] [PubMed]
- Amari, S.I.; Nakahara, H. Correlation and independence in the neural code. Neural Comput. 2006, 18, 1259–1267. [Google Scholar] [CrossRef] [PubMed]
- Berkes, P.; Orbán, G.; Lengyel, M.; Fiser, J. Spontaneous cortical activity reveals hallmarks of an optimal internal model of the environment. Science 2011, 331, 83–87. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, B.; Stemmler, M.B.; Friston, K.J. Information and efficiency in the nervous system—A synthesis. PLoS Comput. Biol. 2013, 9, e1003157. [Google Scholar] [CrossRef] [PubMed]
- Frémaux, N.; Gerstner, W. Neuromodulated Spike-Timing-Dependent Plasticity, and Theory of Three-Factor Learning Rules. Front. Neural Circuits 2016, 9. [Google Scholar] [CrossRef] [PubMed]
- Isomura, T.; Toyoizumi, T. A Local Learning Rule for Independent Component Analysis. Sci. Rep. 2016, 6, 28073. [Google Scholar] [CrossRef] [PubMed]
- Kuśmierz, A.; Isomura, T.; Toyoizumi, T. Learning with three factors: Modulating Hebbian plasticity with errors. Curr. Opin. Neurobiol. 2017, 46, 170–177. [Google Scholar]
- Isomura, T.; Sakai, K.; Kotani, K.; Jimbo, Y. Linking neuromodulated spike-timing dependent plasticity with the free-energy principle. Neural Comput. 2016, 28, 1859–1888. [Google Scholar] [CrossRef] [PubMed]
- Markram, H.; Lübke, J.; Frotscher, M.; Sakmann, B. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 1997, 275, 213–215. [Google Scholar] [CrossRef] [PubMed]
- Bi, G.Q.; Poo, M.M. Synaptic modifications in cultured hippocampal neurons: Dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 1998, 18, 10464–10472. [Google Scholar] [CrossRef] [PubMed]
- Karnani, M.; Pääkkönen, K.; Annila, A. The physical character of information. Proc. R. Soc. A Math. Phys. Eng. Sci. 2009, 465, 2155–2175. [Google Scholar] [CrossRef]
- Annila, A. On the character of consciousness. Front. Syst. Neurosci. 2016, 10, 27. [Google Scholar] [CrossRef] [PubMed]
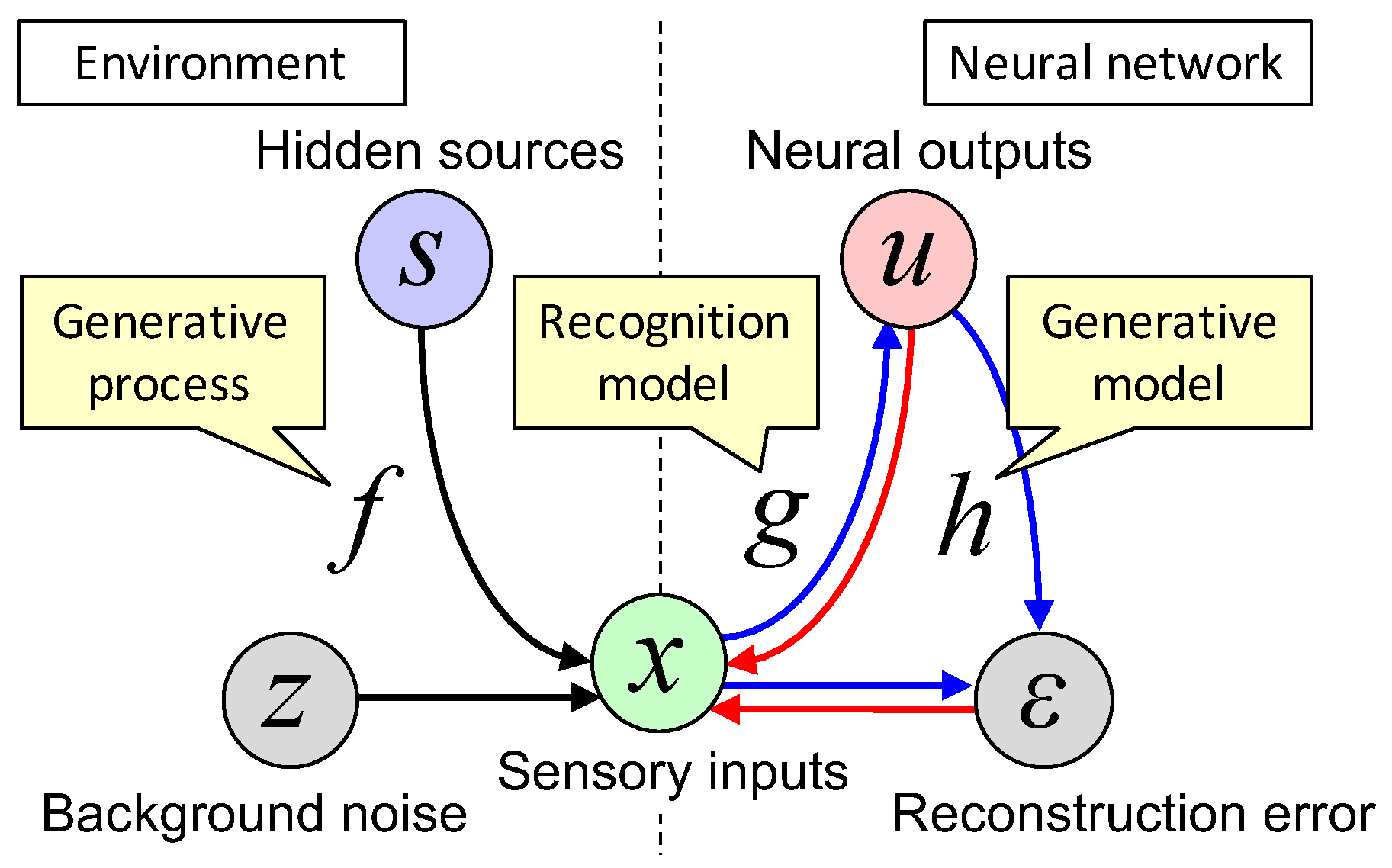

| Expression | Description |
|---|---|
| Generative process | A set of stochastic equations that generate the external world dynamics |
| Recognition model | A model in the neural network that imitates the inverse of the generative process |
| Generative model | A model in the neural network that imitates the generative process |
| Hidden sources | |
| Sensory inputs | |
| A set of parameters | |
| A set of hyper-parameters | |
| A set of hidden states of the external world | |
| Neural outputs | |
| Synaptic strength matrices | |
| State of neuromodulators | |
| A set of the internal states of the neural network | |
| Background noises | |
| Reconstruction errors | |
| The actual probability density of x | |
| Actual probability densities (posterior densities) | |
| Prior densities | |
| Likelihood function | |
| Statistical models | |
| Finite spatial resolution of x, | |
| Expectation of · over | |
| Shannon entropy of | |
| Cross entropy of over | |
| KLD between and | |
| Mutual information between x and | |
| Surprise | |
| Surprise expectation | |
| Free energy | |
| Free energy expectation | |
| Utilizable information between x and |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isomura, T. A Measure of Information Available for Inference. Entropy 2018, 20, 512. https://doi.org/10.3390/e20070512
Isomura T. A Measure of Information Available for Inference. Entropy. 2018; 20(7):512. https://doi.org/10.3390/e20070512
Chicago/Turabian StyleIsomura, Takuya. 2018. "A Measure of Information Available for Inference" Entropy 20, no. 7: 512. https://doi.org/10.3390/e20070512
APA StyleIsomura, T. (2018). A Measure of Information Available for Inference. Entropy, 20(7), 512. https://doi.org/10.3390/e20070512





