On Bohmian Mechanics, Particle Creation, and Relativistic Space-Time: Happy 100th Birthday, David Bohm!
Abstract
1. Introduction
1.1. Significance of Bohmian Mechanics
1.2. Laws of Bohmian Mechanics
1.3. Properties of Bohmian Mechanics
“This idea seems to me so natural and simple, to resolve the wave-particle dilemma in such a clear and ordinary way, that it is a great mystery to me that it was so generally ignored.”
2. Extension of Bohmian Mechanics to Particle Creation
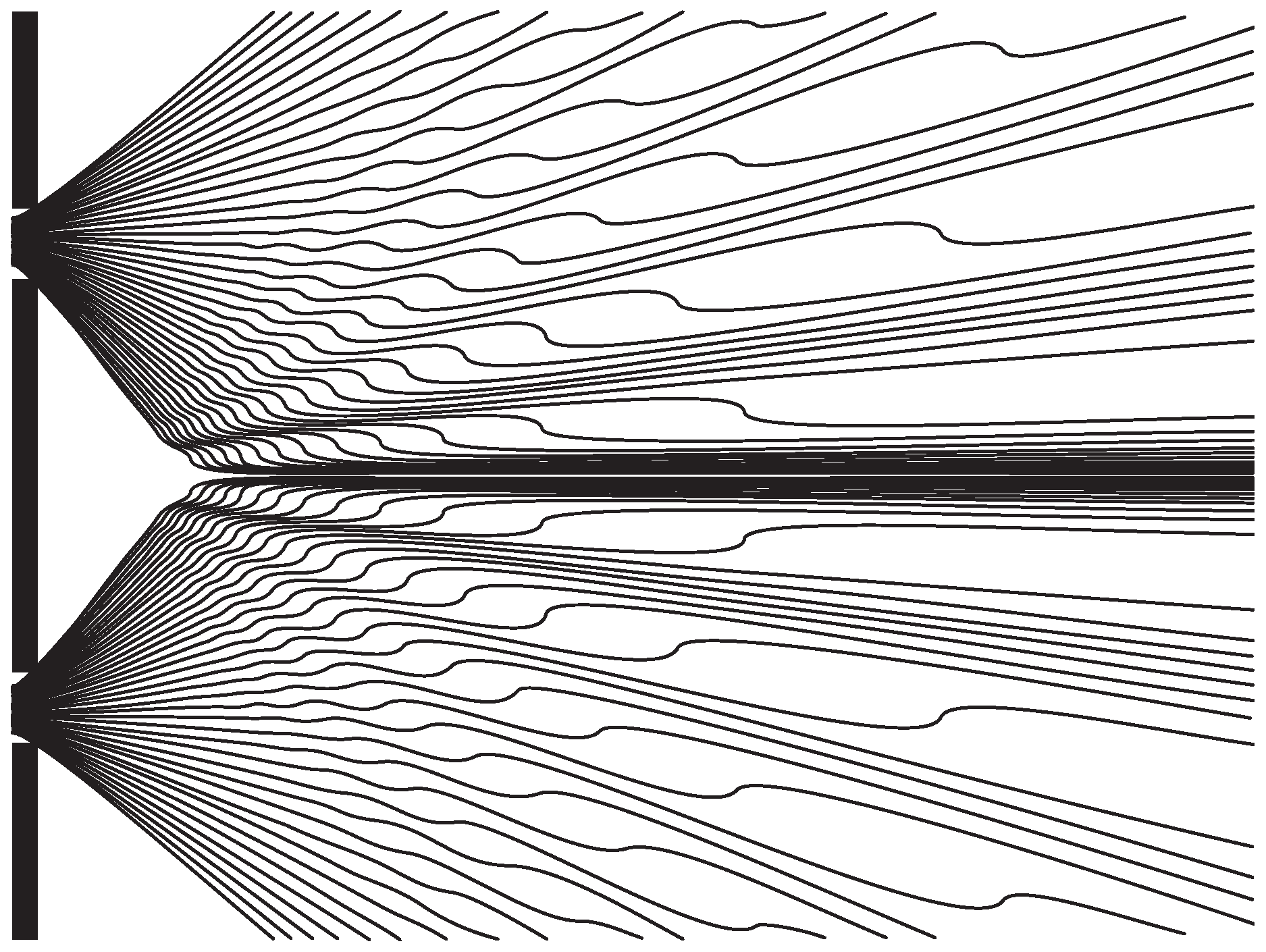
2.1. Bell’s Jump Process (In Its Continuum Version)
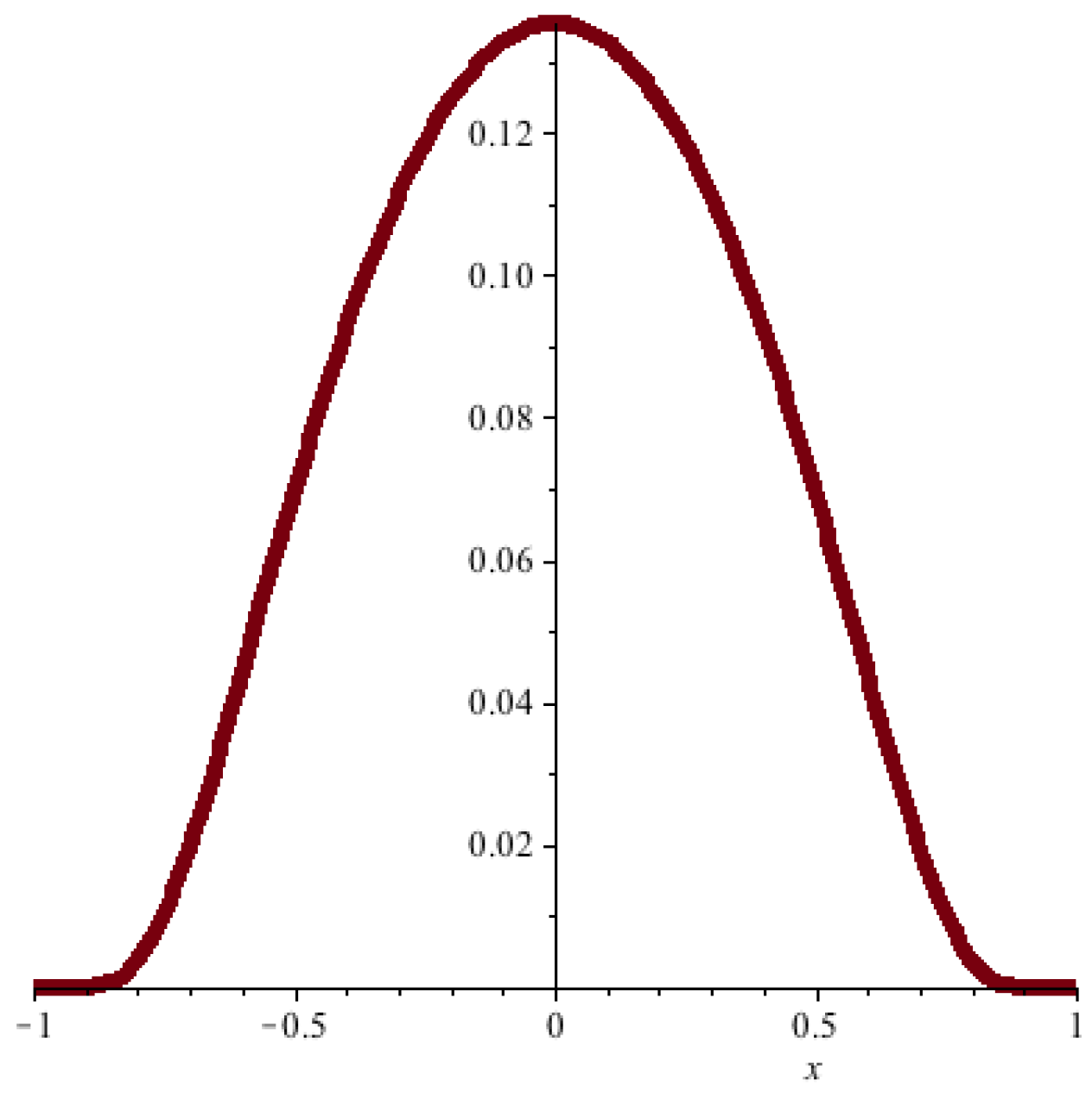
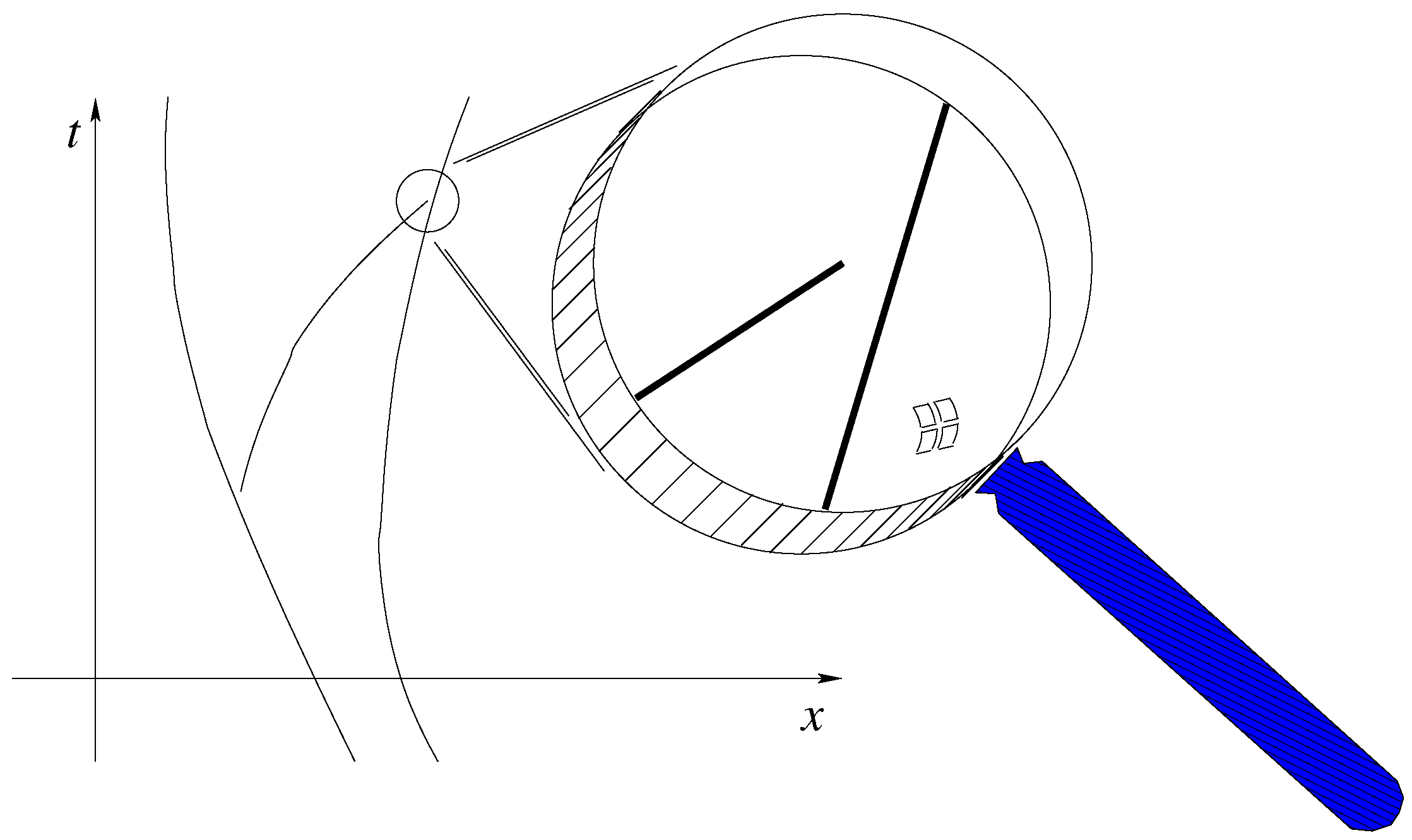
2.2. An Ultraviolet Divergence Problem
2.3. UV Problem Solved!
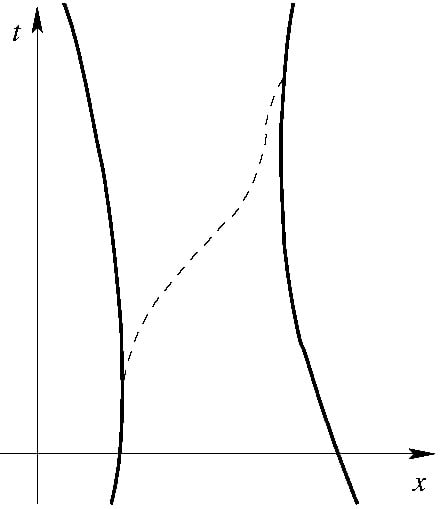
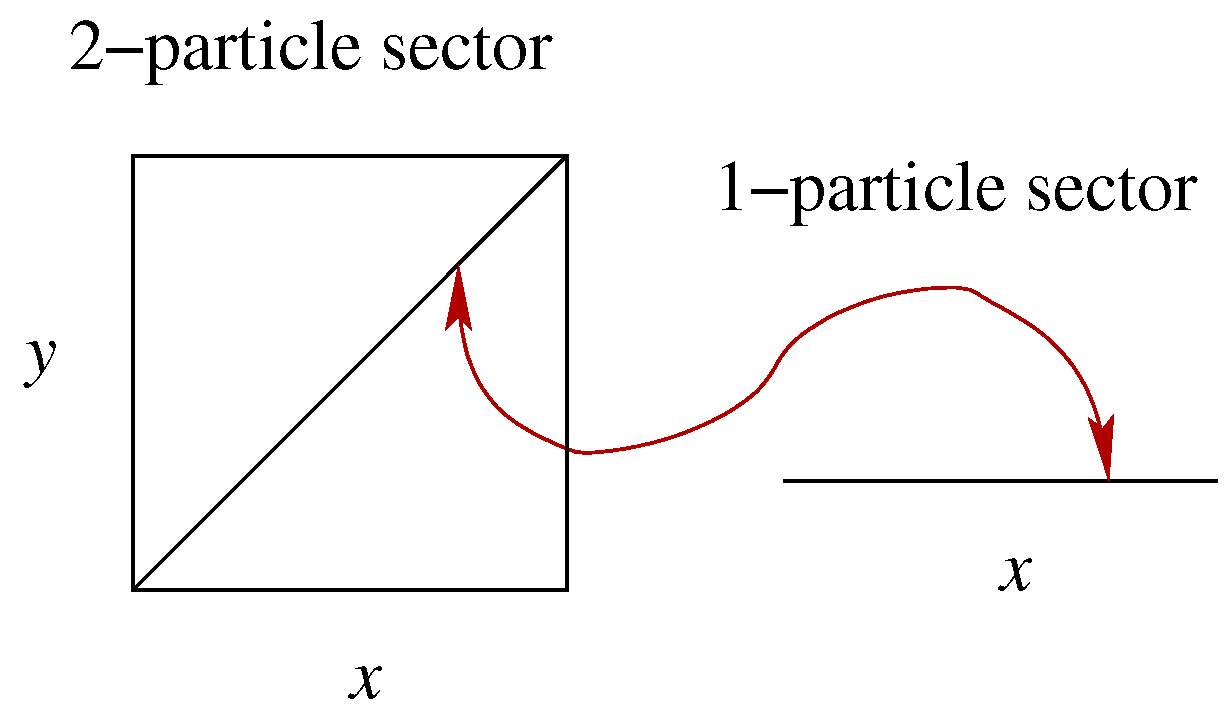
2.4. Particle Trajectories
3. Extension of Bohmian Mechanics to Relativistic Space-Time
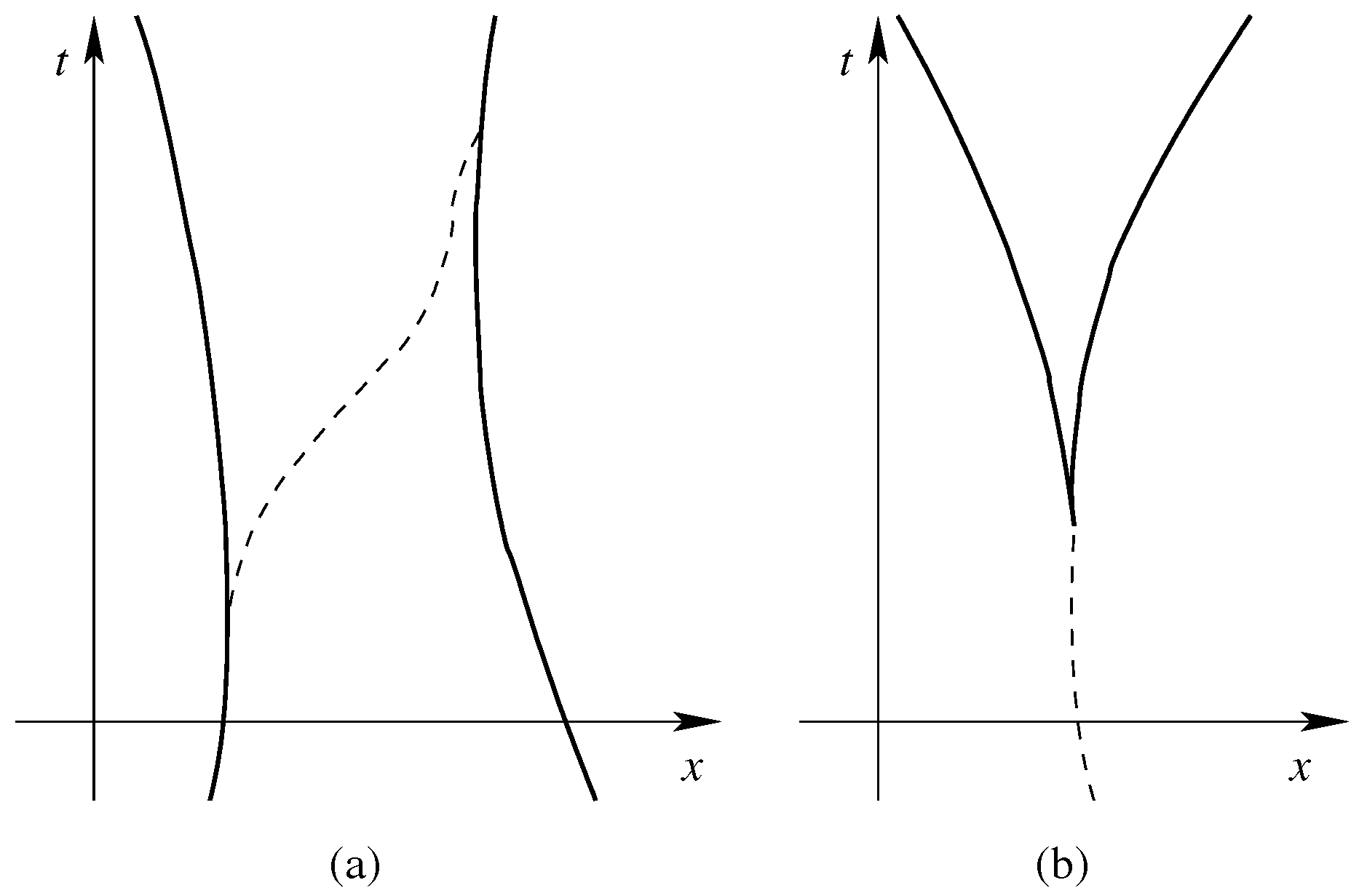
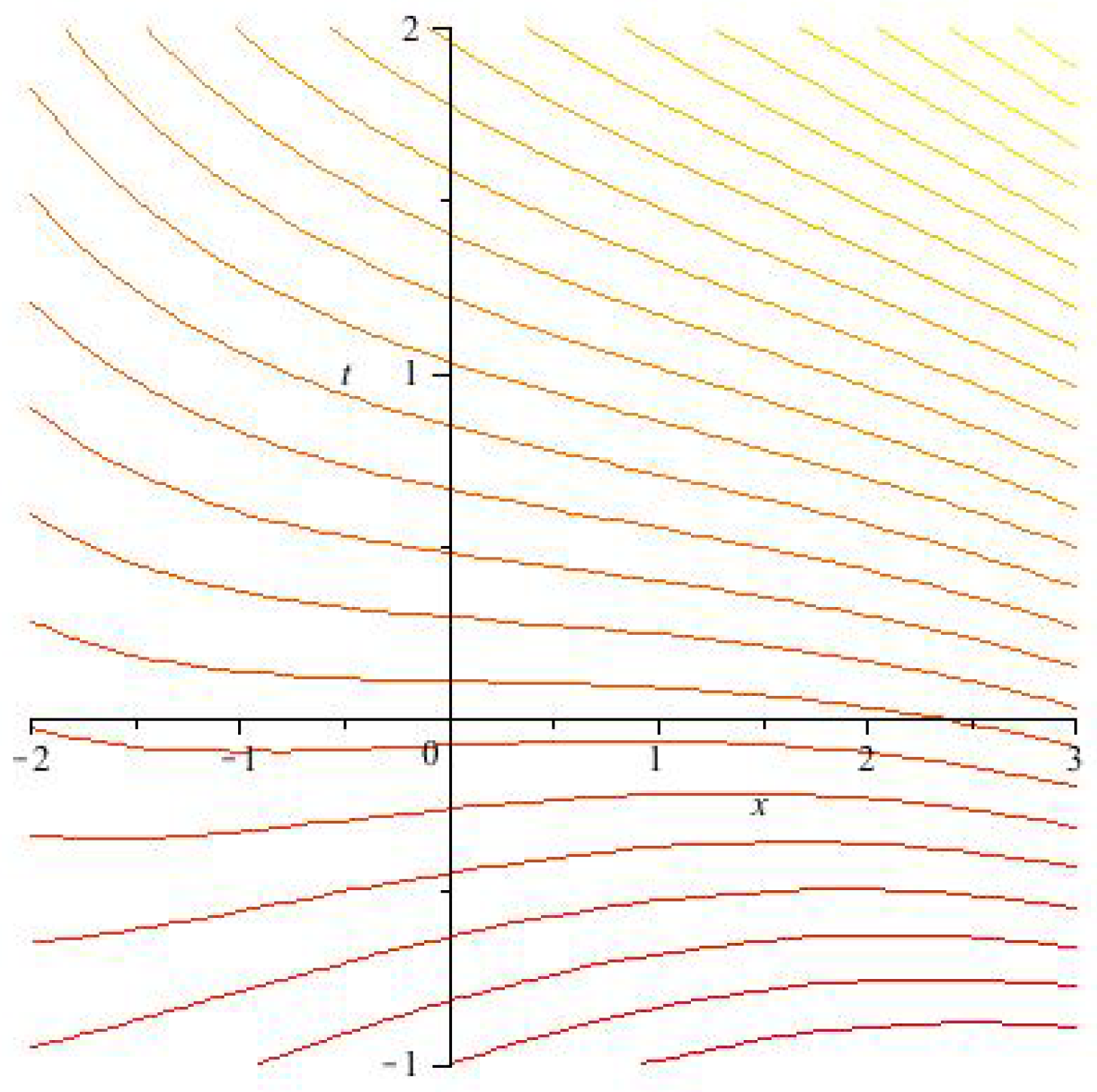
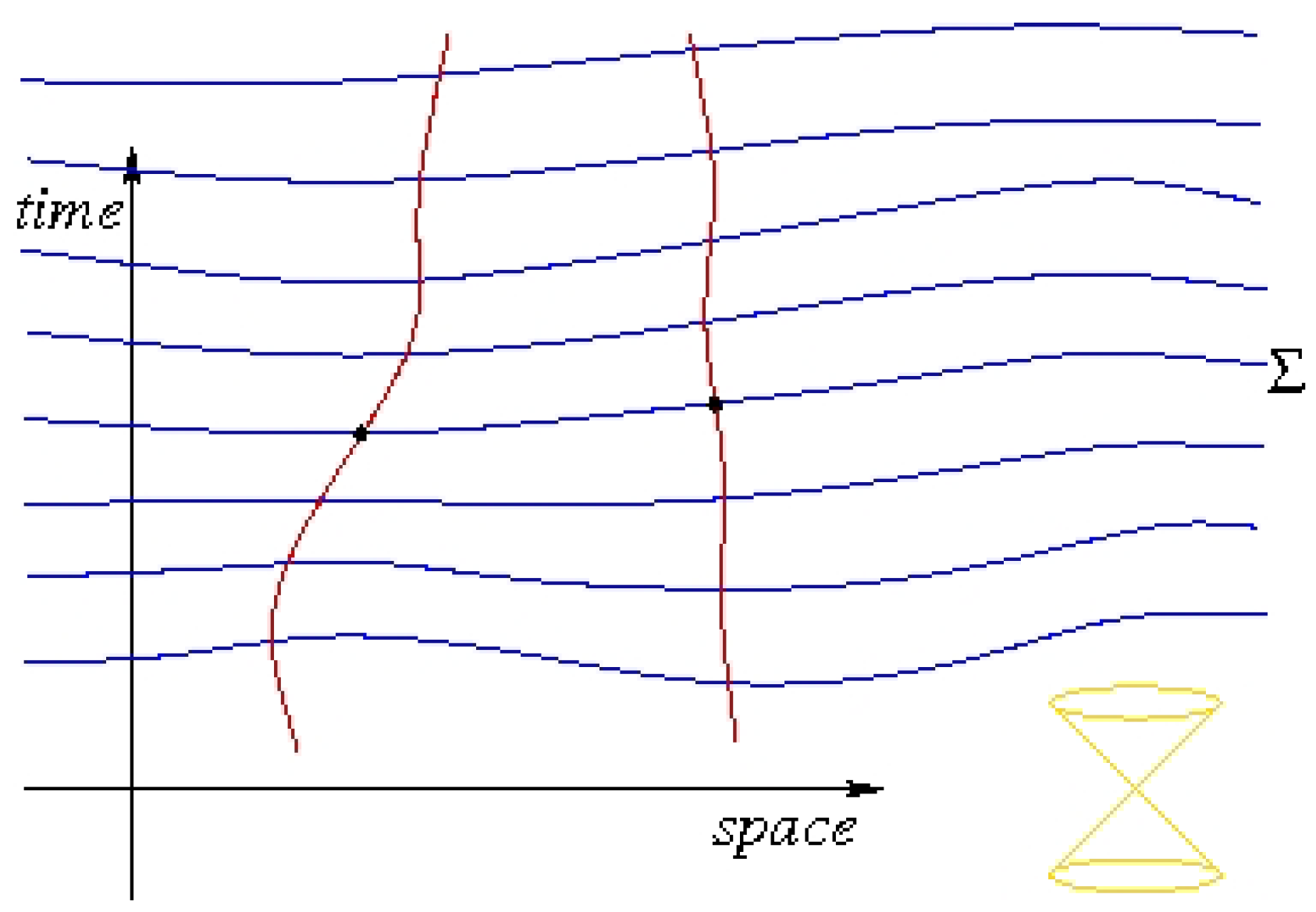
3.1. The Time Foliation
3.2. The Single-Particle Case
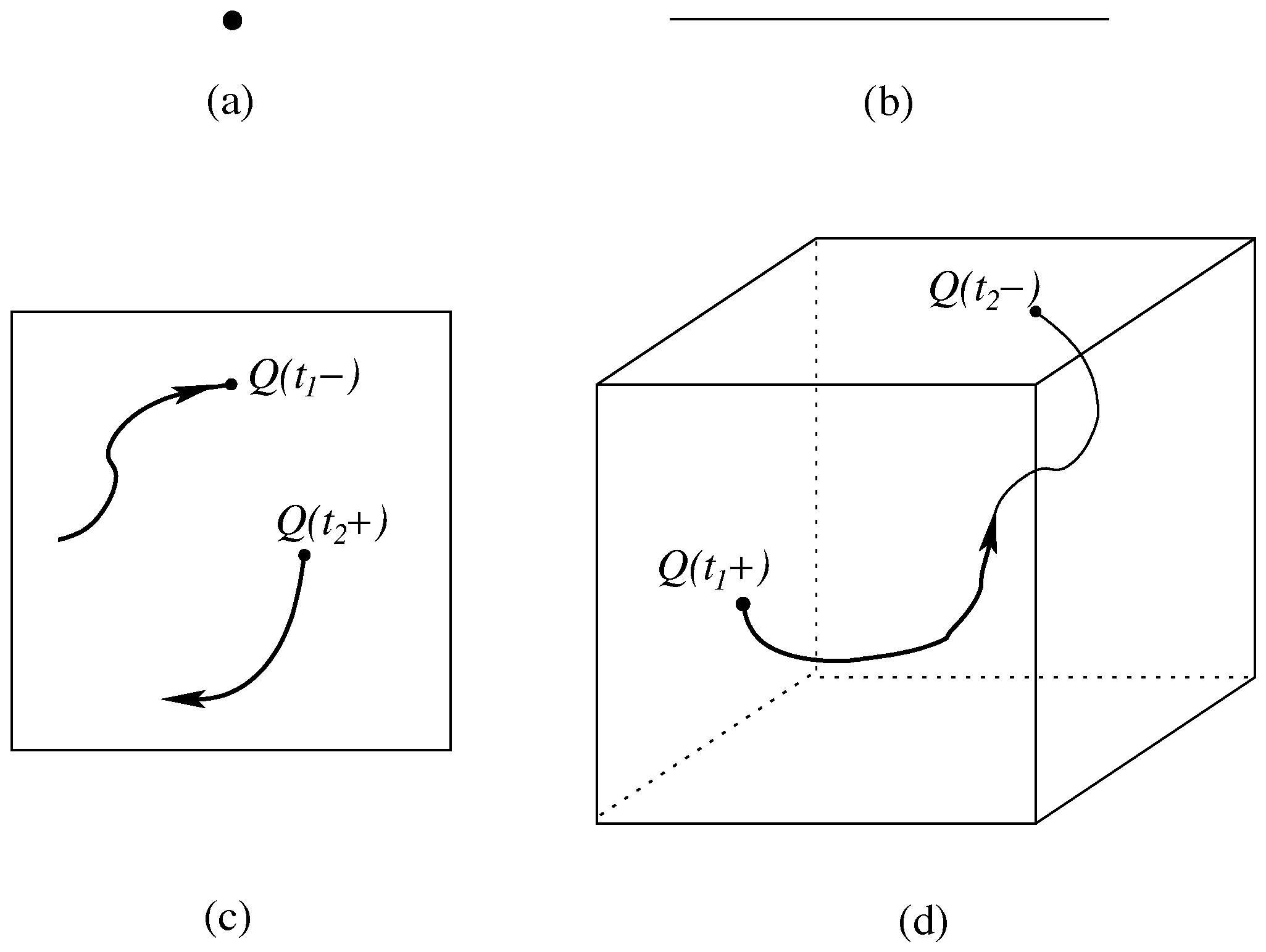
3.3. Law of Motion for Many Particles
3.4. Multi-Time Wave Functions
4. Outlook and Concluding Remarks
Funding
Conflicts of Interest
References
- Bohm, D. A suggested interpretation of the quantum teory in terms of “hidden” variables, I and II. Phys. Rev. 1952, 85, 166–193. [Google Scholar] [CrossRef]
- Einstein, A. Reply to criticisms. In Albert Einstein, Philosopher-Scientist; Schilpp, P.A., Ed.; Open Court: La Salle, IL, USA, 1949; p. 664. [Google Scholar]
- Bell, J.S. Against “measurement”. In Sixty-Two Years of Uncertainty; Miller, A.I., Ed.; Plenum Press: New York, NY, USA, 1990; Reprinted as chapter 23 of Speakable and Unspeakable in Quantum Mechanics, 2nd ed.; Bell, J.S.; Cambridge University Press: Cambridge, UK, 2004. Also reprinted in Phys. World 1990, 3, 33–40. [Google Scholar]
- Bricmont, J. Making Sense of Quantum Mechanics; Springer: Heidelberg, Germany, 2016. [Google Scholar]
- Norsen, T. Foundations of Quantum Mechanics; Springer: Heidelberg, Germany, 2018. [Google Scholar]
- Dürr, D.; Teufel, S. Bohmian Mechanics; Springer: Heidelberg, Germany, 2009. [Google Scholar]
- Bohm, D.; Hiley, B.J. The Undivided Universe: An Ontological Interpretation of Quantum Theory; Routledge: London, UK, 1993. [Google Scholar]
- Tumulka, R. Bohmian mechanics. In The Routledge Companion to the Philosophy of Physics; Wilson, A., Ed.; Routledge: London, UK, 2018. [Google Scholar]
- Dürr, D.; Goldstein, S.; Zanghì, N. Quantum equilibrium and the origin of absolute uncertainty. J. Stat. Phys. 1992, 67, 843–907, Reprinted in Quantum Physics without Quantum Philosophy; Dürr, D.; Goldstein, S.; Zanghì, N.; Springer: Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Bell, J.S. Six possible worlds of quantum mechanics. In Proceedings of the Nobel Symposium 65: Possible Worlds in Arts and Sciences, Stockholm, Sweden, 11–15 August 1986. Reprinted as chapter 20 of Speakable and Unspeakable in Quantum Mechanics, 2nd ed.; Bell, J.S.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Philippidis, C.; Dewdney, C.; Hiley, B.J. Quantum interference and the quantum potential. Il Nuovo Cimento 1979, 52B, 15–28. [Google Scholar] [CrossRef]
- Bell, J.S. Speakable and Unspeakable in Quantum Mechanics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Dürr, D.; Goldstein, S.; Tumulka, R.; Zanghì, N. Bohmian mechanics and quantum field theory. Phys. Rev. Lett. 2004, 93, 090402, Reprinted in Quantum Physics without Quantum Philosophy; Dürr, D.; Goldstein, S.; Zanghì, N.; Springer: Heidelberg, Germany, 2013. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.; Peierls, R. Quantenelektrodynamik im Konfigurationsraum. Z. Phys. 1930, 62, 188–200, English translation: Quantum electrodynamics in configuration space. In Selected Scientific Papers of Sir Rudolf Peierls with Commentary; Dalitz, R.H., Peierls, R., Eds.; World Scientific: Singapore, 1997; pp. 71–82. [Google Scholar] [CrossRef]
- Schweber, S. An Introduction to Relativistic Quantum Field Theory; Harper: New York, NY, USA, 1961. [Google Scholar]
- Nelson, E. Interaction of nonrelativistic particles with a quantized scalar field. J. Math. Phys. 1964, 5, 1190–1197. [Google Scholar] [CrossRef]
- Bell, J.S. Beables for quantum field theory. Phys. Rep. 1986, 137, 49–54, Reprinted in Quantum Implications: Essays in Honour of David Bohm; Peat, F.D., Hiley, B.J., Eds.; Routledge: London, UK, 1987; p. 227. Also reprinted as chapter 19 of Speakable and Unspeakable in Quantum Mechanics, 2nd ed.; Bell, J.S.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Dürr, D.; Goldstein, S.; Tumulka, R.; Zanghì, N. Trajectories and particle creation and annihilation in quantum field theory. J. Phys. A Math. Gen. 2003, 36, 4143–4149. [Google Scholar] [CrossRef]
- Dürr, D.; Goldstein, S.; Tumulka, R.; Zanghì, N. Bell-type quantum field theories. J. Phys. A Math. Gen. 2005, 38, R1–R43. [Google Scholar] [CrossRef]
- Vink, J.C. Quantum mechanics in terms of discrete beables. Phys. Rev. A. 1993, 48, 1808–1818. [Google Scholar] [CrossRef] [PubMed]
- Vink, J.C. Particle trajectories for quantum field theory. Found. Phys. 2018, 48, 209–236. [Google Scholar] [CrossRef]
- Teufel, S.; Tumulka, R. New type of Hamiltonians without ultraviolet divergence for quantum field theories. arXiv, 2015; arXiv:1505.04847. [Google Scholar]
- Lampart, J.; Schmidt, J.; Teufel, S.; Tumulka, R. Particle creation at a point source by means of interior-boundary conditions. Math. Phys. Anal. Geom. 2018, 21, 12. [Google Scholar] [CrossRef]
- Lampart, J.; Schmidt, J. On the domain of Nelson-type Hamiltonians and abstract boundary conditions. arXiv, 2018; arXiv:1803.00872. [Google Scholar]
- Lampart, J. A nonrelativistic quantum field theory with point interactions in three dimensions. arXiv, 2018; arXiv:1804.08295. [Google Scholar]
- Dereziński, J. Van Hove Hamiltonians—Exactly solvable models of the infrared and ultraviolet problem. Ann. Henri Poincaré 2003, 4, 713–738. [Google Scholar] [CrossRef]
- Teufel, S.; Tumulka, R. Avoiding ultraviolet divergence by means of interior-boundary conditions. In Quantum Mathematical Physics—A Bridge between Mathematics and Physics; Finster, F., Kleiner, J., Röken, C., Tolksdorf, J., Eds.; Birkhäuser: Basel, Switzerland, 2016; pp. 293–311. [Google Scholar]
- Georgii, H.-O.; Tumulka, R. Some jump processes in quantum field theory. In Interacting Stochastic Systems; Deuschel, J.-D., Greven, A., Eds.; Springer: Berlin, Germany, 2004; pp. 55–73. [Google Scholar]
- Keppeler, S.; Sieber, M. Particle creation and annihilation at interior boundaries: One-dimensional models. J. Phys. A Math. Theor. 2016, 49, 125204. [Google Scholar] [CrossRef]
- Moshinsky, M. Boundary conditions for the description of nuclear reactions. Phys. Rev. 1951, 81, 347–352. [Google Scholar] [CrossRef]
- Moshinsky, M. Boundary conditions and time-dependent states. Phys. Rev. 1951, 84, 525–532. [Google Scholar] [CrossRef]
- Thomas, L.E. Multiparticle Schrödinger Hamiltonians with point interactions. Phys. Rev. D 1984, 30, 1233–1237. [Google Scholar] [CrossRef]
- Yafaev, D.R. On a zero-range interaction of a quantum particle with the vacuum. J. Phys. A Math. Gen. 1992, 25, 963–978. [Google Scholar] [CrossRef]
- Dürr, D.; Goldstein, S.; Teufel, S.; Tumulka, R.; Zanghì, N. Bohmian trajectories for Hamiltonians with interior–boundary conditions. In preparation. 2018. [Google Scholar]
- Bohm, D. Comments on an article of Takabayasi concerning the formulation of quantum mechanics with classical pictures. Prog. Theor. Phys. 1953, 9, 273–287. [Google Scholar] [CrossRef]
- Dürr, D.; Goldstein, S.; Münch-Berndl, K.; Zanghì, N. Hypersurface Bohm–Dirac models. Phys. Rev. A 1999, 60, 2729–2736, Reprinted in Quantum Physics without Quantum Philosophy; Dürr, D.; Goldstein, S.; Zanghì, N.; Springer: Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Tumulka, R. Closed 3-Forms and Random World Lines. Ph.D. Thesis, Mathematics Institute, Ludwig-Maximilians-Universität, München, Germany, 2001. Available online: http://edoc.ub.uni-muenchen.de/7/ (accessed on 11 June 2018).
- Sutherland, R. Causally symmetric Bohm model. Stud. Hist. Philos. Mod. Phys. 2008, 39, 782–805. [Google Scholar] [CrossRef]
- Sutherland, R. Lagrangian description for particle interpretations of quantum mechanics-entangled many-particle case. Found. Phys. 2017, 47, 174–207. [Google Scholar] [CrossRef]
- Dürr, D.; Goldstein, S.; Norsen, T.; Struyve, W.; Zanghì, N. Can Bohmian mechanics be made relativistic? Proc. R. Soc. A 2014, 470, 20130699. [Google Scholar] [CrossRef] [PubMed]
- Teufel, S.; Tumulka, R. Simple proof for global existence of Bohmian trajectories. Commun. Math. Phys. 2005, 258, 349–365. [Google Scholar] [CrossRef]
- Lienert, M.; Tumulka, R. Born’s rule for arbitrary Cauchy surfaces. arXiv, 2017; arXiv:1706.07074. [Google Scholar]
- Struyve, W.; Tumulka, R. Bohmian trajectories for a time foliation with kinks. J. Geom. Phys. 2014, 82, 75–83. [Google Scholar] [CrossRef]
- Struyve, W.; Tumulka, R. Bohmian mechanics for a degenerate time foliation. Quantum Stud. Math. Found. 2015, 2, 349–358. [Google Scholar] [CrossRef]
- Tumulka, R. Bohmian mechanics at space-time singularities. II. Spacelike singularities. Gen. Relat. Gravit. 2010, 42, 303–346. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Relativistic quantum mechanics. Proc. R. Soc. Lond. A 1932, 136, 453–464. [Google Scholar] [CrossRef]
- Dirac, P.A.M.; Fock, V.A.; Podolsky, B. On quantum electrodynamics. Phys. Z. Sowjetunion 1932, 2, 468–479, Reprinted in Selected Papers on Quantum Electrodynamics; Schwinger, J., Ed.; Dover: New York, USA, 1958. [Google Scholar]
- Bloch, F. Die physikalische Bedeutung mehrerer Zeiten in der Quantenelektrodynamik. Phys. Z. Sowjetunion 1934, 5, 301–305. [Google Scholar]
- Lienert, M.; Petrat, S.; Tumulka, R. Multi-time wave functions. J. Phys. Conf. Ser. 2017, 880, 012006. [Google Scholar] [CrossRef]
- Tomonaga, S. On a relativistically invariant formulation of the quantum theory of wave fields. Prog. Theor. Phys. 1946, 1, 27–42. [Google Scholar] [CrossRef]
- Schwinger, J. Quantum electrodynamics. I. A covariant formulation. Phys. Rev. 1948, 74, 1439–1461. [Google Scholar] [CrossRef]
- Lienert, M. Direct interaction along light cones at the quantum level. arXiv, 2017; arXiv:1801.00060. [Google Scholar]
- Petrat, S.; Tumulka, R. Multi-time Schrödinger equations cannot contain interaction potentials. J. Math. Phys. 2014, 55, 032302. [Google Scholar] [CrossRef]
- Nickel, L.; Deckert, D.-A. Consistency of multi-time Dirac equations with general interaction potentials. J. Math. Phys. 2016, 57, 072301. [Google Scholar]
- Droz-Vincent, P. Relativistic quantum mechanics with non conserved number of particles. J. Geom. Phys. 1985, 2, 101–119. [Google Scholar] [CrossRef]
- Lienert, M. A relativistically interacting exactly solvable multi-time model for two mass-less Dirac particles in 1+1 dimensions. J. Math. Phys. 2015, 56, 042301. [Google Scholar] [CrossRef]
- Lienert, M.; Nickel, L. A simple explicitly solvable interacting relativistic N-particle model. J. Phys. A Math. Theor. 2015, 48, 325301. [Google Scholar] [CrossRef]
- Petrat, S.; Tumulka, R. Multi-time wave functions for quantum field theory. Ann. Phys. 2014, 345, 17–54. [Google Scholar] [CrossRef]
- Petrat, S.; Tumulka, R. Multi-time formulation of pair creation. J. Phys. A Math. Theor. 2014, 47, 112001. [Google Scholar] [CrossRef]
- Tumulka, R. A relativistic version of the Ghirardi–Rimini–Weber model. J. Stat. Phys. 2006, 125, 821–840. [Google Scholar] [CrossRef]
- Bedingham, D.; Dürr, D.; Ghirardi, G.C.; Goldstein, S.; Tumulka, R.; Zanghì, N. Matter density and relativistic models of wave function collapse. J. Stat. Phys. 2014, 154, 623–631. [Google Scholar] [CrossRef]
- Oppenheimer, J.R. Note on light quanta and the electromagnetic field. Phys. Rev. 1931, 38, 725–748. [Google Scholar] [CrossRef]
- Colin, S.; Struyve, W. A Dirac sea pilot-wave model for quantum field theory. J. Phys. A Math. Theor. 2007, 40, 7309–7341. [Google Scholar] [CrossRef]
- Deckert, D.-A.; Esfeld, M.; Oldofredi, A. A persistent particle ontology for QFT in terms of the Dirac sea. arXiv, 2016; arXiv:1608.06141. [Google Scholar]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tumulka, R. On Bohmian Mechanics, Particle Creation, and Relativistic Space-Time: Happy 100th Birthday, David Bohm! Entropy 2018, 20, 462. https://doi.org/10.3390/e20060462
Tumulka R. On Bohmian Mechanics, Particle Creation, and Relativistic Space-Time: Happy 100th Birthday, David Bohm! Entropy. 2018; 20(6):462. https://doi.org/10.3390/e20060462
Chicago/Turabian StyleTumulka, Roderich. 2018. "On Bohmian Mechanics, Particle Creation, and Relativistic Space-Time: Happy 100th Birthday, David Bohm!" Entropy 20, no. 6: 462. https://doi.org/10.3390/e20060462
APA StyleTumulka, R. (2018). On Bohmian Mechanics, Particle Creation, and Relativistic Space-Time: Happy 100th Birthday, David Bohm! Entropy, 20(6), 462. https://doi.org/10.3390/e20060462