Improving the Maximum Transmission Distance of Self-Referenced Continuous-Variable Quantum Key Distribution Using a Noiseless Linear Amplifier
Abstract
1. Introduction
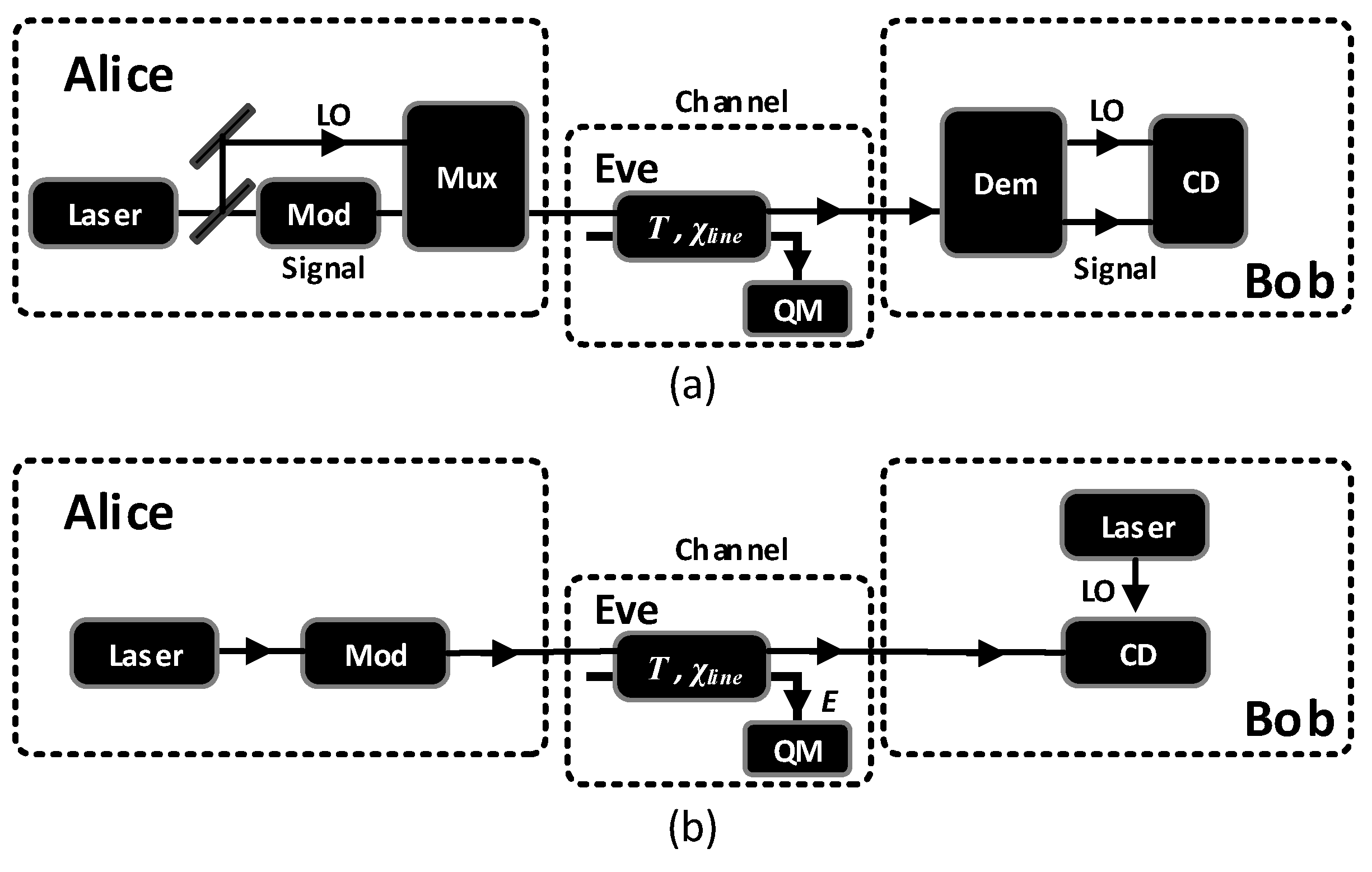
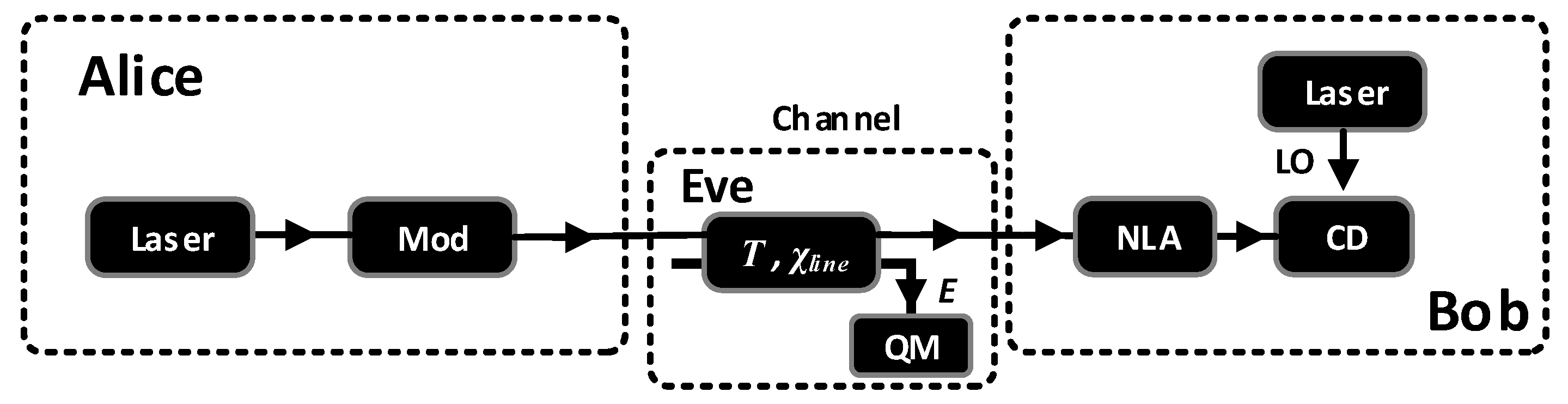
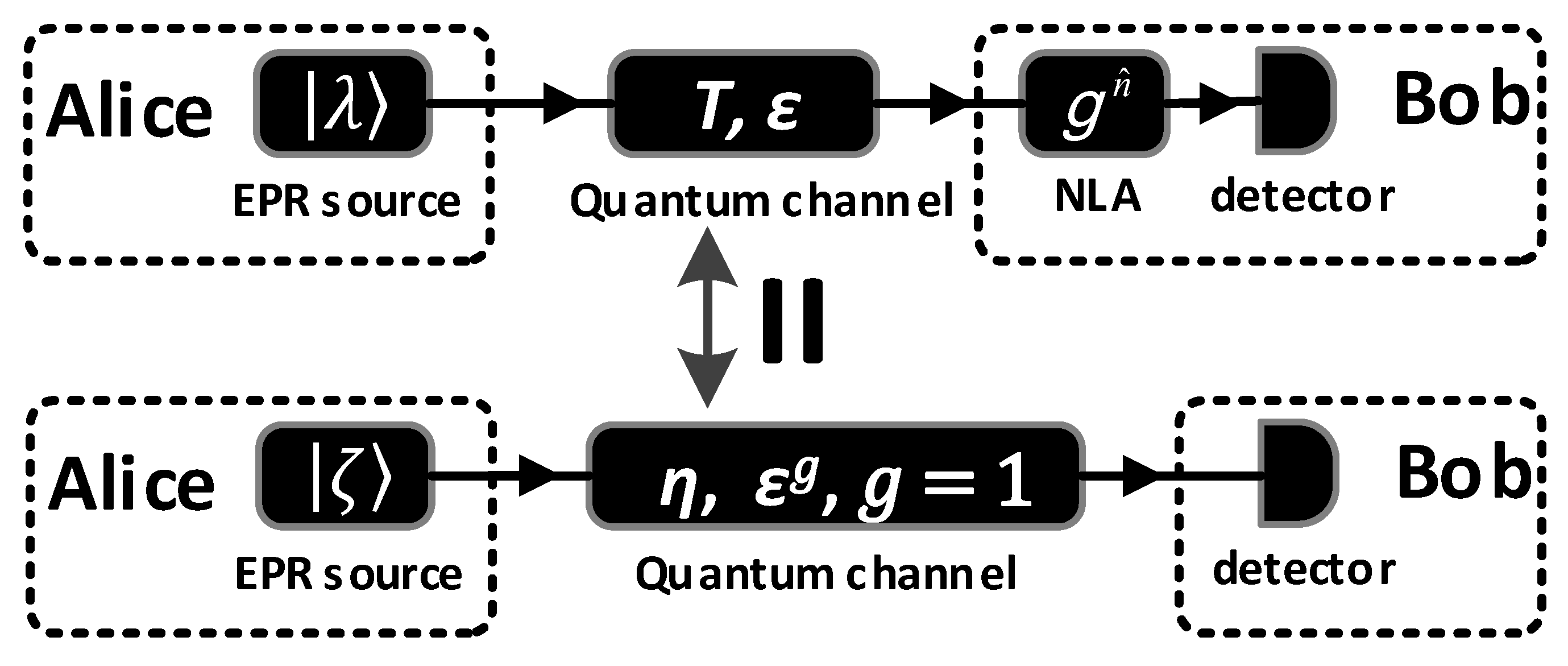
2. The SR CV-QKD Scheme & Our Proposed Scheme
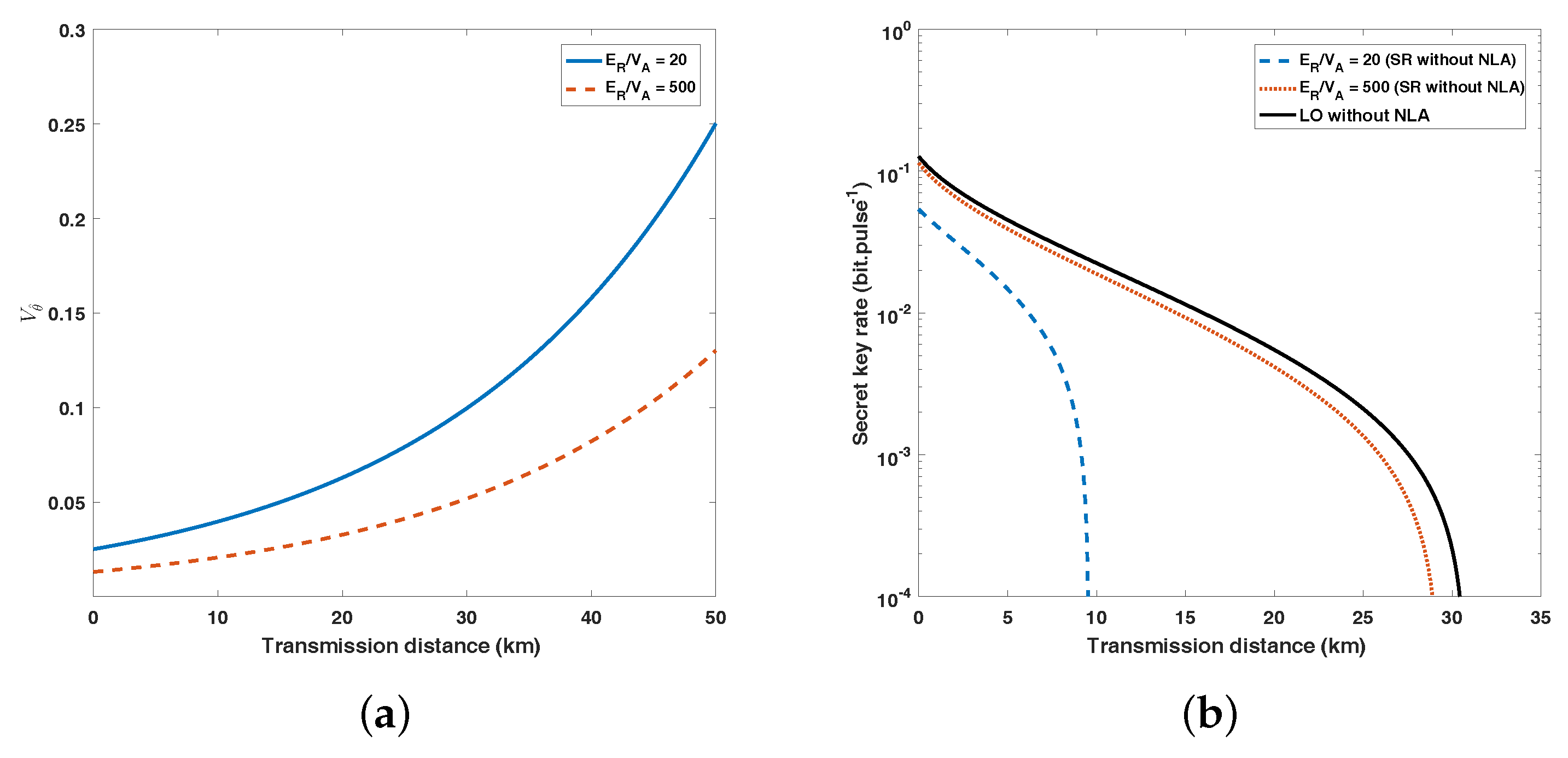
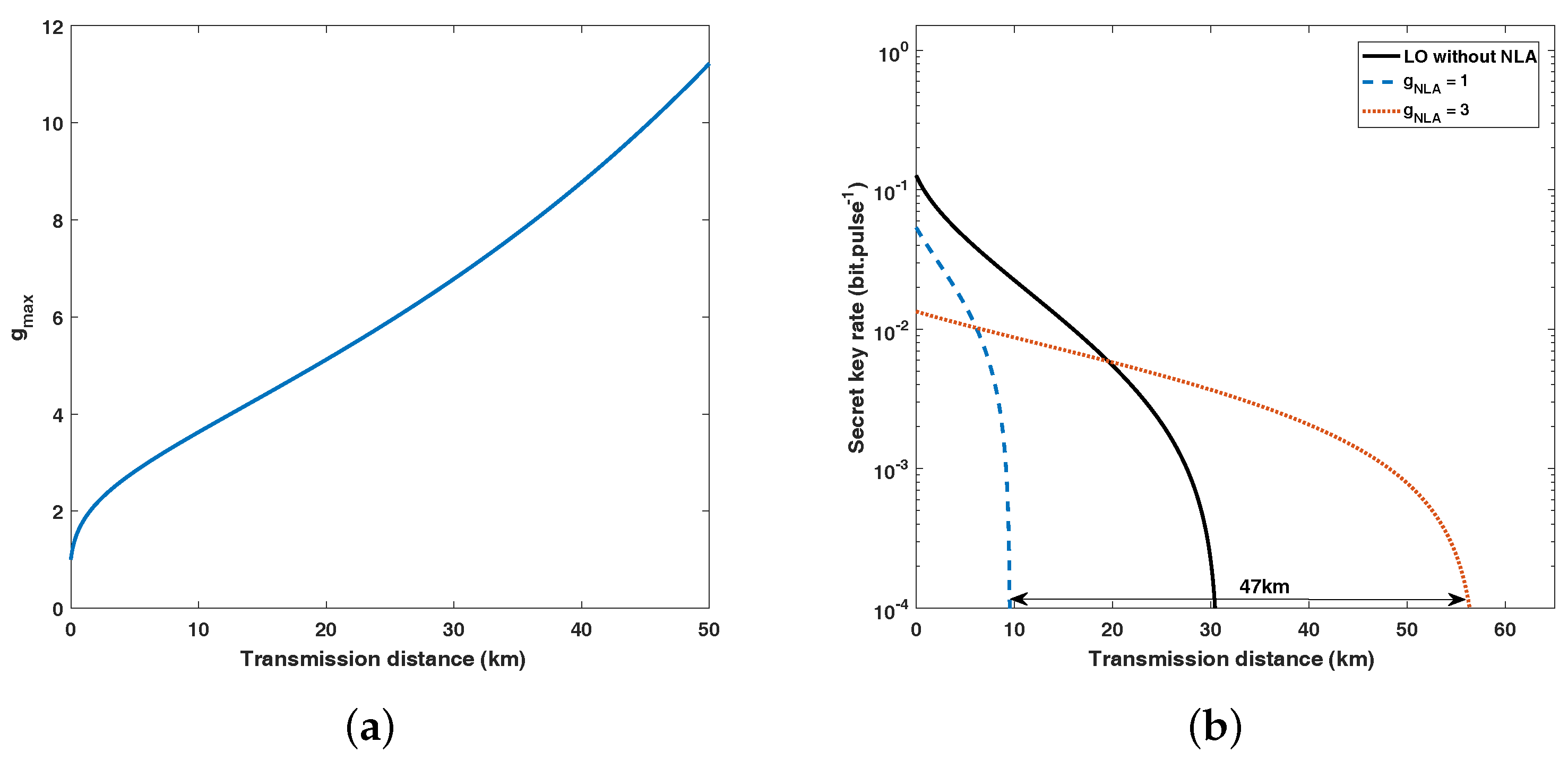
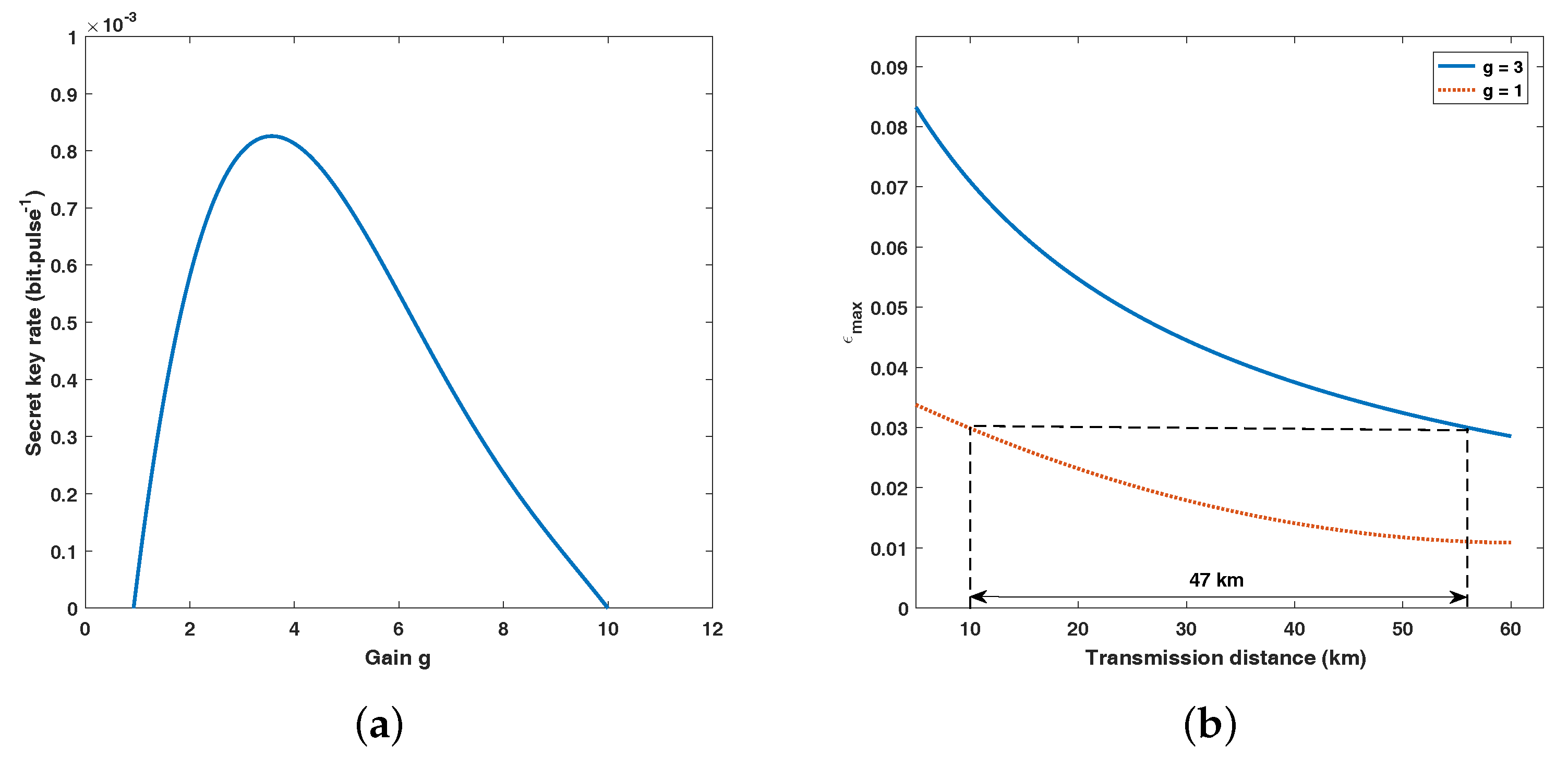
3. Performance Analysis
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India, 9–12 December 1984; pp. 175–179. [Google Scholar]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145. [Google Scholar] [CrossRef]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301. [Google Scholar] [CrossRef]
- Lo, H.-K.; Curty, M.; Tamaki, K. Secure quantum key distribution. Nat. Photonics 2014, 8, 595–604. [Google Scholar] [CrossRef]
- Grosshans, F.; Grangier, P. Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 2002, 88, 057902. [Google Scholar] [CrossRef] [PubMed]
- Braunstein, S.L.; van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 2005, 77, 513. [Google Scholar] [CrossRef]
- Wang, X.B.; Hiroshima, T.; Tomita, A.; Hayashi, M. Quantum information with gaussian states. Phys. Rep. 2007, 44, 1–111. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621. [Google Scholar] [CrossRef]
- Inoue, K.; Waks, E.; Yamamoto, Y. Differential-phase-shift quantum key distribution using coherent light. Phys. Rev. A 2003, 68, 022317. [Google Scholar] [CrossRef]
- Stucki, D.; Brunner, N.; Gisin, N.; Scarani, V.; Zbinden, H. Fast and simple one-way quantum key distribution. Appl. Phys. Lett. 2005, 87, 194108. [Google Scholar] [CrossRef]
- Bacco, D.; Christensen, J.B.; Castaneda, M.A.U.; Ding, Y. Two-dimensional distributed-phase-reference protocol for quantum key distribution. Sci. Rep. 2016, 6, 36756. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.X.; Bao, W.S.; Li, H.W. Quantum hacking of two-way continuous-variable quantum key distribution using trojan-horse attack. Chin. Phys. B 2016, 25, 080309. [Google Scholar] [CrossRef]
- Guo, Y.; Liao, Q.; Huang, D.; Zeng, G.H. Quantum relay schemes for continuous-variable quantum key distribution. Phys. Rev. A 2017, 95, 042326. [Google Scholar] [CrossRef]
- Guo, Y.; Xie, C.L.; Liao, Q.; Zhao, W.; Zeng, G.H.; Huang, D. Entanglement-distillation attack on continuous-variable quantum key distribution in a turbulent atmospheric channel. Phys. Rev. A 2017, 96, 022320. [Google Scholar] [CrossRef]
- Liu, W.Q.; Peng, J.Y.; Huang, P.; Huang, D.; Zeng, G.H. Monitoring of continuous-variable quantum key distribution system in real environment. Opt. Express 2017, 25, 19429–19443. [Google Scholar] [CrossRef] [PubMed]
- Huang, P.; Huang, J.Z.; Wang, T.; Li, H.S.; Huang, D.; Zeng, G.H. Robust continuous-variable quantum key distribution against practical sttacks. Phys. Rev. A 2017, 95, 052302. [Google Scholar] [CrossRef]
- Grosshans, F. Collective attacks and unconditional security in continuous variable quantum key distribution. Phys. Rev. Lett. 2005, 94, 020504. [Google Scholar] [CrossRef] [PubMed]
- Navascues, M.; Acín, A. Security bounds for continuous variables quantum key distribution. Phys. Rev. Lett. 2005, 94, 020505. [Google Scholar] [CrossRef] [PubMed]
- Leverrier, A. Composable security proof for continuous-Variable quantum key distribution with coherent States. Phys. Rev. Lett. 2015, 114, 070501. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.Z.; Weedbrook, C.; Yin, Z.Q.; Wang, S.; Li, H.W.; Chen, W.; Guo, G.C.; Han, Z.F. Quantum hacking of a continuous-variable quantum-key-distribution system using a wavelength attack. Phys. Rev. A 2013, 87, 062329. [Google Scholar] [CrossRef]
- Ma, X.C.; Sun, S.H.; Jiang, M.S.; Liang, L.M. Wavelength attack on practical continuous-variable quantum-key-distribution system with a heterodyne protocol. Phys. Rev. A 2013, 87, 052309. [Google Scholar] [CrossRef]
- Qin, H.; Kumar, R.; Alléaume, R. Saturation attack on continuous-variable quantum key distribution system. Proc. SPIE 2013, 8899, 88990N. [Google Scholar] [CrossRef]
- Jouguet, P.; Kunz-Jacques, S.; Diamanti, E. Preventing calibration attacks on the local oscillator in continuous-variable quantum key distribution. Phys. Rev. A 2013, 87, 062313. [Google Scholar] [CrossRef]
- Ma, X.C.; Sun, S.H.; Jiang, M.S.; Liang, L.M. Local oscillator fluctuation opens a loophole for Eve in practical continuous-variable quantum-key-distribution systems. Phys. Rev. A 2013, 88, 022339. [Google Scholar] [CrossRef]
- Soh, D.B.S.; Brif, C.; Coles, P.J.; Lütkenhaus, N.; Camacho, R.M.; Urayama, J.; Sarovar, M. Self-Referenced continuous-variable quantum key distribution protocol. Phys. Rev. X 2015, 5, 041010. [Google Scholar] [CrossRef]
- Qi, B.; Lougovski, P.; Pooser, R.; Grice, W.; Bobrek, M. Generating the local oscillator locally in continuous-variable quantum key distribution based on coherent detection. Phys. Rev. X 2015, 5, 041009. [Google Scholar] [CrossRef]
- Huang, D.; Huang, P.; Lin, D.K.; Wang, C.; Zeng, G.-H. High-speed continuous-variable quantum key distribution without sending a local oscillator. Opt. Lett. 2015, 40, 3695–3698. [Google Scholar] [CrossRef] [PubMed]
- Marie, A.; Alléaume, R. Self-coherent phase reference sharing for continuous-variable quantum key distribution. Phys. Rev. A 2017, 95, 012316. [Google Scholar] [CrossRef]
- Ralph, T.C.; Lund, A.P. Nondeterministic noiseless linear amplification of quantum systems. AIP Conf. Proc. 2009, 1110, 155–160. [Google Scholar]
- Ferreyrol, F.; Barbieri, M.; Blandino, R.; Fossier, S.; Tualle-Brouri, R.; Grangier, P. Implementation of a nondeterministic optical noiseless amplifier. Phys. Rev. Lett. 2010, 104, 123603. [Google Scholar] [CrossRef] [PubMed]
- Xiang, G.Y.; Ralph, T.C.; Lund, A.P.; Walk, N.; Pryde, G.J. Heralded noiseless linear amplification and distillation of entanglement. Nat. Photonics 2010, 4, 316–319. [Google Scholar] [CrossRef]
- Usuga, M.A.; Müller, C.R.; Wittmann, C.; Marek, P.; Filip, R.; Marquardt, C.; Leuchs, G.; Andersen, U.L. Heralded noiseless linear amplification and distillation of entanglement. Nat. Phys. 2010, 6, 316–319. [Google Scholar]
- Ferreyrol, F.; Blandino, R.; Barbieri, M.; Tualle-Brouri, R.; Grangier, P. Experimental realization of a nondeterministic optical noiseless amplifier. Phys. Rev. A 2011, 83, 063801. [Google Scholar] [CrossRef]
- Barbieri, M.; Ferreyrol, F.; Blandino, R.; Tualle-Brouri, R.; Grangier, P. Nondeterministic noiseless amplification of optical signals: a review of recent experiments. Laser Phys. Lett. 2011, 8, 411–417. [Google Scholar] [CrossRef]
- Zavatta, A.; Fiurasek, J.; Bellini, M. A high-fidelity noiseless amplifier for quantum light states. Nat. Photonics 2011, 5, 52–56. [Google Scholar] [CrossRef]
- McMahon, N.A.; Lund, A.P.; Ralph, T.C. Optimal architecture for a nondeterministic noiseless linear amplifier. Phys. Rev. A 2014, 89, 269–274. [Google Scholar] [CrossRef]
- Blandino, R.; Leverrier, A.; Barbieri, M.; Etesse, J.; Grangier, P.; Tualle-Brouri, R. Improving the maximum transmission distance of continuous-variable quantum key distribution using a noiseless amplifier. Phys. Rev. A 2012, 86, 113–115. [Google Scholar] [CrossRef]
- Jaromír, F.; Nicolas, C.J. Gaussian postselection and virtual noiseless amplification in continuous-variable quantum key distribution. Phys. Rev. A 2012, 86, 060302. [Google Scholar]
- Xu, B.J.; Tang, C.M.; Chen, H.; Zhang, W.Z.; Zhu, F.C. Improving the maximum transmission distance of four-state continuous-variable quantum keydistribution by using a noiseless linear amplifier. Phys. Rev. A 2013, 87, 062311. [Google Scholar] [CrossRef]
- Yang, F.L.; Shi, R.H.; Guo, Y.; Shi, J.J.; Zeng, G.H. Continuous-variable quantum key distribution under the local oscillator intensity attack with noiseless linear amplifier. Quantum Inf. Process. 2015, 14, 3041–3056. [Google Scholar] [CrossRef]
- Bai, D.Y.; Huang, P.; Ma, H.X.; Wang, T.; Zeng, G.H. Performance improvement of plug-and-play dual-phase-modulated quantum key distribution by using a noiseless amplifier. Entropy 2017, 19, 546. [Google Scholar] [CrossRef]
- Walk, N.; Ralph, T.C.; Symul, T.; Lam, P.K. Security of continuous-variable quantum cryptography with gaussian postselection. Phys. Rev. A 2013, 87, 020303. [Google Scholar] [CrossRef]
- Fossier, S. Mise en Oeuvre et Évaluation de Dispositifs de Cryptographie Quantique à Longueur D’onde Télécom. Ph.D. Thesis, Thales Research & Technology France, Palaiseau, France, 2009, unpublished. [Google Scholar]
- García-Patrón, R. Quantum Information with Optical Continuous Variables: From Bell Tests to Key Distribution. Ph.D. Thesis, Université Libre de Bruxelles, Bruxelles, Belgium, 2007. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, X.; Huang, D.; Guo, Y. Improving the Maximum Transmission Distance of Self-Referenced Continuous-Variable Quantum Key Distribution Using a Noiseless Linear Amplifier. Entropy 2018, 20, 461. https://doi.org/10.3390/e20060461
Wang Y, Wang X, Huang D, Guo Y. Improving the Maximum Transmission Distance of Self-Referenced Continuous-Variable Quantum Key Distribution Using a Noiseless Linear Amplifier. Entropy. 2018; 20(6):461. https://doi.org/10.3390/e20060461
Chicago/Turabian StyleWang, Yijun, Xudong Wang, Duan Huang, and Ying Guo. 2018. "Improving the Maximum Transmission Distance of Self-Referenced Continuous-Variable Quantum Key Distribution Using a Noiseless Linear Amplifier" Entropy 20, no. 6: 461. https://doi.org/10.3390/e20060461
APA StyleWang, Y., Wang, X., Huang, D., & Guo, Y. (2018). Improving the Maximum Transmission Distance of Self-Referenced Continuous-Variable Quantum Key Distribution Using a Noiseless Linear Amplifier. Entropy, 20(6), 461. https://doi.org/10.3390/e20060461





