Locating the Sets of Exceptional Points in Dissipative Systems and the Self-Stability of Bicycles
Abstract
1. Introduction
2. Complex Exceptional Points and the Self-Stability of Bicycles
2.1. The TMS Bicycle Model
2.2. Preliminaries on Lyapunov Stability and the Asymptotic Stability of Equilibria
2.3. Asymptotic Stability of the TMS Bike and the Critical Froude Number for the Weaving Motion
2.4. Minimizing the Spectral Abscissa of General TMS Bikes
2.5. Self-Stable and Heavily-Damped TMS Bikes with
2.5.1. The Critical Froude Number and Its Minimum
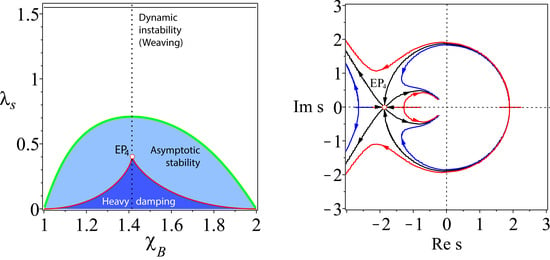
2.5.2. Exact Location of the Real Exceptional Point
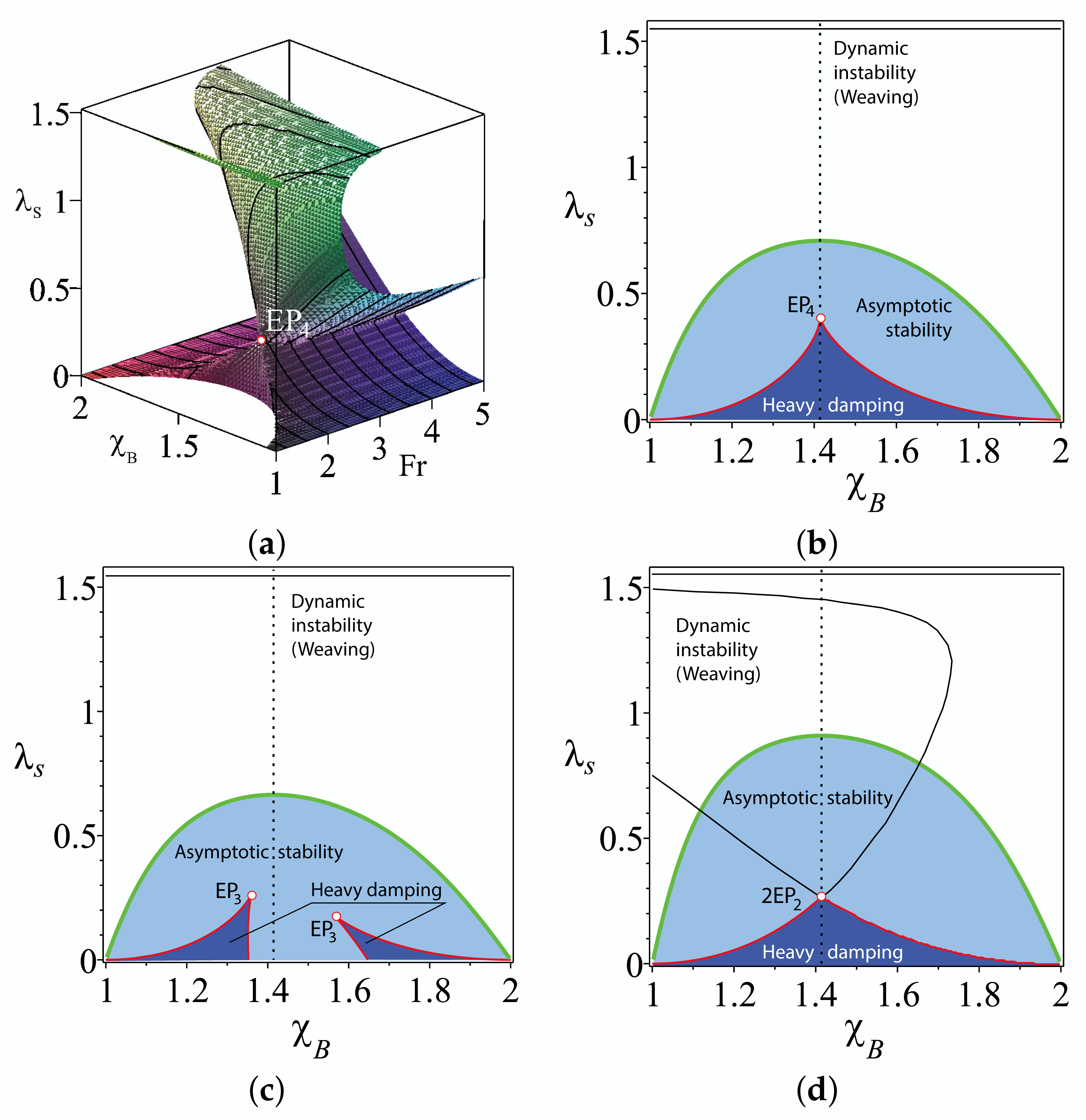
2.5.3. Discriminant Surface and the EP-Set
2.5.4. Location of the EP-Set and Stability Optimization
2.5.5. Mechanism of Self-Stability and as a Precursor to Bike Weaving
2.5.6. How the Scaling Laws Found Match the Experimental TMS Bike Realization
3. Conclusions
Funding
Conflicts of Interest
References
- Bender, C.M.; Berntson, B.K.; Parker, D.; Samuel, E. Observation of PT phase transition in a simple mechanical system. Am. J. Phys. 2013, 81, 173–179. [Google Scholar] [CrossRef]
- Xu, X.-W.; Liu, Y.-X.; Sun, C.-P.; Li, Y. Mechanical PT symmetry in coupled optomechanical systems. Phys. Rev. A 2015, 92, 013852. [Google Scholar] [CrossRef]
- Schindler, S.; Lin, Z.; Lee, J.M.; Ramezani, H.; Ellis, F.M.; Kottos, T. PT symmetric electronics. J. Phys. A Math. Theor. 2012, 45, 444029. [Google Scholar] [CrossRef]
- Freitas, P. On some eigenvalue problems related to the wave equation with indefinite damping. J. Differ. Equ. 1996, 127, 320–335. [Google Scholar] [CrossRef]
- Freitas, P.; Zuazua, E. Stability results for the wave equation with indefinite damping. J. Differ. Equ. 1996, 132, 338–353. [Google Scholar] [CrossRef]
- Freitas, P.; Grinfeld, M.; Knight, P.A. Stability of finite-dimensional systems with indefinite damping. Adv. Math. Sci. Appl. 1997, 7, 437–448. [Google Scholar]
- Freitas, P. Quadratic matrix polynomials with Hamiltonian spectrum and oscillatory damped systems. Z. Angew. Math. Phys. 1999, 50, 64–81. [Google Scholar] [CrossRef]
- Kliem, W.; Pommer, C. Indefinite damping in mechanical systems and gyroscopic stabilization. Z. Angew. Math. Phys. 2009, 60, 785–795. [Google Scholar] [CrossRef]
- Kirillov, O.N. PT symmetry, indefinite damping and dissipation-induced instabilities. Phys. Lett. A 2012, 376, 1244–1249. [Google Scholar] [CrossRef]
- Kirillov, O.N. Stabilizing and destabilizing perturbations of PT symmetric indefinitely damped systems. Philos. Trans. R. Soc. A 2013, 371, 20120051. [Google Scholar] [CrossRef] [PubMed]
- Kirillov, O.N. Exceptional and diabolical points in stability questions. Fortschr. Phys. Prog. Phys. 2013, 61, 205–224. [Google Scholar] [CrossRef]
- Kirillov, O.N. Singular diffusionless limits of double-diffusive instabilities in magnetohydrodynamics. Proc. R. Soc. A 2017, 473, 20170344. [Google Scholar] [CrossRef] [PubMed]
- Jones, C.A. Multiple eigenvalues and mode classification in plane Poiseuille flow. Quart. J. Mech. Appl. Math. 1988, 41, 363–382. [Google Scholar] [CrossRef]
- Dobson, I.; Zhang, J.; Greene, S.; Engdahl, H.; Sauer, P.W. Is strong modal resonance a precursor to power system oscillations? IEEE Trans. Circ. Syst. I 2001, 48, 340–349. [Google Scholar] [CrossRef]
- Friedland, S. Simultaneous similarity of matrices. Adv. Math. 1983, 50, 189–265. [Google Scholar] [CrossRef]
- Christensen, E. On invertibility preserving linear mappings, simultaneous triangularization and Property L. Linear Algebra Appl. 1999, 301, 153–170. [Google Scholar] [CrossRef]
- Kirillov, O.N.; Overton, M.L. Robust stability at the swallowtail singularity. Front. Phys. 2013, 1, 24. [Google Scholar] [CrossRef]
- Borrell, B. Physics on two wheels. Nature 2016, 535, 338–341. [Google Scholar] [CrossRef] [PubMed]
- Meijaard, J.P.; Papadopoulos, J.M.; Ruina, A.; Schwab, A.L. Linearized dynamics equations for the balance and steer of a bicycle: A benchmark and review. Proc. R. Soc. A 2007, 463, 1955–1982. [Google Scholar] [CrossRef]
- Sharp, R.S. On the stability and control of the bicycle. Appl. Mech. Rev. 2008, 61, 060803. [Google Scholar] [CrossRef]
- Meijaard, J.P.; Papadopoulos, J.M.; Ruina, A.; Schwab, A.L. Historical Review of Thoughts on Bicycle Self-Stability; Cornell University: Ithaca, NY, USA, 2011. [Google Scholar]
- Boyer, F.; Porez, M.; Mauny, J. Reduced dynamics of the non-holonomic Whipple bicycle. J. Nonlinear Sci. 2018, 28, 943–983. [Google Scholar] [CrossRef]
- Borisov, A.V.; Mamaev, I.S.; Bizyaev, I.A. Dynamical systems with non-integrable constraints, vakonomic mechanics, sub-Riemannian geometry, and non-holonomic mechanics. Russ. Math. Surv. 2017, 72, 783–840. [Google Scholar] [CrossRef]
- Levi, M.; Tabachnikov, S. On bicycle tire tracks geometry, hatchet planimeter, Menzin’s conjecture, and oscillation of unicycle tracks. Exp. Math. 2009, 18, 173–186. [Google Scholar] [CrossRef]
- Levi, M. Schrödinger’s equation and “bike tracks” —A connection. J. Geom. Phys. 2017, 115, 124–130. [Google Scholar] [CrossRef]
- Bor, G.; Levi, M.; Perline, R.; Tabachnikov, S. Tire tracks and integrable curve evolution. Int. Math. Res. Not. 2018, rny087. [Google Scholar] [CrossRef]
- Kooijman, J.D.G.; Meijaard, J.P.; Papadopoulos, J.M.; Ruina, A.; Schwab, A.L. A bicycle can be self-stable without gyroscopic or caster effects. Science 2011, 332, 339–342. [Google Scholar] [CrossRef] [PubMed]
- Hess, R.; Moore, J.K.; Hubbard, M. Modeling the manually controlled bicycle. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2012, 42, 545–557. [Google Scholar] [CrossRef]
- Ricci, F.; Frosali, G. A symbolic method for the analysis of a nonlinear Two-Mass-Skate model. arXiv, 2016; arXiv:1611.07796. [Google Scholar]
- Collins, S.; Ruina, A.; Tedrake, R.; Wisse, M. Efficient bipedal robots based on passive-dynamic walkers. Science 2005, 307, 1082–1085. [Google Scholar] [CrossRef] [PubMed]
- Borisov, A.V.; Kilin, A.A.; Mamaev, I.S. On the Hadamard-Hamel problem and the dynamics of wheeled vehicles. Reg. Chaot. Dyn. 2015, 20, 752–766. [Google Scholar] [CrossRef]
- Lyapunov, A.M. The general problem of the stability of motion. Int. J. Control 1992, 55, 531–773. [Google Scholar] [CrossRef]
- Kirillov, O.N. Nonconservative Stability Problems of Modern Physics; De Gruyter: Berlin, Germany, 2013. [Google Scholar]
- Barkwell, L.; Lancaster, P. Overdamped and gyroscopic vibrating systems. J. Appl. Mech. 1992, 59, 176–181. [Google Scholar] [CrossRef]
- Veselic, K. Damped Oscillations of Linear Systems: A Mathematical Introduction; Springer: Berlin, Germany, 2011. [Google Scholar]
- Berry, M.V.; Shukla, P. Curl force dynamics: Symmetries, chaos and constants of motion. New J. Phys. 2016, 18, 063018. [Google Scholar] [CrossRef]
- Kirillov, O.N. Classical results and modern approaches to nonconservative stability. Ch. 4. In Dynamic Stability and Bifurcation in Nonconservative Mechanics; Bigoni, D., Kirillov, O., Eds.; CISM International Centre for Mechanical Sciences 586; Springer: Berlin, Germany, 2018; pp. 129–190. [Google Scholar]
- Austin Sydes, G.L. Self-Stable Bicycles; BSc (Hons) Mathematics Final Year Project Report; Northumbria University: Newcastle upon Tyne, UK, 2018. [Google Scholar]
- Freitas, P.; Lancaster, P. On the optimal value of the spectral abscissa for a system of linear oscillators. SIAM J. Matrix Anal. Appl. 1999, 21, 195–208. [Google Scholar] [CrossRef]
- Blondel, V.D.; Gurbuzbalaban, M.; Megretski, A.; Overton, M.L. Explicit solutions for root optimization of a polynomial family with one affine constraint. IEEE Trans. Autom. Control 2012, 57, 3078–3089. [Google Scholar] [CrossRef]




| Dimensional | Meaning | Dimensionless | Meaning |
|---|---|---|---|
| v | Velocity of the bike | ||
| g | Gravity acceleration | Froude number | |
| w | Wheel base | ||
| Steer axis tilt (rad) | Steer axis tilt (rad) | ||
| Front fork and handlebar | |||
| assembly (FHA) mass | Mass ratio () | ||
| Rear frame assembly (RFA) mass | |||
| (≥0) | Horizontal coordinate of the | (≥0) | Horizontal coordinate of the |
| FHA centre of mass | FHA centre of mass | ||
| (≤0) | Vertical coordinate of the | (≤0) | Vertical coordinate of the |
| FHA centre of mass | FHA centre of mass | ||
| (≥0) | Horizontal coordinate of the | (≥0) | Horizontal coordinate of the |
| RFA centre of mass | RFA centre of mass | ||
| (≤0) | Vertical coordinate of the | (≤0) | Vertical coordinate of the |
| RFA centre of mass | RFA centre of mass | ||
| t | Time | Time |
| Bike | (rad) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | ||||||||
| 1 | ≈1.482682090 | ≈2.257421384 | ||||||
| 1 | ≈3.934331969 | ≈4.103508160 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kirillov, O.N. Locating the Sets of Exceptional Points in Dissipative Systems and the Self-Stability of Bicycles. Entropy 2018, 20, 502. https://doi.org/10.3390/e20070502
Kirillov ON. Locating the Sets of Exceptional Points in Dissipative Systems and the Self-Stability of Bicycles. Entropy. 2018; 20(7):502. https://doi.org/10.3390/e20070502
Chicago/Turabian StyleKirillov, Oleg N. 2018. "Locating the Sets of Exceptional Points in Dissipative Systems and the Self-Stability of Bicycles" Entropy 20, no. 7: 502. https://doi.org/10.3390/e20070502
APA StyleKirillov, O. N. (2018). Locating the Sets of Exceptional Points in Dissipative Systems and the Self-Stability of Bicycles. Entropy, 20(7), 502. https://doi.org/10.3390/e20070502