Thermodynamic Explanation of Landau Damping by Reduction to Hydrodynamics
Abstract
1. Introduction
2. Ehrenfest Reduction
2.1. General Formulation
2.2. Hamiltonian Version of Ehrenfest Reduction
2.2.1. Hamiltonian Structure of the Vlasov Equation
2.2.2. Formal Solution of Hamiltonian Evolution
2.2.3. Projection of the Poisson Bracket
2.2.4. Comparing the Solutions on Different Levels
2.2.5. The Special Case of Constant Poisson Bivector
2.2.6. Canonical Hamiltonian System
3. From Vlasov to Mechanical Equilibrium
3.1. Projection
3.2. Construction of the Reduced Evolution
3.3. Features of the Reduced Evolution
3.3.1. Conservation of Total Energy
3.3.2. Dissipativity of Reduced Evolution
3.3.3. Homogeneous Equilibrium Solution
3.3.4. Some Qualitative Insight into Macroscopic Evolution Equations: Linearization.
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Mouhot, C.; Villani, C. On Landau damping. Acta Math. 2011, 207, 29–201. [Google Scholar] [CrossRef]
- Jeans, J.H. The Stability of a Spherical Nebula. Phil. Trans. R. Soc. Lond. A 1902, 199, 1–53. [Google Scholar] [CrossRef]
- Landau, L. On the vibrations of the electronic plasma. Zh. Eksp. Teor. Fiz. 1946, 16, 574–586. [Google Scholar]
- Pitaevskii, L.; Lifshitz, E. Physical Kinetics; Elsevier: New York, NY, USA, 2012. [Google Scholar]
- Villani, C. Particle systems and nonlinear Landau damping. Phys. Plasmas 2014, 21, 030901. [Google Scholar] [CrossRef]
- Chen, F. Introduction to Plasma Physics; Plenum Press: New York, NY, USA, 1974. [Google Scholar]
- Levin, Y.; Pakter, R.; Rizzato, F.B.; Teles, T.N.; Benetti, F.P. Nonequilibrium statistical mechanics of systems with long-range interactions. Phys. Rep. 2014, 535, 1–60. [Google Scholar] [CrossRef]
- Pakter, R.; Levin, Y. Entropy production in systems with long range interactions. J. Stat. Mech. 2017, 2017, 044001. [Google Scholar] [CrossRef]
- Kraus, M.; Kormann, K.; Morrison, P.; Sonnendrücker, E. GEMPIC: Geometric electromagnetic particle-in-cell methods. J. Plasma Phys. 2017, 83. [Google Scholar] [CrossRef]
- Perin, M.; Chandre, C.; Morrison, P.J.; Tassi, E. Hamiltonian closures for fluid models with four moments by dimensional analysis. J. Phys. A 2015, 48, 275501. [Google Scholar] [CrossRef]
- Perin, M.; Chandre, C.; Morrison, P.; Tassi, E. Higher-order Hamiltonian fluid reduction of Vlasov equation. Ann. Phys. 2014, 348, 50–63. [Google Scholar] [CrossRef]
- Grad, H. Principles of Kinetic Theory of Gases. In Encyclopedia of Physics; Springer: Berlin, Germany, 1958. [Google Scholar]
- Grmela, M.; Hong, L.; Jou, D.; Lebon, G.; Pavelka, M. Hamiltonian and Godunov structures of the Grad hierarchy. Phys. Rev. E 2017, 95, 033121. [Google Scholar] [CrossRef] [PubMed]
- Grmela, M.; Klika, V.; Pavelka, M. Reductions and extensions in mesoscopic dynamics. Phys. Rev. E 2015, 92, 032111. [Google Scholar] [CrossRef] [PubMed]
- Villani, C. Bolzano Lecture: Of Triangles, Gases, Prices and Men. Available online: https://www.youtube.com/watch?v=AtOG61tL5hE&feature=youtu.be#t=1h43m (accessed on 1 June 2018).
- Zwanzig, R. Nonequilibrium Statistical Mechanics; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Öttinger, H. Beyond Equilibrium Thermodynamics; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Grmela, M.; Pavelka, M. Landau damping in the multiscale Vlasov theory. Kinet. Relat. Model. 2017, 11, 521–545. [Google Scholar] [CrossRef]
- Gorban, A.N.; Karlin, I.V.; Öttinger, H.C.; Tatarinova, L.L. Ehrenfest’s argument extended to a formalism of nonequilibrium thermodynamics. Phys. Rev. E 2001, 63, 066124. [Google Scholar] [CrossRef] [PubMed]
- Karlin, I.V.; Tatarinova, L.L.; Gorban, A.N.; Öttinger, H.C. Irreversibility in the short memory approximation. Phys. A 2003, 327, 399–424. [Google Scholar] [CrossRef]
- Jaynes, E.T. Foundations of probability theory and statistical mechanics. In Delaware Seminar in the Foundation of Physics; Bunge, M., Ed.; Springer: Berlin, Germany, 1967. [Google Scholar]
- Morrison, P.J.; Greene, J.M. Noncanonical Hamiltonian Density Formulation of Hydrodynamics and Ideal Magnetohydrodynamics. Phys. Rev. Lett. 1980, 45, 790–794. [Google Scholar] [CrossRef]
- Marsden, J.; Weinstein, A. The Hamiltonian-Structure of the Maxwell-Vlasov Equations. Phys. D 1982, 4, 394–406. [Google Scholar] [CrossRef]
- Esen, O.; Gümral, H. Geometry of Plasma Dynamics II: Lie Algebra of Hamiltonian Vector Fields. J. Geom. Mech. 2012, 4, 239–269. [Google Scholar] [CrossRef]
- Pavelka, M.; Klika, V.; Esen, O.; Grmela, M. A hierarchy of Poisson brackets. Phys. D 2016, 335, 54–69. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Fecko, M. Differential Geometry and Lie Groups for Physicists; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Leimkuhler, B.; Reich, S. Simulating Hamiltonian Dynamics; Cambridge Monographs on Applied and Computational Mathematics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Callen, H. Thermodynamics: An Introduction to the Physical Theories of Equilibrium Thermostatics and Irreversible Thermodynamics; Wiley: Hoboken, NJ, USA, 1960. [Google Scholar]
- Clebsch, A. Über die Integration der Hydrodynamische Gleichungen. J. Reine Angew. Math. 1895, 56, 1–10. (In German) [Google Scholar]
- Marsden, J.; Weinstein, A. Coadjoint orbits, vortices, and Clebsch variables for incompressible fluids. Phys. D 1983, 7, 305–323. [Google Scholar] [CrossRef]
- Van Saarloos, W.; Bedeaux, D.; Mazur, P. Hydrodynamics for an ideal fluid: Hamiltonian formalism and Liouville-equation. Phys. A 1981, 107, 109–125. [Google Scholar] [CrossRef]
- De Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; Dover Publications: New York, NY, USA, 1984. [Google Scholar]
- Pavelka, M.; Klika, V.; Grmela, M. Time reversal in nonequilibrium thermodynamics. Phys. Rev. E 2014, 90, 062131. [Google Scholar] [CrossRef] [PubMed]
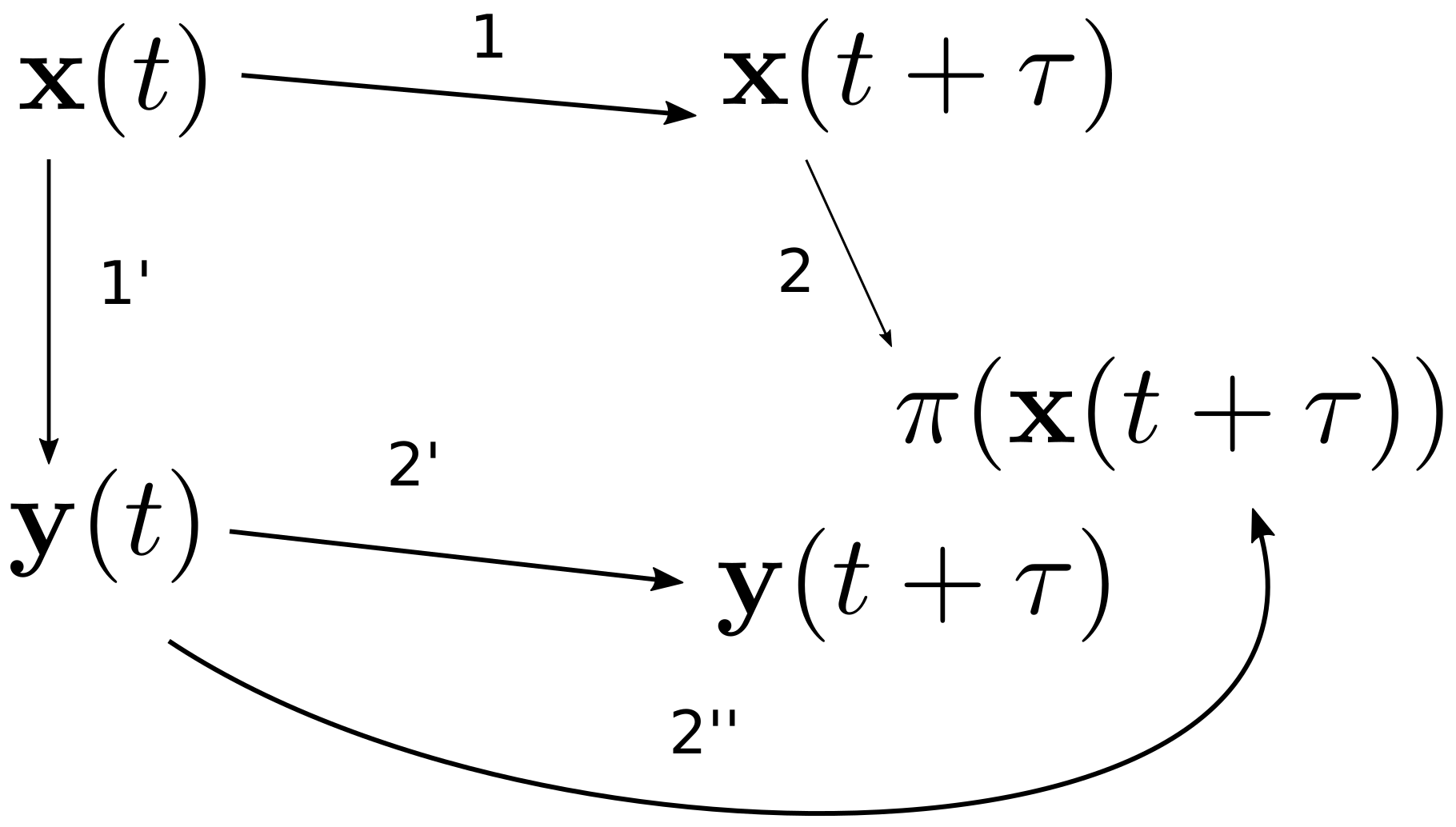
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavelka, M.; Klika, V.; Grmela, M. Thermodynamic Explanation of Landau Damping by Reduction to Hydrodynamics. Entropy 2018, 20, 457. https://doi.org/10.3390/e20060457
Pavelka M, Klika V, Grmela M. Thermodynamic Explanation of Landau Damping by Reduction to Hydrodynamics. Entropy. 2018; 20(6):457. https://doi.org/10.3390/e20060457
Chicago/Turabian StylePavelka, Michal, Václav Klika, and Miroslav Grmela. 2018. "Thermodynamic Explanation of Landau Damping by Reduction to Hydrodynamics" Entropy 20, no. 6: 457. https://doi.org/10.3390/e20060457
APA StylePavelka, M., Klika, V., & Grmela, M. (2018). Thermodynamic Explanation of Landau Damping by Reduction to Hydrodynamics. Entropy, 20(6), 457. https://doi.org/10.3390/e20060457






