Atom-Diffraction from Surfaces with Defects: A Fermatian, Newtonian and Bohmian Joint View
Abstract
1. Introduction
- The Fermatian level, which refers to the analysis of the problem assuming a bare hard-wall-like (fully repulsive) model to describe the He-CO/Pt(111) interaction. Because the trajectories here are of the type of sudden impact (free propagation except at the impact point on the substrate wall, where the trajectory is deflected according to the usual law of reflection), they are going to be straight-like rays, as in optics (this is why it is referred to as Fermatian).
- The Newtonian level, where the He-CO/Pt(111) interaction is modeled in terms of a potential energy surface that smoothly changes from point to point. This model has a repulsive wall that avoids He atoms to approach the substrate beyond a certain distance (for a given incidence energy), and an attractive tail that accounts for van der Waals long-range attraction. The existence of these two regions, repulsive and attractive, gives rise to an attractive channel around the CO adsorbate and that continuous along the flat Pt surface, inducing the possibility of temporary trapping for the He atoms.
- The Bohmian level is the upper one and, to some extent, makes an important difference with the previous models because here the trajectories are not only dependent on the interaction potential model, but also on the particular shape displayed by the wave function at each point of the configuration space at a given time (the “guiding” or “pilot” wave).
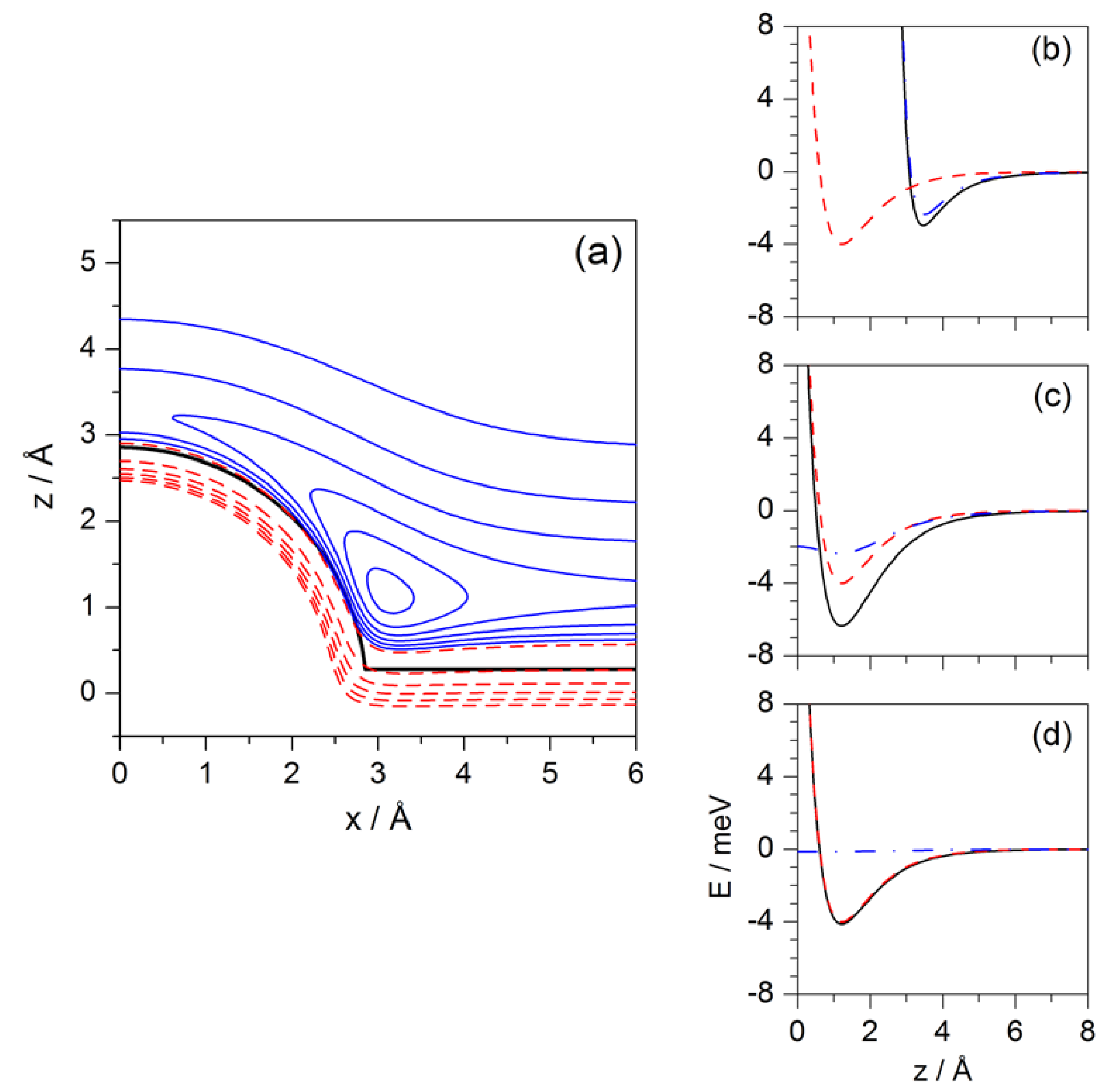
2. Potential Model and Computational Details
3. Wave-Function Approach
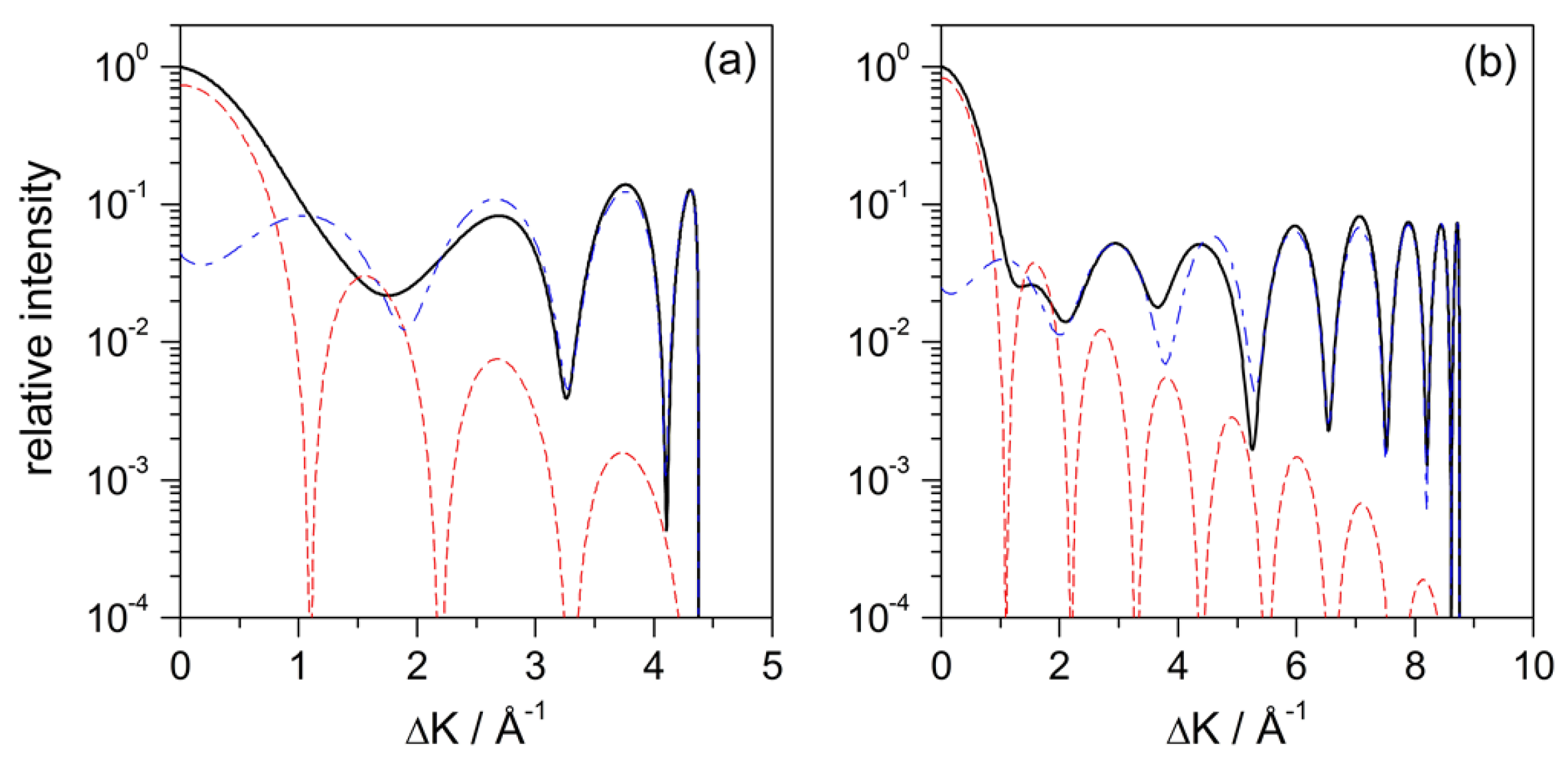
3.1. Diffraction from a Repulsive Hard-Wall Potential
3.2. Diffraction from the Potential Model (2)
4. Trajectory-Based Description
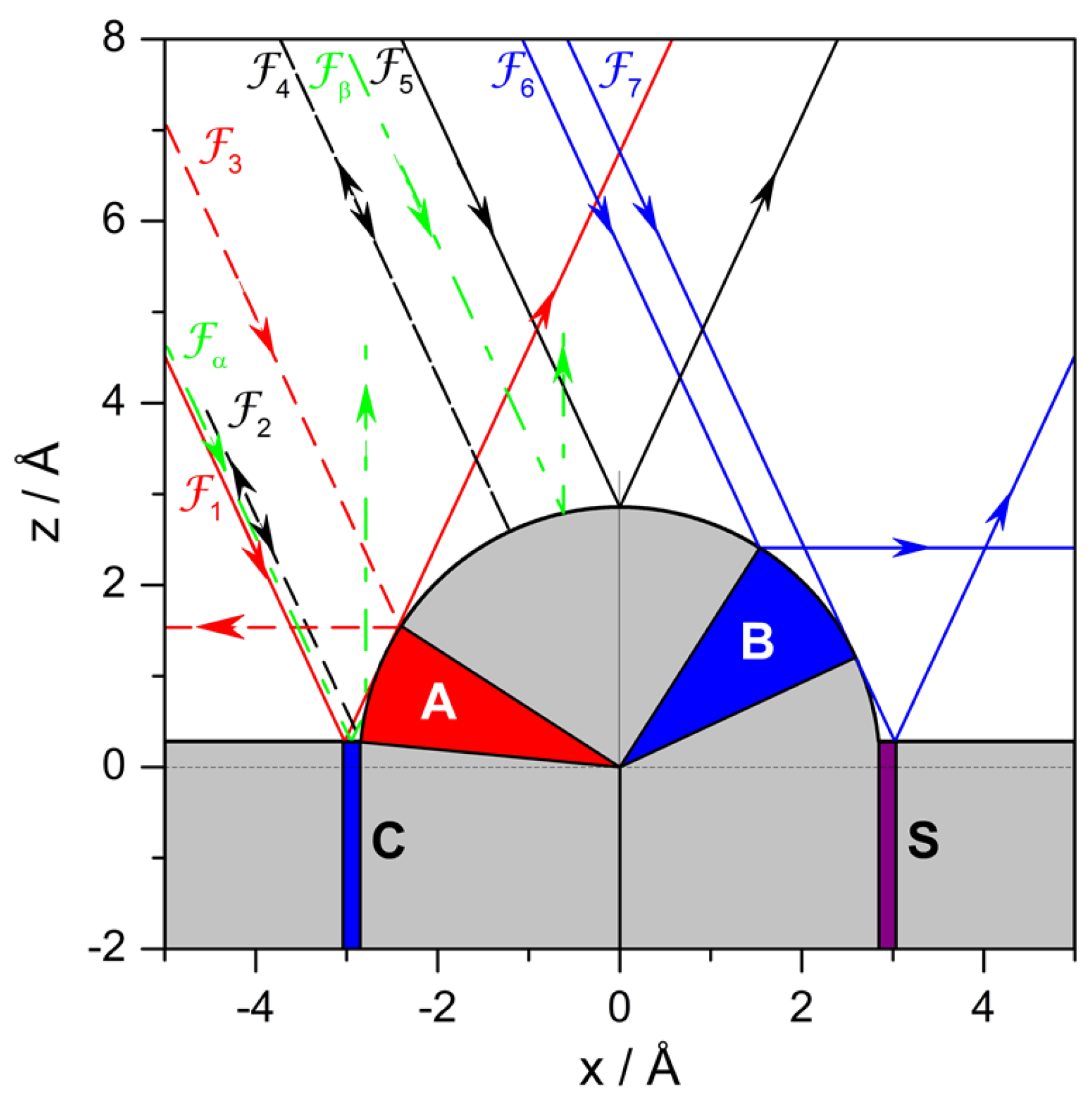
4.1. Fermatian Level
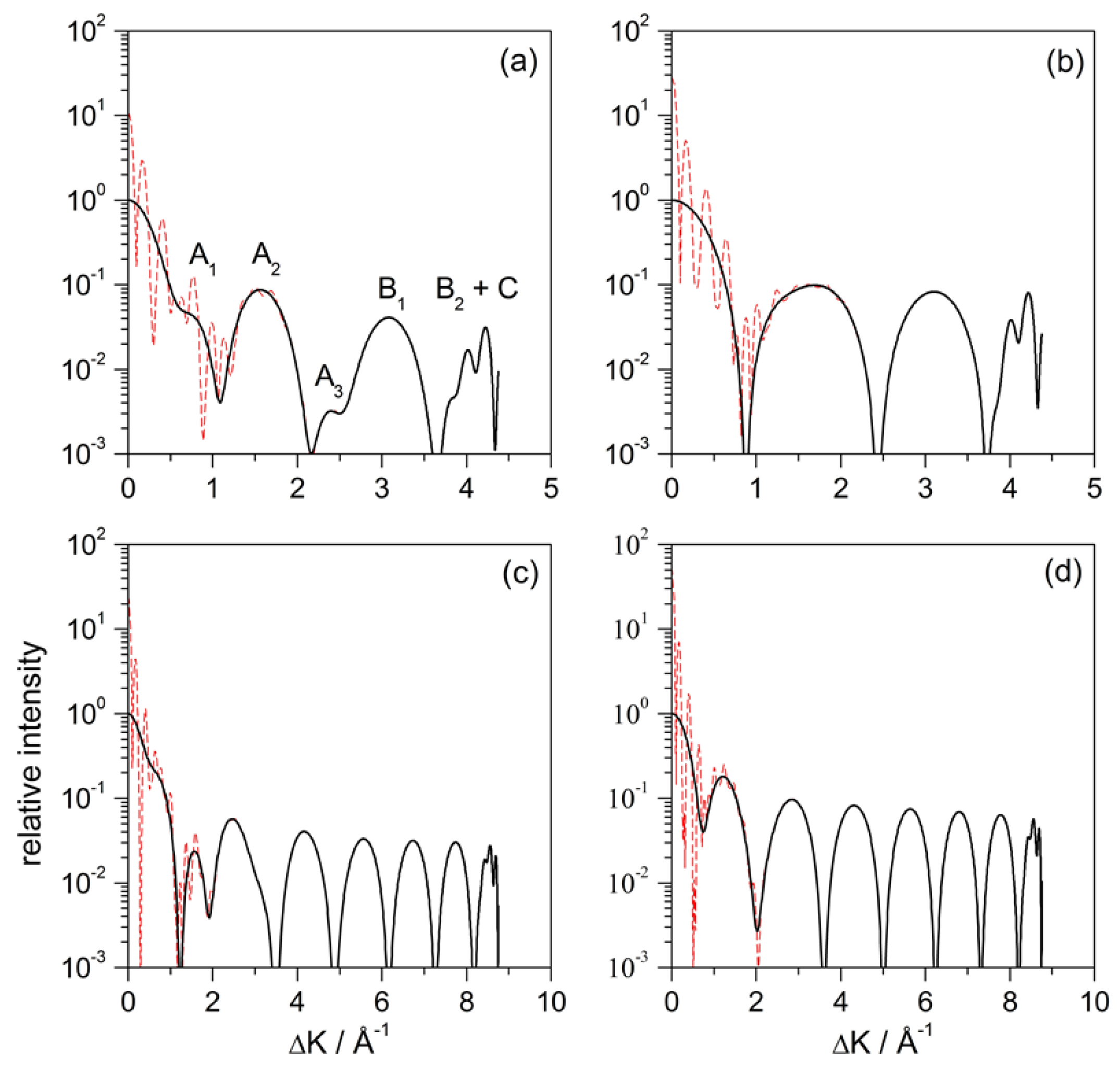
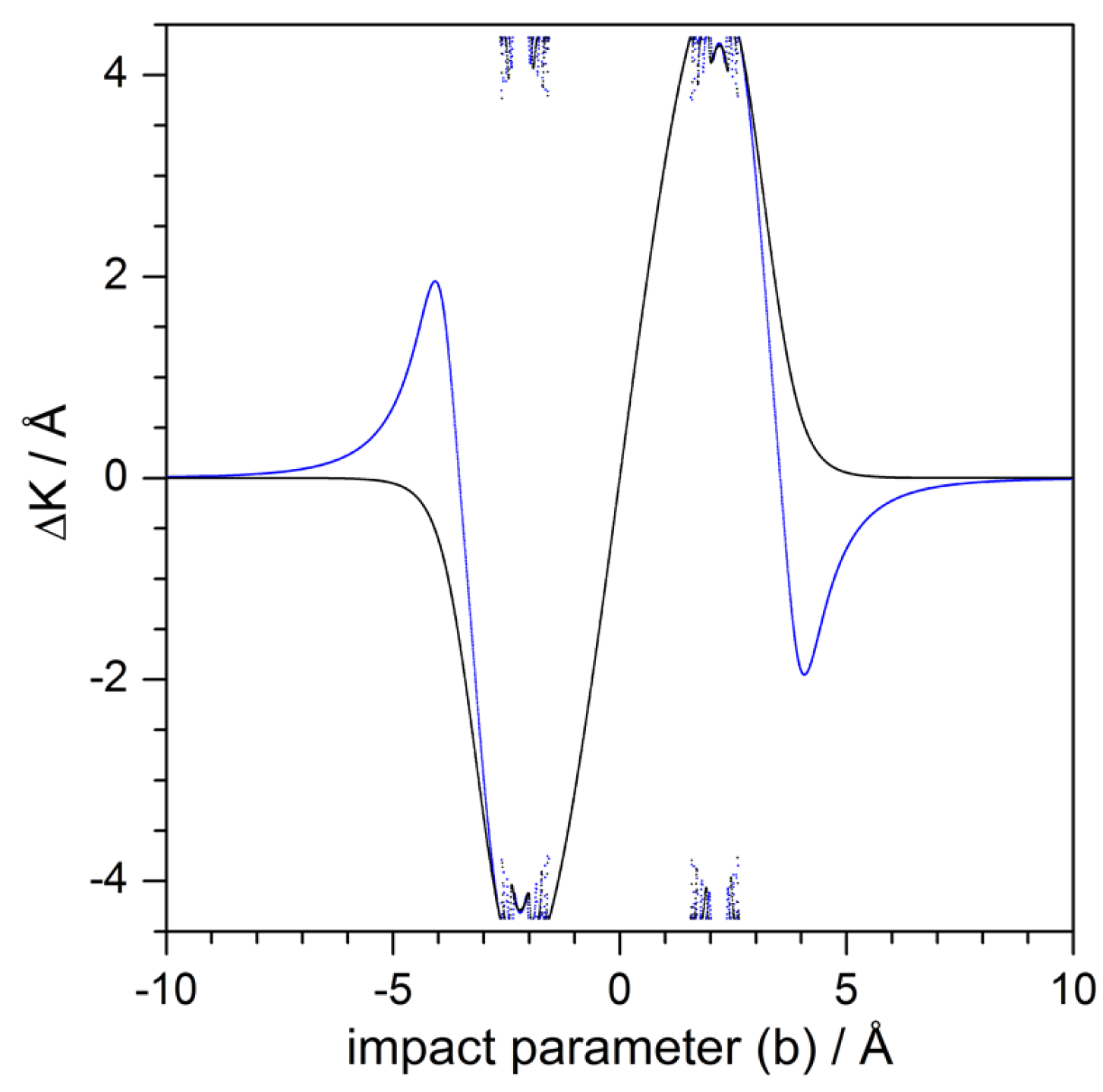
- Trajectories to the left of or to the right of only interact with the clean Pt surface and hence their deflection and incidence angles are equal. These trajectories, plus only contribute to mirror reflection from the flat surface, only contributing the intensity for , since —hence, this contribution will be more prominent as the range of impact parameters increases.
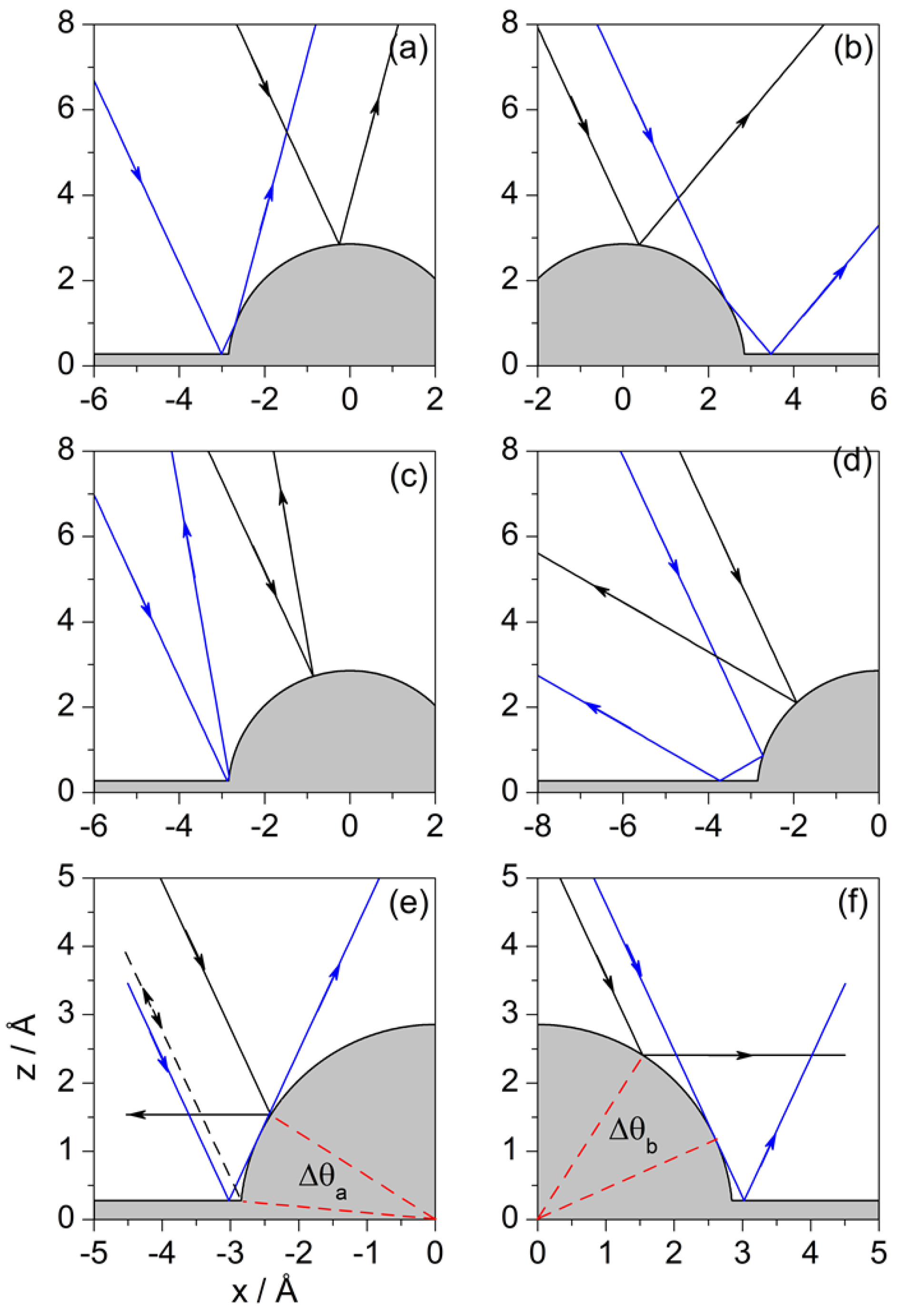
- Any trajectory between and is deflected in an angle that goes from to as the impact parameter increases. The same deflection angles are found for trajectories between and , although here the trend is that the angle increases from to as b increases. Here, we have two sets of pairs of homologous trajectories: trajectories from the first set undergo double collisions (first with the flat surface and then with the adsorbate) and trajectories from the latter only have a single collision (with the flat surface). For any of these pairs, the angular distance between their impact points on the adsorbate surface is , as can be seen in Figure 6a.
- There are also pairs of homologous trajectories with deflection angles between and . These are the trajectories confined between and , with single collisions (with the adsorbate), and between and , with double collisions (first with the adsorbate and then with the flat surface). This second set corresponds to trajectories impinging on the adsorbate within the sector B. In this case, the angular distance between impact points is not a constant, but depends on the deflection angle as . This distance gradually vanishes as both trajectories approach and is maximum when the trajectories coincide with the separatrices and . A representative set is depicted in Figure 6b.
- Trajectories and are both deflected backwards along the incidence direction, i.e., . Accordingly, trajectories between and are deflected between and after undergoing double collisions (first with the flat surface and then with the adsorbate), while trajectories between and (to the right of ) undergo single collisions. The angular distance between impact points of homologous pairs of trajectories is now , although not all trajectories between and have a correspondent between and . This is because the flat surface intersects the adsorbate surface at a distance above its center of mass instead of at . Thus, instead of reaching a maximum deflection of , we have , which is the deflection for the trajectory . An illustrative pair of homologous trajectories of this kind is displayed in Figure 6c.
- The trajectory separates the sets of homologous trajectories that are backward deflected, with the second collision taking place from the flat surface. One set is confined within trajectories and , with double collisions (first with the adsorbate and then with the flat surface), and the other set, with single collisions, is delimited by and (trajectories to the left of ). Unlike the previous set of backward-scattered homologous pairs, here all trajectories are paired, with the angular distance between their impact points being , as before. A representative pair is displayed in Figure 6d.
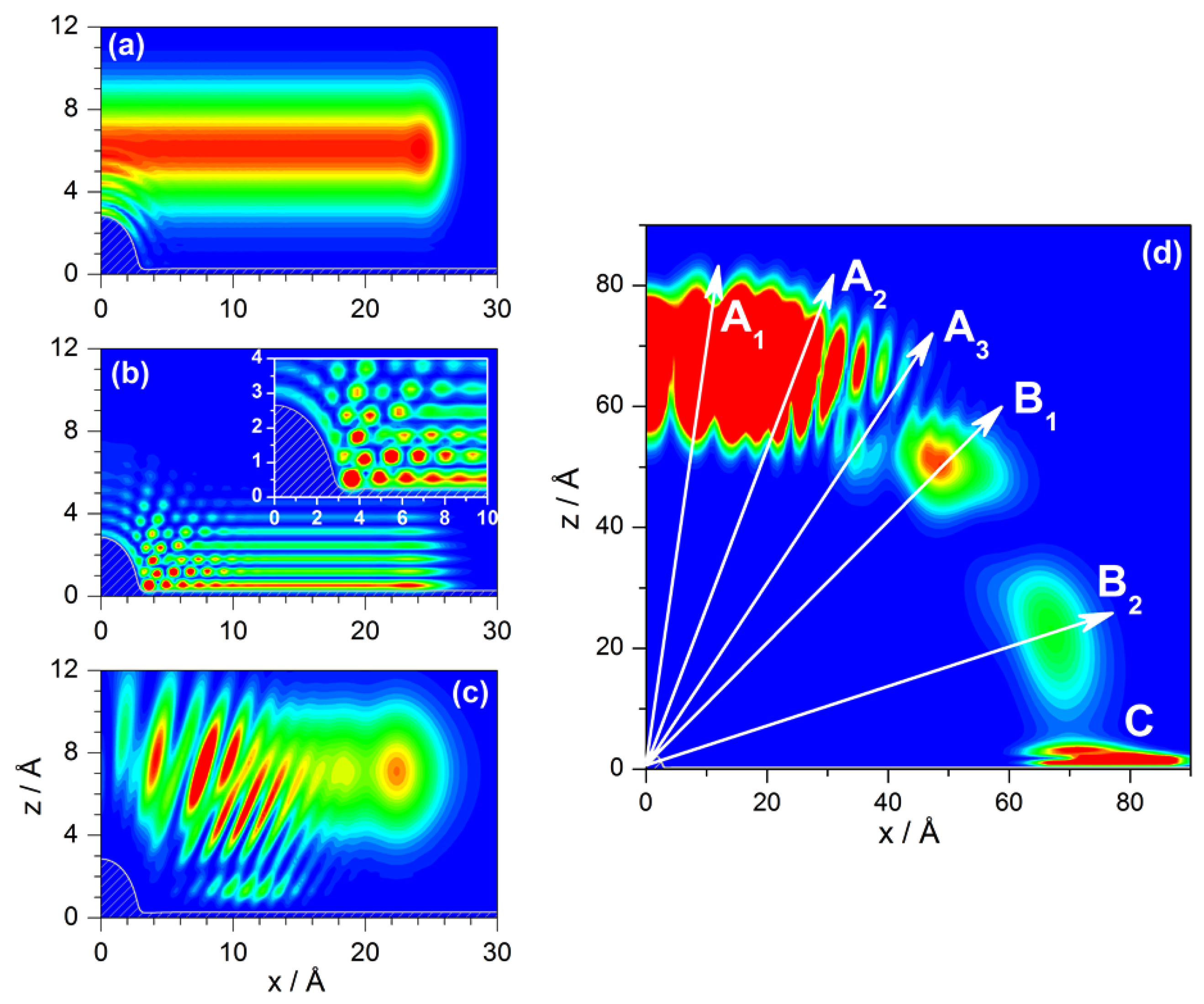
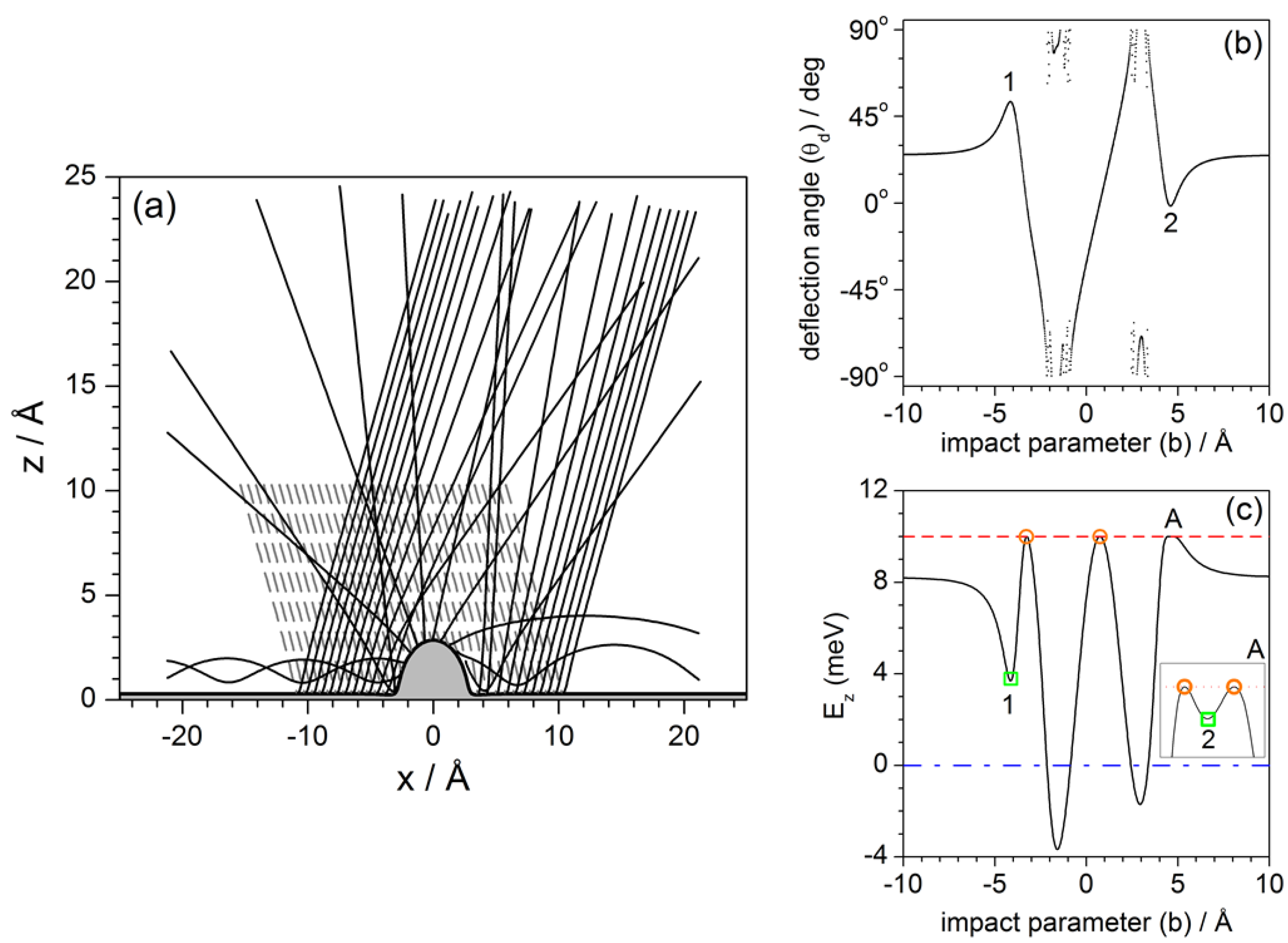
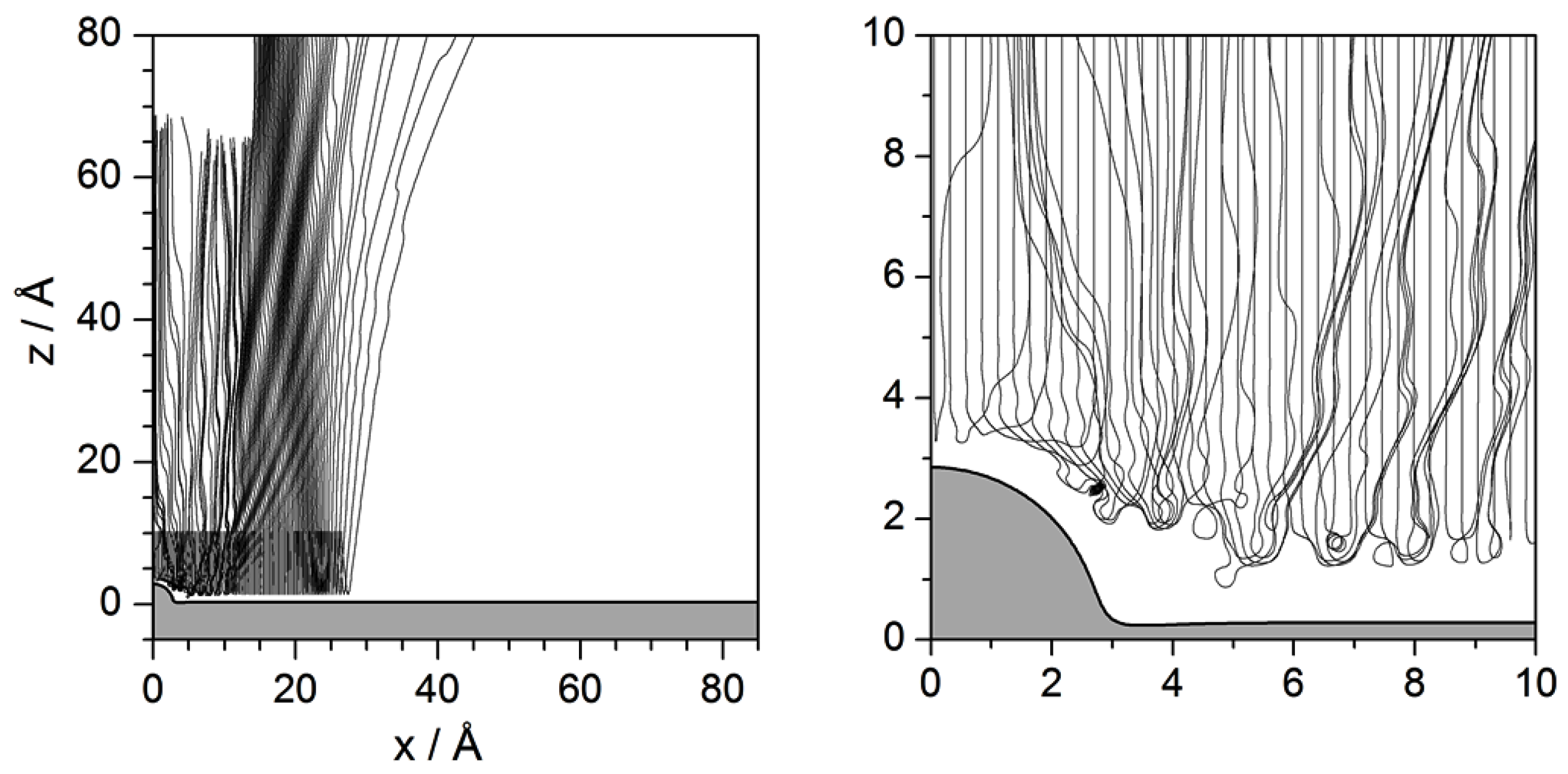
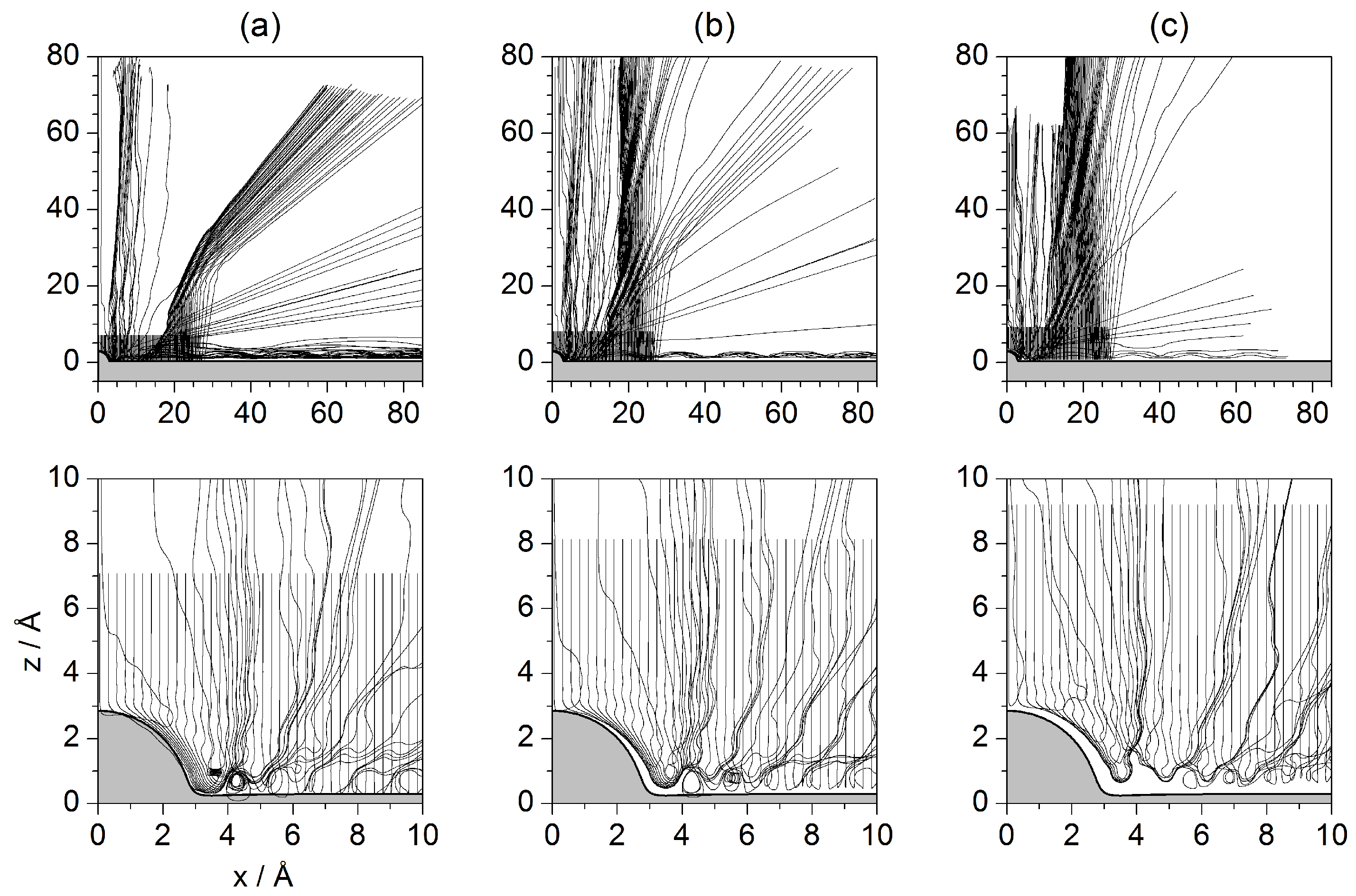
4.2. Newtonian Level
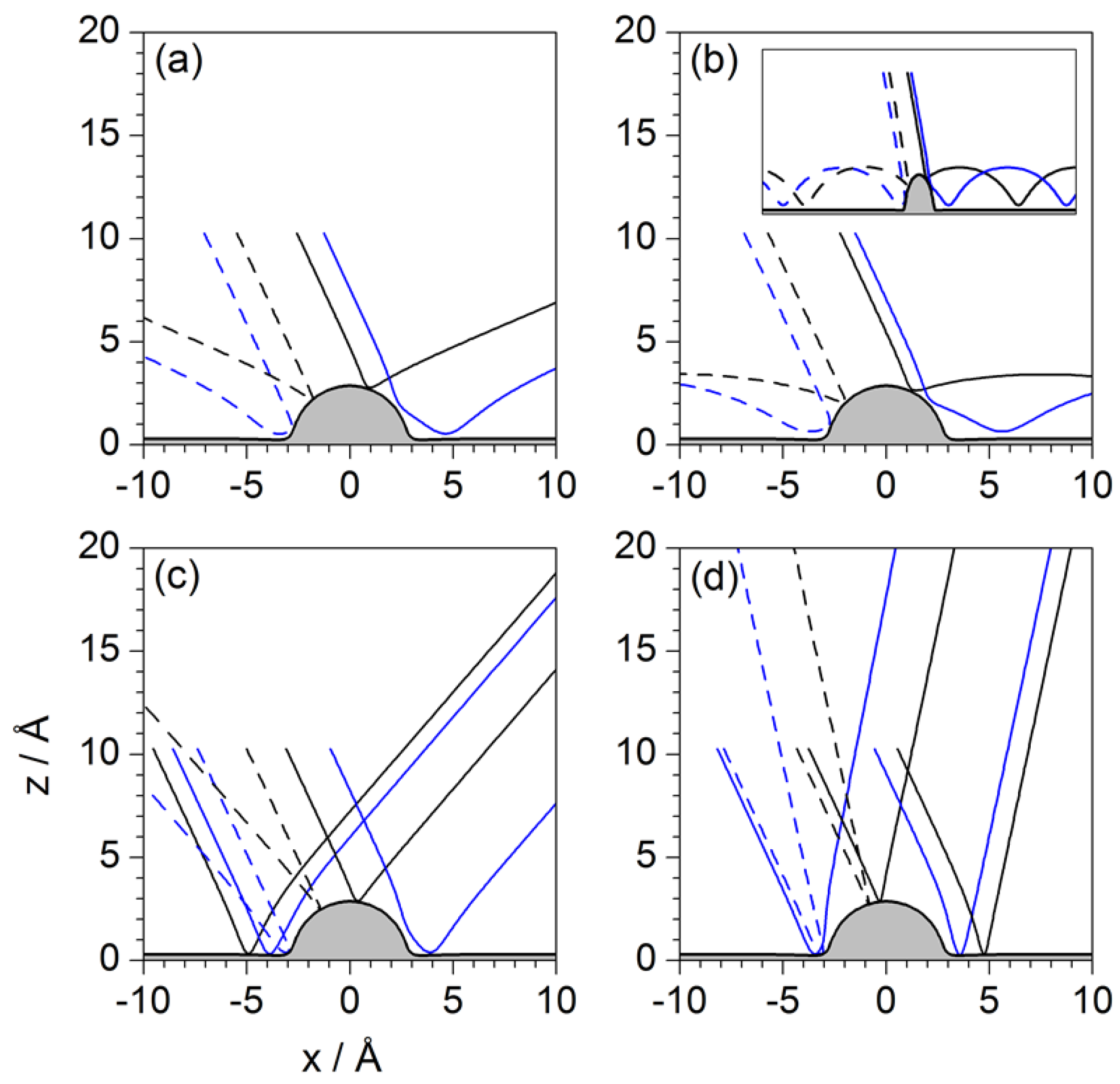
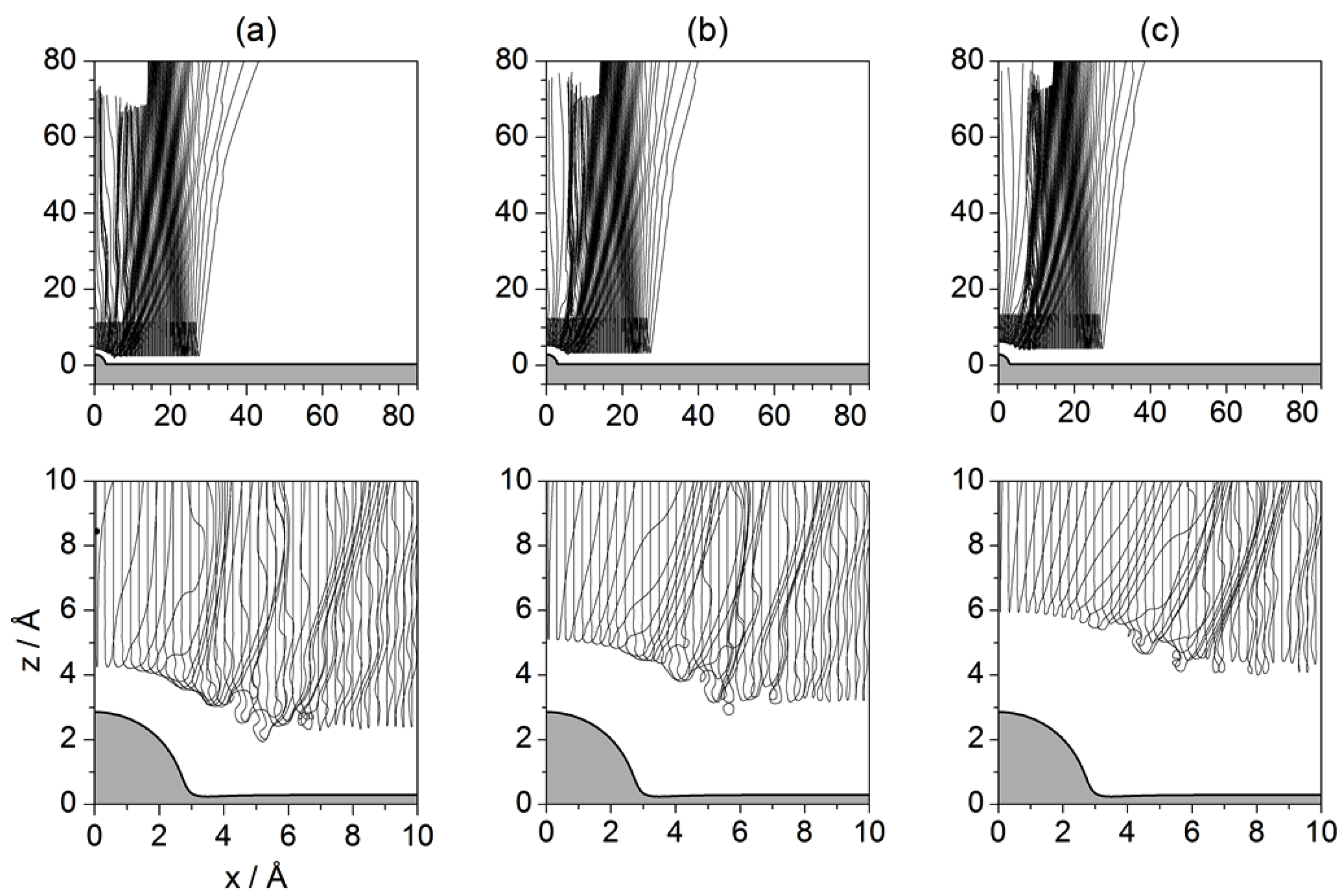
4.3. Bohmian Level
5. Conclusions
- Hard-wall model. This model is in the form of an impenetrable (fully repulsive) wall, where the interaction is reduced to a sudden impact on the He atoms on the such a wall. The first model allows an exact asymptotic analytical treatment, convenient to elucidate the main mechanism observed in the diffraction pattern produced by single adsorbed particles on nearly flat surfaces, namely reflection symmetry interference.
- Potential energy function. This interaction model is determined from fitting to the experimental data and constitutes a refinement of the previous one in the sense that there is detailed information on the intensity of the interaction between the incoming atom and the substrate at each point (in this regard, the hard-wall model is just a crude approximation). Thus, in spite of its lack of analyticity, unlike the hard-wall model, it provides us with a more realistic description of the diffraction process in real time, rendering information on additional physics, such as rainbow features or surface trapping.
- Fermatian level. This first level is the simplest one, based on computing what has been here denoted as Fermatian trajectories, which are just the direct analog to optical rays reflected on a hard wall in a medium with constant refractive index. According to this trajectory model:
- -
- These trajectories have revealed that there are pairs of homologous trajectories, such that one of the peers undergoes single scattering off the interaction potential, while the other undergoes double scattering. The fact that a trajectory collides with the CO/Pt system at one point (single collision) or at two different points (double collision) is a function of the impact parameter. Accordingly, a simple mapping can be establish, which helps to easily localize regions of impact parameters that are going to produce homologous pairs of trajectories.
- -
- The mechanism of reflection symmetry interference is associated with these paired trajectories, which is explained in the same way that we explain interference from two coherent sources: interference maxima and minima arise depending on whether the path difference between the two paths (or virtual rays) joining each source with a given observation point on a distant screen is equal to an integer number of wavelengths or to half an integer, respectively. Although these paths are nonphysical (they are just a mathematical construct), they allow us to understand in simple terms the appearance of the alternating structure of bright and dark interference fringes. In the present case, the path length arises from the extra path length of the trajectory affected by the double collision with respect to the homologous pair with single collision.
- -
- In addition, it has also been seen that two specific trajectories are deflected parallel to the surface, which can be interpreted as a mechanism precursor of the surface trapping mechanism that appears in more refined models, such as the Newtonian and the Bohmian ones.
- Newtonian level. On the next level, the Newtonian one, classical trajectories are obtained for the realistic potential energy surface describing the interaction between the He atoms and the substrate. In this case, it is not so simple to distinguish between single and double collisions, because the deflection of the trajectories near the surface, where the interaction between the He atoms and the CO/Pt surface is stronger, changes gradually very smoothly. However, we have been able to extract a series of interesting conclusions:
- -
- By means of an energy diagram (asymptotic energy along the z direction as a function of the impact parameter), we been able to devise a method that allows to determine in a simple fashion pairs of homologous (Newtonian) trajectories. This diagram is thus a suitable method to determine a behavioral mapping of initial conditions (impact parameters) for a given incidence direction (incident energy).
- -
- Accordingly, also at this level, it is possible to find an underlying mechanism responsible for the reflection symmetry interference found in the corresponding quantum intensity patterns. Actually, interference patterns could be reconstructed in the same way as with the Fermatian model, although in this case we would be dealing with a space-dependent refractive index (the potential function) and the Newtonian trajectories would play the role of Feynman’s paths. Nonetheless, although such a reconstruction is possible and the techniques are well known, this does not mean that trajectories, Fermatian or Newtonian, contain any information on the interference process; in both cases, they are only a tool to determine the interference pattern.
- -
- Regarding the trapping phenomenon, it has been found to be more prominent, with an important amount of trajectories remaining trapped permanently along the surface. This is, however, only a temporary feature, since it may disappear as son as the trapped atoms find another adsorbate. In such a case, the collisions with this adsorbate may provoke an effective transfer of energy from the parallel to the normal direction, such that the will be able to eventually leave the surface.
- -
- Finally, due to the attractive well surrounding the adsorbate, we have also observed the appearance of rainbow features, i.e., high accumulations of trajectories along particular deflection directions. However, rather than contributing with a specific, localized feature in the corresponding quantum intensity pattern, rainbows seem to manifest affecting them globally, i.e., giving rise to features that appear at different places. This has been noticed by computing exactly the same with an alternative repulsive adsorbate model, which lacks the surrounding attractive well and therefore does not give rise to the formation of rainbows.
- Bohmian level. The upper level here considered is the Bohmian one, where things change substantially if we note that the transition from the Fermatian level to the Newtonian one can be seen as a refinement associated with having a more accurate description of the interaction potential model, changing a hard wall by a “soft” wall. These are the main findings at this level:
- -
- First of all, since Bohmian trajectories are associated with a particular wave function, there is no freedom to choose a given set of initial conditions because depending on the positions selected relative to the region covered by the initial wave function, the trajectories are going to exhibit a different behavior. Thus, we have seen that while some of them are deflected quite far from the physical surface (more intense interaction region), other trajectories move just on top of it, displaying signatures of vorticality.
- -
- To better understand that point, notice that Fermatian trajectories are only ruled by the law of reflection, while Newtonian trajectories are ruled by correlations between the two degrees of freedom, x and y, that can be locally established within the interaction region (i.e., the region where the interaction potential is stronger, near the substrate). In the case of Bohmian trajectories, the dynamics is not directly ruled by the interaction potential, but by a wave field that is able to (non-classically) convey information from everywhere in the configuration space (through its phase). This makes a substantial difference between classical (Fermatian or Newtonian) and Bohmian trajectories, which may lead us to think that direct comparisons or analogies must be taken with care. That is, nothing of what has been seen at the previous levels remains at the upper one, since it is not possible to form pairs of homologous trajectories.
- -
- In this case, and contrary to the two previous models, the trajectories contain information about the interference process and, therefore, can be used to determine the fringe structure of the pattern by simply making statistics over them. If they are properly distributed across the region of the configuration space covered by the initial probability density, they will eventually distribute according to the final probability distribution by virtue of the continuity equation that they satisfy.
- -
- Regarding rainbow features, present in the Newtonian model and also, with a weak precursor, in the Fermatian one, the only a similar behavior is observed, although it is difficult to establish a unique correspondence with the phenomenon of the two previous models. In the Bohmian case, taken the trajectories that start with the same value , it is seen that their final positions show, for some range of values, a certain “precession” as increases. However, it has not been possible to uniquely identify this phenomenon with the classical rainbow. In the case of surface trapping, on the contrary, there same effect has been observed in the three models (again, in the Fermatian model it is only a weak precursor).
- -
- Finally, it has also been observed that, depending on how close or far a Bohmian trajectory is started from the physical substrate surface, it will be able to reach this surface or just bounce backwards quite far from it (from what we could call an effective nonphysical surface). Actually, if the trajectories start close to the surface, they are influenced by the web of maxima developed (and sustained for some time) around the adsorbate, displaying a rich vortical dynamics.
Acknowledgments
Conflicts of Interest
References
- Bohm, D. A suggested interpretation of the quantum theory in terms of “hidden” variables. I. Phys. Rev. 1952, 85, 166–179. [Google Scholar] [CrossRef]
- Bohm, D. A suggested interpretation of the quantum theory in terms of “hidden” variables. II. Phys. Rev. 1952, 85, 180–193. [Google Scholar] [CrossRef]
- Bohm, D.; Hiley, B.J. The Undivided Universe; Routledge: New York, NY, USA, 1993. [Google Scholar]
- Holland, P.R. The Quantum Theory of Motion; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Chattaraj, P.K. (Ed.) Quantum Trajectories; CRC Taylor and Francis: New York, NY, USA, 2010. [Google Scholar]
- Hughes, K.H.; Parlant, G. (Eds.) Quantum Trajectories; CCP6: Daresbury, UK, 2011. [Google Scholar]
- Oriols, X.; Mompart, J. (Eds.) Applied Bohmian Mechanics: From Nanoscale Systems to Cosmology; Pan Standford Publishing: Singapore, 2012. [Google Scholar]
- Sanz, A.S.; Miret-Artés, S. A Trajectory Description of Quantum Processes. II. Applications; Lecture Notes in Physics; Springer: Heidelberg/Berlin, Germany, 2014. [Google Scholar]
- Benseny, A.; Albareda, G.; Sanz, A.S.; Mompart, J.; Oriols, X. Applied Bohmian mechanics. Eur. Phys. J. D 2014, 68, 286. [Google Scholar] [CrossRef]
- Dürr, D.; Teufel, S. Bohmian Mechanics: The Physics and Mathematics of Quantum Theory; Springer: Heidelberg/Berlin, Germany, 2009. [Google Scholar]
- Dürr, D.; Goldstein, S.; Zanghì, N. Quantum Physics without Quantum Philosophy; Springer: Heidelberg/Berlin, Germany, 2013. [Google Scholar]
- Sanz, A.S.; Miret-Artés, S. A Trajectory Description of Quantum Processes. I. Fundamentals; Lecture Notes in Physics; Springer: Heidelberg/Berlin, Germany, 2012. [Google Scholar]
- Wyatt, R.E. Quantum Dynamics with Trajectories; Springer: New York, NY, USA, 2005. [Google Scholar]
- Sanz, A.S. Bohm’s approach to quantum mechanics: Alternative theory or practical picture? arXiv, 2017; arXiv:1707.00609v1. [Google Scholar]
- Kocsis, S.; Braverman, B.; Ravets, S.; Stevens, M.J.; Mirin, R.P.; Shalm, L.K.; Steinberg, A.M. Observing the average trajectories of single photons in a two-slit interferometer. Science 2011, 332, 1170–1173. [Google Scholar] [CrossRef] [PubMed]
- Couder, Y.; Protière, S.; Fort, E.; Boudaoud, A. Dynamical phenomena: Walking and orbiting droplets. Nature 2005, 437, 208. [Google Scholar] [CrossRef] [PubMed]
- Couder, Y.; Fort, E. Single-particle diffraction and interference at a macroscopic scale. Phys. Rev. Lett. 2006, 97, 154101. [Google Scholar] [CrossRef] [PubMed]
- Protière, S.; Boudaoud, A.; Couder, Y. Particle-wave association on a fluid interface. J. Fluid. Mech. 2006, 554, 85–108. [Google Scholar] [CrossRef]
- Fort, E.; Eddi, A.; Boudaoud, A.; Moukhtar, J.; Couder, Y. Path-memory induced quantization of classical orbits. Proc. Natl. Acad. Sci. USA 2010, 108, 17515–17520. [Google Scholar] [CrossRef]
- Bush, J.W.M. Quantum mechanics writ large. Proc. Natl. Acad. Sci. USA 2010, 107, 17455–17456. [Google Scholar] [CrossRef]
- Harris, D.M.; Moukhtar, J.; Fort, E.; Couder, Y.; Bush, J.W.M. Wavelike statistics from pilot-wave dynamics in a circular corral. Phys. Rev. E 2013, 88, 011001. [Google Scholar] [CrossRef] [PubMed]
- Bush, J.W.M. Pilot-wave hydrodynamics. Annu. Rev. Fluid Mech. 2015, 47, 269–292. [Google Scholar] [CrossRef]
- Lahee, A.M.; Manson, J.R.; Toennies, J.P.; Wöll, C. Observation of interference oscillations in helium scattering from single surface defects. Phys. Rev. Lett. 1986, 57, 471–474. [Google Scholar] [CrossRef] [PubMed]
- Lahee, A.M.; Manson, J.R.; Toennies, J.P.; Wöll, C. Helium atom differential cross sections for scattering from single adsorbed CO molecules on a Pt(111) surface. J. Chem. Phys. 1987, 86, 7194–7203. [Google Scholar] [CrossRef]
- Drolshagen, G.; Vollmer, R. Atom scattering from surfaces with isolated impurities: Calculations for hard wall and soft potentials. J. Chem. Phys. 1987, 87, 4948–4957. [Google Scholar] [CrossRef]
- Graham, A.P.; Hofman, F.; Toennies, J.P.; Manson, J.R. Helium atom scattering from isolated CO molecules on copper (001). J. Chem. Phys. 1996, 105, 2093–2098. [Google Scholar] [CrossRef]
- Yinnon, A.T.; Kosloff, R.; Gerber, R.B. Atom scattering from isolated adsorbates on surfaces: Rainbows, diffraction interferences, and trapping resonances. J. Chem. Phys. 1988, 88, 7209–7220. [Google Scholar] [CrossRef]
- Carré, M.N.; Lemoine, D. Fully quantum study of the 3D diffractive scattering of He from isolated CO adsorbates on Pt(111). J. Chem. Phys. 1994, 101, 5305–5312. [Google Scholar] [CrossRef]
- Lemoine, D. Atomic scattering from single adsorbates: What can we learn from the gas phase? Phys. Rev. Lett. 1998, 81, 461–464. [Google Scholar] [CrossRef]
- Choi, B.H.; Tang, K.T.; Toennies, J.P. Interpretation of helium atom scattering from isolated CO molecules on copper (001) based on an exact quantum mechanical model. J. Chem. Phys. 1997, 107, 1631–1633. [Google Scholar] [CrossRef]
- Choi, B.H.; Tang, K.T.; Toennies, J.P. Quantum-mechanical scattering of an atom from a rigid hemisphere on a flat surface. J. Chem. Phys. 1997, 107, 9437–9446. [Google Scholar] [CrossRef]
- Sanz, A.S.; Borondo, F.; Miret-Artés, S. Quantum trajectories in atom-surface scattering with single adsorbates: The role of quantum vortices. J. Chem. Phys. 2004, 120, 8794–8806. [Google Scholar] [CrossRef] [PubMed]
- Sanz, A.S.; Borondo, F.; Miret-Artés, S. Role of quantum vortices in atomic scattering from single adsorbates. Phys. Rev. B 2004, 69, 115413. [Google Scholar] [CrossRef]
- Hofmann, F.; Toennies, J.P. High-resolution helium atom time-of-flight spectroscopy of low-frequency vibrations of adsorbates. Chem. Rev. 1996, 96, 1307–1326. [Google Scholar] [CrossRef] [PubMed]
- Kleyn, A.W.; Horn, T.C.M. Rainbow scattering from solid surfaces. Phys. Rep. 1991, 199, 191–230. [Google Scholar] [CrossRef]
- Glebov, A.; Manson, J.R.; Skofronick, J.G.; Toennies, J.P. Defect-mediated diffraction resonances in surface scattering. Phys. Rev. Lett. 1997, 78, 1508–1511. [Google Scholar] [CrossRef]
- Child, M.S. Molecular Collision Theory; Academic Press: London, UK, 1974. [Google Scholar]
- Morse, P.M. Diatomic molecules according to the wave mechanics. II. Vibrational levels. Phys. Rev. 1929, 34, 57–64. [Google Scholar] [CrossRef]
- Dubertrand, R.; Shim, J.B.; Struyve, W. Bohmian trajectories for the half-line barrier. J. Phys. A 2018, 51, 085302. [Google Scholar] [CrossRef]
- Prosser, R.D. The interpretation of diffraction and interference in terms of energy flow. Int. J. Theor. Phys. 1976, 15, 169–180. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Guantes, R.; Sanz, A.S.; Margalef-Roig, J.; Miret-Artés, S. Atom-surface diffraction: A trajectory description. Surf. Sci. Rep. 2004, 53, 199–330. [Google Scholar] [CrossRef]
- Sanz, A.S.; Miret-Artés, S. Selective adsorption resonances: Quantum and stochastic approaches. Phys. Rep. 2007, 451, 37–154. [Google Scholar] [CrossRef]
- Leforestier, C.; Bisseling, R.H.; Cerjan, C.; Feit, M.D.; Friesner, R.; Guldberg, A.; Hammerich, A.; Jolicard, G.; Karrlein, W.; Meyer, H.D.; et al. A comparison of different propagation schemes for the time dependent schrödinger equation. J. Comput. Phys. 1991, 94, 59–80. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in Fortran 77: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Sanz, A.S.; Borondo, F.; Miret-Artés, S. Particle diffraction studied using quantum trajectories. J. Phys. Condens. Matter 2002, 14, 6109–6145. [Google Scholar] [CrossRef]
- Morse, P.M.; Feshbach, H. Methods of Theoretical Physics; McGraw-Hill: New York, NY, USA, 1953. [Google Scholar]
- Joachain, C.J. Quantum Collision Theory; North-Holland: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Farías, D.; Rieder, K.H. Atomic beam diffraction from solid surfaces. Rep. Prog. Phys. 1998, 61, 1575–1664. [Google Scholar] [CrossRef]
- Gerber, R.B.; Yinnon, A.T.; Kosloff, R. Effects of isolated impurities on atom scattering from crystalline surfaces: Exact quantum-mechanical calculations. Chem. Phys. Lett. 1984, 105, 523–526. [Google Scholar] [CrossRef]
- Choi, B.H.; Graham, A.P.; Tang, K.T.; Toennies, J.P. Helium atom scattering from isolated CO molecules on a Pt(111) surface: Experiment versus close-coupling calculations for a realistic He-CO potential. J. Chem. Phys. 2000, 112, 10538–10547. [Google Scholar] [CrossRef]
- McCullough, E.A.; Wyatt, R.E. Quantum dynamics of the collinear (H,H2) reaction. J. Chem. Phys. 1969, 51, 1253–1254. [Google Scholar] [CrossRef]
- McCullough, E.A.; Wyatt, R.E. Dynamics of the collinear H+H2 reaction. I. Probability density and flux. J. Chem. Phys. 1971, 54, 3578–3591. [Google Scholar] [CrossRef]
- McCullough, E.A.; Wyatt, R.E. Dynamics of the collinear H+H2 reaction. II. Energy analysis. J. Chem. Phys. 1971, 54, 3592–3600. [Google Scholar] [CrossRef]
- Schiff, L.I. Quantum Mechanics, 3rd ed.; McGraw-Hill: Singapore, 1968. [Google Scholar]
- Bohm, D.; Vigier, J.P. Model of the causal interpretation of quantum theory in terms of a fluid with irregular fluctuations. Phys. Rev. 1954, 96, 208–216. [Google Scholar] [CrossRef]
- Bohm, D.; Hiley, B.J. Non-Locality and Locality in the Stochastic Interpretation of Quantum Mechanics. Phys. Rep. 1989, 172, 93–122. [Google Scholar] [CrossRef]
- Nelson, E. Derivation of the Schrödinger equation from Newtonian mechanics. Phys. Rev. 1966, 150, 1079–1085. [Google Scholar] [CrossRef]
- Takabayasi, T. On the formulation of quantum mechanics associated with classical pictures. Prog. Theor. Phys. 1952, 8, 143–182. [Google Scholar] [CrossRef]
- Efthymiopoulos, C.; Delis, N.; Contopoulos, G. Wavepacket approach to particle diffraction by thin targets: Quantum trajectories and arrival times. Ann. Phys. 2012, 327, 438–460. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanz, Á.S. Atom-Diffraction from Surfaces with Defects: A Fermatian, Newtonian and Bohmian Joint View. Entropy 2018, 20, 451. https://doi.org/10.3390/e20060451
Sanz ÁS. Atom-Diffraction from Surfaces with Defects: A Fermatian, Newtonian and Bohmian Joint View. Entropy. 2018; 20(6):451. https://doi.org/10.3390/e20060451
Chicago/Turabian StyleSanz, Ángel S. 2018. "Atom-Diffraction from Surfaces with Defects: A Fermatian, Newtonian and Bohmian Joint View" Entropy 20, no. 6: 451. https://doi.org/10.3390/e20060451
APA StyleSanz, Á. S. (2018). Atom-Diffraction from Surfaces with Defects: A Fermatian, Newtonian and Bohmian Joint View. Entropy, 20(6), 451. https://doi.org/10.3390/e20060451




