Entropy Generation on Nanofluid Thin Film Flow of Eyring–Powell Fluid with Thermal Radiation and MHD Effect on an Unsteady Porous Stretching Sheet
Abstract
:1. Introduction
2. Basic Equations
3. Mathematical Formulation
4. Physical Quantities
5. Solution of the Problem by Homotopy Analysis Method
5.1. Equations of Zeroth-Order Deformation
5.2. Equation of the nth Order Deformation
6. Entropy Generation Analysis
- Diffusive irreversibility (DI) (also known as Diffusion).
- Fluid friction irreversibility (FFI).
- Heat transfer irreversibility(HTI) (also known as Conduction effect).
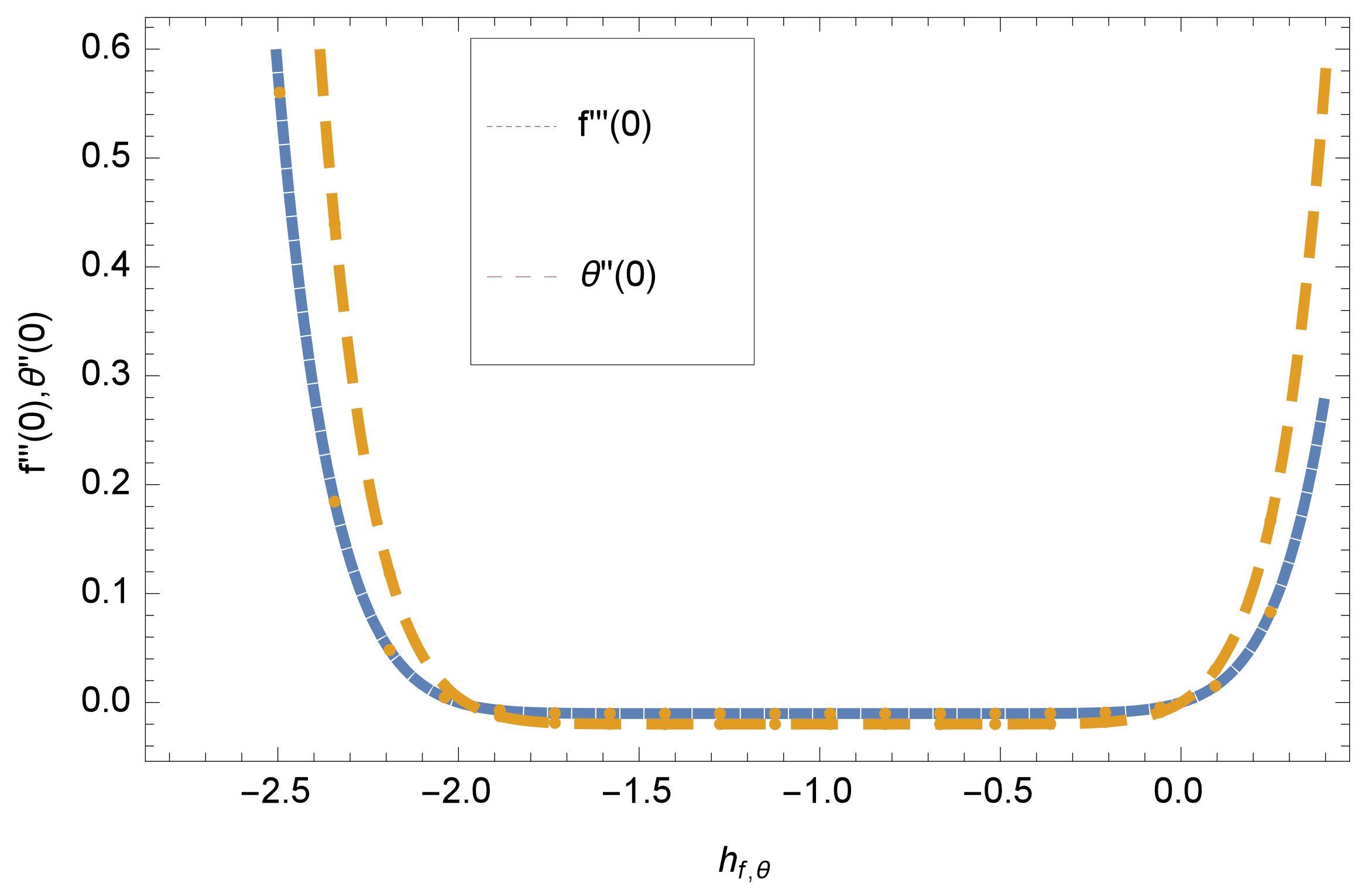
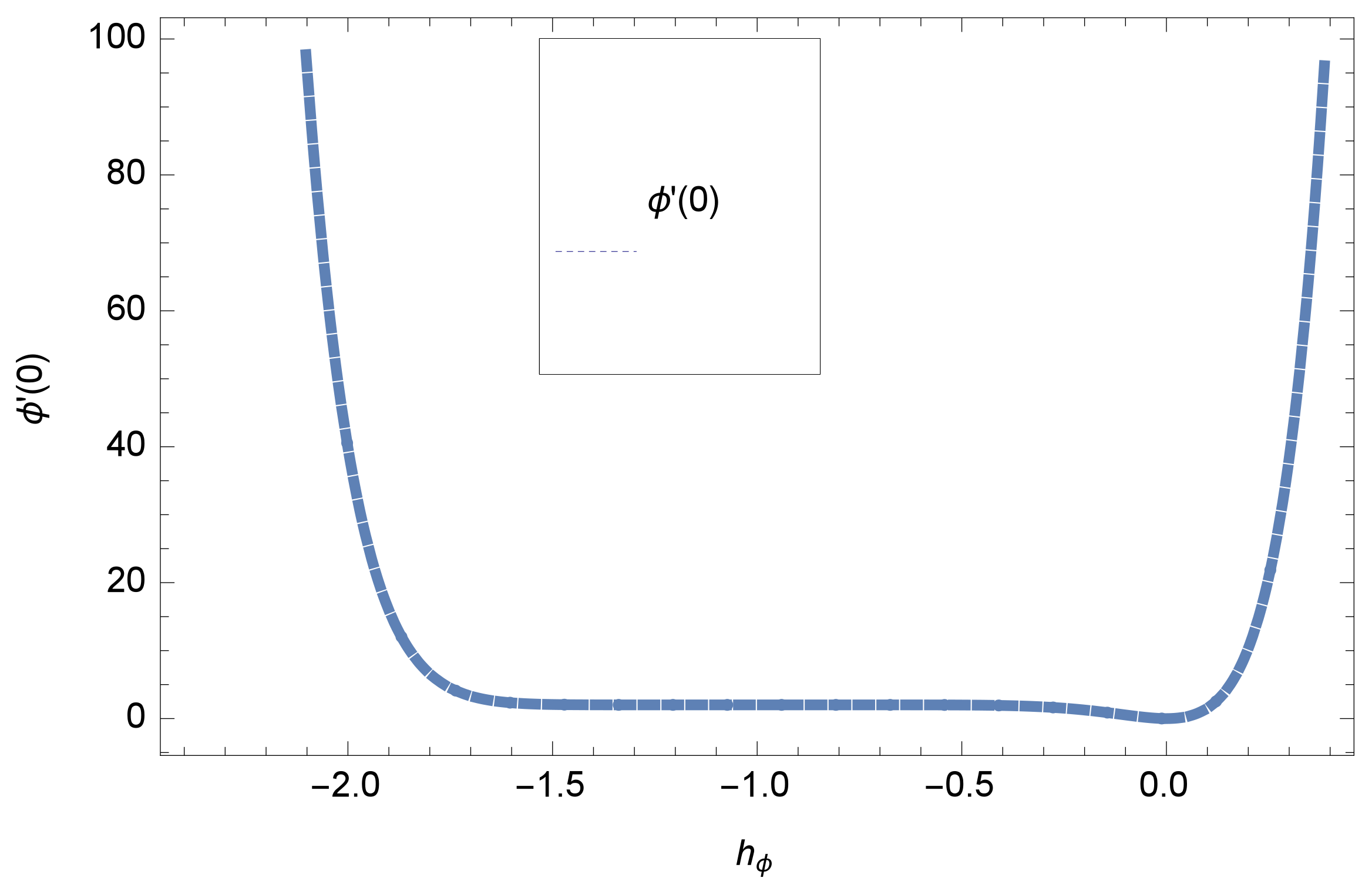
7. Convergence of Solution
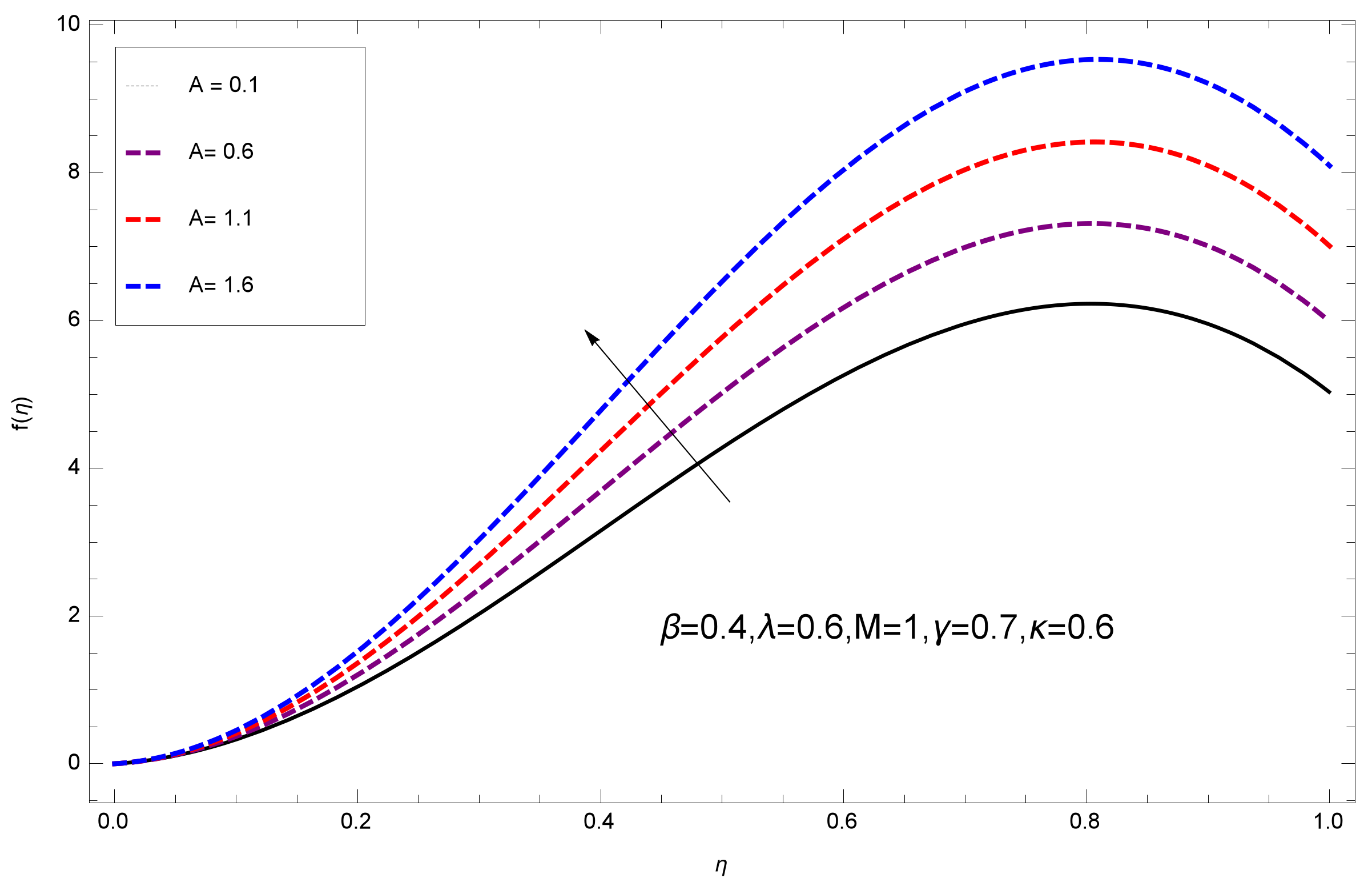
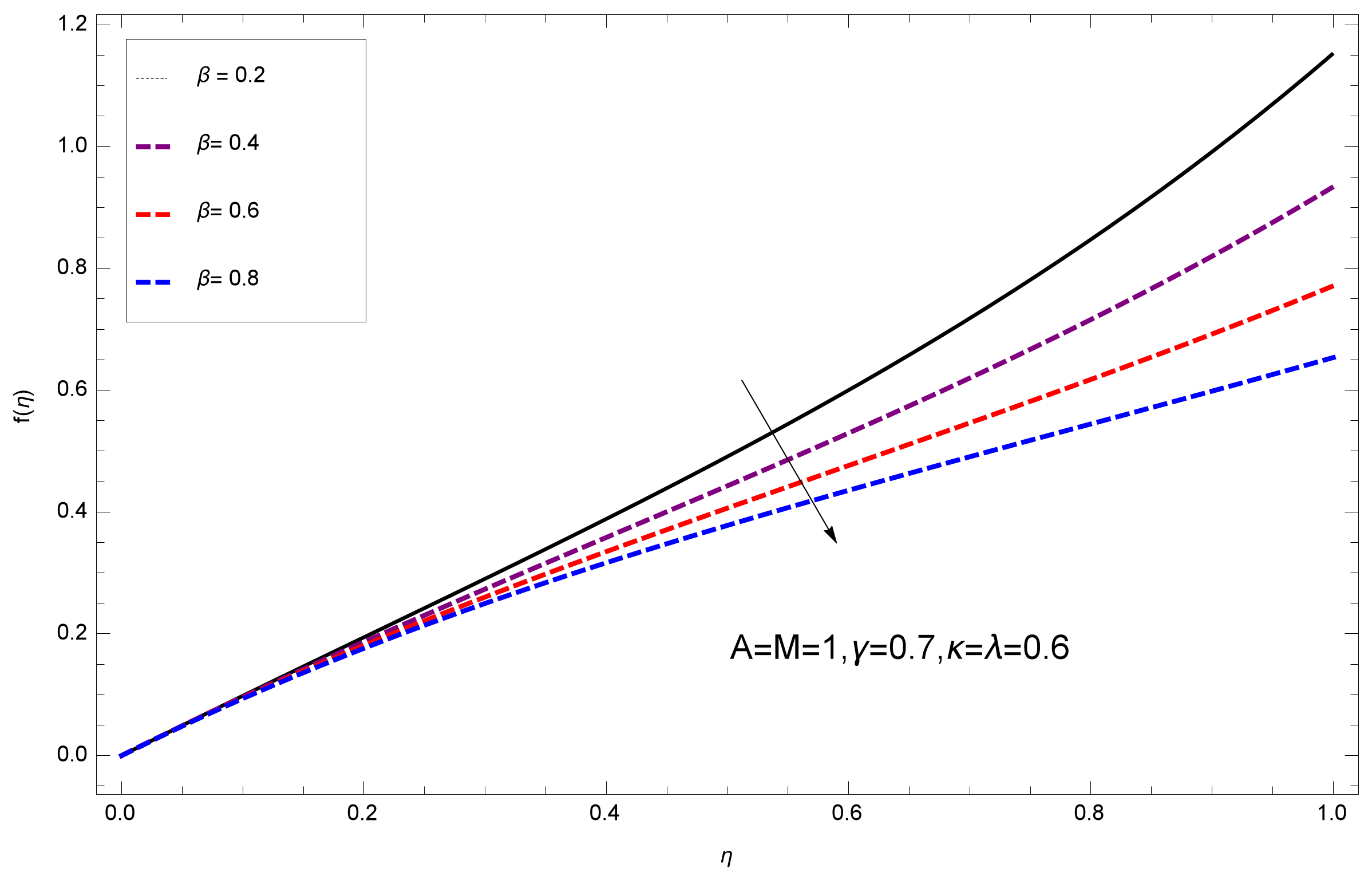
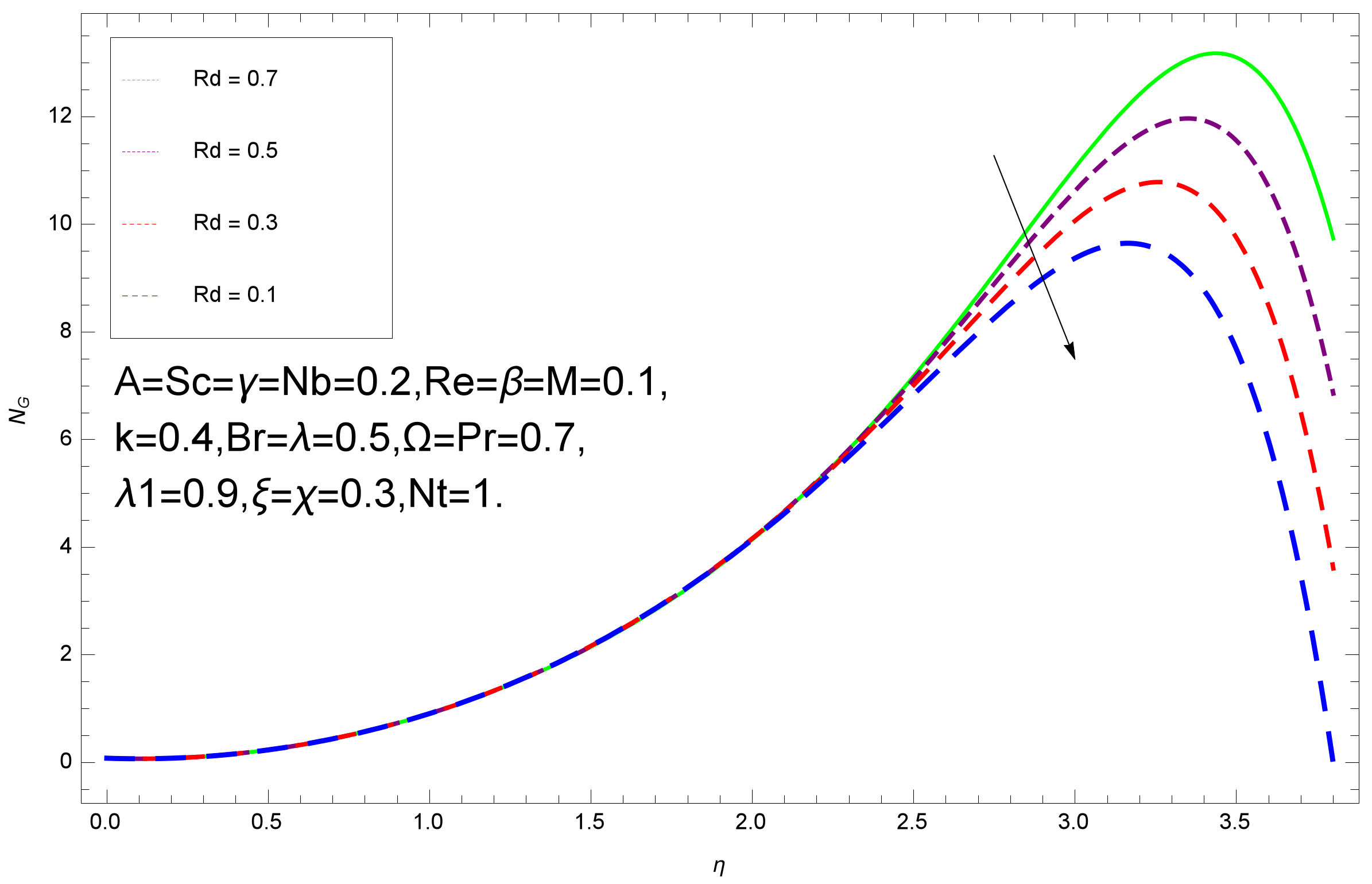
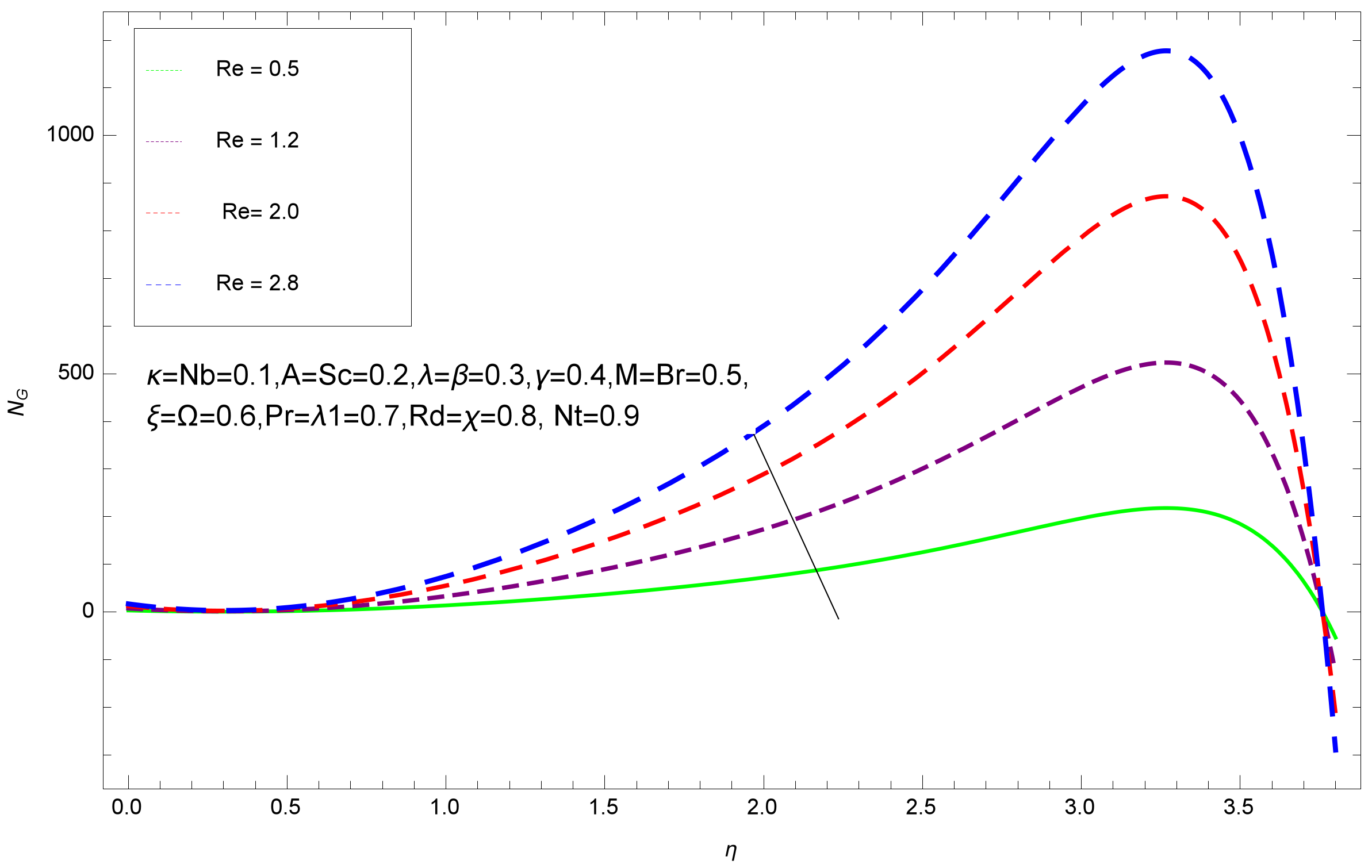
8. Results and Discussion
9. Tables Discussion
10. Conclusions
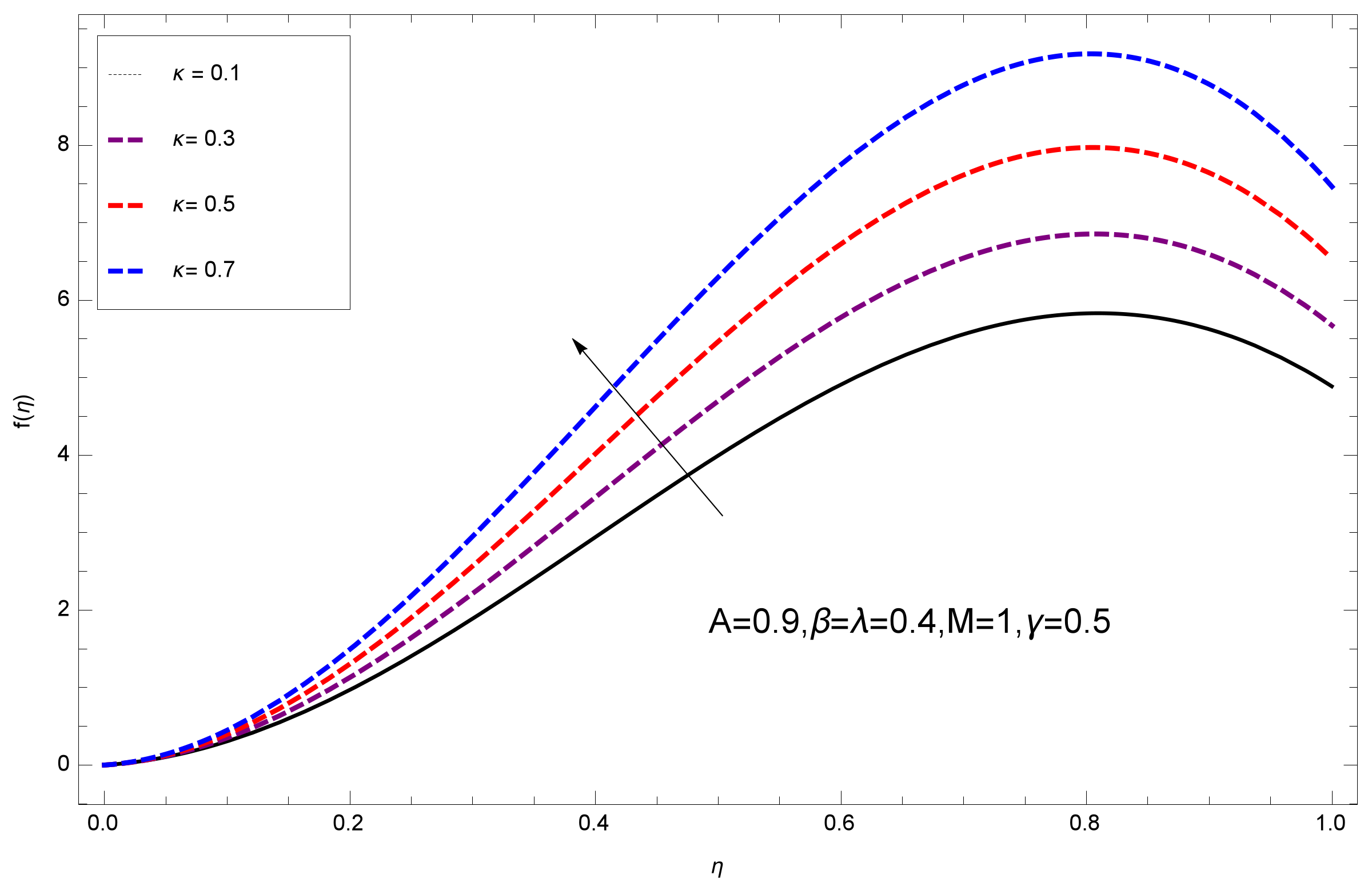
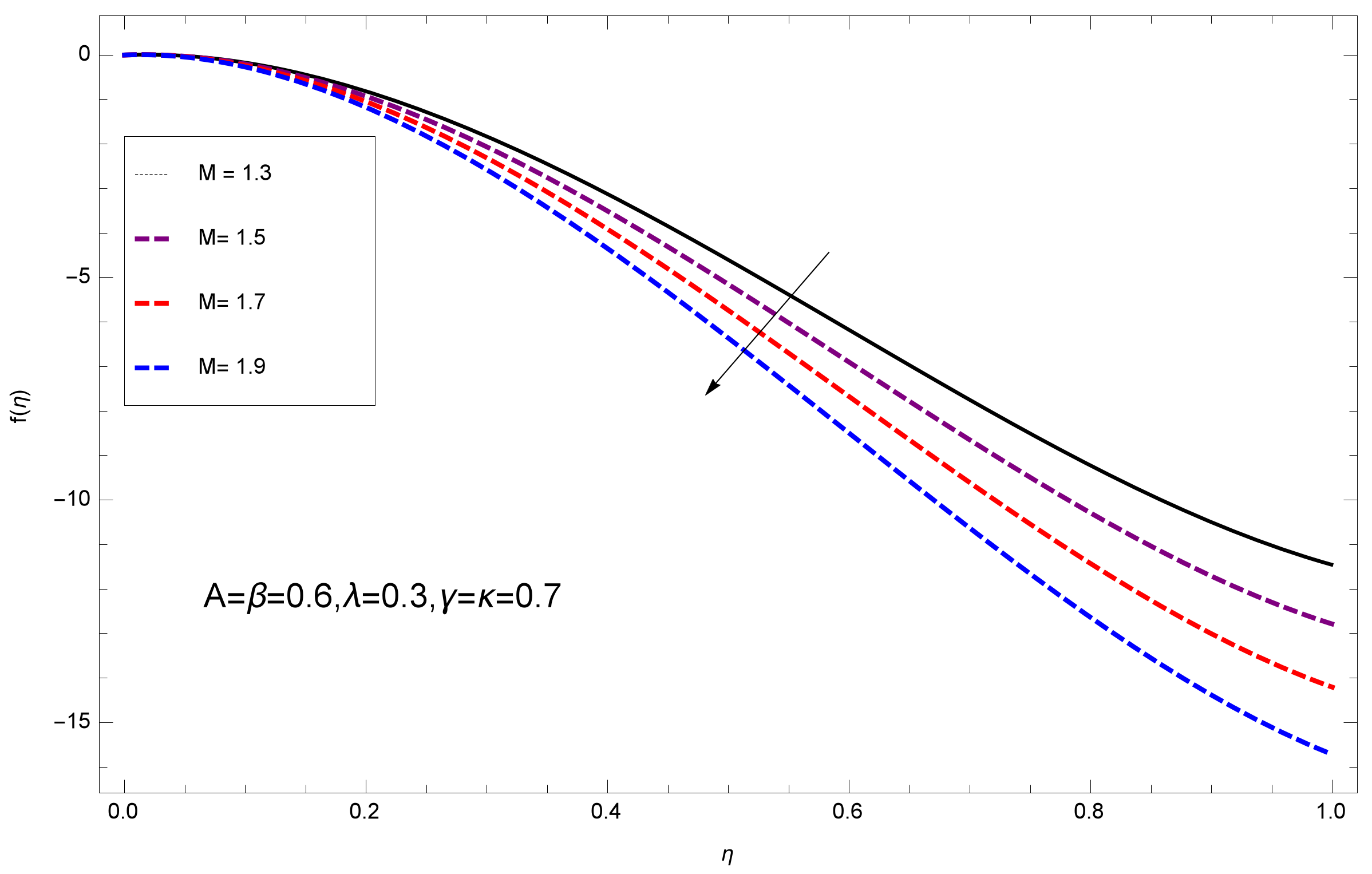
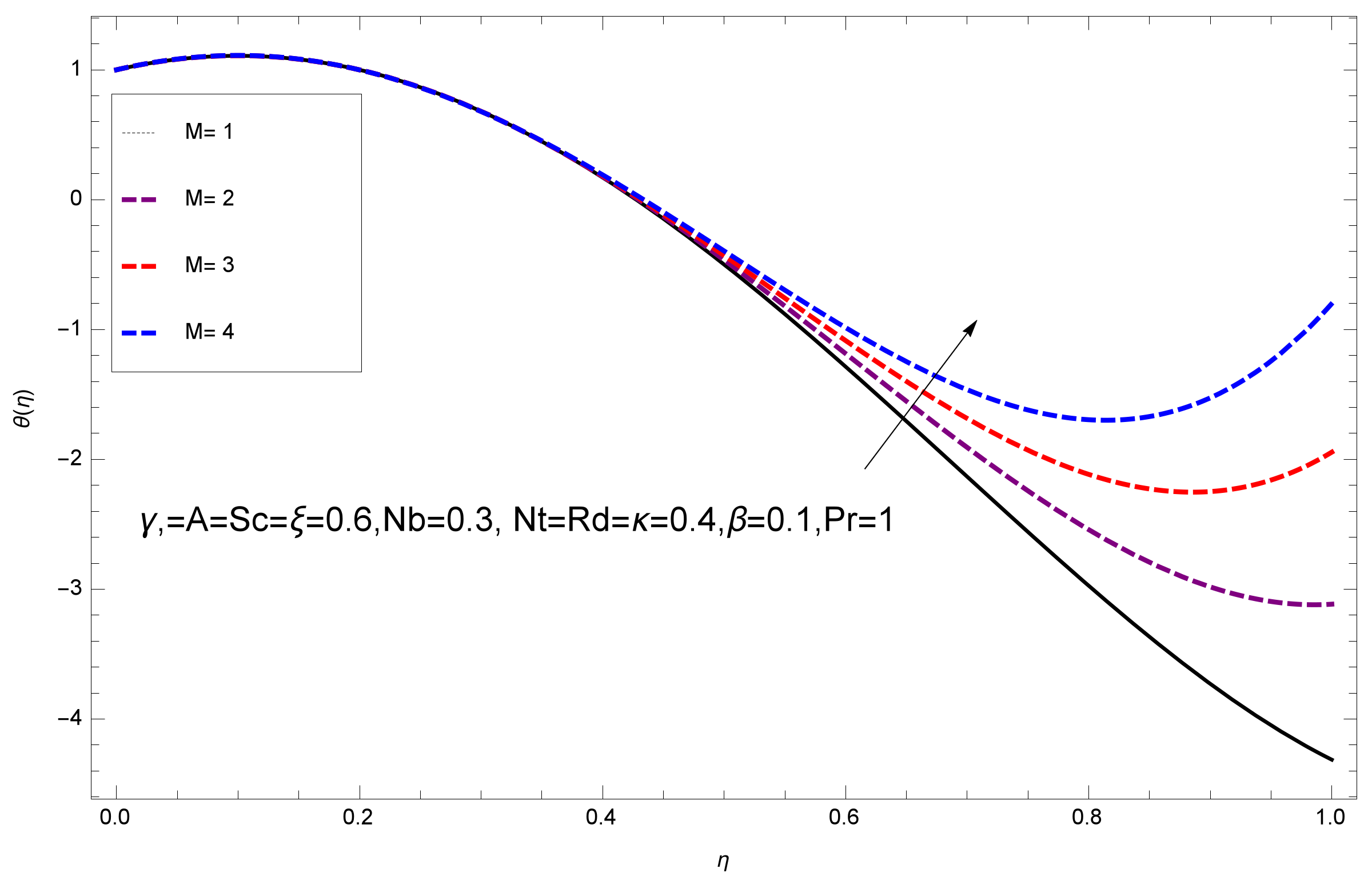
- It is perceived that the large values of Magnetic parameter M drop the velocity distribution of the nanofluid films.
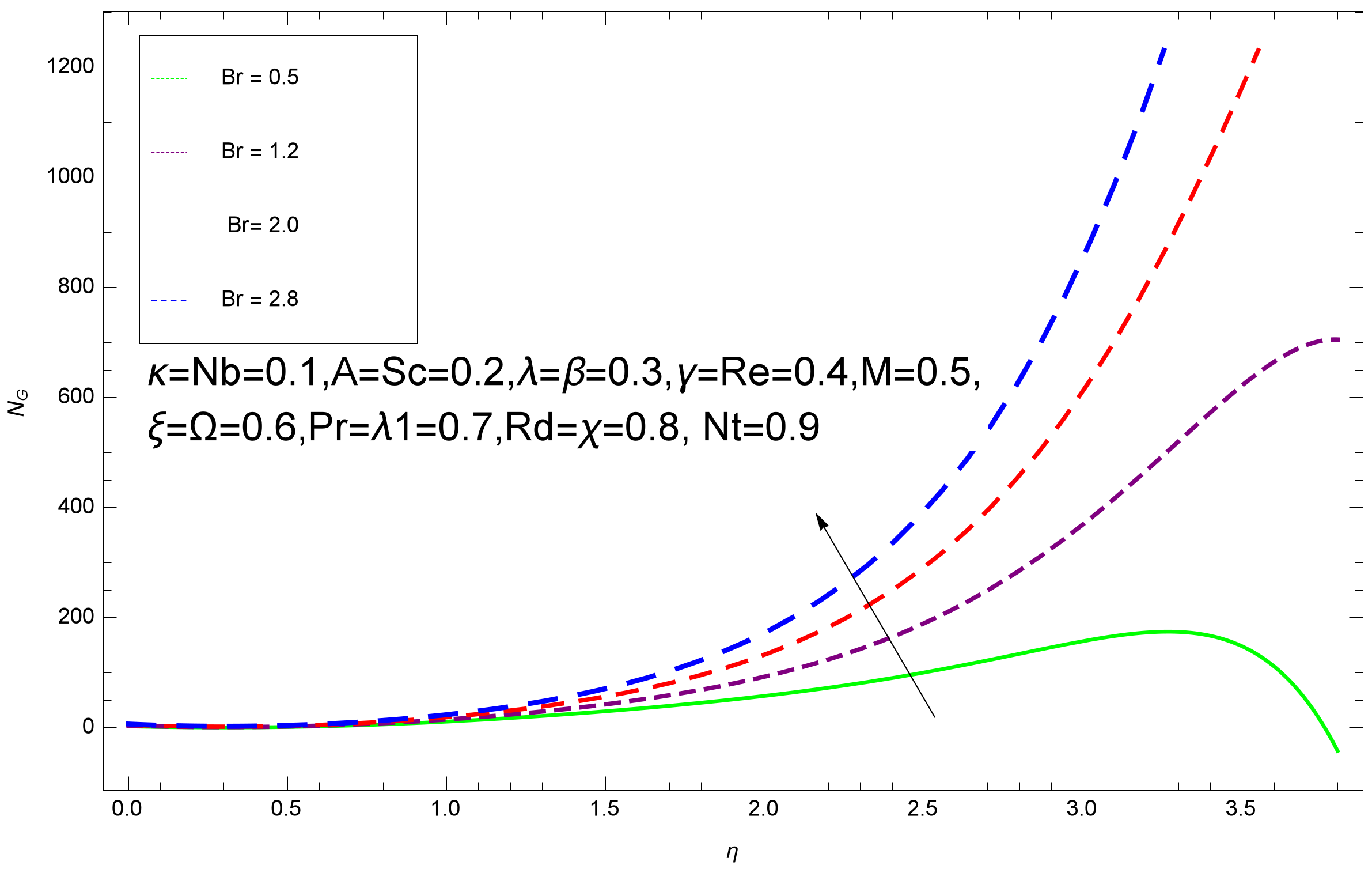
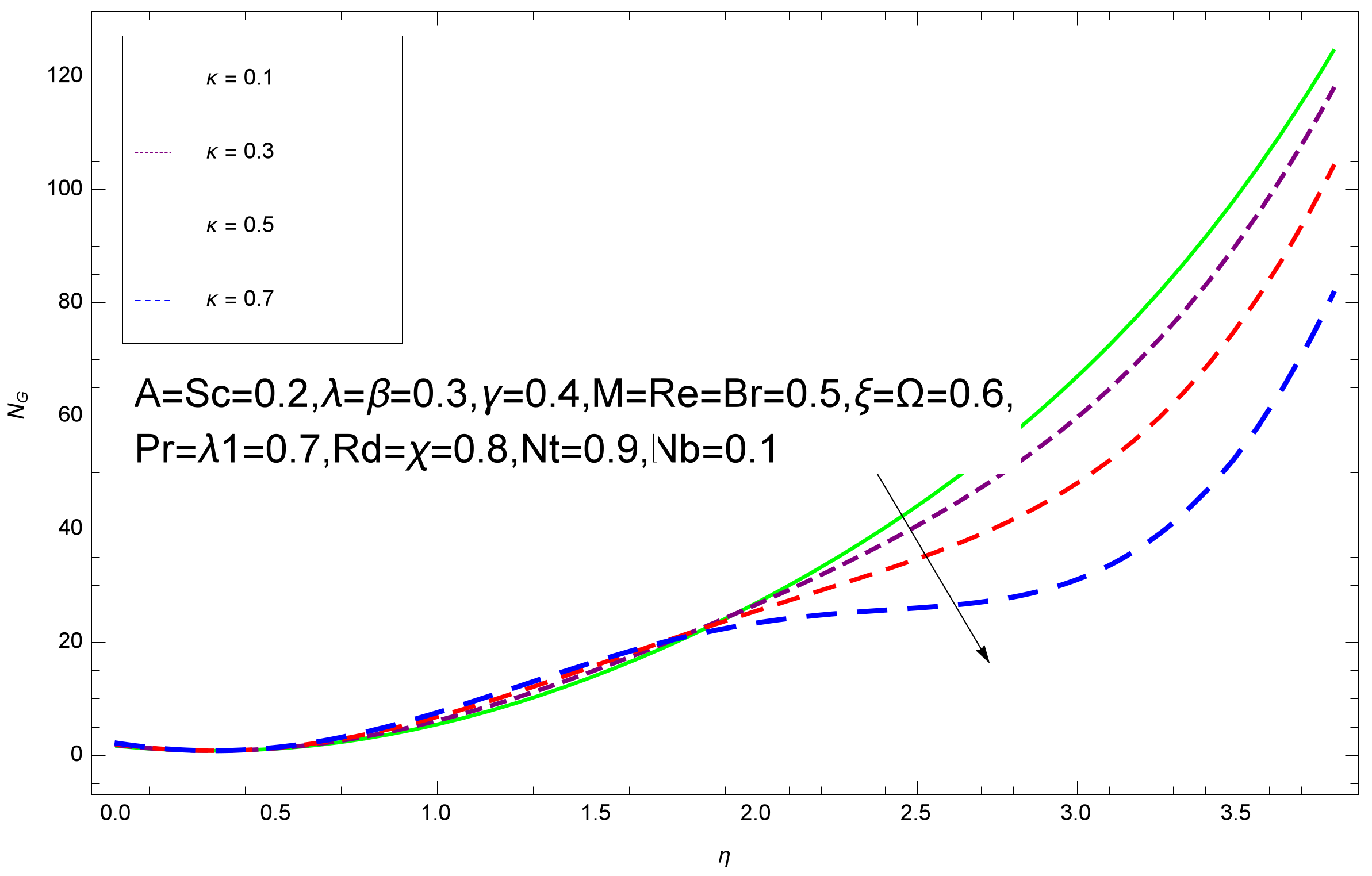
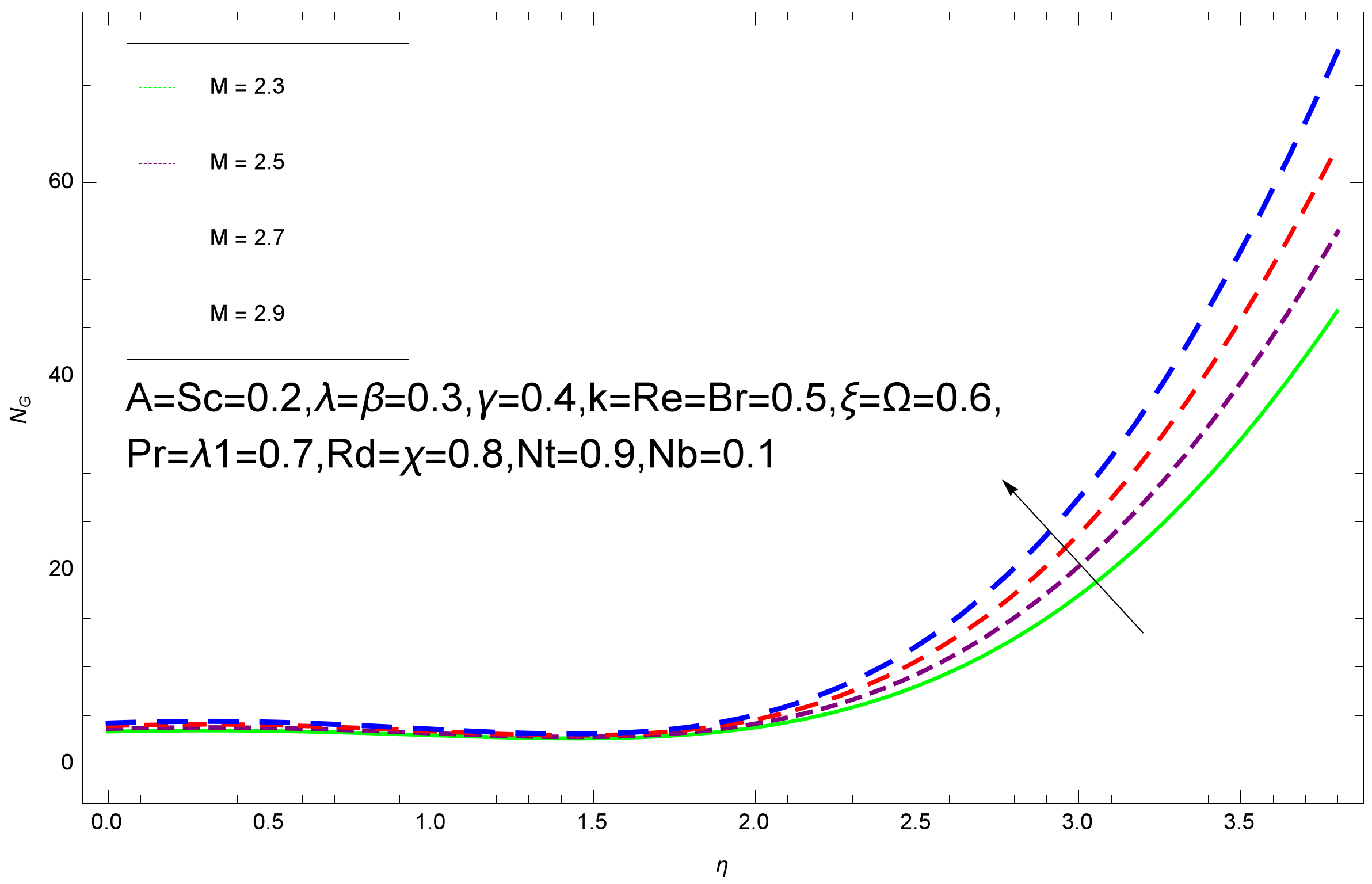
- Entropy profile increases with the increasing values of Brinkmann , Hartmann number M, and Reynolds number .
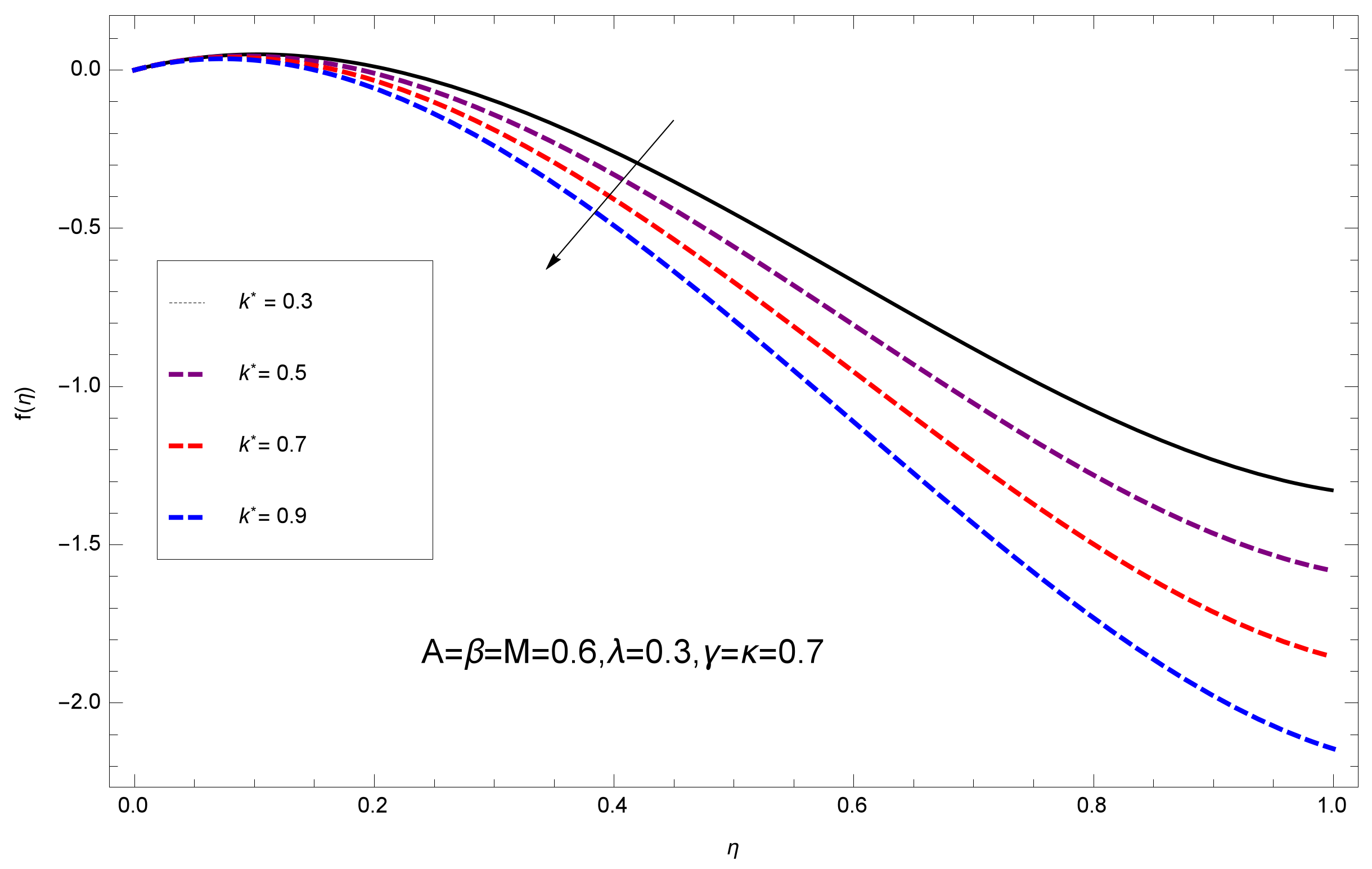
- Entropy profile decreases with the increasing values of Eyring–Powell parameter k and Radiation parameter .
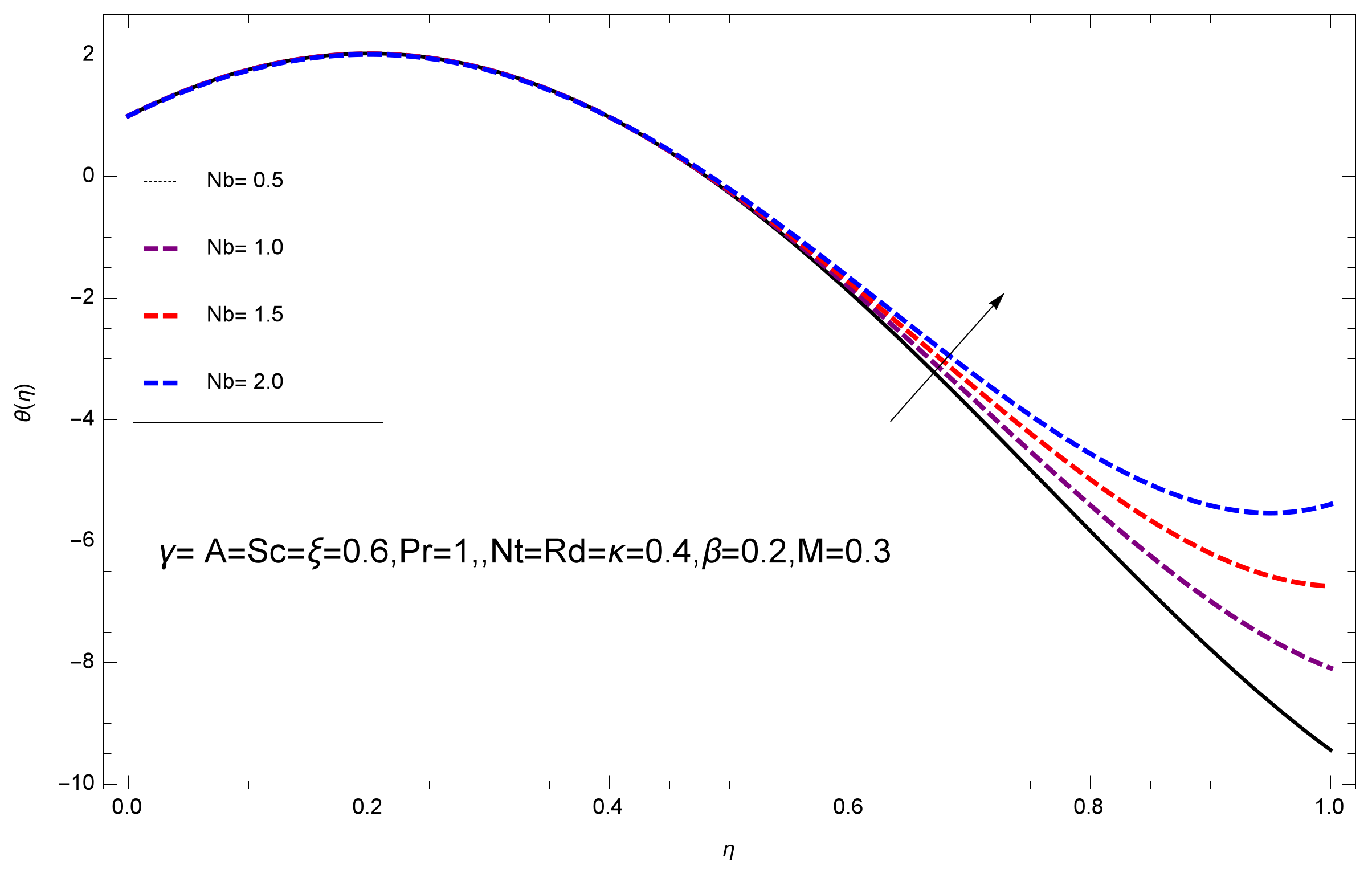
- The larger values of Brownian motion parameter raises the profile of temperature.
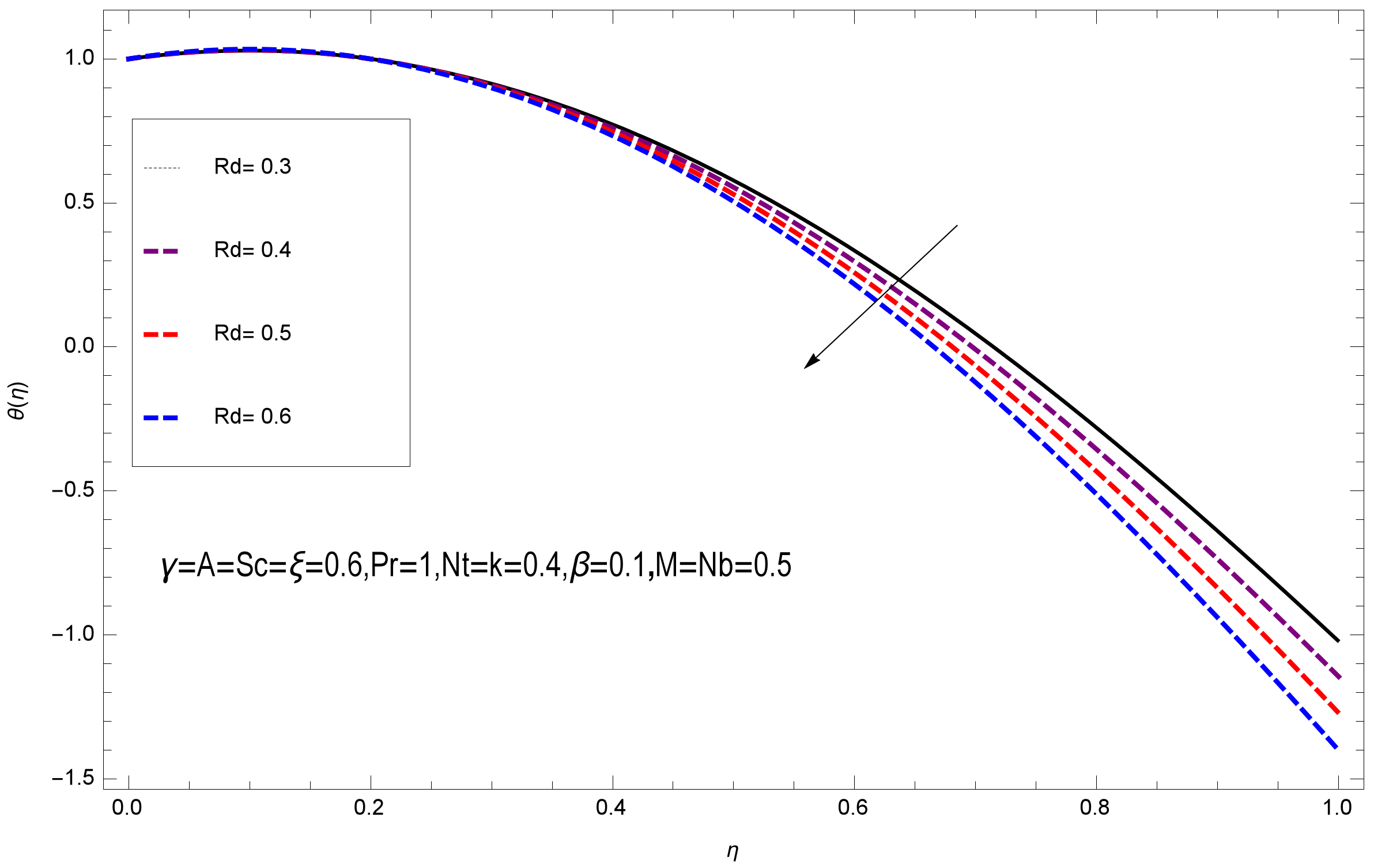
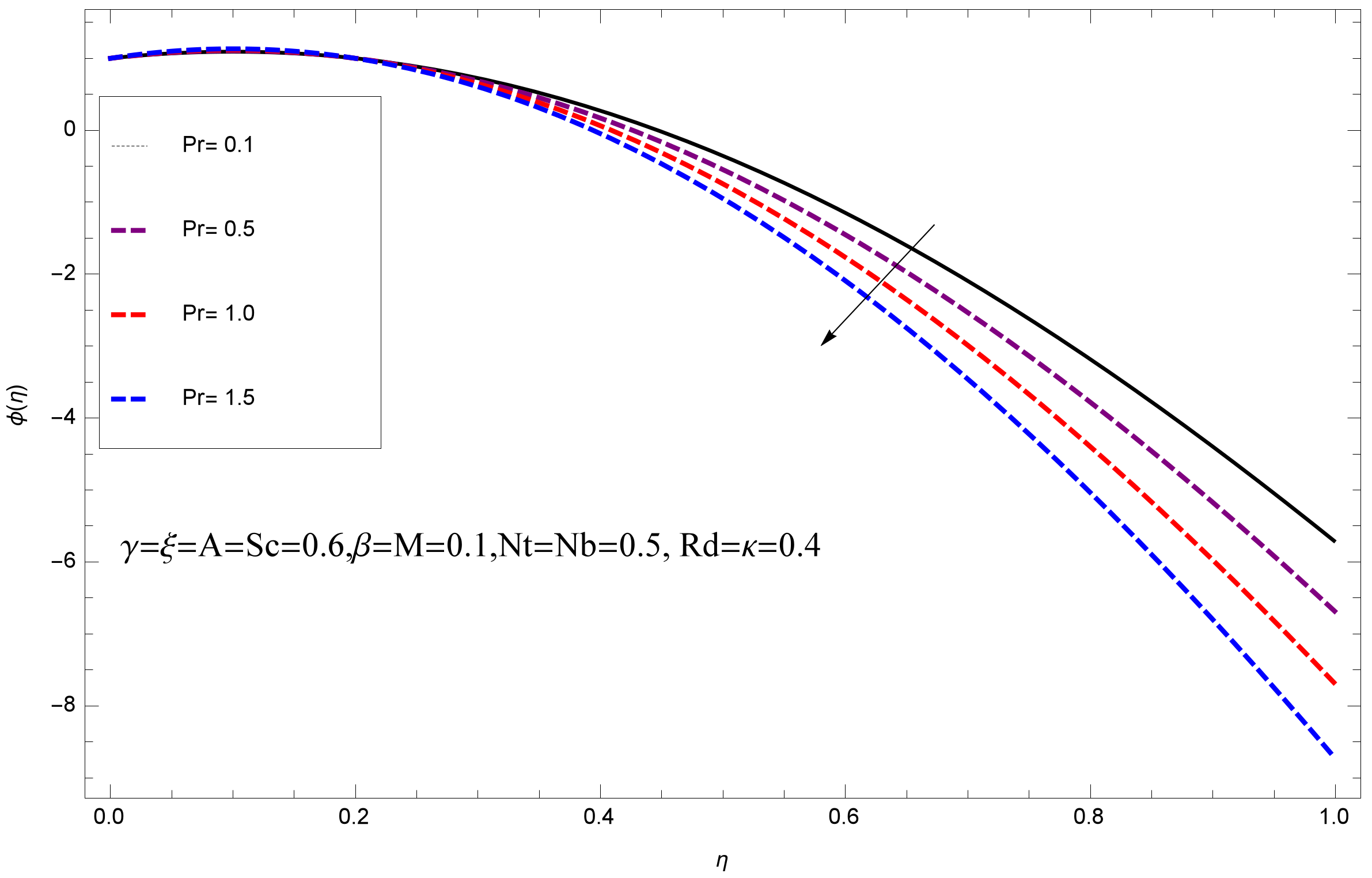
- The thermal boundary layer thickness reduces with rise of and Nusselt number rises with rise in Radiation parameter.
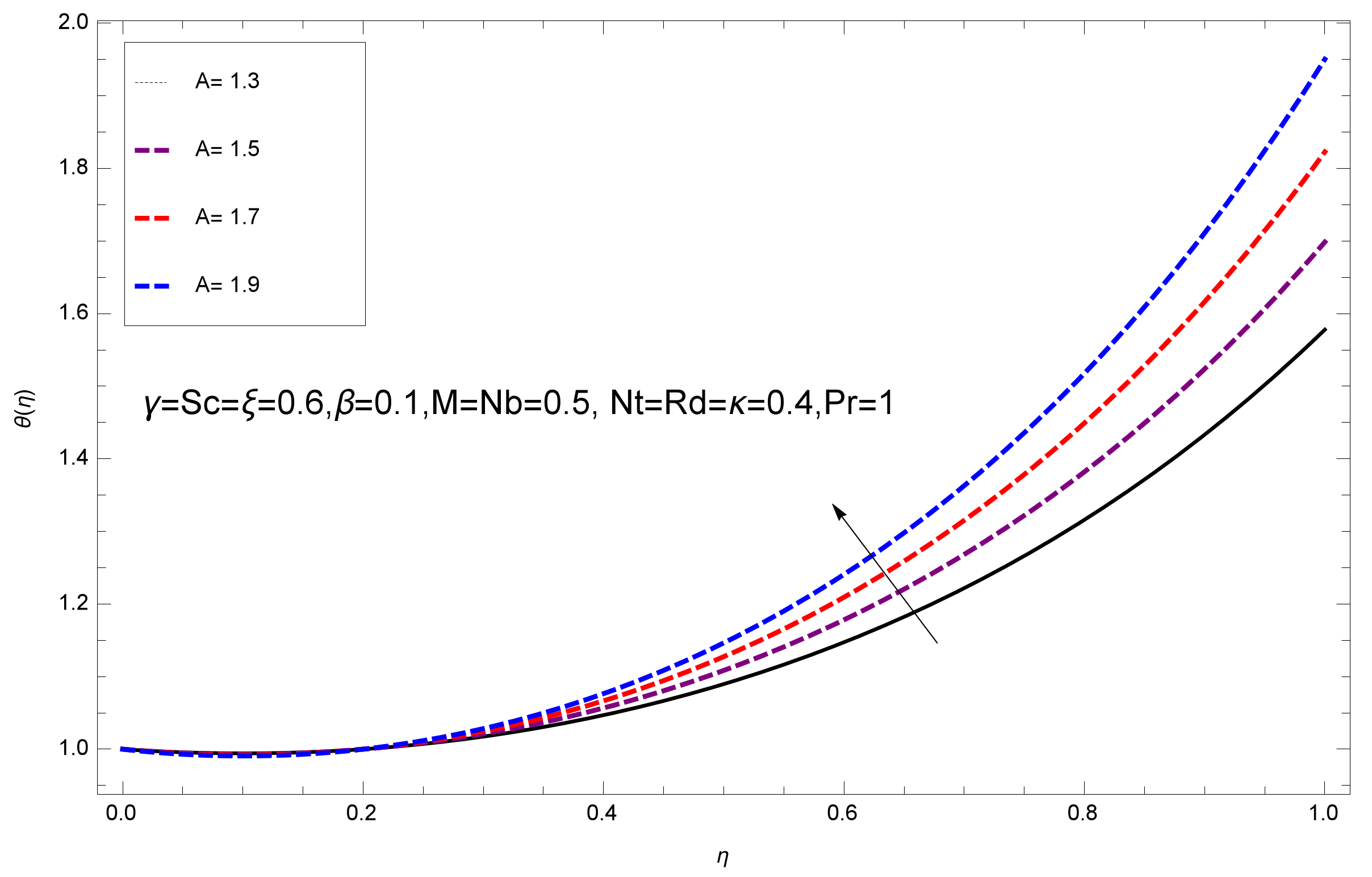
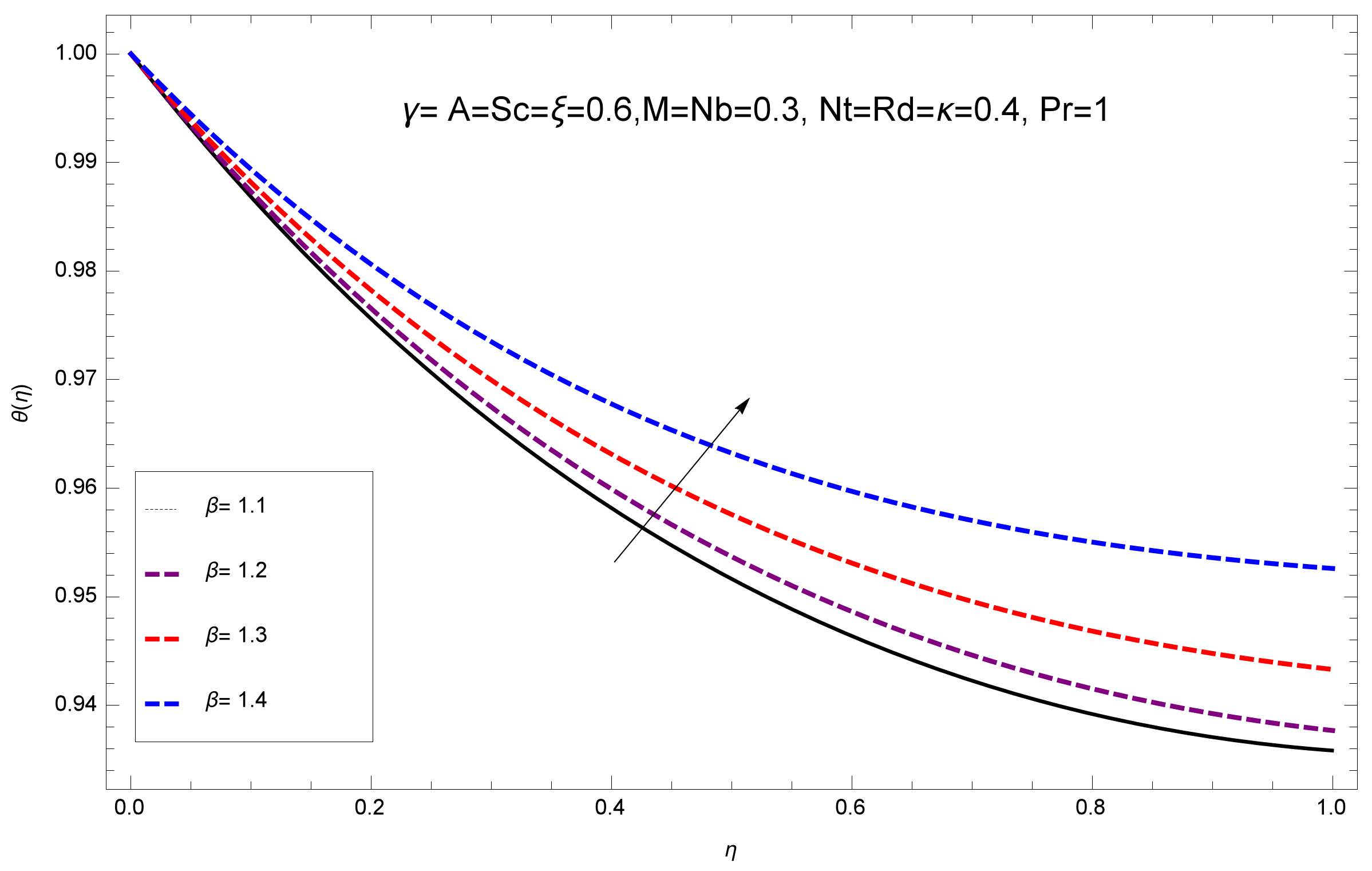
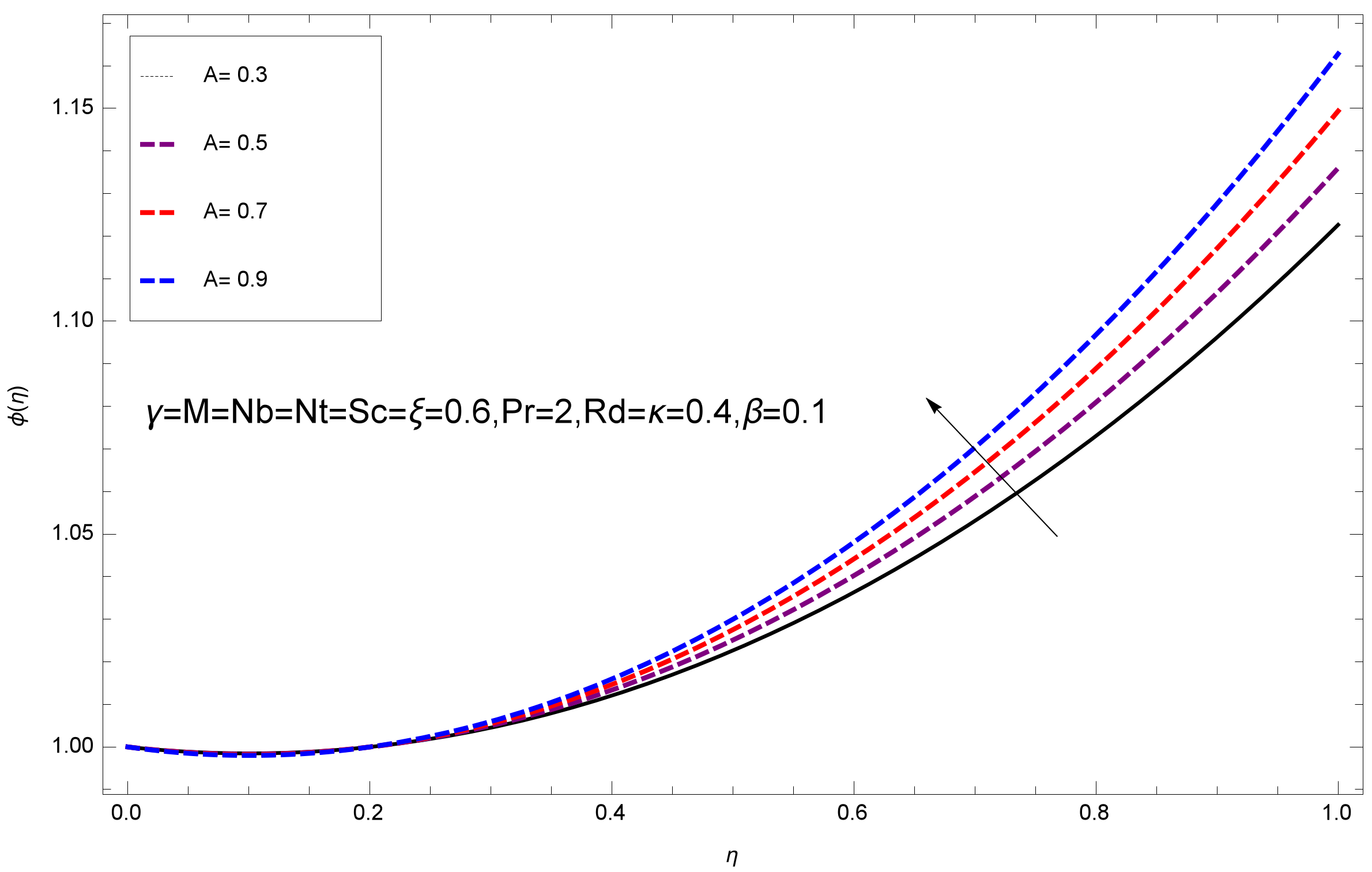
- The growing behavior of increases the surface temperature, where the opposite effect is found for an unsteady parameter A, that is, the large values of A reduce the surface temperature.
- Porosity parameter decreases the motion of the liquid films.
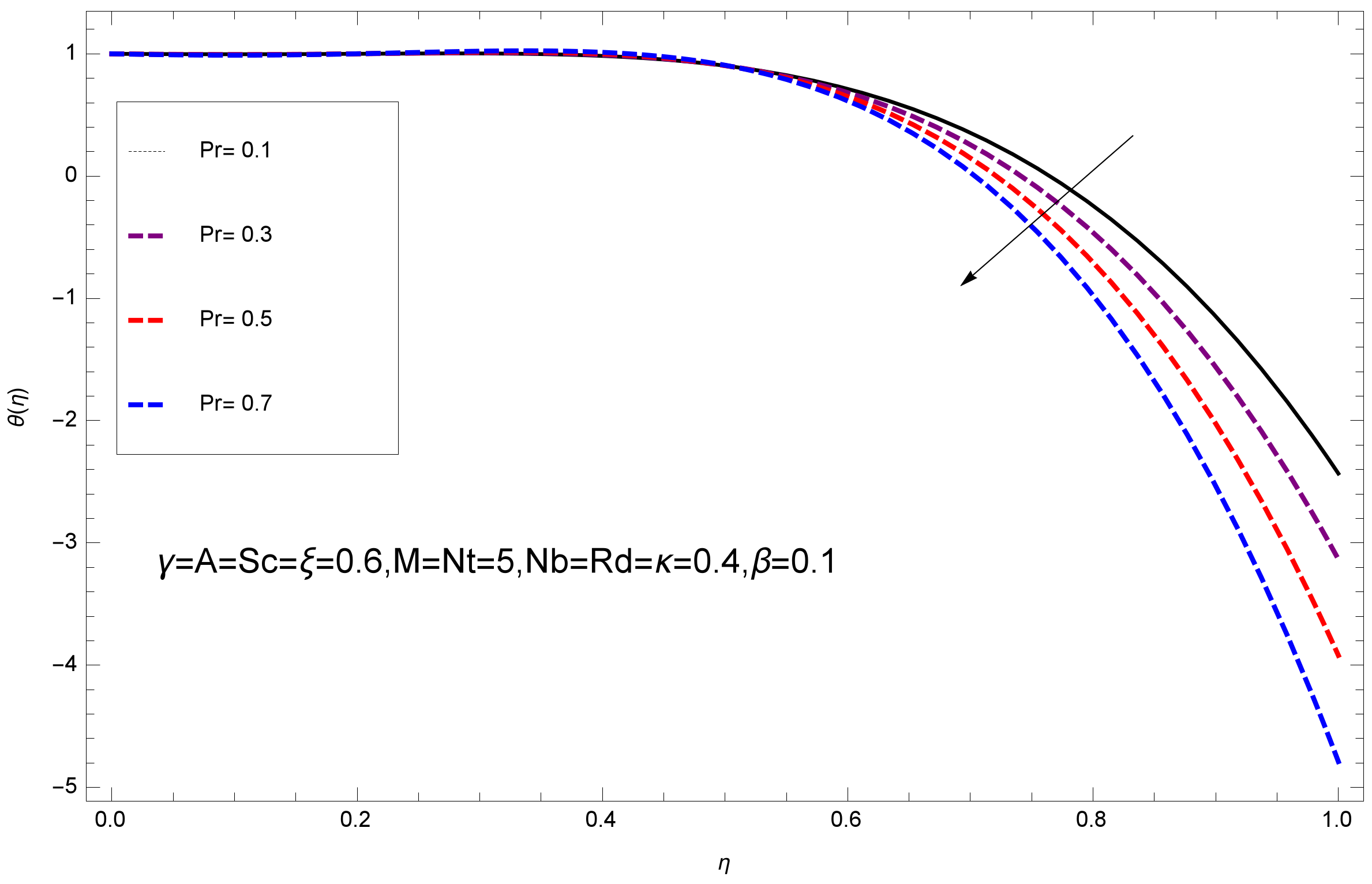
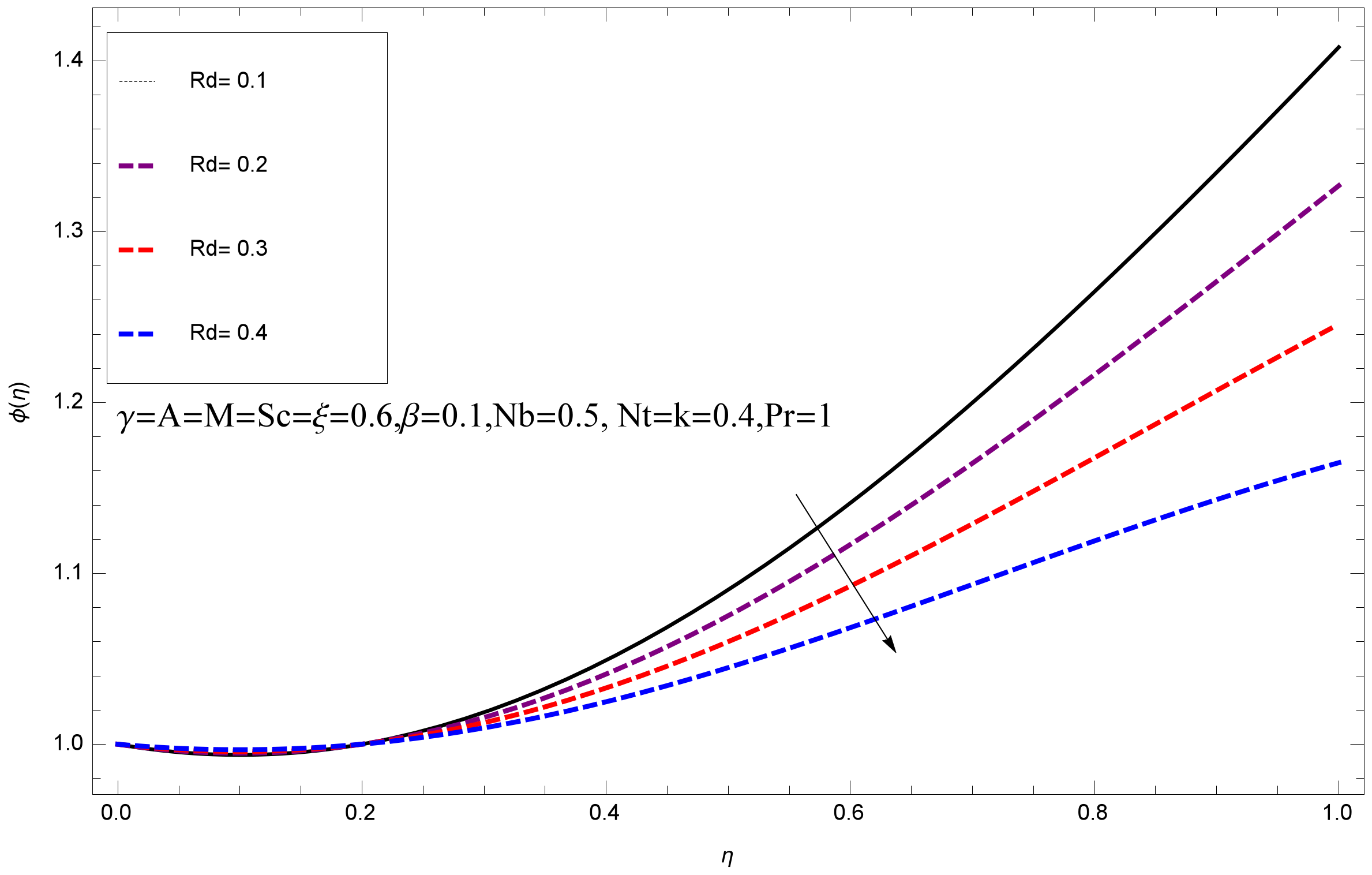
- It is perceived that the Thermal Radiation parameter decreases temperature profile, when it is increased and the same effect is observed for the concentration field.
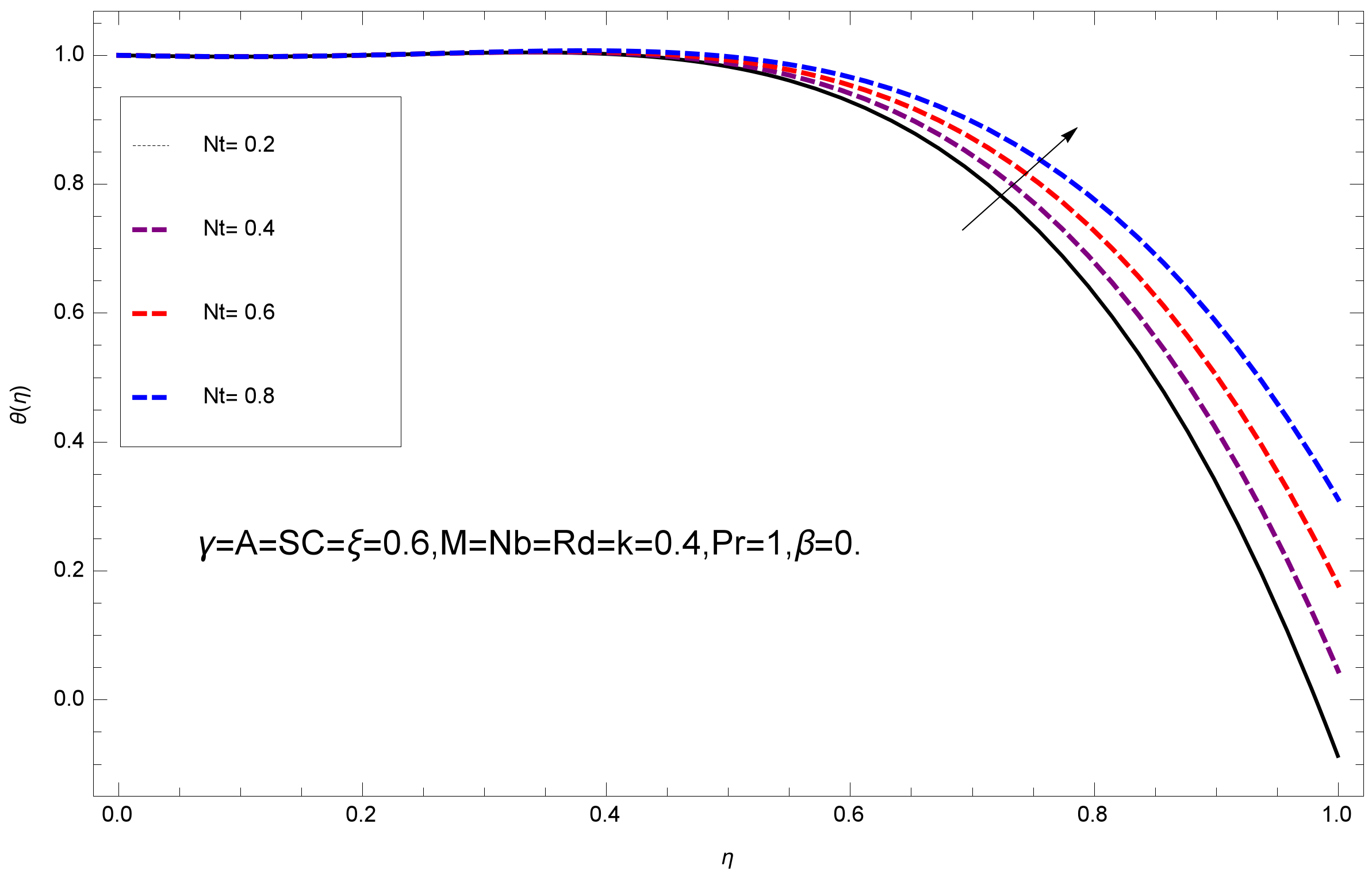
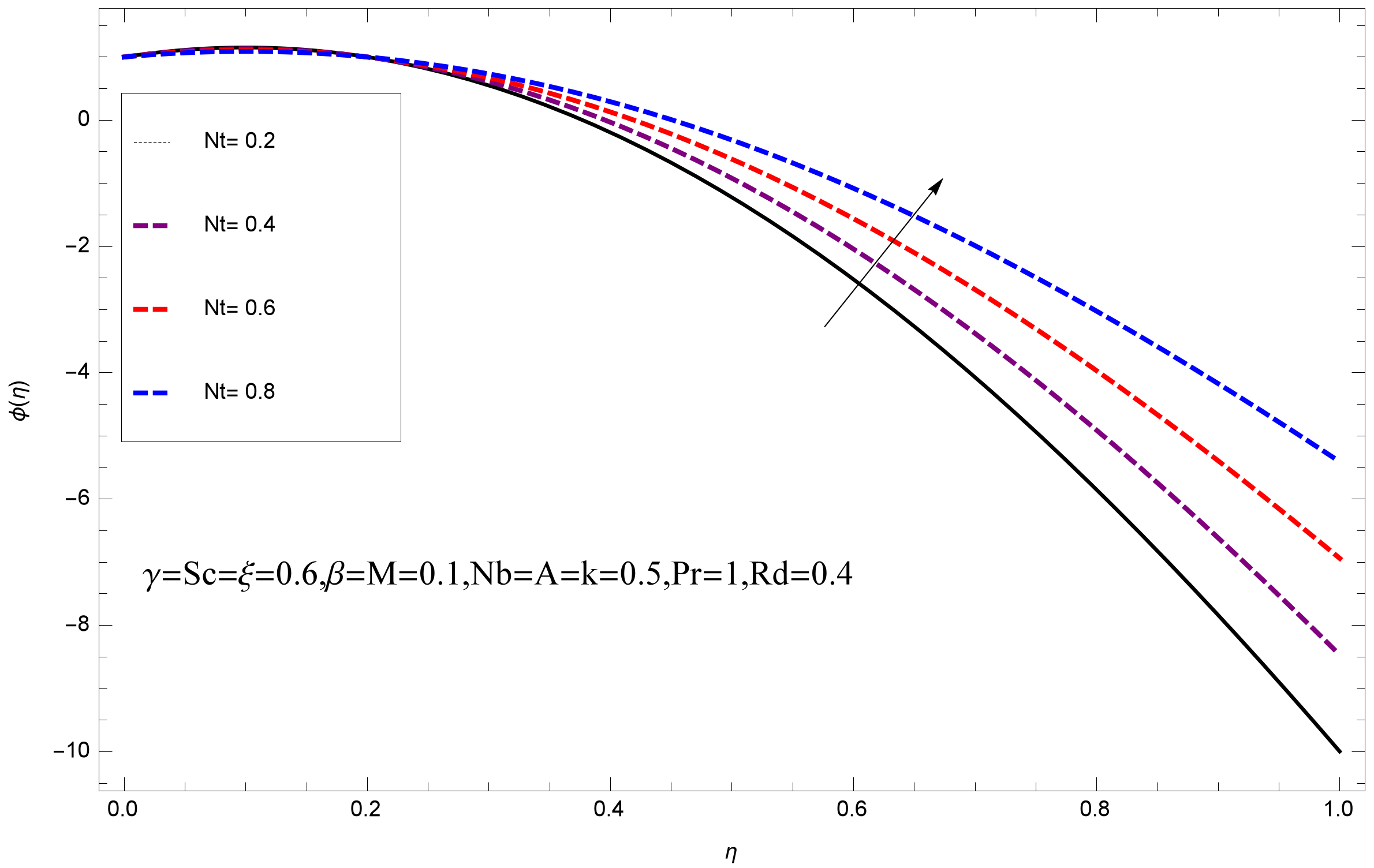
- It is observed that the heat profile falls with the large values of thermophoresis parameter and increases for small values.
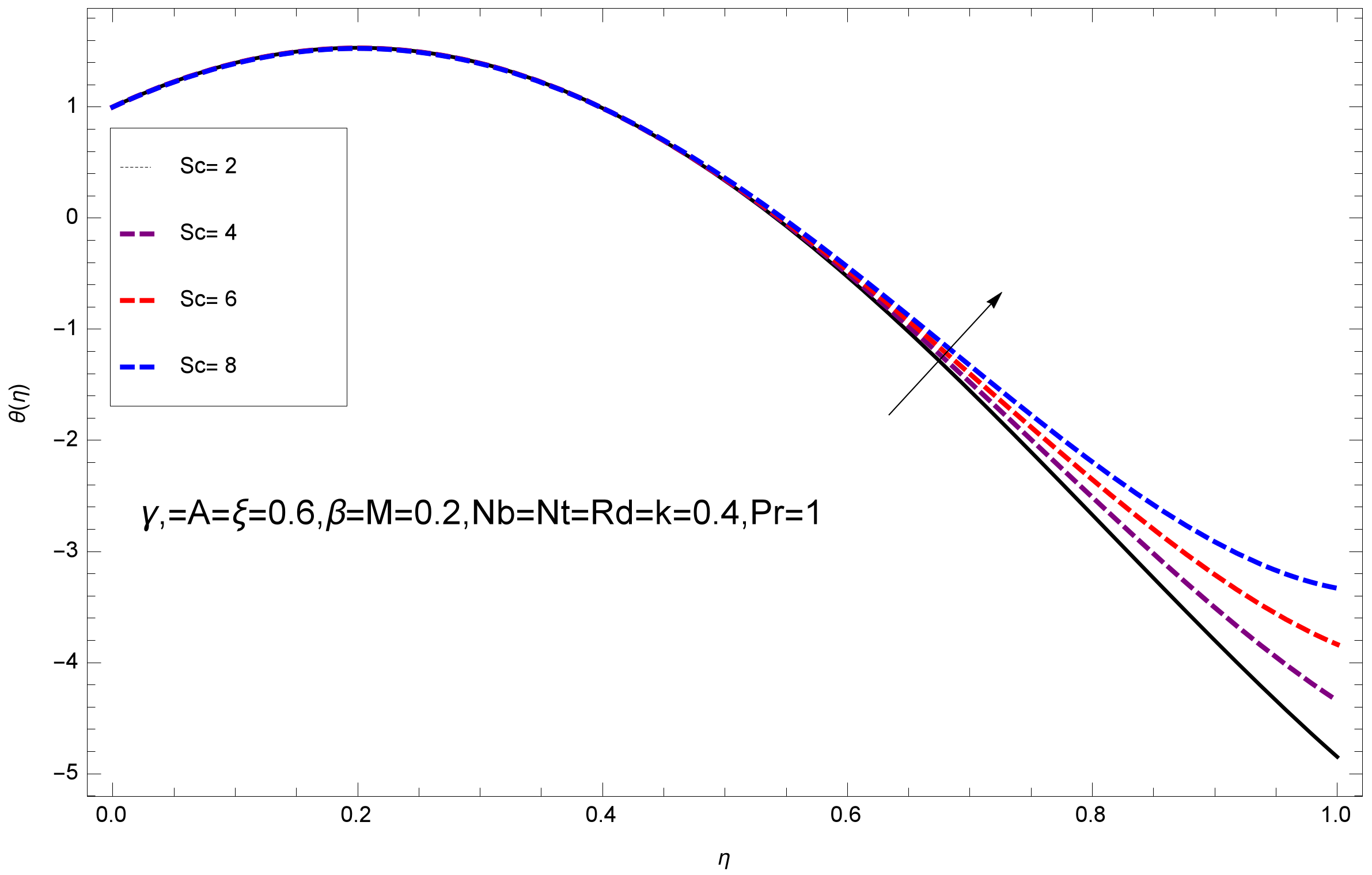
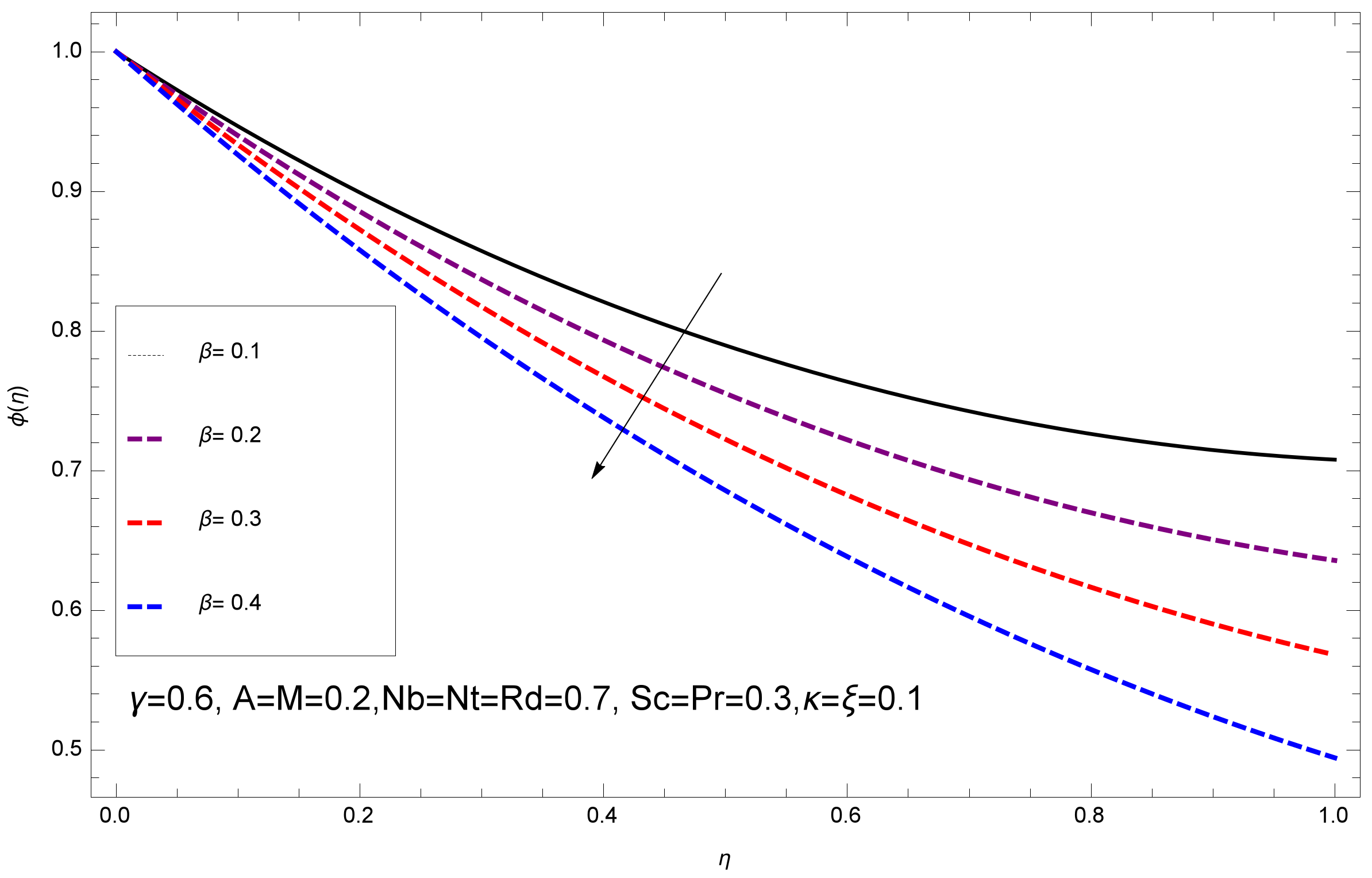
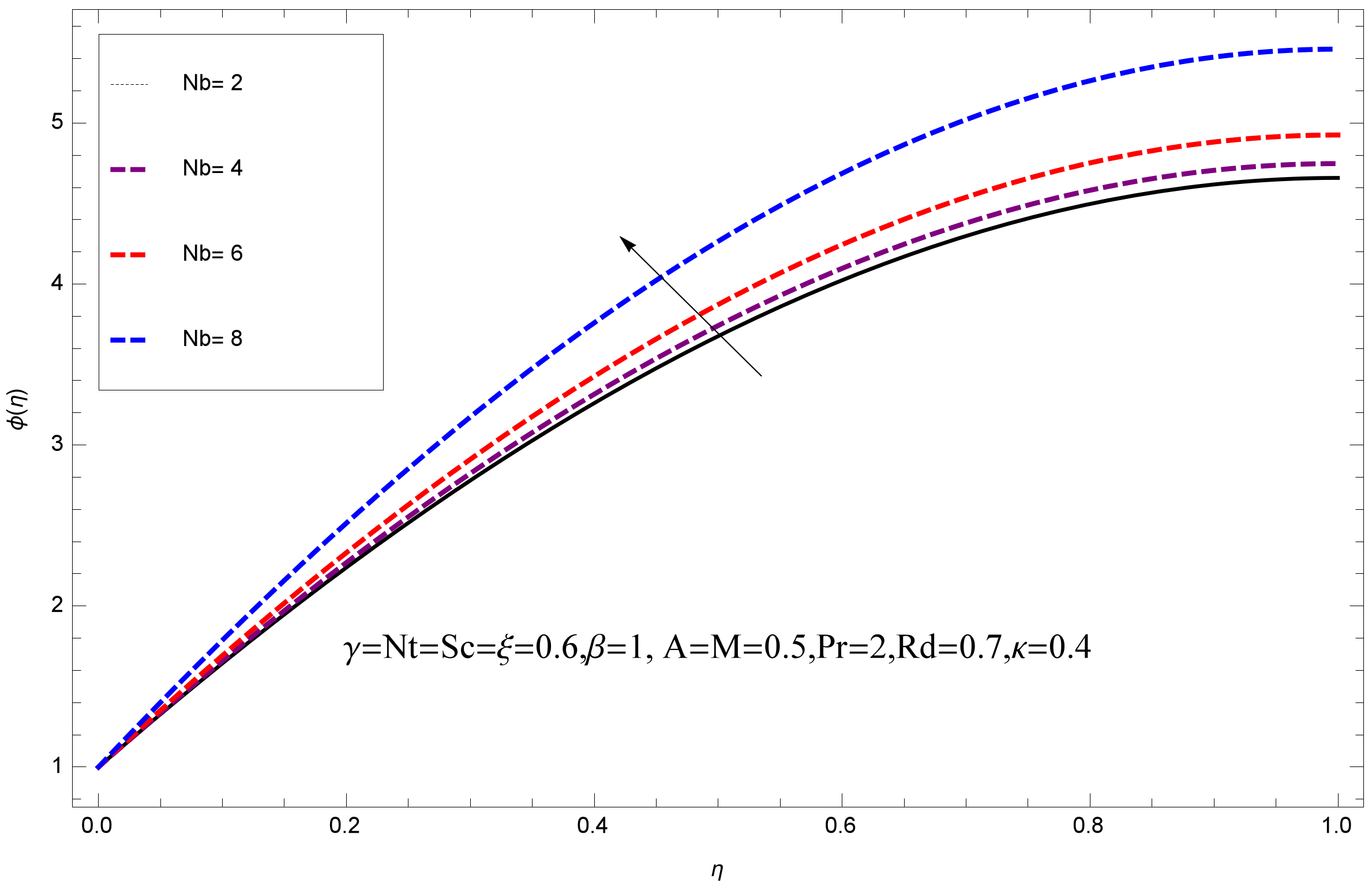
- The increasing values of reduce the mass flux, where increases the mass flux. The higher values of reduce the mass flux, while it rises with rising values of .
- The convergence of the HAM method with the variation of the physical parameters observed numerically.
- Non-dimensional velocity reduces with variable viscosity and magnetic constraints.
- The temperature gradient and concentration fields are both directly related with magnetic field.
- Rise in the nanoparticle concentration efficiently increases the friction feature of Eyring–Powell nanofluid.
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| Sherhood number | |
| Nusslet number | |
| Reynold number | |
| Prandtl number | |
| Schmidth number | |
| Stretching velocity | |
| Reference concentration | |
| Reference temperature | |
| T | Cauchy stress tensor |
| Extra stress tensor | |
| Kinematic viscosity | |
| Dynamic viscosity | |
| T | Temperature |
| Magnetic field strength | |
| Thermal conductivity | |
| Radioactive heat fluctuation | |
| Stefan Boltzmann constant | |
| Stream function | |
| Porosity parameter | |
| Brinkmann number | |
| Film Thickness parameter | |
| A | Unsteady parameter |
| M | Magnetic parameter |
| Stretching parameter | |
| Brownian diffusion of nanofluids | |
| Thermophoretic parameter | |
| Brownian motion parameter | |
| Rediation parameter | |
| Stretching parameter | |
| I | Identity tensor |
| Density | |
| Electrical conductivity | |
| Thermal diffusivity | |
| Specific heat | |
| Brownian diffusion | |
| Thickness of liquid | |
| Absorption coefficient | |
| Stretching parameter | |
| k | Eyring–Powell fluid parameter |
References
- Crane, L.J. Flow past a Stretching Plate. J. Appl. Math. Phys. (ZAMP) 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Dandapat, B.S.; Gupta, A.S. Flow and heat transfer in a viscoelastic fluid over a stretching sheet. Int. J. Nonlinear Mech. 1989, 24, 215–219. [Google Scholar] [CrossRef]
- Wang, C.Y. Liquid film on an unsteady stretching surface. Q. Appl. Math. 1990, 48, 601–610. [Google Scholar] [CrossRef]
- Usha, R.; Sridharan, R. On the motion of a liquid film on an unsteady stretching surface. ASME Fluids Eng. 1993, 150, 43–48. [Google Scholar] [CrossRef]
- Liu, I.C.; Andersson, H.I. Heat Transfer in a Liquid Film on an Unsteady Stretching Sheet. Int. J. Ther. Sci. 2008, 47, 766–772. [Google Scholar] [CrossRef]
- Aziz, R.C.; Hashim, I.; Alomari, A.K. Thin Film Flow and Heat Transfer on an Unsteady Stretching Sheet with Internal Heating. Meccanica 2011, 46, 349–357. [Google Scholar] [CrossRef]
- Tawade, L.; Abel, M.G.; Metrix, P. Kotiya Thin film flow and heat transfer over an unsteady stretching sheet with thermal radiation, internal heating in presence of external magnetic field. Int. J. Adv. Appl. Math. Mech. 2016, 3, 29–40. [Google Scholar]
- Andersson, H.I.; Aarseth, J.B.; Braud, N.; Dandapat, B.S. Flow of a power-law fluid film on an unsteady stretching surface. J. Non-Newton. Fluid Mech. 1996, 62, 1–8. [Google Scholar] [CrossRef]
- Anderssona, H.I.; Aarsetha, J.; Dandapatb, B.S. Heat transfer in a liquid film on an unsteady stretching. Int. J. Heat Mass Transf. 2000, 43, 69–74. [Google Scholar] [CrossRef]
- Chen, C.H. Heat transfer in a power-law liquid fillm over a unsteady stretching sheet. Heat Mass Transf. 2003, 39, 791796. [Google Scholar] [CrossRef]
- Wang, C.; Pop, L. Analysis of the ow of a power-law liquid film on an unsteady stretching surface by means of homotopy analysis method. J. Non-Newton. Fluid 2006, 138, 161–172. [Google Scholar] [CrossRef]
- Chen, C.-H. Effect of viscous dissipation on heat transfer in a non-Newtonian liquid film over an unsteady stretching sheet. J. Non-Newton. Fluid Mech. 2006, 135, 128–135. [Google Scholar] [CrossRef]
- Megahed, A.M. Effect of slip velocity on Casson thin film flow and heat transfer due to unsteady stretching sheet in presence of variable heat flux and viscous dissipation. Appl. Math. Mech. 2015, 36, 1273–1284. [Google Scholar] [CrossRef]
- Abolbashari, M.H.; Freidoonimehr, N.; Nazari, F.; Rashidi, M.M. Analytical modeling of entropy generation for Casson nano-fluid flow induced by a stretching surface. Adv. Powder Technol. 2015, 26, 542–552. [Google Scholar] [CrossRef]
- Qasim, M.; Khan, Z.H.; Lopez, R.J.; Khan, W.A. Heat and mass transfer in nanofluid thin film over an unsteady stretching sheet using Buongiorno’s model. Eur. Phys. J. Plus 2016, 131, 16. [Google Scholar] [CrossRef]
- Hayat, T.; Awats, M.; Asghar, S. Radiative effects in a three-dimensional flow of MHD Eyring-Powell fluid. J. Egypt. Math. Soc. 2013, 21, 379–384. [Google Scholar] [CrossRef]
- Sirohi, V.; Timol, M.G.; Kalathia, N.L. Numerical treatment of Eyring-Powell fluid flow past a 90 degree wedge. Reg. J. Energy Heat Mass Transf. 1984, 6, 219–228. [Google Scholar]
- Eldabe, N.T.M.; Hassan, A.A.; Mohamed, M.A. Effect of couple stresses on the MHD of a non-Newton. unsteady flow between two parallel porous plates. Z. Naturforschung A 2003, 58, 204–210. [Google Scholar]
- Patel, M.; Timol, M.G. Numerical treatment of Powell–Eyring fluid flow using method of satisfaction of asymptotic boundary conditions (MSABC). Appl. Numer. Math. 2009, 59, 2584–2592. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization: The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Oztop, H.F.; Al-Salem, K. A review on entropy generation in natural and mixed convection heat transfer for energy systems. Renew. Sustain. Energy Rev. 2012, 16, 911–920. [Google Scholar] [CrossRef]
- Ozawa, H.; Ohmura, A.; Lorenz, R.D.; Pujol, T. The second law of thermodynamics and the global climate system: A review of the maximum entropy production principle. Rev. Geophys. 2003, 41. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Abelman, S.; Mehr, N.F. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Transf. 2013, 62, 515–525. [Google Scholar] [CrossRef]
- Qing, J.; Bhatti, M.M.; Abbas, M.A.; Rashidi, M.M.; Ali, M.E.S. Entropy generation on MHD Casson nanofluid flow over a porous stretching/shrinking surface. Entropy 2016, 18, 123. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Bhatti, M.M.; Abbas, M.A.; Ali, M.E.S. Entropy generation on MHD blood flow of nanofluid due to peristaltic waves. Entropy 2016, 18, 117. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bai, Y.; Rashidi, M.M.; Bhatti, M.M. Analysis of entropy generation in the flow of peristaltic nanofluids in channels with compliant walls. Entropy 2016, 18, 90. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Entropy generation of nanofluid in presence of magnetic field using Lattice Boltzmann Method. Phys. A Stat. Mech. Its Appl. 2015, 417, 273–286. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Ali, M.; Freidoonimehr, N.; Nazari, F. Parametric analysis and optimization of entropy generation in unsteady MHD flow over a stretching rotating disk using artificial neural network and particle swarm optimization algorithm. Energy 2013, 55, 497–510. [Google Scholar] [CrossRef]
- Abolbashari, M.H.; Freidoonimehr, N.; Nazari, F.; Rashidi, M.M. Entropy analysis for an unsteady MHD flow past a stretching permeable surface in nano-fluid. Powder Technol. 2014, 267, 256–267. [Google Scholar] [CrossRef]
- Liao, S.J. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Liao, S.J. An explicit, totally analytic approximate solution for Blasius’ viscous flow problems. Int. J. Non-Linear Mech. 1999, 34, 759–778. [Google Scholar] [CrossRef]
- Liao, S. Beyond Perturbation: Introduction to the Homotopy Analysis Method; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Liao, S.J. On the analytic solution of magnetohydrodynamic flows of non-Newton. fluids over a stretching sheet. J. Fluid Mech. 2003, 488, 189–212. [Google Scholar] [CrossRef]
- Liao, S. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Liao, S. An analytic solution of unsteady boundary-layer flows caused by an impulsively stretching plate. Commun. Nonlinear Sci. Numer. Simul. 2006, 11, 326–339. [Google Scholar] [CrossRef]
- Liao, S. Homotopy Analysis Method in Nonlinear Differential Equations; Higher Education Press: Beijing, China, 2012; pp. 153–165. [Google Scholar]
- Liao, S. An optimal homotopy-analysis approach for strongly nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2003–2016. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Siddiqui, A.M.; Asadi, M. Application of homotopy analysis method to the unsteady squeezing flow of a second-grade fluid between circular plates. Math. Prob. Eng. 2010, 2010, 706840. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Pour, S.M. Analytic approximate solutions for unsteady boundary-layer flow and heat transfer due to a stretching sheet by homotopy analysis method. Nonlinear Anal. Model. Control 2010, 15, 83–95. [Google Scholar]
- Abbasbandy, S. Homotopy analysis method for heat radiation equations. Int. Commun. Heat Mass Transf. 2007, 34, 380–387. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Shirzadi, A. A new application of the homotopy analysis method: Solving the Sturm–Liouville problems. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 112–126. [Google Scholar] [CrossRef]
- Abbasbandy, S. The application of homotopy analysis method to nonlinear equations arising in heat transfer. Phys. Lett. A 2006, 360, 109–113. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S.; Asghar, S. Hydromagnetic Couette flow of an Oldroyd-B fluid in a rotating system. Int. J. Eng. Sci. 2004, 42, 65–78. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, S.B.; Sajid, M.; Asghar, S. Rotating flow of a third grade fluid in a porous space with Hall current. Nonlinear Dyn. 2007, 49, 83–91. [Google Scholar] [CrossRef]
- Nadeem, S.; Awais, M. Thin film flow of an unsteady shrinking sheet through porous medium with variable viscosity. Phys. Lett. A 2008, 372, 4965–4972. [Google Scholar] [CrossRef]
- Nadeem, S.; Hussain, M.; Naz, M. MHD stagnation flow of a micropolar fluid through a porous medium. Meccanica 2010, 45, 869–880. [Google Scholar] [CrossRef]
- Xiao, B.; Chen, H.; Xiao, S.; Cai, J. Research on relative permeability of nanofibers with capillary pressure effect by means of Fractal-Monte Carlo technique. J. Nanosci. Nanotechnol. 2017, 17, 6811–6817. [Google Scholar] [CrossRef]
- Shah, Z.; Gul, T.; Khan, A.M.; Ali, I.; Islam, S. Effects of hall current on steady three dimensional non-newtonian nanofluid in a rotating frame with brownian motion and thermophoresis effects. J. Eng. Technol. 2017, 6, 280–296. [Google Scholar]
- Shah, Z.; Islam, S.; Gul, T.; Bonyah, E.; Khan, M.A. The electrical MHD and hall current impact on micropolar nanofluid flow between rotating parallel plates. Results Phys. 2018, 9, 1201–1214. [Google Scholar] [CrossRef]


| A | Wang [3] | Narayana and Sibanda [39] | Qasim [15] | Present Results |
|---|---|---|---|---|
| 0.4 | 5.122490 | 4.981455 | 4.981454 | 5.523451 |
| 0.6 | 3.131250 | 3.131713 | 3.131710 | 4.002111 |
| 0.8 | 2.151990 | 2.151994 | 2.151994 | 3.992358 |
| 1.0 | 1.543620 | 1.543618 | 1.543616 | 3.113001 |
| 1.2 | 1.127780 | 1.127780 | 1.127781 | 1.625391 |
| 1.4 | 0.821032 | 0.821032 | 0.821032 | 1.896541 |
| 1.6 | 0.576173 | 0.576173 | 0.576173 | 0.876512 |
| 1.8 | 0.356389 | 0.356389 | 0.356389 | 0.266156 |
| A | Wang [3] | Narayana and Sibanda [39] | Qasim [15] | Present Results |
|---|---|---|---|---|
| 0.4 | −6.699120 | −5.6494483 | −5.6494474 | −4.33027 |
| 0.6 | −3.742330 | −3.7427896 | −3.7427863 | −3.94882 |
| 0.8 | −2.680940 | −2.6809660 | −2.6809656 | −2.64208 |
| 01 | −1.972380 | −1.9723877 | −1.9723819 | −1.33999 |
| 1.2 | −1.442631 | −1.4426237 | −1.4426252 | −0.92157 |
| 1.4 | −1.012784 | −1.0127798 | −1.0127802 | −0.56897 |
| 1.6 | −0.642397 | −0.6423970 | −0.6423970 | −0.34227 |
| 1.8 | −0.309137 | −0.3091369 | −0.3091367 | −0.03027 |
| M | Nt | A | Pr | Tawade et al. (2016) Results | Qasim et al. (2016) Results | Present (2017) Results |
|---|---|---|---|---|---|---|
| 0 | 0.1 | 1.0 | 0.1 | 0.257696 | 0.9604803 | 0.223456 |
| 1 | 0.420739 | 0.6925326 | 0.432111 | |||
| 2 | 0.01 | 0.526782 | 0.0978841 | 0.712351 | ||
| 0.1 | 0.0 | 0.695757 | 0.0248625 | 1.023001 | ||
| 1.0 | 0.1 | 1.030899 | 0.0083111 | 1.625341 | ||
| 0.2 | 0.931433 | 0.0013612 | 1.236540 |
| Ec | β | Pr | Nt | −Θ′(0) | −Θ′(0) | −Φ′(0) | −Φ′(0) |
|---|---|---|---|---|---|---|---|
| Tawad et al. (2016) Results | Present (2017) Results | Qasim et al. (2016) Results | Present (2017) Results | ||||
| 0.0 | 0.2 | 1.0 | 0.1 | 2.46682 | 0.682385 | 4.69946 | 6.68238 |
| 0.5 | 1.66004 | 0.541422 | 5.63125 | 4.94142 | |||
| 1.0 | 1.17173 | 0.440569 | 5.73992 | 5.44569 | |||
| 0.2 | 2.08356 | 0.321022 | 4.96867 | 5.12101 | |||
| 0.3 | 1.37004 | 0.300420 | 5.68398 | 5.70742 | |||
| 0.4 | 0.94740 | 0.291420 | 5.75820 | 5.29140 | |||
| 0.5 | 2.46062 | 0.371420 | 4.65665 | 5.37143 | |||
| 1.5 | 1.65905 | 0.182285 | 5.59404 | 6.78223 | |||
| 5.0 | 1.17298 | 0.011422 | 5.70473 | 7.01147 | |||
| 0.4 | 1.96299 | 0.612427 | 5.01443 | 4.11207 | |||
| 0.6 | 1.28112 | 0.691428 | 5.66638 | 4.69458 | |||
| 0.8 | 0.87980 | 0.500987 | 5.73093 | 7.50097 |
| Solution Approximation | f′′(0) | θ′(0) | ϕ′(0) |
|---|---|---|---|
| 1 | −0.05401 | −0.10070 | −1.10075 |
| 4 | −0.10218 | −0.18890 | −1.38506 |
| 7 | −0.10813 | −0.19903 | −1.88867 |
| 10 | −0.10888 | −0.20281 | −1.99293 |
| 13 | −0.10894 | −0.20154 | −2.01113 |
| 14 | −0.10896 | −0.20475 | −2.01406 |
| 17 | −0.10897 | −0.20478 | −2.01451 |
| 20 | −0.10897 | −0.20479 | −2.01458 |
| 25 | −0.10897 | −0.20479 | −2.01458 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishaq, M.; Ali, G.; Shah, Z.; Islam, S.; Muhammad, S. Entropy Generation on Nanofluid Thin Film Flow of Eyring–Powell Fluid with Thermal Radiation and MHD Effect on an Unsteady Porous Stretching Sheet. Entropy 2018, 20, 412. https://doi.org/10.3390/e20060412
Ishaq M, Ali G, Shah Z, Islam S, Muhammad S. Entropy Generation on Nanofluid Thin Film Flow of Eyring–Powell Fluid with Thermal Radiation and MHD Effect on an Unsteady Porous Stretching Sheet. Entropy. 2018; 20(6):412. https://doi.org/10.3390/e20060412
Chicago/Turabian StyleIshaq, Mohammad, Gohar Ali, Zahir Shah, Saeed Islam, and Sher Muhammad. 2018. "Entropy Generation on Nanofluid Thin Film Flow of Eyring–Powell Fluid with Thermal Radiation and MHD Effect on an Unsteady Porous Stretching Sheet" Entropy 20, no. 6: 412. https://doi.org/10.3390/e20060412
APA StyleIshaq, M., Ali, G., Shah, Z., Islam, S., & Muhammad, S. (2018). Entropy Generation on Nanofluid Thin Film Flow of Eyring–Powell Fluid with Thermal Radiation and MHD Effect on an Unsteady Porous Stretching Sheet. Entropy, 20(6), 412. https://doi.org/10.3390/e20060412






