Sparse-Aware Bias-Compensated Adaptive Filtering Algorithms Using the Maximum Correntropy Criterion for Sparse System Identification with Noisy Input
Abstract
1. Introduction
2. Review of the BCNMCC
2.1. NMCC
2.2. BCNMCC
3. Sparse-Aware BCNMCC Algorithms
3.1. CIM-BCNMCC
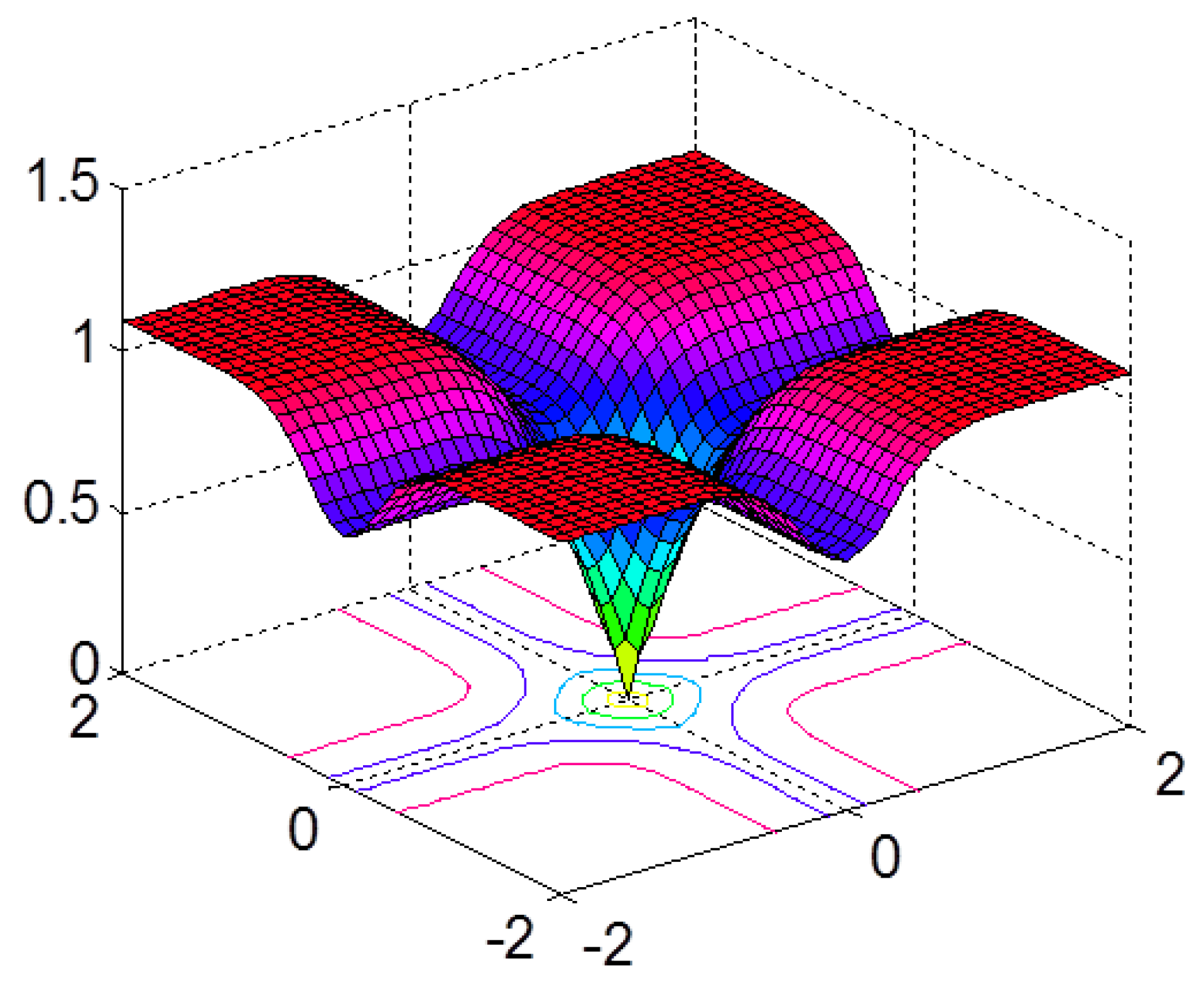
3.1.1. Correntropy-Induced Metric
3.1.2. CIM-BCNMCC
3.2. BCPNMCC
3.2.1. PMCC
3.2.2. BCPNMCC
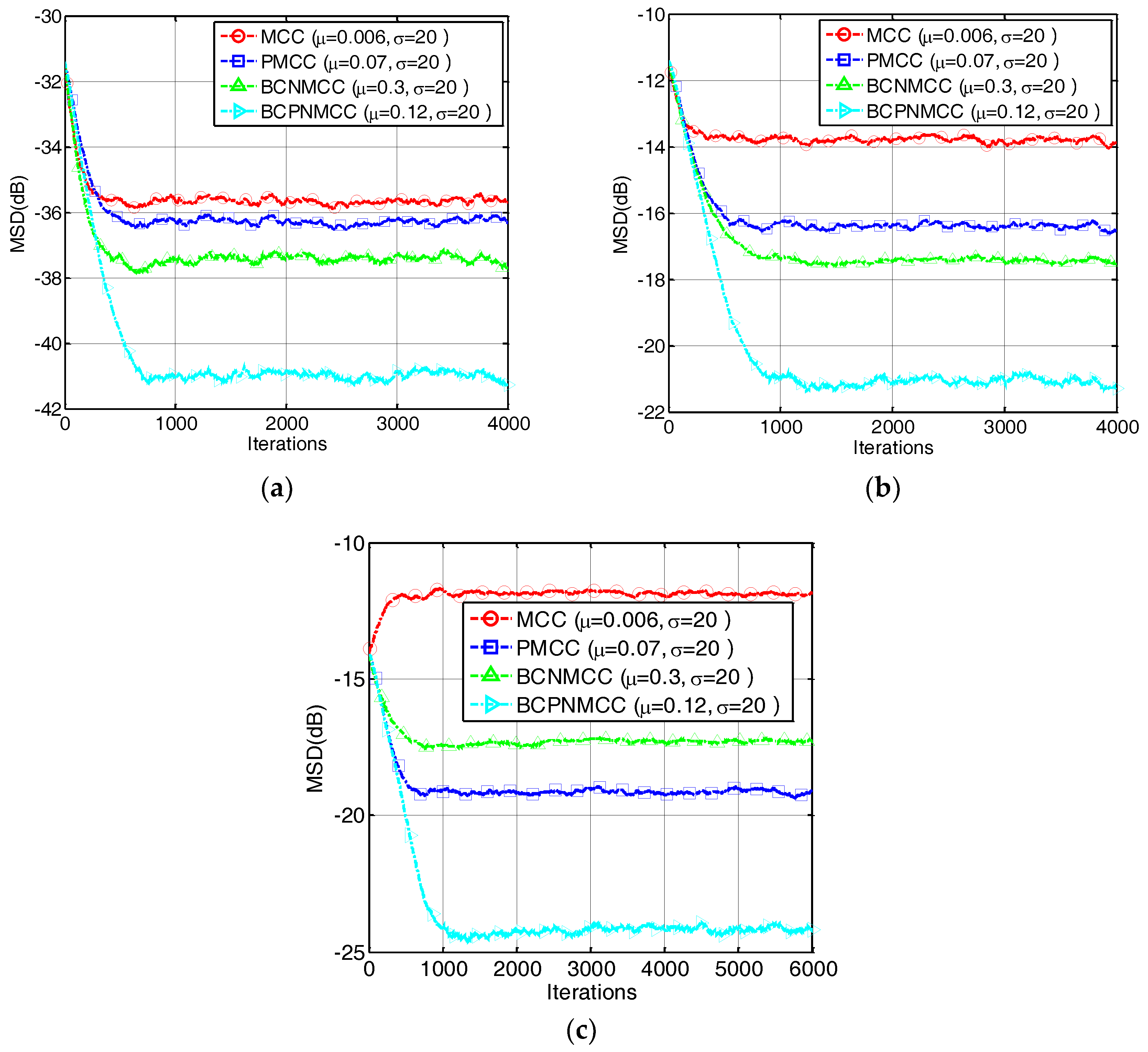
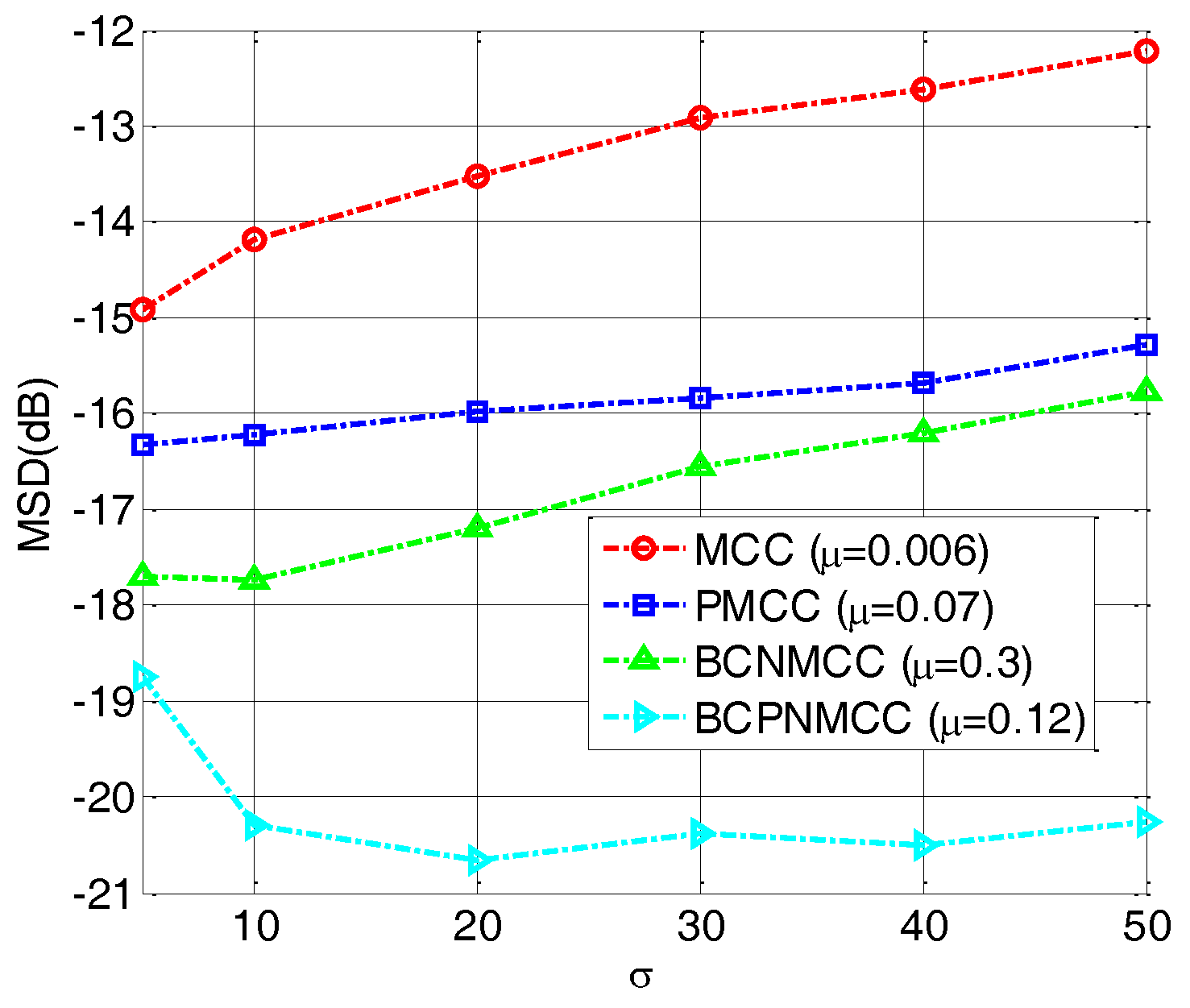
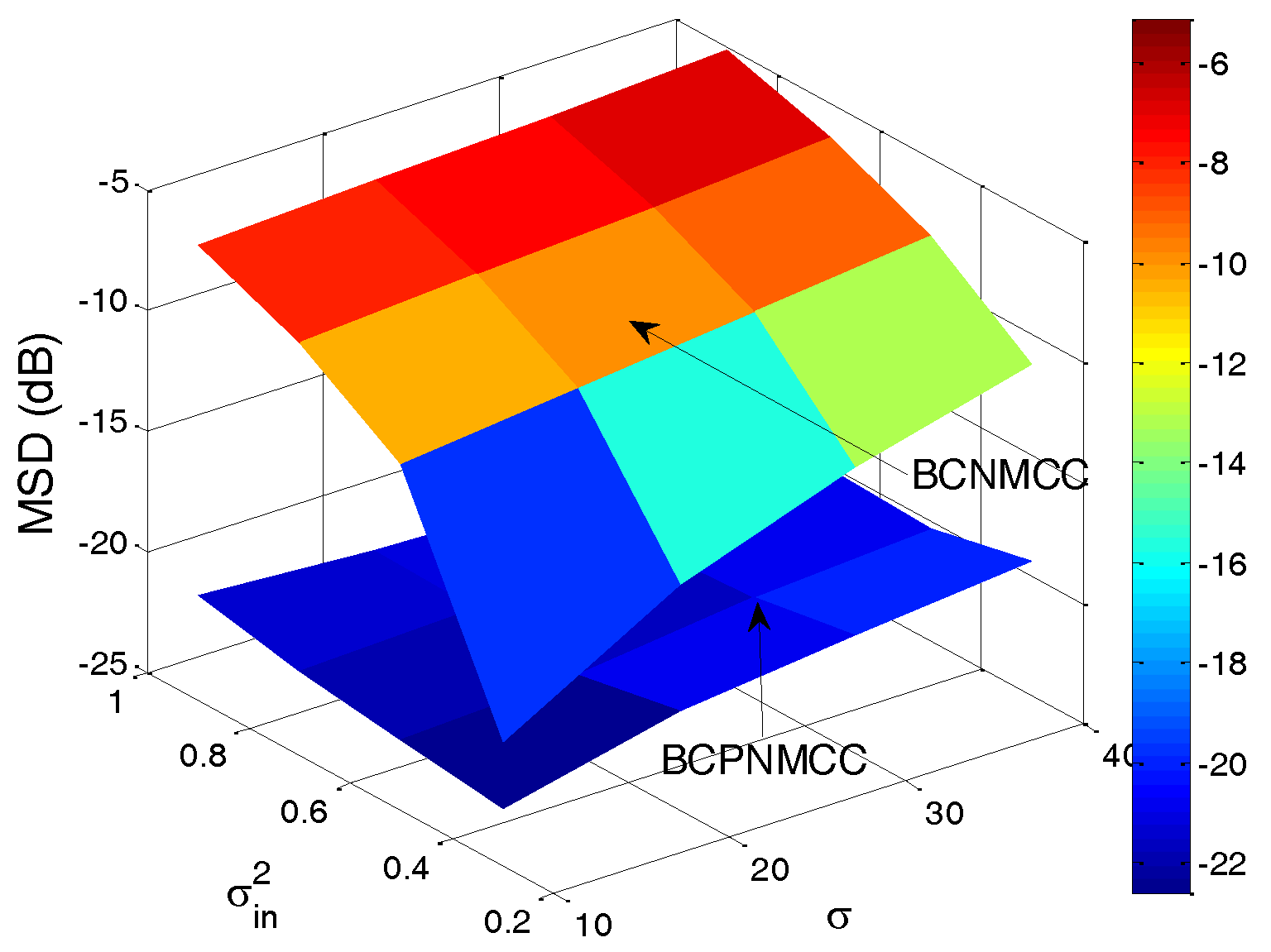
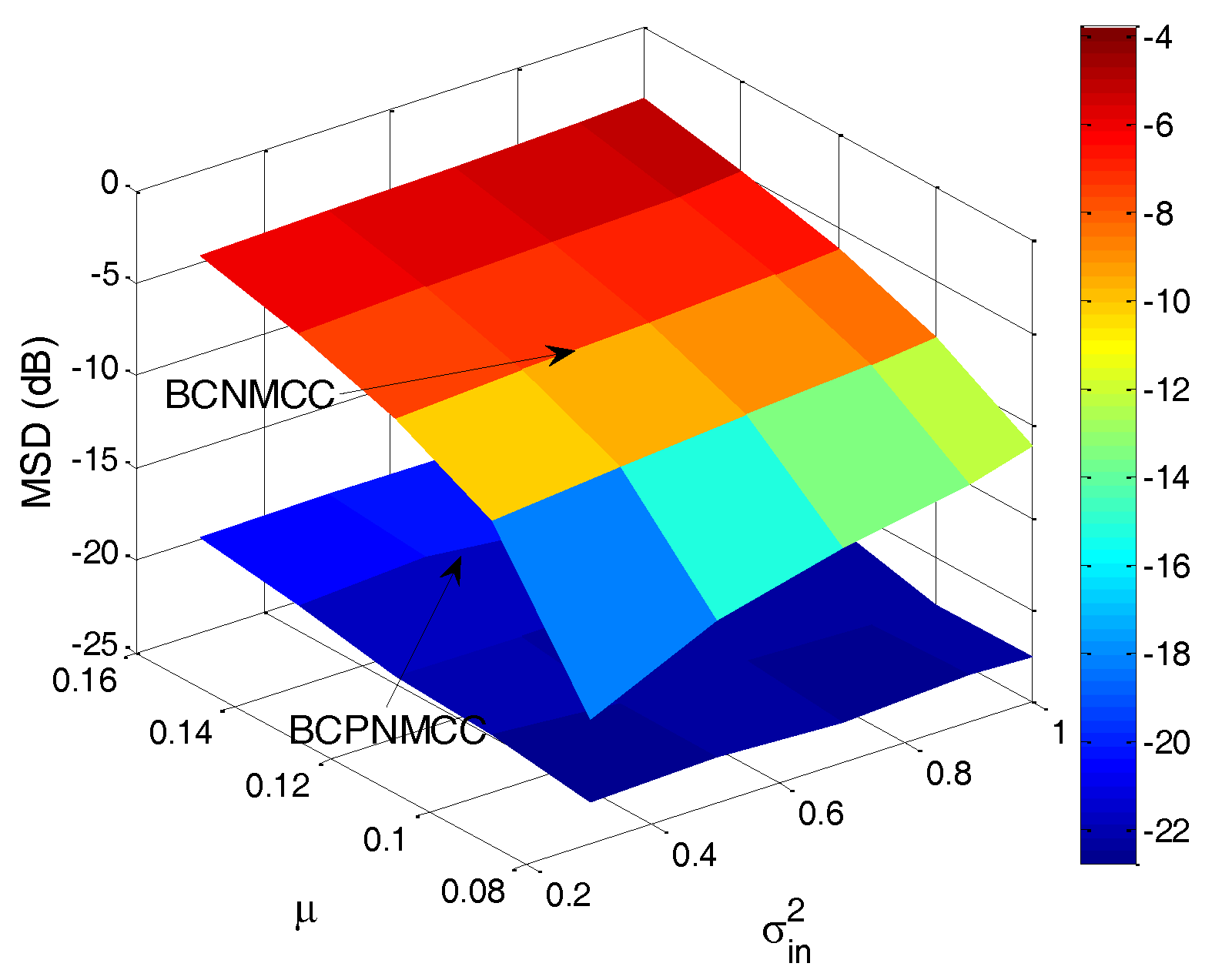
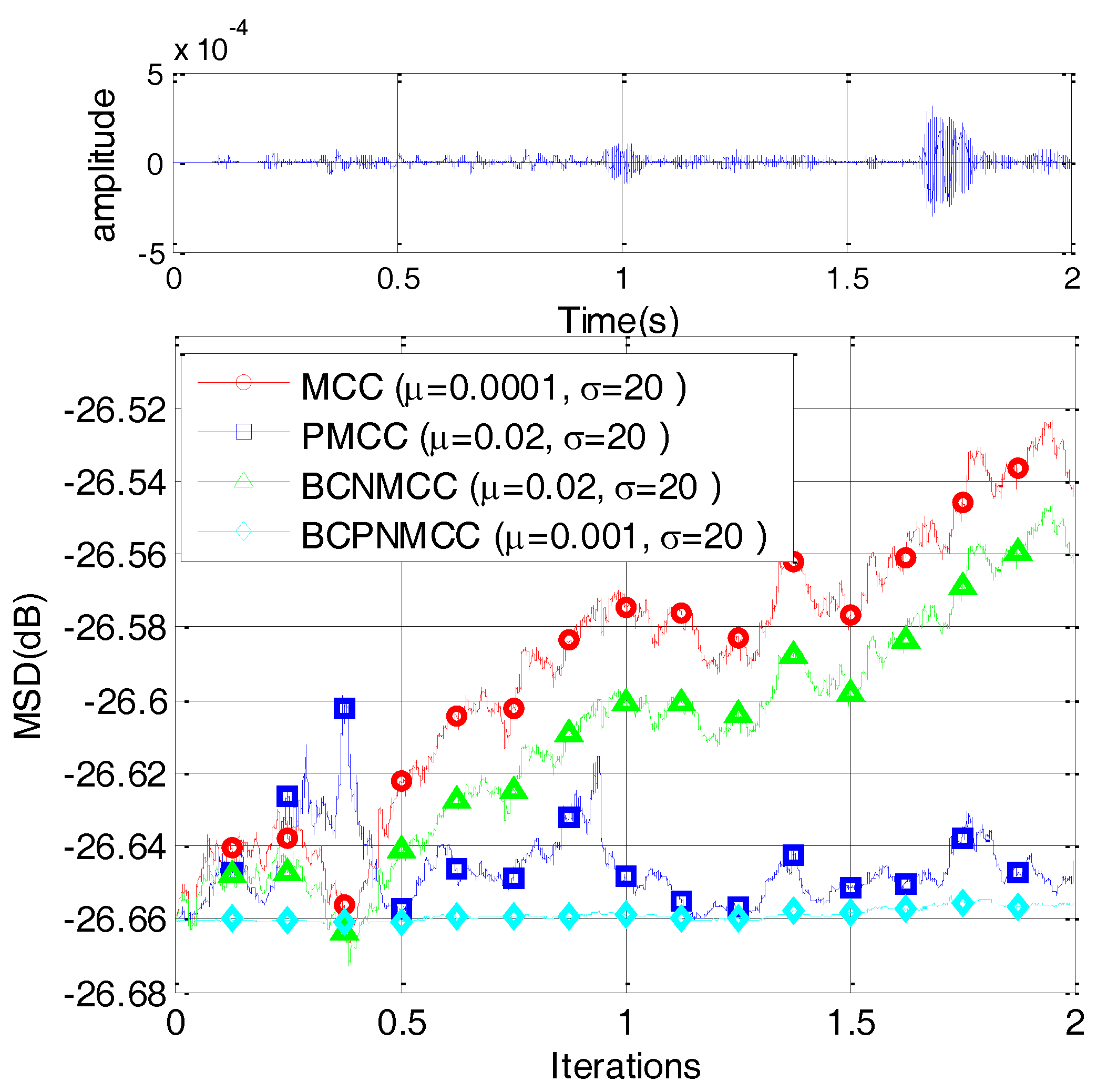
4. Simulation Results
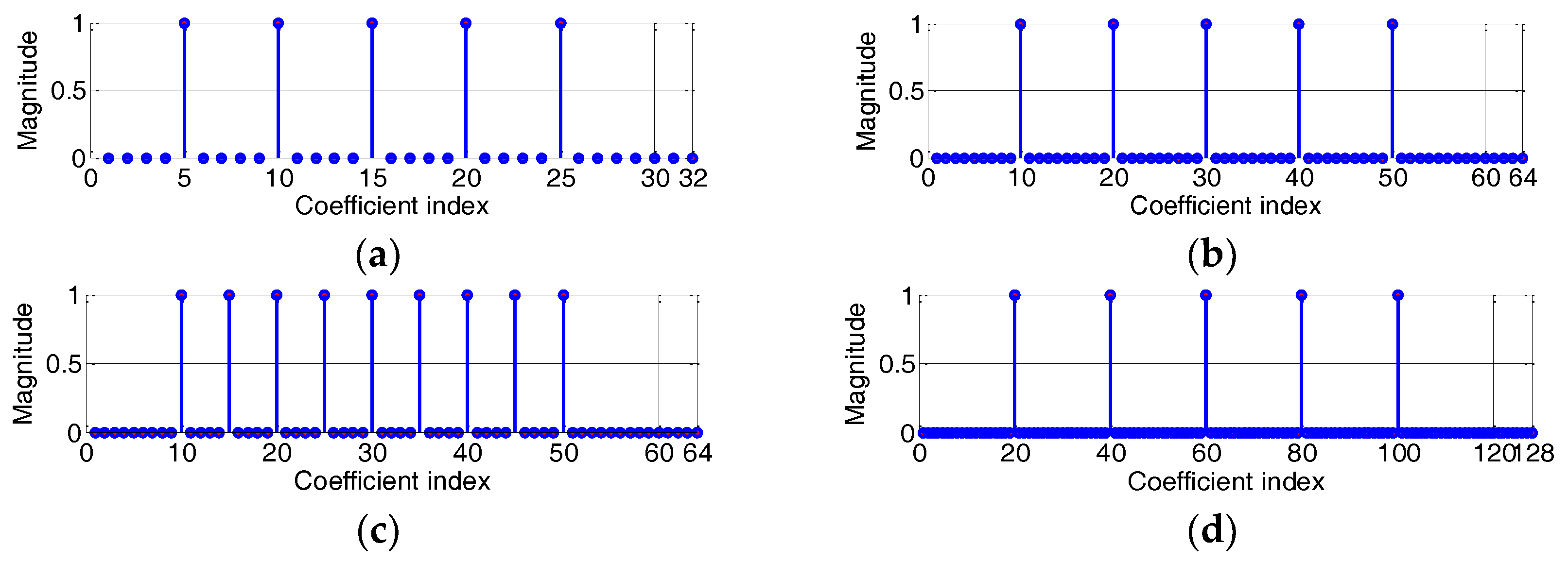
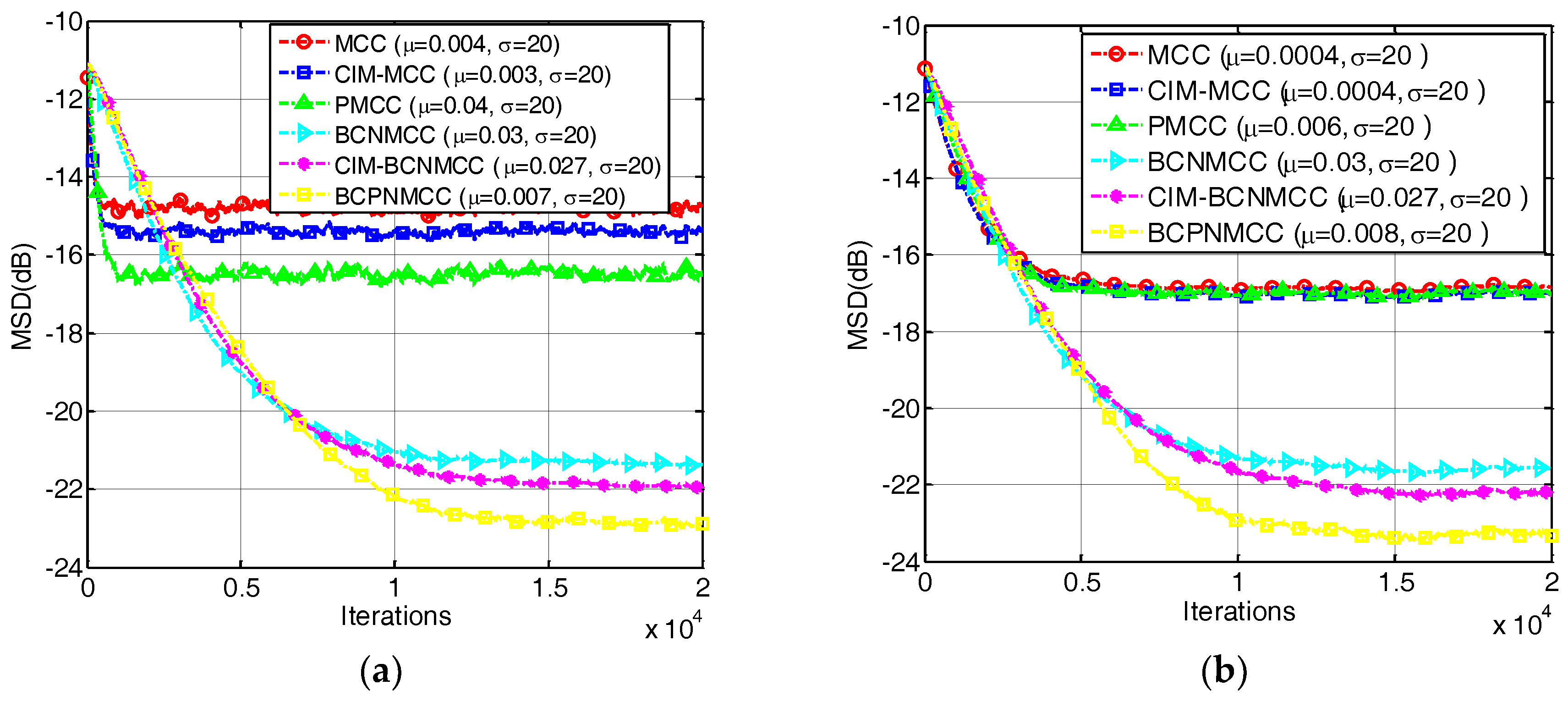
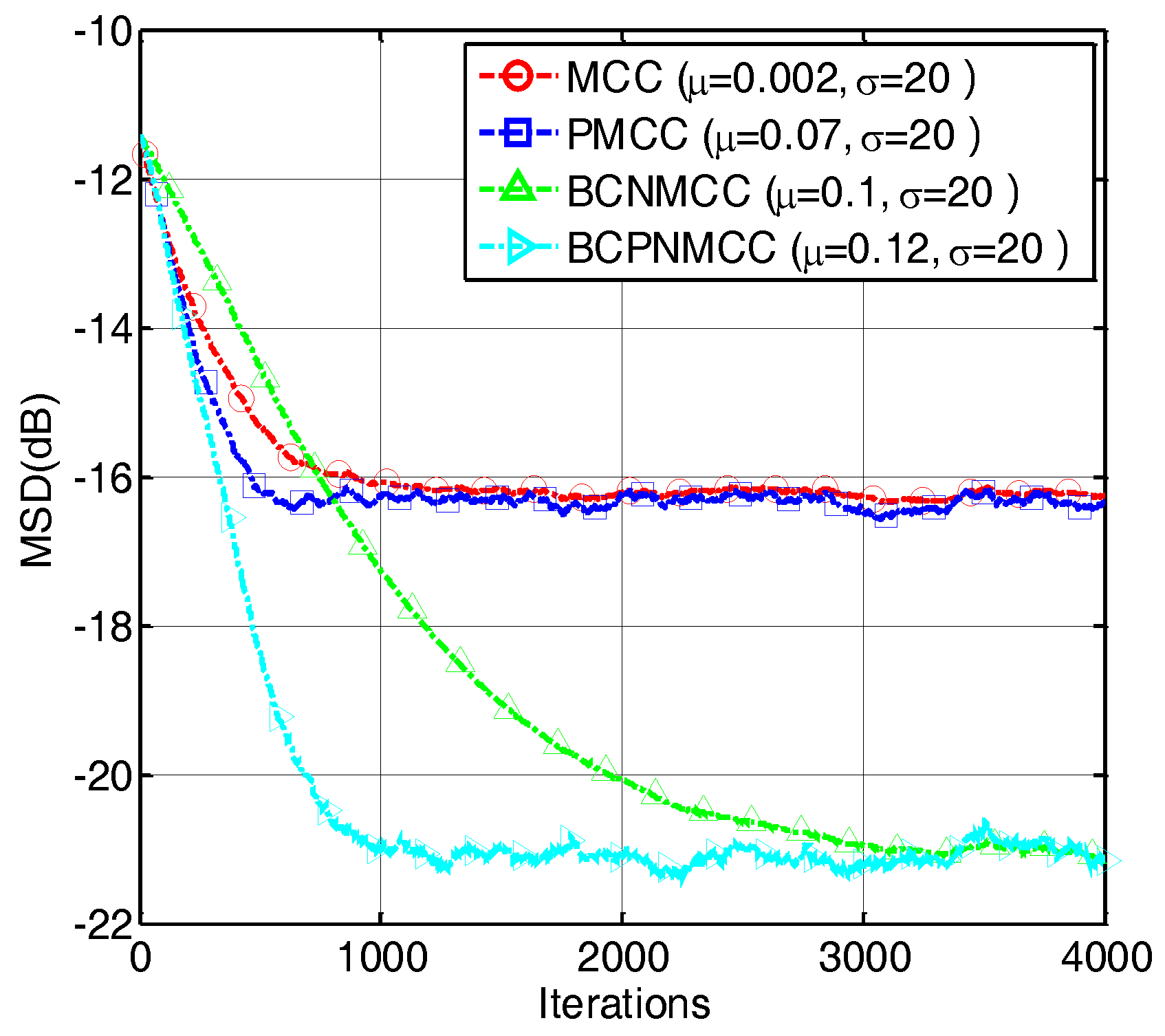
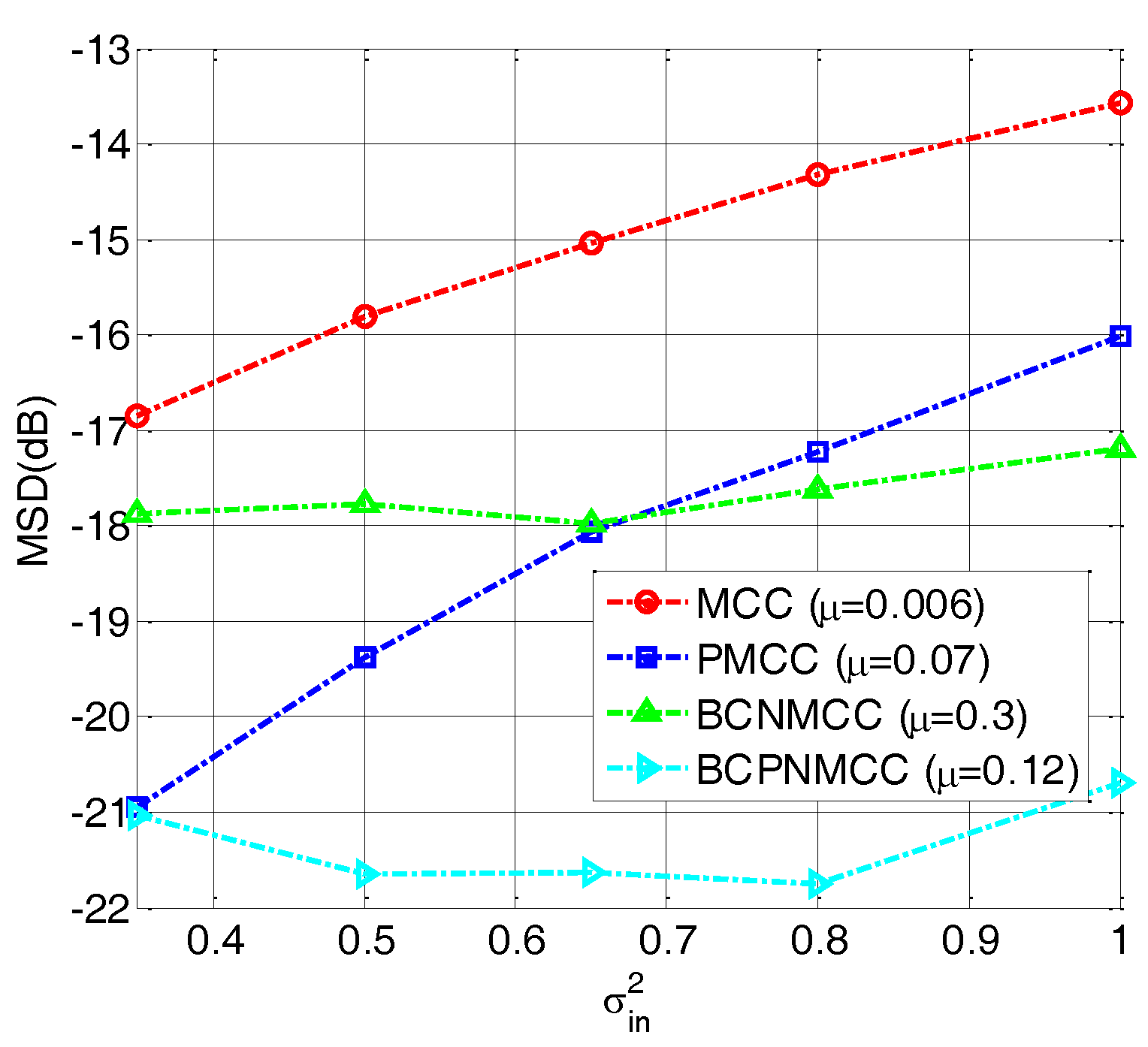
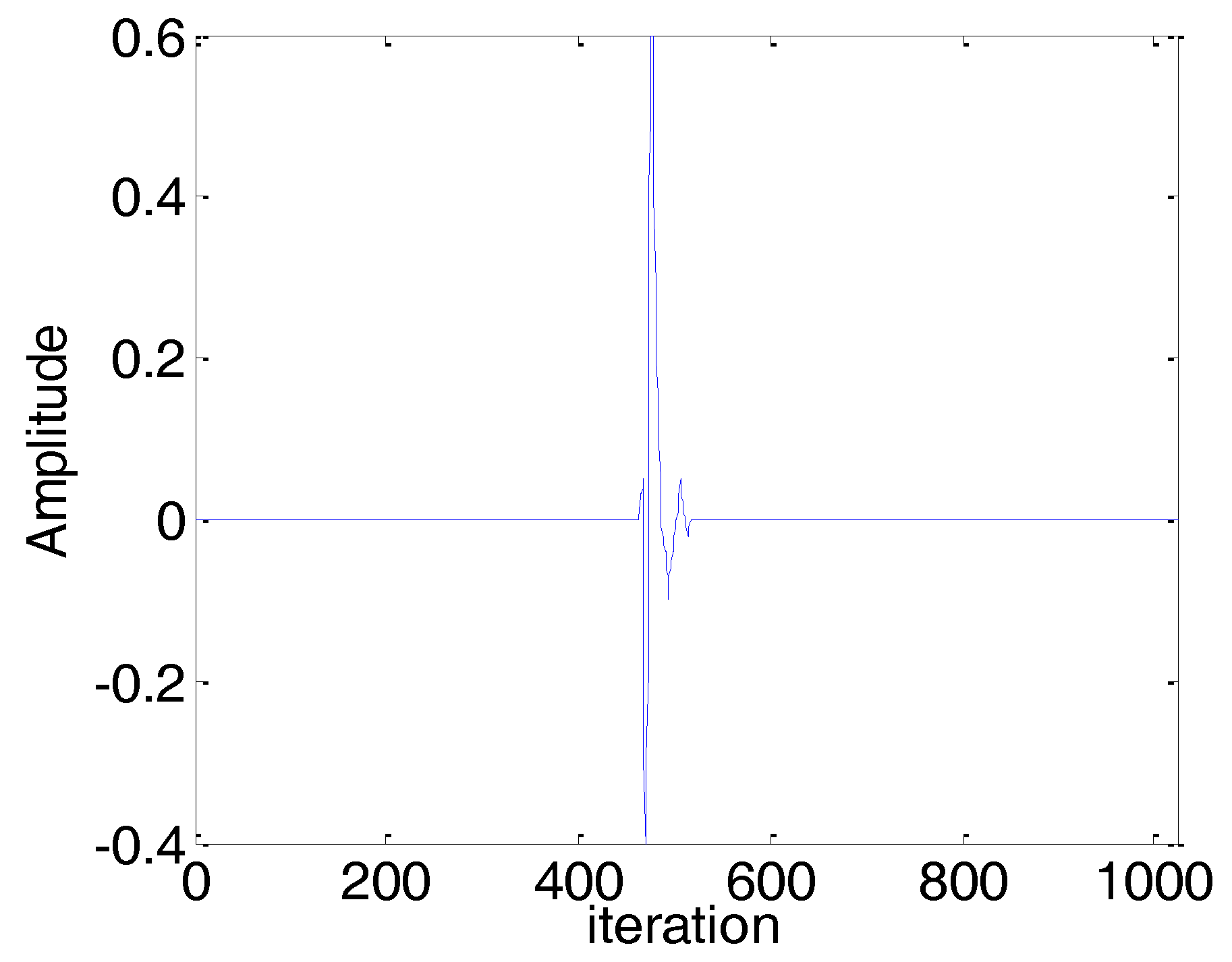
4.1. Sparse System Identification
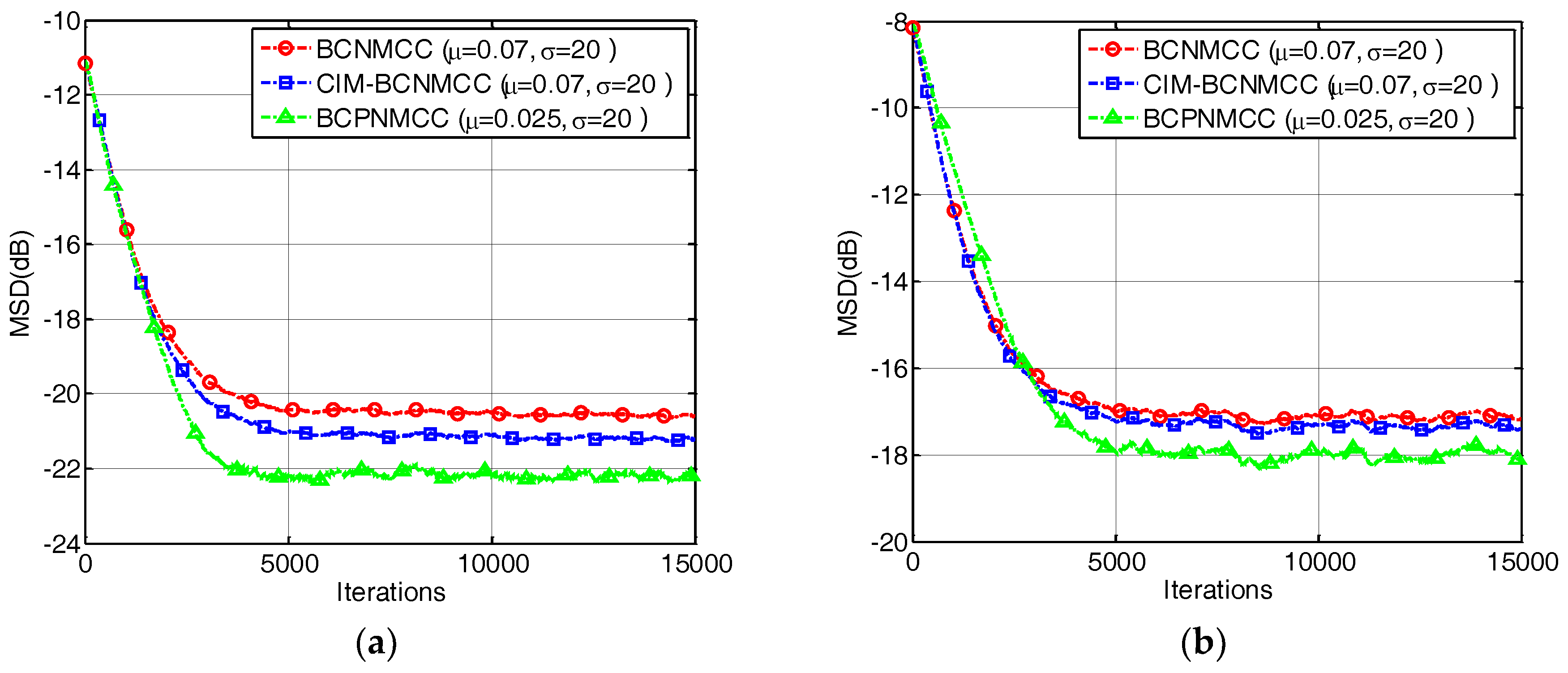
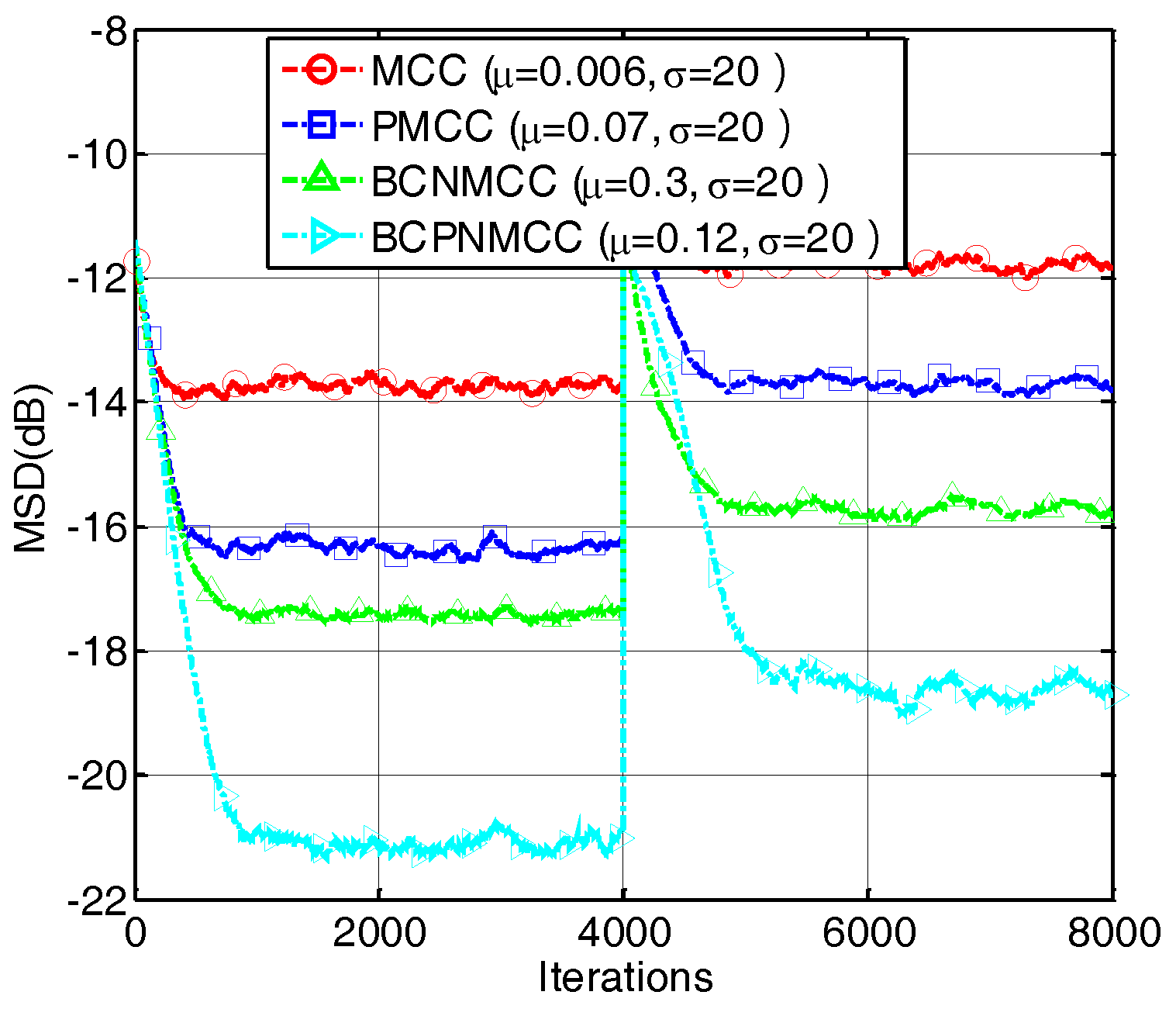
4.2. Sparse Echo Channel Estimation
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kalouptsidis, N.; Mileounis, G.; Babadi, B. Adaptive algorithms for sparse system identification. Signal Process. 2011, 91, 1910–1919. [Google Scholar] [CrossRef]
- Slock, D.T.M. On the convergence behavior of the LMS and the normalized LMS algorithms. IEEE Trans. Signal Process. 1993, 41, 2811–2825. [Google Scholar] [CrossRef]
- Walach, E.; Widrow, B. The least mean fourth (LMF) adaptive algorithm and its family. IEEE Trans. Inf. Theory 1984, 30, 275–283. [Google Scholar] [CrossRef]
- Zerguine, A. Convergence and steady-state analysis of the normalized least mean fourth algorithm. Digit. Signal Process. 2007, 17, 17–31. [Google Scholar] [CrossRef]
- Liu, W.; Pokharel, P.; Principe, J.C. Correntropy: Properties and applications in non-Gaussian signal processing. IEEE Trans. Signal Process. 2007, 55, 5286–5298. [Google Scholar] [CrossRef]
- Chen, B.; Xing, L.; Liang, J.; Zheng, N.; Principe, J.C. Steady-state mean-square error analysis for adaptive filtering under the maximum correntropy criterion. IEEE Signal Process. Lett. 2014, 21, 880–884. [Google Scholar]
- Chen, B.; Principe, J.C. Maximum correntropy estimation is a smoothed MAP estimation. IEEE Signal Process. Lett. 2012, 19, 491–494. [Google Scholar] [CrossRef]
- Chen, B.; Wang, J.; Zhao, H.; Zheng, N.; Principe, J.C. Convergence of a fixed-point algorithm under maximum correntropy criterion. IEEE Signal Process. Lett. 2015, 22, 1723–1727. [Google Scholar] [CrossRef]
- Chambers, J.; Avlonitis, A. A robust mixed-norm adaptive filter algorithm. IEEE Signal Process. Lett. 1997, 4, 46–48. [Google Scholar] [CrossRef]
- Breidt, F.J.; Davis, R.A.; Trindade, A.A. Least absolute deviation estimation for all-pass time series models. Ann. Stat. 2001, 29, 919–946. [Google Scholar]
- Ma, W.; Chen, B.; Duan, J.; Zhao, H. Diffusion maximum correntropy criterion algorithms for robust distributed estimation. Digit. Signal Process. 2016, 155, 10–19. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, J.; Zhang, X.; Chen, B. Kernel recursive maximum correntropy. Signal Process. 2015, 117, 11–16. [Google Scholar] [CrossRef]
- Chen, B.; Xing, L.; Zhao, H.; Zheng, N.; Principe, J.C. Generalized correntropy for robust adaptive filtering. IEEE Trans. Signal Process. 2016, 64, 3376–3387. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Albu, F.; Yang, R. Group-constrained maximum correntropy criterion algorithms for estimating sparse mix-noised channels. Entropy 2017, 19, 432. [Google Scholar] [CrossRef]
- Wu, Z.; Peng, S.; Chen, B.; Zhao, H. Robust Hammerstein adaptive filtering under maximum correntropy criterion. Entropy 2015, 17, 7149–7166. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Yang, R.; Albu, F. A soft parameter function penalized normalized maximum correntropy criterion algorithm for sparse system identification. Entropy 2017, 19, 45. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Baraniuk, R.G. Compressive sensing. IEEE Signal Process. Mag. 2007, 24, 21–30. [Google Scholar] [CrossRef]
- Duttweiler, D.L. Proportionate normalized least-mean-squares adaptation in echo cancelers. IEEE Trans. Speech Audio Process. 2000, 8, 508–518. [Google Scholar] [CrossRef]
- Gu, Y.; Jin, J.; Mei, S. l0 norm constraint LMS algorithm for Sparse system identification. IEEE Signal Process. Lett. 2009, 16, 774–777. [Google Scholar]
- Gui, G.; Adachi, F. Sparse least mean fourth algorithm for adaptive channel estimation in low signal-to-noise ratio region. Int. J. Commun. Syst. 2014, 27, 3147–3157. [Google Scholar] [CrossRef]
- Ma, W.; Qu, H.; Gui, G.; Xu, L.; Zhao, J.; Chen, B. Maximum correntropy criterion based sparse adaptive filtering algorithms for robust channel estimation under non-Gaussian environments. J. Franklin Inst. 2015, 352, 2708–2727. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Albu, F.A.; Jiang, J. General Zero Attraction Proportionate Normalized Maximum Correntropy Criterion Algorithm for Sparse System Identification. Symmetry 2017, 9, 229. [Google Scholar] [CrossRef]
- Li, Y.; Jin, Z.; Wang, Y.; Yang, R. A robust sparse adaptive filtering algorithm with a correntropy induced metric constraint for broadband multipath channel estimation. Entropy 2016, 18, 380. [Google Scholar] [CrossRef]
- Ma, W.; Chen, B.; Qu, H.; Zhao, J. Sparse least mean p-power algorithms for channel estimation in the presence of impulsive noise. Signal Image Video Process. 2016, 10, 503–510. [Google Scholar] [CrossRef]
- Sayin, M.O.; Yilmaz, Y.; Demir, A. The Krylov-proportionate normalized least mean fourth approach: Formulation and performance analysis. Signal Process. 2015, 109, 1–13. [Google Scholar] [CrossRef]
- Ma, W.; Zheng, D.; Zhang, Z. Robust proportionate adaptive filter based on maximum correntropy criterion for sparse system identification in impulsive noise environments. Signal Image Video Process. 2018, 12, 117–124. [Google Scholar] [CrossRef]
- Jung, S.M.; Park, P.G. Normalized least-mean-square algorithm for adaptive filtering of impulsive measurement noises and noisy inputs. Electron. Lett. 2013, 49, 1270–1272. [Google Scholar] [CrossRef]
- Yoo, J.W.; Shin, J.W.; Park, P.G. An improved NLMS algorithm in sparse systems against noisy input signals. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 271–275. [Google Scholar] [CrossRef]
- Ma, W.; Zheng, D.; Tong, X.; Zhang, Z.; Chen, B. Proportionate NLMS with Unbiasedness Criterion for Sparse System Identification in the Presence of Input and Output Noises. IEEE Trans. Circuits Syst. II Express Briefs 2017. [Google Scholar] [CrossRef]
- Zheng, Z.; Liu, Z.; Zhao, H. Bias-compensated normalized least-mean fourth algorithm for noisy input. Circuits Syst. Signal Process. 2017, 36, 3864–3873. [Google Scholar] [CrossRef]
- Zhao, H.; Zheng, Z. Bias-compensated affine-projection-like algorithms with noisy input. Electron. Lett. 2016, 52, 712–714. [Google Scholar] [CrossRef]
- Ma, W.; Zheng, D.; Li, Y.; Zhang, Z.; Chen, B. Bias-compensated normalized maximum correntropy criterion algorithm for system identification with noisy Input. arXiv, 2017; arXiv:1711.08677. [Google Scholar]
- Shin, H.C.; Sayed, A.H.; Song, W.J. Variable step-size NLMS and affine projection algorithms. IEEE. Signal Process. Lett. 2004, 11, 132–135. [Google Scholar] [CrossRef]
- Jo, S.E.; Kim, S.W. Consistent normalized least mean square filtering with noisy data matrix. IEEE Trans. Signal Process. 2015, 53, 2112–2123. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, W.; Zheng, D.; Zhang, Z.; Duan, J.; Qiu, J.; Hu, X. Sparse-Aware Bias-Compensated Adaptive Filtering Algorithms Using the Maximum Correntropy Criterion for Sparse System Identification with Noisy Input. Entropy 2018, 20, 407. https://doi.org/10.3390/e20060407
Ma W, Zheng D, Zhang Z, Duan J, Qiu J, Hu X. Sparse-Aware Bias-Compensated Adaptive Filtering Algorithms Using the Maximum Correntropy Criterion for Sparse System Identification with Noisy Input. Entropy. 2018; 20(6):407. https://doi.org/10.3390/e20060407
Chicago/Turabian StyleMa, Wentao, Dongqiao Zheng, Zhiyu Zhang, Jiandong Duan, Jinzhe Qiu, and Xianzhi Hu. 2018. "Sparse-Aware Bias-Compensated Adaptive Filtering Algorithms Using the Maximum Correntropy Criterion for Sparse System Identification with Noisy Input" Entropy 20, no. 6: 407. https://doi.org/10.3390/e20060407
APA StyleMa, W., Zheng, D., Zhang, Z., Duan, J., Qiu, J., & Hu, X. (2018). Sparse-Aware Bias-Compensated Adaptive Filtering Algorithms Using the Maximum Correntropy Criterion for Sparse System Identification with Noisy Input. Entropy, 20(6), 407. https://doi.org/10.3390/e20060407




