Thermoelectric Efficiency of a Topological Nano-Junction
Abstract
1. Introduction
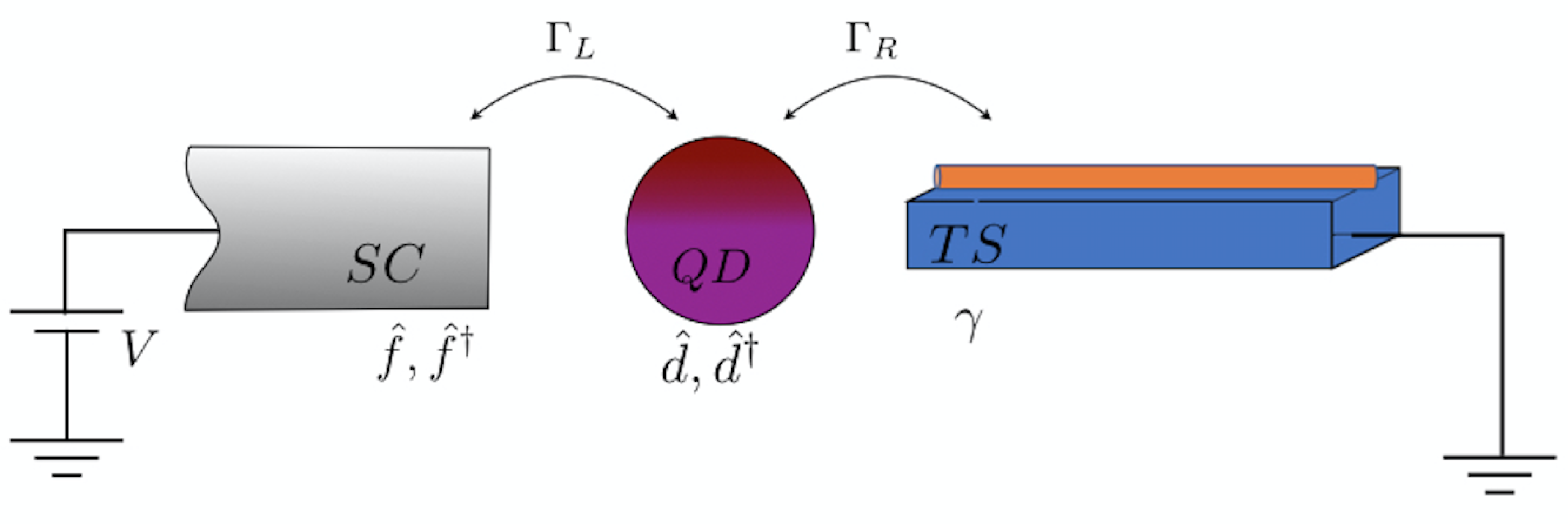
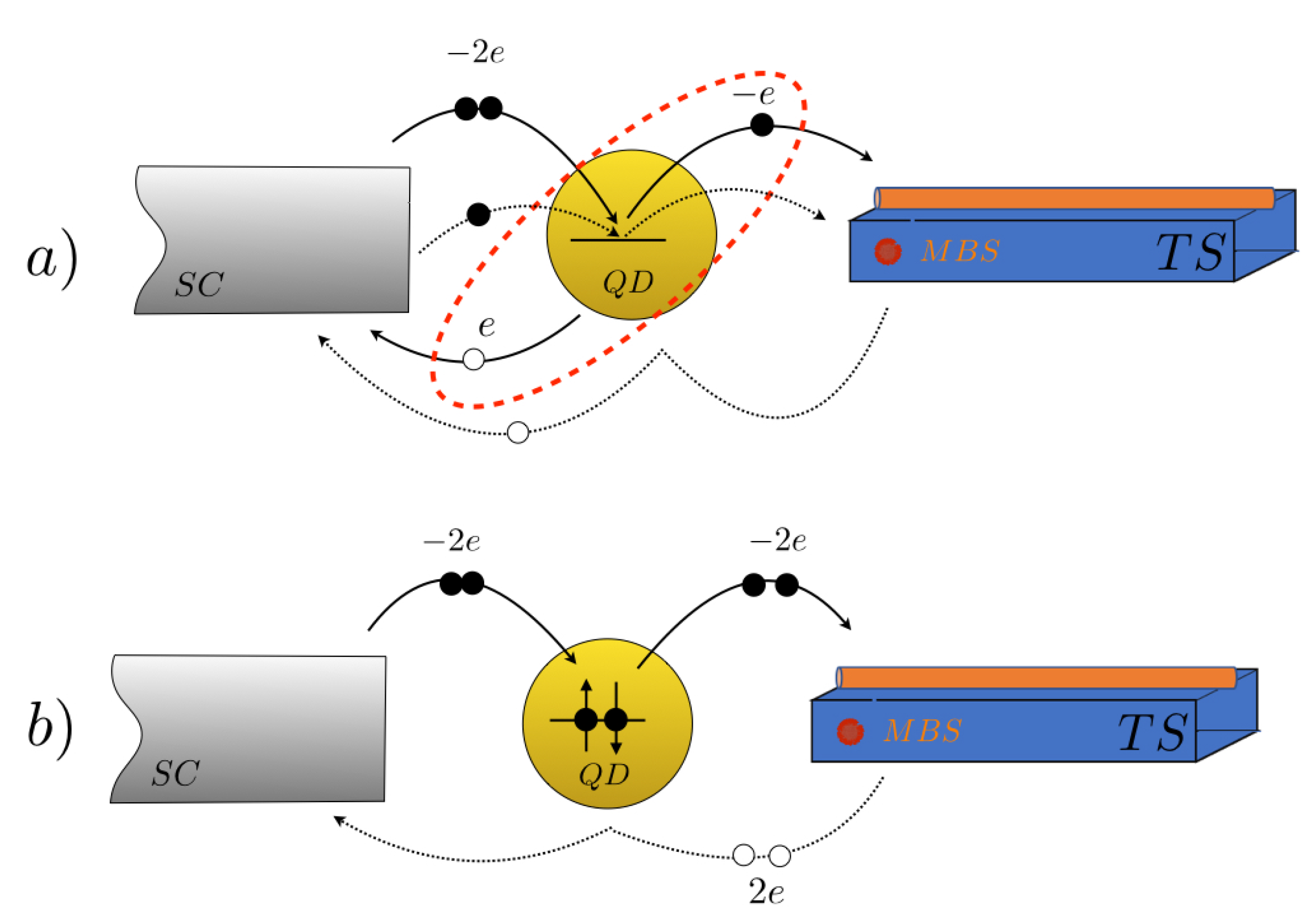
2. The Hybrid Nano-Junction
The Model
3. Non-Equilibrium Transport Through the Nano-Junction
Non-Equilibrium Green’s Function in the Floquet Basis
4. Results
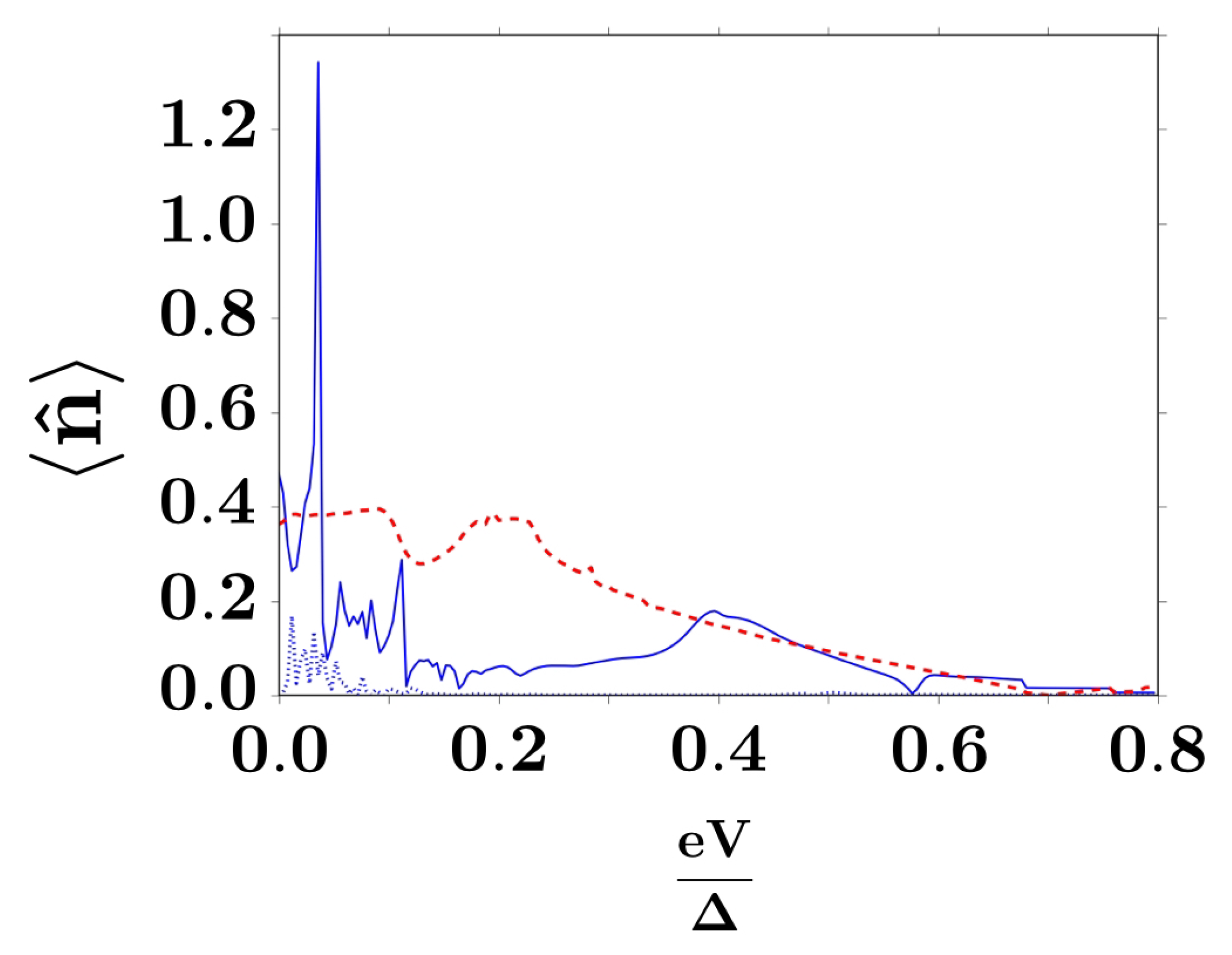
4.1. Electrical Current
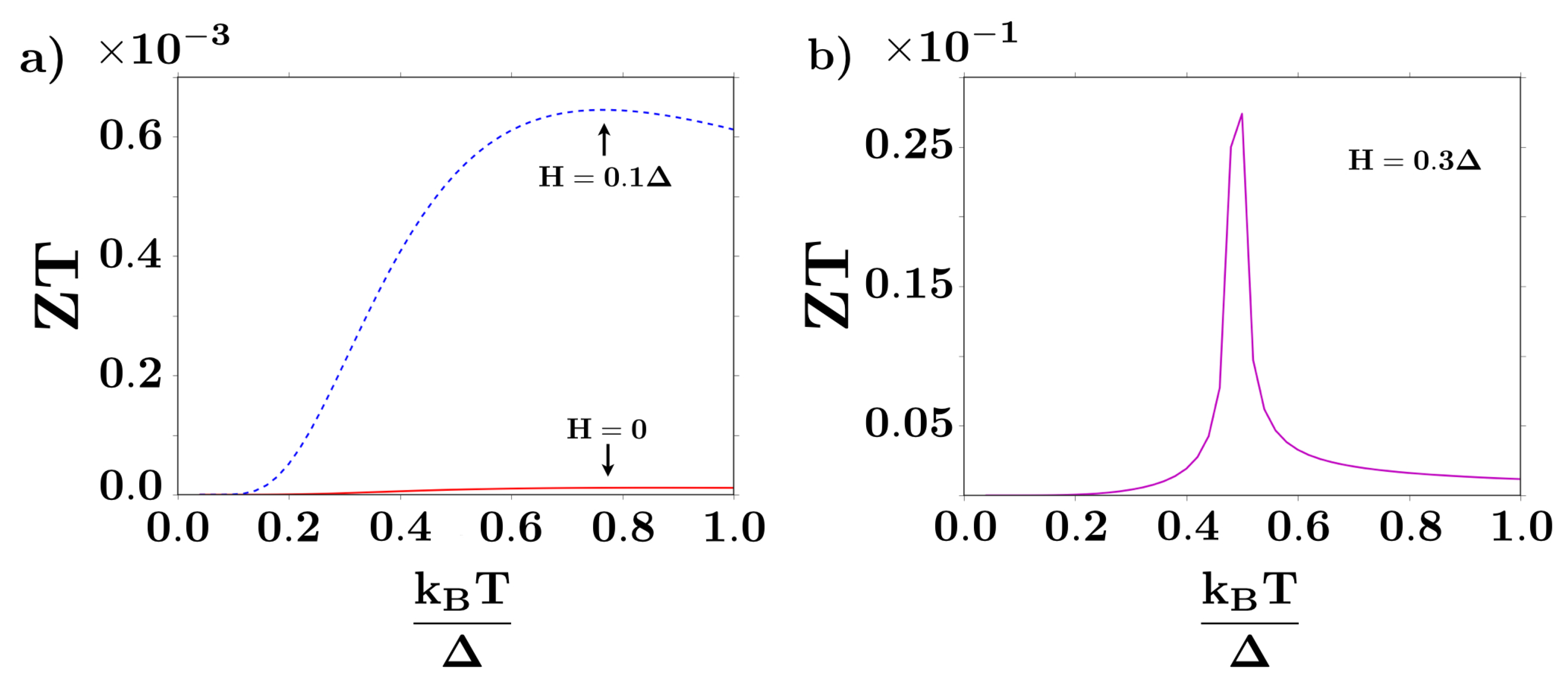
4.2. Thermoelectric Performance
5. Discussion
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Non-Equilibrium Green’s Function Method
Appendix A.1. Closed-Time Contour Formalism

Appendix A.2. Non-Equilibrium Keldysh Formalism

Appendix B. Thermoelectric Transport Coefficients and Onsager Relations
References
- Nayak, C.; Simon, S.H.; Stern, A.; Freedman, M.; Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 2000, 80, 1083. [Google Scholar] [CrossRef]
- Alicea, J.; Oreg, Y.; Refael, G.; von Oppen, F.; Fisher, P.A. Non-Abelian statistics and topological quantum information processing in 1D wire networks. Nat. Phys. 2010, 7, 412–417. [Google Scholar] [CrossRef]
- Beenakker, C. Search for Majorana fermions in superconductors. Annu. Rev. Condens. Matter Phys. 2013, 4, 113–136. [Google Scholar] [CrossRef]
- Read, N.; Green, D. Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries and the fractional quantum Hall effect. Phys. Rev. B 2000, 61, 10267. [Google Scholar] [CrossRef]
- Kitaev, A. Unpaired Majorana fermions in quantum wires. Phys. Usp. 2001, 44, 131. [Google Scholar] [CrossRef]
- Bolech, C.J.; Demler, E. Observing Majorana bound States in p-Wave Superconductors Using Noise Measurements in Tunneling Experiments. Phys. Rev. Lett. 2007, 98, 237002. [Google Scholar] [CrossRef] [PubMed]
- San-Jose, P.; Prada, E.; Aguado, R. Ac Josephson Effect in Finite-Length Nanowire Junction with Majorana Modes. Nano Energy 2012, 108, 1462–1524. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, J.; Akhmerov, A.R.; Beenakker, C. Splitting of a Cooper Pair by a Pair of Majorana Bound States. Phys. Rev. Lett. 2008, 101, 120403. [Google Scholar] [CrossRef] [PubMed]
- Law, K.T.; Lee, P.A.; Ng, T.K. Majorana Fermion Induced Resonant Andreev Reflection. Phys. Rev. Lett. 2009, 103, 237001. [Google Scholar] [CrossRef] [PubMed]
- Wimmer, M.; Akhmerov, A.R.; Dahlhaus, J.P.; Beenakker, C. Quantum point contact as a probe of a topological superconductor. New. J. Phys. 2011, 13, 053016. [Google Scholar] [CrossRef]
- Oreg, Y.; Rafael, G.; von Oppen, F. Helical Liquids and Majorana Bound States in Quantum Wires. Phys. Rev. Lett. 2010, 105, 177002. [Google Scholar] [CrossRef] [PubMed]
- Lutchyn, R.M.; Sau, J.D.; Das Sarma, S. Majorana Fermions and a Topological Phase Transition in Semiconductor-Superconductor Heterostructures. Phys. Rev. Lett. 2010, 105, 077001. [Google Scholar] [CrossRef] [PubMed]
- Mourik, V.; Kuo, K.; Frolov, S.M.; Plissard, S.R.; Bakkers, E.P.A.M.; Kouwenhoven, L.P. Signatures of Majorana Fermions in Hybrid Superconductor-Semiconductor Nanowire Devices. Science 2012, 336, 1003. [Google Scholar] [CrossRef] [PubMed]
- Golub, A. Multiple Andreev reflections in s-wave superconductor-quantum dot-topological superconductor tunnel junction and Majorana Bound states. Phys. Rev. B 2015, 91, 205105. [Google Scholar] [CrossRef]
- Ricco, L.S.; Dessotti, F.A.; Shelykh, I.A.; Figueira, M.S.; Seridonio, A.C. Tuning of heat and charge transport by Majorana fermions. Sci. Rep. 2018, 8, 2790. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, D.; Feldman, D.; Mirlin, A.D.; Shnirman, A. Themoelectric transport in junction of Majorana and Dirac channels. Phys. Rev. B 2017, 95, 195425. [Google Scholar] [CrossRef]
- Sothmann, B.; Giazotto, F.; Hankiewicz, E.M. High-efficiency thermal switch based on topological Josephson junctions. New J. Phys. 2017, 19, 023056. [Google Scholar] [CrossRef]
- Li, H.; Zhao, Y. Thermal transport in topological-insulator- based superconducting hybrid structures with mixed singlet and triplet pairing states. J. Phys. Condens. Matter 2017, 29, 465001. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Chen, Z.G.; Liu, W.; Yang, L.; Hong, M.; Moshwan, R.; Huang, L.; Zou, J. Achieving high Figure of Merit in p-type polycrystalline Sn0.98Se via self-doping and anisotropy-strengthening. Energy Storage Mater. 2018, 10, 465001. [Google Scholar]
- Yang, L.; Chen, Z.G.; Dargush, M.; Zou, J. High Performance Thermoelectric Materials: Progress and Their Applications. Adv. Energy Mater. 2018, 8, 1701797. [Google Scholar] [CrossRef]
- Moshwan, R.; Yang, L.; Zou, J.; Chen, Z.G. Eco Friendly SnTe Themoelectric Materials: Progress and Future Challenges. Adv. Funct. Mater. 2017, 8, 1703278. [Google Scholar] [CrossRef]
- Yang, L.; Chen, Z.G.; Hong, M.; Wang, L.; Kong, D.; Huang, L.; Han, G.; Zou, Y.; Dargusch, M.; Zou, J. n-type Bi-doped PbTe Nanocubes with Enhanced Thermoelectric Performance. Nano Energy 2017, 31, 105–112. [Google Scholar] [CrossRef]
- Öttinger, H. Beyond Equilibrium Thermodynamics, 1st ed.; Wiley: Hoboken, NY, USA, 2005. [Google Scholar]
- Kirchner, S.; Zamani, F.; Muñoz, E. Nonlinear thermoelectric response of quantum dots: Renormalized dual fermions out of equilibrium. In New Materials for Thermoelectric Applications: Theory and Experiment; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Lifshitz, E.M.; Pitaevskii, L.P. Physical Kinetics. Landau Course of Theoretical Physics, 1st ed.; Butterworth- Heinemann: Oxford, UK, 1997. [Google Scholar]
- Klika, V.; Pavelka, M.; Benziger, J. Functional constraints on phenomenological coefficients. Phys. Rev. E 2017, 95, 022125. [Google Scholar] [CrossRef] [PubMed]
- Ziman, J.M. Electrons and Phonons; Oxford University Press: Cambridge, UK, 1960. [Google Scholar]
- Muñoz, E. Thermal and Thermoelectric Transport in Graphene. In Graphene Science Handbook: Electrical and Optical Properties; CRC Press, Taylor and Francis Group: Abingdon, UK, 2016. [Google Scholar]
- Kubo, R.; Toda, M.; Hashitume, N. Statistical Physics II: Nonequilibrium Statistical Mechanics, 2nd ed.; Springer: Heidelberg, Germany, 1998. [Google Scholar]
- De Groot, S.; Mazur, P. Non-Equilibrium Thermodynamics; Dover: New York, NJ, USA, 1984. [Google Scholar]
- Keldysh, L. Diagram technique for nonequilibrium processes. Zh. Eksp. Teor. Fiz. 1964, 47, 1515. [Google Scholar]
- Kamenev, A. Field Theory of Non-Equilibrium Systems; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Thuberg, D.; Muñoz, E.; Eggert, S.; Reyes, S.A. Perfect Spin Filter by Periodic Drive of a Ferromagnetic Quantum Barrier. Phys. Rev. Lett. 2017, 119, 267701. [Google Scholar] [CrossRef] [PubMed]
- Pottier, N. Non-Equilibrium Statistical Physics; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Goldhaber-Gordon, D.; Göres, J.; Kastner, M.A.; Shtrikman, H.; Mahalu, D.; Meirav, U. From the Kondo Regime to the Mixed-Valence Regime in a Single-Electron Transistor. Phys. Rev. Lett. 1998, 81, 5225. [Google Scholar] [CrossRef]
- Muñoz, E.; Bolech, C.J.; Kirchner, S. Universal Out-of-Equilibrium Transport in Kondo-Correlated Quantum Dots: Renormalized Dual Fermions on the Keldysh Contour. Phys. Rev. Lett. 2013, 110, 016601. [Google Scholar] [CrossRef] [PubMed]
- Ashcroft, N.W.; Mermin, N. Solid State Physics; Harcourt College Publishers: San Diego, CA, USA, 1976. [Google Scholar]
- Benenti, G.; Saito, K.; Casati, G. Thermodynamic bounds on efficiency for systems with broken time-reversal symmetry. Phys. Rev. Lett. 2011, 106, 230602. [Google Scholar] [CrossRef] [PubMed]
- Stefanucci, G.; van Leeuwen, R. Nonequilibrium Many-Body Theory of Quantum Systems; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Larkin, A.I.; Ovchinnikov, Y.N. Nonlinear conductivity of superconductors in the mixed state. Zh. Eksp. Teor. Fiz. 1975, 68, 1915. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Álamo, M.; Muñoz, E. Thermoelectric Efficiency of a Topological Nano-Junction. Entropy 2018, 20, 366. https://doi.org/10.3390/e20050366
Álamo M, Muñoz E. Thermoelectric Efficiency of a Topological Nano-Junction. Entropy. 2018; 20(5):366. https://doi.org/10.3390/e20050366
Chicago/Turabian StyleÁlamo, Manuel, and Enrique Muñoz. 2018. "Thermoelectric Efficiency of a Topological Nano-Junction" Entropy 20, no. 5: 366. https://doi.org/10.3390/e20050366
APA StyleÁlamo, M., & Muñoz, E. (2018). Thermoelectric Efficiency of a Topological Nano-Junction. Entropy, 20(5), 366. https://doi.org/10.3390/e20050366





