1. Introduction
The composition of systems and operations is a fundamental primitive in our modelling of the world. It has been investigated in depth in quantum information theory [
1,
2], and in the foundations of quantum mechanics, where composition has played a key role from the early days of Einstein–Podolski–Rosen [
3] and Schroedinger [
4]. At the level of frameworks, the most recent developments are the compositional frameworks of general probabilistic theories [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15] and categorical quantum mechanics [
16,
17,
18,
19,
20].
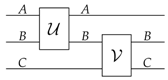
The mathematical structure underpinning most compositional approaches is the structure of monoidal category [
18,
21]. Informally, a monoidal category describes circuits, in which wires represent systems and boxes represent operations, as in the following diagram:
The composition of systems is described by a binary operation denoted by ⊗, and referred to as the “tensor product” (note that ⊗ is not necessarily a tensor product of vector spaces). The system is interpreted as the composite system made of subsystems A and B. Larger systems are built in a bottom-up fashion, by combining subsystems together. For example, a quantum system of dimension can arise from the composition of n single qubits.
In some situations, having a rigid decomposition into subsystems is neither the most convenient nor the most natural approach. For example, in algebraic quantum field theory [
22], it is natural to start from a single system—the field—and then to identify subsystems, e.g., spatial or temporal modes. The construction of the subsystems is rather flexible, as there is no privileged decomposition of the field into modes. Another example of flexible decomposition into subsystems arises in quantum information, where it is crucial to identify degrees of freedom that can be treated as “qubits”. Viola, Knill, and Laflamme [
23] and Zanardi, Lidar, and Lloyd [
24] proposed that the partition of a system into subsystems should depend on which operations are experimentally accessible. This flexible definition of subsystem has been exploited in quantum error correction, where decoherence free subsystems are used to construct logical qubits that are untouched by noise [
25,
26,
27,
28,
29,
30]. The logical qubits are described by “virtual subsystems" of the total Hilbert space [
31], and in general such subsystems are spread over many physical qubits. In all these examples, the subsystems are constructed through an algebraic procedure, whereby the subsystems are associated with algebras of observables [
32]. However, the notion of “algebra of observables” is less appealing in the context of general physical theories, because the multiplication of two observables may not be defined. For example, in the framework of general probabilistic theories [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15], observables represent measurement procedures, and there is no notion of “multiplication of two measurement procedures”.
In this paper, we propose a construction of subsystems that can be applied to general physical theories, even in scenarios where observables and measurements are not included in the framework. The core of our construction is to associate subsystems to sets of
operations, rather than observables. To fix ideas, it is helpful to think that the operations can be performed by some
agent. Given a set of operations, the construction extracts the degrees of freedom that are acted upon
only by those operations, identifying a “private space” that only the agent can access. Such a private space then becomes the subsystem, equipped with its own set of states and its own set of operations. This construction is closely related to an approach proposed by Krämer and del Rio, in which the states of a subsystem are identified with equivalence classes of states of the global system [
33]. In this paper, we extend the equivalence relation to transformations, providing a complete description of the subsystems. We illustrate the construction in a several examples, including
quantum subsystems associated with the tensor product of two Hilbert spaces,
subsystems associated with an subalgebra of self-adjoint operators on a given Hilbert space,
classical systems of quantum systems,
subsystems associated with the action of a group representation on a given Hilbert space.
The example of the classical systems has interesting implications for the resource theory of coherence [
34,
35,
36,
37,
38,
39,
40,
41]. Our construction implies that different types of agents, corresponding to different choices of free operations, are associated with the same subsystem, namely the largest classical subsystem of a given quantum system. Specifically, classical systems arise from strictly incoherent operations [
41], physically incoherent operations [
38,
39], phase covariant operations [
38,
39,
40], and multiphase covariant operations (to the best of our knowledge, multiphase covariant operations have not been considered so far in the resource theory of coherence). Notably, we do not obtain classical subsystems from the maximally incoherent operations [
34] and from the incoherent operations [
35,
36], which are the first two sets of free operations proposed in the resource theory of coherence. For these two types of operations, we find that the associated subsystem is the whole quantum system.
After examining the above examples, we explore the general features of our construction. An interesting feature is that certain properties, such as the impossibility of instantaneous signalling between two distinct subsystems, arise
by fiat, rather then being postulated as physical requirements. This fact is potentially useful for the project of finding new axiomatizations of quantum theory [
42,
43,
44,
45,
46,
47,
48] because it suggests that some of the axioms assumed in the usual (compositional) framework may turn out to be consequences of the very definition of subsystem. Leveraging on this fact, one could hope to find axiomatizations with a smaller number of axioms that pinpoint exactly the distinctive features of quantum theory. In addition, our construction suggests a
desideratum that every truly fundamental axiom should arguably satisfy:
an axiom for quantum theory should hold for all possible subsystems of quantum systems. We call this requirement
Consistency Across Subsystems. If one accepts our broad definition of subsystems, then Consistency Across Subsystems is a very non-trivial requirement, which is not easily satisfied. For example, the Subspace Axiom [
5], stating that all systems with the same number of distinguishable states are equivalent, does not satisfy Consistency Across Subsystems because classical subsystems are not equivalent to the corresponding quantum systems, even if they have the same number of distinguishable states.
In general, proving that Consistence Across Subsystems is satisfied may require great effort. Rather than inspecting the existing axioms and checking whether or not they are consistent across subsystems, one can try to formulate the axioms in a way that guarantees the validity of this property. We illustrate this idea in the case of the Purification Principle [
8,
12,
13,
15,
49,
50,
51], which is the key ingredient in the quantum axiomatization of Refs. [
13,
15,
42] and plays a central role in the axiomatic foundation of quantum thermodynamics [
52,
53,
54] and quantum information protocols [
8,
15,
55,
56,
57]. Specifically, we show that the Purification Principle holds for
closed systems, defined as systems where all transformations are invertible, and where every state can be generated from a fixed initial state by the action of a suitable transformation. Closed systems satisfy the Conservation of Information [
58], i.e., the requirement that physical dynamics should send distinct states to distinct states. Moreover, the states of the closed systems can be interpreted as “pure”. In this setting, the general notion of subsystem captures the idea of purification, and extends it to a broader setting, allowing us to regard coherent superpositions as the “purifications” of classical probability distributions.
The paper is structured as follows. In
Section 2, we outline related works. In
Section 3, we present the main framework and the construction of subsystems. The framework is illustrated with five concrete examples in
Section 4. In
Section 5, we discuss the key structures arising from our construction, such as the notion of partial trace and the validity of the no-signalling property. In
Section 6, we identify two requirements, concerning the existence of agents with non-overlapping sets of operations, and the ability to generate all states from a given initial state. We also highlight the relation between the second requirement and the notion of causality. We then move to systems satisfying the Conservation of Information (
Section 7) and we formalize an abstract notion of closed systems (
Section 8). For such systems, we provide a dynamical notion of pure states, and we prove that every subsystem satisfies the Purification Principle (
Section 9). A macro-example, dealing with group representations in quantum theory is provided in
Section 10. Finally, the conclusions are drawn in
Section 11.
2. Related Works
In quantum theory, the canonical route to the definition of subsystems is to consider commuting algebras of observables, associated with independent subsystems. The idea of defining independence in terms of commutation has a long tradition in quantum field theory and, more recently, quantum information theory. In algebraic quantum field theory [
22], the local subsystems associated with causally disconnected regions of spacetime are described by commuting
C*-algebras. A closely related approach is to associate quantum systems to von Neumann algebras, which can be characterized as double commutants [
59]. In quantum error correction, decoherence free subsystems are associated with the commutant of the noise operators [
28,
29,
31]. In this context, Viola, Knill, and Laflamme [
23] and Zanardi, Lidar, and Lloyd [
24] made the point that subsystems should be defined operationally, in terms of the experimentally accessible operations. The canonical approach of associating subsystems to subalgebras was further generalized by Barnum, Knill, Ortiz, and Viola [
60,
61], who proposed the notion of generalized entanglement, i.e., entanglement relative to a subspace of operators. Later, Barnum, Ortiz, Somma, and Viola explored this notion in the context of general probabilistic theories [
62].
The above works provided a concrete model of subsystems that inspired the present work. An important difference, however, is that here we will not use the notions of observable and expectation value. In fact, we will not use any probabilistic notion, making our construction usable also in frameworks where no notion of measurement is present. This makes the construction appealingly simple, although the flip side is that more work will have to be done in order to recover the probabilistic features that are built-in in other frameworks.
More recently, del Rio, Krämer, and Renner [
63] proposed a general framework for representing the knowledge of agents in general theories (see also the Ph.D. theses of del Rio [
64] and Krämer [
65]). Krämer and del Rio further developed the framework to address a number of questions related to locality, associating agents to monoids of operations, and introducing a relation, called
convergence through a monoid, among states of a global system [
33]. Here, we will extend this relation to transformations, and we will propose a general definition of subsystem, equipped with its set of states and its set of transformations.
Another related work is the work of Brassard and Raymond-Robichaud on no-signalling and local realism [
66]. There, the authors adopt an equivalence relation on transformations, stating that two transformations are equivalent iff they can be transformed into one another through composition with a local reversible transformation. Such a relation is related to the equivalence relation on transformations considered in this paper, in the case of systems satisfying the Conservation of Information. It is interesting to observe that, notwithstanding the different scopes of Ref. [
66] and this paper, the Conservation of Information plays an important role in both. Ref. [
66], along with discussions with Gilles Brassard during QIP 2017 in Seattle, provided inspiration for the present paper.
3. Constructing Subsystems
Here, we outline the basic definitions and the construction of subsystems.
3.1. A Pre-Operational Framework
Our starting point is to consider a single system S, with a given set of states and a given set of transformations. One could think S to be the whole universe, or, more modestly, our “universe of discourse”, representing the fragment of the world of which we have made a mathematical model. We denote by the set of states of the system (sometimes called the “state space”), and by be the set of transformations the system can undergo. We assume that is equipped with a composition operation ∘, which maps a pair of transformations and into the transformation . The transformation is interpreted as the transformation occurring when happens right before . We also assume that there exists an identity operation , satisfying the condition for every transformation . In short, we assume that the physical transformations form a monoid.
We do not assume any structure on the state space : in particular, we do not assume that is convex. We do assume, however, is that there is an action of the monoid on the set : given an input state and a transformation , the action of the transformation produces the output state .
Example 1 (Closed quantum systems)
. Let us illustrate the basic framework with a textbook example, involving a closed quantum system evolving under unitary dynamics. Here, S is a quantum system of dimension d, and the state space is the set of pure quantum states, represented as rays on the complex vector space , or equivalently, as rank-one projectors. With this choice, we have The physical transformations are represented by unitary channels, i.e., by maps of the form , where is a unitary d-by-d matrix over the complex field. In short, we havewhere I is the d-by-d identity matrix. The physical transformations form a monoid, with the composition operation induced by the matrix multiplication . Example 2 (Open quantum systems)
. Generally, a quantum system can be in a mixed state and can undergo an irreversible evolution. To account for this scenario, we must take the state space to be the set of all density matrices. For a system of dimension d, this means that the state space iswhere denotes the matrix trace, and means that the matrix ρ is positive semidefinite. is the set of all quantum channels [67], i.e., the set of all linear, completely positive, and trace-preserving maps from to itself. The action of the quantum channel on a generic state ρ can be specified through the Kraus representation [68]where is a set of matrices satisfying the condition . The composition of two transformations and S is given by the composition of the corresponding linear maps. Note that, at this stage, there is no notion of measurement in the framework. The sets and are meant as a model of system S irrespectively of anybody’s ability to measure it, or even to operate on it. For this reason, we call this layer of the framework pre-operational. One can think of the pre-operational framework as the arena in which agents will act. Of course, the physical description of such an arena might have been suggested by experiments done earlier on by other agents, but this fact is inessential for the scope of our paper.
3.2. Agents
Let us introduce agents into the picture. In our framework, an agent A is identified a set of transformations, denoted as and interpreted as the possible actions of A on S. Since the actions must be allowed physical processes, the inclusion must hold. It is natural, but not strictly necessary, to assume that the concatenation of two actions is a valid action, and that the identity transformation is a valid action. When these assumptions are made, is a monoid. Still, the construction presented in the following will hold not only for monoids, but also for generic sets . Hence, we adopt the following minimal definition:
Definition 1 (Agents)
. An agent A is identified by a subset .
Note that this definition captures only one aspect of agency. Other aspects—such as the ability to gather information, make decisions, and interact with other agents—are important too, but not necessary for the scope of this paper.
We also stress that the interpretation of the subset as the set of actions of an agent is not strictly necessary for the validity of our results. Nevertheless, the notion of “agent” here is useful because it helps explaining the rationale of our construction. The role of the agent is somehow similar to the role of a “probe charge” in classical electromagnetism. The probe charge need not exist in reality, but helps—as a conceptual tool—to give operational meaning to the magnitude and direction of the electric field.
In general, the set of actions available to agent A may be smaller than the set of all physical transformations on S. In addition, there may be other agents that act on system S independently of agent A. We define the independence of actions in the following way:
Definition 2. Agents A and B act independently
if the order in which they act is irrelevant, namely In a very primitive sense, the above relation expresses the fact that A and B act on “different degrees of freedom” of the system.
Remark 1 (Commutation of transformations vs. commutation of observables)
. Commutation conditions similar to Equation (6) are of fundamental importance in quantum field theory, where they are known under the names of “Einstein causality” [69] and “Microcausality” [70]. However, the similarity should not mislead the reader. The field theoretic conditions are expressed in terms of operator algebras. The condition is that the operators associated with independent systems commute. For example, a system localized in a certain region could be associated with the operator algebra , and another system localized in another region could be associated with the operator algebra . In this situation, the commutation condition reads In contrast, Equation (6) is a condition on the transformations
, and not on the observables, which are not even described by our framework. In quantum theory, Equation (6) is a condition on the completely positive maps, and not to the elements of the algebras and . In Section 4, we will bridge the gap between our framework and the usual algebraic framework, focussing on the scenario where and are finite dimensional von Neumann algebras. 3.3. Adversaries and Degradation
From the point of view of agent A, it is important to identify the degrees of freedom that no other agent B can affect. In an adversarial setting, agent B can be viewed as an adversary that tries to control as much of the system as possible.
Definition 3 (Adversary)
. Let A be an agent and let be her set of operations. An adversary
of A is an agent B that acts independently of A, i.e., an agent B whose set of actions satisfies Like the agent, the adversary is a conceptual tool, which will be used to illustrate our notion of subsystem. The adversary need not be a real physical entity, localized outside the agent’s laboratory, and trying to counteract the agent’s actions. Mathematically, the adversary is just a subset of the commutant of . The interpretation of B as an “adversary” is a way to “give life to to the mathematics”, and to illustrate the rationale of our construction.
When
B is interpreted as an adversary, we can think of his actions as a “degradation”, which compromises states and transformations. We denote the degradation relation as
, and write
for
or
.
The states that can be obtained by degrading
will be denoted as
The transformations that can be obtained by degrading
will be denoted as
The more operations
B can perform, the more powerful
B will be as an adversary. The most powerful adversary compatible with the independence condition (
6) is the adversary that can implement all transformations in the commutant of
:
Definition 4. The maximal adversary of agent A is the agent that can perform the actions .
Note that the actions of the maximal adversary are automatically a monoid, even if the set is not. Indeed,
the identity map commutes with all operations in , and
if and commute with every operation in , then also their composition will commute with all the operations in .
In the following, we will use the maximal adversary to define the subsystem associated with agent A.
3.4. The States of the Subsystem
Given an agent A, we think of the subsystem to be the collection of all degrees of freedom that are unaffected by the action of the maximal adversary . Consistently with this intuitive picture, we partition the states of S into disjoint subsets, with the interpretation that two states are in the same subset if and only if they correspond to the same state of subsystem .
We denote by the subset of containing the state . To construct the state space of the subsystem, we adopt the following rule:
Rule 1. If the state ψ is obtained from the state ϕ through degradation, i.e., if , then ψ and ϕ must correspond to the same state of subsystem , i.e., one must have .
Rule 1 imposes that all states in the set must be contained in the set . Furthermore, we have the following fact:
Proposition 1. If the sets and have non-trivial intersection, then
Proof. By Rule 1, every element of is contained in . Similarly, every element of is contained in . Hence, if and have non-trivial intersection, then also and have non-trivial intersection. Since the sets and belong to a disjoint partition, we conclude that . ☐
Generalizing the above argument, it is clear that two states
and
must be in the same subset
if there exists a finite sequence
such that
When this is the case, we write . Note that the relation is an equivalence relation. When the relation holds, we say that and are equivalent for agent A. We denote the equivalence class of the state by .
By Rule 1, the whole equivalence class
must be contained in the set
, meaning that all states in the equivalence class must correspond to the same state of subsystem
. Since we are not constrained by any other condition, we make the minimal choice
In summary, the state space of system
is
3.5. The Transformations of a Subsystem
The transformations of system
can also be constructed through equivalence classes. Before taking equivalence classes, however, we need a candidate set of transformations that can be interpreted as acting exclusively on subsystem
. The largest candidate set is the set of all transformations that commute with the actions of the maximal adversary
, namely
In general, could be larger than , in agreement with the fact the set of physical transformations of system could be larger than the set of operations that agent A can perform. For example, agent A could have access only to noisy operations, while another, more technologically advanced agent could perform more accurate operations on the same subsystem.
For two transformations
and
in
, the degradation relation
takes the simple form
As we did for the set of states, we now partition the set into disjoint subsets, with the interpretation that two transformations act in the same way on the subsystem if and only if they belong to the same subset.
Let us denote by the subset containing the transformation . To find the appropriate partition of into disjoint subsets, we adopt the following rule:
Rule 2. If the transformation is obtained from the transformation through degradation, i.e., if , then and must act in the same way on the subsystem , i.e., they must satisfy .
Intuitively, the motivation for the above rule is that system is defined as the system that is not affected by the action of the adversary.
Rule 2 implies that all transformations in must be contained in . Moreover, we have the following:
Proposition 2. If the sets and have non-trivial intersection, then .
Proof. By Rule 2, every element of is contained in . Similarly, every element of is contained in . Hence, if and have non-trivial intersection, then also and have non-trivial intersection. Since the sets and belong to a disjoint partition, we conclude that . ☐
Using the above proposition, we obtain that the equality
holds whenever there exists a finite sequence
such that
When the above relation is satisfied, we write and we say that and are equivalent for agent A. It is immediate to check that is an equivalence relation. We denote the equivalence class of the transformation as .
By Rule 2, all the elements of
must be contained in the set
, i.e., they should correspond to the same transformation on
. Again, we make the minimal choice: we stipulate that the set
coincides exactly with the equivalence class
. Hence, the transformations of subsystem
are
The composition of two transformations
and
is defined in the obvious way, namely
Similarly, the action of the transformations on the states is defined as
In
Appendix A, we show that definitions (
20) and (
21) are well-posed, in the sense that their right-hand sides are independent of the choice of representatives within the equivalence classes.
Remark 1. It is important not to confuse the transformation with the equivalence class : the former is a transformation on the whole system
S, while the latter is a transformation only on subsystem . To keep track of the distinction, we define the restriction
of the transformation to the subsystem via the map Proposition 3. The restriction map is a monoid homomorphism, namely and for every pair of transformations .
Proof. Immediate from the definition (
20). ☐
4. Examples of Agents, Adversaries, and Subsystems
In this section, we illustrate the construction of subsystems in five concrete examples.
4.1. Tensor Product of Two Quantum Systems
Let us start from the obvious example, which will serve as a sanity check for the soundness of our construction. Let
S be a quantum system with Hilbert space
. The states of
S are all the density operators on the Hilbert space
. The space of all linear operators from
to itself will be denoted as
, so that
The transformations are all the quantum channels (linear, completely positive, and trace-preserving linear maps) from to itself. We will denote the set of all channels on system S as . Similarly, we will use the notation [] for the spaces of linear operators from [] to itself, and the notation [] for the quantum channels from [] to itself.
We can now define an agent
A whose actions are all quantum channels acting locally on system
A, namely
where
denotes the identity map on
. It is relatively easy to see that the commutant of
is
(see
Appendix B for the proof). Hence, the maximal adversary of agent
A is the adversary
that has full control on the Hilbert space
. Note also that one has
.
Now, the following fact holds:
Proposition 4. Two states are equivalent for agent A if and only if , where denotes the partial trace over the Hilbert space .
Proof. Suppose that the equivalence
holds. By definition, this means that there exists a finite sequence
such that
In turn, the condition of non-trivial intersection implies that, for every
, one has
where
and
are two quantum channels in
. Since
and
are trace-preserving, Equation (
27) implies
, as one can see by taking the partial trace on
on both sides. In conclusion, we obtained the equality
.
Conversely, suppose that the condition
holds. Then, one has
where
is the erasure channel defined as
,
being a fixed (but otherwise arbitrary) density matrix in
. Since
is an element of
, Equation (
28) shows that the intersection between
and
is non-empty. Hence,
and
correspond to the same state of system
. ☐
We have seen that two global states
are equivalent for agent
A if and only if they have the same partial trace over
B. Hence, the state space of the subsystem
is
consistently with the standard prescription of quantum mechanics.
Now, let us consider the transformations. It is not hard to show that two transformations
are equivalent if and only if
(see
Appendix B for the details). Recalling that the transformations in
are of the form
, for some
, we obtain that the set of transformations of
is
In summary, our construction correctly identifies the quantum subsystem associated with the Hilbert space , with the right set of states and the right set of physical transformations.
4.2. Subsystems Associated with Finite Dimensional Von Neumann algebras
In this example, we show that our notion of subsystem encompasses the traditional notion of subsystem based on an algebra of observables. For simplicity, we restrict our attention to a quantum system S with finite dimensional Hilbert space , . With this choice, the state space is the set of all density matrices in and the transformation monoid is the set of all quantum channels (linear, completely positive, trace-preserving maps) from to itself.
We now define an agent
A associated with a von Neumann algebra
. In the finite dimensional setting, a von Neumann algebra is just a matrix algebra that contains the identity operator and is closed under the matrix adjoint. Every such algebra can be decomposed in a block diagonal form. Explicitly, one can decompose the Hilbert space
as
for appropriate Hilbert spaces
and
. Relative to this decomposition, the elements of the algebra
are characterized as
where
is an operator in
, and
is the identity on
. The elements of the commutant algebra
are characterized as
where
is the identity on
and
is an operator in
.
We grant agent
A the ability to implement all quantum channels with Kraus operators in the algebra
, i.e., all quantum channels in the set
The maximal adversary of agent
A is the agent
B who can implement all the quantum channels that commute with the channels in
, namely
In
Appendix C, we prove that
coincides with the set of quantum channels with Kraus operators in the commutant of the algebra
: in formula,
As in the previous example, the states of subsystem
can be characterized as “partial traces” of the states in
S, provided that one adopts the right definition of “partial trace”. Denoting the commutant of the algebra
by
, one can define the “partial trace over the algebra
” as the channel
specified by the relation
where
is the projector on the subspace
, and
denotes the partial trace over the space
. With definition (
37), is not hard to see that two states are equivalent for
A if and only if they have the same partial trace over
:
Proposition 5. Two states are equivalent for A if and only if .
The proof is provided in
Appendix C. In summary, the states of system
are obtained from the states of
S via partial trace over
, namely
Our construction is consistent with the standard algebraic construction, where the states of system
are defined as restrictions of the global states to the subalgebra
: indeed, for every element
, we have the relation
meaning that the restriction of the state
to the subalgebra
is in one-to-one correspondence with the state
.
Alternatively, the states of subsystem
can be characterized as density matrices of the block diagonal form
where
is a probability distribution, and each
is a density matrix in
. In
Appendix C, we characterize the transformations of the subsystem
as quantum channels
of the form
where
is a linear, completely positive, and trace-preserving map. In summary, the subsystem
is a direct sum of quantum systems.
4.3. Coherent Superpositions vs. Incoherent Mixtures in Closed-System Quantum Theory
We now analyze an example involving only pure states and reversible transformations. Let
S be a single quantum system with Hilbert space
, equipped with a distinguished orthonormal basis
. As the state space, we consider the set of pure quantum states: in formula,
As the set of transformations, we consider the set of all unitary channels: in formula,
To agent
A, we grant the ability to implement all unitary channels corresponding to diagonal unitary matrices, i.e., matrices of the form
where each phase
can vary independently of the other phases. In formula, the set of actions of agent
A is
The peculiarity of this example is that the actions of the maximal adversary are exactly the same as the actions of A. It is immediate to see that is included in because all operations of agent A commute. With a bit of extra work, one can see that, in fact, and coincide.
Let us look at the subsystem associated with agent A. The equivalence relation among states takes a simple form:
Proposition 6. Two pure states with unit vectors are equivalent for A if and only if for some diagonal unitary matrix U.
Proof. Suppose that there exists a finite sequence
such that
This means that, for every
, there exist two diagonal unitary matrices
and
such that
, or equivalently,
Using the above relation for all values of i, we obtain with .
Conversely, suppose that the condition holds for some diagonal unitary matrix U. Then, the intersection is non-empty, which implies that and are in the same equivalence class. ☐
Using Proposition 6, it is immediate to see that the equivalence class
is uniquely identified by the diagonal density matrix
. Hence, the state space of system
is the set of diagonal density matrices
The set of transformations of system
is trivial because the actions of
A coincide with the actions of the adversary
, and therefore they are all in the equivalence class of the identity transformation. In formula, one has
4.4. Classical Subsystems in Open-System Quantum Theory
This example is of the same flavour as the previous one but is more elaborate and more interesting. Again, we consider a quantum system S with Hilbert space . Now, we take to be the whole set of density matrices in and to be the whole set of quantum channels from to itself.
We grant to agent
A the ability to perform every multiphase covariant channel, that is, every quantum channel
satisfying the condition
where
is the unitary channel corresponding to the diagonal unitary
. Physically, we can interpret the restriction to multiphase covariant channels as the lack of a reference for the definition of the phases in the basis
.
It turns out that the maximal adversary of agent
A is the agent
that can perform every
basis-preserving channel , that is, every channel satisfying the condition
Indeed, we have the following:
Theorem 1. The monoid of multiphase covariant channels and the monoid of basis-preserving channels are the commutant of one another.
The proof, presented in
Appendix D.1, is based on the characterization of the basis-preserving channels provided in [
71,
72].
We now show that states of system can be characterized as classical probability distributions.
Proposition 7. For every pair of states , the following are equivalent:
- 1.
ρ and σ are equivalent for agent A,
- 2.
, where is the completely dephasing channel .
Proof. Suppose that Condition 1 holds, meaning that there exists a sequence
such that
where
and
are basis-preserving channels. The above equation implies
Now, the relation
is valid for every basis-preserving channel
and for every state
[
71]. Applying this relation on both sides of Equation (
52), we obtain the condition
valid for every
. Hence, all the density matrices
must have the same diagonal entries, and, in particular, Condition 2 must hold.
Conversely, suppose that Condition 2 holds. Since the dephasing channel is obviously basis-preserving, we obtained the condition , which implies that and are equivalent for agent A. In conclusion, Condition 1 holds. ☐
Proposition 7 guarantees that the states of system
is in one-to-one correspondence with diagonal density matrices, and therefore, with classical probability distributions: in formula,
The transformations of system
can be characterized as
transition matrices, namely
In summary, agent A has control on a classical system, whose states are probability distributions, and whose transformations are classical transition matrices.
4.5. Classical Systems From Free Operations in the Resource Theory of Coherence
In the previous example, we have seen that classical systems arise from agents who have access to the monoid of multiphase covariant channels. In fact, classical systems can arise in many other ways, corresponding to agents who have access to different monoids of operations. In particular, we find that several types of free operations in the resource theory of coherence [
34,
35,
36,
37,
38,
39,
40,
41] identify classical systems. Specifically, consider the monoids of
Strictly incoherent operations [
41], i.e., quantum channels
with the property that, for every Kraus operator
, the map
satisfies the condition
, where
is the completely dephasing channel.
Dephasing covariant operations [
38,
39,
40], i.e., quantum channels
satisfying the condition
.
Phase covariant channels [40], i.e., quantum channels
satisfying the condition
,
, where
is the unitary channel associated with the unitary matrix
.
Physically incoherent operations [
38,
39], i.e., quantum channels that are convex combinations of channels
admitting a Kraus representation where each Kraus operator
is of the form
where
is a unitary that permutes the elements of the computational basis,
is a diagonal unitary, and
is a projector on a subspace spanned by a subset of vectors in the computational basis.
For each of the monoids 1–4, our construction yields the classical subsystem consisting of diagonal density matrices. The transformations of the subsystem are just the classical channels. The proof is presented in
Appendix E.1.
Notably, other choices of free operations, such as the
maximally incoherent operations [34] and the
incoherent operations [
35], do
not identify classical subsystems. The maximally incoherent operations are the quantum channels
that map diagonal density matrices to diagonal density matrices, namely
, where
is the completely dephasing channel. The incoherent operations are the quantum channels
with the property that, for every Kraus operator
, the map
sends diagonal matrices to diagonal matrices, namely
.
In
Appendix E.2, we show that incoherent and maximally incoherent operations do not identify classical subsystems: the subsystem associated with these operations is the whole quantum system. This result can be understood from the analogy between these operations and non-entangling operations in the resource theory of entanglement [
38,
39]. Non-entangling operations do not generate entanglement, but nevertheless they cannot (in general) be implemented with local operations and classical communication. Similarly, incoherent and maximally incoherent operations do not generate coherence, but they cannot (in general) be implemented with incoherent states and coherence non-generating unitary gates. An agent that performs these operations must have access to more degrees of freedom than just a classical subsystem.
At the mathematical level, the problem is that the incoherent and maximally incoherent operations do not necessarily commute with the dephasing channel . In our construction, commutation with the dephasing channel is essential for retrieving classical subsystems. In general, we have the following theorem:
Theorem 2. Every set of operations that
- 1.
contains the set of classical channels, and
- 2.
commutes with the dephasing channel
identifies a d-dimensional classical subsystem of the original d-dimensional quantum system.
6. Non-Overlapping Agents, Causality, and the Initialization Requirement
In the previous sections, we developed a general framework, applicable to arbitrary physical systems. In this section, we identify some desirable properties that the global systems may enjoy.
6.1. Dual Pairs of Agents
So far, we have taken the perspective of agent
A. Let us now take the perspective of the maximal adversary
. We consider
as the agent, and denote his maximal adversary as
. By definition,
can perform every action in the commutant of
, namely
Obviously, the set of actions allowed to agent includes the set of actions allowed to agent A. At this point, one could continue the construction and consider the maximal adversary of agent . However, no new agent would appear at this point: the maximal adversary of agent is agent again. When two agents have this property, we call them a dual pair:
Definition 6. Two agents A and B form a dual pair iff and .
All the examples in
Section 4 are examples of dual pairs of agents.
It is easy to see that an agent A is part of a dual pair if and only if the set coincides with its double commutant .
6.2. Non-Overlapping Agents
Suppose that agents
A and
B form a dual pair. In general, the actions in
may have a non-trivial intersection with the actions in
. This situation does indeed happen, as we have seen in
Section 4.3 and
Section 4.4. Still, it is important to examine the special case where the actions of
A and
B have only trivial intersection, corresponding to the identity action
. When this is the case, we say that the agents
A and
B are
non-overlapping:Definition 7. Two agents A and B are non-overlapping iff .
Dual pairs of non-overlapping agents are characterized by the fact that the sets of actions have trivial center:
Proposition 8. Let A and B be a dual pair of agents. Then, the following are equivalent:
- 1.
A and B are non-overlapping,
- 2.
has trivial center,
- 3.
has trivial center.
Proof. Since agents A and B are dual to each other, we have and . Hence, the intersection coincides with the center of , and with the center of . The non-overlap condition holds if and only if the center is trivial. ☐
Note that the existence of non-overlapping dual pairs is a condition on the transformations of the whole system S:
Proposition 9. The following are equivalent:
- 1.
system S admits a dual pair of non-overlapping agents,
- 2.
the monoid has trivial center.
Proof. Assume that Condition 1 holds for a pair of agents A and B. Let be the center of . By definition, is contained into because contains all the transformations that commute with those in . Moreover, the elements of commute with all elements of , and therefore they are in the center of . Since A and B are a non-overlapping dual pair, the center of must be trivial (Proposition 8), and therefore must be trivial. Hence, Condition 2 holds.
Conversely, suppose that Condition 2 holds. In that case, it is enough to take A to be the maximal agent, i.e., the agent with . Then, the maximal adversary of is the agent with . By definition, the two agents form a non-overlapping dual pair. Hence, Condition 1 holds. ☐
The existence of dual pairs of non-overlapping agents is a desirable property, which may be used to characterize “good systems”:
Definition 8 (Non-Overlapping Agents)
. We say that system S satisfies the Non-Overlapping Agents Requirement if there exists at least one dual pair of non-overlapping agents acting on S.
The Non-Overlapping Agents Requirement guarantees that the total system
S can be regarded as a subsystem: if
is the
maximal agent (i.e., the agent who has access to all transformations on
S), then the subsystem
is the whole system
S. A more formal statement of this fact is provided in
Appendix G.
6.3. Causality
The Non-Overlapping Agents Requirement guarantees that the subsystem associated with a maximal agent (i.e., an agent who has access to all possible transformations) is the whole system
S. On the other hand, it is natural to expect that a minimal agent, who has no access to any transformation, should be associated with the trivial system, i.e., the system with a single state and a single transformation. The fact that the minimal agent is associated with the trivial system is important because it equivalent to a property of causality [
8,
13,
75,
76]: indeed, we have the following
Proposition 10. Let be the minimal agent and let be its maximal adversary, coinciding with the maximal agent. Then, the following conditions are equivalent
- 1.
is the trivial system,
- 2.
one has for every pair of states .
Proof. : By definition, the state space of consists of states of the form , . Hence, the state space contains only one state if and only if Condition 2 holds. : Condition 2 implies that every two states of system S are equivalent for agent . The fact that has only one transformation is true by definition: since the adversary of is the maximal agent, one has for every transformation . Hence, every transformation is in the equivalence class of the identity. ☐
With a little abuse of notation, we may denote the trace over
as
because
has access to all transformations on system
S. With this notation, the causality condition reads
It is interesting to note that, unlike no signalling, causality does not necessarily hold in the framework of this paper. This is because the trace
is defined as the quotient with respect to all possible transformations, and having a single equivalence class is a non-trivial property. One possibility is to demand the validity of this property, and to call a system
proper, only if it satisfies the causality condition (
62). In the following subsection, we will see a requirement that guarantees the validity of the causality condition.
6.4. The Initialization Requirement
The ability to prepare states from a fixed initial state is important in the circuit model of quantum computation, where qubits are initialized to the state , and more general states are generated by applying quantum gates. More broadly, the ability to initialize the system in a given state and to generate other states from it is important for applications in quantum control and adiabatic quantum computing. Motivated by these considerations, we formulate the following definition:
Definition 9. A system S satisfies the Initialization Requirement if there exists a state from which any other state can be generated, meaning that, for every other state there exists a transformation such that . When this is the case, the state is called cyclic.
The Initialization Requirement is satisfied in quantum theory, both at the pure state level and at the mixed state level. At the pure state level, every unit vector
can be generated from a fixed unit vector
via a unitary transformation
U. At the mixed state level, every density matrix
can be generated from a fixed density matrix
via the erasure channel
. By the same argument, the initialization requirement is also satisfied when
S is a system in an operational-probabilistic theory [
8,
10,
11,
12,
13] and when
S is a system in a causal process theory [
75,
76].
The Initialization Requirement guarantees that minimal agents are associated with trivial systems:
Proposition 11. Let S be a system satisfying the Initialization Requirement, and let be the minimal agent , i.e., the agent that can only perform the identity transformation. Then, the subsystem is trivial: contains only one state and contains only one transformation.
Proof. By definition, the maximal adversary of is the maximal agent , who has access to all physical transformations. Then, every transformation is in the equivalence class of the identity transformation, meaning that system has a single transformation. Now, let be the cyclic state. By the Initialization Requirement, the set is the whole state space . Hence, every state is equivalent to the state . In other words, contains only one state. ☐
The Initialization Requirement guarantees the validity of causality, thanks to Proposition 10. In addition, the Initialization Requirement is important independently of the causality property. For example, we will use it to formulate an abstract notion of closed system.
8. Closed Systems
Here, we define an abstract notion of “closed systems”, which captures the essential features of what is traditionally called a closed system in quantum theory. Intuitively, the idea is that all the states of the closed system are “pure” and all the evolutions are reversible.
An obvious problem in defining closed system is that our framework does not include a notion of “pure state”. To circumvent the problem, we define the closed systems in the following way:
Definition 15. System S is closed iff it satisfies the Logical Conservation of Information and the Initialiation Requirement, that is, iff
- 1.
every transformation is logically invertible,
- 2.
there exists a state such that, for every other state , one has for some suitable transformation .
For a closed system, we nominally say that all the states in
are “pure”, or, more precisely, “dynamically pure”. This definition is generally different from the usual definition of pure states as extreme points of convex sets, or from the compositional definition of pure states as states with only product extensions [
77]. First of all, dynamically pure states are
not a subset of the state space: provided that the right conditions are met, they are
all the states. Other differences between the usual notion of pure states and the notion of dynamically pure states are highlighted by the following example:
Example 4. Let S be a system in which all states are of the form , where U is a generic 2-by-2 unitary matrix, and is a fixed 2-by-2 density matrix. For the transformations, we allow all unitary channels . By construction, system S satisfies the initialization Requirement, as one can generate every state from the initial state . Moreover, all the transformations of system S are unitary and therefore the Conservation of Information is satisfied, both at the physical and the logical level. Therefore, the states of system S are dynamically pure. Of course, the states need not be extreme points of the convex set of all density matrices, i.e., they need not be rank-one projectors. They are so only when the cyclic state is rank-one.
On the other hand, consider a similar example, where
system S is a qubit,
the states are pure states, of the form for a generic unit vector
the transformations are unitary channels , where the unitary matrix V has real entries.
Using the Bloch sphere picture, the physical transformations are rotations around the y axis. Clearly, the Initialization Requirement is not satisfied because there is no way to generate arbitrary points on the sphere using only rotations around the y-axis. In this case, the states of S are pure in the convex set sense, but not dynamically pure.
For closed systems satisfying the Physical Conservation of Information, every pair of pure states are interconvertible:
Proposition 13 (Transitive action on the pure states)
. If system S is closed and satisfies the Physical Conservation of Information, then, for every pair of states there exists a reversible transformation such that .
Proof. By the Initialization Requirement, one has and for suitable . By the Physical Conservation of Information, all the tranformations in are physically reversible. Hence, , having defined . ☐
The requirement that all pure states be connected by reversible transformations has featured in many axiomatizations of quantum theory, either directly [
5,
44,
45,
46], or indirectly as a special case of other axioms [
42,
48]. Comparing our framework with the framework of general probabilistic theories, we can see that the dynamical definition of pure states refers to a rather specific situation, in which all pure states are connected, either to each other (in the case of physical reversibility) or with to a fixed cyclic state (in the case of logical reversibility).
10. Example: Group Representations on Quantum State Spaces
We conclude the paper with a macro-example, involving group representations in closed-system quantum theory. The point of this example is to illustrate the general notion of purification introduced in this paper and to characterize the sets of mixed states associated with different agents.
As system S, we consider a quantum system with Hilbert space , possibly of infinite dimension. We let be the set of pure quantum states, and let be the group of all unitary channels. With this choice, the total system is closed and satisfies the Physical Conservation of Information.
Suppose that agent
A is able to perform a group of transformations, such as e.g., the group of phase shifts on a harmonic oscillator, or the group of rotations of a spin
j particle. Mathematically, we focus our attention on unitary channels arising from some representation of a given compact group
. Denoting the representation as
, the group of Alice’s actions is
The maximal adversary of
A is the agent
who is able to perform all unitary channels
that commute with those in
, namely, the unitary channels in the group
Specifically, the channels
correspond to unitary operators
V satisfying the relation
where, for every fixed
V, the function
is a multiplicative character, i.e., a one-dimensional representation of the group
.
Note that, if two unitaries
V and
W satisfy Equation (
86) with multiplicative characters
and
, respectively, then their product
satisfies Equation (
86) with multiplicative character
. This means that the function
is a multiplicative
bicharacter: is a multiplicative character for
for every fixed
, and, at the same time,
is a multiplicative character for
for every fixed
.
The adversarial group
contains the commutant of the representation
, consisting of all the unitaries
V such that
The unitaries in the commutant satisfy Equation (
86) with the trivial multiplicative character
,
. In general, the adversarial group may contain other unitary operators, corresponding to non-trivial multiplicative characters. The full characterization of the adversarial group is provided by the following theorem:
Theorem 3. Let be a compact group, let be a projective representation of , and let be the group of channels . Then, the adversarial group is isomorphic to the semidirect product , where is the commutant of the set , and is an Abelian subgroup of the group of permutations of , the set of irreducible representations contained in the decomposition of the representation .
In the following, we will illustrate the construction of the state space in a the prototypical example where the group is a compact connected Lie group.
Compact Connected Lie Groups
When is a compact connected Lie group, the characterization of the adversarial group is simplified by the following theorem:
Theorem 4. If is a compact connected Lie group, then the Abelian subgroup of Theorem 3 is trivial, and all the solutions of Equation (86) have . For compact connected Lie groups, the the adversarial group coincides exactly with the commutant of the representation
. An explicit expression can be obtained in terms of the isotypic decomposition [
78]
where
is the set of irreducible representations (irreps) of
contained in the decomposition of
U,
is the irreducible representation of
acting on the representation space
, and
is the identity acting on the multiplicity space
. From this expression, it is clear that the adversarial group
consists of unitary gates
V of the form
where
is the identity operator on the representation space
, and
is a generic unitary operator on the multiplicity space
.
In general, the agents
A and
do not form a dual pair. Indeed, it is not hard to see that the maximal adversary of
B is the agent
that can perform every unitary channel
where
U is a unitary operator of the form
being a generic unitary operator on the representation space
. When
A and
B form a dual par, the groups
and
are sometimes called
gauge groups [
79].
It is now easy to characterize the subsystem
. Its states are equivalence classes of pure states under the relation
iff
It is easy to see that two states in the same equivalence class must satisfy the condition
where the “partial trace over agent
B” is
is the map
being the projector on the subspace
.
Conversely, it is possible to show that the state completely identifies the equivalence class .
Proposition 16. Let be two unit vectors such that . Then, there exists a unitary operator such that .
We have seen that the states of system
are in one-to-one correspondence with the density matrices of the form
, where
is a generic pure state. Note that the rank of the density matrices
in Equation (
A109) cannot be larger than the dimensions of the spaces
and
, denoted as
and
, respectively. Taking this fact into account, we can represent the states of
as
where
is a generic probability distribution. The state space of system
is
not convex, unless the condition
is satisfied. Basically, in order to obtain a convex set of density matrices, we need the total system
S to be “sufficiently large” compared to its subsystem
. This observation is a clue suggesting that the standard convex framework could be considered as the effective description of subsystems of “large” closed systems.
Finally, note that, in agreement with the general construction, the pure states of system S are “purifications" of the states of the system . Every state of system can be obtained from a pure state of system S by “tracing out" system . Moreover, every two purifications of the same state are connected by a unitary transformation in .
11. Conclusions
In this paper, we adopted rather minimalistic framework, in which a single physical system was described solely in terms of states and transformations, without introducing measurements. Or at least, without introducing measurements in an explicit way: of course, one could always interpret certain transformations as “measurement processes", but this interpretation is not necessary for any of the conclusions drawn in this paper.
Our framework can be interpreted in two ways. One way is to think of it as a fragment of the larger framework of operational-probabilistic theories [
8,
11,
12,
13], in which systems can be freely composed and measurements are explicitly described. The other way is to regard our framework as a dynamicist framework, meant to describe physical systems
per se, independently of any observer. Both approaches are potentially fruitful.
On the operational-probabilistic side, it is interesting to see how the definition of subsystem adopted in this paper interacts with probabilities. For example, we have seen in a few examples that the state space of a subsystem is not always convex: convex combination of allowed states are not necessarily allowed states. It is then natural to ask: under which condition is convexity retrieved? In a different context, the non-trivial relation between convexity and the dynamical notion of system has been emerged in a work of Galley and Masanes [
80]. There, the authors studied alternatives to quantum theory where the closed systems have the same states and the same dynamics of closed quantum systems, while the measurements are different from the quantum measurements. Among these theories, they found that quantum theory is the only theory where subsystems have a convex state space. These and similar clues are an indication that the interplay between dynamical notions and probabilistic notions plays an important role in determining the structure of physical theories. Studying this interplay is a promising avenue of future research.
On the opposite end of the spectrum, it is interesting to explore how far the measurement-free approach can reach. An interesting research project is to analyze the notions of subsystem, pure state, and purification, in the context of algebraic quantum field theory [
22] and quantum statistical mechanics [
32]. This is important because the notion of pure state as an extreme point of the convex set breaks down for type III von Neumann algebras [
81], whereas the notions used in this paper (commutativity of operations, cyclicity of states) would still hold. Another promising clue is the existence of dual pairs of non-overlapping agents, which amounts to the requirement that the set of operations of each agent has trivial center and coincides with its double commutant. A similar condition plays an important role in the algebraic framework, where the operator algebras with trivial center are known as factors, and are at the basis of the theory of von Neumann algebras [
82,
83].
Finally, another interesting direction is to enrich the structure of system with additional features, such as a metric, quantifying the proximity of states. In particular, one may consider a strengthened formulation of the Conservation of Information, in which the physical transformations are required not only to be invertible, but also to preserve the distances. It is then interesting to consider how the metric on the pure states of the whole system induces a metric on the subsystems, and to search for relations between global metric and local metric. Also in this case, there is a promising precedent, namely the work of Uhlmann [
84], which led to the notion of fidelity [
85]. All these potential avenues of future research suggest that the notions investigated in this work may find application in a variety of different contexts, and for a variety of interpretational standpoints.