Divergence from, and Convergence to, Uniformity of Probability Density Quantiles
Abstract
:1. Introduction
2. Divergences between Probability Density Quantiles
2.1. Definitions
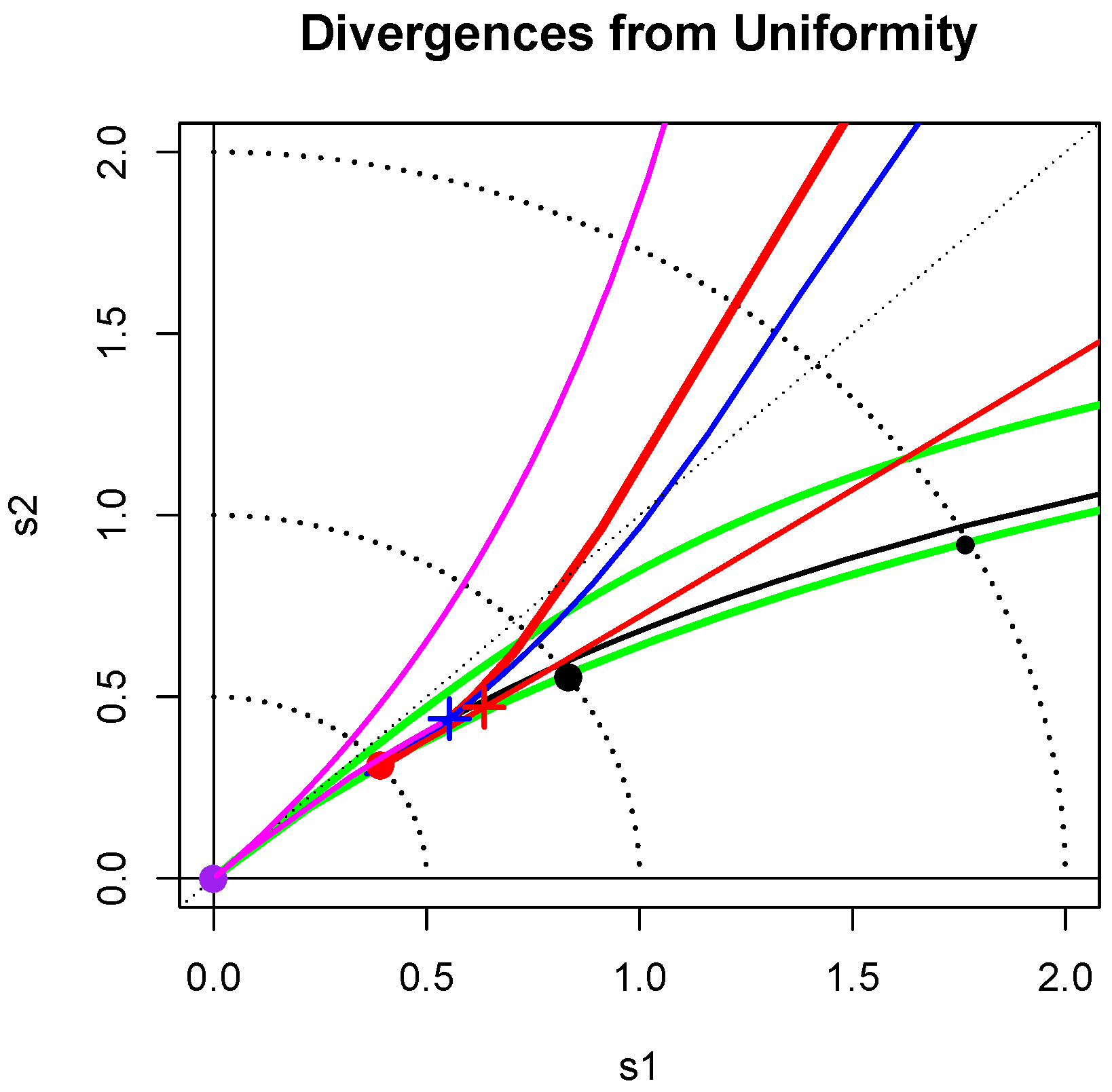
2.2. Divergence Map
2.3. Uniformity Testing
3. Convergence of Density Shapes to Uniformity via Fixed Point Theorems
3.1. Conditions for Convergence to Uniformity
- (i)
- ,
- (ii)
- for all ,
- (iii)
- and for all .
- (i)
- ;
- (ii)
- For all , ;
- (iii)
- as .
- (i)
- for all , and the inequality becomes equality if and only if ;
- (ii)
- for all .
- (i*)
- ;
- (ii)
- For all , ;
- (iii)
- as .
3.2. Examples of Convergence to Uniformity
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Staudte, R. The shapes of things to come: Probability density quantiles. Statistics 2017, 51, 782–800. [Google Scholar] [CrossRef]
- Parzen, E. Nonparametric statistical data modeling. J. Am. Stat. Assoc. 1979, 7, 105–131. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Kullback, S. Information Theory and Statistics; Dover: Mineola, NY, USA, 1968. [Google Scholar]
- Abbas, A.; Cadenbach, A.; Salimi, E. A Kullback–Leibler View of Maximum Entropy and Maximum Log-Probability Methods. Entropy 2017, 19, 232. [Google Scholar] [CrossRef]
- Jeffreys, H. An invariant form for the prior probability in estimation problems. Proc. R. Soc. Lond. A 1946, 186, 453–461. [Google Scholar] [CrossRef]
- Freimer, M.; Kollia, G.; Mudholkar, G.; Lin, C. A study of the generalized Tukey lambda family. Commun. Stat. Theory Methods 1988, 17, 3547–3567. [Google Scholar] [CrossRef]
- Stephens, M. Uniformity, Tests of. In Encyclopedia of Statistical Sciences; John Wiley & Sons: Hoboken, NJ, USA, 2006; Volume 53, pp. 1–8. [Google Scholar] [CrossRef]
- Lockhart, R.; O’Reilly, F.; Stephens, M. Tests of Fit Based on Normalized Spacings. J. R. Stat. Soc. B 1986, 48, 344–352. [Google Scholar]
- Schader, M.; Schmid, F. Power of tests for uniformity when limits are unknown. J. Appl. Stat. 1997, 24, 193–205. [Google Scholar] [CrossRef]
- Prendergast, L.; Staudte, R. Exploiting the quantile optimality ratio in finding confidence Intervals for a quantile. Stat 2016, 5, 70–81. [Google Scholar] [CrossRef]
- Dudewicz, E.; Van Der Meulen, E. Entropy-Based Tests of Uniformity. J. Am. Stat. Assoc. 1981, 76, 967–974. [Google Scholar] [CrossRef]
- Bowman, A. Density based tests for goodness-of-fit. J. Stat. Comput. Simul. 1992, 40, 1–13. [Google Scholar] [CrossRef]
- Fan, Y. Testing the Goodness of Fit of a Parametric Density Function by Kernel Method. Econ. Theory 1994, 10, 316–356. [Google Scholar] [CrossRef]
- Pavia, J. Testing Goodness-of-Fit with the Kernel Density Estimator: GoFKernel. J. Stat. Softw. 2015, 66, 1–27. [Google Scholar] [CrossRef]
- Noughabi, H. Entropy-based tests of uniformity: A Monte Carlo power comparison. Commun. Stat. Simul. Comput. 2017, 46, 1266–1279. [Google Scholar] [CrossRef]
- Arellano-Valle, R.; Contreras-Reyes, J.; Stehlik, M. Generalized Skew-Normal Negentropy and Its Application to Fish Condition Factor Time Series. Entropy 2017, 19, 528. [Google Scholar] [CrossRef]
- R Core Team. R Foundation for Statistical Computing; R Core Team: Vienna, Austria, 2008; ISBN 3-900051-07-0. [Google Scholar]
- Luenberger, D. Optimization by Vector Space Methods; Wiley: New York, NY, USA, 1969. [Google Scholar]
- Bessenyei, M.; Páles, Z. A contraction principle in semimetric spaces. J. Nonlinear Convex Anal. 2017, 18, 515–524. [Google Scholar]
- Feller, W. An Introduction to Probability Theory and Its Applications; John Wiley & Sons: New York, NY, USA, 1971; Volume 2. [Google Scholar]
- Johnson, N.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions; John Wiley & Sons: New York, NY, USA, 1994; Volume 1. [Google Scholar]
- Johnson, N.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions; John Wiley & Sons: New York, NY, USA, 1995; Volume 2, ISBN 0-471-58494-0. [Google Scholar]
- Azzalini, A. A Class of Distributions which Includes the Normal Ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Jones, M.; Pewsey, A. Sinh-arcsinh distributions. Biometrika 2009, 96, 761–780. [Google Scholar] [CrossRef]
- Brockwell, P.; Davis, R. Time Series: Theory and Methods; Springer: New York, NY, USA, 2009. [Google Scholar]
| Normal | 0.153 | 0.097 | 0.250 | |||
| Logistic | 0.208 | 0.125 | 0.333 | |||
| Laplace | 0.307 | 0.193 | 0.500 | |||
| 0.391 | 0.200 | 0.591 | ||||
| Cauchy | 0.693 | 0.307 | 1.000 | |||
| Exponential | 0.307 | 0.193 | 0.500 | |||
| Gumbel | 0.191 | 0.116 | 0.307 | |||
| Lognormal () | - | |||||
| Pareto (a) | - | |||||
| Power (b) | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Staudte, R.G.; Xia, A. Divergence from, and Convergence to, Uniformity of Probability Density Quantiles. Entropy 2018, 20, 317. https://doi.org/10.3390/e20050317
Staudte RG, Xia A. Divergence from, and Convergence to, Uniformity of Probability Density Quantiles. Entropy. 2018; 20(5):317. https://doi.org/10.3390/e20050317
Chicago/Turabian StyleStaudte, Robert G., and Aihua Xia. 2018. "Divergence from, and Convergence to, Uniformity of Probability Density Quantiles" Entropy 20, no. 5: 317. https://doi.org/10.3390/e20050317
APA StyleStaudte, R. G., & Xia, A. (2018). Divergence from, and Convergence to, Uniformity of Probability Density Quantiles. Entropy, 20(5), 317. https://doi.org/10.3390/e20050317






