Deconstructing Cross-Entropy for Probabilistic Binary Classifiers
Abstract
:1. Introduction
- We analyze the contribution to cross-entropy of two sources of information: the prior knowledge about the classes, and the value of the observations expressed as a likelihood ratio. Apart from its advantages for general classifiers [13], this analysis is of particular interest in many applications such as forensic science [17,24], where prior probabilities and likelihood ratios are computed by different agents, with different responsibilities in the decision process. Moreover, this prior-dependent analysis allows system designers to work on the likelihood ratio computed by the classifier without having to be focused on particular prior probabilities or decision costs. This way of designing classifiers has been referred to as application-independent [12,13]. To the best of our knowledge, there are not many works in the literature offering tools to analyze the cross-entropy function under this dichotomy.
- We introduce a decomposition of cross-entropy into two additive components: discrimination loss and calibration loss, showing its information-theoretical properties. A better discrimination component of cross-entropy will indicate a classifier that separates the classes more effectively; and a better calibration component will indicate more reliable probabilities [18]. Moreover, the decomposition enables improving calibration without changing discrimination, by means of an invertible function, theoretically justifying approaches as in [2,3,5,12,13].
- We propose several interpretations of cross-entropy that offer useful communication tools to present results of systems performance to non-expert end users, which can be of great utility for many applications such as forensic science [24].
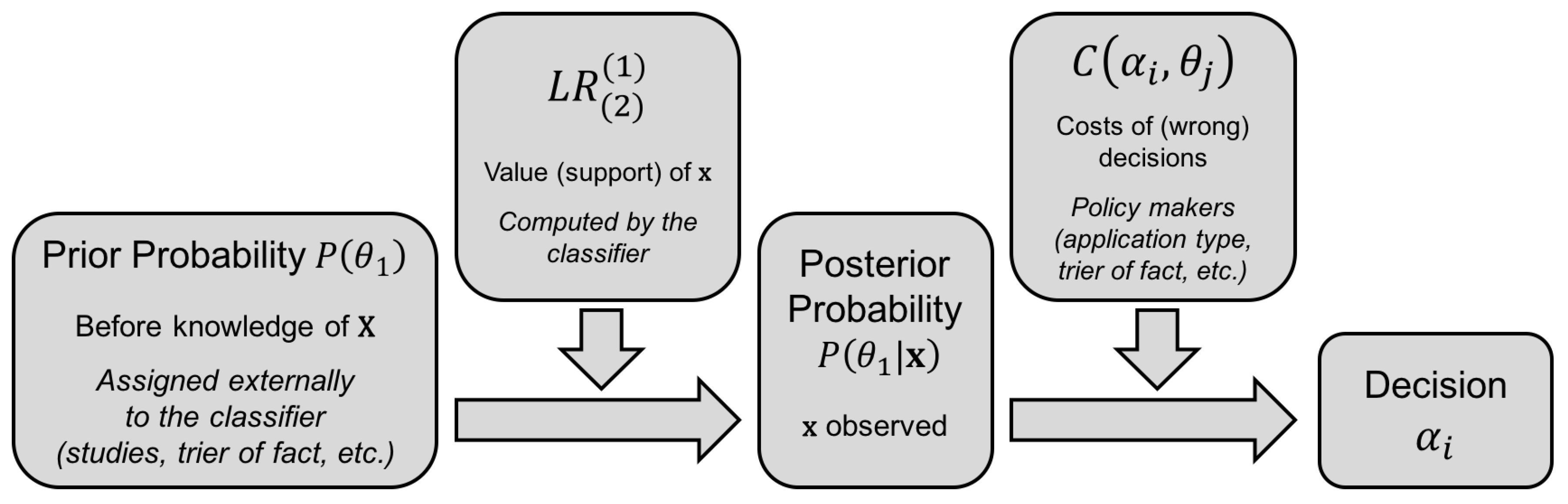
2. Review of Bayesian Decision Theory
2.1. Definitions, Notation and Examples
- Speaker recognition techniques [26] are used to perform a comparison between the speech of the person who tries to access the system and the speech stored in the system for that particular identity claimed. If the system yields a higher support that the person has the claimed identity, it will increase the chances of a successful access, and vice-versa.
- In order to make the decision, the speaker verification system must take also into account the prior probability, i.e., whether it is probable or not that an impostor attempt will happen for this particular application.
- Moreover, the bank policy should evaluate the consequences of an error when it occurs. Perhaps the application gives access to very sensitive information (e.g., operations with bank accounts), and then avoiding false attempts is critical, or, perhaps, the application yields access to personalized publicity for that particular client, and false rejections are to be avoided.
- The report of a forensic examiner, who compares the glass in the burglary window with the glass in the clothes of the suspect. She or he uses analytical chemistry techniques for this, as well as forensic statistic models, in order to assign a quantitative value to those findings in the form of a likelihood ratio, according to recommendations from forensic institutions worldwide [24].
- In order to make the decision, the trier of fact must also take into account the prior probability that the glass in the suspect’s clothes could be originated by the window at the scene of the crime, even before the findings are analyzed by the forensic examiner. Perhaps the suspect was arrested next to the house at the time of the burglary, and/or witnesses have seen her or him smashing the window, and/or she or he has been typically arrested in the past for similar crimes, etc., in which case the prior probability should increase. However, the suspect could present a convincing alibi, and/or witnesses could testify that they saw other people smashing the window, etc., and in those cases the prior probability should be low.
- Moreover, justice systems around the globe have legal standards and policies that influence decisions of triers of fact. In modern, advanced democracies, it is typical that a presumption of innocence is always respected, meaning that condemning a person must be supported by solid evidence. In this sense, it is naturally much more critical not to imprison an innocent person, even though this means that false acquittals may then be more probable. Thus, a trier of fact will only condemn a suspect if the probability that the suspect committed the crime is very high.
- Classification categories will be referred to as and , and they will be assumed to be observed from a random variable . It is assumed that both classes are complementary in probabilistic terms.
- –
- In the speaker verification example, stands for the person accessing is who she or he claims to be, and stands for the person accessing is an impostor.
- –
- In the forensic case example, stands for the glass of the suspect’s clothes comes from the window at the crime scene, and stands for the glass of the suspect’s clothes does not come from the window at the crime scene.
- The features observed in the classification problem will be assumed to be multivariate, and referred to as generated by .
- –
- In the speaker verification example, , where are the speech features extracted from the utterance spoken by the person attempting to enter the system, and are the features already stored in the system, which are known to come from the claimed identity.
- –
- In the forensic case example, , where are the chemical features extracted from the glass fragments recovered in the suspect’s clothes, and are the chemical features extracted from the window at the scene of the crime, known as control glass.
- The action of deciding will be denoted as .
- –
- In the speaker verification example, means that the system decides to accept the speaker, and means deciding to reject the speaker.
- –
- In the forensic case example, means that the trier of fact decides that the suspect glass came from the window at the scene of the crime, and means deciding that the suspect glass came from a different source than the window at the crime scene.
- Decision costs will be referred to as where is the decision made, but is the actual category to which a particular feature vector belongs. Without loss of generality, costs are assumed to be non-negative. In addition, it is typically assumed that , i.e., right decisions are costless.
- –
- In the speaker verification example, the costs are defined depending on the risk policy of the bank, and depending on the application. For instance, if we talk about access to personalized publicity, perhaps and , being then flexible with false acceptances, but rigorous with false rejections. On the other hand, if the application involves accessing sensitive bank account data, perhaps the priority is to avoid false acceptances, and therefore we can set and , for example.
- –
- In the forensic case example, costs are typically designed to avoid false condemns, even though it means that false acquittals are more frequent. Thus, a possible selection of decision costs could be and . In any case, it would correspond to the trier of fact to establish the values of the costs.
2.2. Optimal Bayesian Decisions
- The likelihood ratio , expressing the value of the observation of in support of each of the two classes and .
- The prior probabilities for both classes, namely and .
- The costs associated to each action towards deciding a class , given that class is actually true, namely .
2.3. Empirical Performance of Probabilistic Classifiers
- In speaker verification, imagine that we have a black-box speaker recognition system that receives two sets of speech files, where all utterances in each of the two sets belong to a given putative speaker. The system compares both sets and outputs a likelihood ratio , for (same speaker), and (different speakers). With a database of speech utterances, each one with a label indicating an index of speaker identity, we compare them according to a given protocol to generate LR values. The ground-truth labels of the experimental set of LR values are same-speaker () or different-speakers () labels.
- In forensic interpretation of glass samples, we can work analogously with a black-box glass interpretation model yielding likelihood ratios, and a database of feature vectors measured from glass objects, each vector with a label indicating a different index for each glass object. Thus, LR values generated are accompanied by ground-truth labels like same-source () and different-source ().
3. Calibration of Probabilities
Calibration and Discrimination of Posterior Probabilities
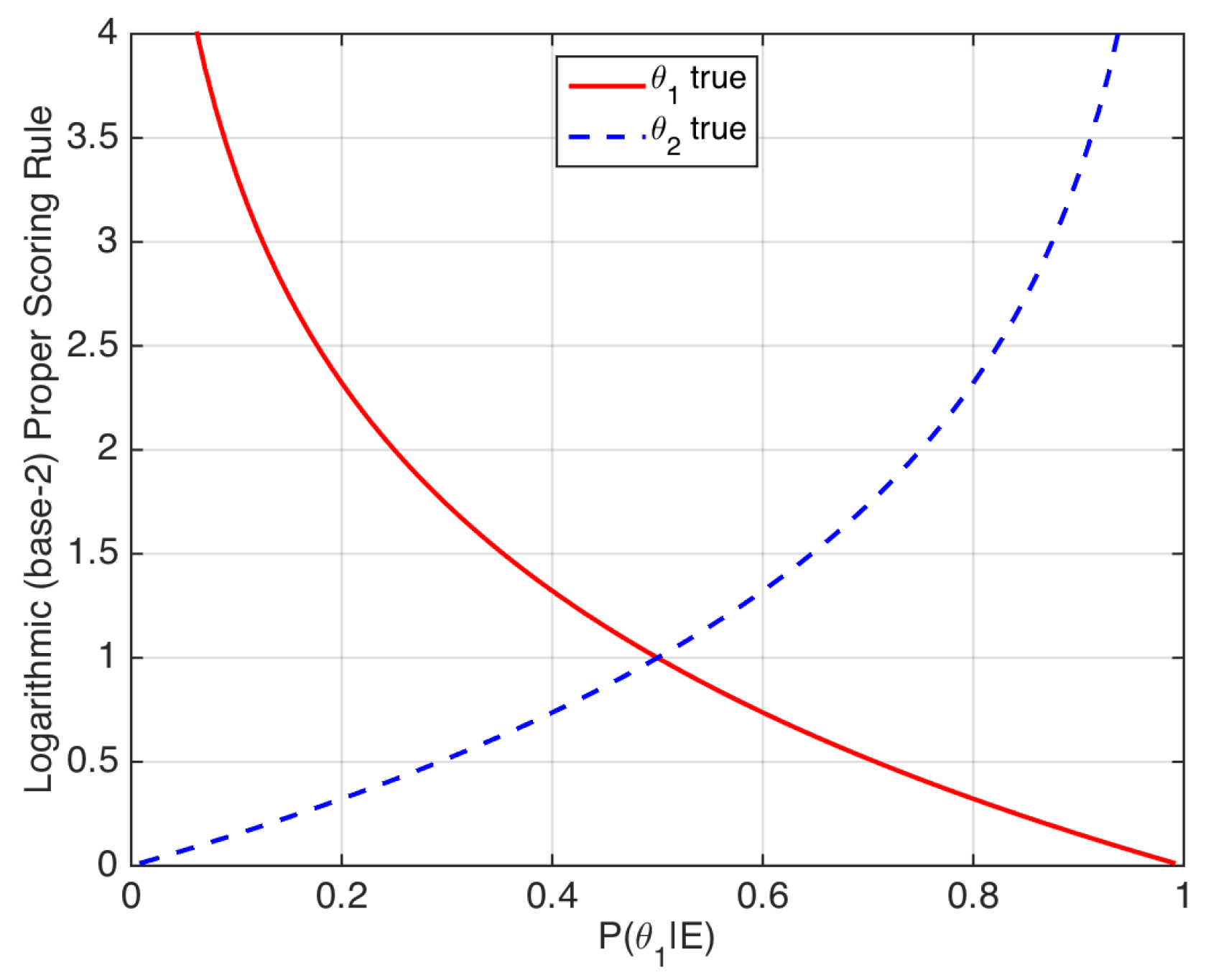
- In our speaker verification example, a posterior probability is obtained. We can define the mean value of the proper scoring rule with respect to a reference probability distribution , according to [18]. This reference probability can be viewed as a desired value P of the posterior probability distribution, to which the actual posterior probability distribution is compared. For the logarithmic scoring rule:By definition, the mean value of a strictly proper scoring rule is minimized if and only if (for instance, this is easy to prove for the logarithmic rule by simply deriving Equation (8) with respect to ). In other words, if a classifier aims at minimizing a strictly proper scoring rule, it should yield a likelihood ratio value as close as possible to , which will lead to the desired probability .
- In [18], the overall measure of goodness of an empirical set of posterior probabilities is defined as the empirical average of a strictly proper scoring rule. An example is the logarithmic score ():where and are the number of comparisons where or are respectively true. Thus, is an overall loss. Moreover, it is also demonstrated in [18] that such a measure of accuracy can be divided into two components:
- A calibration loss component, which measures how similar the posterior probabilities are to the frequency of occurrence of . Low calibration loss means that, for a given range of values of closely around a value k, the frequency of cases where tends to be k.
- A refinement loss, also known as sharpness loss or discrimination loss, component. It measures how sharp or how spread the posterior probabilities are. Roughly speaking, lower refinement loss means that, if the calibration loss is low, will tend to be closer either to 0 or to 1, on average.
4. Cross-Entropy: An Information-Theoretical Performance Measure
- , the posterior entropy of the reference probability, which measures the uncertainty about the hypotheses if the reference probability distribution is used.
- , the divergence of the classifier posterior from the reference posterior P. This is an additional information loss because it was expected that the system computed P, not .
4.1. Proposed Measure of Accuracy: Empirical Cross-Entropy (ECE)
- increases (decreases) and
- decreases (increases)
4.2. Choosing a Reference Probability Distribution for Intuitive Interpretation
4.2.1. Oracle Reference
4.2.2. PAV-Calibrated Reference
- The discrimination component, namely , that represents the information loss due to a lack of discriminating power of the classifier.
- The calibration component, namely , that represents the information loss due to a lack of calibration of the classifier.
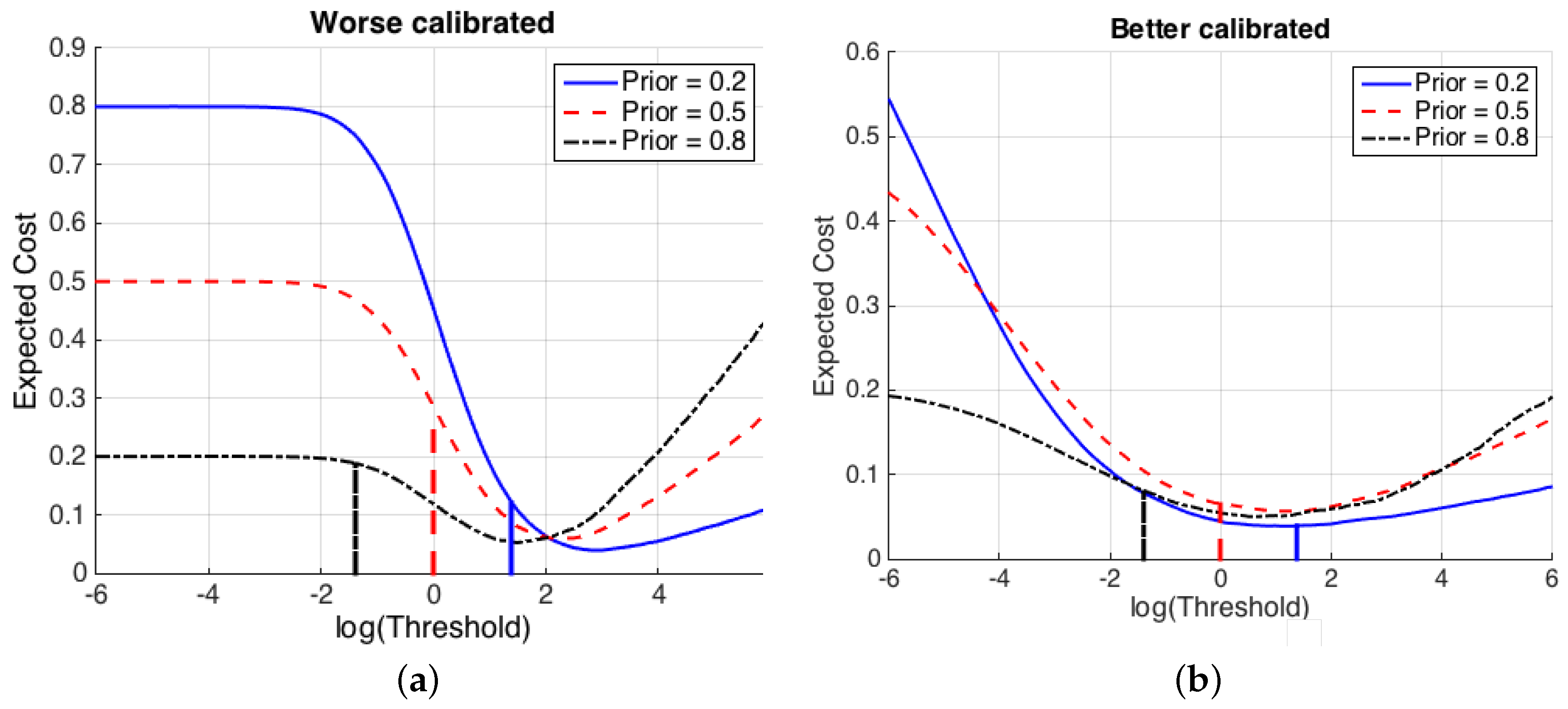
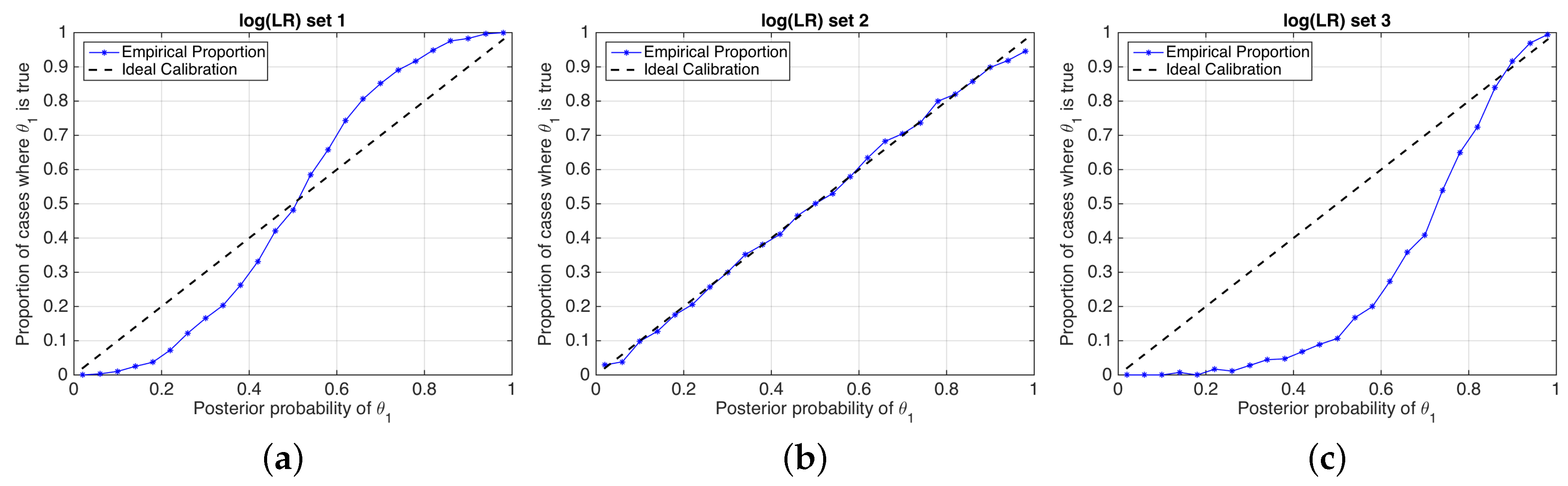
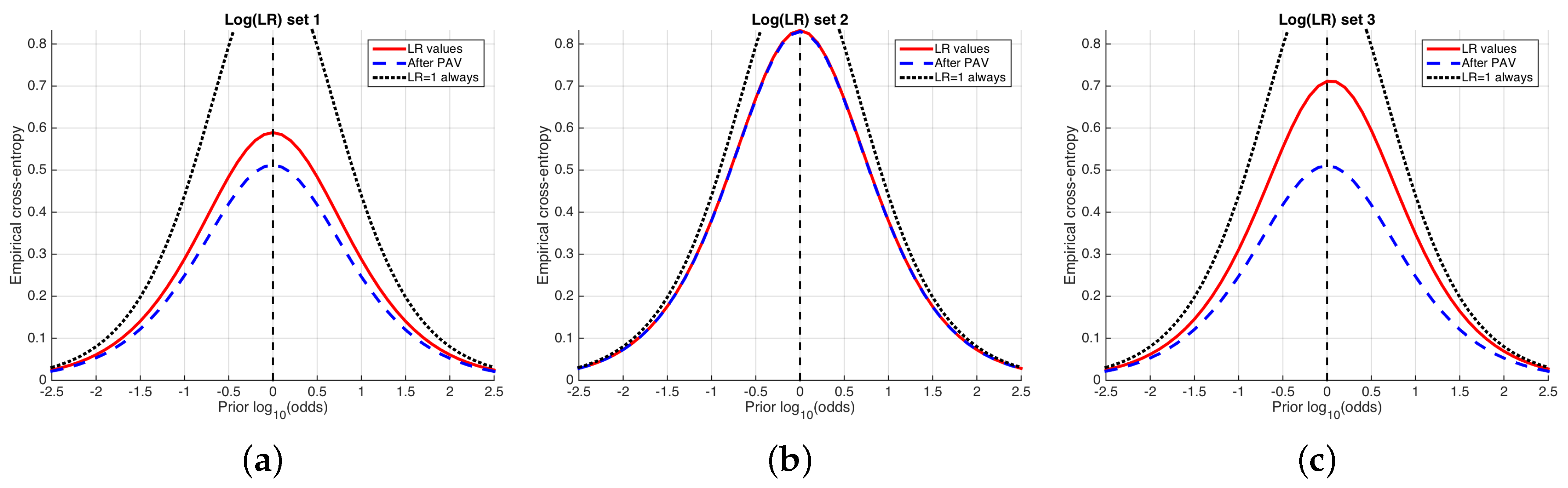
5. The ECE Plot
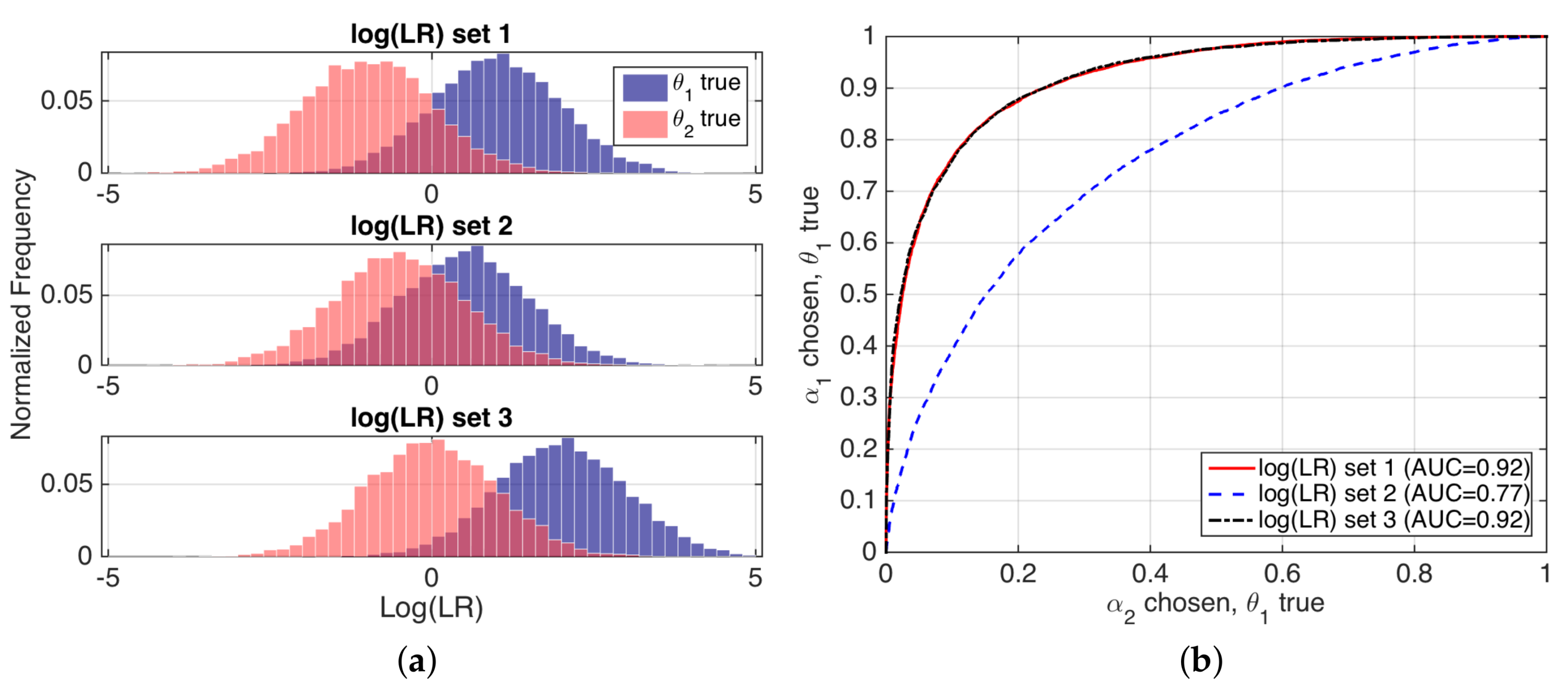
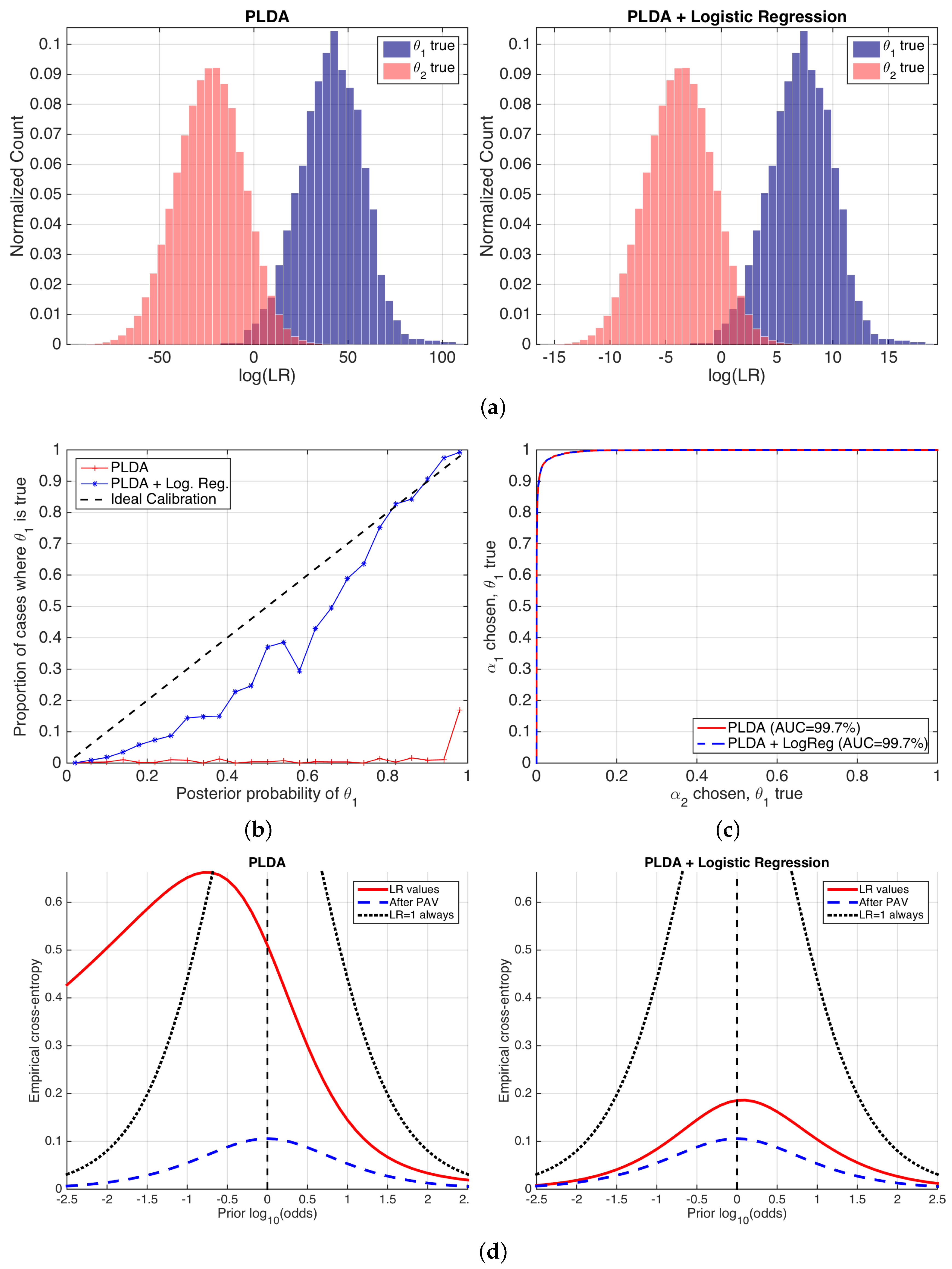
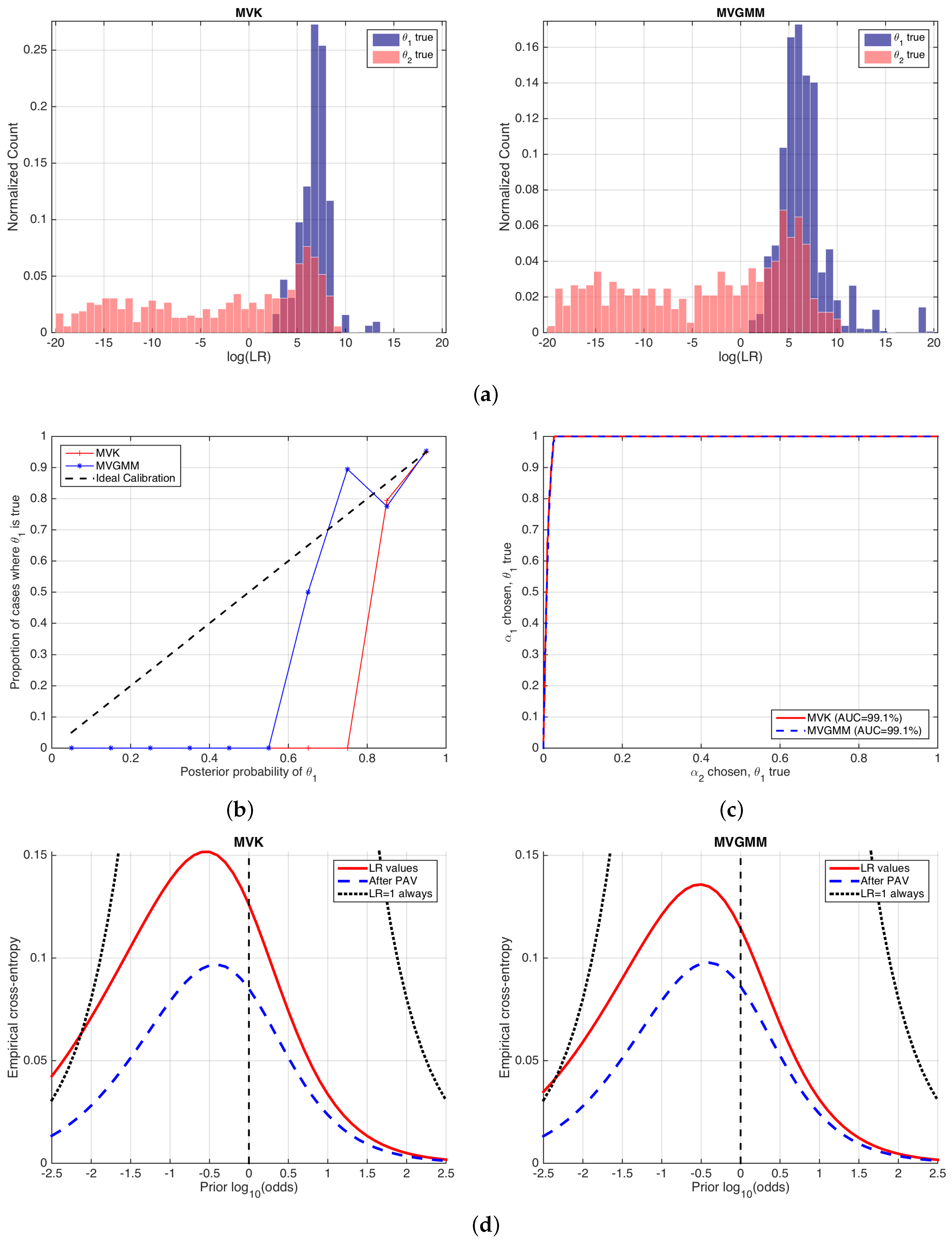
6. Experimental Examples
6.1. Speaker Verification
- We need bits to know the true value of the ground-truth label of a comparison (i.e., we use as the reference).
- The best possible calibrated classifier needs bits to know the true value of the ground-truth label of a comparison. However, as our classifier is not so well calibrated, it will need bits more (i.e., we use as reference).
6.2. Forensic Case Involving Glass Findings
7. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Platt, J. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. In Advances in Large Margin Classifiers, Book ed.; Smola, A.J., Bartlett, P., Sholkopf, B., Shchuurmans, D., Eds.; MIT Press: Cambridge, MA, USA, 1999; Chapter 10; pp. 61–74. [Google Scholar]
- Zadrozny, B.; Elkan, C. Transforming classifier scores into accurate multiclass probability estimates. In Proceeding of the Eight International Conference on Knowledge Discovery and Data Mining (KDD’02), Edmonton, AB, Canada, 23–26 July 2002. [Google Scholar]
- Cohen, I.; Goldszmidt, M. Properties and benefits of calibrated classifiers. In Lecture Notes in Computer Science; Knowledge Discovery in Databases: PKDD 2004; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3202. [Google Scholar]
- Niculescu-Mizil, A.; Caruana, R. Predicting Good Probabilities With Supervised Learning. In Proceedings of the 22nd International Conference on Machine Learning, Bonn, Germany, 7–11 August 2005; pp. 625–632. [Google Scholar]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On Calibration of Modern Neural Networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Kittler, J.; Hatef, M.; Duin, R.; Matas, J. On combining classifiers. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 226–239. [Google Scholar] [CrossRef]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques—Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Sim, I.; Gorman, P.; Greenes, R.A.; Haynes, R.B.; Kaplan, B.; Lehmann, H.; Tang, P.C. Clinical Decision Support Systems for the Practice of Evidence-based Medicine. J. Am. Med. Inform. Assoc. 2001, 8, 527–534. [Google Scholar] [CrossRef] [PubMed]
- Tversky, A.; Kahneman, D. Judgment under Uncertainty: Heuristics and Biases. Science 1974, 185, 1124–1131. [Google Scholar] [CrossRef] [PubMed]
- Gigerenzer, G.; Hoffrage, U.; Kleinbölting, H. Probabilistic Mental Models: A Brunswikian Theory of Confidence. Psychol. Rev. 1991, 98, 506–528. [Google Scholar] [CrossRef] [PubMed]
- Van Leeuwen, D.; Brümmer, N. An introduction to application-independent evaluation of speaker recognition systems. In Speaker Classification; Müller, C., Ed.; Lecture Notes in Computer Science/Artificial Intelligence; Springer: Heidelberg/Berlin, Germany; New York, NY, USA, 2007; Volume 4343. [Google Scholar]
- Brümmer, N.; du Preez, J. Application Independent Evaluation of Speaker Detection. Comput. Speech Lang. 2006, 20, 230–275. [Google Scholar] [CrossRef]
- Ramos, D.; Krish, R.P.; Fierrez, J.; Meuwly, D. From Bometric Scores to Forensic Likelihood Ratios. In Handbook of Biometrics for Forensic Science, Book ed.; Tistarelli, M., Champod, C., Eds.; Springer: Cham, Switzerland, 2017; Chapter 14; pp. 305–327. [Google Scholar]
- Murphy, A.H.; Winkler, R.L. Reliability of Subjective Probability Forecasts of Precipitation and Temperature. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1977, 26, 41–47. [Google Scholar] [CrossRef]
- Ramos, D.; Gonzalez-Rodriguez, J. Reliable support: measuring calibration of likelihood ratios. Forensic Sci. Int. 2013, 230, 156–169. [Google Scholar] [CrossRef] [PubMed]
- Berger, C.E.H.; Buckleton, J.; Champod, C.; Evett, I.W.; Jackson, G. Expressing evaluative opinions: A position statement. Sci. Justice 2011, 51, 1–2. [Google Scholar]
- DeGroot, M.H.; Fienberg, S.E. The Comparison and Evaluation of Forecasters. Statistician 1983, 32, 12–22. [Google Scholar] [CrossRef]
- Gneiting, T.; Balabdaoui, F.; Raftery, A.E. Probabilistic forecasts, calibration and sharpness. J. R. Stat. Soc. Ser. B 2007, 69, 243–268. [Google Scholar] [CrossRef]
- Dawid, A.P. The well-calibrated Bayesian. J. Am. Stat. Assoc. 1982, 77, 605–610. [Google Scholar] [CrossRef]
- Savage, L. The elicitation of personal probabilities and expectations. J. Am. Stat. Assoc. 1971, 66, 783–801. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A. Strictly Proper Scoring Rules, Prediction and Estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Richard, M.D.; Lippmann, R.P. Neural network classifiers estimate Bayesian a posteriori probabilities. Neural Comput. 1991, 3, 461–483. [Google Scholar] [CrossRef]
- Willis, S. ENFSI Guideline for the Formulation of Evaluative Reports in Forensic Science. Monopoly Project MP2010: The Development and Implementation of an ENFSI Standard for Reporting Evaluative Forensic Evidence; Technical Report; European Network of Forensic Science Institutes: Wiesbaden, Germany, 2015. [Google Scholar]
- Ramos, D.; Gonzalez-Rodriguez, J.; Zadora, G.; Aitken, C. Information-Theoretical Assessment of the Performance of Likelihood Ratio Models. J. Forensic Sci. 2013, 58, 1503–1518. [Google Scholar] [CrossRef] [PubMed]
- Kinnunen, T.; Li, H. An overview of text-independent speaker recognition: From features to supervectors. Speech Commun. 2010, 52, 12–40. [Google Scholar] [CrossRef]
- Brier, G. Verification of forecasts expressed in terms of probability. Mon. Weather Rev. 1950, 78, 1–3. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley Interscience: New York, NY, USA, 2006. [Google Scholar]
- Fawcett, T.; Niculescu-Mizil, A. PAV and the ROC convex hull. Mach. Learn. 2007, 68, 97–106. [Google Scholar] [CrossRef]
- Brümmer, N. Measuring, Refining and Calibrating Speaker and Language Information Extracted from Speech. Ph.D. Thesis, School of Electrical Engineering, University of Stellenbosch, Stellenbosch, South Africa, 2010. Available online: http://sites.google.com/site/nikobrummer/ (accessed on 31 January 2018).
- Brümmer, N.; du Preez, J. The PAV Algorithm Optimizes Binary Proper Scoring Rules. Technical Report, Agnitio, 2009. Available online: https://sites.google.com/site/nikobrummer/ (accessed on 31 January 2018).
- Dehak, N.; Kenny, P.; Dehak, R.; Dumouchel, P.; Ouellet, P. Front-End Factor Analysis for Speaker Verification. IEEE Trans. Audio Speech Lang. Process. 2010, 19, 788–798. [Google Scholar] [CrossRef]
- Kenny, P. Bayesian speaker verification with heavy-tailed priors. In Odyssey: The Speaker and Language Recognition Workshop; International Speech Communication Association: Brno, Czech Republic, 2010. [Google Scholar]
- Brümmer, N.; Burget, L.; Cernocky, J.; Glembek, O.; Grezl, F.; Karafiat, M.; van Leeuwen, D.A.; Matejka, P.; Scwartz, P.; Strasheim, A. Fusion of heterogeneous speaker recognition systems in the STBU submission for the NIST speaker recognition evaluation 2006. IEEE Trans. Audio Speech Signal Process. 2007, 15, 2072–2084. [Google Scholar] [CrossRef]
- Martin, A.; Greenberg, C. The NIST 2010 speaker recognition evaluation. In Proceedings of the Interspeech 2010, Makuhari, Chiba, Japan, 26–30 September 2010; pp. 2726–2729. [Google Scholar]
- Martin, A.; Greenberg, C. NIST 2008 Speaker Recognition Evaluation: Performance Across Telephone and Room Microphone Channels. In Proceedings of the Interspeech 2009, Brighton, UK, 6–10 September 2009; pp. 2579–2582. [Google Scholar]
- Aitken, C.G.G.; Lucy, D. Evaluation of trace evidence in the form of multivariate data. Appl. Stat. 2004, 53, 109–122, With corrigendum 665–666. [Google Scholar]
- Franco-Pedroso, J.; Ramos, D.; Gonzalez-Rodriguez, J. Gaussian Mixture Models of Between-Source Variation for Likelihood Ratio Computation from Multivariate Data. PLoS ONE 2016, 11, e0149958. [Google Scholar] [CrossRef] [PubMed]
- Thompson, W.C.; Newman, E.J. Lay understanding of forensic statistics: Evaluation of random match probabilities, likelihood ratios, and verbal equivalents. Law Hum. Behav. 2015, 39, 332–349. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.M.; Yuan, X.J.; Hub, Q.H.; Wangc, S.Q. A novel measure for evaluating classifiers. Expert Syst. Appl. 2010, 37, 3799–3809. [Google Scholar] [CrossRef]
- Jurman, G.; Riccadonna, S.; Furlanello, C. A Comparison of MCC and CEN Error Measures in Multi-Class Prediction. PLoS ONE 2012, 7, e41882. [Google Scholar] [CrossRef] [PubMed]
- Corzo, R.; Hoffman, T.; Weis, P.; Franco-Pedroso, J.; Ramos, D.; Almirall, J. The Use of LA-ICP-MS Databases to Estimate Likelihood Ratios for the Forensic Analysis of Glass Evidence. Talanta 2018, in press. [Google Scholar] [CrossRef]
- Gonzalez-Rodriguez, J.; Rose, P.; Ramos, D.; Toledano, D.T.; Ortega-Garcia, J. Emulating DNA: Rigorous Quantification of Evidential Weight in Transparent and Testable Forensic Speaker Recognition. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 2072–2084. [Google Scholar] [CrossRef]
- Morrison, G.S. Tutorial on logistic-regression calibration and fusion: Converting a score to a likelihood ratio. Aust. J. Forensic Sci. 2013, 45, 173–197. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos, D.; Franco-Pedroso, J.; Lozano-Diez, A.; Gonzalez-Rodriguez, J. Deconstructing Cross-Entropy for Probabilistic Binary Classifiers. Entropy 2018, 20, 208. https://doi.org/10.3390/e20030208
Ramos D, Franco-Pedroso J, Lozano-Diez A, Gonzalez-Rodriguez J. Deconstructing Cross-Entropy for Probabilistic Binary Classifiers. Entropy. 2018; 20(3):208. https://doi.org/10.3390/e20030208
Chicago/Turabian StyleRamos, Daniel, Javier Franco-Pedroso, Alicia Lozano-Diez, and Joaquin Gonzalez-Rodriguez. 2018. "Deconstructing Cross-Entropy for Probabilistic Binary Classifiers" Entropy 20, no. 3: 208. https://doi.org/10.3390/e20030208
APA StyleRamos, D., Franco-Pedroso, J., Lozano-Diez, A., & Gonzalez-Rodriguez, J. (2018). Deconstructing Cross-Entropy for Probabilistic Binary Classifiers. Entropy, 20(3), 208. https://doi.org/10.3390/e20030208





