Statistics of Correlations and Fluctuations in a Stochastic Model of Wealth Exchange
Abstract
1. Introduction
2. Simulations for a Fixed Value of the Initial Total Income and Gini Index
2.1. Langevin Equation. Deterministic Solutions
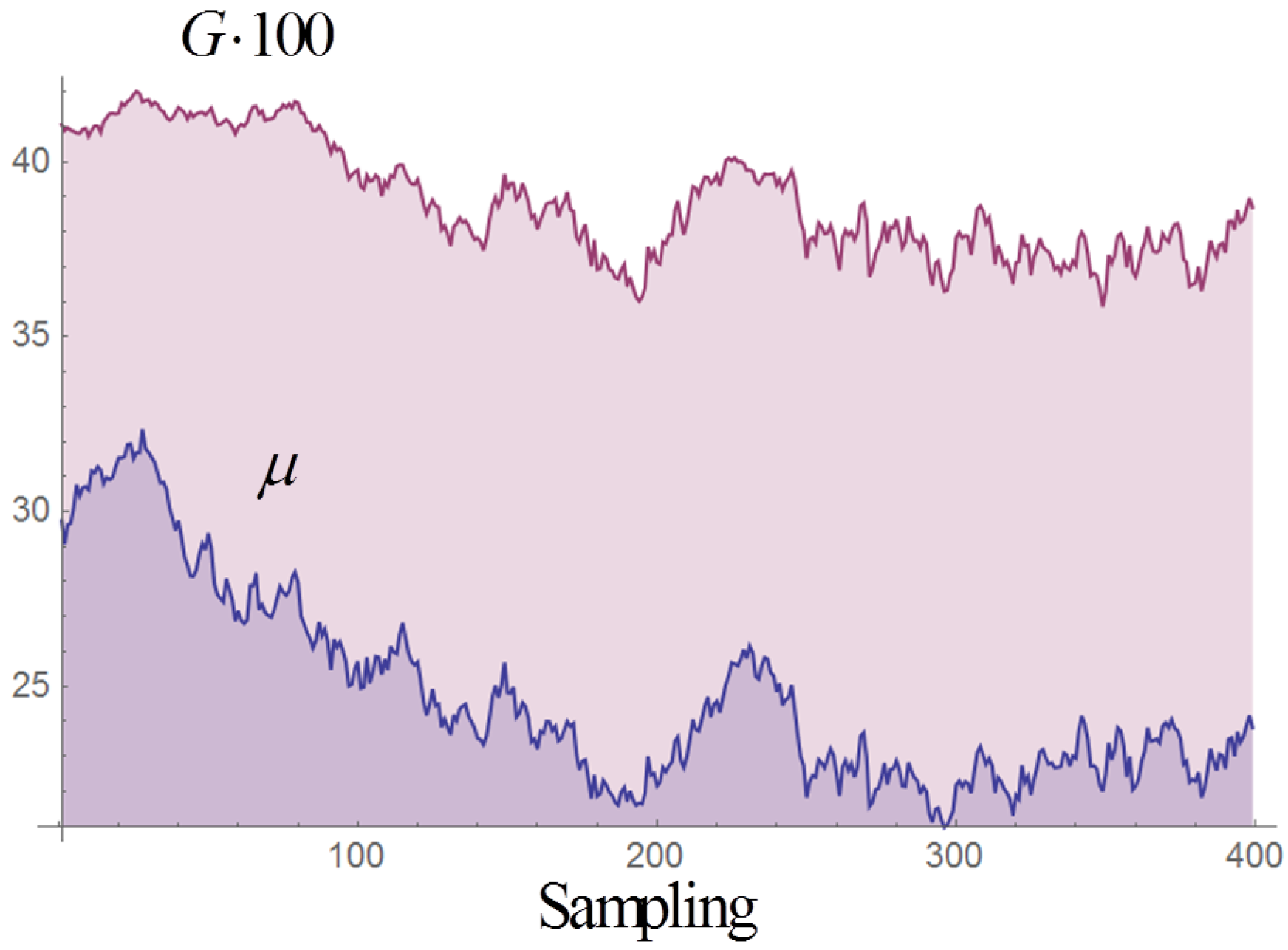
2.2. Stochastic Time-Series
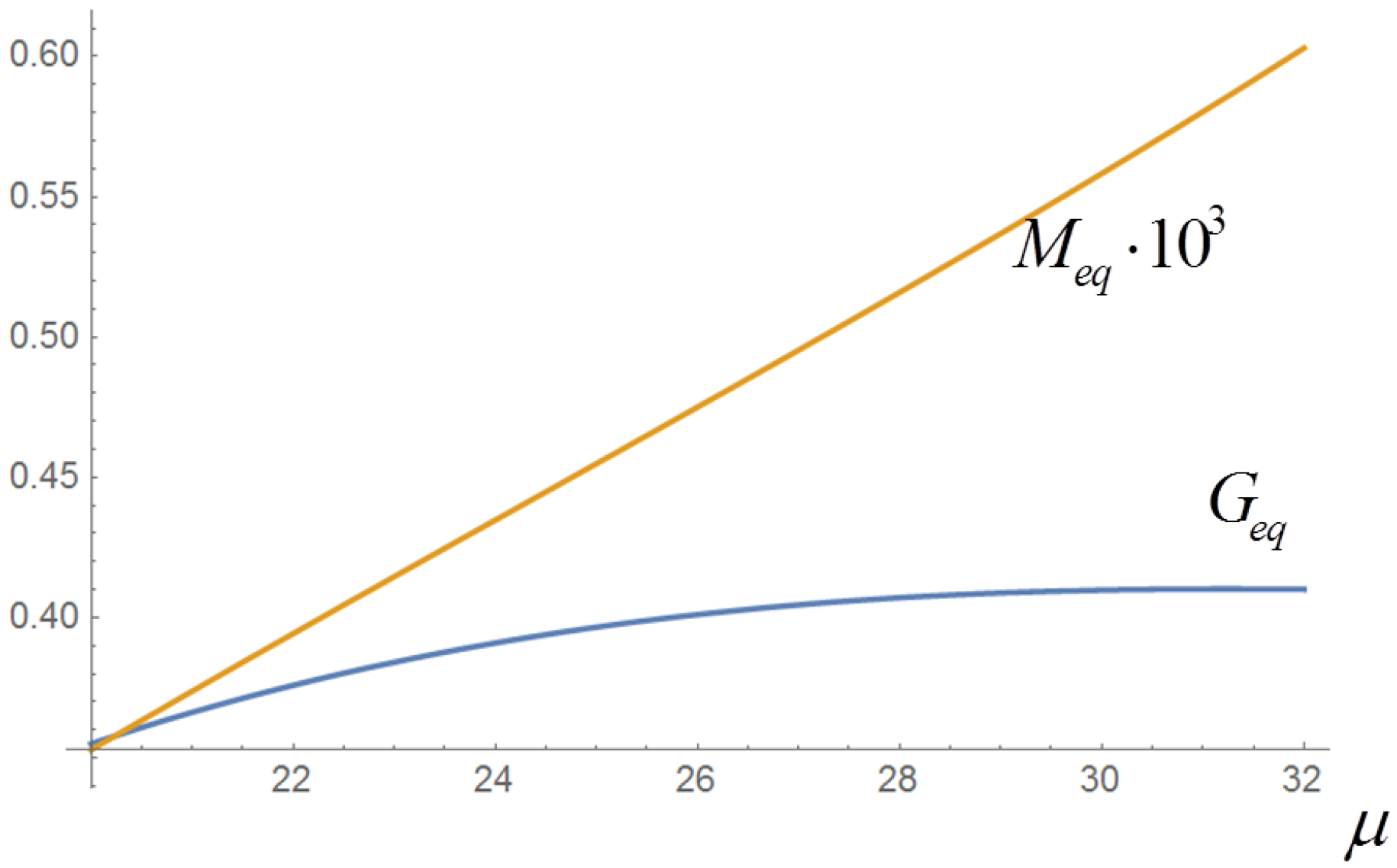
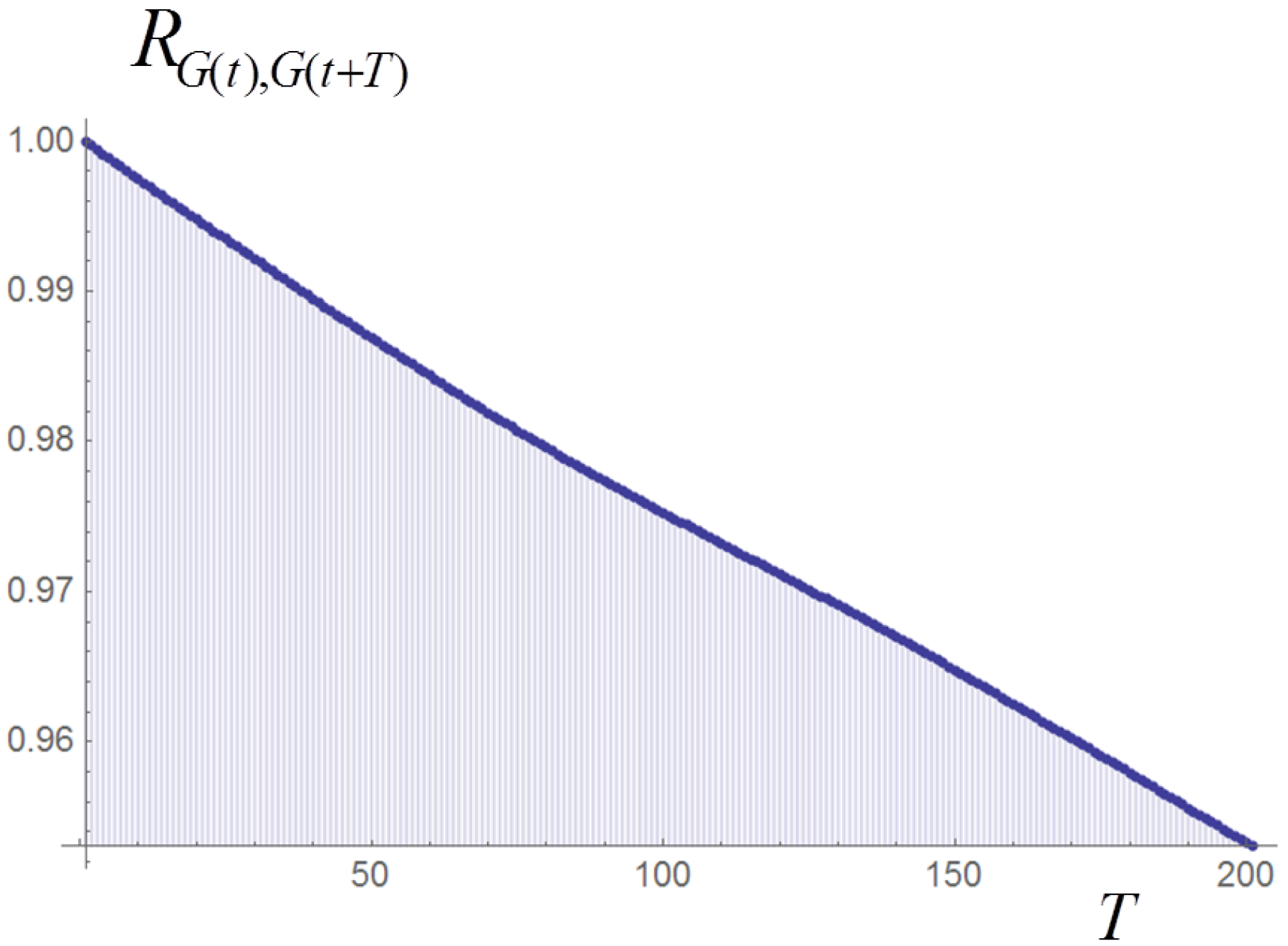
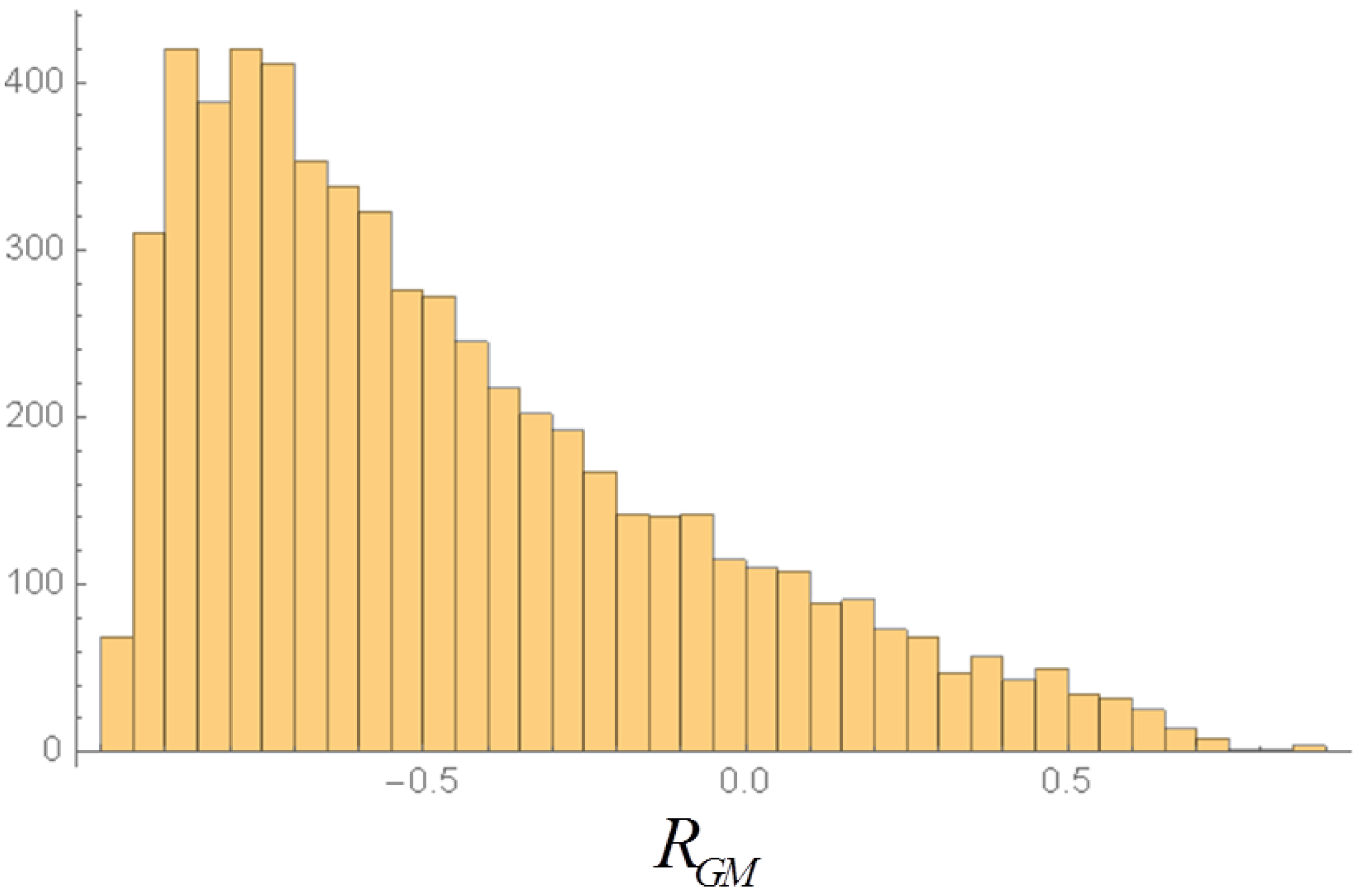
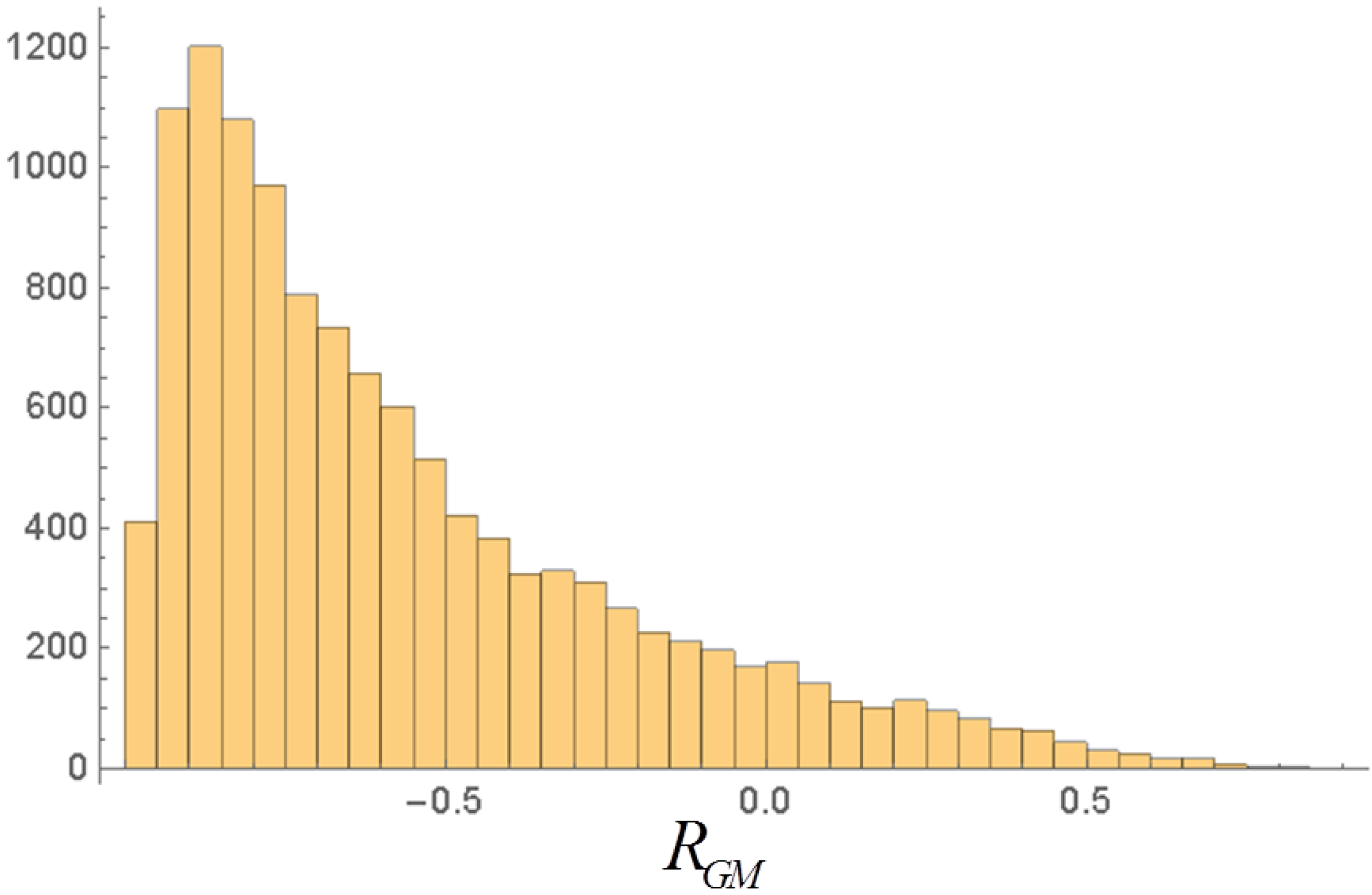
3. Dependence of the Correlations on the Total Income and on G
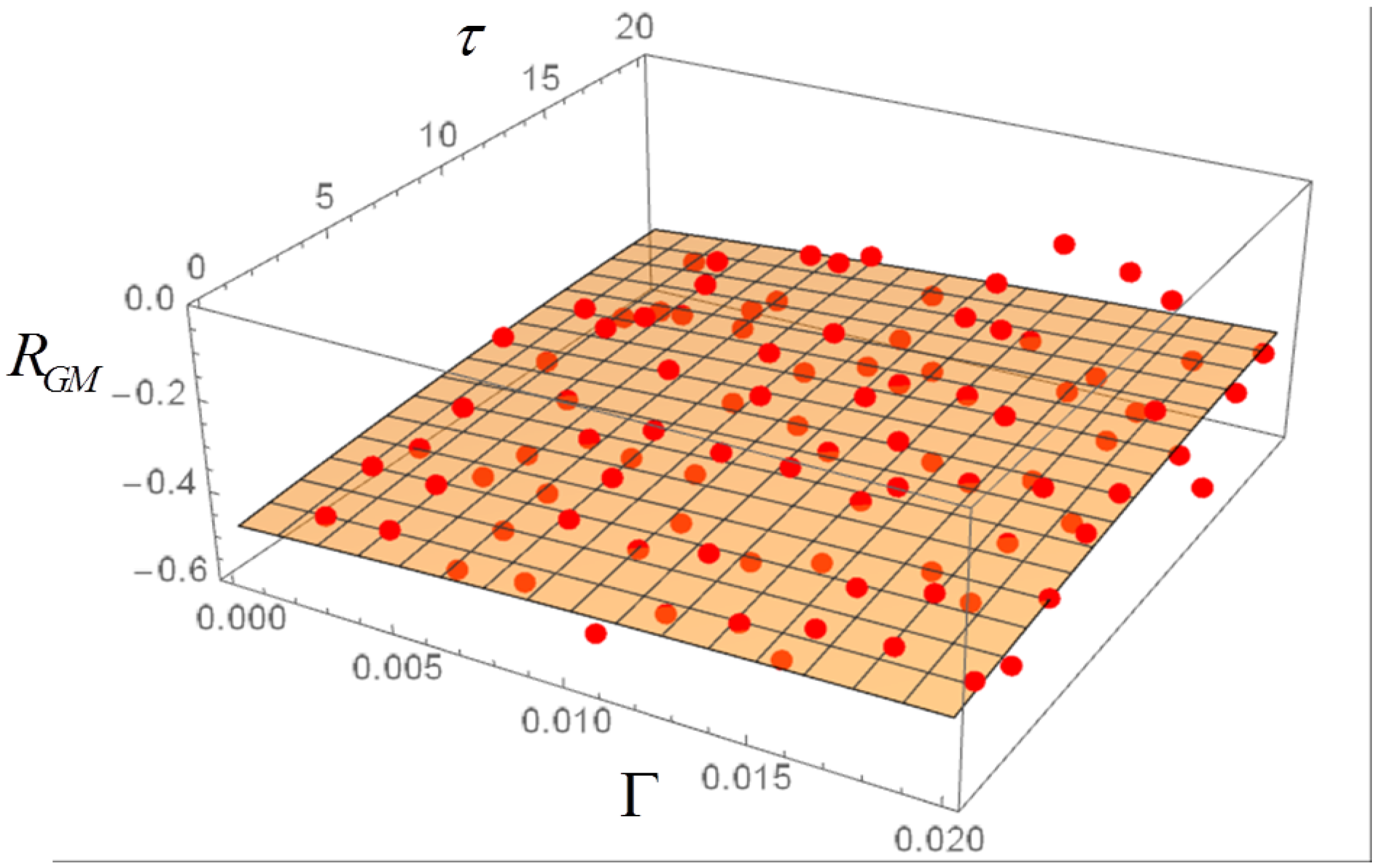
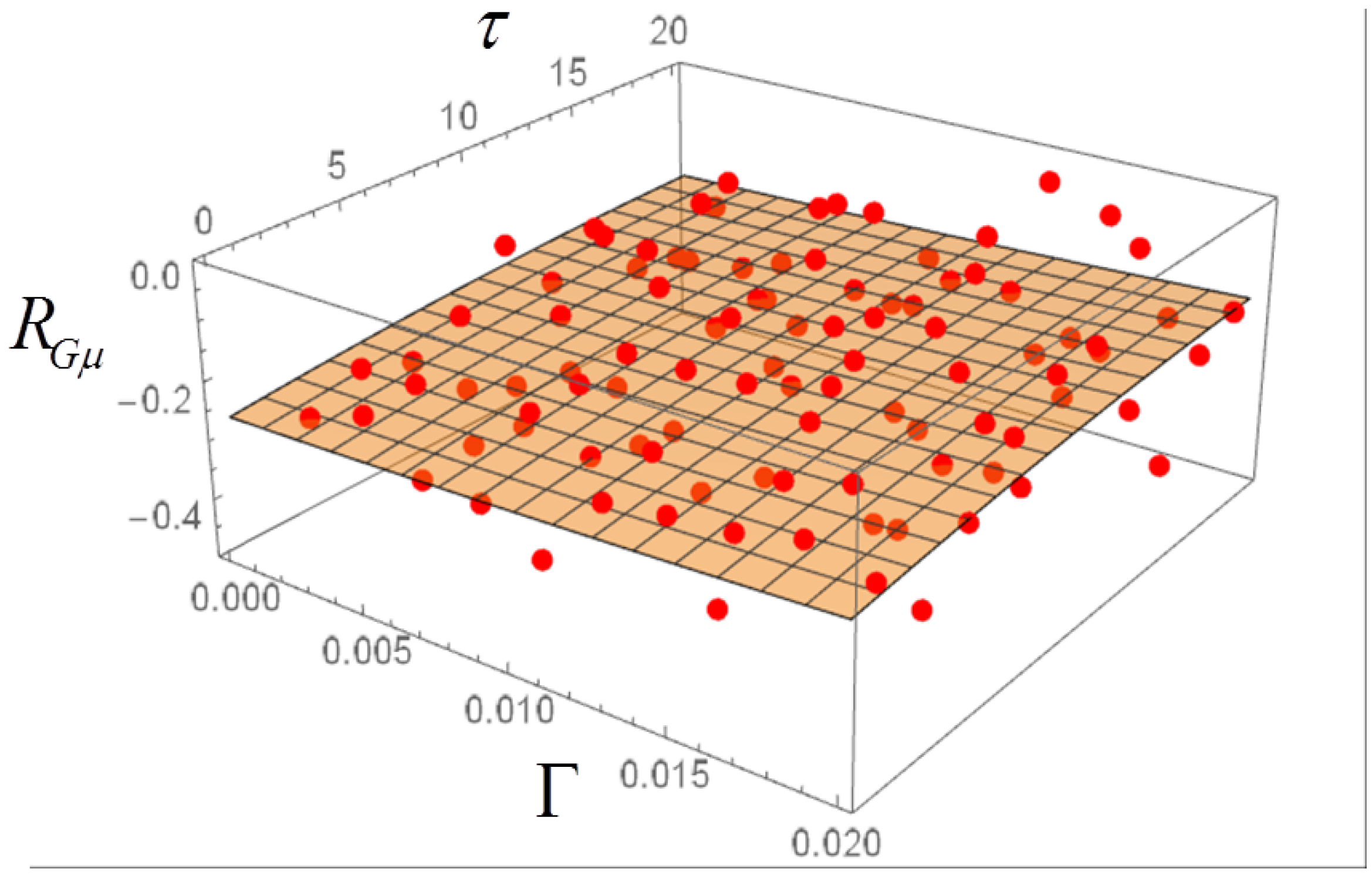
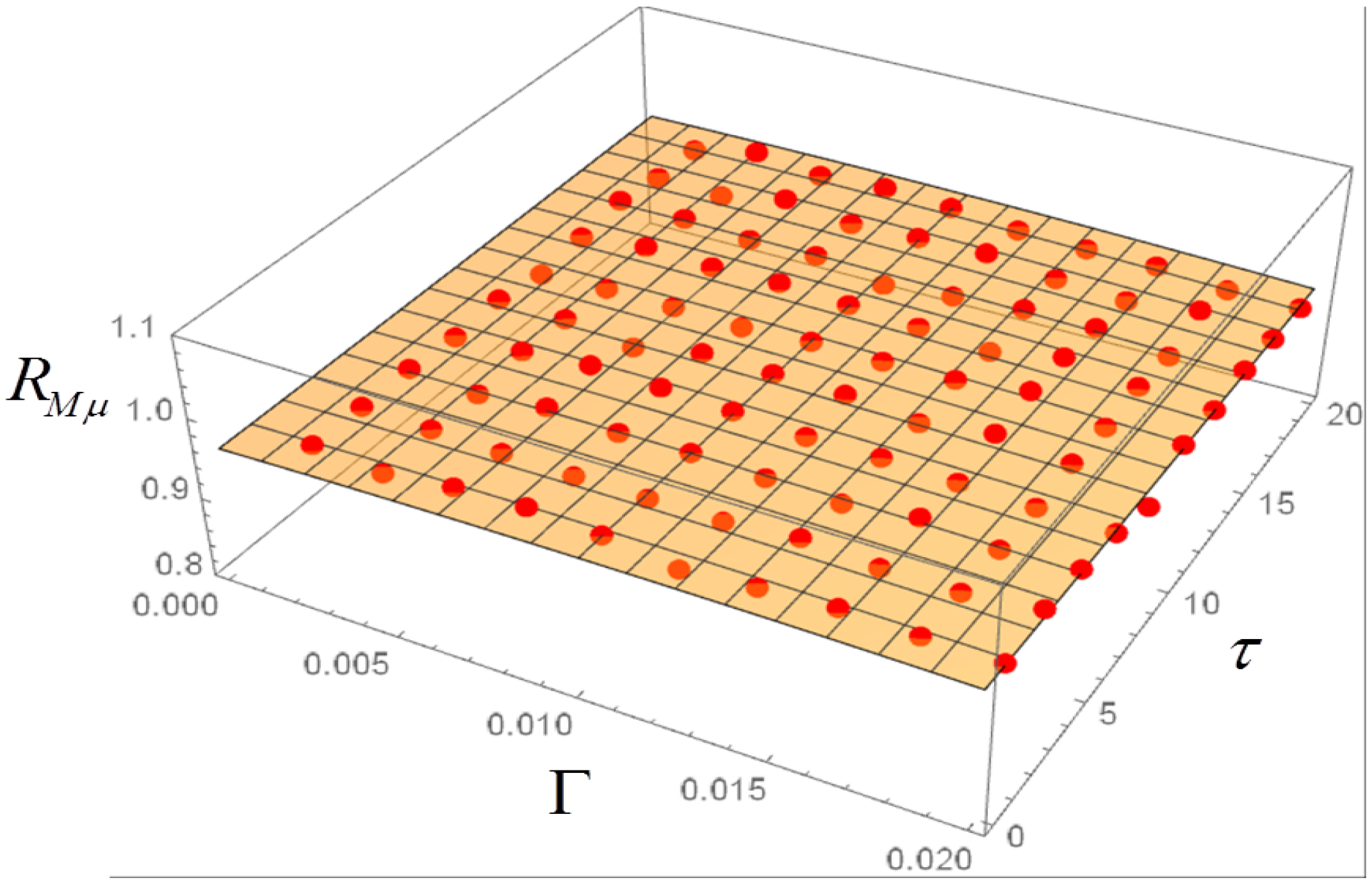
4. Langevin Equation with Ornstein–Uhlenbeck Noise and Dependence of the Correlations on and
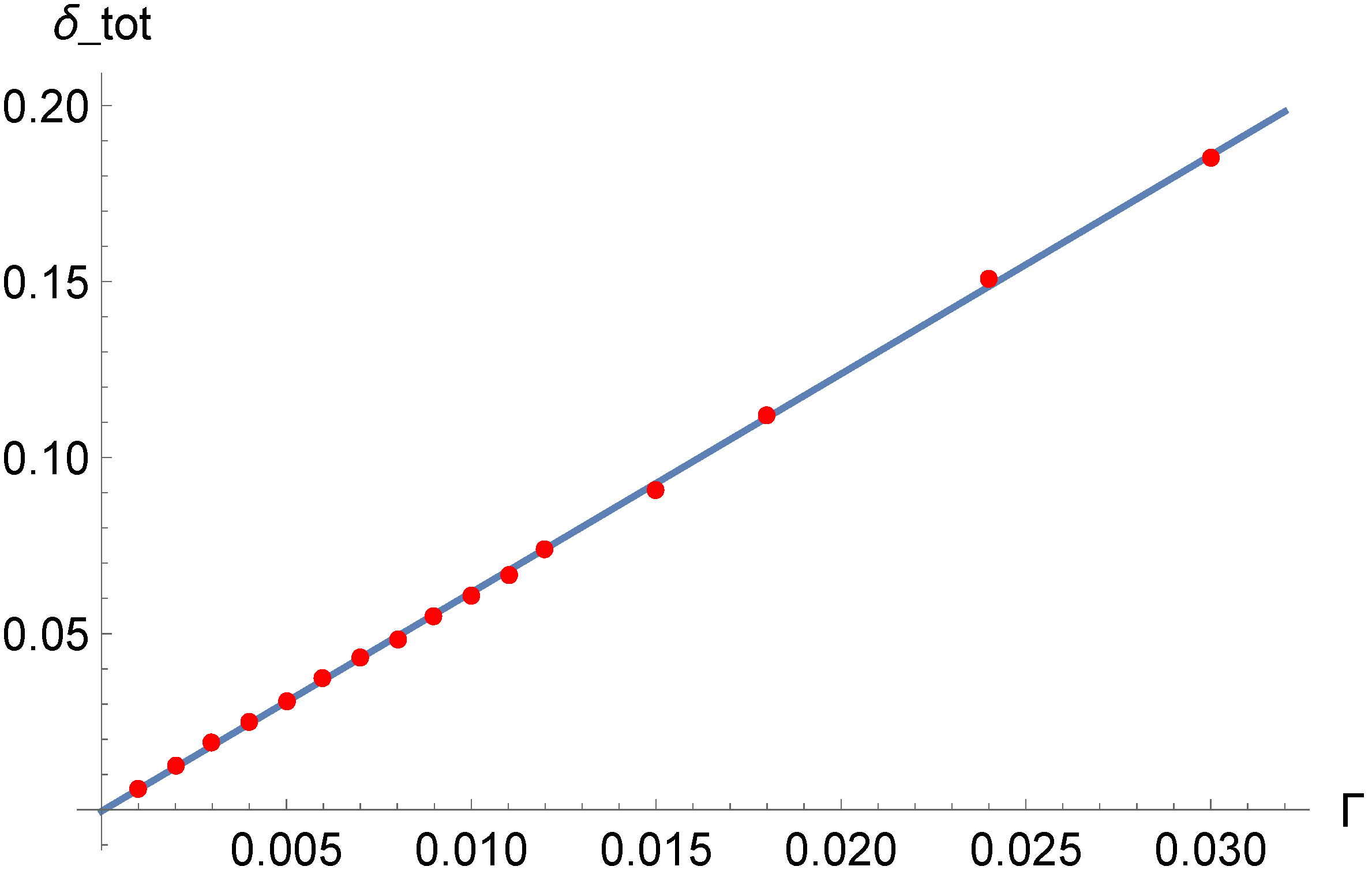
5. Fluctuations of the Populations in Dependence from
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Patriarca, M.; Chakraborti, A. Kinetic exchange models: From molecular physics to social science. Am. J. Phys. 2013, 81, 618. [Google Scholar] [CrossRef]
- Pareschi, L.; Toscani, G. Interacting Multiagent Systems: Kinetic Equations and Monte Carlo Methods; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Dragulescu, A.; Yakovenko, V.M. Statistical mechanics of money. Eur. Phys. J. B 2000, 17, 723–729. [Google Scholar] [CrossRef]
- Schinckus, C. Between complexity of modelling and modelling of complexity: An essay of econophysics. Physica A 2013, 392, 3654–3665. [Google Scholar] [CrossRef]
- Gallegati, M.; Kirman, A. Reconstructing Economics: Agent Based Models and Complexity. Complex. Econ. 2012, 1, 5–31. [Google Scholar] [CrossRef]
- Tesfatsion, L.; Judd, K.L. Handbook of Computational Economics, Volume 2: Agent Based Computational Economics; North-Holland: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Bertotti, M.L. Modelling taxation and redistribution: A discrete active particle kinetic approach. Appl. Math Comput. 2010, 217, 752–762. [Google Scholar] [CrossRef]
- Bertotti, M.L.; Modanese, G. Micro to macro models for income distribution in the absence and in the presence of tax evasion. Appl. Math. Comput. 2014, 244, 836–846. [Google Scholar] [CrossRef]
- Bertotti, M.L.; Modanese, G. Discretized kinetic theory on scale-free networks. Eur. Phys. J. Spec. Top. 2016, 225, 1879–1891. [Google Scholar] [CrossRef]
- Bertotti, M.L.; Modanese, G. Microscopic models for the study of taxpayer audit effects. Int. J. Mod. Phys. C 2016, 27. [Google Scholar] [CrossRef]
- Bertotti, M.L.; Chattopadhyay, A.K.; Modanese, G. Stochastic effects in a discretized kinetic model of economic exchange. Physica A 2017, 471, 724–732. [Google Scholar] [CrossRef][Green Version]
- Bertotti, M.L.; Chattopadhyay, A.K.; Modanese, G. Economic inequality and mobility for stochastic models with multiplicative noise. arXiv, 2017; arXiv:1702.08391. [Google Scholar]
- Stiglitz, J.E. The Price of Inequality: How Today’s Divided Society Endangers Our Future; W.W. Norton & Company: New York, NY, USA, 2012. [Google Scholar]
- Atkinson, A.B. Inequality: What Can Be Done? Harvard University Press: Cambridge, UK, 2015. [Google Scholar]
- Corak, M. Income inequality, equality of opportunity, and intergenerational mobility. J. Econ. Perspect. 2013, 27, 79–102. [Google Scholar] [CrossRef]
- Andrews, D.; Leigh, A. More inequality, less social mobility. Appl. Econ. Lett. 2009, 16, 1489–1492. [Google Scholar] [CrossRef]
- Bertotti, M.L.; Modanese, G. Economic inequality and mobility in kinetic models for social sciences. Eur. Phys. J. Spec. Top. 2016, 225, 1945–1958. [Google Scholar] [CrossRef]
- Spannagel, D.; Broschinski, S. Reichtum in Deutschland Wächst Weiter; WSI Report; Wirtschafts- und Sozialwissenschaftliches Institut: Duesseldorf, Germany, 17 September 2014. [Google Scholar]
- Jerrim, J.; Macmillan, L. Income inequality, intergenerational mobility, and the Great Gatsby curve: Is education the key? Soc. Forces 2015, 94, 505–533. [Google Scholar] [CrossRef]
- Aghion, P.; Caroli, E.; Garcia-Penalosa, C. Inequality and economic growth: The perspective of the new growth theories. Appl. Econ. Lett. 1999, 37, 1615–1660. [Google Scholar] [CrossRef]
- Bertotti, M.L.; Chattopadhyay, A.K.; Modanese, G. Uncertainty dynamics in a model of economic inequality. Int. J. Des. Nat. Ecodyn. 2017, 13, 16–22. [Google Scholar] [CrossRef]

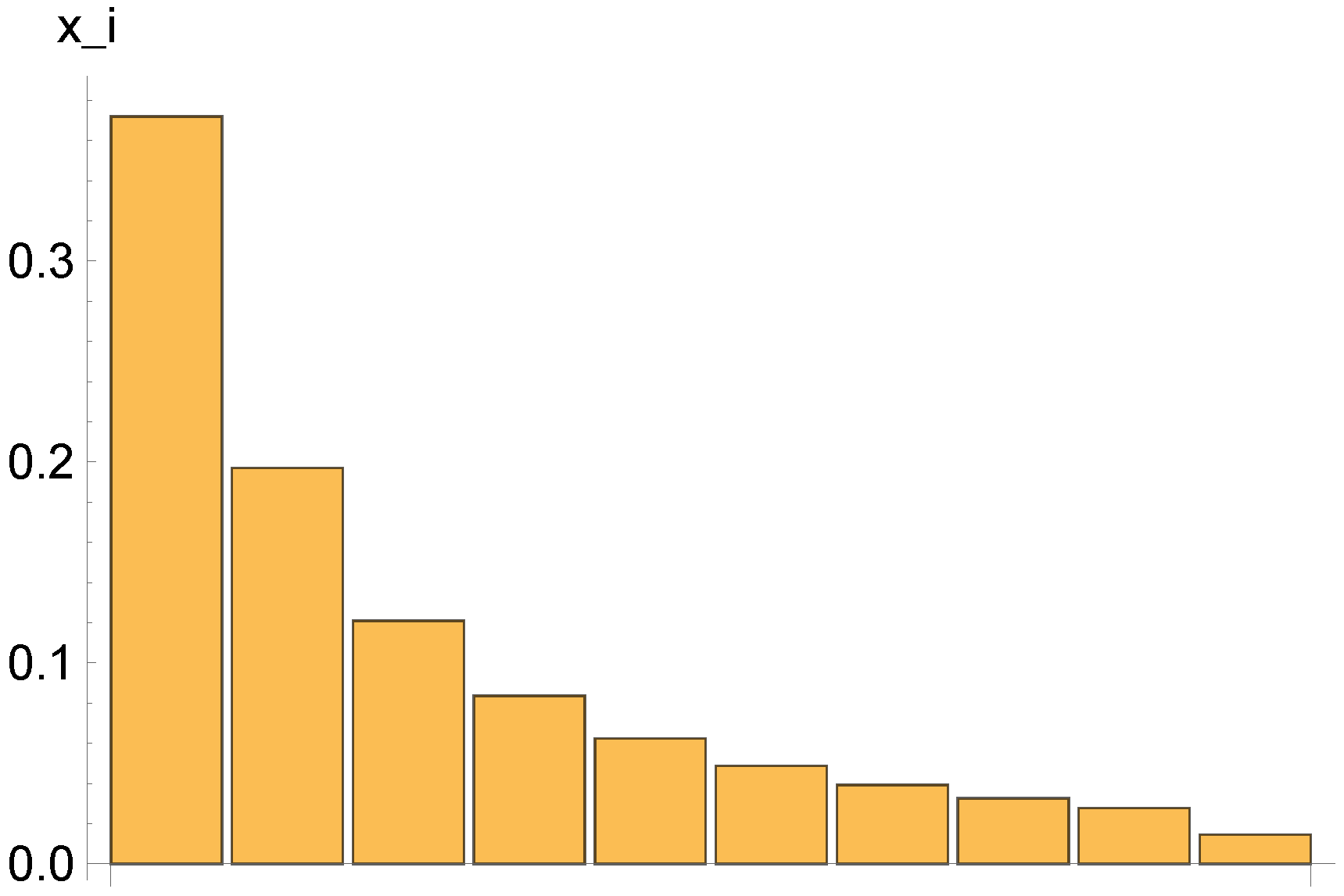
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bertotti, M.L.; Chattopadhyay, A.K.; Modanese, G. Statistics of Correlations and Fluctuations in a Stochastic Model of Wealth Exchange. Entropy 2018, 20, 166. https://doi.org/10.3390/e20030166
Bertotti ML, Chattopadhyay AK, Modanese G. Statistics of Correlations and Fluctuations in a Stochastic Model of Wealth Exchange. Entropy. 2018; 20(3):166. https://doi.org/10.3390/e20030166
Chicago/Turabian StyleBertotti, Maria Letizia, Amit K. Chattopadhyay, and Giovanni Modanese. 2018. "Statistics of Correlations and Fluctuations in a Stochastic Model of Wealth Exchange" Entropy 20, no. 3: 166. https://doi.org/10.3390/e20030166
APA StyleBertotti, M. L., Chattopadhyay, A. K., & Modanese, G. (2018). Statistics of Correlations and Fluctuations in a Stochastic Model of Wealth Exchange. Entropy, 20(3), 166. https://doi.org/10.3390/e20030166






