Thermodynamic Optimization for an Endoreversible Dual-Miller Cycle (DMC) with Finite Speed of Piston
Abstract
1. Introduction
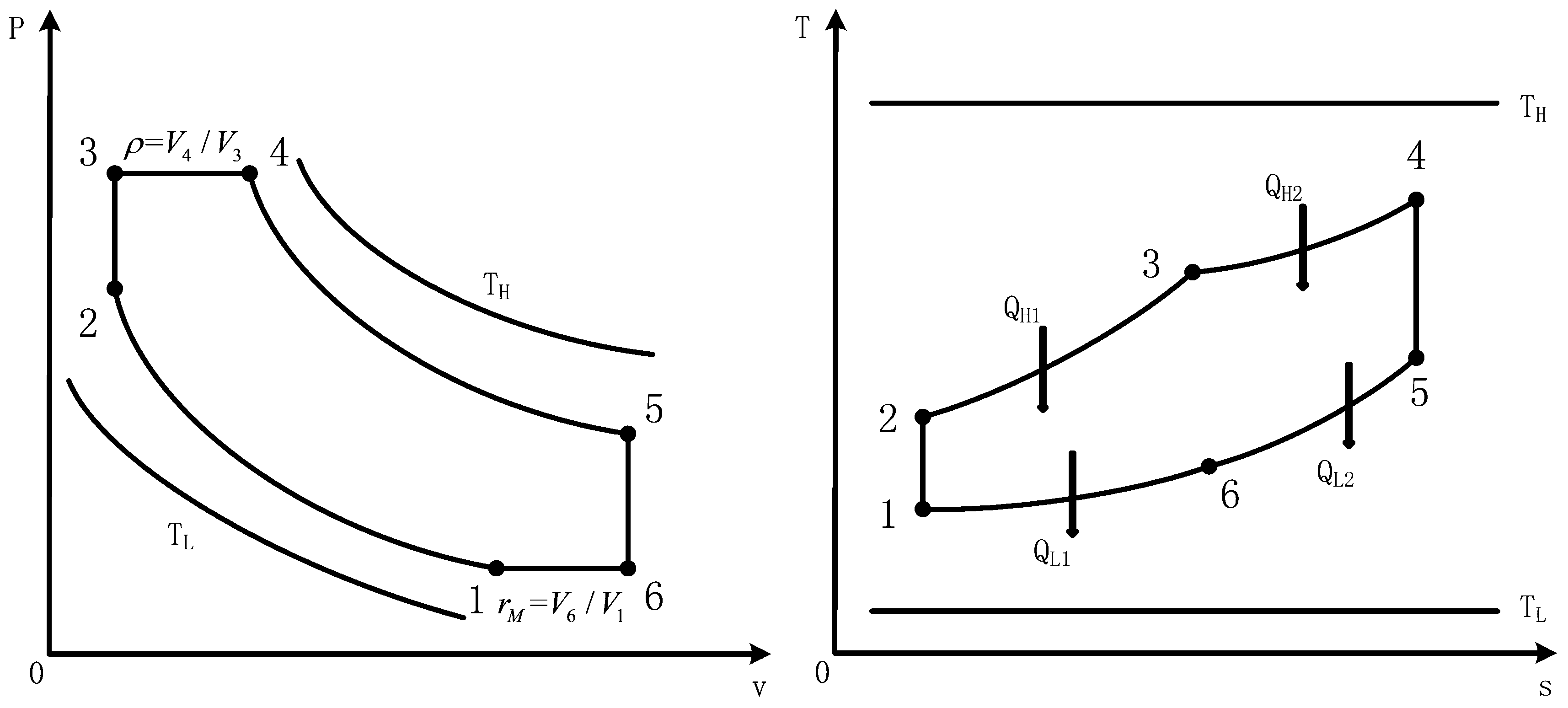
2. Cycle Model and Performance Analyses
3. Analyses of Special Cases
- (1)
- When , i.e., , Equations (19), (28) and (32) are transformed into expressions of , and of an endoreversible DiMC with finite speed of the piston and finite rate of HT:
- (2)
- When , i.e., , Equations (19), (28) and (32) are transformed into expressions of , and of an endoreversible OMC with finite speed of the piston and finite rate of HT:
- (3)
- When , i.e., , Equations (19), (28) and (32) are transformed into expressions of , and of an endoreversible DAC with finite speed of the piston and finite rate of HT:
- (4)
- When , i.e., , Equations (19), (28) and (32) are transformed into expressions of , and of an endoreversible DDC with finite speed of the piston and finite rate of HT:
- (5)
- When and , i.e., and , Equations (19), (28) and (32) are transformed into expressions of , and of an endoreversible Diesel-Atkinson cycle with finite speed of the piston and finite rate of HT:
- (6)
- When and , i.e., and , Equations (19), (28) and (32) are transformed into expressions of , and of an endoreversible DC with finite speed of the piston and finite rate of HT:
- (7)
- When and , i.e., and , Equations (19), (28) and (32) are transformed into expressions of , and of an endoreversible Otto-Atkinson cycle with finite speed of the piston and finite rate of HT:
- (8)
- When and , i.e., and , Equations (19), (28) and (32) are transformed into expressions of , and of an endoreversible OC with finite speed of the piston and finite rate of HT:
4. Numerical Examples
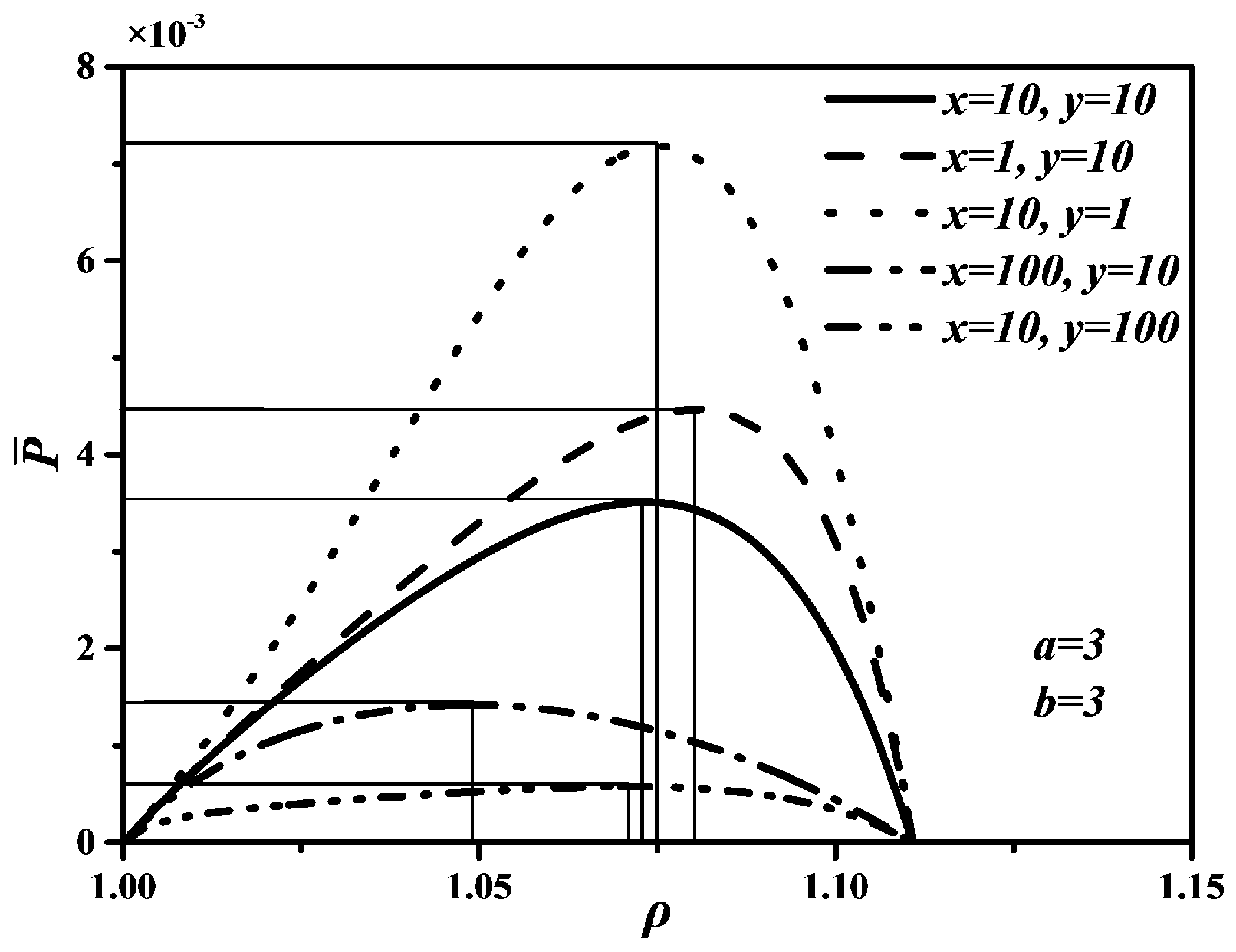
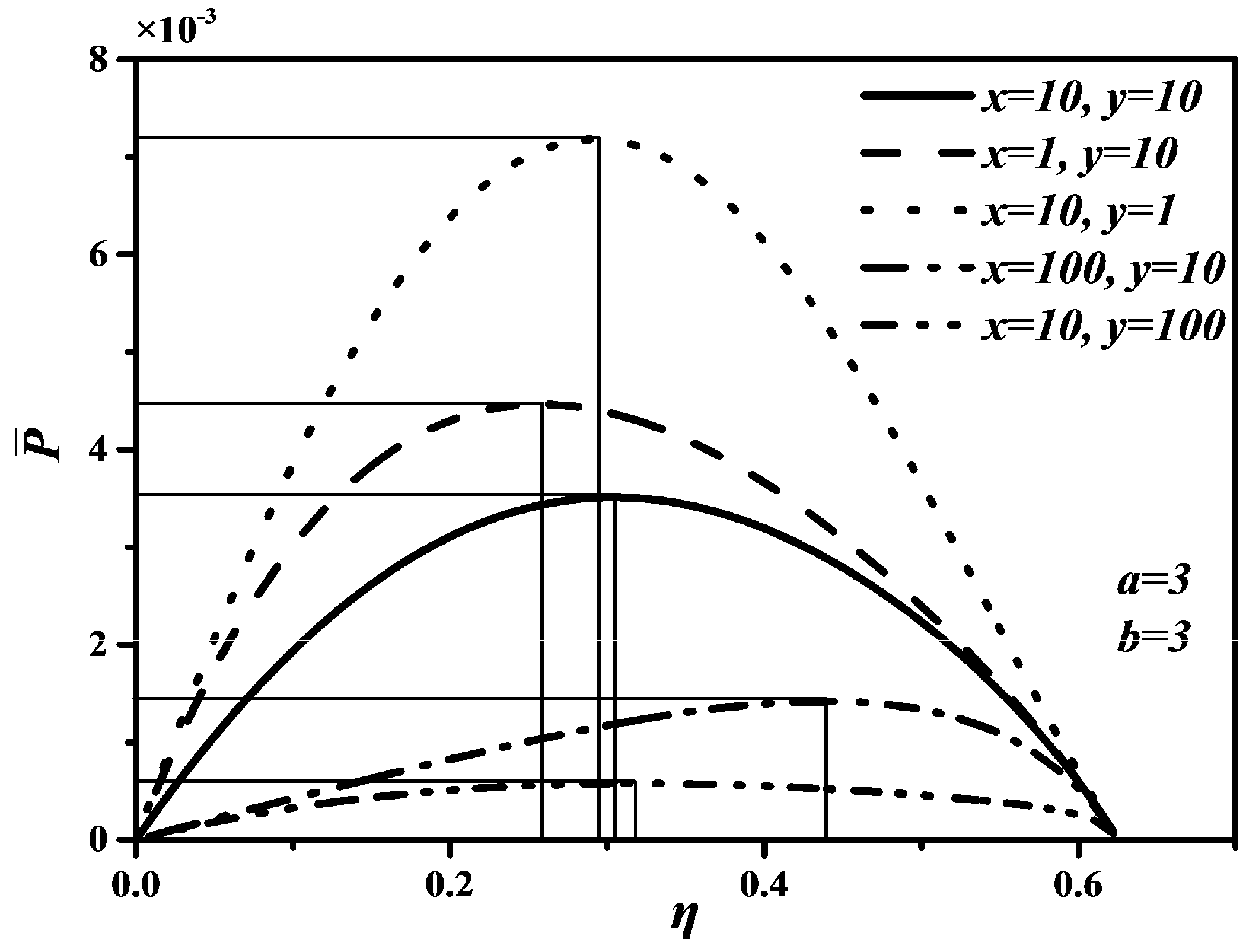
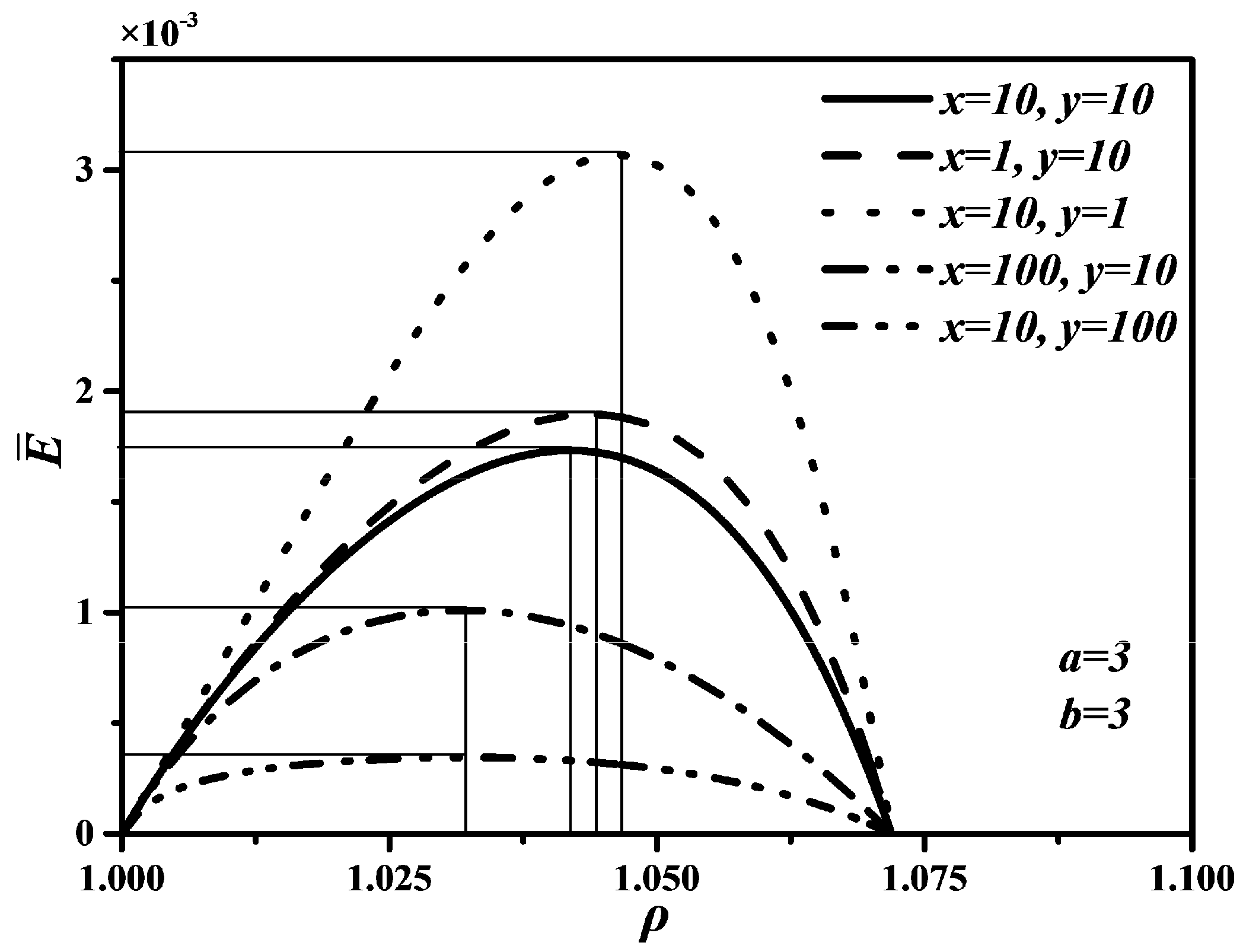
4.1. Effects of x and y on , and
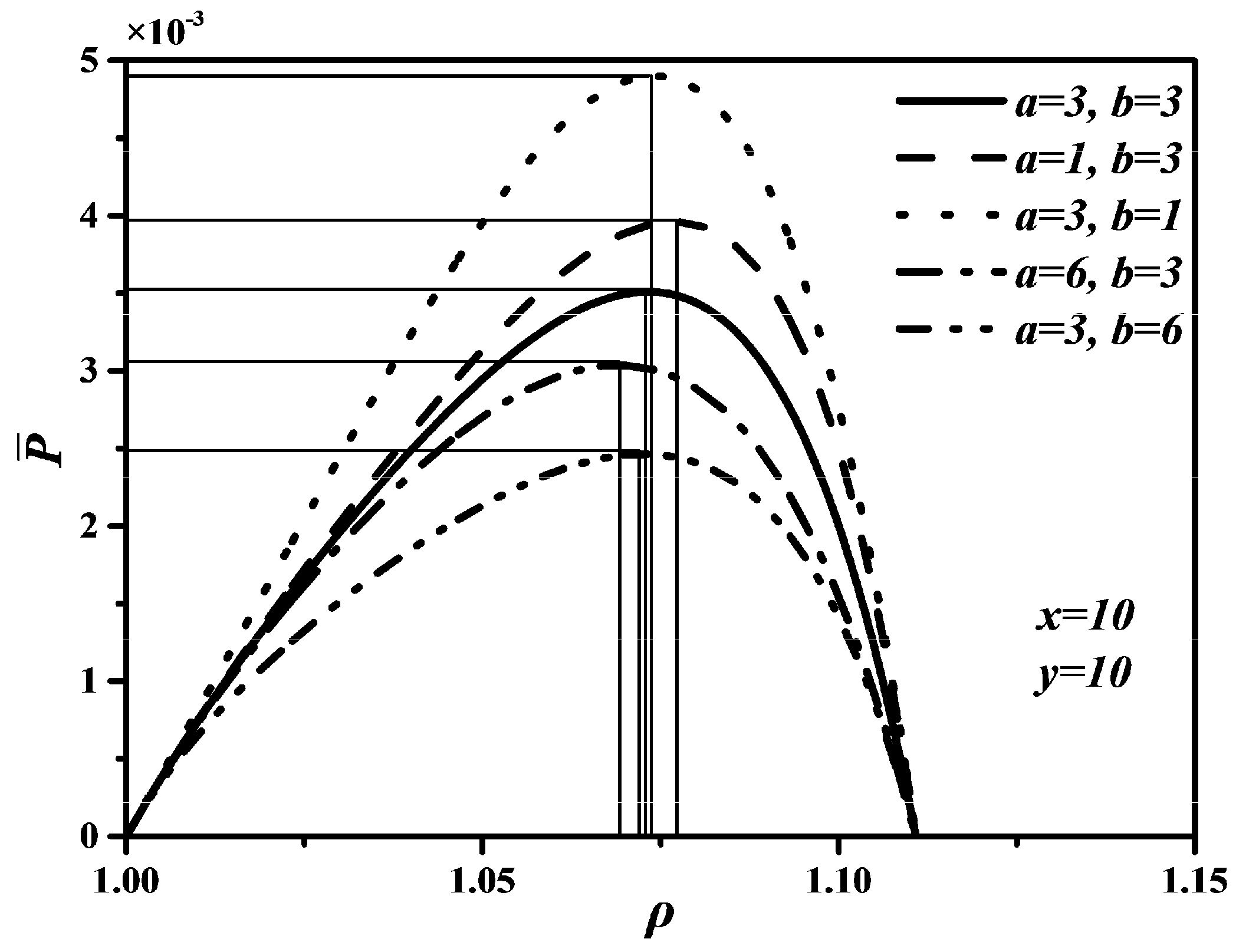
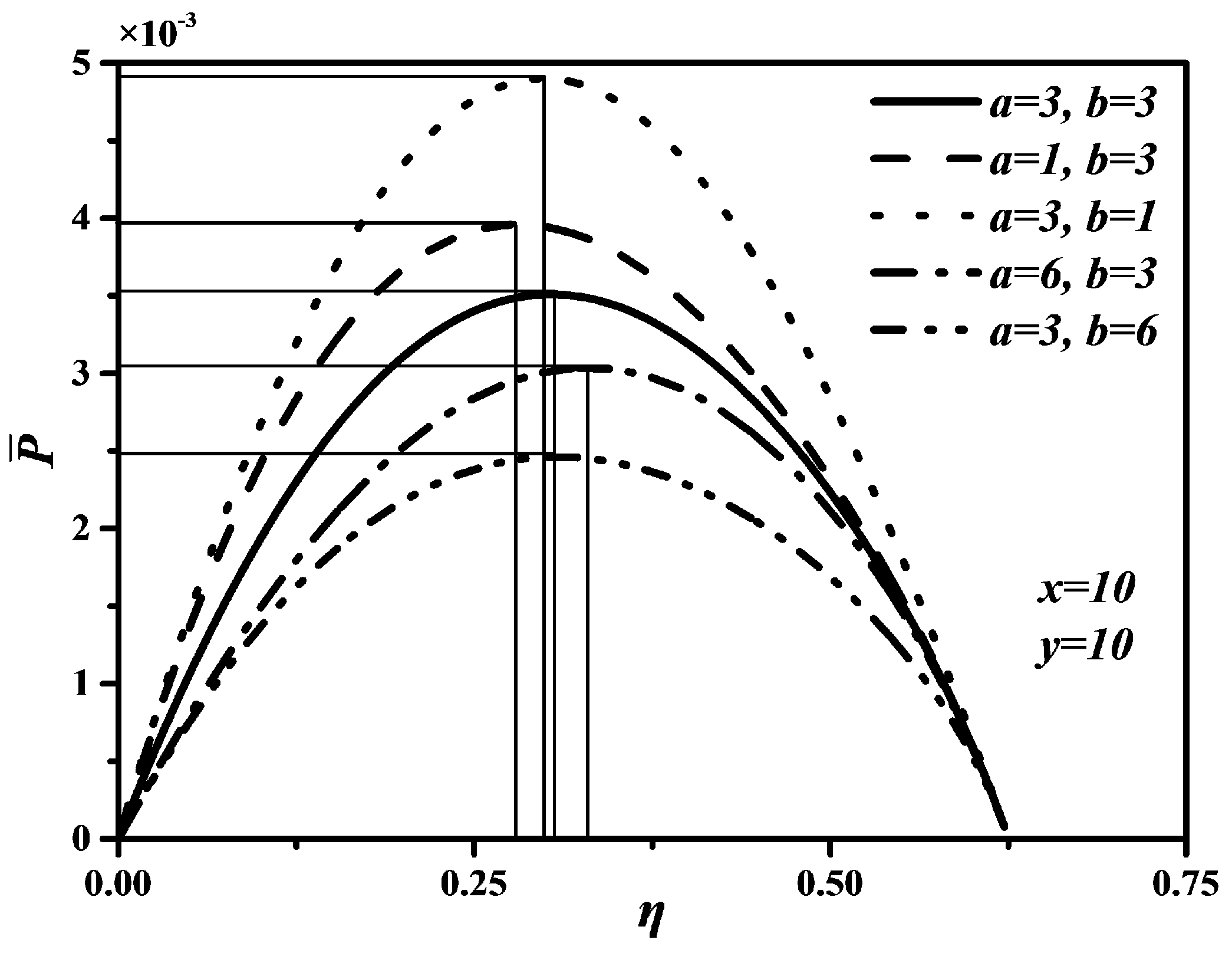
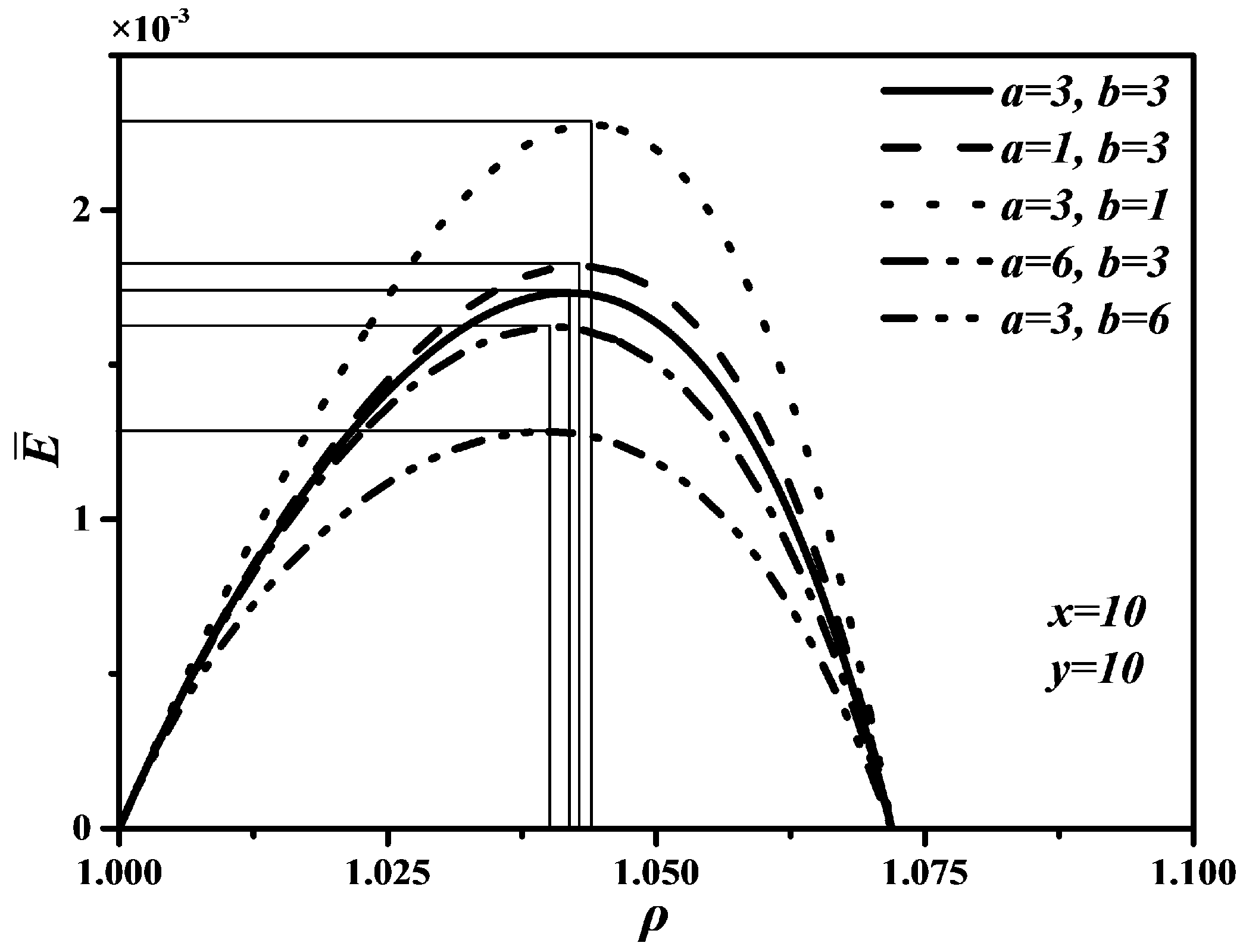
4.2. Effects of a and b on , and
4.3. Performance Comparison
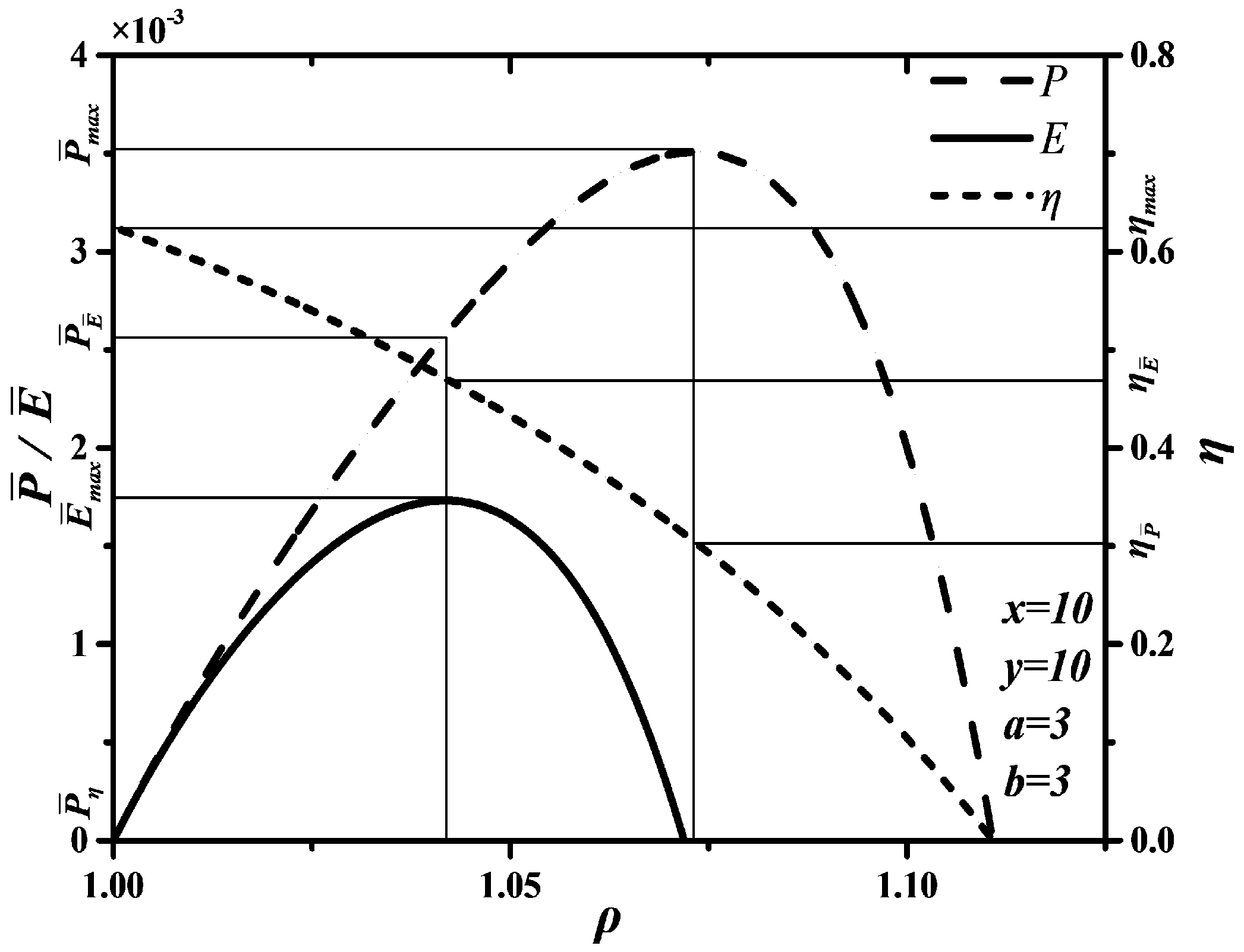
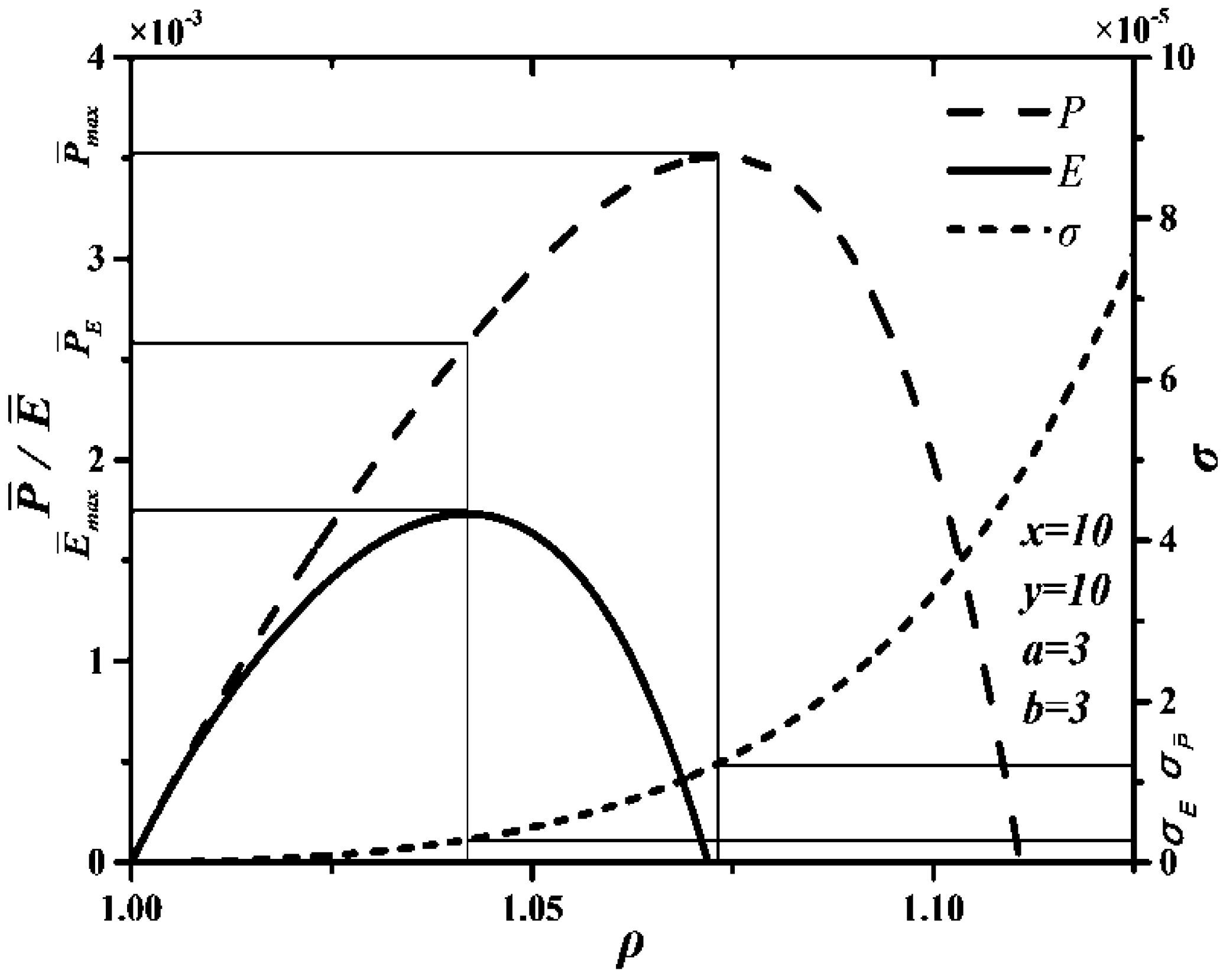
- (1)
- When is chosen as optimization objective function, the maximum is , corresponding to the maximum is . However, the maximum is , , so choosing as optimization objective function sacrifices most of .
- (2)
- When is chosen as optimization objective function, corresponding to the maximum is , . Although can reach the maximum, is zero when optimizing . Thus, choosing as optimization objective function is unreasonable.
- (3)
- When is chosen as optimization objective function, the maximum is , corresponding to the maximum is , , corresponding to the maximum is , . Thus, choosing as optimization objective function can improve compared with choosing as optimization objective function and can also improve compared with choosing as optimization objective function.
- (4)
- There are and . When is chosen as optimization objective function, and may be smaller than their maxima, but they can reach relatively large values at the same time. Hence, optimizing is the best compromise optimization between optimizing and optimizing .
4.4. Corollary 75–25
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclatures
| constant | |
| area of piston face () | |
| constant | |
| specific heat at constant pressure () | |
| specific heat at constant volume () | |
| ecological function () | |
| ecological coefficient of performance | |
| area of heat transfer () | |
| specific heat ratio | |
| stroke length () | |
| mass of working fluid () | |
| number of heat transfer unites | |
| power output () | |
| quantity of heat transfer () | |
| entropy generation () | |
| temperature () | |
| piston speed () | |
| heat transfer coefficient () | |
| volume () | |
| Greek symbols | |
| effectiveness of heat exchanger | |
| η | thermal efficiency |
| entropy generation rate () | |
| cycle period () | |
| Subscripts | |
| H | high temperature heat reservoir |
| low temperature heat reservoir | |
| optimal value | |
| cycle state points | |
| Superscripts | |
| rate | |
| non-dimensional |
Abbreviations
| DAC | Dual-Atkinson cycle |
| DC | Diesel cycle |
| DDC | Dual-Diesel cycle |
| DiMC | Diesel-Miller cycle |
| DMC | Dual-Miller cycle |
| FST | finite speed thermodynamics |
| HEC | heat engine cycle |
| HL | heat leakage |
| HT | heat transfer |
| ICE | internal combustion engine |
| OC | Otto cycle |
| OMC | Otto-Miller cycle |
| TFS | thermodynamics with finite speed |
References
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Andresen, B. Finite-Time Thermodynamics; Physics Laboratory II, University of Copenhagen: Copenhagen, Denmark, 1983. [Google Scholar]
- Andresen, B.; Salamon, P.; Berry, R.S. Thermodynamics in finite time. Phys. Today 1984, 37, 62–70. [Google Scholar] [CrossRef]
- Bejan, A. Entropy generation on minimization: The new thermodynamics of finite-size device and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Chen, L.G.; Wu, C.; Sun, F.R. Finite time thermodynamic optimization or entropy generation minimization of energy systems. J. Non-Equilib. Thermodyn. 1999, 24, 327–359. [Google Scholar] [CrossRef]
- Chen, L.G. Finite-Time Thermodynamic Analysis of Irreversible Processes and Cycles; High Education Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Feidt, M. Optimal Thermodynamics-New Upperbounds. Entropy 2009, 11, 529–547. [Google Scholar] [CrossRef]
- Andresen, B. Current trends in finite-time thermodynamics. Angew. Chem. Int. Ed. 2011, 50, 2690–2704. [Google Scholar] [CrossRef] [PubMed]
- Quijano, J.; Lin, H. Entropy in the critical zone: A comprehensive review. Entropy 2014, 16, 3482–3536. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. Constructal design for a rectangular body with nonuniform heat generation. Eur. Phys. J. Plus 2016, 131, 274. [Google Scholar] [CrossRef]
- Feidt, M. The history and perspectives of efficiency at maximum power of the Carnot engine. Entropy 2017, 19, 369. [Google Scholar] [CrossRef]
- Honig, J. On the entropy of a class of irreversible processes. Entropy 2013, 15, 2975–2988. [Google Scholar] [CrossRef]
- Chen, L.G.; Feng, H.J.; Xie, Z.H. Generalized thermodynamic optimization for iron and steel production processes: Theoretical exploration and application cases. Entropy 2016, 18, 353. [Google Scholar] [CrossRef]
- Chen, L.G.; Xia, S.J. Generalized Thermodynamic Dynamic-Optimization for Irreversible Processes; Science Press: Beijing, China, 2017. (In Chinese) [Google Scholar]
- Acikkalp, E. Models for optimum thermo-ecological criteria of actual thermal cycles. Therm. Sci. 2013, 17, 915–930. [Google Scholar] [CrossRef]
- Açıkkalp, E.; Yamik, H. Limits and optimization of power input or output of actual thermal cycles. Entropy 2013, 15, 3309–3338. [Google Scholar] [CrossRef]
- Açıkkalp, E. Methods used for evaluation of actual power generating thermal cycles and comparing them. Int. J. Electr. Power Energy Syst. 2015, 69, 85–89. [Google Scholar] [CrossRef]
- Chen, L.G.; Xia, S.J. Generalized Thermodynamic Dynamic-Optimization for Irreversible Cycles: Thermodynamic and Chemical Theoretical Cycles; Science Press: Beijing, China, 2017. (In Chinese) [Google Scholar]
- Chen, L.G.; Xia, S.J. Generalized Thermodynamic Dynamic-Optimization for Irreversible Cycles: Engineering Thermodynamic Plants and Generalized Engine Cycles; Science Press: Beijing, China, 2017. (In Chinese) [Google Scholar]
- Reyes-Ramírez, I.; Barranco-Jiménez, M.A.; Rojas-Pacheco, A.; Guzmán-Vargas, L. Global stability analysis of a Curzon-Ahlborn heat engine using the Lyapunov method. Phys. A Stat. Mech. Appl. 2014, 399, 98–105. [Google Scholar] [CrossRef]
- Açıkkalp, E.; Yamik, H. Modeling and optimization of maximum available work for irreversible gas power cycles with temperature dependent specific heat. J. Non-Equilib. Thermodyn. 2015, 40, 25–39. [Google Scholar] [CrossRef]
- Xia, S.J.; Chen, L.G.; Sun, F.R. Maximum cycle work output optimization for generalized radiative law Otto cycle engines. Eur. Phys. J. Plus 2016, 131, 394. [Google Scholar] [CrossRef]
- Qin, X.Y.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Thermodynamic modeling and performance analysis of variable-temperature heat reservoir absorption heat pump cycle. Phys. A Stat. Mech. Appl. 2015, 436, 788–797. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, L.G.; Sun, F.R. Power optimization chemically driven heat engine based on first and second order reaction kinetic theory and probability theory. Phys. A Stat. Mech. Appl. 2016, 445, 221–230. [Google Scholar] [CrossRef]
- Kosloff, R. Quantum thermodynamics: A dynamical viewpoint. Entropy 2013, 15, 2100–2128. [Google Scholar] [CrossRef]
- Von Spakovsky, M.R.; Gemmer, J. Some trends in quantum thermodynamics. Entropy 2014, 16, 3434–3470. [Google Scholar] [CrossRef]
- Açıkkalp, E.; Caner, N. Determining of the optimum performance of a nano scale irreversible Dual cycle with quantum gases as working fluid by using different methods. Phys. A Stat. Mech. Appl. 2015, 433, 247–258. [Google Scholar] [CrossRef]
- Açıkkalp, E.; Caner, N. Determining performance of an irreversible nano scale dual cycle operating with Maxwell-Boltzmann gas. Phys. A Stat. Mech. Appl. 2015, 424, 342–349. [Google Scholar] [CrossRef]
- Açıkkalp, E.; Caner, N. Application of exergetic sustainable index to the quantum irreversible Diesel refrigerator cycles for 1D box system. Eur. Phys. J. Plus 2015, 130, 73. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ahmadi, M.A.; Pourfayaz, F. Performance assessment and optimization of an irreversible nano-scale Stirling engine cycle operating with Maxwell-Boltzmann gas. Eur. Phys. J. Plus 2015, 130, 190. [Google Scholar] [CrossRef]
- Kosloff, R.; Rezek, Y. The quantum harmonic Otto cycle. Entropy 2017, 19, 136. [Google Scholar] [CrossRef]
- Ding, Z.M.; Chen, L.G.; Wang, W.H.; Ge, Y.L.; Sun, F.R. Exploring the operation of a microscopic energy selective electron engine. Phys. A Stat. Mech. Appl. 2015, 431, 94–108. [Google Scholar] [CrossRef]
- Ding, Z.M.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Performance optimization of total momentum filtering double-resonance energy selective electron heat pump. Phys. A Stat. Mech. Appl. 2016, 447, 49–61. [Google Scholar] [CrossRef]
- Zhou, J.L.; Chen, L.G.; Ding, Z.M.; Sun, F.R. Exploring the optimal performance of irreversible single resonance energy selective electron refrigerator. Eur. Phys. J. Plus 2016, 131, 149. [Google Scholar] [CrossRef]
- Ge, Y.L.; Chen, L.G.; Sun, F.R. Progress in finite time thermodynamic studies for internal combustion engine cycles. Entropy 2016, 18, 139. [Google Scholar] [CrossRef]
- Sun, F.R.; Chen, L.G.; Chen, W.Z. Finite time Thermodynamics analysis and evaluation for a heat engine with steady-state energy conversion between heat sources. J. Eng. Therm. Energy Power 1989, 4, 1–6. (In Chinese) [Google Scholar]
- Wu, C. Specific power optimization of a closed-cycle OTEC plants. Ocean Eng. 1990, 17, 307–314. [Google Scholar] [CrossRef]
- Sahin, B.; Kodal, A.; Yavuz, H. Maximum power density analysis of an endoreversible Carnot heat engine. Energy 1996, 21, 1219–1225. [Google Scholar] [CrossRef]
- Sahin, B.; Kodal, A.; Yavuz, H. Efficiency of Joule-Brayton engine at maximum power density. J. Phys. D Appl. Phys. 1995, 28, 1309–1313. [Google Scholar] [CrossRef]
- Jubeh, N.M. Exergy analysis and second law efficiency of a regenerative Brayton cycle with isothermal heat addition. Entropy 2005, 7, 172–187. [Google Scholar] [CrossRef]
- Labrecque, R. Exergy as a useful variable for quickly assessing the theoretical maximum power of salinity gradient energy systems. Entropy 2009, 11, 798–806. [Google Scholar] [CrossRef]
- Açıkkalp, E.; Caner, N. Performance assessment of an irreversible nano Brayton cycle operating with Maxwell-Boltzmann gas. Eur. Phys. J. Plus 2015, 130, 93. [Google Scholar] [CrossRef]
- Açıkkalp, E. Exergetic sustainability evaluation of irreversible Carnot refrigerator. Phys. A Stat. Mech. Appl. 2015, 436, 311–320. [Google Scholar] [CrossRef]
- Chen, L.G.; Sun, F.R.; Chen, W.Z. Finite time exergoeconomic performance bound and optimization criteria for two-heat-reservoir heat engine. Chin. Sci. Bull. 1991, 36, 233–235. (In Chinese) [Google Scholar]
- Wu, C.; Chen, L.G.; Sun, F.R. Effect of heat transfer law on finite-time exergoeconomic performance of heat engines. Energy 1996, 21, 1127–1134. [Google Scholar] [CrossRef]
- Angulo-Brown, F. An ecological optimization criterion for finite-time heat engines. J. Appl. Phys. 1991, 69, 7465–7469. [Google Scholar] [CrossRef]
- Yan, Z.J. Comment on “ecological optimization criterion for finite-time heat engines”. J. Appl. Phys. 1993, 73, 3583. [Google Scholar] [CrossRef]
- Chen, L.G.; Sun, F.R.; Chen, W.Z. The ecological figures of merit for thermodynamic cycles. J. Eng. Therm. Energy Power 1994, 9, 374–376. (In Chinese) [Google Scholar]
- Barranco-Jiménez, M.A.; Chimal-Eguía, J.C.; Angulo-Brown, F. The Gordon and Zarmi model for convective atmospheric cells under the ecological criterion applied to the planets of the solar system. Rev. Mex. Fís. 2006, 52, 205–212. [Google Scholar]
- Barranco-Jimenez, M.A.; Angulo-Brown, F. Thermo-economic optimization of a Novikov power plant model under maximum ecological conditions. J. Energy Inst. 2007, 80, 96–104. [Google Scholar] [CrossRef]
- Arias-Hernandez, L.A.; Barranco-Jimenez, M.A.; Angulo-Brown, F. Comparative analysis of two ecological type modes of performance for a simple energy converter. J. Energy Inst. 2009, 82, 223–227. [Google Scholar] [CrossRef]
- Angulo-Brown, F.; Fernandez-Betanzos, J.; Diaz-Pico, C.A. Compression ratio of an optimized Otto cycle model. Eur. J. Phys. 1994, 15, 38–42. [Google Scholar] [CrossRef]
- Ust, Y.; Safa, A.; Sahin, B. Ecological performance analysis of an endoreversible regenerative Brayton heat-engine. Appl. Energy 2005, 80, 247–260. [Google Scholar] [CrossRef]
- Ust, Y.; Sahin, B.; Kodal, A. Ecological coefficient of performance (ECOP) optimization for generalized irreversible Carnot heat engines. J. Energy Inst. 2005, 78, 145–151. [Google Scholar] [CrossRef]
- Barranco-Jiménez, M.A.; Angulo-Brown, F. Thermoeconomic optimisation of endoreversible heat engine under maximum modified ecological criterion. J. Energy Inst. 2007, 80, 232–238. [Google Scholar] [CrossRef]
- Moscato, A.L.S.; del Rio Oliveira, S. Net power optimization of an irreversible Otto cycle using ECOP and ecological function. Int. Rev. Mech. Eng. 2015, 9, 1970–8734. [Google Scholar] [CrossRef]
- Gonca, G.; Sahin, B. Performance optimization of an air-standard irreversible Dual-Atkinson cycle engine based on the ecological coefficient of performance criterion. Sci. World J. 2014, 2014, 815787. [Google Scholar] [CrossRef] [PubMed]
- Long, R.; Liu, W. Ecological optimization for general heat engines. Phys. A Stat. Mech. Appl. 2015, 434, 232–239. [Google Scholar] [CrossRef]
- Chen, L.G.; Zhang, W.L.; Sun, F.R. Power, efficiency, entropy-generation rate and ecological optimization for a class of generalized irreversible universal heat-engine cycles. Appl. Energy 2007, 84, 512–525. [Google Scholar] [CrossRef]
- Ge, Y.L. Finite Time Thermodynamic Analysis and Optimization for Irreversible Internal Combustion Engine Cycles. Ph.D. Thesis, Naval University of Engineering, Wuhan, China, 2011. (In Chinese). [Google Scholar]
- Chen, L.G.; Zhu, X.Q.; Sun, F.R.; Wu, C. Ecological optimization for generalized irreversible Carnot refrigerators. J. Phys. D Appl. Phys. 2005, 38, 113–118. [Google Scholar] [CrossRef]
- Wu, X.H.; Chen, L.G.; Sun, F.R. Local stability of a non-endoreversible Carnot refrigerator working at the maximum ecological function. Appl. Math. Model. 2015, 39, 1689–1700. [Google Scholar] [CrossRef]
- Long, R.; Liu, W. Ecological optimization and coefficient of performance bounds of general refrigerators. Phys. A Stat. Mech. Appl. 2016, 443, 14–21. [Google Scholar] [CrossRef]
- Liu, X.W.; Chen, L.G.; Wu, F.; Sun, F.R. Ecological optimization of an irreversible quantum Carnot heat engine with spin-1/2 systems. Phys. Scripta 2010, 81, 025003. [Google Scholar] [CrossRef]
- Chen, L.G.; Kan, X.X.; Sun, F.R.; Wu, F.; Guo, F.Z. Ecological performance optimization of a thermoacoustic heat engine. Rev. Mex. Fis. 2010, 56, 386–393. [Google Scholar]
- Chen, L.G.; Xia, D.; Sun, F.R. Ecological optimization of generalized irreversible chemical engines. Int. J. Chem. React. Eng. 2010. [Google Scholar] [CrossRef]
- Wang, H.; Wu, G.X. Ecological optimization for generalized irreversible macro/nano thermosize engine. J. Appl. Phys. 2013, 113, 054309. [Google Scholar] [CrossRef]
- Ma, K.; Chen, L.G.; Sun, F.R. Ecological performance improved by controlling piston motion: Linear phenomenological system bimolecular, light-driven engine. J. Energy Inst. 2013, 86, 210–219. [Google Scholar] [CrossRef]
- Zhou, J.L.; Chen, L.G.; Ding, Z.M.; Sun, F.R. Analysis and optimization with ecological objective function of irreversible single resonance energy selective electron heat engines. Energy 2016, 111, 306–312. [Google Scholar] [CrossRef]
- Long, R.; Li, B.D.; Liu, Z.C.; Liu, W. Ecological analysis of a thermally regenerative electro-chemical cycle. Energy 2016, 107, 95–102. [Google Scholar] [CrossRef]
- Ramírez-Moreno, M.A.; Angulo-Brown, F. Ecological optimization of a family of n-Müser engines for an arbitrary value of the solar concentration factor. Phys. A Stat. Mech. Appl. 2017, 469, 250–255. [Google Scholar] [CrossRef]
- Qin, X.Y.; Chen, L.G.; Sun, F.R. The universal power and efficiency characteristics for irreversible reciprocating heat engine cycles. Eur. J. Phys. 2003, 24, 359–366. [Google Scholar] [CrossRef]
- Ge, Y.L.; Chen, L.G.; Sun, F.R. Reciprocating heat-engine cycles. Appl. Energy 2005, 81, 397–408. [Google Scholar] [CrossRef]
- Agrawal, D.C.; Menon, V.J. Power of a finite speed Carnot engine. Eur. J. Phys. 2009, 30, 295–301. [Google Scholar] [CrossRef]
- Agrawal, D.C. A finite speed Curzon-Ahlborn engine. Eur. J. Phys. 2009, 30, 587–593. [Google Scholar] [CrossRef]
- Petrescu, S.; Cristea, A.F.; Boriaru, N.; Costea, M. Optimization of the irreversible Otto cycle using finite speed thermodynamics and the direct method. In Proceedings of the 10th WSEAS International Conference on Mathematical and Computational Methods Science and Engineering (MACMESE’08), Computers and Simulation in Modern Science, Bucharest, Romania, 7–9 November 2008; Volume 2, pp. 51–56. [Google Scholar]
- Petrescu, S.; Boriaru, N.; Costea, M. Optimization of the irreversible Diesel cycle using finite speed thermodynamics and the direct method. Eng. Sci. 2009, 2, 87–94. [Google Scholar]
- Petrescu, S.; Harman, C.; Bejan, A.; Costea, M.; Dobre, C. Carnot cycle with external and internal irreversibilities analyzed in thermodynamics with finite speed with the direct method. Rev. Termotehnica 2012, 2, 7–17. [Google Scholar]
- Petrescu, S.; Harman, C.; Petre, C.; Costea, M. Irreversibility generation analysis of reversed cycle Carnot machine by using the finite speed thermodynamics. Rev. Termotehnica 2009, 2, 43–48. [Google Scholar]
- Petrescu, S.; Costea, M. Development of Thermodynamics with Finite Speed and Direct Method; Editura AGIR: Bucuresti, Romania, 2012. [Google Scholar]
- Petrescu, S. Thermodynamics with Finite Speed and Thermodynamics in Finite Time; Editura AGIR: Bucuresti, Romania, 2015. [Google Scholar]
- Petrescu, S.; Feidt, M.; Enache, V.; Costea, M.; Stanciu, C.; Boriaru, N. Unification perspective of finite physical dimensions thermodynamics and finite speed thermodynamics. Int. J. Energy Environ. Eng. 2015, 6, 245–254. [Google Scholar] [CrossRef]
- Yang, B.; Chen, L.G.; Sun, F.R. Performance analysis and optimization for an endreversible Carnot heat pump cycle with finite speed of the piston. Int. J. Energy Environ. 2011, 2, 1133–1140. [Google Scholar]
- Feng, H.J.; Chen, L.G.; Sun, F.R. Optimal ratios of the piston speeds for a finite speed endoreversible Carnot heat engine cycle. Rev. Mex. Fis. 2010, 56, 135–140. [Google Scholar]
- Feng, H.J.; Chen, L.G.; Sun, F.R. Optimal ratios of the piston speeds for a finite speed irreversible Carnot heat engine cycle. Int. J. Sustain. Energy 2011, 56, 321–335. [Google Scholar] [CrossRef]
- Chen, L.G.; Feng, H.J.; Sun, F.R. Optimal piston speed ratio analyses for irreversible Carnot refrigerator and heat pump using finite time thermodynamics, finite speed thermodynamics and direct method. J. Energy Inst. 2011, 84, 105–112. [Google Scholar] [CrossRef]
- Hosseinzade, H.; Sayyaadi, H.; Babaelahi, M. A new closed-form analytical thermal model for simulating Stirling engines based on polytropic-finite speed thermodynamics. Energy Convers. Manag. 2015, 90, 395–408. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ahmadi, M.A.; Pourfayaz, F.; Bidi, M.; Hosseinzade, H.; Feidt, M. Optimization of powered Stirling heat engine with finite speed thermodynamics. Energy Convers. Manag. 2016, 108, 96–105. [Google Scholar] [CrossRef]
- Gonca, G.; Sahin, B.; Ust, Y. Performance maps for an air-standard irreversible Dual-Miller cycle (DMC) with late inlet valve closing (LIVC) version. Energy 2013, 54, 285–290. [Google Scholar] [CrossRef]
- Ust, Y.; Arslan, F.; Ozsari, I.; Cakir, M. Thermodynamic performance analysis and optimization of DMC (Dual Miller Cycle) cogeneration system by considering exergetic performance coefficient and total exergy output criteria. Energy 2015, 90, 552–559. [Google Scholar] [CrossRef]
- Gonca, G.; Sahin, B.; Ust, Y. Investigation of heat transfer influences on performance of air-standard irreversible Dual-Miller cycle. J. Thermophys. Heat Transf. 2015, 29, 678–683. [Google Scholar] [CrossRef]
- Gonca, G. Comparative performance analyses of irreversible OMCE (Otto Miller cycle engine)-DiMCE (Diesel Miller cycle engine)-DMCE (Dual Miller cycle engine). Energy 2016, 109, 152–159. [Google Scholar] [CrossRef]
- Gonca, G.; Sahin, B. Thermo-ecological performance analyses and optimizations of irreversible gas cycle engines. Appl. Therm. Eng. 2016, 105, 566–576. [Google Scholar] [CrossRef]
- Wu, Z.X.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Optimization of the power, efficiency and ecological function for an air-standard irreversible Dual-Miller cycle. Front. Energy 2018, in press. [Google Scholar]
- Wu, Z.X.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Thermodynamic optimization for an air-standard irreversible Dual-Miller cycle with linearly variable specific heat ratio of working fluid. Int. J. Heat Mass Transf. 2018, in press. [Google Scholar]
- Wu, Z.X.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Power, efficiency, ecological function and ecological coefficient of performance of an irreversible Dual-Miller cycle (DMC) with nonlinear variable specific heat ratio of working fluid. Eur. Phys. J. Plus 2017, 132, 203. [Google Scholar] [CrossRef]
- You, J.; Chen, L.G.; Wu, Z.X.; Sun, F.R. Thermodynamic performance of Dual-Miller cycle (DMC) with polytropic processes based on power output, thermal efficiency and ecological function. Sci. China Tech. Sci. 2018, 61. [Google Scholar] [CrossRef]
- Arias-Hernández, L.A.; Angulo-Brown, F. Reply to Comment on A general property of endoreversible thermal engines. J. Appl. Phys. 2001, 89, 1520–1523. [Google Scholar]
- Barranco-Jiménez, M.A. Finite-time thermoeconomic optimization of a non endoreversible heat engine. Rev. Mex. Fis. 2009, 55, 211–220. [Google Scholar]
| Optimal Conditions | Power Output | Entropy Generation Rate |
|---|---|---|
| 2.63 × 10−3 | 3.013 × 10−6 | |
| 3.51 × 10−3 | 1.222 × 10−5 | |
| ratio | 74.9% | 24.7% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Chen, L.; Feng, H. Thermodynamic Optimization for an Endoreversible Dual-Miller Cycle (DMC) with Finite Speed of Piston. Entropy 2018, 20, 165. https://doi.org/10.3390/e20030165
Wu Z, Chen L, Feng H. Thermodynamic Optimization for an Endoreversible Dual-Miller Cycle (DMC) with Finite Speed of Piston. Entropy. 2018; 20(3):165. https://doi.org/10.3390/e20030165
Chicago/Turabian StyleWu, Zhixiang, Lingen Chen, and Huijun Feng. 2018. "Thermodynamic Optimization for an Endoreversible Dual-Miller Cycle (DMC) with Finite Speed of Piston" Entropy 20, no. 3: 165. https://doi.org/10.3390/e20030165
APA StyleWu, Z., Chen, L., & Feng, H. (2018). Thermodynamic Optimization for an Endoreversible Dual-Miller Cycle (DMC) with Finite Speed of Piston. Entropy, 20(3), 165. https://doi.org/10.3390/e20030165





