Information Thermodynamics Derives the Entropy Current of Cell Signal Transduction as a Model of a Binary Coding System
Abstract
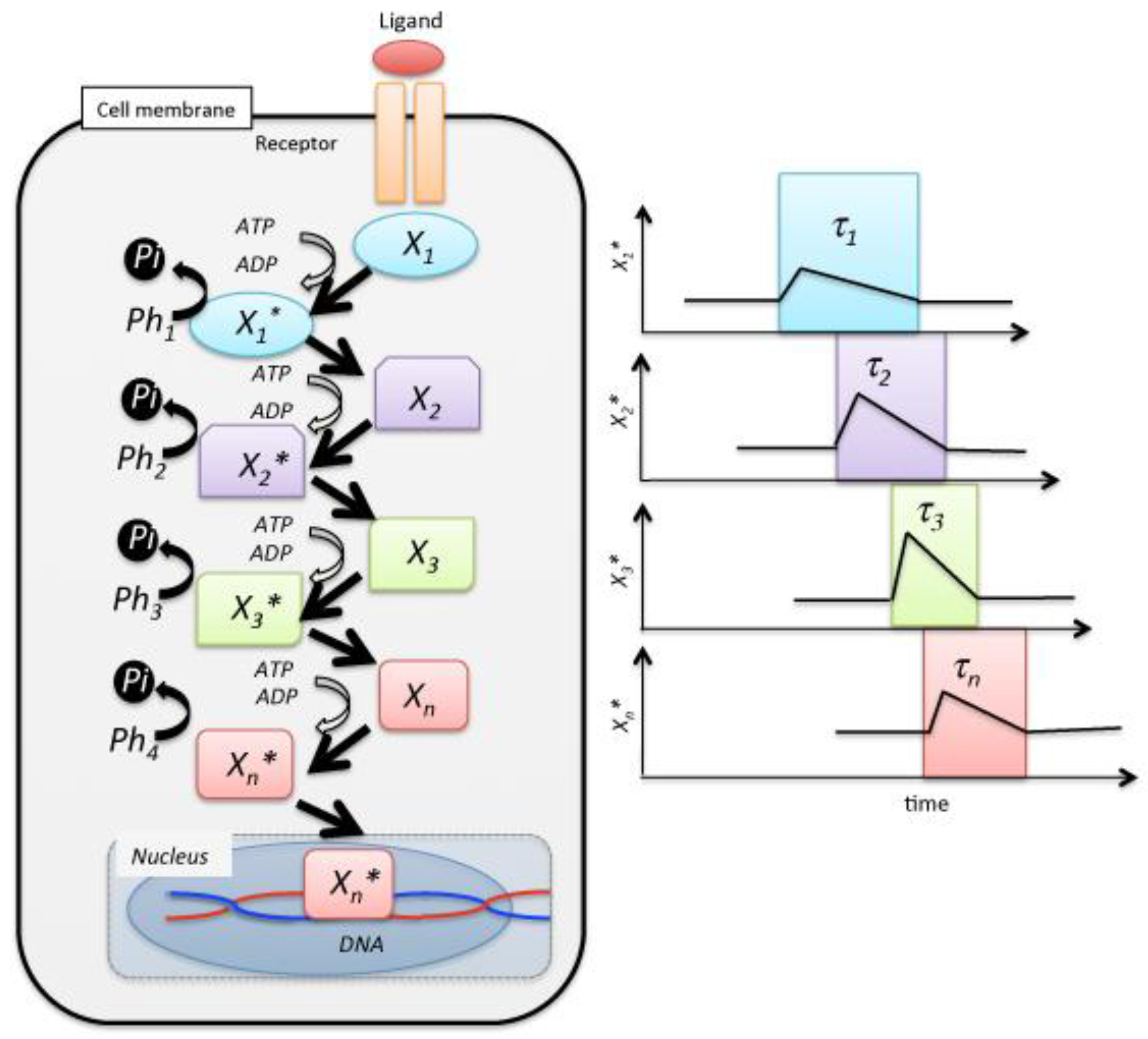
1. Introduction
2. Mixing Entropy in Signal Transduction
3. Entropy Current and Signal Transduction
4. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A
References
- Selimkhanov, J.; Taylor, B.; Yao, J.; Pilko, A.; Albeck, J.; Hoffmann, A.; Tsimring, L.; Wollman, R. Systems biology. Accurate information transmission through dynamic biochemical signaling networks. Science 2014, 346, 1370–1373. [Google Scholar] [CrossRef] [PubMed]
- Sagawa, T.; Kikuchi, Y.; Inoue, Y.; Takahashi, H.; Muraoka, T.; Kinbara, K.; Ishijima, A.; Fukuoka, H. Single-cell E. coli response to an instantaneously applied chemotactic signal. Biophys. J. 2014, 107, 730–739. [Google Scholar] [CrossRef] [PubMed]
- Cheong, R.; Rhee, A.; Wang, C.J.; Nemenman, I.; Levchenko, A. Information transduction capacity of noisy biochemical signaling networks. Science 2011, 334, 354–358. [Google Scholar] [CrossRef] [PubMed]
- Watters, N.; Reeke, G.N. Neuronal spike train entropy estimation by history clustering. Neural Comput. 2014, 26, 1840–1872. [Google Scholar] [CrossRef] [PubMed]
- Hanel, R.; Thurner, S.; Gell-Mann, M. How multiplicity determines entropy and the derivation of the maximum entropy principle for complex systems. Proc. Natl. Acad. Sci. USA 2014, 111, 6905–6910. [Google Scholar] [CrossRef] [PubMed]
- Teschendorff, A.E. Increased entropy of signal transduction in the cancer metastasis phenotype. BMC Syst. Biol. 2010, 4, e104. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.S.; Park, M.; Han, J.; Lee, J.H.; Bae, I.H.; Choi, H.; Son, E.D.; Park, Y.H.; Lim, K.M. Liver X receptor activation inhibits melanogenesis through the acceleration of ERK-mediated MITF degradation. J. Investig. Dermatol. 2013, 133, 1063–1071. [Google Scholar] [CrossRef] [PubMed]
- Mackeigan, J.P.; Murphy, L.O.; Dimitri, C.A.; Blenis, J. Graded mitogen-activated protein kinase activity precedes switch-like c-Fos induction in mammalian cells. Mol. Cell. Biol. 2005, 25, 4676–4682. [Google Scholar] [CrossRef] [PubMed]
- Newman, D.R.; Li, C.M.; Simmons, R.; Khosla, J.; Sannes, P.L. Heparin affects signaling pathways stimulated by fibroblast growth factor-1 and-2 in type II cells. Am. J. Physiol. Lung Cell. Mol. Physiol. 2004, 287, L191–L200. [Google Scholar] [CrossRef] [PubMed]
- Petropavlovskaia, M.; Daoud, J.; Zhu, J.; Moosavi, M.; Ding, J.; Makhlin, J.; Assouline-Thomas, B.; Rosenberg, L. Mechanisms of action of islet neogenesis-associated protein, comparison of the full-length recombinant protein and a bioactive peptide. Am. J. Physiol. Endocrinol. Metab. 2012, 303, E917–E927. [Google Scholar] [CrossRef] [PubMed]
- Tao, R.; Hoover, H.E.; Honbo, N.; Kalinowski, M.; Alano, C.C.; Karliner, J.S.; Raffai, R. High-density lipoprotein determines adult mouse cardiomyocyte fate after hypoxia-reoxygenation through lipoprotein-associated sphingosine 1-phosphate. Am. J. Physiol. Heart Circ. Physiol. 2010, 298, H1022–H1028. [Google Scholar] [CrossRef] [PubMed]
- Mina, M.; Magi, S.; Jurman, G.; Itoh, M.; Kawaji, H.; Lassmann, T.; Arner, E.; Forrest, A.R.R.; Carninci, P.; Hayashizaki, Y. Promoter-level expression clustering identifies time development of transcriptional regulatory cascades initiated by ErbB receptors in breast cancer cells. Sci. Rep. 2015, 5, 11999. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Ubl, J.J.; Stricker, R.; Reiser, G. Thrombin (PAR-1)-induced proliferation in astrocytes via MAPK involves multiple signaling pathways. Am. J. Physiol. Cell Physiol. 2002, 283, C1351–C1364. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.Y.; Liu, Y.; Ni, X.Y.; Bai, Z.H.; Chen, Q.Y.; Zhang, Y.; Gao, F.G. Nicotine promotes cell proliferation and induces resistance to cisplatin by alpha7 nicotinic acetylcholine receptormediated activation in Raw264.7 and El4 cells. Oncol. Rep. 2014, 31, 1480–1488. [Google Scholar] [CrossRef] [PubMed]
- Yeung, K.; Seitz, T.; Li, S.; Janosch, P.; McFerran, B.; Kaiser, C.; Fee, F.; Katsanakis, K.D.; Rose, D.W.; Mischak, H.; et al. Suppression of Raf-1 kinase activity and MAP kinase signalling by RKIP. Nature 1999, 401, 173–177. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.Z.; Yano, N.; Deng, M.; Mao, Q.; Shaw, S.K.; Tseng, Y.-T. β-Adrenergic Receptor-PI3K Signaling Crosstalk in Mouse Heart, Elucidation of Immediate Downstream Signaling Cascades. PLoS ONE 2011, 6, e26581. [Google Scholar] [CrossRef] [PubMed]
- Jung, P.; Menssen, A.; Mayr, D.; Hermeking, H. AP4 encodes a c-MYC-inducible repressor of p21. Proc. Natl. Acad. Sci. USA 2008, 105, 15046–15051. [Google Scholar] [CrossRef] [PubMed]
- Blossey, R.; Bodart, J.F.; Devys, A.; Goudon, T.; Lafitte, P. Signal propagation of the MAPK cascade in Xenopus oocytes, role of bistability and ultrasensitivity for a mixed proble. J. Math. Biol. 2012, 64, 1–39. [Google Scholar] [CrossRef] [PubMed]
- Hollenberg, M.D. PARs in the stars, proteinase-activated receptors and astrocyte function. Focus on “Thrombin (PAR-1)-induced proliferation in astrocytes via MAPK involves multiple signaling pathways’. Am. J. Physiol. Cell Physiol. 2002, 283, C1347–C1350. [Google Scholar] [CrossRef] [PubMed]
- Purutçuoğlu, V.; Wit, E. Estimating Network Kinetics of the MAPK/ERK Pathway Using Biochemical Data. Math. Probl. Eng. 2012, 2012, 1–34. [Google Scholar] [CrossRef]
- Qiao, L.; Nachbar, R.B.; Kevrekidis, I.G.; Shvartsman, S.Y. Bistability and oscillations in the Huang-Ferrell model of MAPK signaling. PLoS Comput. Biol. 2007, 3, 1819–1826. [Google Scholar] [CrossRef] [PubMed]
- Xin, X.; Zhou, L.; Reyes, C.M.; Liu, F.; Dong, L.Q. APPL1 mediates adiponectin-stimulated p38 MAPK activation by scaffolding the TAK1-MKK3-p38 MAPK pathway. Am. J. Physiol. Endocrinol. Metab. 2011, 300, E103–E110. [Google Scholar] [CrossRef] [PubMed]
- Yoon, J.; Deisboeck, T.S. Investigating differential dynamics of the MAPK signaling cascade using a multi-parametric global sensitivity analysis. PLoS ONE 2009, 4, e4560. [Google Scholar] [CrossRef] [PubMed]
- Zumsande, M.; Gross, T. Bifurcations and chaos in the MAPK signaling cascade. J. Theor. Biol. 2010, 265, 481–491. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, K.L.; Hayakawa, H. Geometric fluctuation theorem for a spin-boson system. Phys. Rev. E 2017, 96, 022118. [Google Scholar] [CrossRef] [PubMed]
- Tsuruyama, T. Channel Capacity of Coding System on Tsallis Entropy and q-Statistics. Entropy 2017, 19, 682. [Google Scholar] [CrossRef]
- Brillouin, L. Science and Information Theory, 2nd ed.; Dover Publication Inc.: New York, NY, USA, 2013. [Google Scholar]
- Andrieux, D.; Gaspard, P. Fluctuation theorem and Onsager reciprocity relations. J. Chem. Phys. 2004, 121, 6167–6174, Erratum in: J. Chem. Phys. 2006, 125, 219902. [Google Scholar] [CrossRef] [PubMed]
- Andrieux, D.; Gaspard, P. Fluctuation theorem and mesoscopic chemical clocks. J. Chem. Phys. 2008, 128, 154506. [Google Scholar] [CrossRef] [PubMed]
- Gaspard, P. Fluctuation theorem for nonequilibrium reactions. J. Chem. Phys. 2004, 120, 8898–8905. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsuruyama, T. Information Thermodynamics Derives the Entropy Current of Cell Signal Transduction as a Model of a Binary Coding System. Entropy 2018, 20, 145. https://doi.org/10.3390/e20020145
Tsuruyama T. Information Thermodynamics Derives the Entropy Current of Cell Signal Transduction as a Model of a Binary Coding System. Entropy. 2018; 20(2):145. https://doi.org/10.3390/e20020145
Chicago/Turabian StyleTsuruyama, Tatsuaki. 2018. "Information Thermodynamics Derives the Entropy Current of Cell Signal Transduction as a Model of a Binary Coding System" Entropy 20, no. 2: 145. https://doi.org/10.3390/e20020145
APA StyleTsuruyama, T. (2018). Information Thermodynamics Derives the Entropy Current of Cell Signal Transduction as a Model of a Binary Coding System. Entropy, 20(2), 145. https://doi.org/10.3390/e20020145



