A Simple and Adaptive Dispersion Regression Model for Count Data
Abstract
:1. Introduction
2. Discrete Weibull Distribution
2.1. The Distribution
- The discrete Rayleigh distribution in [13] is a special case of a DW distribution with and .
- The geometric distribution is a special case of a DW distribution, with and . Moreover, for the geometric distribution, the variance is always greater than its mean. Therefore, a DW distribution with is a case of overdispersion relative to Poisson regression, regardless of the value of q. In particular, when and , the distribution is the discrete exponential distribution introduced by [14].
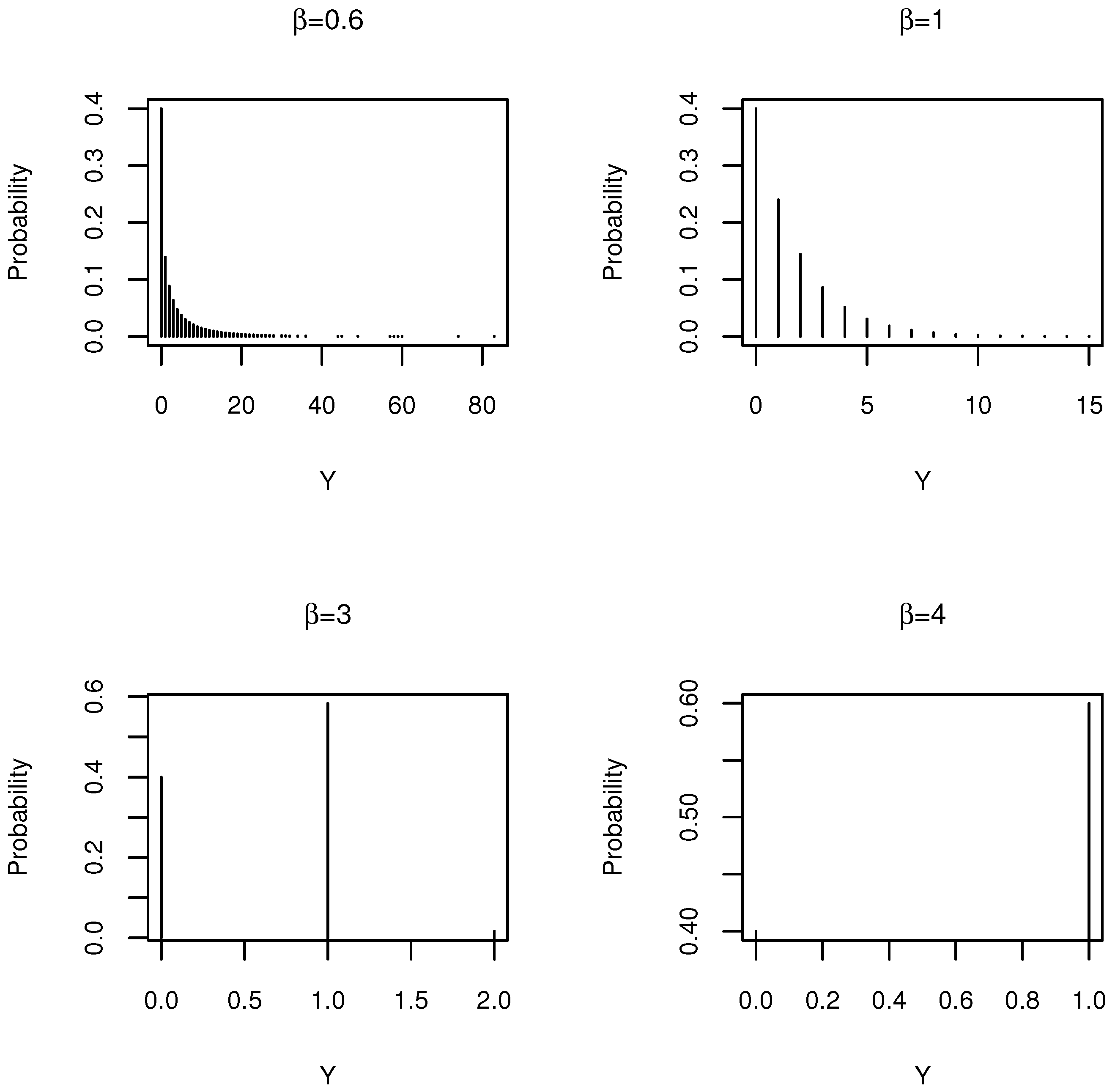
- can be considered as controlling the range of values of the variable. In other words, this parameter controls the skewness of the DW distribution. In order to show this, Figure 1 plots the probability mass functions for a fixed parameter q and different values of . The plot shows how the the probability of 0 stays constant, while the tail of the distribution becomes increasingly longer as , and the distribution approaches a Bernoulli distribution with probability q as .
2.2. Moments and Quantiles
2.3. Parameter Estimation
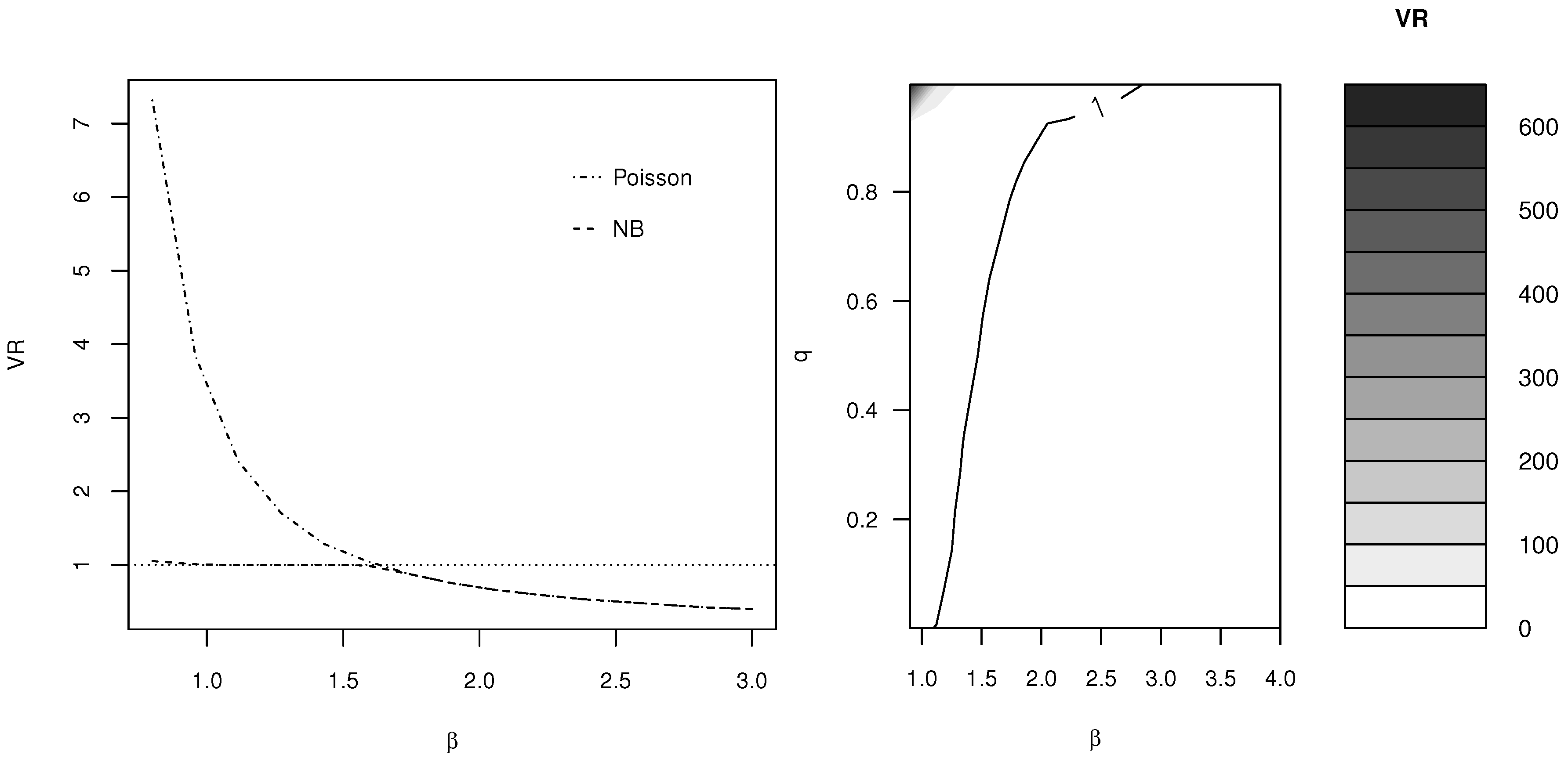
3. DW Accounts for Different Types of Dispersion
- is a case of overdispersion, regardless of the value of q.
- is a case of underdispersion, regardless of the value of q. In fact, the DW distribution approaches the Bernoulli distribution with mean p and variance for .
- leads to both cases of overdispersion and underdispersion depending on the value of q.
4. DW Regression Model
4.1. Model Formulation
4.2. Interpretation of the Regression Coefficients
- The fitted values for the central trend of the conditional distribution, namely, the following:
- -
- -
- Median: The quantile formula provided in Equation (5) can be applied. Because of the skewness, which is common for count data, the median is more appropriate than the mean. The fitted conditional median can be obtained easily from the closed-form expression of quantiles for DW regression, as
- The conditional quantile for any can be obtained from Equation (5).
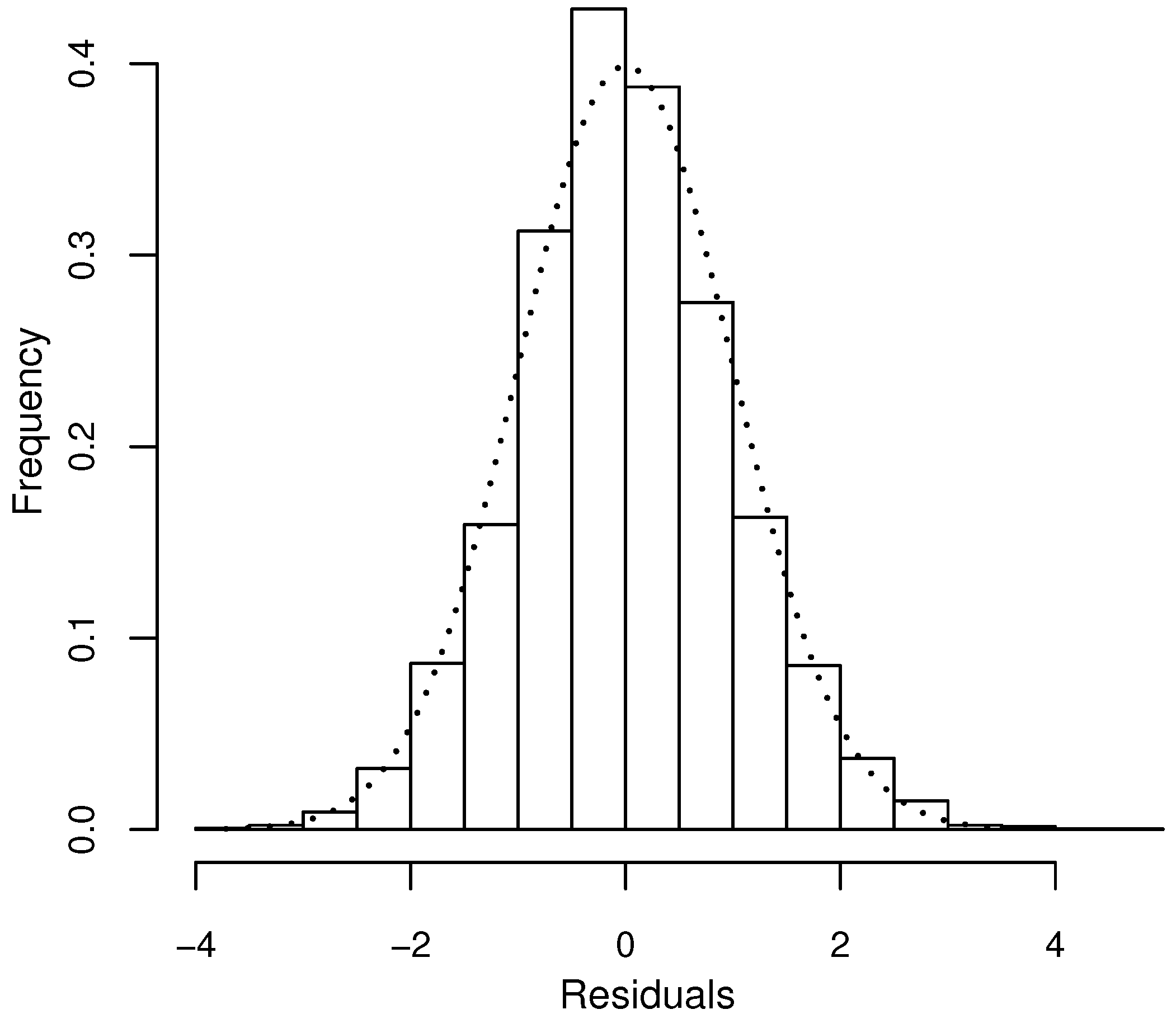
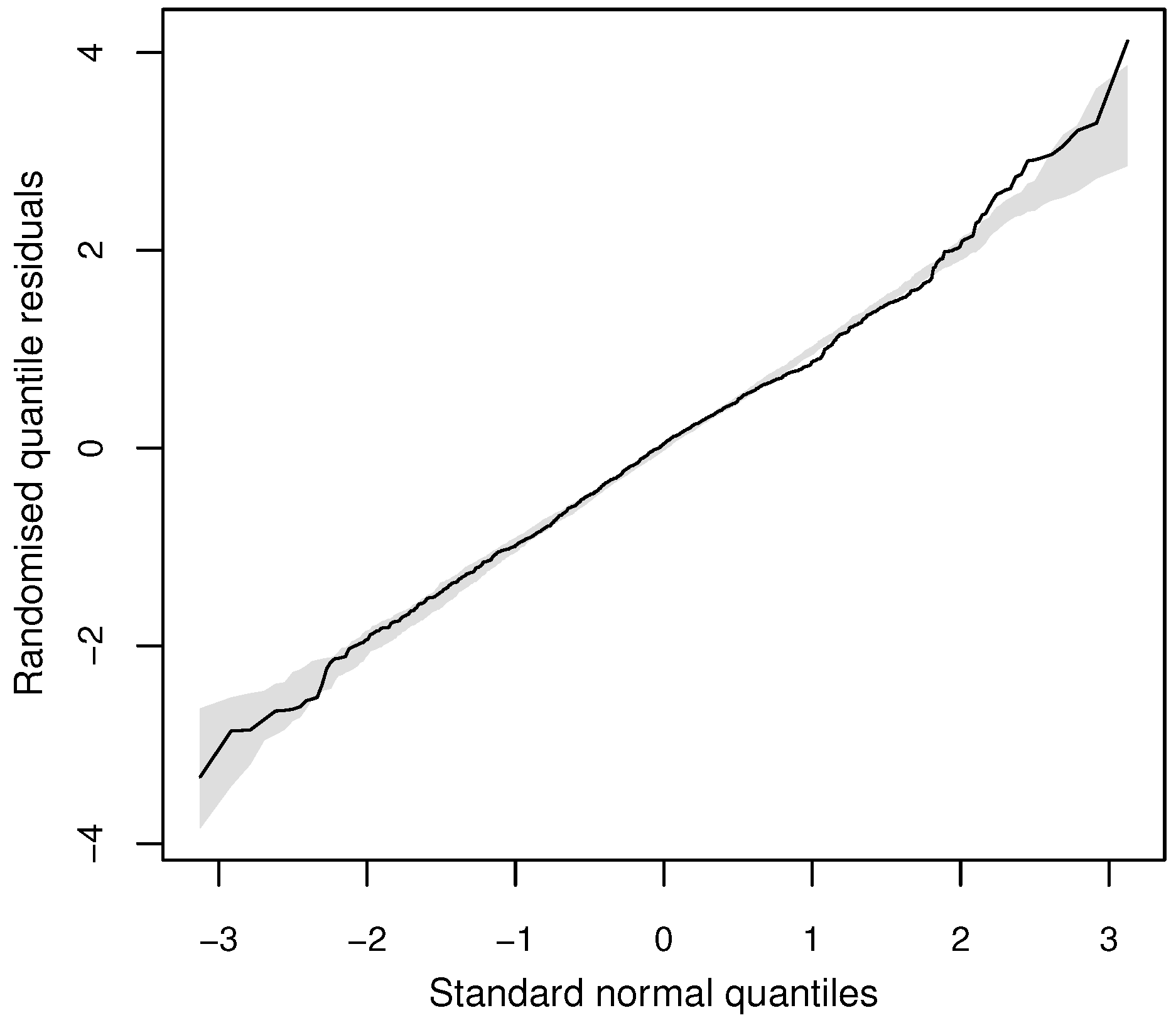
4.3. Diagnostics Checks
5. DW Regression Naturally Handles Covariate-Specific Dispersion
6. Application to Real Datasets
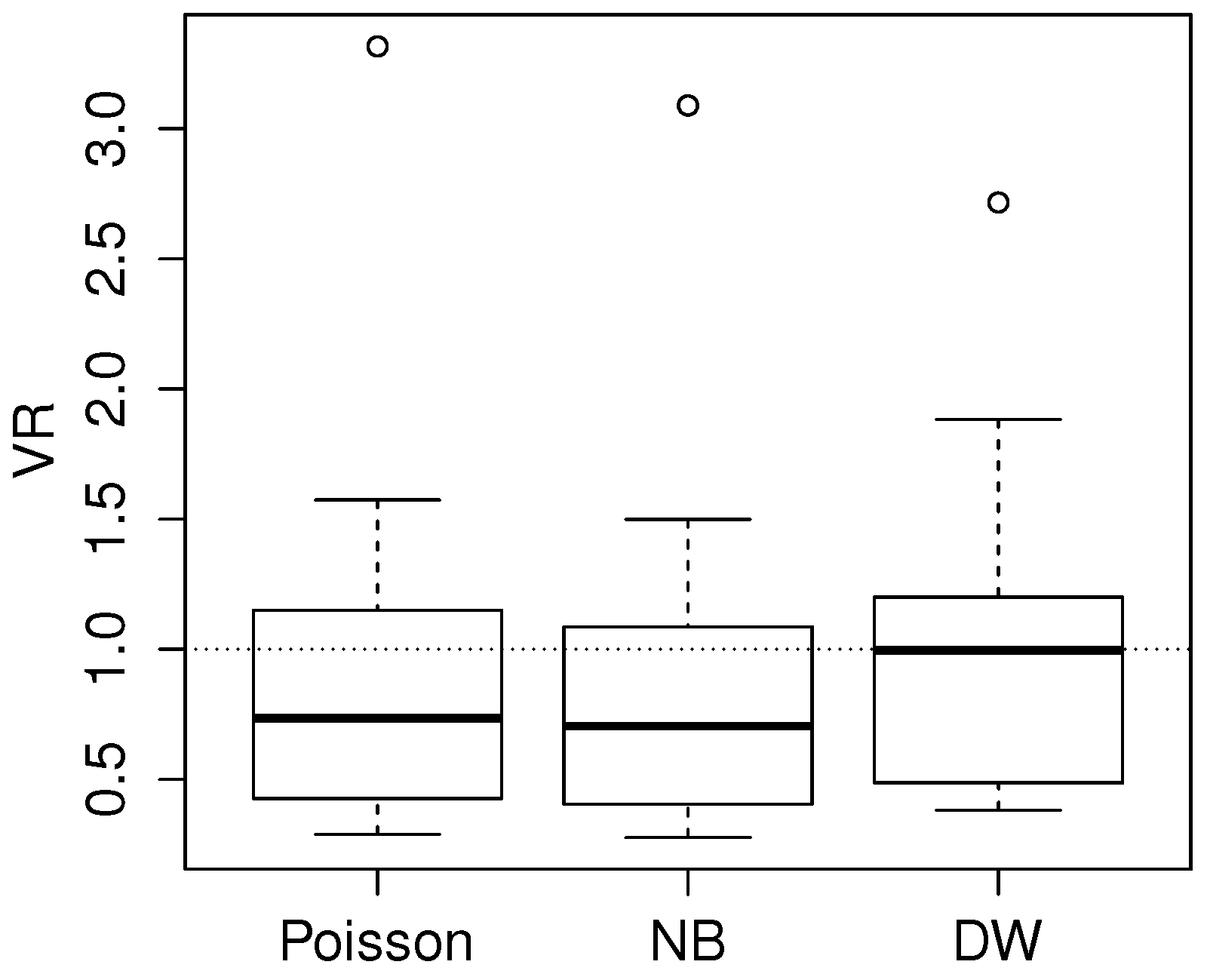
6.1. The Case of Underdispersion: Inhaler Usage Data
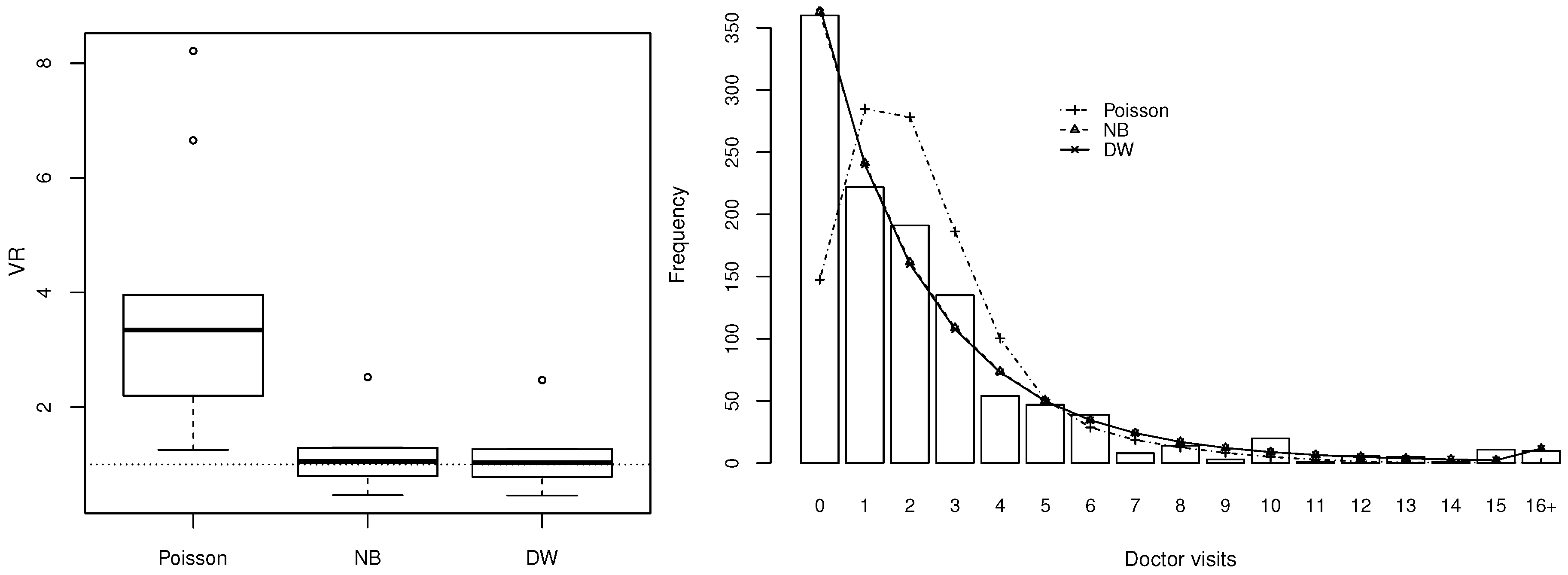
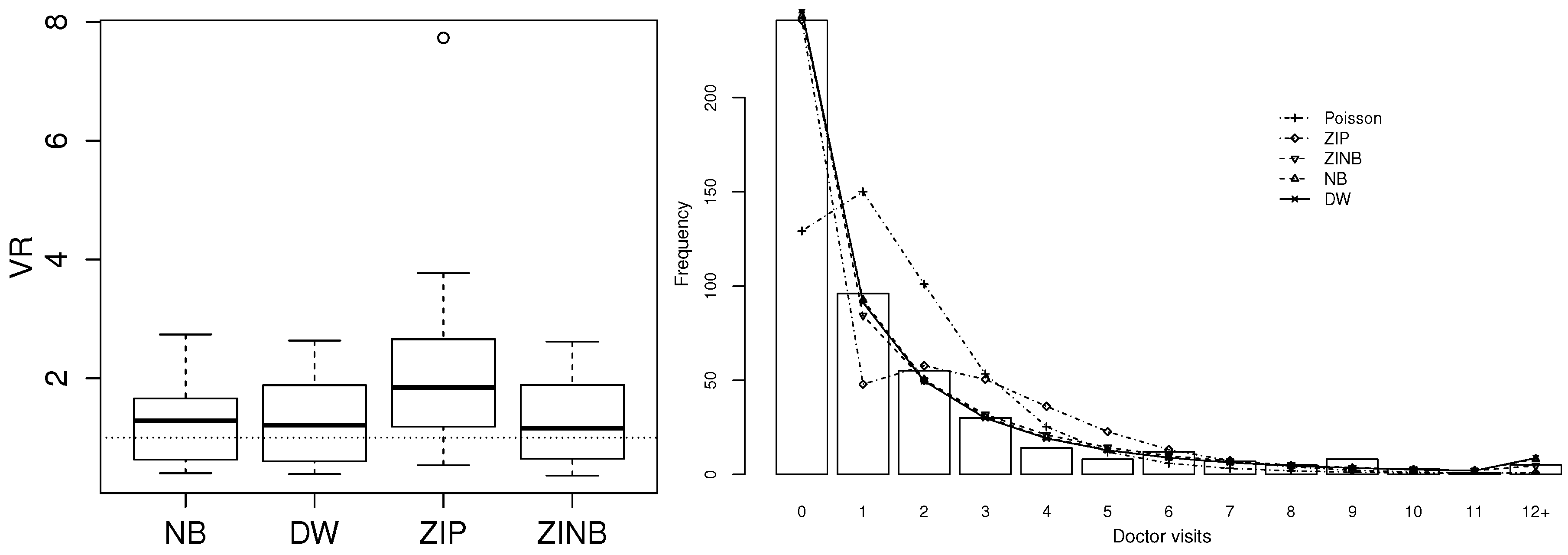
6.2. The Case of Overdispersion: Doctor Visits from German Health Survey Data
6.3. The Case of Excessive Zeros: Doctor Visits from the United States Data
6.4. The Case of a Mixed Level of Dispersion: Bids Data
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DW | Discrete Weibull |
| NB | Negative binomial |
| GP | Generalised Poisson |
| ZIP | Zero-inflated Poisson |
| ZINB | Zero-inflated negative binomial |
| HP | Hurdle Poisson |
| ZINB | Hurdle negative binomial |
| MSE | Mean-squared error |
| MLE | Maximum likelihood estimator |
| VR | Variance ratio |
| KS | Kolmogorov–Smirnov |
References
- Cameron, A.C.; Trivedi, P.K. Regression Analysis of Count Data; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Hilbe, J.M. Modeling Count Data; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Nelder, J.A.; Wedderburn, R.W. Generalized linear models. J. R. Stat. Soc. Ser. A 1972, 135, 370–384. [Google Scholar] [CrossRef]
- Efron, B. Double exponential families and their use in generalized linear regression. J. Am. Stat. Assoc. 1986, 81, 709–721. [Google Scholar] [CrossRef]
- Famoye, F. Restricted generalized Poisson regression model. Commun. Stat. Theory Methods 1993, 22, 1335–1354. [Google Scholar] [CrossRef]
- Sellers, K.F.; Shmueli, G. A flexible regression model for count data. Ann. Appl. Stat. 2010, 4, 943–961. [Google Scholar] [CrossRef]
- Sáez-Castillo, A.; Conde-Sánchez, A. A hyper-Poisson regression model for overdispersed and underdispersed count data. Comput. Stat. Data Anal. 2013, 61, 148–157. [Google Scholar] [CrossRef]
- Nakagawa, T.; Osaki, S. The discrete Weibull distribution. IEEE Trans. Reliab. 1975, 24, 300–301. [Google Scholar] [CrossRef]
- Khan, M.A.; Khalique, A.; Abouammoh, A. On estimating parameters in a discrete Weibull distribution. IEEE Trans. Reliab. 1989, 38, 348–350. [Google Scholar] [CrossRef]
- Kulasekera, K. Approximate MLE’s of the parameters of a discrete Weibull distribution with type I censored data. Microelectron. Reliab. 1994, 34, 1185–1188. [Google Scholar] [CrossRef]
- Englehardt, J.D.; Li, R. The discrete Weibull distribution: An alternative for correlated counts with confirmation for microbial counts in water. Risk Anal. 2011, 31, 370–381. [Google Scholar] [CrossRef] [PubMed]
- Englehardt, J.D.; Ashbolt, N.J.; Loewenstine, C.; Gadzinski, E.R.; Ayenu-Prah, A.Y. Methods for assessing long-term mean pathogen count in drinking water and risk management implications. J. Water Health 2012, 10, 197–208. [Google Scholar] [CrossRef] [PubMed]
- Roy, D. Discrete Rayleigh distribution. IEEE Trans. Reliab. 2004, 53, 255–260. [Google Scholar] [CrossRef]
- Sato, H.; Ikota, M.; Sugimoto, A.; Masuda, H. A new defect distribution metrology with a consistent discrete exponential formula and its applications. IEEE Trans. Semicond. Manuf. 1999, 12, 409–418. [Google Scholar] [CrossRef]
- Barbiero, A. DiscreteWeibull: Discrete Weibull Distributions (Type 1 and 3), 2015. R Package Version 1.0.1. Available online: https://cran.r-project.org/web/packages/DiscreteWeibull/index.html (accessed on 17 February 2018).
- Da Silva, M.F.; Ferrari, S.L.; Cribari-Neto, F. Improved likelihood inference for the shape parameter in Weibull regression. J. Stat. Comput. Simul. 2008, 78, 789–811. [Google Scholar] [CrossRef]
- Lee, E.T.; Wang, J. Statistical Methods for Survival Data Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Dunn, P.K.; Smyth, G.K. Randomized quantile residuals. J. Comput. Graph. Stat. 1996, 5, 236–244. [Google Scholar]
- Ospina, R.; Ferrari, S.L. A general class of zero-or-one inflated beta regression models. Comput. Stat. Data Anal. 2012, 56, 1609–1623. [Google Scholar] [CrossRef]
- Vanegas, L.H.; Rondón, L.M.; Cordeiro, G.M. Diagnostic tools in generalized Weibull linear regression models. J. Stat. Comput. Simul. 2013, 83, 2315–2338. [Google Scholar] [CrossRef]
- Ferrari, S.; Cribari-Neto, F. Beta regression for modelling rates and proportions. J. Appl. Stat. 2004, 31, 799–815. [Google Scholar] [CrossRef]
- Garay, A.M.; Hashimoto, E.M.; Ortega, E.M.; Lachos, V.H. On estimation and influence diagnostics for zero-inflated negative binomial regression models. Comput. Stat. Data Anal. 2011, 55, 1304–1318. [Google Scholar] [CrossRef]
- Atkinson, A.C. Plots, Transformations, and Regression: An Introduction to Graphical Methods of Diagnostic Regression Analysis; Clarendon Press Oxford: Oxford, UK, 1985. [Google Scholar]
- Sellers, K.; Lotze, T. COMPoissonReg: Conway-Maxwell Poisson (COM-Poisson) Regression. 2011. R Package Version 0.3.4. Available online: https://mran.microsoft.com/snapshot/2014-11-09/web/packages/COMPoissonReg/index.html (accessed on 17 February 2018).
- Yee, T.W. The VGAM package for categorical data analysis. J. Stat. Softw. 2010, 32, 1–34. [Google Scholar] [CrossRef]
- Zeileis, A.; Kleiber, C.; Jackman, S. Regression Models for Count Data in R. J. Stat. Softw. 2008, 27. [Google Scholar] [CrossRef]
- Dayton, C.M. Model comparisons using information measures. J. Mod. Appl. Stat. Methods 2003, 2, 2. [Google Scholar] [CrossRef]
- Grunwald, G.K.; Bruce, S.L.; Jiang, L.; Strand, M.; Rabinovitch, N. A statistical model for under-or overdispersed clustered and longitudinal count data. Biom. J. 2011, 53, 578–594. [Google Scholar] [CrossRef] [PubMed]
- Hilbe, J.M. COUNT: Functions, Data and Code for Count Data. 2014. R Package Version 1.3.2. Available online: https://cran.r-project.org/web/packages/COUNT/index.html (accessed on 17 February 2018).
- Zeileis, A.; Hothorn, T. Diagnostic Checking in Regression Relationships. R News 2002, 2, 7–10. [Google Scholar]
- Cameron, A.C.; Johansson, P. Count data regression using series expansions: With applications. J. Appl. Econom. 1997, 12, 203–223. [Google Scholar] [CrossRef]
- DWreg: Parametric Regression for Discrete Response. Available online: https://cran.r-project.org/web/packages/DWreg/index.html (accessed on 17 February 2018).



| MLE | Bias | MSE | 95% CI Length | ||
|---|---|---|---|---|---|
| 0.6467 | 0.1467 | 0.2932 | 1.7324 | ||
| 0.4908 | 0.0908 | 0.0763 | 0.8821 | ||
| −0.3651 | −0.0651 | 0.0241 | 0.4694 | ||
| 2.5924 | 0.4924 | 0.8455 | 2.4718 | ||
| 0.5074 | 0.0074 | 0.009 | 0.3611 | ||
| 0.402 | 0.002 | 0.0021 | 0.1782 | ||
| −0.3033 | −0.0033 | 0.0004 | 0.0789 | ||
| 2.1196 | 0.0196 | 0.0086 | 0.3549 |
| Humidity | Pressure | Temperature | Particles | Other | AIC | BIC | |
|---|---|---|---|---|---|---|---|
| Poisson | −0.1125 | 4.0950 | −0.2035 | 0.0225 | — | 13915.47 | 13948.26 |
| NB | −0.1125 | 4.0950 | −0.2035 | 0.0225 | 13917.54 | 13956.89 | |
| COM–Poisson | −0.1724 | 6.2864 | −0.3128 | 0.0348 | 13450.77 | 13490.12 | |
| DW | −0.1050 | 2.6376 | −0.1735 | 0.0136 | 13484.36 | 13523.71 |
| Bad Health | Age | Other | AIC | BIC | |
|---|---|---|---|---|---|
| Poisson | 1.1083 | 0.0058 | — | 5638.552 | 5653.634 |
| NB | 1.1073 | 0.0070 | 4475.285 | 4495.394 | |
| DW | 1.0068 | 0.0120 | 4474.973 | 4495.083 |
| Children | Access | Health | Other | AIC | BIC | |
|---|---|---|---|---|---|---|
| Poisson | −0.1759 | 0.9369 | 0.2898 | — | 2179.487 | 2196.223 |
| NB | −0.1706 | 0.4197 | 0.3154 | 1581.88 | 1602.801 | |
| Zero-inflated models | ||||||
| Poisson | ||||||
| Count model | −0.1498 | 0.8053 | 0.1736 | — | 1885.813 | 1919.287 |
| Logit model | 0.0843 | −0.1048 | −0.4147 | — | ||
| NB | ||||||
| Count model | −0.1414 | 0.6491 | 0.2239 | 1578.5 | 1616.158 | |
| Logit model | 0.2465 | 1.2085 | −2.0676 | — | ||
| Hurdle models | ||||||
| Logit model | −0.1462 | 0.4252 | 0.4524 | — | — | — |
| Poisson count model | −0.1506 | 0.8143 | 0.1733 | — | 1885.808 | 1919.281 |
| NB count model | −0.1664 | 0.5404 | 0.2157 | 1576.302 | 1613.959 | |
| DW | −0.1309 | 0.3403 | 0.2758 | 1575.796 | 1596.717 |
| Price | Size | Regulator | Other | AIC | BIC | |
|---|---|---|---|---|---|---|
| Poisson | −0.7849 | 0.0362 | 0.0547 | — | 402.2602 | 413.6054 |
| NB | −0.7824 | 0.0369 | 0.0544 | 403.9481 | 418.1295 | |
| DW | −0.6761 | 0.0552 | 0.0293 | 395.1214 | 409.3028 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klakattawi, H.S.; Vinciotti, V.; Yu, K. A Simple and Adaptive Dispersion Regression Model for Count Data. Entropy 2018, 20, 142. https://doi.org/10.3390/e20020142
Klakattawi HS, Vinciotti V, Yu K. A Simple and Adaptive Dispersion Regression Model for Count Data. Entropy. 2018; 20(2):142. https://doi.org/10.3390/e20020142
Chicago/Turabian StyleKlakattawi, Hadeel S., Veronica Vinciotti, and Keming Yu. 2018. "A Simple and Adaptive Dispersion Regression Model for Count Data" Entropy 20, no. 2: 142. https://doi.org/10.3390/e20020142
APA StyleKlakattawi, H. S., Vinciotti, V., & Yu, K. (2018). A Simple and Adaptive Dispersion Regression Model for Count Data. Entropy, 20(2), 142. https://doi.org/10.3390/e20020142





