Coarse-Graining Approaches in Univariate Multiscale Sample and Dispersion Entropy
Abstract
1. Introduction
- The complexity of a biological or physiological time series indicates its ability to adapt and function in an ever-changing environment.
- A biological time series requires operating across multiple temporal and spatial scales and so its complexity is similarly multiscaled and hierarchical.
- A wide class of disease states, in addition to ageing, which decrease the adaptive capacity of the individual, appear to degrade the information carried by output variables.
2. Multiscale Entropy-Based Approaches
2.1. MDE Based on Moving Average (MA) and Butterworth (BW) Filters with and without Downsampling (DS)
2.1.1. Coarse-Graining Approaches
2.1.2. Calculation of DispEn or SampEn at Every Scale Factor
2.2. Refined Composite Multiscale Dispersion Entropy (RCMDE)
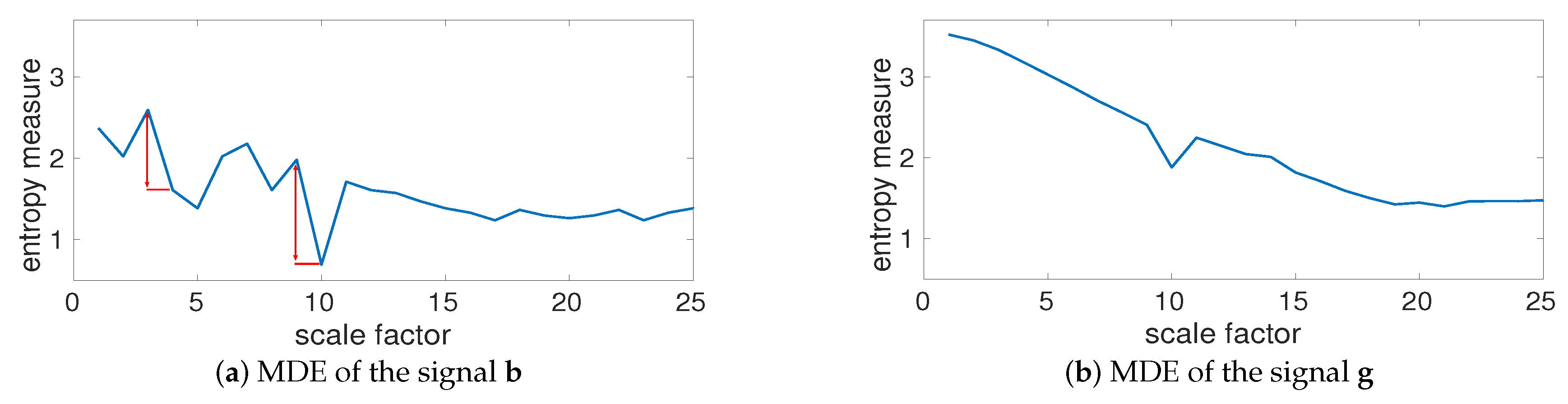
2.3. Intrinsic Mode Dispersion Entropy (InMDE)
- Calculation of the sum of the intrinsic mode functions (IMFs) obtained by EMD: In this step, the original signal u is decomposed to and a residual signal . It is worth noting that the first IMF, , shows the highest frequency component in a signal, while the last IMF, , reflects the trend of the time series. Next, the cumulative sums of IMFs (CSI) for each scale factor are defined as follows [15]:where denotes the IMF obtained by EMD. Thus, is equal to the original signal u.
- Calculation of DispEn of at each scale factor: The DispEn value is calculated at each scale factor. Like MDE and RCMDE, and of NCDF are respectively set at the average and SD of the original signal and they remain constant for all scale factors in InMDE.
2.4. Parameters of the Multiscale Entropy Approaches
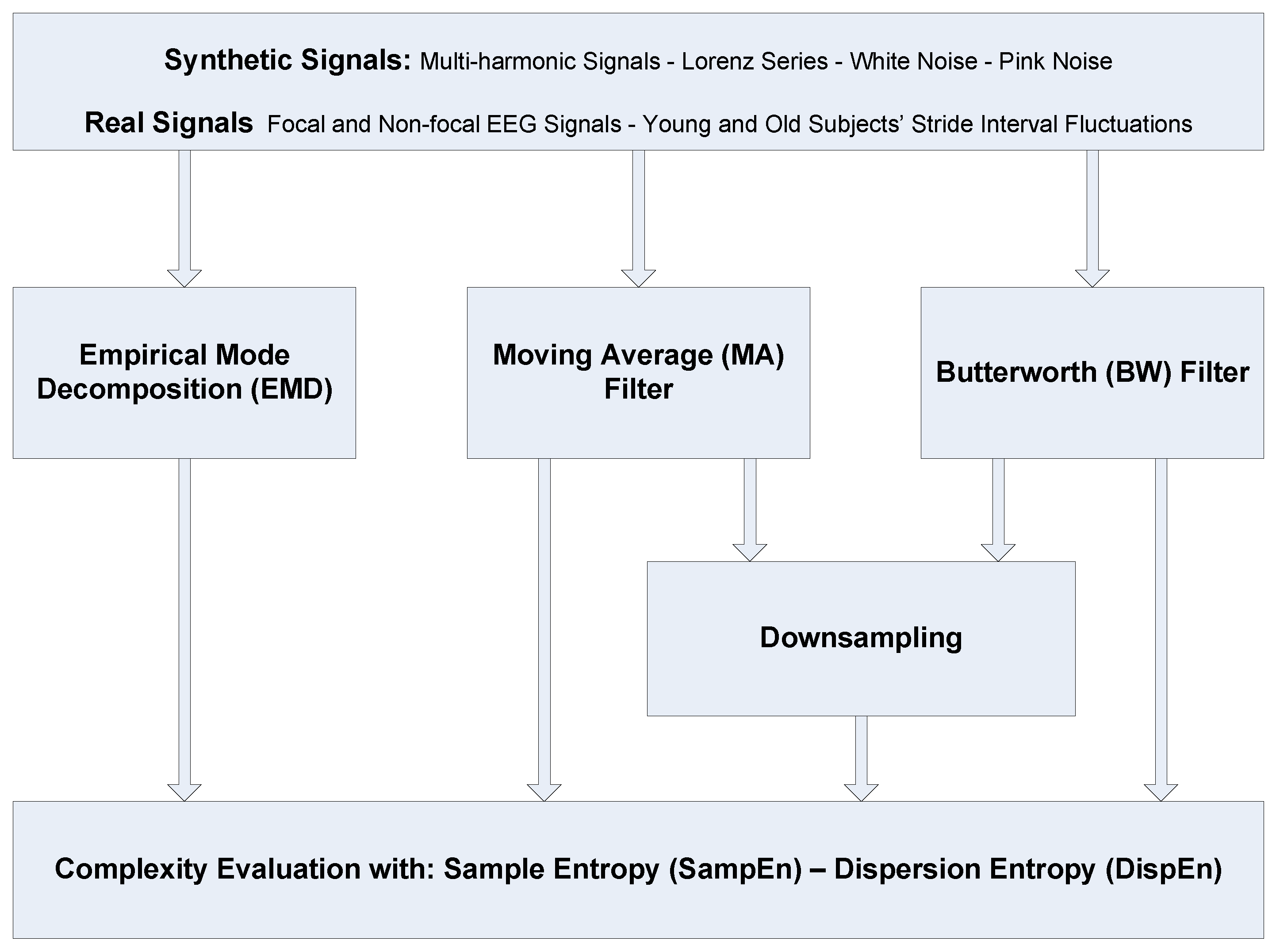
3. Evaluation Signals
3.1. Synthetic Signals
3.2. Real Biomedical Datasets
3.2.1. Dataset of Focal and Non-Focal Brain Activity
3.2.2. Dataset of Stride Internal Fluctuations
4. Results and Discussion
4.1. Synthetic Signals
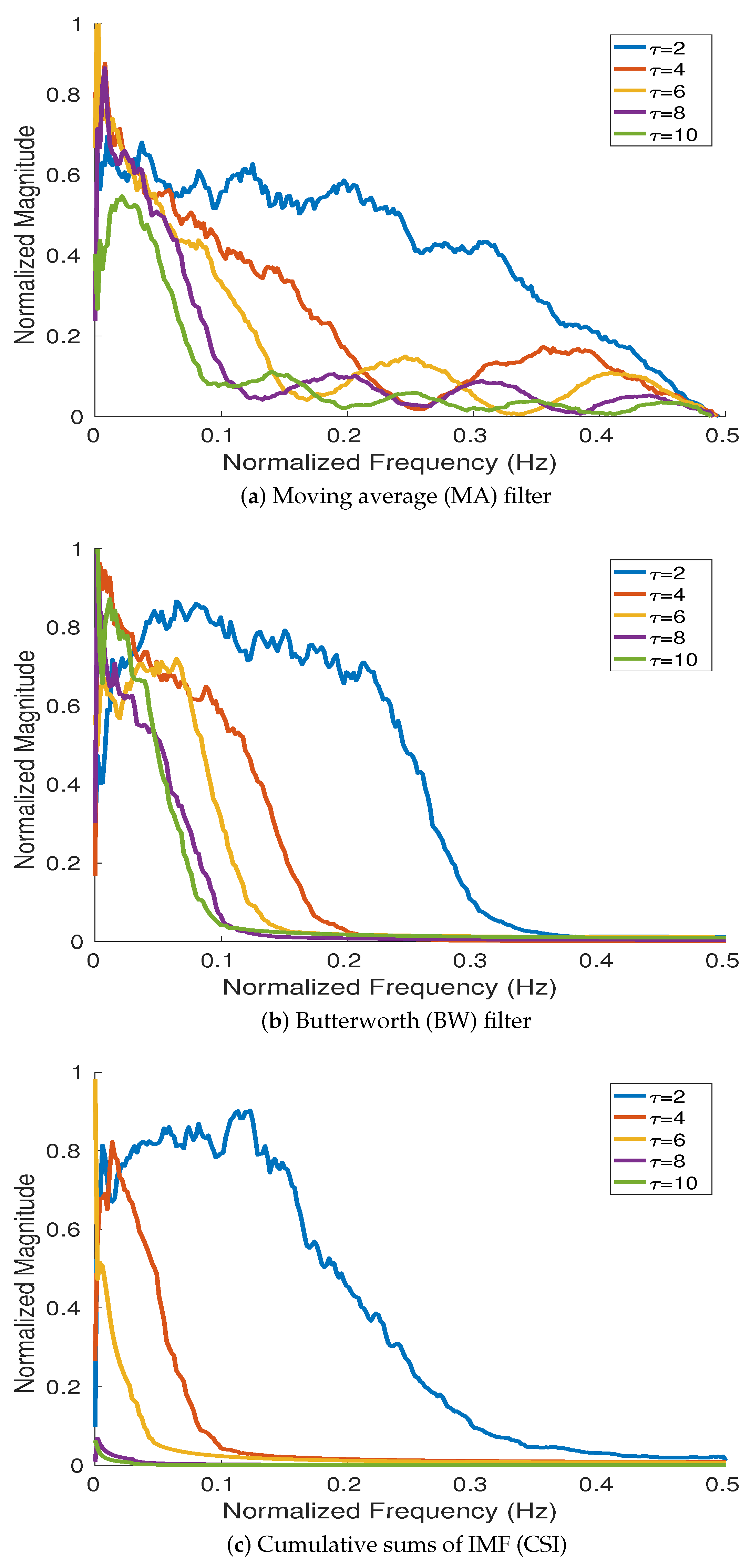
4.1.1. Frequency Responses of Cumulative Sums of IMFs (CSI), and Moving Average (MA) and Butterworth (BW) Filters
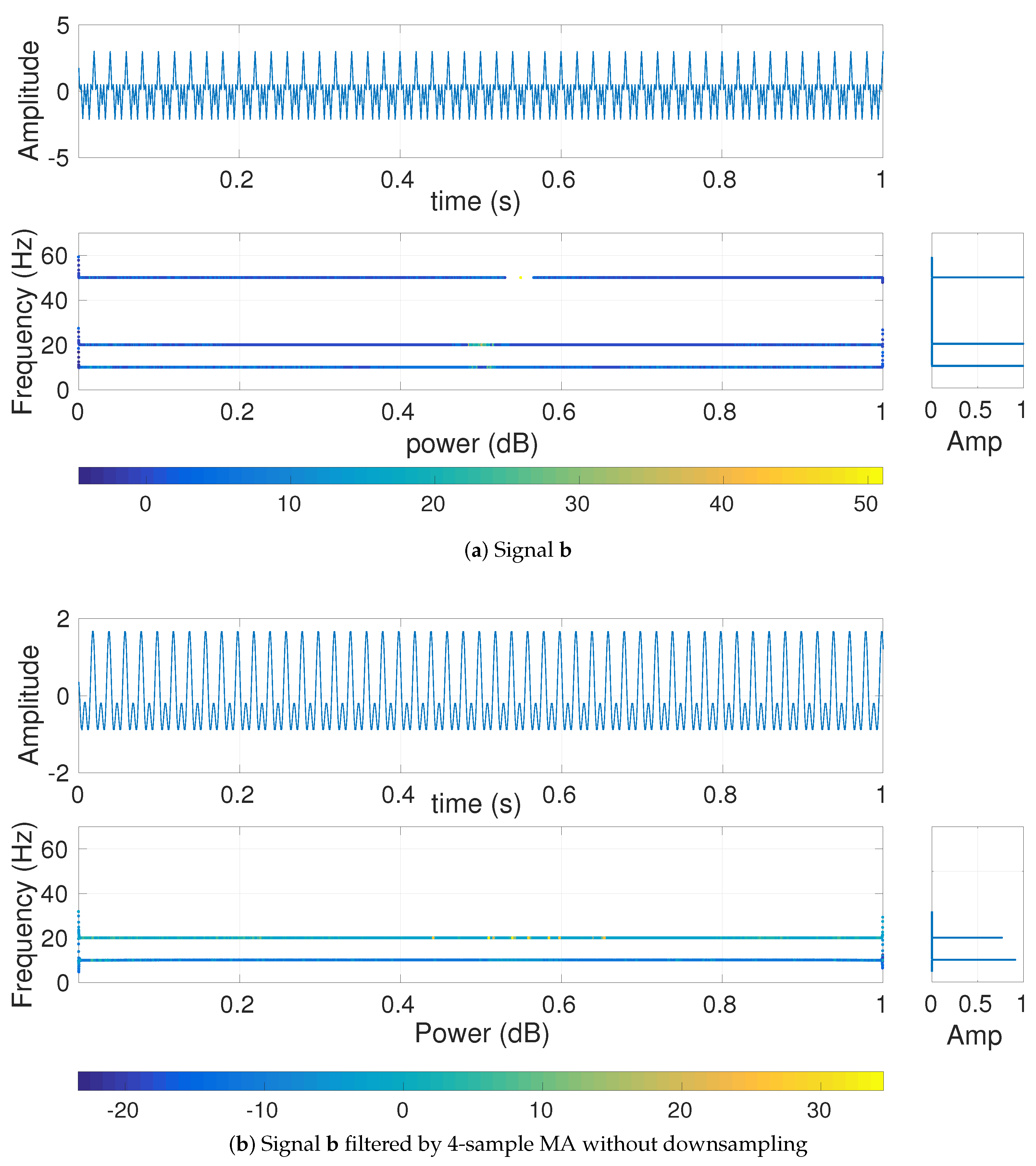
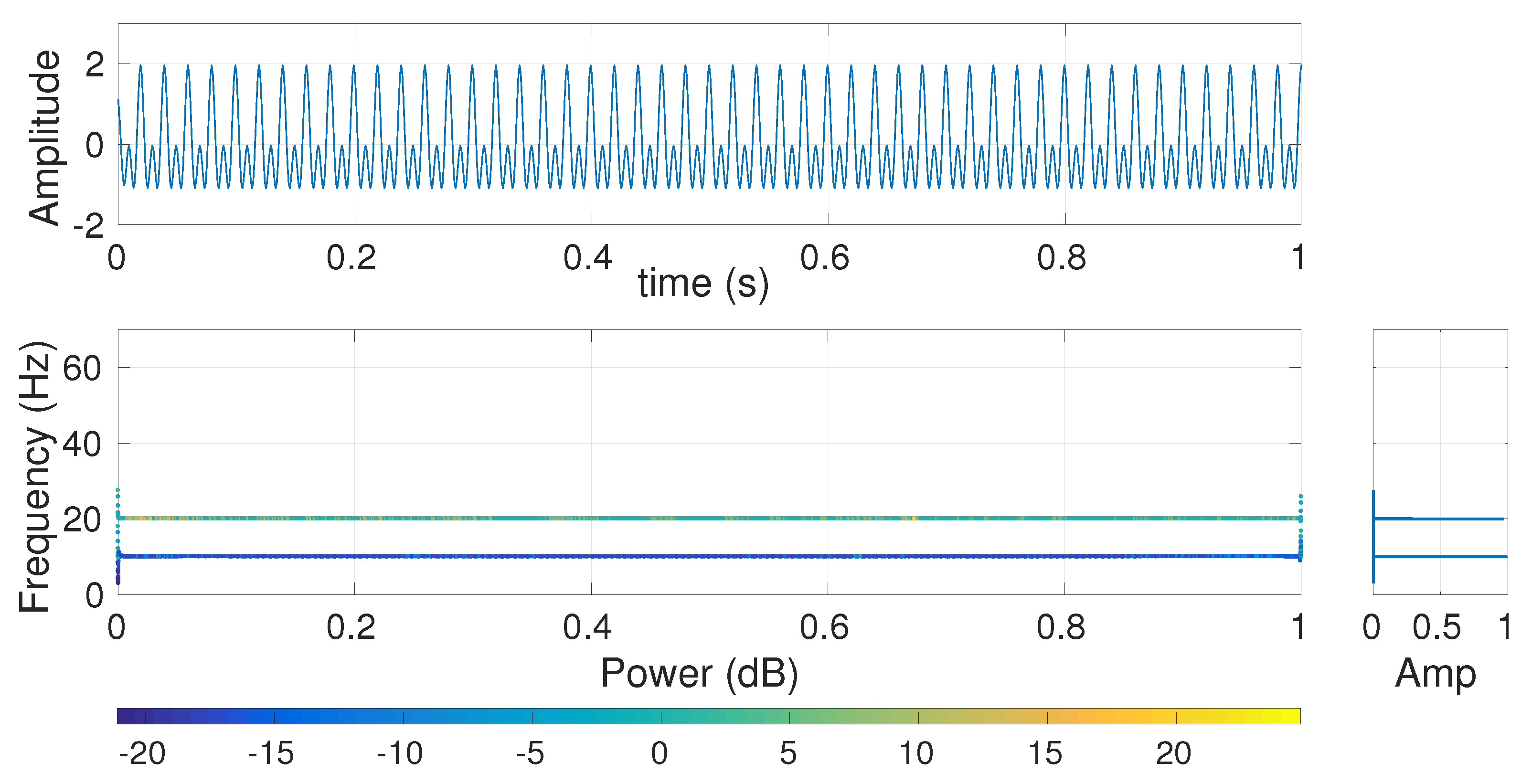
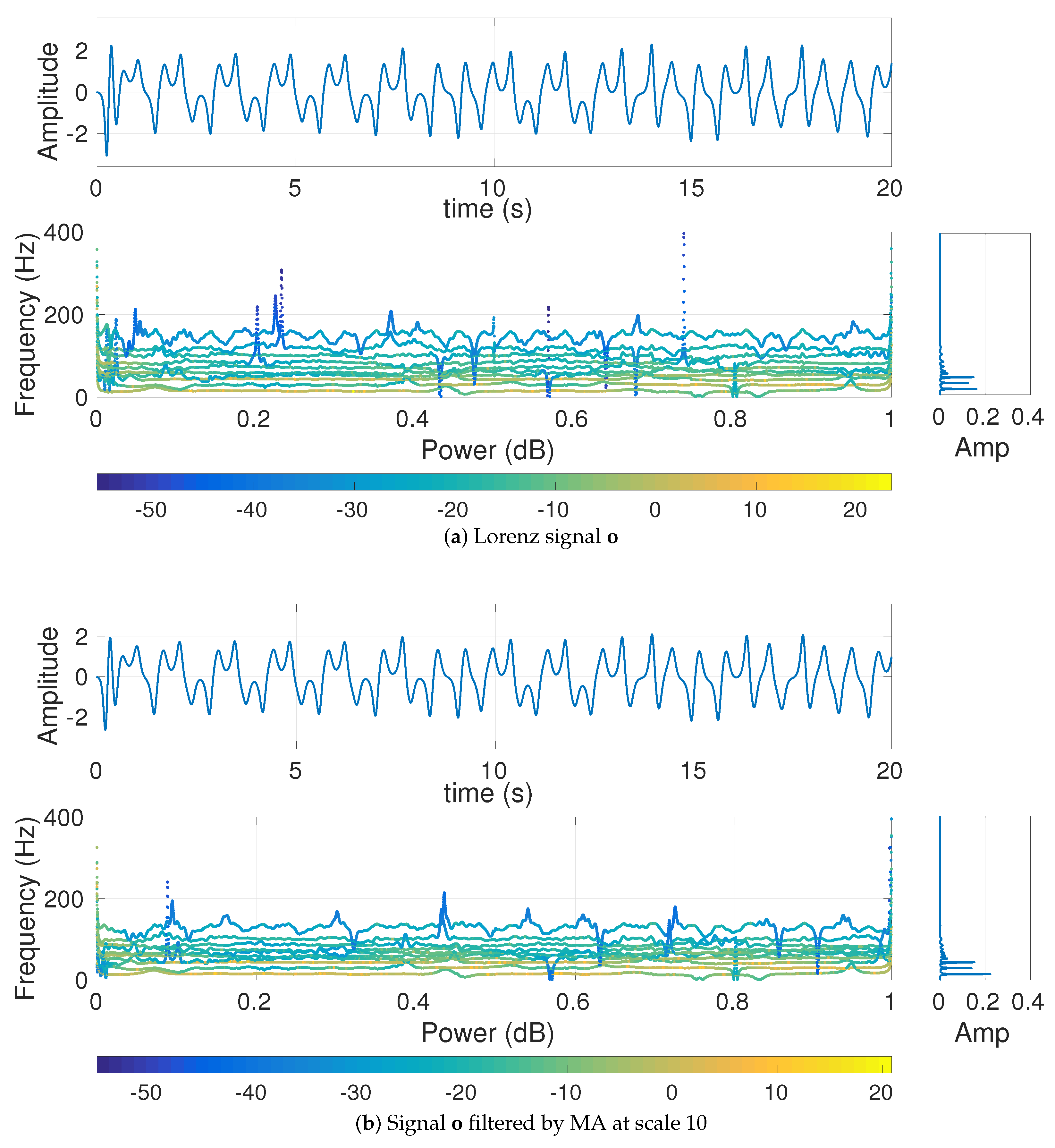
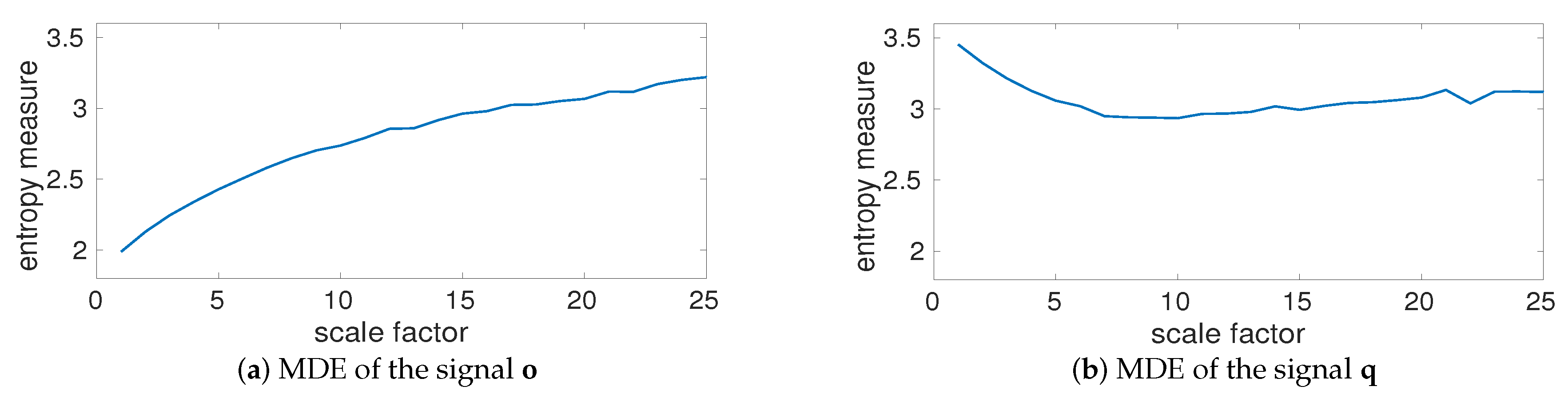
4.1.2. Effect of Different Low-Pass Filters on Multi-Harmonic and Lorenz Series
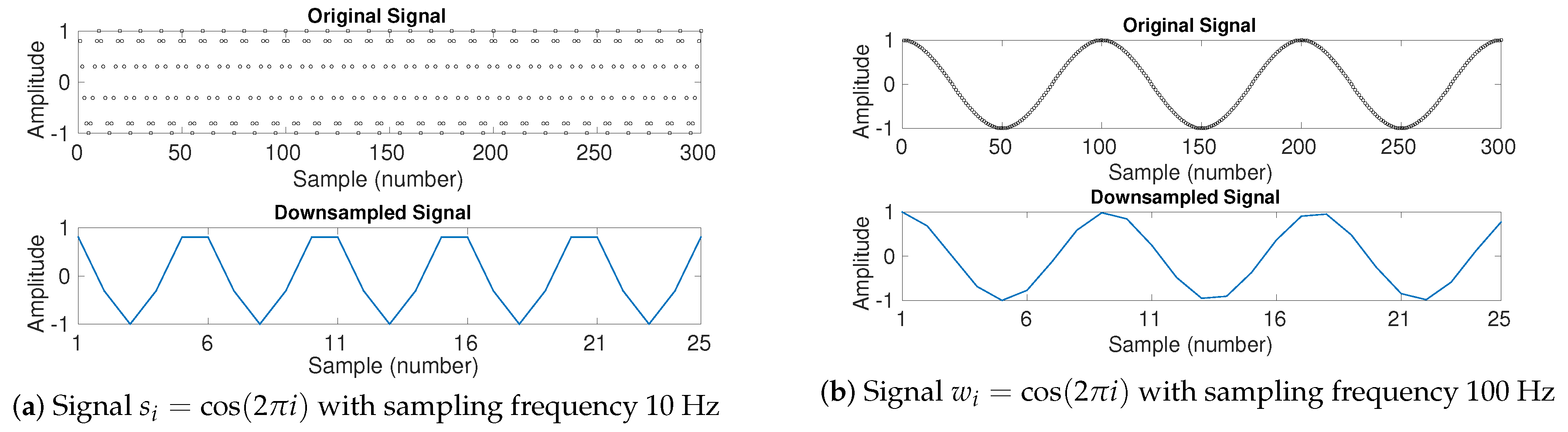
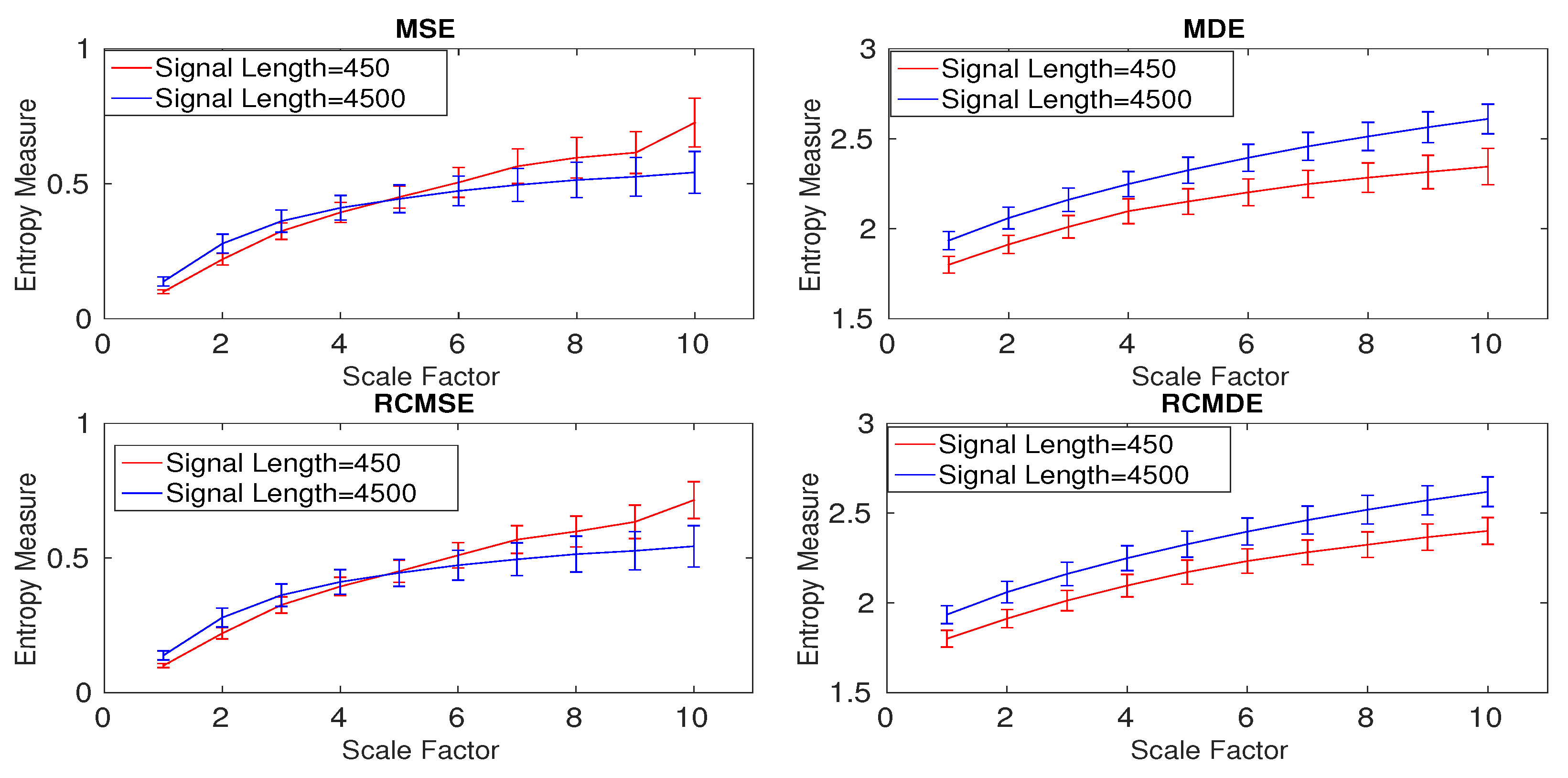
4.1.3. Effect of Downsampling and Sampling Frequency on Multiscale Entropy Methods
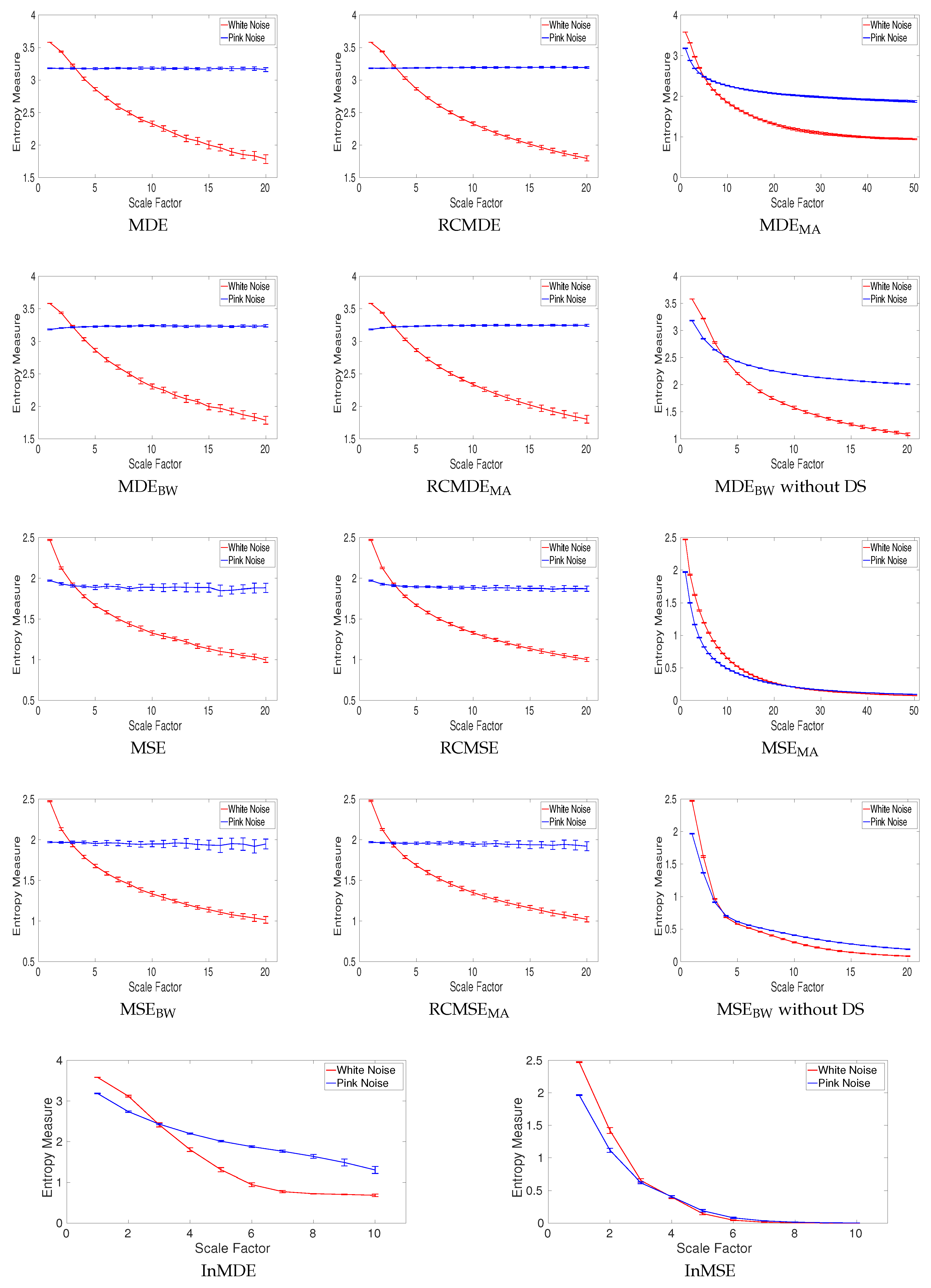
4.1.4. Multiscale Entropy Methods vs. Noise
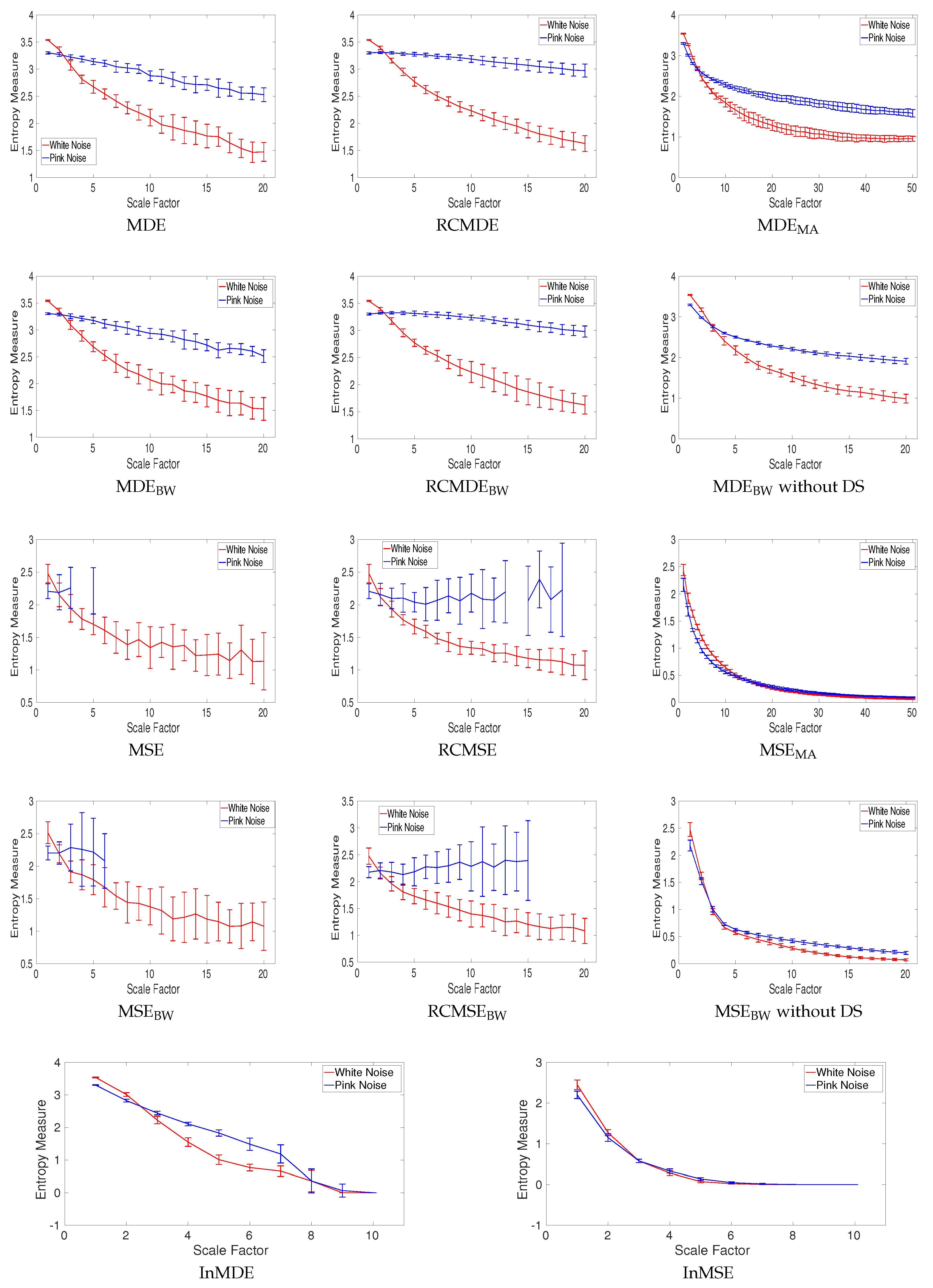
4.1.5. Effect of Refined Composite on Nonlinear Systems without Noise
4.2. Real Signals
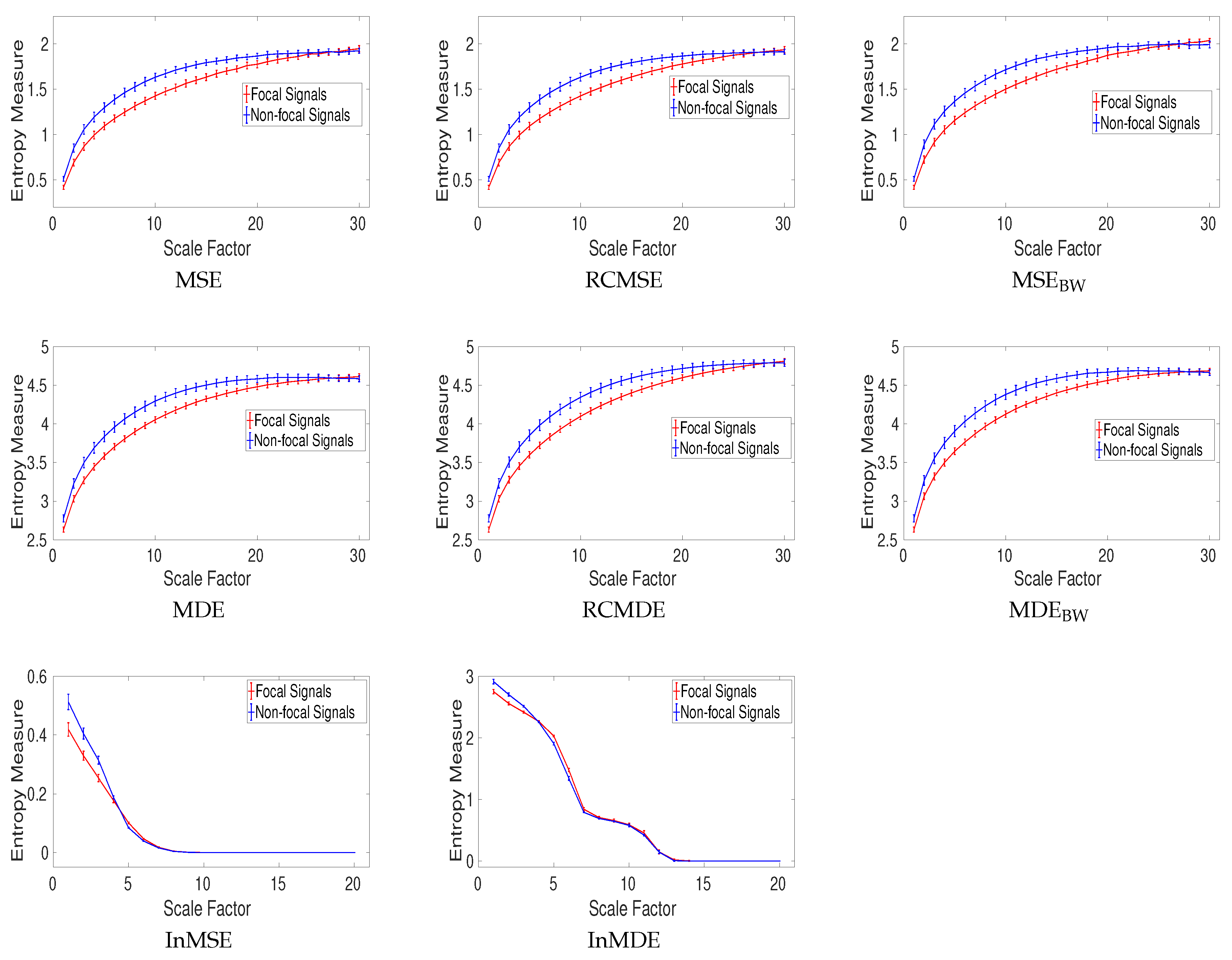
4.2.1. Dataset of Focal and Non-Focal Brain Activity
4.2.2. Dataset of Stride Internal Fluctuations
5. Time Delay, Downsampling, and Nyquist Frequency
6. Future Work
7. Conclusions
Author Contributions
Conflicts of Interest
Appendix. Matlab Codes used in this Article
References
- Yang, A.C.; Tsai, S.J. Is mental illness complex? From behavior to brain. Prog. Neuro-Psychopharmacol. Biol. Psychiatry 2013, 45, 253–257. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Bar-Yam, Y. Dynamics of Complex Systems; Addison-Wesley Reading: Boston, MA, USA, 1997. [Google Scholar]
- Fogedby, H.C. On the phase space approach to complexity. J. Stat. Phys. 1992, 69, 411–425. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion entropy: A measure for time series analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Zhang, Y.C. Complexity and 1/f noise. A phase space approach. J. Phys. I 1991, 1, 971–977. [Google Scholar] [CrossRef]
- Silva, L.E.V.; Cabella, B.C.T.; da Costa Neves, U.P.; Junior, L.O.M. Multiscale entropy-based methods for heart rate variability complexity analysis. Phys. A Stat. Mech. Appl. 2015, 422, 143–152. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Peng, C.K.; Lipsitz, L.A. What is physiologic complexity and how does it change with aging and disease? Neurobiol. Aging 2002, 23, 23–26. [Google Scholar] [CrossRef]
- Hayano, J.; Yamasaki, F.; Sakata, S.; Okada, A.; Mukai, S.; Fujinami, T. Spectral characteristics of ventricular response to atrial fibrillation. Am. J. Physiol. Heart Circ. Physiol. 1997, 273, H2811–H2816. [Google Scholar] [CrossRef]
- Valencia, J.F.; Porta, A.; Vallverdu, M.; Claria, F.; Baranowski, R.; Orlowska-Baranowska, E.; Caminal, P. Refined multiscale entropy: Application to 24-h holter recordings of heart period variability in healthy and aortic stenosis subjects. IEEE Trans. Biomed. Eng. 2009, 56, 2202–2213. [Google Scholar] [CrossRef] [PubMed]
- Humeau-Heurtier, A. The multiscale entropy algorithm and its variants: A review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef]
- Azami, H.; Rostaghi, M.; Abasolo, D.; Escudero, J. Refined Composite Multiscale Dispersion Entropy and its Application to Biomedical Signals. IEEE Trans. Biomed. Eng. 2017, 64, 2872–2879. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Lee, K.Y.; Peng, C.K. Analysis of complex time series using refined composite multiscale entropy. Phys. Lett. A 2014, 378, 1369–1374. [Google Scholar] [CrossRef]
- Amoud, H.; Snoussi, H.; Hewson, D.; Doussot, M.; Duchêne, J. Intrinsic mode entropy for nonlinear discriminant analysis. IEEE Signal Process. Lett. 2007, 14, 297–300. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Unser, M.; Aldroubi, A.; Eden, M. B-spline signal processing. I. Theory. IEEE Trans. Signal Process. 1993, 41, 821–833. [Google Scholar] [CrossRef]
- Fliege, N.J. Multirate Digital Signal Processing; John Wiley: Hoboken, NJ, USA, 1994. [Google Scholar]
- Oppenheim, A.V. Discrete-Time Signal Processing; Pearson Education India: Delhi, India, 1999. [Google Scholar]
- Castiglioni, P.; Coruzzi, P.; Bini, M.; Parati, G.; Faini, A. Multiscale sample entropy of cardiovascular signals: Does the choice between fixed-or varying-tolerance among scales influence its evaluation and interpretation? Entropy 2017, 19, 590. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of surface EMG signal based on fuzzy entropy. Neural Syst. Rehabil. Eng. IEEE Trans. 2007, 15, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.D.; Wu, C.W.; Humeau-Heurtier, A. Refined scale-dependent permutation entropy to analyze systems complexity. Phys. A Stat. Mech. Appl. 2016, 450, 454–461. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A.; Wu, C.W.; Wu, S.D.; Mahé, G.; Abraham, P. Refined Multiscale Hilbert–Huang Spectral Entropy and Its Application to Central and Peripheral Cardiovascular Data. IEEE Trans. Biomed. Eng. 2016, 63, 2405–2415. [Google Scholar] [CrossRef] [PubMed]
- Azami, H.; Fernández, A.; Escudero, J. Refined multiscale fuzzy entropy based on standard deviation for biomedical signal analysis. Med. Biol. Eng. Comput. 2017, 55, 2037–2052. [Google Scholar] [CrossRef] [PubMed]
- Baker, G.L.; Gollub, J.P. Chaotic dynamics: an introduction; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Thuraisingham, R.A.; Gottwald, G.A. On multiscale entropy analysis for physiological data. Phys. A Stat. Mech. Appl. 2006, 366, 323–332. [Google Scholar] [CrossRef]
- Andrzejak, R.G.; Schindler, K.; Rummel, C. Nonrandomness, nonlinear dependence, and nonstationarity of electroencephalographic recordings from epilepsy patients. Phys. Rev. E 2012, 86, 046206. [Google Scholar] [CrossRef] [PubMed]
- Gait in Aging and Disease Database. Available online: https://www.physionet.org/physiobank/database/gaitdb (accessed on 17 February 2018).
- The Bern-Barcelona EEG database. Available online: http://ntsa.upf.edu/downloads/andrzejak-rg-schindler-k-rummel-c-2012-nonrandomness-nonlinear-dependence-and (accessed on 17 February 2018).
- Hausdorff, J.M.; Purdon, P.L.; Peng, C.; Ladin, Z.; Wei, J.Y.; Goldberger, A.L. Fractal dynamics of human gait: stability of long-range correlations in stride interval fluctuations. J. Appl. Physiol. 1996, 80, 1448–1457. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2004, 460, 1597–1611. [Google Scholar] [CrossRef]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Process. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Gow, B.J.; Peng, C.K.; Wayne, P.M.; Ahn, A.C. Multiscale entropy analysis of center-of-pressure dynamics in human postural control: methodological considerations. Entropy 2015, 17, 7926–7947. [Google Scholar] [CrossRef]
- Sharma, R.; Pachori, R.B.; Acharya, U.R. Application of entropy measures on intrinsic mode functions for the automated identification of focal electroencephalogram signals. Entropy 2015, 17, 669–691. [Google Scholar] [CrossRef]
- Nemati, S.; Edwards, B.A.; Lee, J.; Pittman-Polletta, B.; Butler, J.P.; Malhotra, A. Respiration and heart rate complexity: effects of age and gender assessed by band-limited transfer entropy. Respir. Physiol. Neurobiol. 2013, 189, 27–33. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy: A tool for complexity analysis of multichannel data. Phys. Rev. E 2011, 84, 061918. [Google Scholar] [CrossRef] [PubMed]
- Kaffashi, F.; Foglyano, R.; Wilson, C.G.; Loparo, K.A. The effect of time delay on approximate & sample entropy calculations. Phys. D Nonlinear Phenom. 2008, 237, 3069–3074. [Google Scholar]
- Berger, S.; Schneider, G.; Kochs, E.F.; Jordan, D. Permutation Entropy: Too Complex a Measure for EEG Time Series? Entropy 2017, 19, 692. [Google Scholar] [CrossRef]
- Strang, G.; Nguyen, T. Wavelets Filter Banks; Wellesley: Cambridge, UK, 1996. [Google Scholar]
- Costa, M.D.; Goldberger, A.L. Generalized multiscale entropy analysis: application to quantifying the complex volatility of human heartbeat time series. Entropy 2015, 17, 1197–1203. [Google Scholar] [CrossRef] [PubMed]
- Azami, H.; Escudero, J. Refined composite multivariate generalized multiscale fuzzy entropy: A tool for complexity analysis of multichannel signals. Phys. A Stat. Mech. Appl. 2017, 465, 261–276. [Google Scholar] [CrossRef]
- Xu, M.; Shang, P. Analysis of financial time series using multiscale entropy based on skewness and kurtosis. Phys. A Stat. Mech. Appl. 2018, 490, 1543–1550. [Google Scholar] [CrossRef]
- Azami, H.; Fernández, A.; Escudero, J. Multivariate Multiscale Dispersion Entropy of Biomedical Times Series. arXiv, 2017; arXiv:1704.03947. [Google Scholar]
| Methods | Filtering | Downsampling | Applicability of Refined Composite |
|---|---|---|---|
| MSE [2] and MDE [13] | Moving average | yes | yes |
| MSEMA and MDEMA | Moving average | no | no |
| MSEBW [11] and MDEBW | Butterworth | yes | yes |
| MSEBW [11] and MDEBW without downsampling | Butterworth | no | no |
| InMSE [15] and InMDE | Cumulative sums of IMFs | no | no |
| Noise | MDE | RCMDE | MDEMA (Scale 25) | MDEBW | RCMDEBW | MDEBW without DS | InMDE (Scale 5) |
| Pink | 0.0058 | 0.0038 | 0.0069 | 0.0044 | 0.0038 | 0.0031 | 0.0091 |
| White | 0.0174 | 0.0124 | 0.0246 | 0.0166 | 0.0115 | 0.0182 | 0.0394 |
| Noise | MSE | RCMSE | MSEMA (Scale 25) | MSEBW | RCMSEBW | MSEBW without DS | InMSE (Scale 5) |
| Pink | 0.0186 | 0.0105 | 0.0131 | 0.0176 | 0.0124 | 0.0130 | 0.0982 |
| White | 0.0201 | 0.0133 | 0.0135 | 0.0219 | 0.0203 | 0.0308 | 0.1330 |
| Noise | MDE | RCMDE | MDEMA (Scale 25) | MDEBW | RCMDEBW | MDEBW without DS | InMDE (Scale 5) |
| Pink | 0.0317 | 0.0194 | 0.0473 | 0.0320 | 0.0141 | 0.0204 | 0.0522 |
| White | 0.0726 | 0.0415 | 0.1116 | 0.0929 | 0.0876 | 0.0726 | 0.1435 |
| Noise | MSE | RCMSE | MSEMA (Scale 25) | MSEBW | RCMSEBW | MSEBW without DS | InMSE (Scale 5) |
| Pink | undefined | 0.1327 | 0.0434 | undefined | 0.2008 | 0.0822 | 0.2351 |
| White | 0.2385 | 0.0738 | 0.0605 | 0.2024 | 0.1736 | 0.1060 | 0.3779 |
| Signal Length | MSE | MDE | RCMSE | RCMDE |
|---|---|---|---|---|
| 450 sample points | 0.1000 | 0.0898 | 0.0700 | 0.0309 |
| 4500 sample points | 0.1156 | 0.0310 | 0.1134 | 0.0312 |
| Signals | MSE | RCMSE | MSEBW | MDE | RCMDE | MDEBW |
|---|---|---|---|---|---|---|
| Focal EEGs | 0.0229 | 0.0229 | 0.0224 | 0.0083 | 0.0089 | 0.0083 |
| Non-focal EEGs | 0.0178 | 0.0191 | 0.0172 | 0.0111 | 0.0121 | 0.0109 |
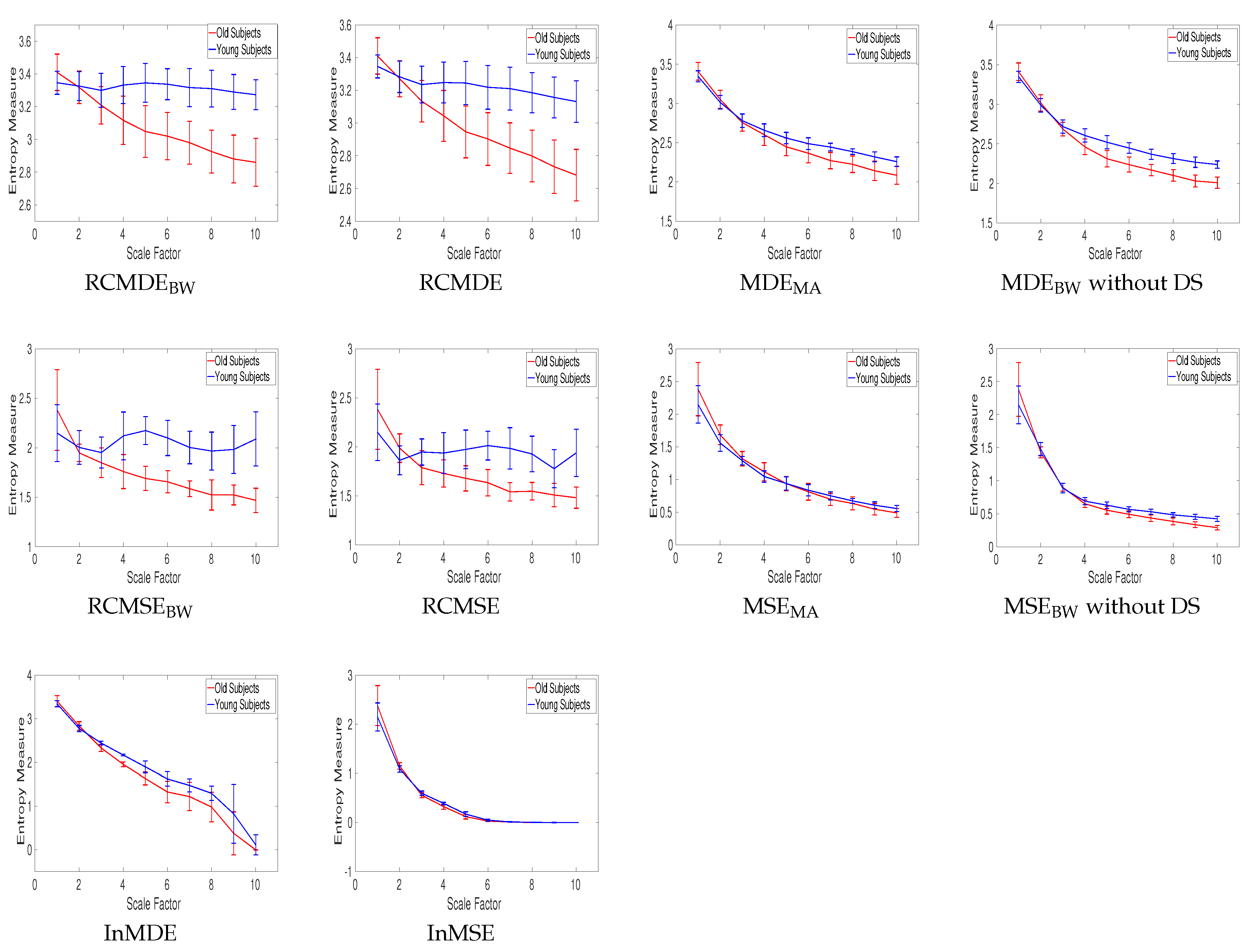
| Signals | RCMDEBW | RCMDE | MDEBW without DS | RCMSEBW |
|---|---|---|---|---|
| Young subjects | 0.0355 | 0.0410 | 0.0334 | 0.0644 |
| Old subjects | 0.0517 | 0.0540 | 0.0449 | 0.0723 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azami, H.; Escudero, J. Coarse-Graining Approaches in Univariate Multiscale Sample and Dispersion Entropy. Entropy 2018, 20, 138. https://doi.org/10.3390/e20020138
Azami H, Escudero J. Coarse-Graining Approaches in Univariate Multiscale Sample and Dispersion Entropy. Entropy. 2018; 20(2):138. https://doi.org/10.3390/e20020138
Chicago/Turabian StyleAzami, Hamed, and Javier Escudero. 2018. "Coarse-Graining Approaches in Univariate Multiscale Sample and Dispersion Entropy" Entropy 20, no. 2: 138. https://doi.org/10.3390/e20020138
APA StyleAzami, H., & Escudero, J. (2018). Coarse-Graining Approaches in Univariate Multiscale Sample and Dispersion Entropy. Entropy, 20(2), 138. https://doi.org/10.3390/e20020138






