Stochastic Proximal Gradient Algorithms for Multi-Source Quantitative Photoacoustic Tomography
Abstract
1. Introduction
1.1. Multi-Source QPAT
1.2. Stochastic Proximal Gradient Algorithms
1.3. Outline
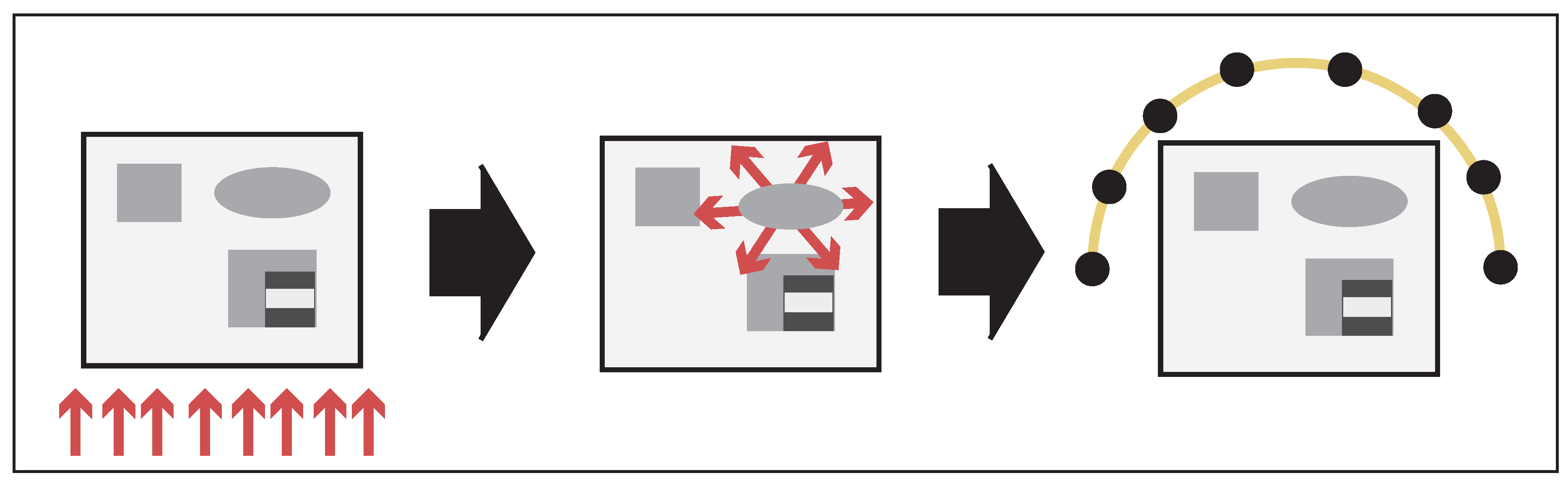
2. The Forward Problem in QPAT
2.1. Mathematical Notation
2.2. The Radiative Transfer Equation
2.3. Heating Operator
2.4. The Wave Equation
2.5. Analysis of the Forward Problem in Multi-Source QPAT
- (1)
- The operators , and are sequentially continuous and Lipschitz-continuous.
- (2)
- For every , the one-sided directional derivatives , of , at μ in any feasible direction h exist, and are given by
3. The Stochastic Proximal Gradient Method for QPAT
3.1. Formulation of the Inverse Problem
3.2. Tikhonov Regularization in QPAT
- (1)
- For any and any , the Tikhonov functional has at least one minimizer.
- (2)
- Let , , with . Suppose further that satisfies and as . Then:
- ■
- Every sequence with has a weakly converging subsequence.
- ■
- The limit of every weakly convergent subsequence of is an -minimizing solution of .
- ■
- If the -minimizing solution of is unique and denoted by , then .
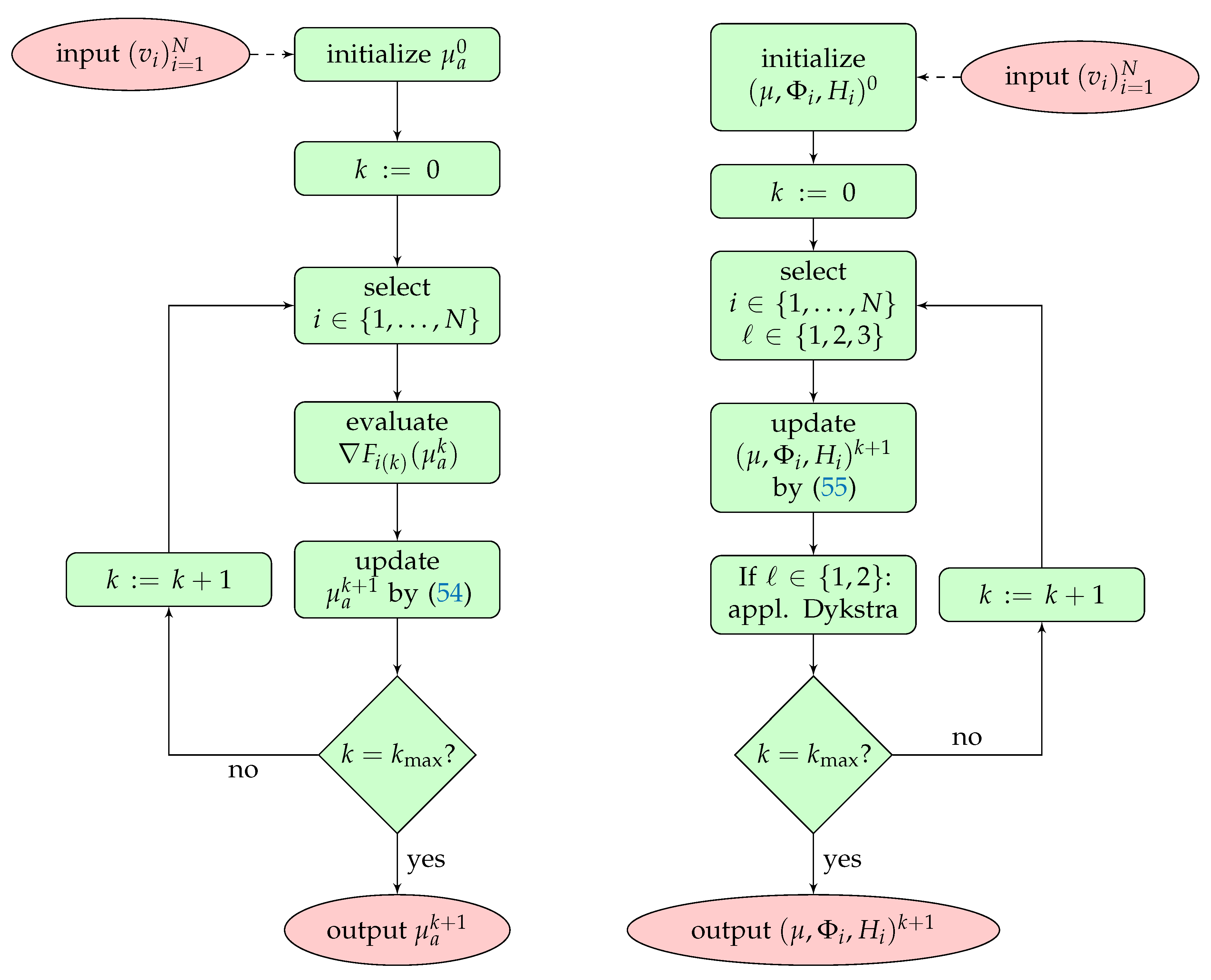
3.3. The Proximal Stochastic Gradient Algorithm for QPAT
3.4. Iterative Regularization Methods
4. QPAT as Multilinear Inverse Problem
4.1. Reformulation as Multilinear Inverse Problem
4.2. Application of Tikhonov Regularization
4.3. Solution of the MULL Formulation of QPAT Using Stochastic Gradient Methods
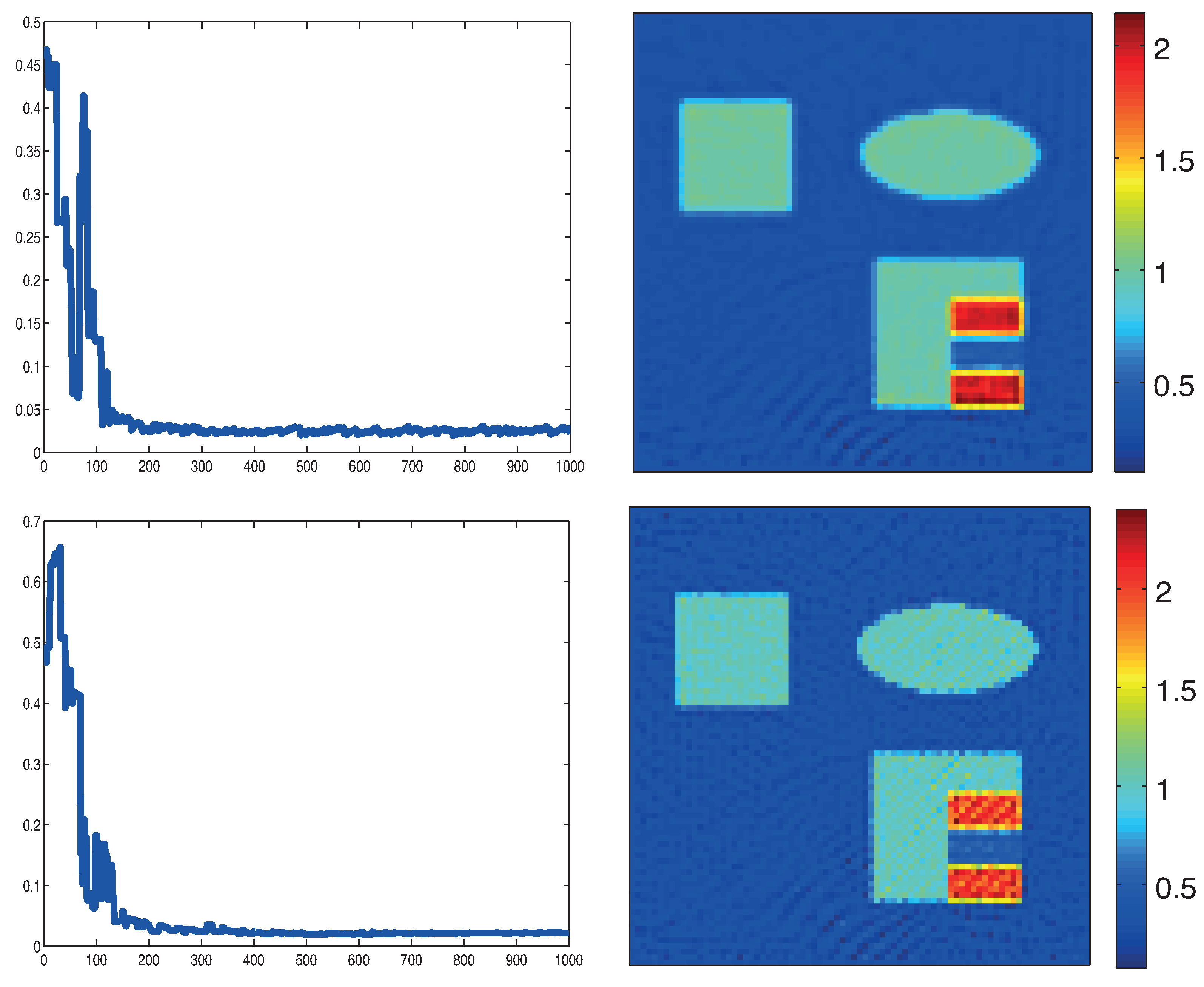
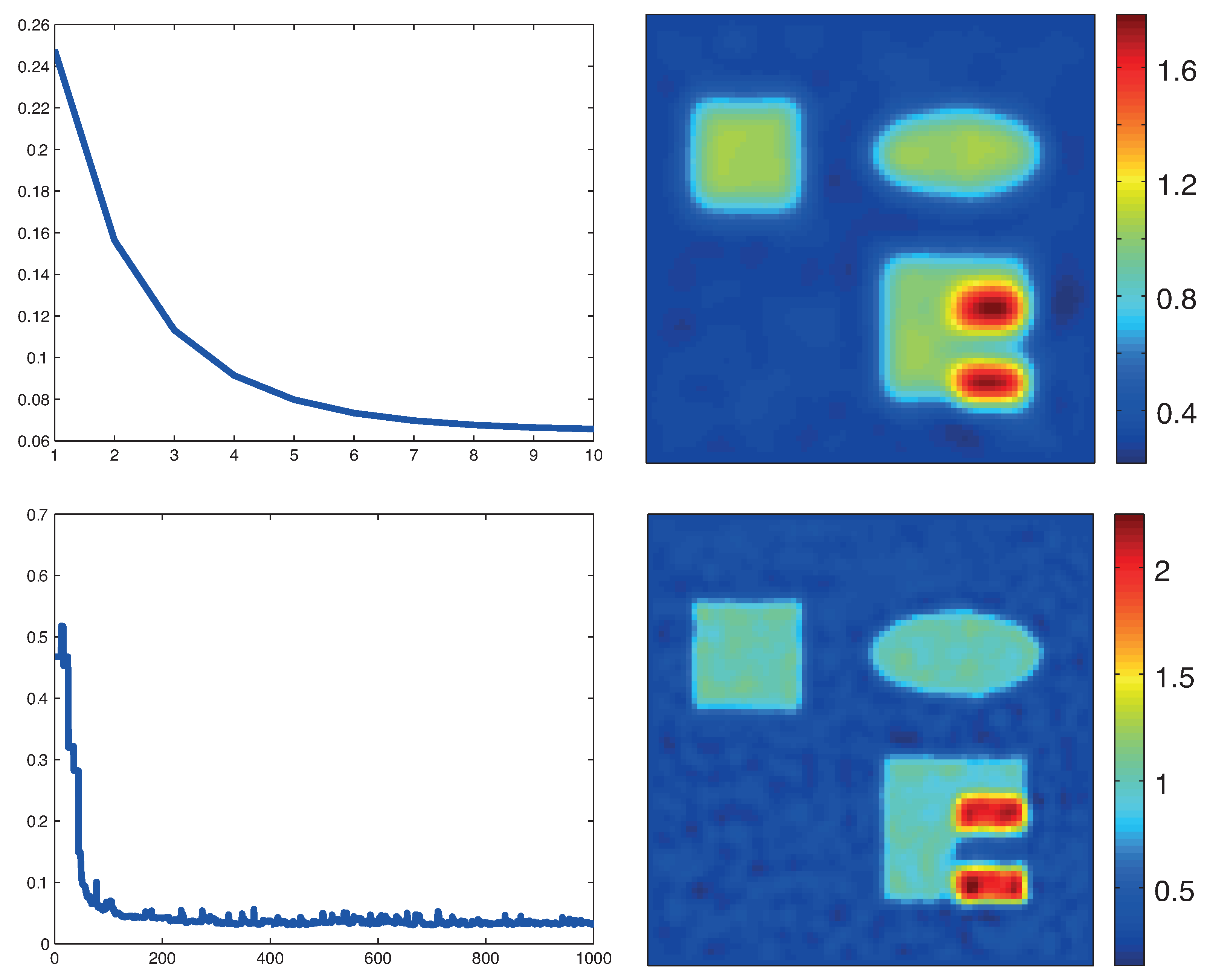
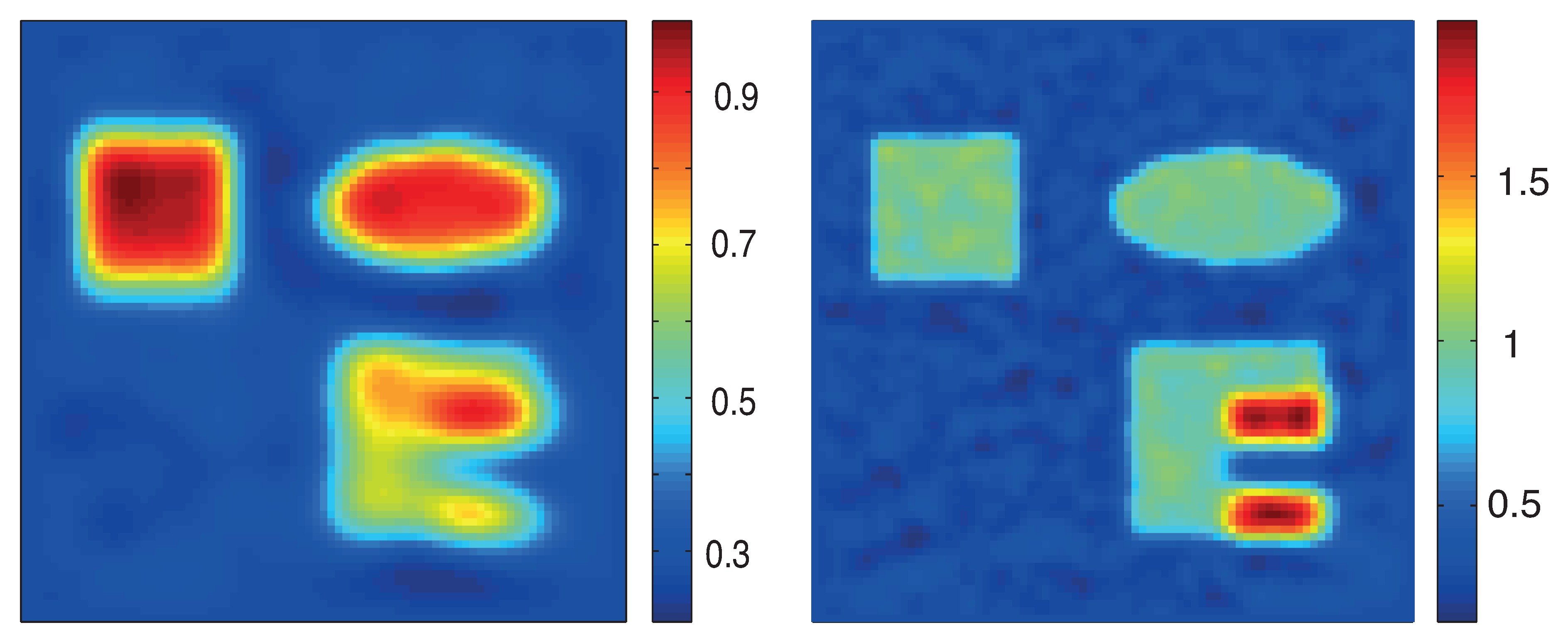
5. Numerical Simulations
5.1. Numerical Solution of the RTE
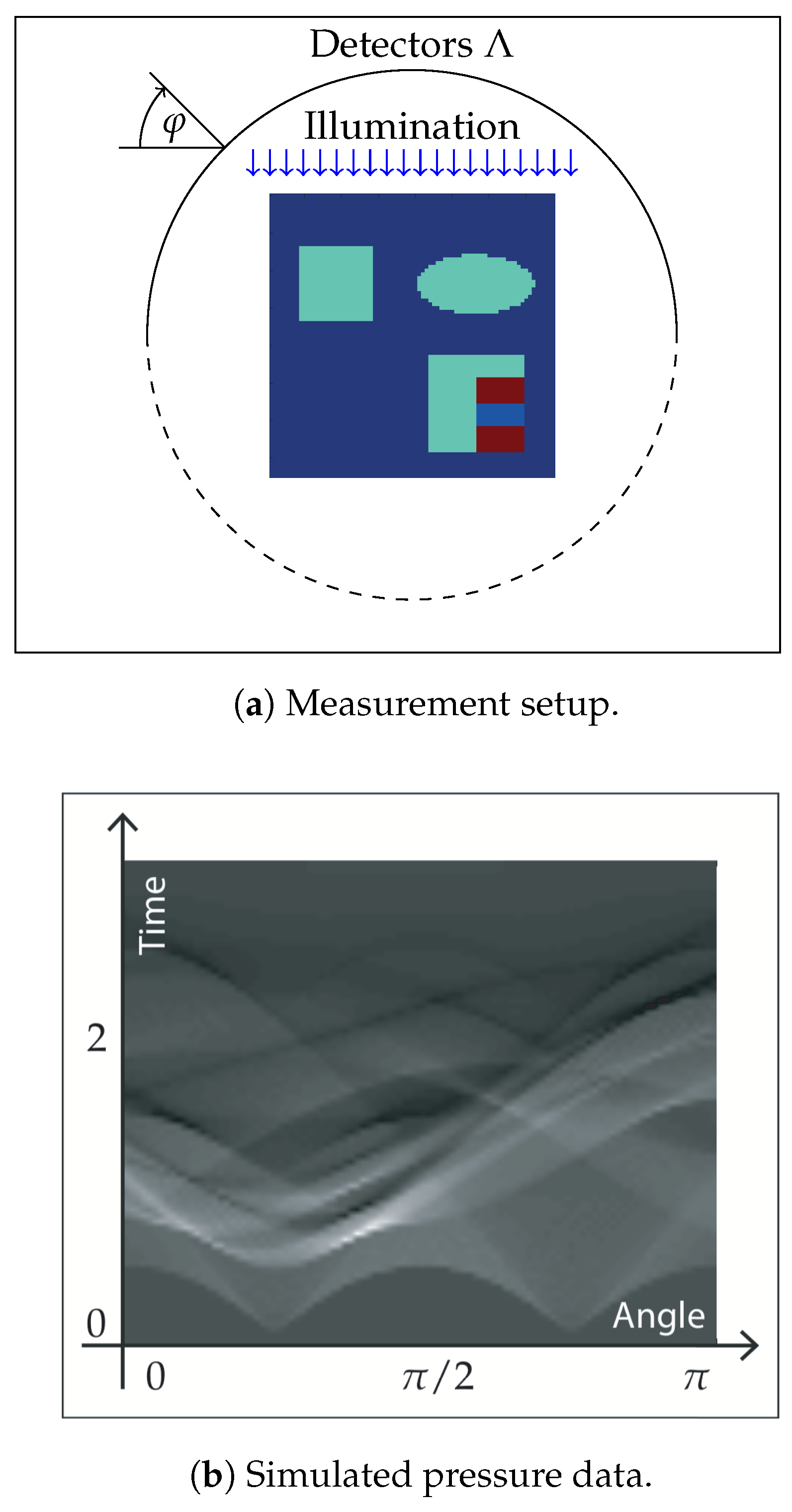
5.2. Test Scenario for Multiple Illumination
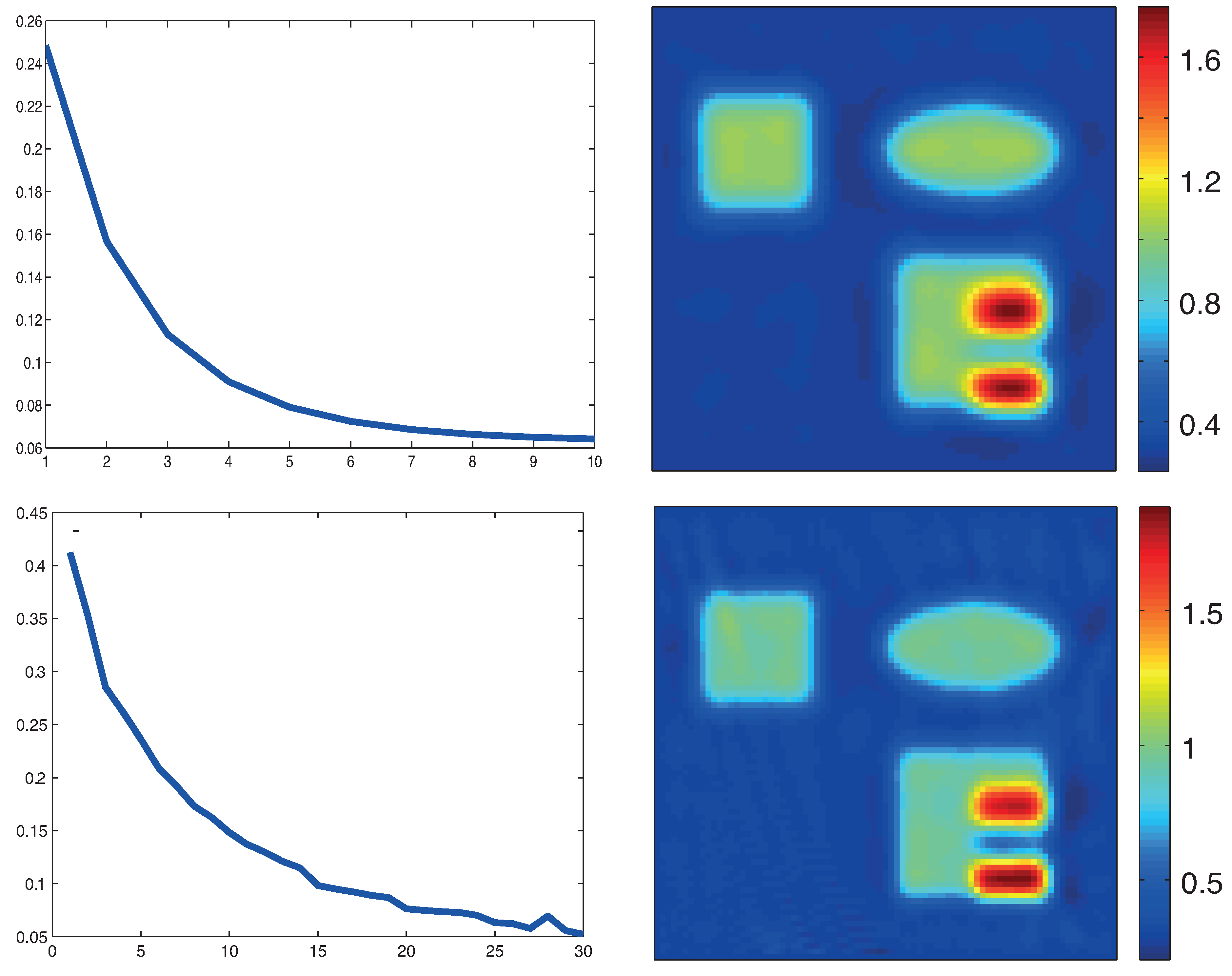
5.3. Numerical Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Beard, P. Biomedical photoacoustic imaging. Interface Focus 2011, 1, 602–631. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.V. Multiscale photoacoustic microscopy and computed tomography. Nat. Photonics 2009, 3, 503–509. [Google Scholar] [CrossRef] [PubMed]
- Agranovsky, M.; Kuchment, P.; Kunyansky, L. On reconstruction formulas and algorithms for the thermoacoustic tomography. In Photoacoustic Imaging and Spectroscopy; Wang, L.V., Ed.; CRC Press: Boca Raton, FL, USA, 2009; pp. 89–101. [Google Scholar]
- Burgholzer, P.; Bauer-Marschallinger, J.; Grün, H.; Haltmeier, M.; Paltauf, G. Temporal back-projection algorithms for photoacoustic tomography with integrating line detectors. Inverse Probl. 2007, 23, S65–S80. [Google Scholar] [CrossRef]
- Haltmeier, M. Universal inversion formulas for recovering a function from spherical means. SIAM J. Math. Anal. 2014, 46, 214–232. [Google Scholar] [CrossRef]
- Haltmeier, M.; Nguyen, L.V. Analysis of iterative methods in photoacoustic tomography with variable sound speed. SIAM J. Imaging Sci. 2017, 10, 751–781. [Google Scholar] [CrossRef]
- Haltmeier, M.; Schuster, T.; Scherzer, O. Filtered backprojection for thermoacoustic computed tomography in spherical geometry. Math. Methods Appl. Sci. 2005, 28, 1919–1937. [Google Scholar] [CrossRef]
- Huang, C.; Wang, K.; Nie, L.; Wang, L.V.; Anastasio, M.A. Full-wave iterative image reconstruction in photoacoustic tomography with acoustically inhomogeneous media. IEEE Trans. Med. Imaging 2013, 32, 1097–1110. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, L.V.; Kunyansky, L.A. A Dissipative Time Reversal Technique for Photoacoustic Tomography in a Cavity. SIAM J. Imaging Sci. 2016, 9, 748–769. [Google Scholar] [CrossRef]
- Rosenthal, A.; Ntziachristos, V.; Razansky, D. Acoustic Inversion in Optoacoustic Tomography: A Review. Curr. Med. Imaging Rev. 2013, 9, 318–336. [Google Scholar] [CrossRef] [PubMed]
- Ammari, H.; Bossy, E.; Jugnon, V.; Kang, H. Reconstruction of the Optical Absorption Coefficient of a Small Absorber from the Absorbed Energy Density. SIAM J. Appl. Math. 2011, 71, 676–693. [Google Scholar] [CrossRef]
- Bal, G.; Jollivet, A.; Jugnon, V. Inverse transport theory of photoacoustics. Inverse Probl. 2010, 26, 025011. [Google Scholar] [CrossRef]
- Bal, G.; Ren, K. Multi-source quantitative photoacoustic tomography in a diffusive regime. Inverse Probl. 2011, 27, 075003. [Google Scholar] [CrossRef]
- Chen, J.; Yang, Y. Quantitative photo-acoustic tomography with partial data. Inverse Probl. 2012, 28, 115014. [Google Scholar] [CrossRef]
- Cox, B.T.; Arridge, S.A.; Beard, P.C. Gradient-Based Quantitative Photoacoustic Image Reconstruction for Molecular Imaging. Proc. SPIE 2007, 6437, 64371T. [Google Scholar]
- Cox, B.T.; Arridge, S.R.; Köstli, P.; Beard, P.C. Two-dimensional quantitative photoacoustic image reconstruction of absorption distributions in scattering media by use of a simple iterative method. Appl. Opt. 2006, 45, 1866–1875. [Google Scholar] [CrossRef] [PubMed]
- Cox, B.T.; Laufer, J.G.; Arridge, S.R.; Beard, P.C. Quantitative spectroscopic photoacoustic imaging: A review. J. Biomed. Opt. 2012, 17, 0612021. [Google Scholar] [CrossRef] [PubMed]
- Haltmeier, M.; Neumann, L.; Rabanser, S. Single-stage reconstruction algorithm for quantitative photoacoustic tomography. Inverse Probl. 2015, 31, 065005. [Google Scholar] [CrossRef]
- Haltmeier, M.; Neumann, L.; Nguyen, L.V.; Rabanser, S. Analysis of the Linearized Problem of Quantitative Photoacoustic Tomography. arXiv, 2017; arXiv:1702.04560. [Google Scholar]
- Kruger, R.A.; Lui, P.; Fang, Y.R.; Appledorn, R.C. Photoacoustic Ultrasound (PAUS)–Reconstruction Tomography. Med. Phys. 1995, 22, 1605–1609. [Google Scholar] [CrossRef] [PubMed]
- Mamonov, A.V.; Ren, K. Quantitative photoacoustic imaging in radiative transport regime. Commun. Math. Sci. 2014, 12, 201–234. [Google Scholar] [CrossRef]
- Naetar, W.; Scherzer, O. Quantitative Photoacoustic Tomography with Piecewise Constant Material Parameters. SIAM J. Imaging Sci. 2014, 7, 1755–1774. [Google Scholar] [CrossRef]
- Ren, K.; Gao, H.; Zhao, H. A hybrid reconstruction method for quantitative PAT. SIAM J. Imaging Sci. 2013, 6, 32–55. [Google Scholar] [CrossRef]
- Rosenthal, A.; Razansky, D.; Ntziachristos, V. Fast Semi-Analytical Model-Based Acoustic Inversion for Quantitative Optoacoustic Tomography. IEEE Trans. Med. Imaging 2010, 29, 1275–1285. [Google Scholar] [CrossRef] [PubMed]
- Tarvainen, T.; Cox, B.T.; Kaipio, J.P.; Arridge, S.A. Reconstructing absorption and scattering distributions in quantitative photoacoustic tomography. Inverse Probl. 2012, 28, 084009. [Google Scholar] [CrossRef]
- Yao, L.; Sun, Y.; Jiang, H. Transport-based quantitative photoacoustic tomography: Simulations and experiments. Phys. Med. Biol. 2010, 55, 1917–1934. [Google Scholar] [CrossRef] [PubMed]
- Arridge, S.R. Optical tomography in medical imaging. Inverse Probl. 1999, 15, R41–R93. [Google Scholar] [CrossRef]
- Dautray, R.; Lions, J. Mathematical Analysis and Numerical Methods for Science and Technology; Springer: Berlin, Germany, 1993. [Google Scholar]
- Egger, H.; Schlottbom, M. Numerical methods for parameter identification in stationary radiative transfer. Comput. Optim. Appl. 2015, 62, 67–83. [Google Scholar] [CrossRef]
- Kanschat, G. Solution of radiative transfer problems with finite elements. In Numerical Methods in Multidimensional Radiative Transfer; Springer: Berlin, Germany, 2009; pp. 49–98. [Google Scholar]
- Gao, H.; Feng, J.; Song, L. Limited-view multi-source quantitative photoacoustic tomography. Inverse Probl. 2015, 31, 065004. [Google Scholar] [CrossRef]
- Engl, H.W.; Hanke, M.; Neubauer, A. Regularization of Inverse Problems; Springer Science & Business Media: Berlin, Germany, 1996. [Google Scholar]
- Kaltenbacher, B.; Neubauer, A.; Scherzer, O. Iterative Regularization Methods for Nonlinear Ill-Posed Problems; Walter de Gruyter: Berlin, Geramny, 2008. [Google Scholar]
- Scherzer, O.; Grasmair, M.; Grossauer, H.; Haltmeier, M.; Lenzen, F. Variational Methods in Imaging; Applied Mathematical Sciences; Springer: New York, NY, USA, 2009. [Google Scholar]
- Combettes, P.L.; Wajs, V.R. Signal recovery by proximal forward-backward splitting. Multiscale Model. Simul. 2005, 4, 1168–1200. [Google Scholar] [CrossRef]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces; Springer: Berlin, Germany, 2011. [Google Scholar]
- Bertsekas, D.P. Incremental gradient, subgradient, and proximal methods for convex optimization: A survey. In Optimization for Machine Learing; Sra, S., Nowozin, S., Wright, S.J., Eds.; The MIT Press: London, UK, 2012. [Google Scholar]
- Bertsekas, D.P. Incremental proximal methods for large scale convex optimization. Math. Program. 2011, 129, 163–195. [Google Scholar] [CrossRef]
- Xiao, L.; Zhang, T. A proximal stochastic gradient method with progressive variance reduction. SIAM J. Optim. 2014, 24, 2057–2075. [Google Scholar] [CrossRef]
- Duchi, J.; Singer, Y. Efficient online and batch learning using forward backward splitting. J. Mach. Learn. Res. 2009, 10, 2899–2934. [Google Scholar]
- Li, H.; Haltmeier, M. The Averaged Kaczmarz Iteration for Solving Inverse Problems. arXiv, 2017; arXiv:1709.00742. [Google Scholar]
- Pereyra, M.; Schniter, P.; Chouzenoux, E.; Pesquet, J.-C.; Tourneret, J.Y.; Hero, A.O.; McLaughlin, S. A survey of stochastic simulation and optimization methods in signal processing. IEEE J. Sel. Top. Signal Process. 2016, 10, 224–241. [Google Scholar] [CrossRef]
- De Cezaro, A.; Haltmeier, M.; Leitão, A.; Scherzer, O. On steepest-descent-Kaczmarz methods for regularizing systems of nonlinear ill-posed equations. Appl. Math. Comput. 2008, 202, 596–607. [Google Scholar] [CrossRef]
- Haltmeier, M.; Leitao, A.; Scherzer, O. Kaczmarz methods for regularizing nonlinear ill-posed equations I: convergence analysis. Inverse Probl. Imaging 2007, 1, 289–298. [Google Scholar]
- Haltmeier, M.; Kowar, R.; Leitao, A.; Scherzer, O. Kaczmarz methods for regularizing nonlinear ill-posed equations II: Applications. Inverse Probl. Imaging 2007, 1, 507–523. [Google Scholar]
- Alberti, G.; Ammari, H. Disjoint sparsity for signal separation and applications to hybrid inverse problems in medical imaging. Appl. Comput. Harmon. Anal. 2017, 42, 319–349. [Google Scholar] [CrossRef]
- Ammari, H.; Garnier, J.; Kang, H.; Nguyen, L.; Seppecher, L. Multi-Wave Medical Imaging, Mathematical Modelling & Imaging Reconstruction; World Scientific Publishing: London, UK, 2017. [Google Scholar]
- Saratoon, T.; Tarvainen, T.; Cox, B.T.; Arridge, S.R. A gradient-based method for quantitative photoacoustic tomography using the radiative transfer equation. Inverse Probl. 2013, 29, 075006. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, T. On iterative algorithms for quantitative photoacoustic tomography in the radiative transport regime. Inverse Probl. 2017, 33, 115006. [Google Scholar] [CrossRef]
- Egger, H.; Schlottbom, M. Stationary radiative transfer with vanishing absorption. Math. Models Methods Appl. Sci. 2014, 24, 973–990. [Google Scholar] [CrossRef]
- Finch, D.; Patch, S.K.; Rakesh. Determining a function from its mean values over a family of spheres. SIAM J. Math. Anal. 2004, 35, 1213–1240. [Google Scholar] [CrossRef]
- Finch, D.; Haltmeier, M.; Rakesh. Inversion of spherical means and the wave equation in even dimensions. SIAM J. Appl. Math. 2007, 68, 392–412. [Google Scholar] [CrossRef]
- Combettes, P.L.; Pesquet, J.C. Proximal splitting methods in signal processing. In Fixed-Point Algorithms for Inverse Problems in Science and Engineering; Springer: New York, NY, USA, 2011; pp. 185–212. [Google Scholar]
- Ito, K.; Kunisch, K. Lagrange Multiplier Approach to Variational Problems and Applications; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2008. [Google Scholar]
- John, F. Partial Differential Equations, 4th ed.; Applied Mathematical Sciences; Springer: New York, NY, USA, 1982. [Google Scholar]
- Evans, L.C. Partial Differential Equations; Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 1998. [Google Scholar]

| Algorithm | Model | Update | No. Iterations | Reconstruction Time |
|---|---|---|---|---|
| Proximal gradient | (19) | (23) | 10 | h |
| Proximal stochastic gradient | (19) | (31) | 30 | h |
| MULL-proximal stochastic gradient | (35) | (49) | 1000 | h |
| MULL-projected stochastic gradient | (35) | (50) | 1000 | h |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rabanser, S.; Neumann, L.; Haltmeier, M. Stochastic Proximal Gradient Algorithms for Multi-Source Quantitative Photoacoustic Tomography. Entropy 2018, 20, 121. https://doi.org/10.3390/e20020121
Rabanser S, Neumann L, Haltmeier M. Stochastic Proximal Gradient Algorithms for Multi-Source Quantitative Photoacoustic Tomography. Entropy. 2018; 20(2):121. https://doi.org/10.3390/e20020121
Chicago/Turabian StyleRabanser, Simon, Lukas Neumann, and Markus Haltmeier. 2018. "Stochastic Proximal Gradient Algorithms for Multi-Source Quantitative Photoacoustic Tomography" Entropy 20, no. 2: 121. https://doi.org/10.3390/e20020121
APA StyleRabanser, S., Neumann, L., & Haltmeier, M. (2018). Stochastic Proximal Gradient Algorithms for Multi-Source Quantitative Photoacoustic Tomography. Entropy, 20(2), 121. https://doi.org/10.3390/e20020121






