Glass Transition, Crystallization of Glass-Forming Melts, and Entropy
Abstract
:1. Introduction
2. Glass and the Glass Transition
2.1. Basic Definitions and Some Comments
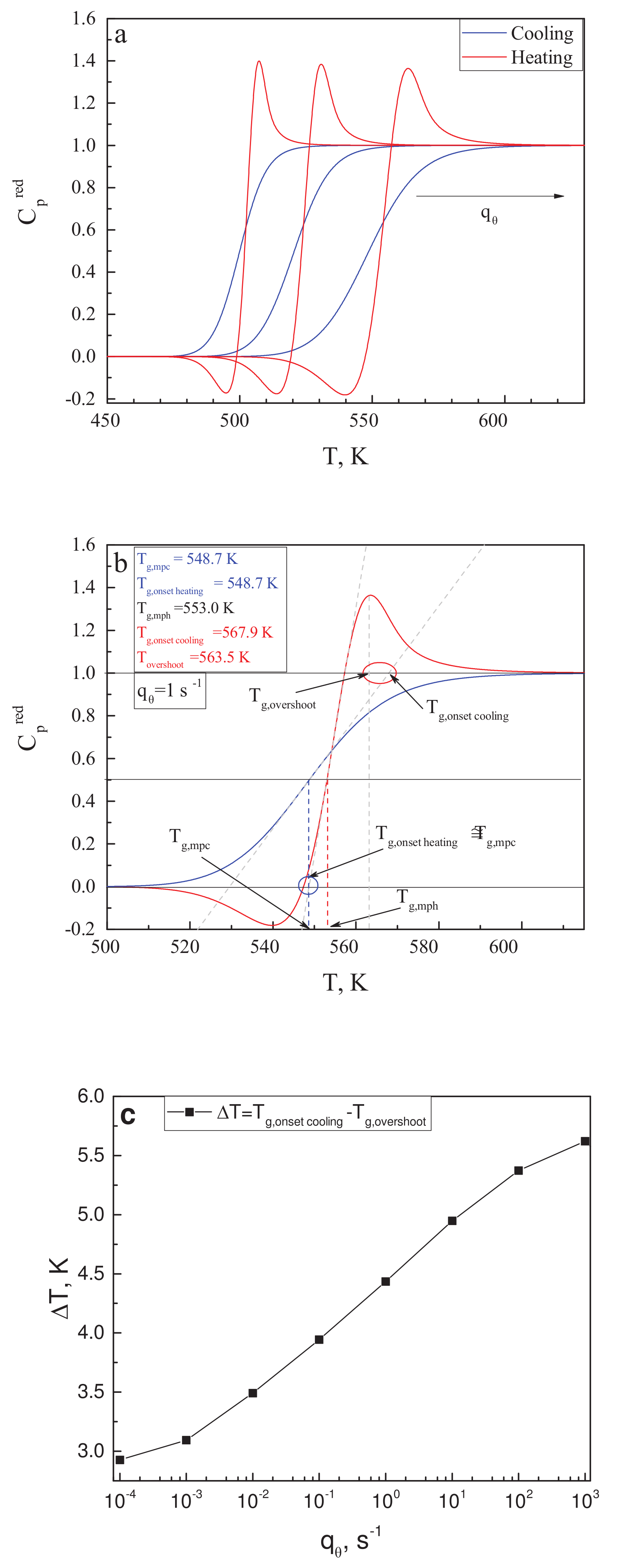
2.2. What Is the Right Deborah Number?
3. Residual Entropy of Glasses
3.1. A Brief Overview of Some Recent Discussions
3.2. Residual Entropy: A Simple Model
3.3. On the Behavior of the Thermodynamic Coefficients in the Glass-Transition Range
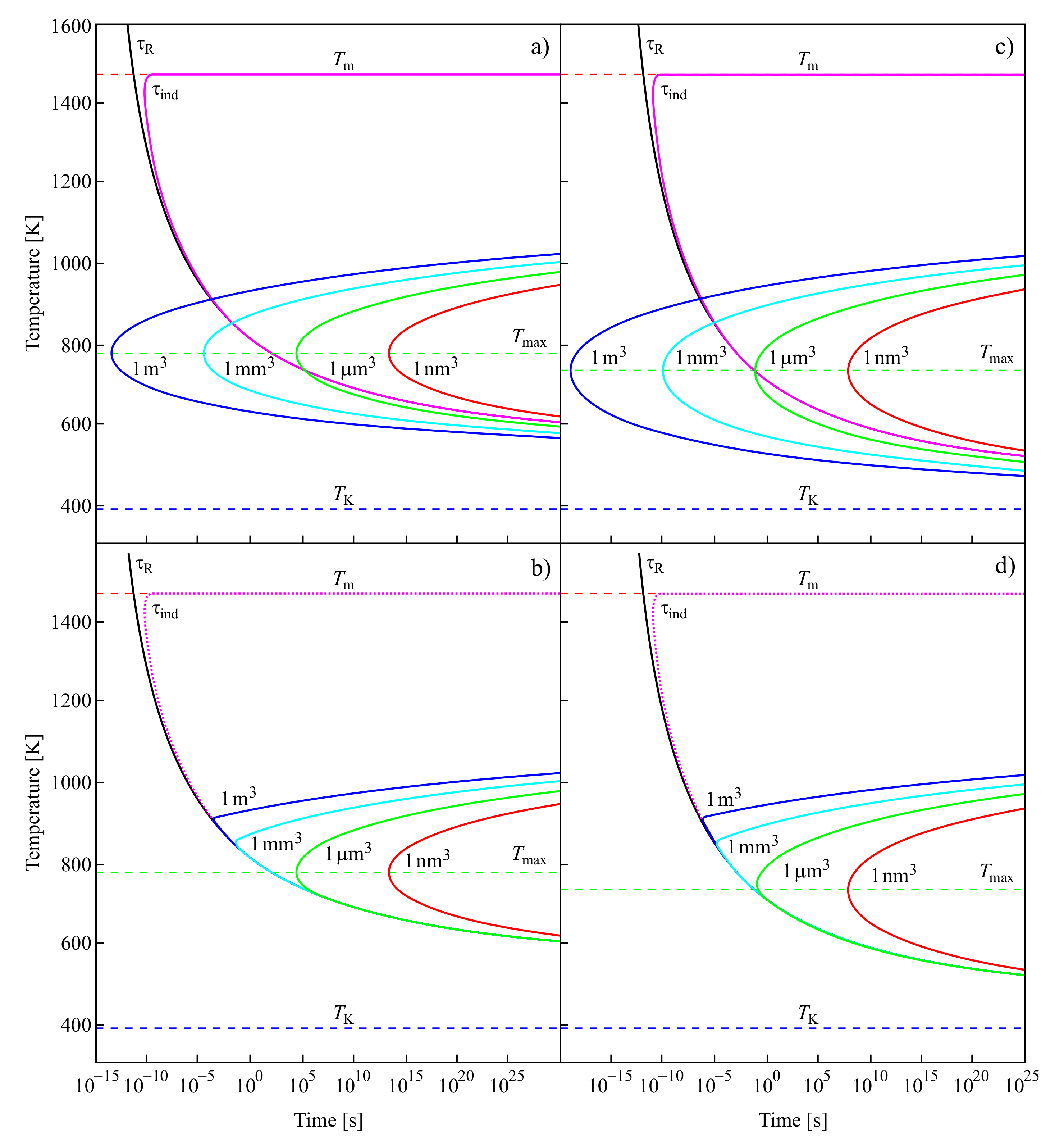
4. Is the Kauzmann Paradox Really in Conflict with Basic Laws of Nature?
5. Summary of Results and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gibbs, J.W. Graphical Methods in the Thermodynamics of Fluids; Longmans & Green: London, UK; New York, NY, USA; Bombay, India, 1906; Volume 1. [Google Scholar]
- Gibbs, J.W. Elementare Grundlagen der Statistischen Mechanik (Elementary Foundation of Statistical Mechanics); Johann Ambrosius Barth: Leipzig, Germany, 1905. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 1980. [Google Scholar]
- Koverda, V.P.; Skokov, V.N. Maximum entropy in a nonlinear system with a (1/f)-power spectrum. Physica A 2012, 391, 21–28. [Google Scholar] [CrossRef]
- Feistel, R.; Ebeling, W. Physics of Self-Organization and Evolution; Wiley-VCH: Weinheim, Germany, 2011. [Google Scholar]
- Kondepudi, D.; Prigogine, I. The Second Law of Thermodynamics and the Arrow of Time. In Modern Thermodynamics: From Heat Engines to Dissipative Structures, 2nd ed.; John Wiley & Sons: Chichester, UK, 2014. [Google Scholar]
- Feistel, R. Self-organisation of symbolic information. Eur. Phys. J. Spec. Top. 2017, 226, 207–228. [Google Scholar] [CrossRef]
- Feistel, R.; Ebeling, W. Entropy and the Self-Organization of Information and Value. Entropy 2016, 18, 193/1–193/14. [Google Scholar] [CrossRef]
- Gujrati, P.D. On Equivalence of Nonequilibrium Thermodynamic and Statistical Entropies. Entropy 2015, 17, 710–754. [Google Scholar] [CrossRef]
- Ebeling, W.; Kremp, D.; Parthey, H.; Ulbricht, H. Reversibilität und Irreversibilität als physikalisches Problem in philosophischer Sicht (Reversibility and irreversibility as a physical problem from a philosophical point of view). Wiss. Z. Univ. Rostock 1970, 1, 127–138. [Google Scholar]
- Schmelzer, J.W.P. Über eine Möglichkeit der Lösung des Widerspruchs zwischen mikroskopischer Reversibilität und makroskopischer Irreversibilität der Bewegung (On one possibility of resolution of the contradiction between microscopic reversibility and macroscopic irreversibility of motion). Rostocker Philos. Manuskr. 1981, 21, 111–122. [Google Scholar]
- Boltachev, G.S.; Schmelzer, J.W.P. On the definition of temperature and its fluctuations in small systems. J. Chem. Phys. 2010, 133, 134509/1–134509/11. [Google Scholar] [CrossRef] [PubMed]
- Chua, Y.Z.; Schulz, G.; Shoifet, E.; Huth, H.; Zorn, R.; Schmelzer, J.W.P.; Schick, C. Glass transition cooperativity from broad band heat capacity spectroscopy. Colloid Polym. Sci. 2014, 292, 1893–1904. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Boltachev, G.S.; Baidakov, V.G. Classical and Generalized Gibbs’ Approaches and the Work of Critical Cluster Formation in Nucleation Theory. J. Chem. Phys. 2006, 124, 194503/1–194503/18. [Google Scholar] [CrossRef] [PubMed]
- Nernst, W. Die Theoretischen und Experimentellen Grundlagen des Neuen Wärmesatzes (Theoretical and Experimental Foundation of the New Heat Theorem); Verlag W. Knapp: Halle, Germany, 1918. [Google Scholar]
- Haase, R. 50 Jahre Nernstscher Wärmesatz (50 years of Nernst’s heat theorem). Die Naturwiss. 1956, 43, 481–486. [Google Scholar] [CrossRef]
- Gutzow, I.S.; Schmelzer, J.W.P. Glasses and the Third Law of Thermodynamics. In Glasses and the Glass Transition; Schmelzer, J.W.P., Gutzow, I.S., Eds.; WILEY-VCH: Berlin-Weinheim, Germany, 2011; Chapter 9; pp. 357–378. [Google Scholar]
- Einstein, A. Beiträge zur Quantentheorie (Contributions to quantum theory). Verh. Deutsch. Phys. Ges. 1914, 16, 820–828. [Google Scholar]
- Simon, F. On the Third Law of Thermodynamics. Physica 1937, 4, 1089–1096. [Google Scholar] [CrossRef]
- Planck, M. Theorie der Wärme (Theory of Heat); Hirzel Verlag: Leipzig, Germany, 1930. [Google Scholar]
- Planck, M. Vorlesungen über Thermodynamik (Lectures on Thermodynamics), 10th ed.; Extended by von Laue, M.; De Gryuter: Berlin, Germany, 1954. [Google Scholar]
- Bazarow, I.P. Thermodynamik (Thermodynamics); Deutscher Verlag der Wissenschaften: Berlin, Germany, 1974. [Google Scholar]
- Nernst, W. Theoretische Chemie (Theoretical Chemistry), 16th ed.; F. Enke Verlag: Stuttgart, Germany, 1926. [Google Scholar]
- Gutzow, I.S.; Schmelzer, J.W.P. The Vitreous State: Thermodynamics, Structure, Rheology, and Crystallization, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Nemilov, S.V. Thermodynamic and Kinetic Aspects of the Vitreous State; CRC Press: Boca Raton, FL, USA; Ann Arbor, MI, USA; London, UK; Tokyo, Japan, 1995. [Google Scholar]
- Simon, F.; Lange, F. Zur Frage der Entropie amorpher Substanzen (On the question concerning the entropy of amorphous substances). Z. Phys. 1926, 38, 227–236. [Google Scholar] [CrossRef]
- Tammann, G. Die Entropien eines Kristalls und seiner Schmelze in Abhängigkeit von der Temperatur (The entropies of a crystal and its melt in dependence on temperature). Ann. Phys. 1930, 397, 107–112. [Google Scholar] [CrossRef]
- Tammann, G.; Jenckel, E. Die Kristallisationsgeschwindigkeit und die Kernzahl des Glycerins in Abhängigkeit von der Temperatur (Rate of crystallization and the number of nuclei in dependence on temperature). Z. Anorg. Allg. Chem. 1930, 103, 76–80. [Google Scholar] [CrossRef]
- Gibson, G.E.; Giauque, W.F. The Third Law of Thermodynamics. Evidence from the Specific Heats of Glycerol that the Entropy of a Glass Exceeds that of a Crystal at the Absolute Temperature. J. Am. Chem. Soc. 1923, 45, 93–104. [Google Scholar] [CrossRef]
- Simon, F. Zum Prinzip on der Unerreichbarkeit des absoluten Nullpunktes (On the principle of unattainability of the absolute zero). Z. Phys. 1927, 41, 806–809. [Google Scholar] [CrossRef]
- Simon, F. Fünfundzwanzig Jahre Nernstscher Wärmesatz (Twenty-five years of Nernst’s heat theorem). Ergebnisse der exakten Naturwiss. 1930, 9, 222–274. [Google Scholar]
- Simon, F. Über den Zustand der unterkühlten Flüssigkeiten und Gläser (On the state of undercooled liquids and glasses). Z. Anorg. Allg. Chem. 1931, 203, 219–227. [Google Scholar] [CrossRef]
- Wolynes, P.G. Entropy Crises in Glasses and Random Heteropolymers. J. Res. Natl. Inst. Stand. Technol. 1997, 102, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Gutzow, I.; Petroff, B.; Möller, J.; Schmelzer, J.W.P. Glass transition and the Third Principle of thermodynamics: Reconsideration of a classical problem. Phys. Chem. Glasses 2007, 48, 168–177. [Google Scholar]
- Gutzow, I.; Schmelzer, J.W.P. The Third Principle of thermodynamics and the zero-point entropy of glasses: History and new developments. J. Non-Cryst. Solids 2009, 355, 581–594. [Google Scholar] [CrossRef]
- Johari, G.P. Configurational and residual entropies of nonergodic crystals and the entropy’s behavior on glass formation. J. Chem. Phys. 2010, 132, 124509/1–124509/7. [Google Scholar] [CrossRef] [PubMed]
- Gutzow, I.S.; Petroff, B.P.; Todorova, S.V.; Schmelzer, J.W.P. Thermodynamics of Amorphous Solids, Glasses, and Disordered Crystals. In Glasses and the Glass Transition; Schmelzer, J.W.P., Gutzow, I.S., Eds.; WILEY-VCH: Berlin-Weinheim, Germany, 2011; pp. 179–221. [Google Scholar]
- Pauling, L. The Structure and Entropy of Ice and of Other Crystals with Some Randomness of Atomic Arrangement. J. Am. Chem. Soc. 1935, 57, 2680–2684. [Google Scholar] [CrossRef]
- Aji, D.P.B.; Johari, G.P. Fictive temperature, structural relaxation, and reality of residual entropy. J. Phys. Chem. B 2010, 114, 9578–9585. [Google Scholar] [CrossRef] [PubMed]
- Tammann, G. Der Glaszustand (The Vitreous State); Leopold Voss Verlag: Leipzig, Germany, 1933. [Google Scholar]
- Tammann, G.; Kohlhaas, A. Die Begrenzung des Erweichungsintervalles der Gläser und die abnorme Änderung der spezifischen Wärme und des Volumens im Erweichungsgebiet (The boundaries of the softening interval of glasses and the abnormal variation of the specific heat and the volume in the softening interval). Z. Anorg. Allg. Chem. 1929, 182, 49–73. [Google Scholar]
- Parks, G.S.; Huffmann, H.M. Studies on glass. I. The transition between the glassy and liquid states in the case of some simple organic compounds. J. Phys. Chem. 1927, 31, 1842–1855. [Google Scholar] [CrossRef]
- Schick, C.; Zhuravlev, E.; Androsch, R.; Wurm, A.; Schmelzer, J.W.P. Influence of Thermal Prehistory on Crystal Nucleation and Growth in Polymers. In Glass: Selected Properties and Crystallization; Schmelzer, J.W.P., Ed.; De Gruyter: Berlin, Germany, 2014; pp. 1–93. [Google Scholar]
- Dyre, J. Colloquium: The glass transition and elastic models of glass-forming liquids. Rev. Mod. Phys. 2006, 78, 953–972. [Google Scholar] [CrossRef]
- Wool, R.P. Twinkling fractal theory of the glass transition. J. Polym. Sci. Polym. Phys. 2008, 46, 2765–2778. [Google Scholar] [CrossRef]
- Ojovan, M.I. Ordering and structural changes at the glass-liquid transition. J. Non-Cryst. Solids 2013, 382, 79–86. [Google Scholar] [CrossRef]
- Sanditov, D.S. Model of delocalized atoms in the physics of the vitreous state. J. Exp. Theor. Phys. 2012, 115, 112–124. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, B.A.; Bai, H.Y.; Wang, W.H. Evolution of hidden localized flow during glass-to-liquid transition in metallic glass. Nat. Commun. 2014, 5, 5823. [Google Scholar] [CrossRef] [PubMed]
- Tropin, T.V.; Schmelzer, J.W.P.; Aksenov, V.L. Modern aspects of the kinetic theory of glass transition. Phys. Usp. 2016, 59, 42–66. [Google Scholar] [CrossRef]
- Debenedetti, P.G. Metastable Liquids: Concepts and Principles; Princeton University Press: Princeton, NJ, USA, 1996. [Google Scholar]
- Anderson, P.W. Viewpoint: The future. Science 1995, 267, 1615–1616. [Google Scholar] [CrossRef] [PubMed]
- Zanotto, E.D.; Mauro, J.C. The glassy state of matter: Its definition and ultimate fate. J. Non-Cryst. Solids 2017, 471, 490–495. [Google Scholar] [CrossRef]
- Tool, A.Q. Relation between inelastic deformability and thermal expansion of glass in its annealing range. J. Am. Ceram. Soc. 1946, 29, 240–253. [Google Scholar] [CrossRef]
- Gutzow, I.; Grigorova, T.; Avramov, I.; Schmelzer, J.W.P. Generic phenomenology of vitrification and relaxation and the Kohlrausch and Maxwell equations. Phys. Chem. Glasses 2002, 43C, 477–486. [Google Scholar]
- Zanotto, E.D. Do cathedral glasses flow? Am. J. Phys. 1998, 66, 392–395. [Google Scholar] [CrossRef]
- Zanotto, E.D.; Gupta, P.K. Do cathedral glasses flow?—Additional remarks. Am. J. Phys. 1999, 67, 260–262. [Google Scholar] [CrossRef]
- Davies, R.O.; Jones, G.O. Thermodynamic and kinetic properties of glasses. Adv. Phys. 1953, 2, 370–410. [Google Scholar] [CrossRef]
- Ojovan, M.I. Viscous flow and the viscosity of melts and glasses. Phys. Chem. Glasses 2012, 53, 143–150. [Google Scholar]
- Priven, A.I. Methods of Prediction of Glass Properties from Chemical Compositions. In Glasses and the Glass Transition; Schmelzer, J.W.P., Gutzow, I.S., Eds.; WILEY-VCH: Berlin, Germany, 2011; pp. 255–309. [Google Scholar]
- Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M.; Schick, C.; Zanotto, E.D. Crystallization in glass-forming liquids: Maxima of nucleation, growth, and overall crystallization rates. J. Non-Cryst. Solids 2015, 429, 24–32. [Google Scholar] [CrossRef]
- Fokin, V.M.; Yuritsyn, N.S.; Zanotto, E.D.; Schmelzer, J.W.P. Homogeneous crystal nucleation in silicate glasses: A 40 years perspective. J. Non-Cryst. Solids 2006, 352, 2681–2714. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M.; Schick, C.; Zanotto, E.D. Crystallization in glass-forming liquids: Effects of decoupling of diffusion and viscosity on crystal growth. J. Non-Cryst. Solids 2015, 429, 45–53. [Google Scholar] [CrossRef]
- Tammann, G. Über die Abhängigkeit der Zahl der Kerne, welche sich in verschiedenen unterkühlten Flüssigkeiten bilden, von der Temperatur (On the dependence of the number of nuclei, which are formed in undercooled liquids, on temperature). Z. Phys. Chem. 1898, 25, 441–479. [Google Scholar]
- Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M.; Schick, C. Kauzmann paradox and the crystallization of glass-forming melts. J. Non-Cryst. Solids 2017. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M. Crystallization of glass: What we know, what we need to know. Int. J. Appl. Glass Sci. 2016, 7, 253–261. [Google Scholar] [CrossRef]
- Available online: https://en.wikipedia.org/wiki/Amber (accessed on 31 January 2018).
- Available online: http://geology.com/rocks/obsidian.shtml (accessed on 31 January 2018).
- Schmelzer, J.W.P.; Gutzow, I.S. Glasses and the Glass Transition; WILEY-VCH: Berlin-Weinheim, Germany, 2011. [Google Scholar]
- Schmelzer, J.W.P. Glass: Selected Properties and Crystallization; De Gruyter: Berlin, Germany, 2014. [Google Scholar]
- Berthier, L.; Ediger, M.D. Facets of glass physics. Phys. Today 2016, 69, 41–46. [Google Scholar] [CrossRef]
- Gibbs, J.W. The Collected Works; Thermodynamics; Longmans & Green: New York; NY, USA; London, UK; Toronto, ON, Canada, 1928; p. 96. [Google Scholar]
- Bartenev, G.M. On the vitrification of high-polymer bodies at periodic deformation. Dokl. Akad. Nauk SSSR 1949, 69, 373–376. (In Russian) [Google Scholar]
- Bartenev, G.M. On the relation between the glass transition temperature of silicate glass and rate of cooling or heating. Dokl. Akad. Nauk SSSR 1951, 76, 227–230. (In Russian) [Google Scholar]
- Bartenev, G.M.; Lukyanov, I.A. Dependence of the glass-transition temperature of amorphous substances on the heating rate and the relation between glass transition temperature and activation energy. Zhurnal Fizicheskoi Khimii 1955, 29, 1486–1498. (In Russian) [Google Scholar]
- Ritland, H.N. Density phenomena in the transformation range of a borosilicate crown glass. J. Am. Ceram. Soc. 1954, 37, 370–377. [Google Scholar] [CrossRef]
- Volkenstein, M.V.; Ptizyn, O.B. Relaxation theory of glass transition. Dokl. Akad. Nauk USSR 1955, 103, 795–798. (In Russian) [Google Scholar]
- Volkenstein, M.V.; Ptizyn, O.B. Relaxation theory of glass transition: Solution of the basic equation and its analysis. Zhurnal Tekhnicheskoi Fiziki 1956, 26, 2204–2222. (In Russian) [Google Scholar]
- Cooper, A.R.; Gupta, P.K. A dimensionless parameter to characterize the glass transition. Phys. Chem. Glasses 1982, 23, 44–45. [Google Scholar]
- Bragg, W.L.; Williams, E.J. The effect of thermal agitation on atomic arrangement in alloys. Proc. R. Soc. Lond. A 1934, 145, 699–730. [Google Scholar] [CrossRef]
- Reiner, M. The Deborah number. Phys. Today 1964, 17, 62. [Google Scholar] [CrossRef]
- Mazurin, O.V.; Cooper, A.R. An analysis of the suitability of the Lillie number to characterize the glass transition of real glass-forming substances. J. Non-Cryst. Solids 1985, 72, 65–71. [Google Scholar] [CrossRef]
- Möller, J.; Gutzow, I.; Schmelzer, J.W.P. Freezing-in and production of entropy in vitrification. J. Chem. Phys. 2006, 125, 094505/1–094505/13. [Google Scholar] [CrossRef] [PubMed]
- Schmelzer, J.W.P. Kinetic criteria of glass formation and the pressure dependence of the glass transition temperature. J. Chem. Phys. 2012, 136, 074512/1–074512/11. [Google Scholar] [CrossRef] [PubMed]
- Schmelzer, J.W.P.; Tropin, T.V. Kinetic criteria of glass-formation, pressure dependence of the glass-transition temperature, and the Prigogine-Defay ratio. J. Non-Cryst. Solids 2015, 407, 170–178. [Google Scholar] [CrossRef]
- Johari, G.P. On relative merits of the criteria of glass formation and effects of ultraviscous liquid properties. J. Non-Cryst. Solids 2017, 471, 439–445. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Tropin, T.V. Dependence of the width of the glass transition interval on cooling and heating rates. J. Chem. Phys. 2013, 138, 034507/1–034507/11. [Google Scholar] [CrossRef] [PubMed]
- Tropin, T.V.; Schmelzer, J.W.P.; Gutzow, I.; Schick, C. On the theoretical determination of the Prigogine-Defay ratio in glass transition. J. Chem. Phys. 2012, 136, 124502/1–124502/14. [Google Scholar] [CrossRef] [PubMed]
- Gujrati, P.D. Nonequilibrium thermodynamics: Structural relaxation, fictive temperature, and Tool-Narayanaswamy phenomenology in glasses. Phys. Rev. E 2010, 81, 051130/1–051130/13. [Google Scholar] [CrossRef] [PubMed]
- Johari, G.P. Determining Temperature-Invariant Enthalpy Change and Other Thermodynamic Functions on Transformation of Proteins and Other Biopolymers. J. Phys. Chem. B 1997, 101, 6780–6785. [Google Scholar] [CrossRef]
- Kivelson, D.; Reiss, H. Metastable Systems in Thermodynamics: Consequences, Role of Constraints. J. Phys. Chem. B 1999, 103, 8337–8343. [Google Scholar] [CrossRef]
- Reiss, H. Apparent entropy, residual entropy, causality, metastability, constraints, and the glass transition. J. Non-Cryst. Solids 2009, 355, 617–623. [Google Scholar] [CrossRef]
- Yang, C.N.; Lee, T.D. Statistical Theory of Equations of State and Phase Transitions. I. Theory of Condensation. Phys. Rev. 1952, 87, 404–409. [Google Scholar] [CrossRef]
- Baidakov, V.G. On the Thermodynamic Properties of Metastable Systems. In Nucleation Theory and Applications; Workshop Proceedings 2005–2008; Schmelzer, J.W.P., Röpke, G., Priezzhev, V.B., Eds.; Joint Institute for Nuclear Research Publishing Department: Dubna, Russia, 2008; pp. 11–16. [Google Scholar]
- Baidakov, V.G. Thermophysical properties of superheated liquids. In Soviet Technology Reviews; Gordon and Breach Publishers: Reading, UK, 1994; Volume 5, pp. 1–88. [Google Scholar]
- Davies, R.O.; Jones, G.O. The irreversible approach to equilibrium in glasses. Proc. R. Soc. A 1953, 217, 26–42. [Google Scholar] [CrossRef]
- Gupta, P.K.; Mauro, J.C. The configurational entropy of glass. J. Non-Cryst. Solids 2009, 355, 595–599. [Google Scholar] [CrossRef]
- Mauro, J.C.; Gupta, P.K.; Loucks, R.J.; Varshneya, A.K. Non-equilibrium entropy of glasses formed by continuous cooling. J. Non-Cryst. Solids 2009, 355, 600–606. [Google Scholar] [CrossRef]
- Mauro, J.C.; Loucks, R.J.; Sabyasachi, S. Heat capacity, enthalpy fluctuations, and configurational entropy in broken ergodic systems. J. Chem. Phys. 2010, 133, 164503/1–164503/9. [Google Scholar] [CrossRef] [PubMed]
- Patrascioiu, A. The Ergodic Hypothesis: A Complicated Problem in Mathematics and Physics; Los Alamos Science Special Issue; Los Alamos National Laboratory Publishers: Los Alamos, NM, USA, 1987; pp. 262–279. [Google Scholar]
- Brush, S.G. The Kinetic Theory of Gases; Imperial College Press: London, UK, 2003. [Google Scholar]
- Palmer, R.G. Broken ergodicity. Adv. Phys. 1982, 31, 669–735. [Google Scholar] [CrossRef]
- Goldstein, M. On the reality of residual entropies of glasses and disordered crystals. J. Chem. Phys. 2008, 128, 154510/1–154510/7. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, M. On the reality of the residual entropy of glasses and disordered crystals: The entropy of mixing. J. Non-Cryst. Solids 2011, 357, 463–465. [Google Scholar] [CrossRef]
- Goldstein, M. On the reality of the residual entropies of glasses and disordered crystals: Counting microstates, calculating fluctuations, and comparing averages. J. Chem. Phys. 2011, 134, 124502/1–124502/4. [Google Scholar] [CrossRef] [PubMed]
- Johari, G.P. Mechanical relaxation and the notion of time-dependent extent of ergodicity during the glass transition. Phys. Rev. E 2011, 84, 021501/1–021501/17. [Google Scholar] [CrossRef] [PubMed]
- Johari, G.P. Specific heat relaxation-based critique of isothermal glass transition, zero residual entropy and time-average formalism for ergodicity loss. Thermochim. Acta 2011, 523, 97–104. [Google Scholar] [CrossRef]
- Richet, P. Residual and configurational entropy: Quantitative checks through applications of Adam—Gibbs theory to the viscosity of silicate melts. J. Non-Cryst. Solids 2009, 355, 628–635. [Google Scholar] [CrossRef]
- Conradt, R. On the entropy difference between the vitreous and the crystalline state. J. Non-Cryst. Solids 2009, 355, 636–641. [Google Scholar] [CrossRef]
- Fotheringham, U.; Baltes, A.; Müller, R.; Conradt, R. The residual configurational entropy below the glass transition: Determination for two commercial optical glasses. J. Non-Cryst. Solids 2009, 355, 642–652. [Google Scholar] [CrossRef]
- Nemilov, S.V. Zero-point entropy of glasses as physical reality. J. Non-Cryst. Solids 2009, 355, 607–616. [Google Scholar] [CrossRef]
- Johari, G.P. On resolving the statistical and calorimetric entropies of glass and non-crystalline solids, and the residual entropy problem. Thermochim. Acta 2010, 500, 111–118. [Google Scholar] [CrossRef]
- Johari, G.P.; Khouri, J. Entropy change on the cooling and heating paths between liquid and glass and the residual entropy. J. Chem. Phys. 2011, 134, 034515/1–034515/6. [Google Scholar] [CrossRef] [PubMed]
- Johari, G.P.; Aji, D.P.B.; Gunawan, L. Clausius limits on cooling and heating through the liquid—Glass range of three pharmaceuticals and one metal alloy-Annealing effects and residual entropy. Thermochim. Acta 2011, 522, 173–181. [Google Scholar] [CrossRef]
- Tombari, E.; Johari, G.P. Change in entropy in thermal hysteresis of liquid-glass-liquid transition and consequences of violating the Clausius theorem. J. Chem. Phys. 2014, 141, 074502/1–074502/5. [Google Scholar] [CrossRef] [PubMed]
- Schmelzer, J.W.P.; Gutzow, I. Structural order-parameters, the Prigogine-Defay ratio, and the behavior of the entropy in vitrification. J. Non-Cryst. Solids 2009, 355, 653–662. [Google Scholar] [CrossRef]
- Tropin, T.V.; Schmelzer, J.W.P.; Schick, C. On the dependence of the properties of glasses on cooling and heating rates. I. Entropy, entropy production, and glass transition temperature. J. Non-Cryst. Solids 2011, 357, 1291–1302. [Google Scholar] [CrossRef]
- Tropin, T.V.; Schmelzer, J.W.P.; Schick, C. On the Dependence of the Properties of Glasses on Cooling and Heating Rates. II. Prigogine-Defay Ratio, Fictive Temperature, and Fictive Pressure. J. Non-Cryst. Solids 2011, 357, 1303–1309. [Google Scholar] [CrossRef]
- Jordanov, N.; Wondraczek, L.; Gutzow, I. Thermodynamic properties of vitreous electrodes in a Ni/NiP glass-crystal Galvanic cell. J. Non-Cryst. Solids 2015, 382, 125–132. [Google Scholar] [CrossRef]
- Angell, C.A. Liquid Fragility and the Glass Transition in Water and Aqueous Solutions. Chem. Rev. 2002, 102, 2627–2650. [Google Scholar] [CrossRef] [PubMed]
- Mazurin, O.V. Problems of Compatibility of the Values of Glass Transition Temperatures Published in the World Literature. Glass Phys. Chem. 2007, 33, 22–36. [Google Scholar] [CrossRef]
- Cahn, R.W. Missing atoms and melting. Nature 1992, 356, 108–109. [Google Scholar] [CrossRef]
- Stillinger, F.H.; Debenedetti, P.G. Glass transition: Thermodynamics and kinetics. Annu. Rev. Condens. Matter Phys. 2013, 4, 263–285. [Google Scholar] [CrossRef]
- Gupta, P.K.; Cassar, D.R.; Zanotto, E.D. Role of dynamic heterogeneities in crystal nucleation kinetics in an oxide supercooled liquid. J. Chem. Phys. 2016, 145, 211920/1–211920/7. [Google Scholar] [CrossRef] [PubMed]
- Kauzmann, W. The Nature of the Glassy State and the Behavior of Liquids at Low Temperatures. Chem. Rev. 1948, 43, 219–256. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M. Thermodynamic Aspects of Pressure-Induced Crystallization: Kauzmann Pressure. Int. J. Appl. Glass Sci. 2016, 7, 474–485. [Google Scholar] [CrossRef]
- Kauzmann, W. Reminiscences from a life in protein physical chemistry. Protein Sci. 1993, 2, 671–691. [Google Scholar] [CrossRef] [PubMed]
- Skripov, V.P. Metastable Liquids; WILEY: New York, NY, USA; Toronto, ON, Canada, 1974. [Google Scholar]
- Schmelzer, J.W.P.; Abyzov, A.S. On the theoretical description of nucleation in confined space. AIP Adv. 2011, 1, 042160/1–042160/9. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S.; Baidakov, V.G. Time of formation of the first supercritical nucleus, time-lag, and the steady-state nucleation rate. Int. J. Appl. Glass Sci. 2017, 8, 48–60. [Google Scholar] [CrossRef]
- Angell, C.A.; MacFarlane, D.R.; Oguni, M. The Kauzmann Paradox, Metastable Liquids, and Glasses: A Summary. In Dynamic Aspects of Structural Change in Liquids and Glasses; Angell, C.A., Goldstein, M., Eds.; Annals New York Academy of Sciences: New York, NY, USA, 1986; Volume 484, pp. 241–247. [Google Scholar]
- Kalinina, A.M.; Filipovich, V.N.; Fokin, V.M. Stationary and non-stationary crystal nucleation rate in a glass of 2Na2O·CaO·3SiO2 stoichiometric composition. J. Non-Cryst. Solids 1980, 38, 723–728. [Google Scholar] [CrossRef]
- Rouxel, T. Elastic properties and short-to medium-range order in glasses. J. Am. Ceram. Soc. 2007, 90, 3019–3039. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S. Pressure-induced crystallization of liquids: Maxima of nucleation, growth, and overall crystallization rates. Int. J. Appl. Glass Sci. 2018. [Google Scholar] [CrossRef]
- Schick, C.; Androsch, R.; Schmelzer, J.W.P. Homogeneous crystal nucleation in polymers. J. Phys. 2017, 29, 453002/1–453002/36. [Google Scholar] [CrossRef] [PubMed]
- Schmelzer, J.W.P.; Abyzov, A.S. Crystallization of glass-forming melts: New answers to old questions. J. Non-Cryst. Solids 2017. [Google Scholar] [CrossRef]
- Zhuravlev, E.; Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M.; Androsch, R.; Schick, C. Experimental test of Tammann’s nuclei development approach in crystallization of macromolecules. Cryst. Growth Des. 2015, 15, 786–798. [Google Scholar] [CrossRef]
- Takada, A.; Conradt, R.; Richet, P. Residual entropy and structural disorder in glass: A review of history and an attempt to resolve two apparently conflicting views. J. Non-Cryst. Solids 2015, 429, 33–44. [Google Scholar] [CrossRef]
- Simon, F. On the range of stability of the fluid state. Trans. Faraday Soc. 1937, 33, 65–73. [Google Scholar] [CrossRef]
- Bernal, J.D. An attempt at a molecular theory of liquid structure. Trans. Faraday Soc. 1937, 33, 27–40. [Google Scholar] [CrossRef]
- Frenkel, Y.I. The Kinetic Theory of Liquids; Oxford University Press: Oxford, UK, 1946. [Google Scholar]
- Skripov, V.P.; Baidakov, V.G. Absence of a spinodal in undercooled liquids. Teplofizika Vysokikh Temperatur 1972, 10, 1226–1230, English version is available in High Temp. 10, 1102 (1972). [Google Scholar]
- Skripov, V.P.; Faizullin, M.Z. Crystal-Liquid-Gas Phase Transitions and Thermodynamic Similarity; Wiley: Weinheim, Germany, 2006. [Google Scholar]
- Angell, C.A. On the uncertain distinction between fast landscape exploration and second amorphous phase (ideal glass) interpretations of the ultrastable glass phenomenon. J. Non-Cryst.Solids 2015, 407, 246–255. [Google Scholar] [CrossRef]
- Stillinger, F.H.; Debenedetti, P.G.; Truskett, T.M. The Kauzmann Paradox Revisited. J. Phys. Chem. B 2001, 105, 11809–11816. [Google Scholar] [CrossRef]
- Das, S.P. Statistical Physics of Liquids at Freezing; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Androsch, R.; Schick, C.; Schmelzer, J.W.P. Sequence of enthalpy relaxation, homogeneous nucleation, and crystal growth in glassy Polyamide 6. Eur. Polym. J. 2014, 53, 100–108. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Schick, C. Dependence of Crystallization Processes of Glass-forming Melts on Prehistory: A Theoretical Approach to a Quantitative Treatment. Phys. Chem. Glasses B 2012, 53, 99–106. [Google Scholar]
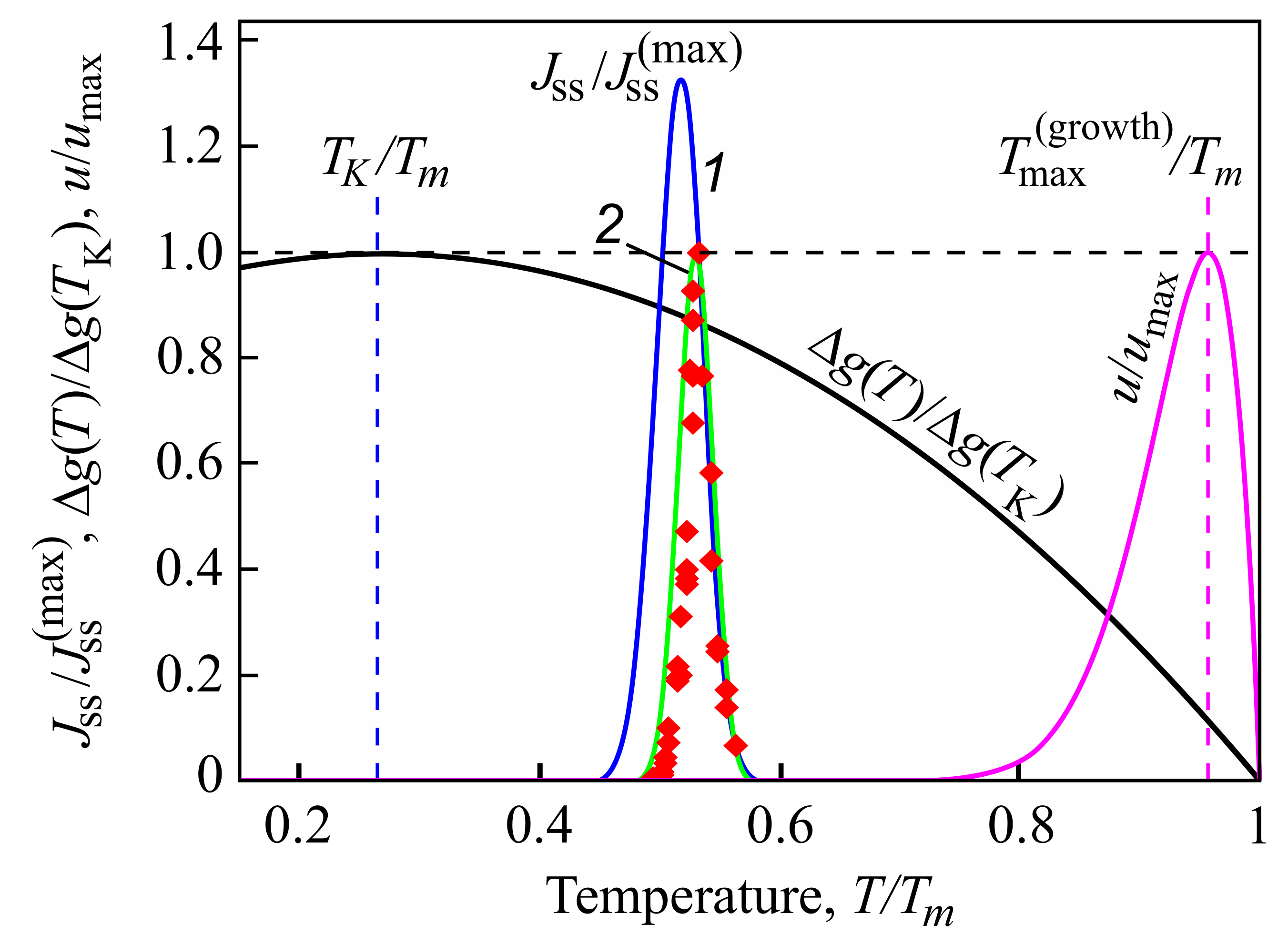
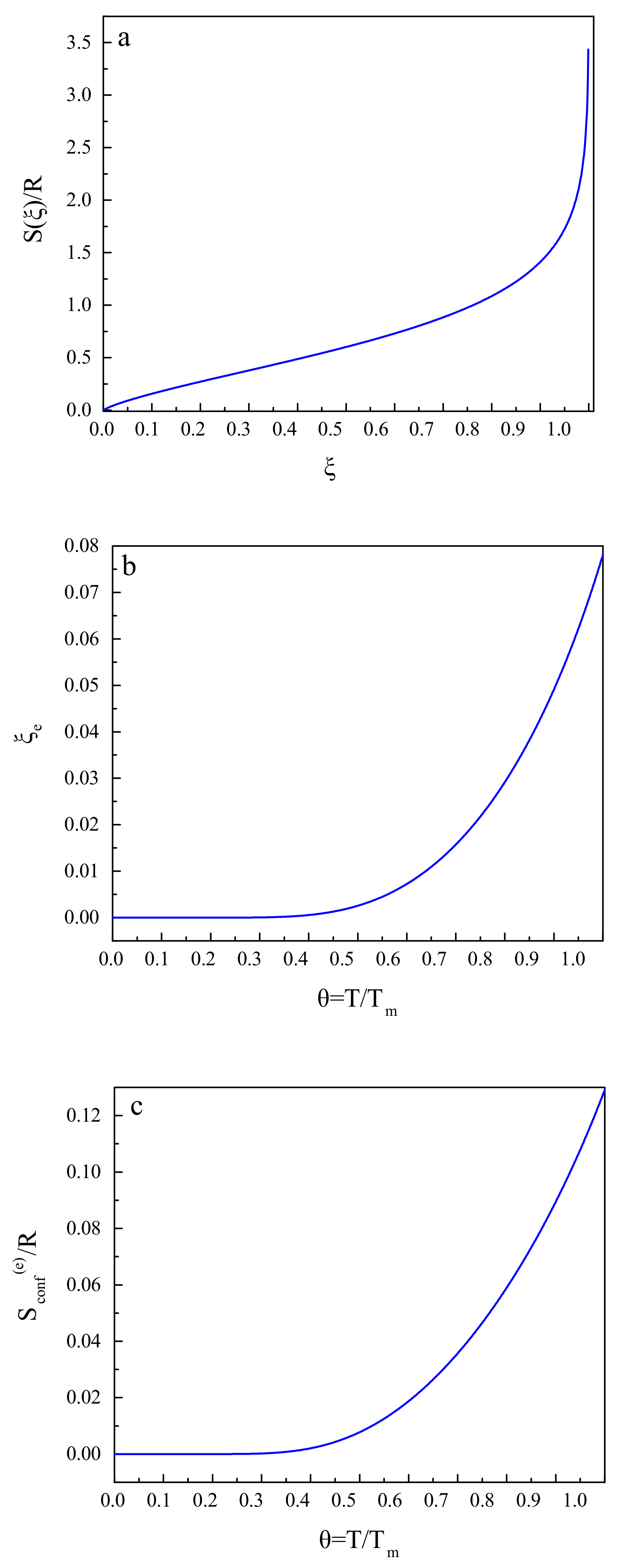
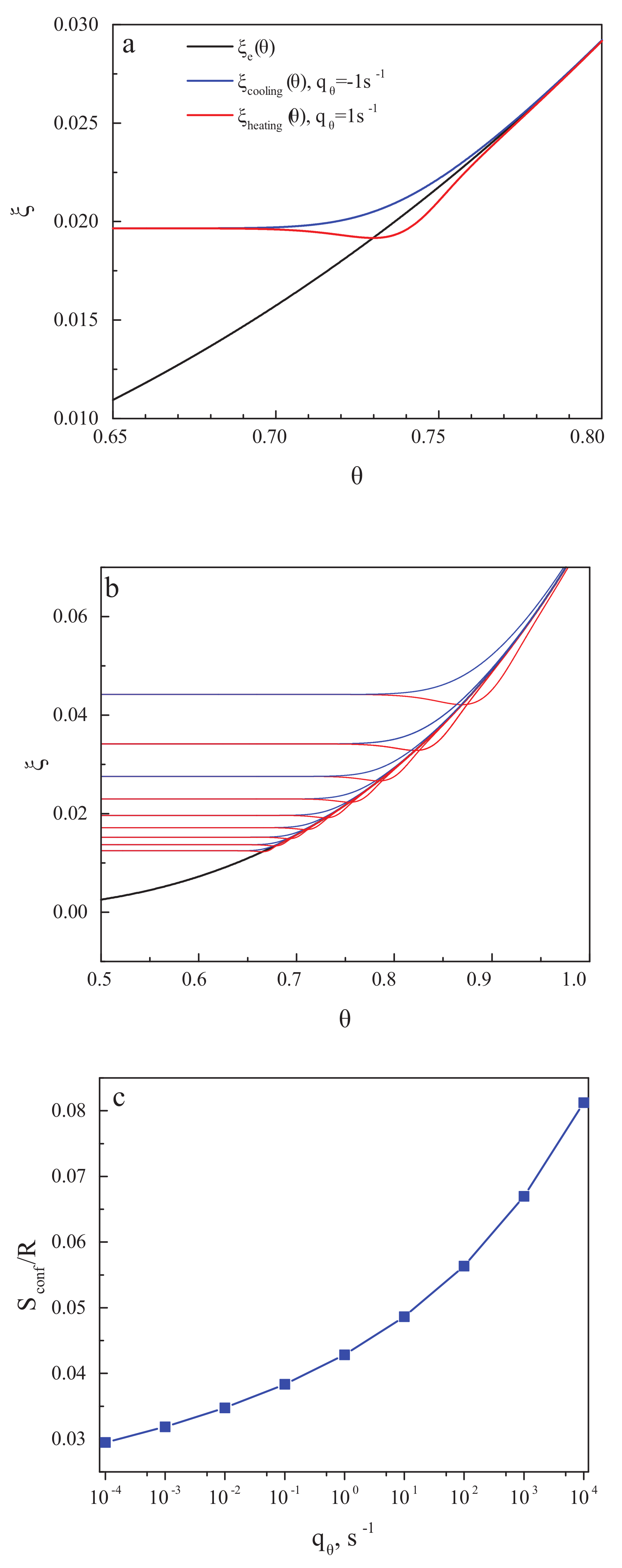
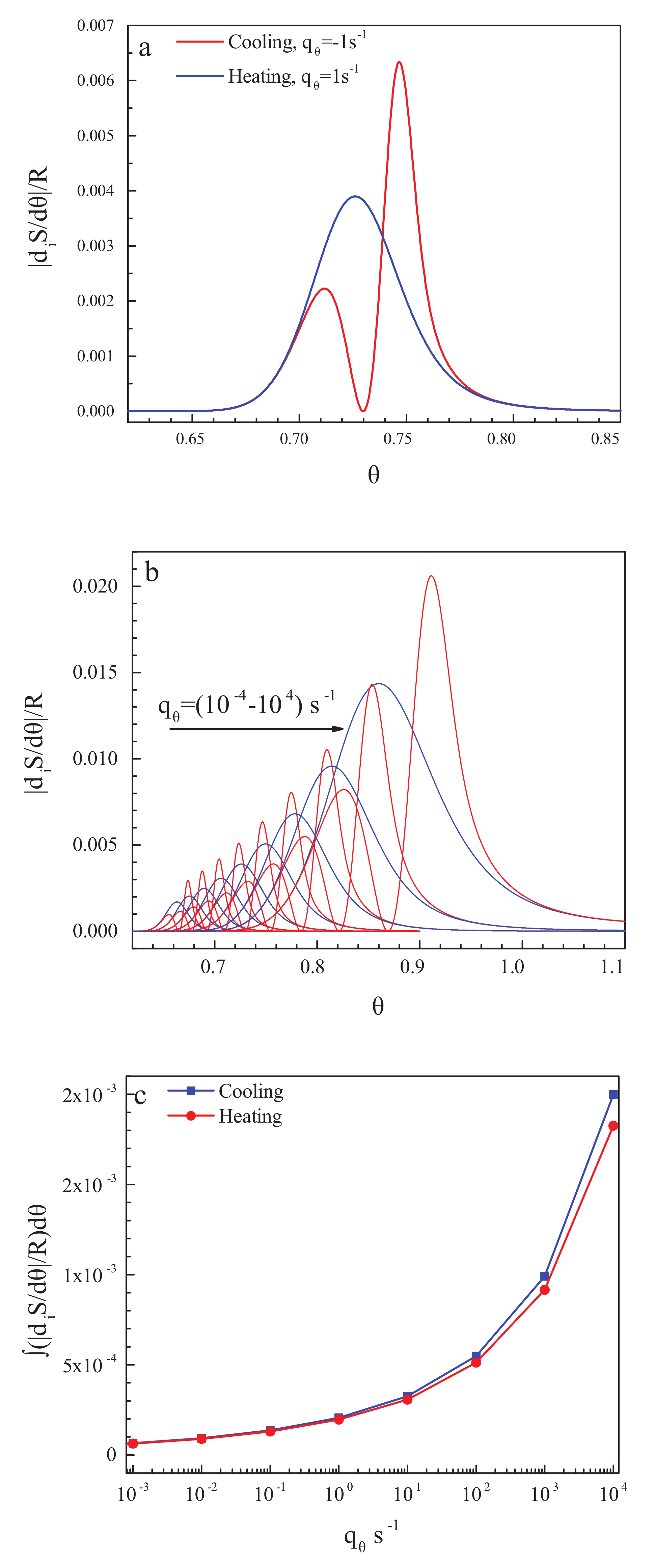

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmelzer, J.W.P.; Tropin, T.V. Glass Transition, Crystallization of Glass-Forming Melts, and Entropy. Entropy 2018, 20, 103. https://doi.org/10.3390/e20020103
Schmelzer JWP, Tropin TV. Glass Transition, Crystallization of Glass-Forming Melts, and Entropy. Entropy. 2018; 20(2):103. https://doi.org/10.3390/e20020103
Chicago/Turabian StyleSchmelzer, Jürn W. P., and Timur V. Tropin. 2018. "Glass Transition, Crystallization of Glass-Forming Melts, and Entropy" Entropy 20, no. 2: 103. https://doi.org/10.3390/e20020103
APA StyleSchmelzer, J. W. P., & Tropin, T. V. (2018). Glass Transition, Crystallization of Glass-Forming Melts, and Entropy. Entropy, 20(2), 103. https://doi.org/10.3390/e20020103





