1. Introduction
Diverse methods from complexity studies have been applied to evaluate spatio-temporal organization of seismic activity from different regions of the world. An important aspect of some of these studies is that they intend to identify potential anomalous patterns prior to the occurrence of a mainshock. Although there is some debate about the universality of these features, there are efforts to elucidate the dominance of some peculiar spatio-temporal organizational patterns in specific regions with high seismic activity. The occurrence of earthquakes is a complex phenomenon which results from interactions covering a wide range of spatio-temporal scales, with some statistical properties frequently expressed as power-law functions with fractal behavior. In many cases, the use of a single scaling exponent is not sufficient to fully characterize the variety of dynamical behaviors displayed by earthquake activity, and the use of multifractality is necessary, where a broad distribution of fractal scaling exponents is associated with the richness of the dynamics. For instance, a multifractal structure of inter-event time series has been reported for various earthquake sequences [
1,
2,
3,
4,
5,
6,
7]. However, it is widely accepted that the complexity of earthquake activity is observed in both spatial and temporal domains, the use of parameters which contain information from both sides being necessary. This is compatible, for example, with the findings of the analysis in natural time [
8] of the seismicity in Japan for 1994–2011, which revealed that the spatiotemporal variations of the order parameter of seismicity enable the estimation of the epicentral location of forthcoming major earthquakes [
9].
In a related way, the identification of a seismic quiescence, defined as a temporal window where a function associated with the rate of seismic process attains an abnormal value, represents a potential source of information to characterize anomalous seismic activity [
10]. Probably the seismic quiescence is the most reported seismicity pattern, prior to the occurrence of a large earthquake [
11,
12]. The Mexican coast of the Pacific is not the exception; for the last five decades, four earthquakes of magnitude
have been preceded by important patterns of seismic quiescence [
13,
14]. As we said, on 7 September 2017, a great earthquake of
occurred at Tehuantepec Isthmus in Mexico. For a long time, some seismologists thought that in this section of the Pacific trench, an aseismic slip of the Cocos plate could occur or a recurrence period for big earthquakes could be abnormally large [
15]. However, the great earthquake of 7 September 2017 helps to better understand the dynamics of the subduction process [
16,
17]. Motivated by this event, we decided to investigate if this great earthquake had some particular statistical features and precursor quietude patterns similar to those we have reported previously [
14]. We report that the spatio-temporal organization represented by the pseudo-velocities exhibits changes in the multifractality with a narrower and asymmetric spectrum for the years 2013 until almost the end of 2016. We also found that the Schreider algorithm shows an important period of seismic quietude, for six to seven years, from 2008 to 2015 approximately, known as the alpha stage, and a beta stage of resumption of seismic activity, with a duration of approximately three years until the occurrence of the great earthquake of magnitude
, occurred on 7 September 2017, with an epicenter in the region of the Tehuantepec Isthmus in Mexico. The alpha and beta stages are taken in the sense of Ohtake [
18]. The paper is organized as follows. In
Section 2, a description of the dataset and methods is presented. The results and discussion are described in
Section 3. Finally, some conclusions are given in
Section 4.
3. Multifractality of Pseudo-Velocities
Prior to the description of multifractal properties of the pseudo-velocities, we describe some representative statistical parameters of the corresponding velocity distributions along the time. Specifically, a sliding window which contains
data values is considered with an overlapping of 990 values. For each window, we calculated the usual statistical parameters: the skewness
, the Kurtosis
K, and the coefficient of variation
C.
is a measure of the lack of symmetry. Negative (positive) values are associated with the existence of left (right) asymmetric tails longer than the right (left) tail.
K is a measure of whether the data are peaked (
K ) or flat (
) relative to a normal distribution. The coefficient of variation is defined as the ratio between the standard deviation and the mean value.
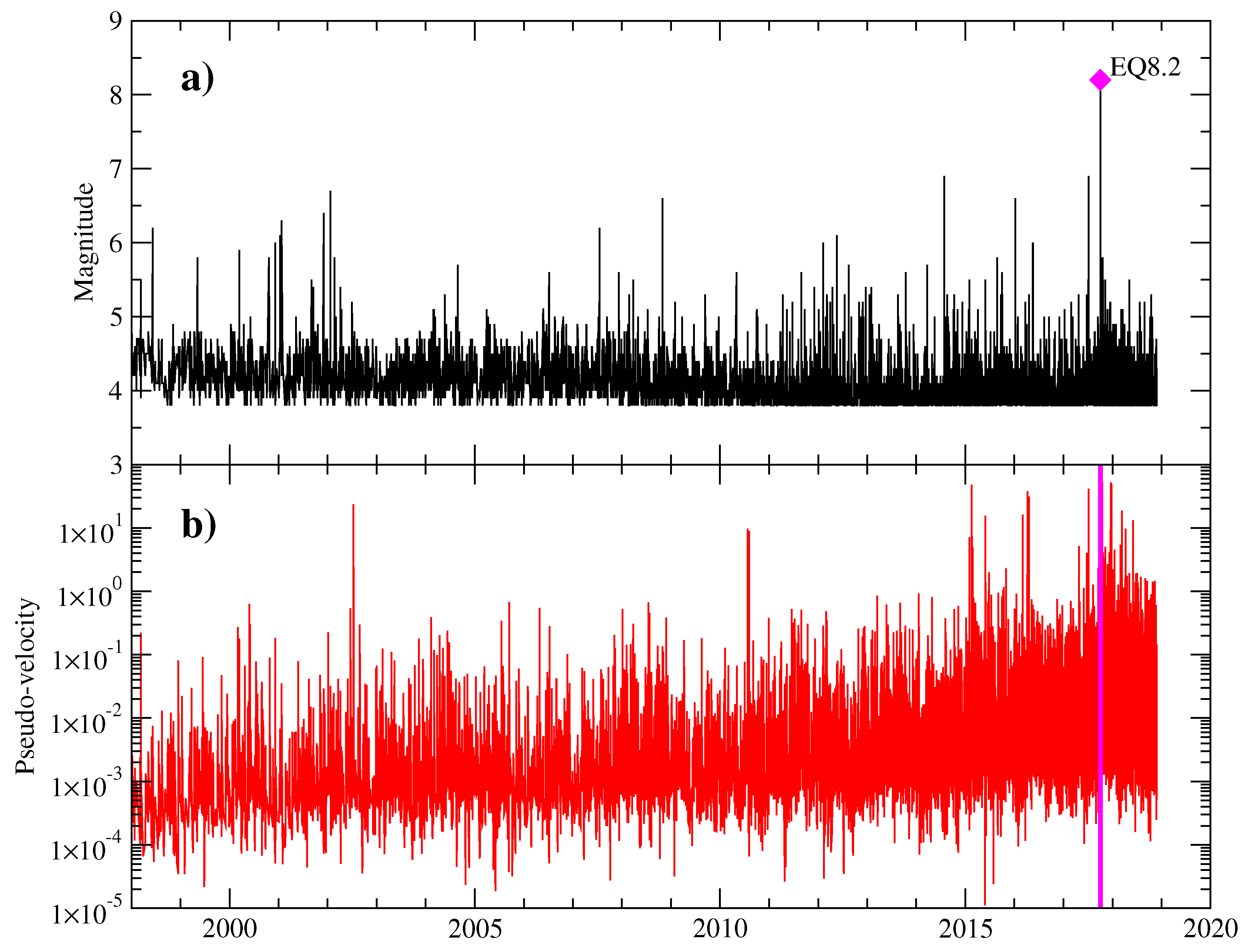
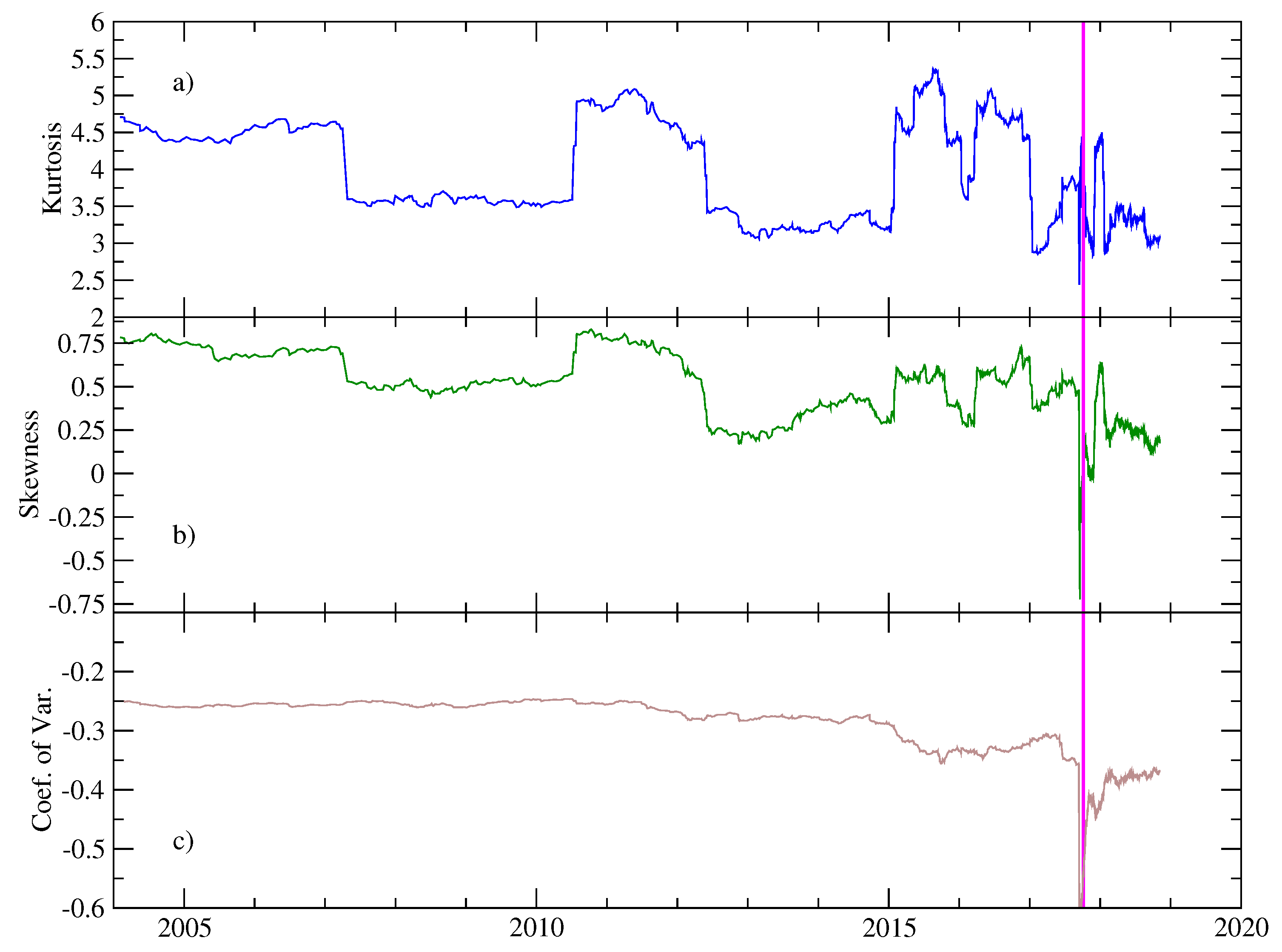
Figure 3a–c shows the results of these metrics as a function of time for the period before the main shock. We observe that
is positive along the whole period, starting from 1 with fluctuations around
, indicating that distributions are positively skewed. There are some periods for which
is close to the neutral zero value. We will discuss this property later in the Results section. After the EQ8.2,
is also close to zero, indicating that pseudo-velocities are well described by a normal distribution. For the Kurtosis
K, the evolution displays values between 3 and 5, denoting that pseudo-velocities distributions are relatively more peaked compared to the Gaussian distribution. We roughly identify several periods for which
K has a lower local value, revealing that, for these windows, the distributions are identified as quasi-symmetrical and close to the Gaussian one. The coefficient of variation exhibits a slowly decreasing behavior with some fluctuations until the occurrence of the main shock. This behavior is expected due to the fact that the mean value decreases for the whole interval before the mainshock (see
Figure 3c).
Next, we applied the MDFA method to the same windows (with
values) as described above.
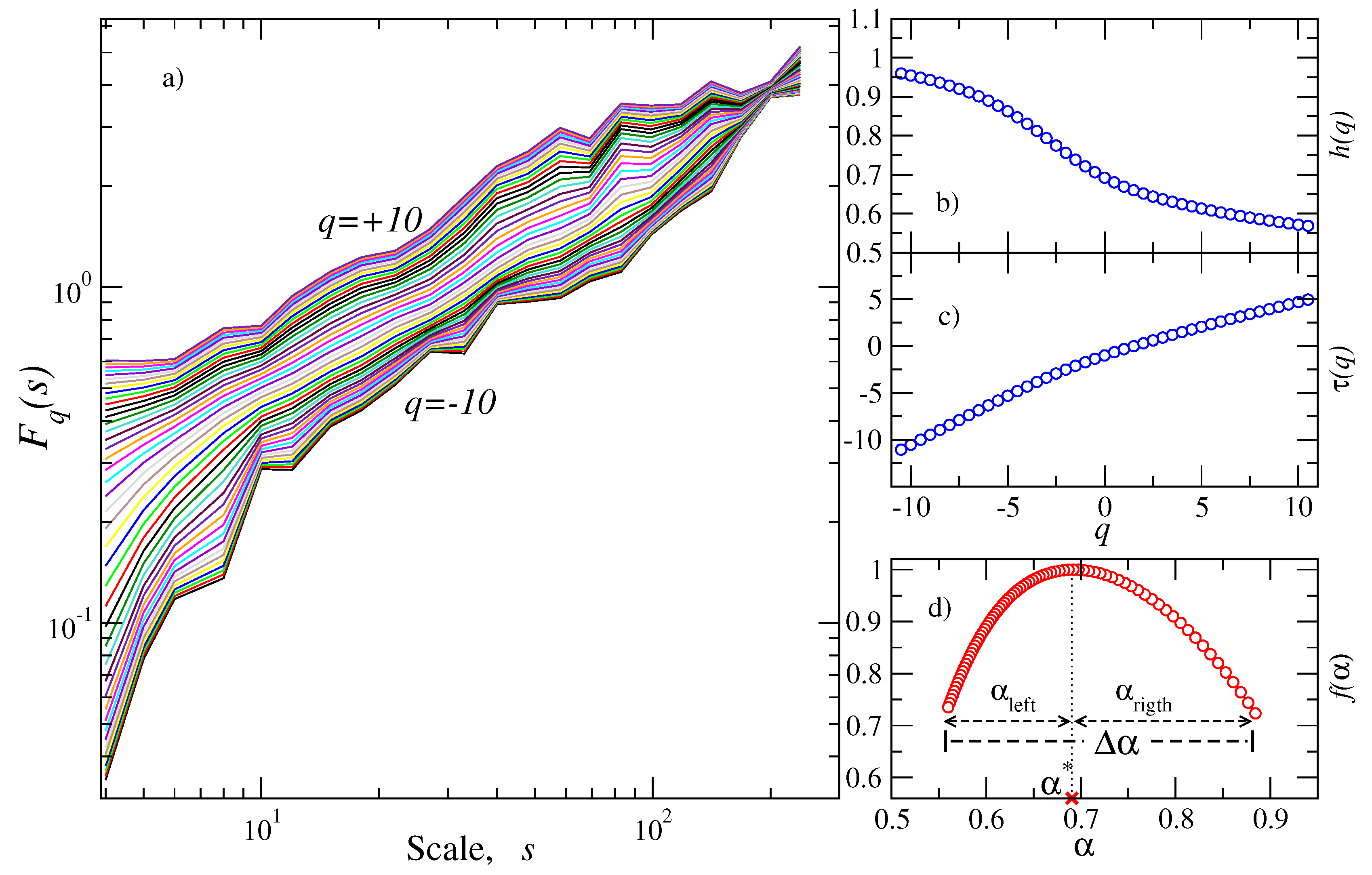
Figure 4a shows representative cases of the spectra
vs.
s for several values of
q within the interval
. The estimation of the scaling exponents
(and
) permits determining the dependence of these exponents in terms of the
q-moments as shown in
Figure 4b,c, and, finally, the multifractal spectrum is constructed (see
Figure 4d). We focused our attention on the evolution of the parameters which characterize the multifractality within each window. The results are depicted in
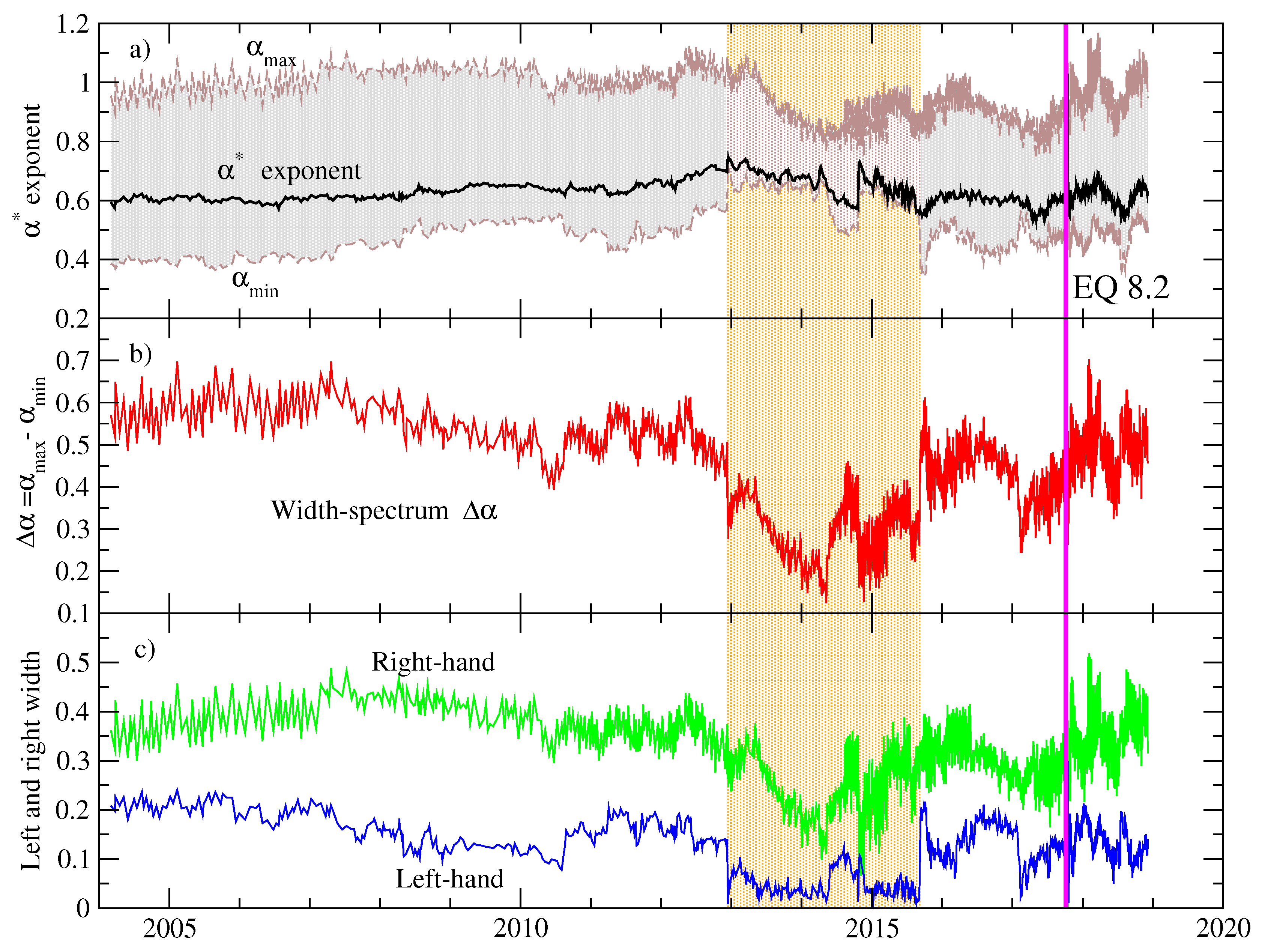
Figure 5. The exponent
exhibits a slight upward trend from 0.6 to 0.7 for the period 2004 until the end of 2012 (see
Figure 5a); from the beginning of 2013 until approximately the end of 2015, the
-exponent fluctuates between 0.6 and 0.7 and then fluctuations around 0.6 are observed until the main shock occurred. Interestingly, a noticeable decrease in the width of the spectrum (
) is clearly observed for the period 2013 until the end of 2015 (vertical shaded area shown in
Figure 5a), suggesting that a more monofractal behavior is present for this period (see
Figure 5b). Outside this interval, the width of the spectrum exhibits higher values (
before 2013 and
after 2015) until the mainshock, revealing a broad multifractality. Regarding the asymmetry parameters (see
Figure 5c), the left-hand width that corresponds to positive moments (large fluctuations) suffers the most noticeable reduction for the period where the width is narrower, while, for the right-hand width (small fluctuations), the reduction is smaller. This indicates that large fluctuations are the ones that contribute to the reduction of the spectrum. For the periods outside this region, the asymmetry parameters are higher except for a short interval just before the main shock.
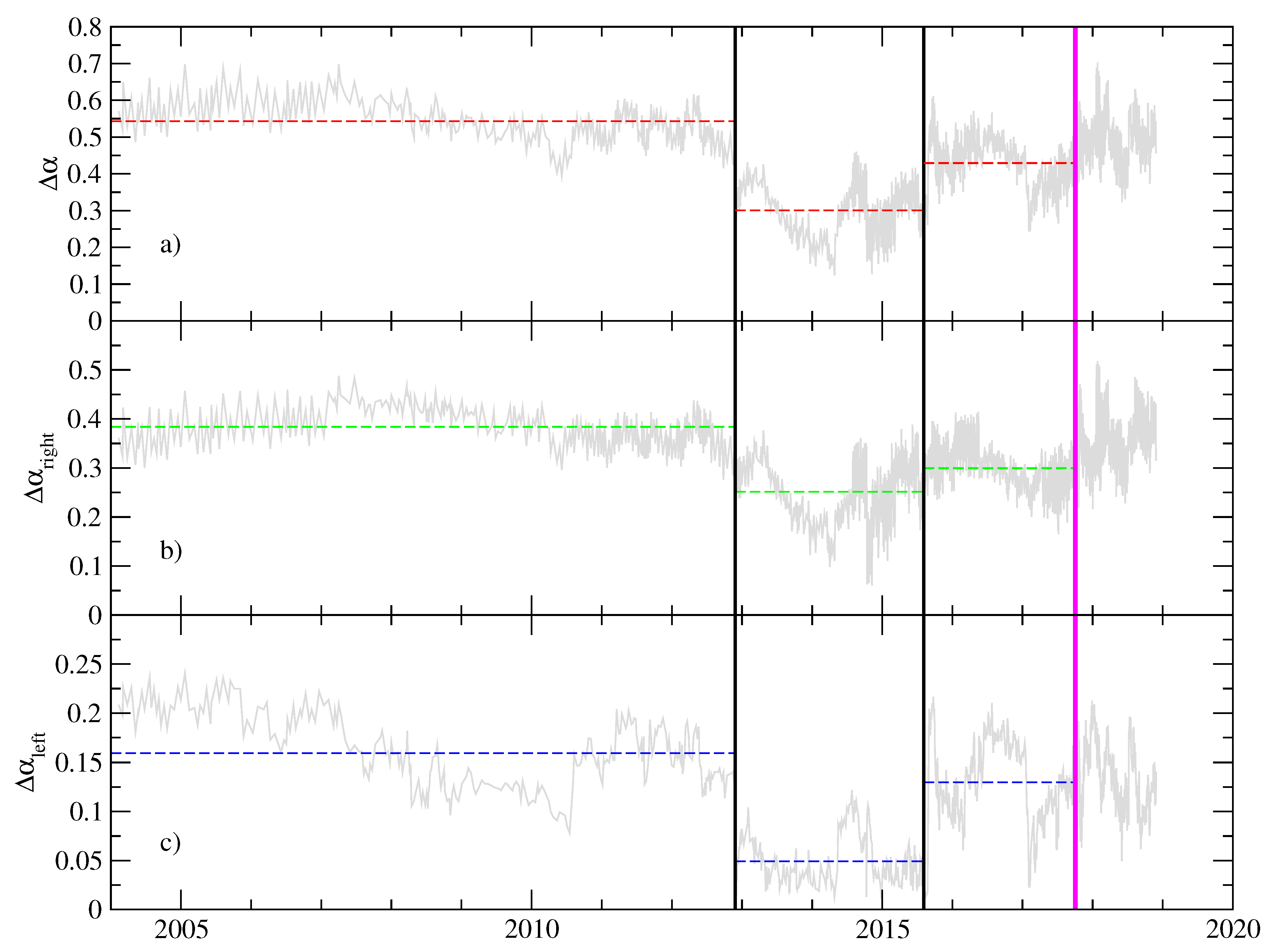
In order to provide a statistical assessment of the differences between the periods described above, we apply a segmentation method based on significant differences between the mean values of adjacent segments in a non-stationary sequence [
22]. The method is able to separate two segments with a statistically different mean. A significance level is applied to cut the series into two new segments (typically set to 0.9), as long as the means of the two new segments are significantly different from the mean of the adjacent segments (see details in [
22,
23]). The segmentation procedure was applied to the multifractal parameters:
,
and
. The results are shown in
Figure 6. Clearly, the segmentation procedure separates the three regions previously identified by inspection (see
Figure 5), confirming that the mean values of the multifractal parameters of adjacent segments are significantly different. We remark that the segment which corresponds to the period with a narrower spectrum, roughly also corresponds to the interval for which both the kurtosis and the skewness were concomitant with a Gaussian distribution (see
Figure 3).
4. Quiescence Analysis
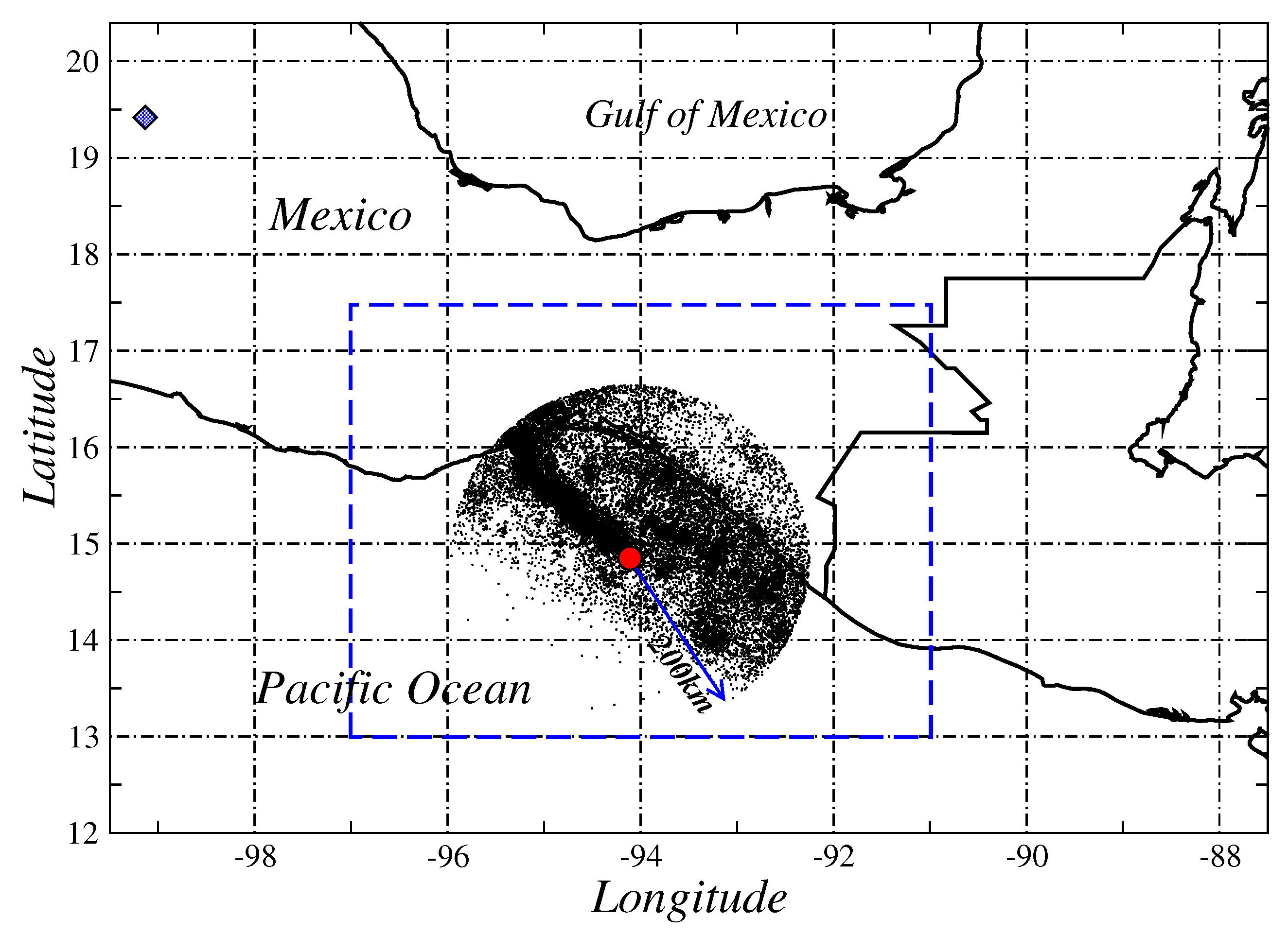
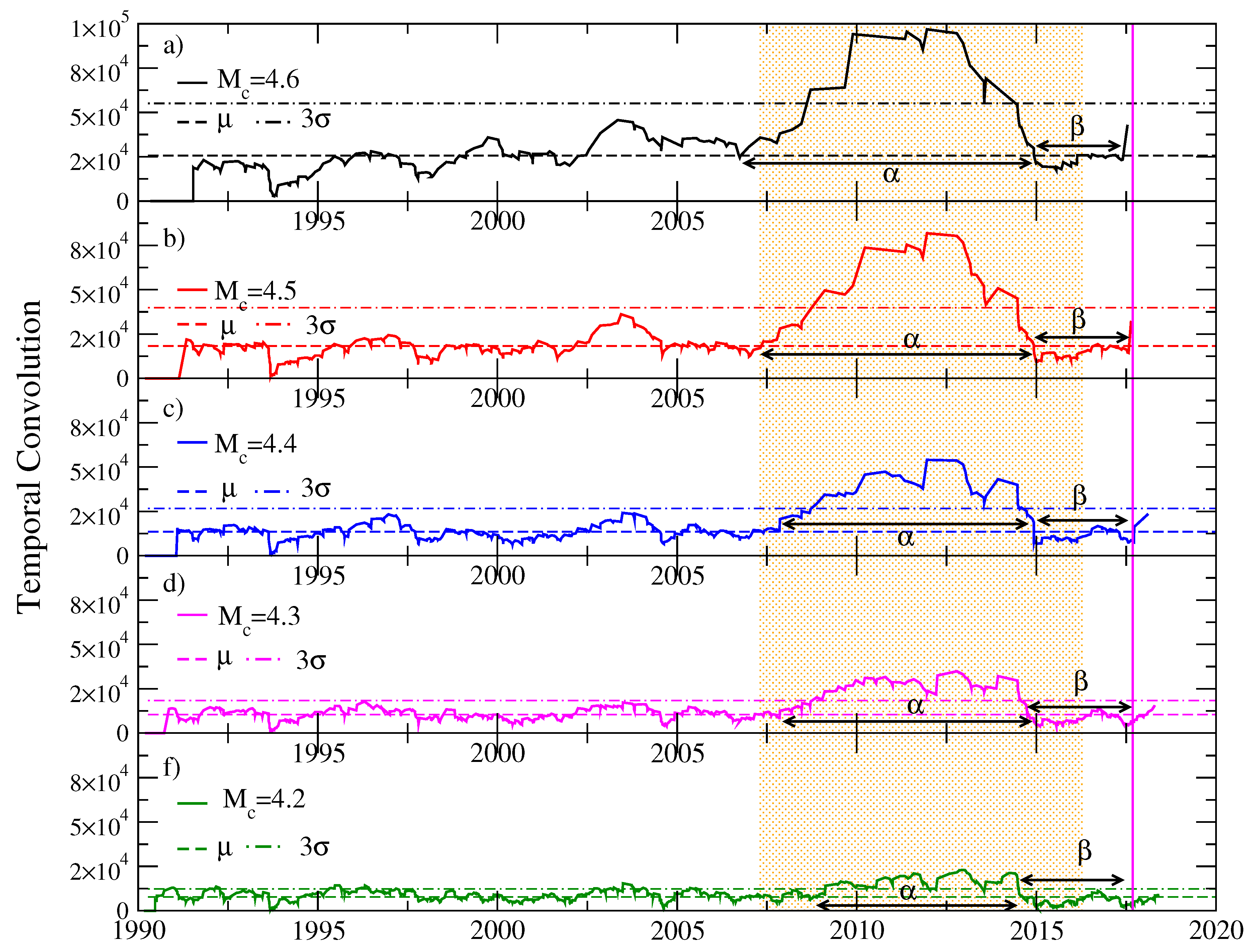
We applied the Schreider algorithm for earthquakes of coda magnitude
that occurred between January 1990 and September 2017 in the region of Tehuantepec Isthmus, considering a cylindrical volume of exploration centered in the epicenter of the earthquake of magnitude
, latitude
N, and longitude
W. We considered an interval of 60 km for the depth of the events inside the exploration cylinder, which we were moving down and found an important episode of seismic quiescence for events between 30 and 90 km deep. In each of
Figure 7,
Figure 8 and
Figure 9, horizontal dotted lines represent the average of each time series and the value
. We will call
Schreider’s critical value the value of
, given that values of the convolution
that exceed this critical value are considered abnormally large.
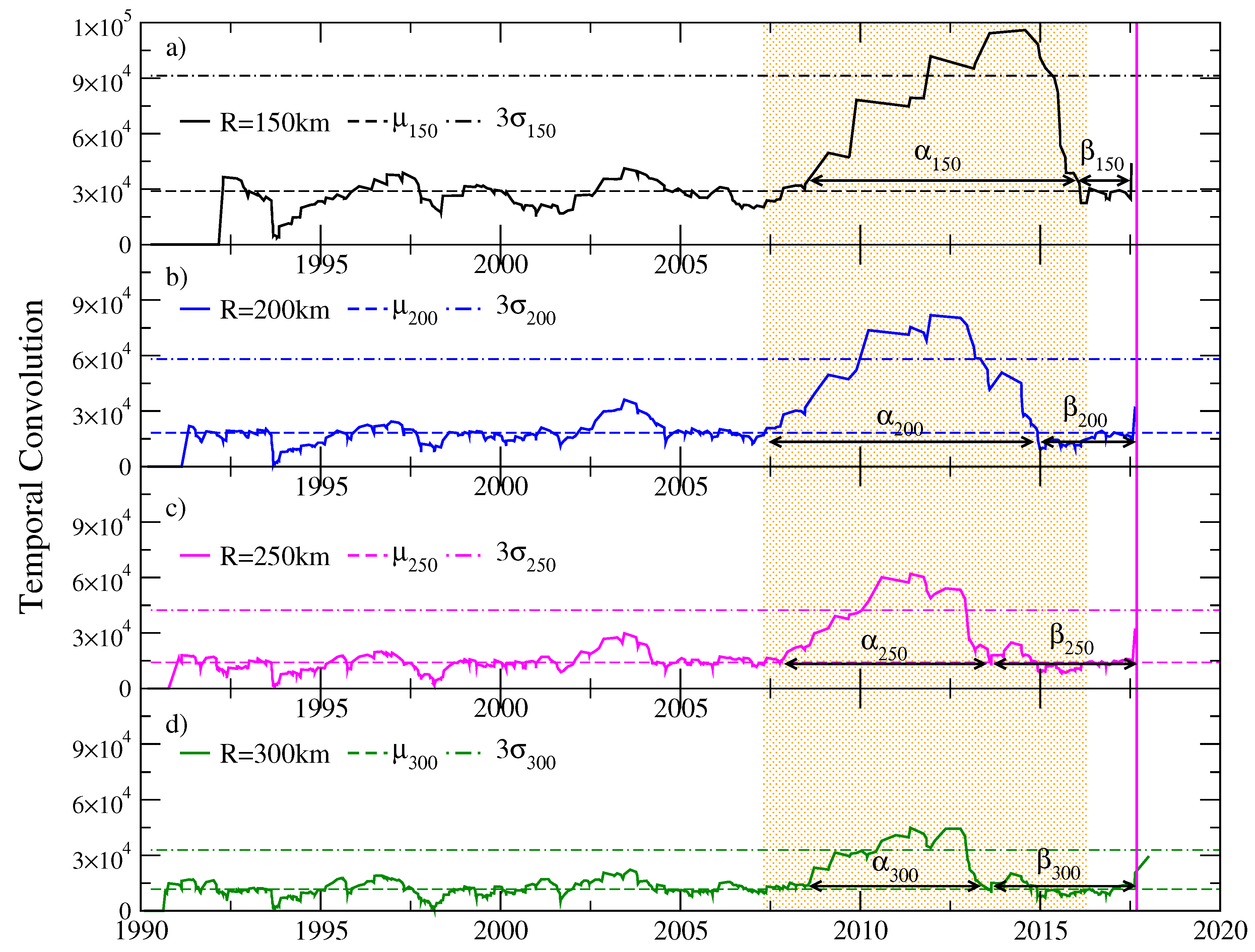
Figure 7 shows four temporal convolution functions for earthquakes of magnitude
occurring between January 1990 and September 2017. The exploration cylinders for the calculation of the convolution function considered events with depths between 30 and 90 km. The graphs correspond to cylinders with different radii:
km (black line),
km (blue line),
km (magenta line) and
km (green line). In
Figure 7a–d, it can be seen that the duration of the alpha and beta stages depend on the radius of the exploration cylinder; these figures allow us to see that, for a radius of 200 km, the temporal convolution function acquires the highest values within the quiet period. For this reason, the following analyses were made keeping that radius of the cylinder.
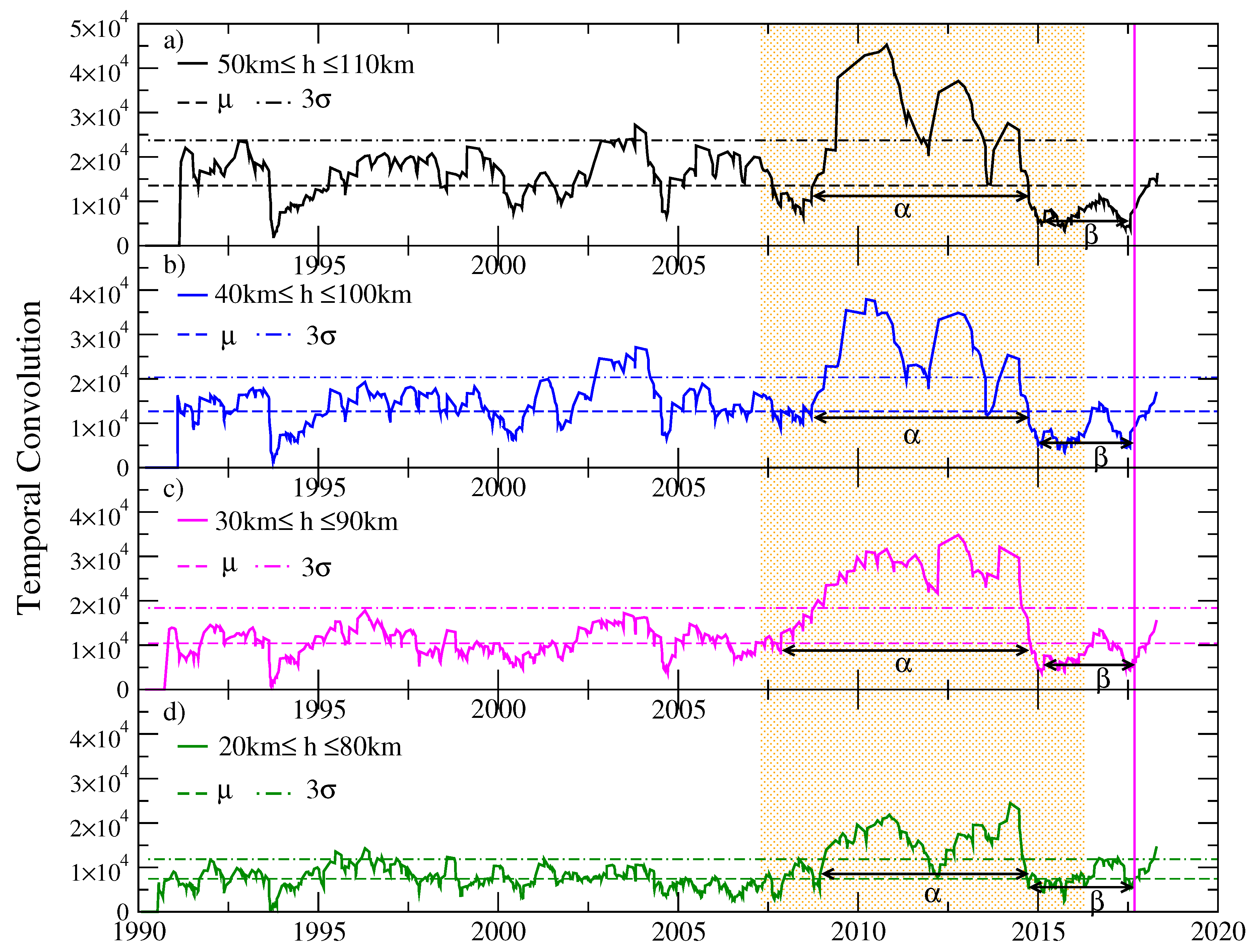
Figure 8 shows four temporal convolution functions for earthquakes of magnitude
, for different exploration cylinders with 200 km radius and 60 km height, whose depth of the upper face varies between 20 and 50 km deep. This figure shows the temporal convolution function for different depths of the exploration cylinders. We observe that, at the beginning of 2009, a significant increase in the value of the convolution function began, exceeding the critical value of Schreider between the beginning of 2010 and the end of 2014, which we consider as the alpha stage. At the beginning of 2015, the beta stage of resumption of seismic activity can be seen, with values below the average, which indicates a period of important activity, until the occurrence of the earthquake on 7 September 2017. It is noted, for a depth of events between 30 and 90 km, that the function of temporal convolution is maintained, within the quiet period (alpha stage), with the highest number of values above Schreider’s critical value; for this reason, in the following analysis, interval of depths is considered.
In
Figure 9, we have five temporal convolution graphs, evaluated for a cylindrical volume of 200 km radius between 30 and 90 km depth and centered at the epicenter of the Tehuantepec earthquake, for different values of the threshold coda magnitude
. Different alpha and beta stages are observed, for each magnitude whose duration varies between six years for threshold magnitude
and eight years for
. The duration of the beta stage is approximately three years. The durations of both of these stages, alpha and beta, are consistent with the results obtained from the application of natural time analysis (e.g., see Ref. [
24] as follows: Ramirez-Rojas and Flores-Marquez [
25] studied the fluctuations of the order parameter of seismicity by employing natural time analysis of seismicity for the period 1974–2012 in six tectonic regions of the Mexican Pacific coast and identified the following two key properties in the Chiapas region discussed later by Sarlis et al. [
26]: first, the probability density of the order parameter fluctuations had a bimodal feature. Second, the feature of the scaled distribution was non-Gaussian having a left exponential tail. These two features that have been identified almost five years before the occurrence of the M8.2 earthquake on 7 September 2017 signaled a forthcoming large earthquake. In addition, Ramirez-Rojas et al. [
27] using sliding windows comprising
and
events of magnitude 3.5 or larger identified in natural time important precursory variations in the entropy change under time reversal.
5. Conclusions
We have presented results of multifractal properties of pseudo-velocities and quescience obtained from spatio-temporal information of the 1998–2017 earthquake activity in the Tehuantepec region. Our results of multifractality revealed that a reduction in the width of the spectrum is observed for the years 2013–2015, indicating that, for this interval, the pseudo-velocity exhibited a less multifractal (more monofractal) behavior with a notorious reduction of the left-hand width of the spectrum for a period that comprises the beginning of 2013 until the end of 2015. The monofractality (narrow spectrum) indicates that the pseudo-velocity sequence exhibits less nonlinear features compared to a broad multifractal spectrum. Moreover, the Schreider algorithm was used for the identification of the pattern of significant seismic quietude within a cylindrical volume of a 200 km radius, located between 30 and 90 km depth and centered at the epicenter of the earthquake of magnitude
. The analysis of the temporal series of earthquakes that occurred between January 1990 and September 2017, in the Tehuantepec region, considering a range of threshold magnitudes
for the application of the algorithm, shows a pattern of significant seismic stillness that begins in the year 2008 and ends at the end of 2015, a temporary interval of approximately seven years (alpha stage), which ends with the resumption of seismic activity in the region, activity superior to the average historical activity of the last three decades (beta stage) that lasts until the occurrence of the main event of magnitude
. This pattern of seismic stillness is similar to those reported by [
14] for earthquakes occurring in the Mexican subduction zone of the Pacific with
. Finally, we remark that the two methods used in our study identified significant patterns from spatio-temporal information of earthquake activity for approximately the same period before the main shock, and additional studies are needed in this direction.