An Analysis of Deterministic Chaos as an Entropy Source for Random Number Generators
Abstract
:1. Introduction
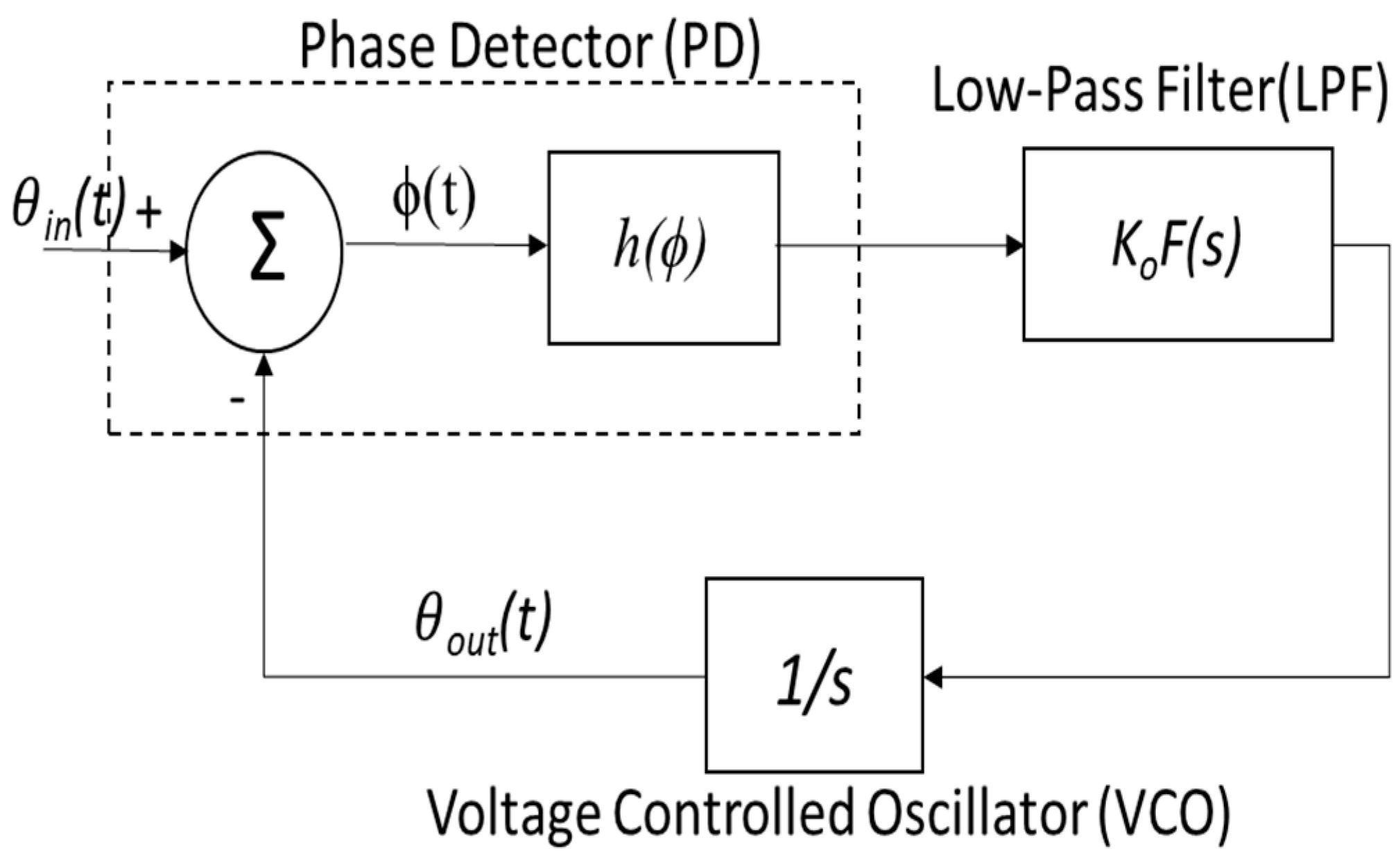
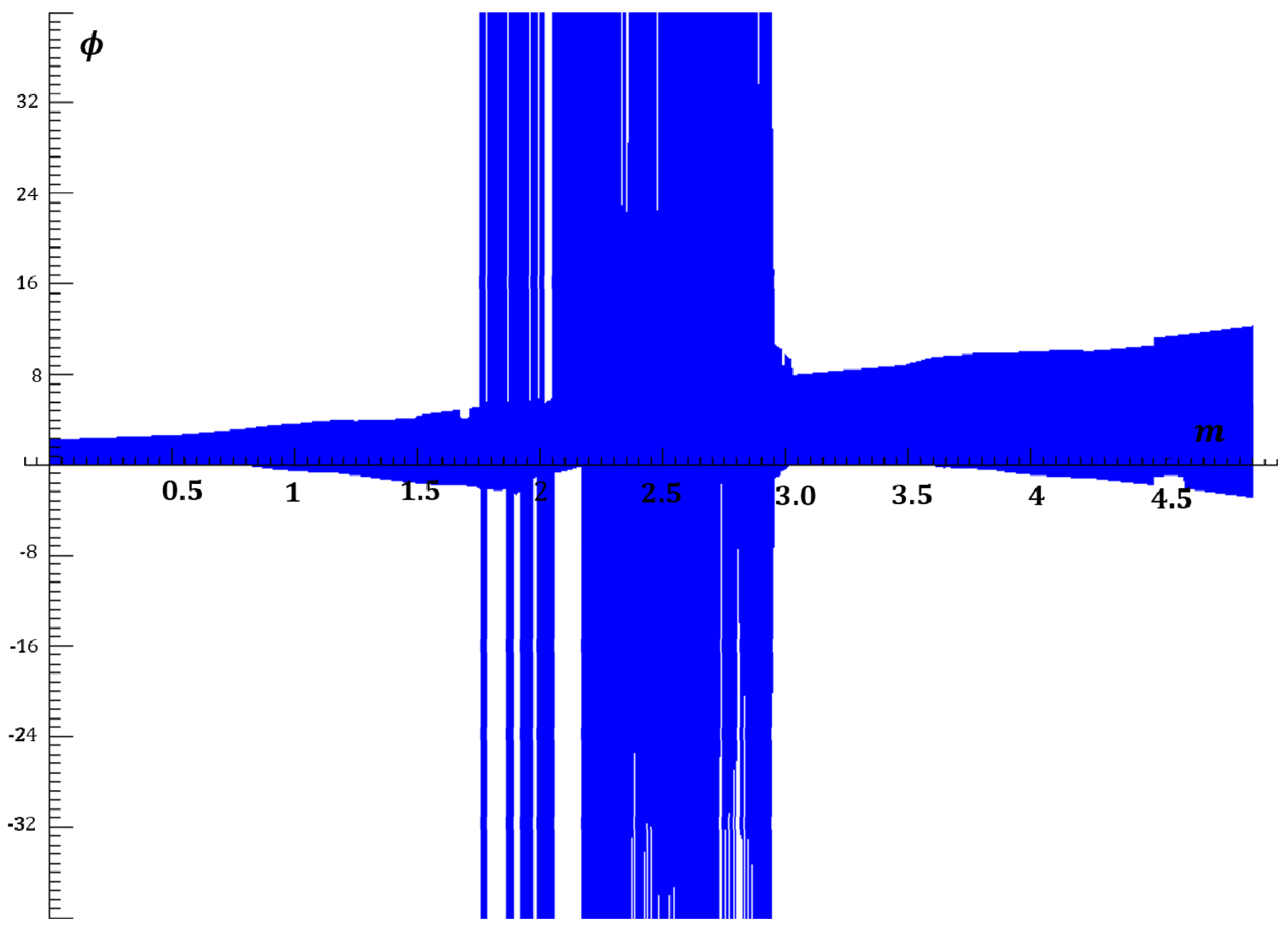
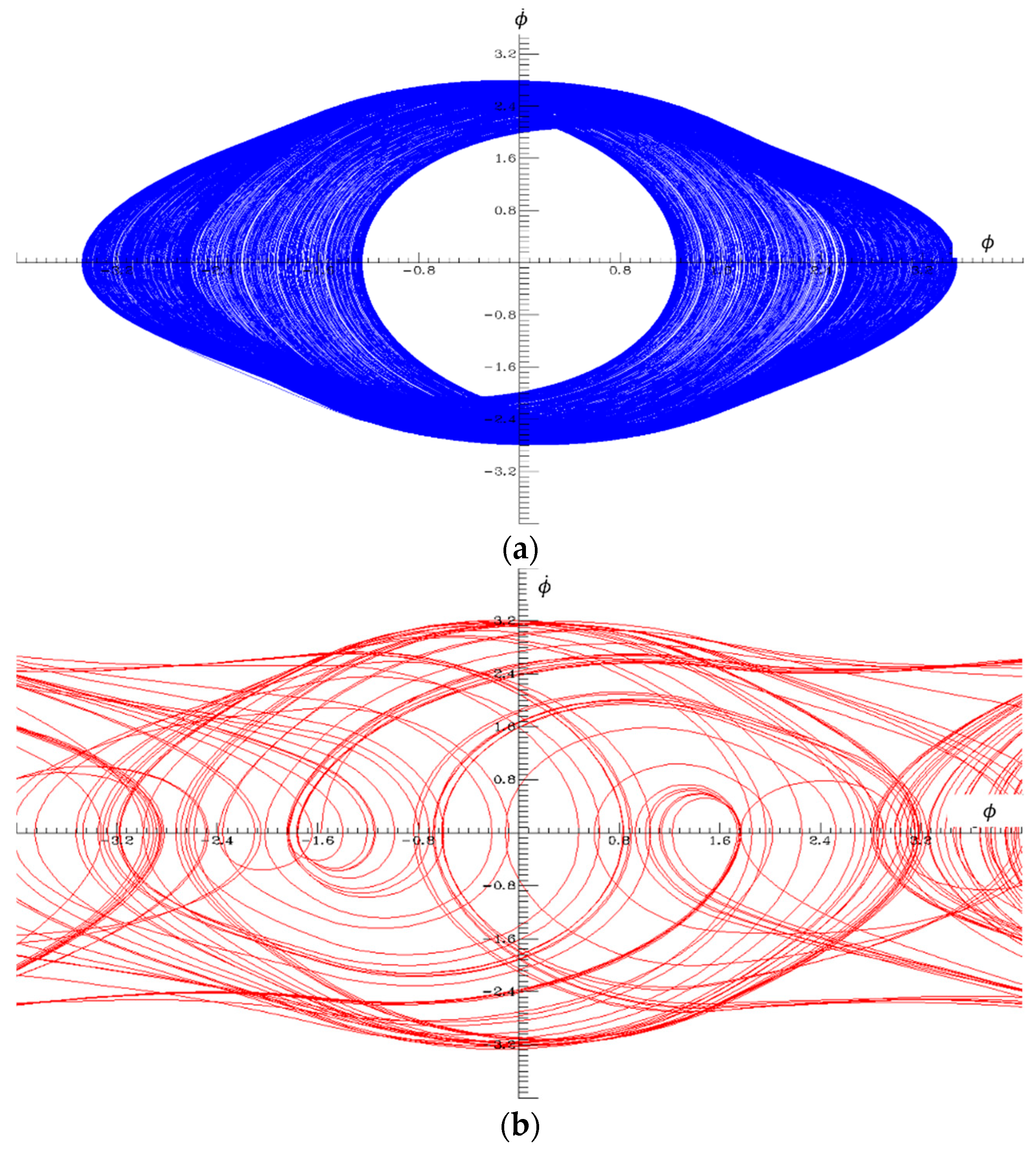
2. Chaotic System
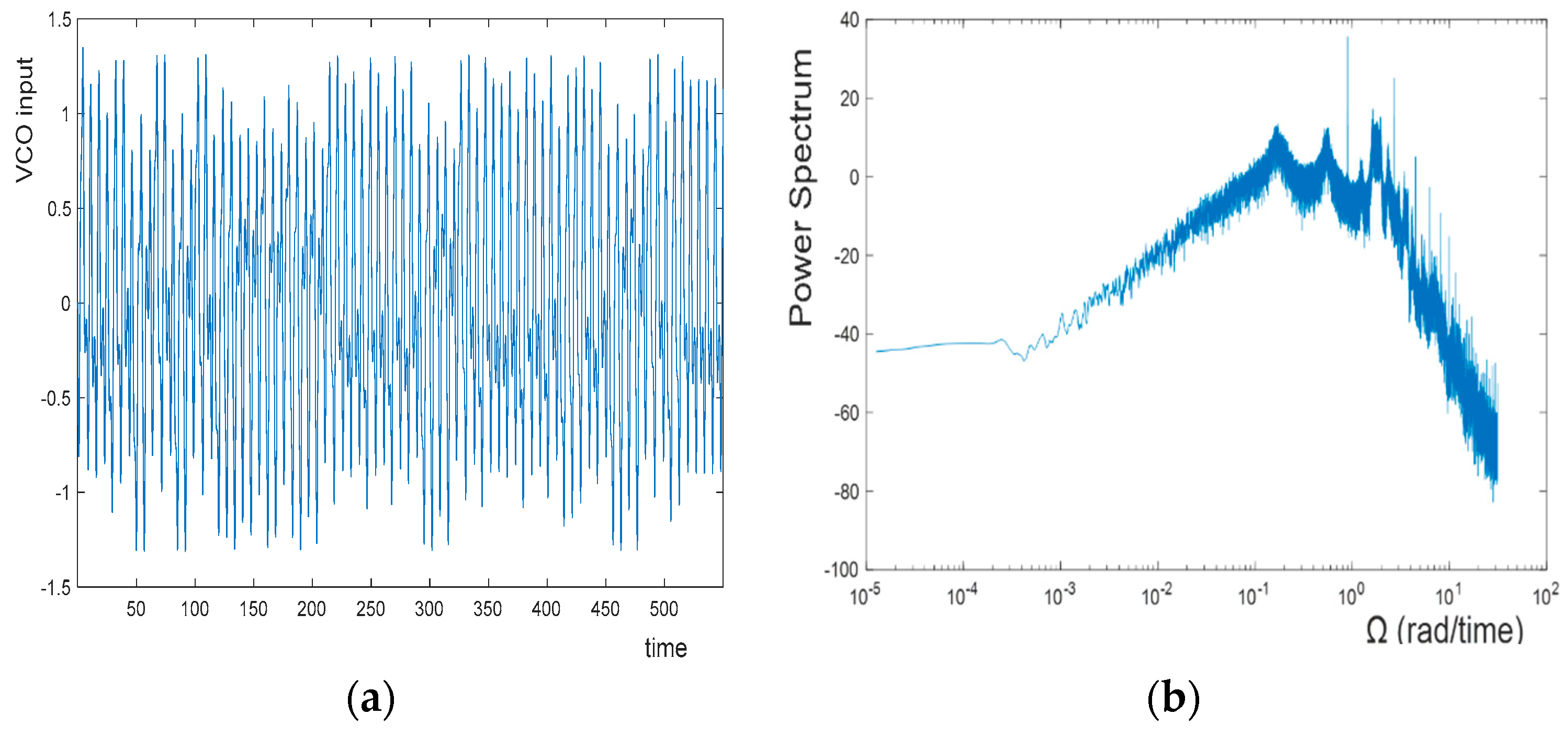
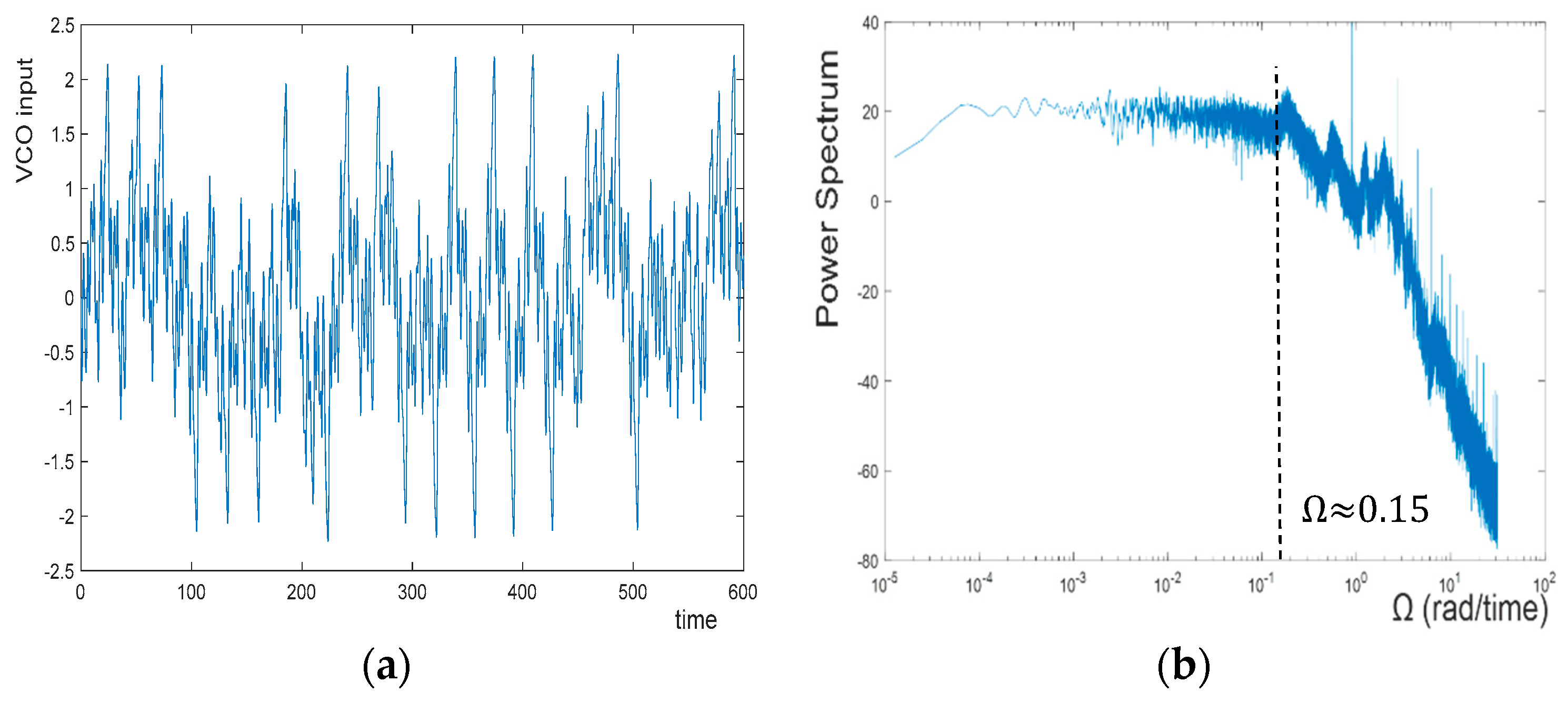
3. Chaotic Signal Formation
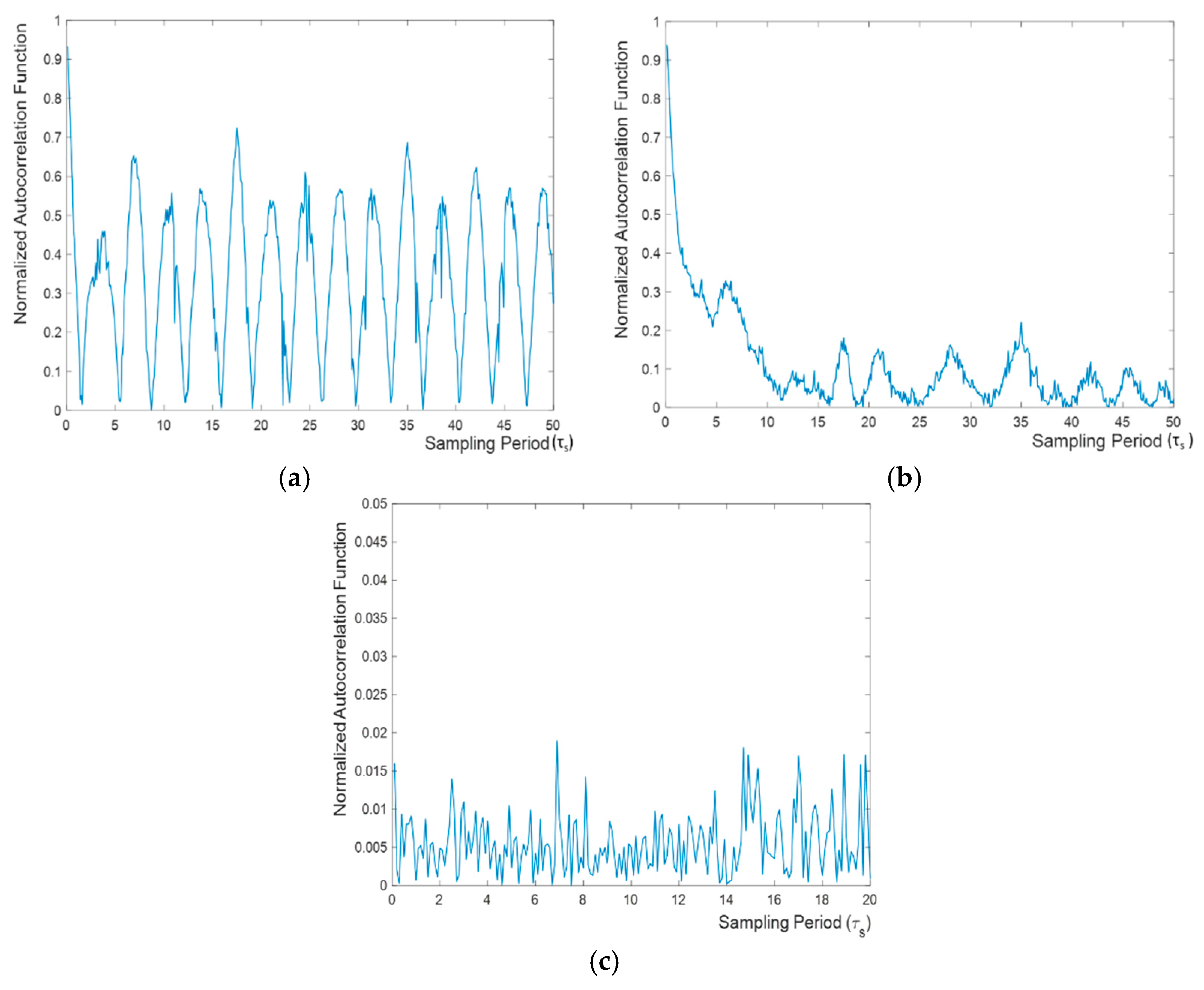
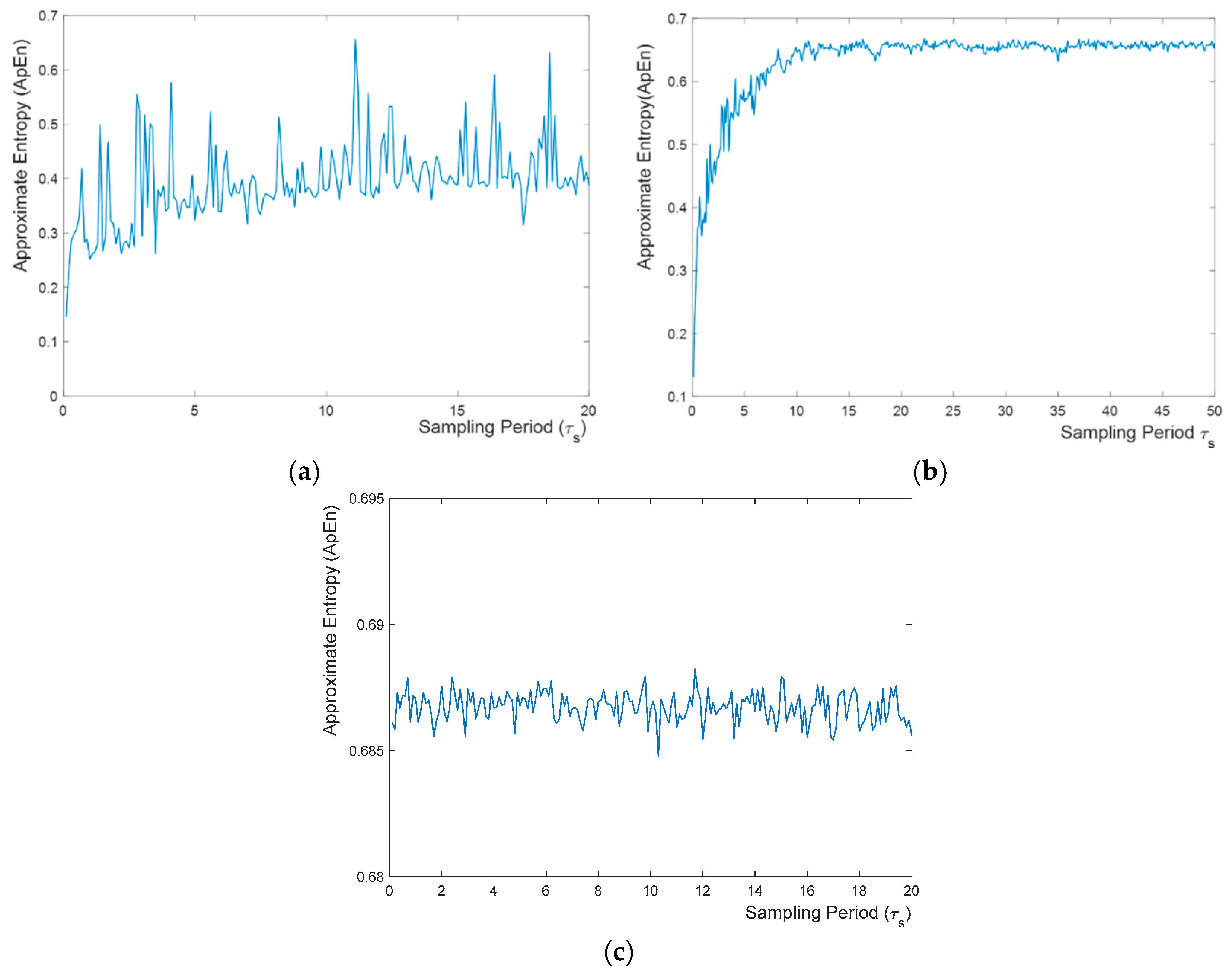
4. Random Bit Generation and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jun, B.; Kocher, P. The Intel Random Number Generator; White Paper; Cryptography Research Inc.: San Francisco, CA, USA, 1999. [Google Scholar]
- Menezes, A.; Oorscot, P.V.; Vanstone, S.A. Handbook of Applied Cryptography, 1st ed.; CRC Press: Boca Raton, FL, USA, 1996; ISBN 9781439821916. [Google Scholar]
- Gov, N.C.; Mihcak, M.K.; Ergün, S. True Random Number Generation via Sampling from Flat Band-Limited Gaussian Process. IEEE Trans. Circuits Syst. I 2011, 58, 1044–1051. [Google Scholar] [CrossRef]
- Holman, W.T.; Connelly, J.A.; Dowlatabadi, A.B. An integrated analog/digital random noise source. IEEE Trans. Circuits Syst. I 1997, 44, 521–528. [Google Scholar] [CrossRef]
- Bagini, V.; Bucci, M. A design of reliable true random number generator for cryptographic applications. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems (CHES), Worcester, MA, USA, 12–13 August 1999; Springer: Berlin, Heidelberg, 1999; pp. 204–218. [Google Scholar]
- Kautz, R.L. Using Chaos to Generate White Noise. J. Appl. Phys. 1999, 86, 5794–5800. [Google Scholar] [CrossRef]
- Ergün, S.; Asada, K. Numerical verification of chaos-based random number generators by using bootstrap method. Nonlinear Theory Its Appl. 2011, 2, 43–53. [Google Scholar] [CrossRef]
- Ozoguz, S.; Elwakil, A.S.; Ergün, S. Cross-coupled chaotic oscillators and application to random bit generation. IEE Proc. Circuits Devices Syst. 2006, 153, 506–510. [Google Scholar] [CrossRef]
- Ergün, S.; Güler, Ü.; Asada, K. IC truly random number generators based on regular & chaotic sampling of chaotic waveforms. IEICE Nonlinear Theory Its Appl. 2011, 2, 246–261. [Google Scholar]
- Ergün, S. Modeling and analysis of chaos-modulated dual oscillator-based random number generators. In Proceedings of the European Signal Processing Conference (EUSIPCO), Lausanne, Switzerland, 25–29 August 2008; pp. 1–5. [Google Scholar]
- Liu, Y.; Tong, X. Hyperchaotic system-based pseudorandom number generator. IET Inf. Secur. 2016, 10, 433–441. [Google Scholar] [CrossRef]
- Buscarino, A.; Fortuna, L.; Frasca, M. Experimental robust synchronization of hyperchaotic circuits. Phys. D Nonlinear Phenom. 2009, 238, 1917–1922. [Google Scholar] [CrossRef]
- Ergün, S. On the security of chaos based true random generators. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2016, 99, 363–369. [Google Scholar] [CrossRef]
- Fischer, V.; Drutarovskỳ, M. True random number generator embedded in reconfigurable hardware. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems (CHES), Redwood Shores, CA, USA, 13–15 August 2002; Springer: Berlin, Heidelberg, 2003; pp. 415–430. [Google Scholar]
- Šimka, M.; Drutarovskỳ, M.; Fischer, V. Embedded true random number generator in actel FPGAs. In Proceedings of the Workshop on Cryptographic Advances in Secure Hardware (CRASH), Leuven, Belgium, 6–7 September 2005; pp. 6–7. [Google Scholar]
- Varchola, M.; Drutarovskỳ, M.; Fouquet, R.; Fischer, V. Hardware platform for testing performance of TRNGs embedded in actel fusion FPGA. In Proceedings of the 18th International Conference Radioelektronika, Prague, Czech Republic, 24–25 April 2008; pp. 1–4. [Google Scholar]
- Bakiri, M.; Guyeux, C.; Couchot, J.F.; Oudjida, A.K. Survey on hardware implementation of random number generators on FPGA: Theory and experimental analyses. Comput. Sci. Rev. 2018, 27, 135–153. [Google Scholar] [CrossRef]
- Takada, A. White noise generation in a chaotic phase-locked loop. IEICE Tech. Rep. Circuits Syst. 2005, 105, 55–60. [Google Scholar]
- Endo, T.; Chua, L. Chaos from Phase-Locked Loops. IEEE Trans. Circuits Syst. I 1988, 35, 987–1003. [Google Scholar] [CrossRef]
- Endo, T.; Yokota, J. Generation of White Noise by Using Chaos in Practical Phase-Locked Loop Integrated Circuit Module. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), New Orleans, LA, USA, 27–30 May 2007; pp. 201–204. [Google Scholar]
| Statistical Tests | p-Value |
|---|---|
| Frequency | 0.777297 |
| Block Frequency | 0.543739 |
| Runs | 0.041646 |
| Longest Run | 0.496469 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demir, K.; Ergün, S. An Analysis of Deterministic Chaos as an Entropy Source for Random Number Generators. Entropy 2018, 20, 957. https://doi.org/10.3390/e20120957
Demir K, Ergün S. An Analysis of Deterministic Chaos as an Entropy Source for Random Number Generators. Entropy. 2018; 20(12):957. https://doi.org/10.3390/e20120957
Chicago/Turabian StyleDemir, Kaya, and Salih Ergün. 2018. "An Analysis of Deterministic Chaos as an Entropy Source for Random Number Generators" Entropy 20, no. 12: 957. https://doi.org/10.3390/e20120957
APA StyleDemir, K., & Ergün, S. (2018). An Analysis of Deterministic Chaos as an Entropy Source for Random Number Generators. Entropy, 20(12), 957. https://doi.org/10.3390/e20120957





