Characterization of Self-Assembled 2D Patterns with Voronoi Entropy
Abstract
1. Introduction
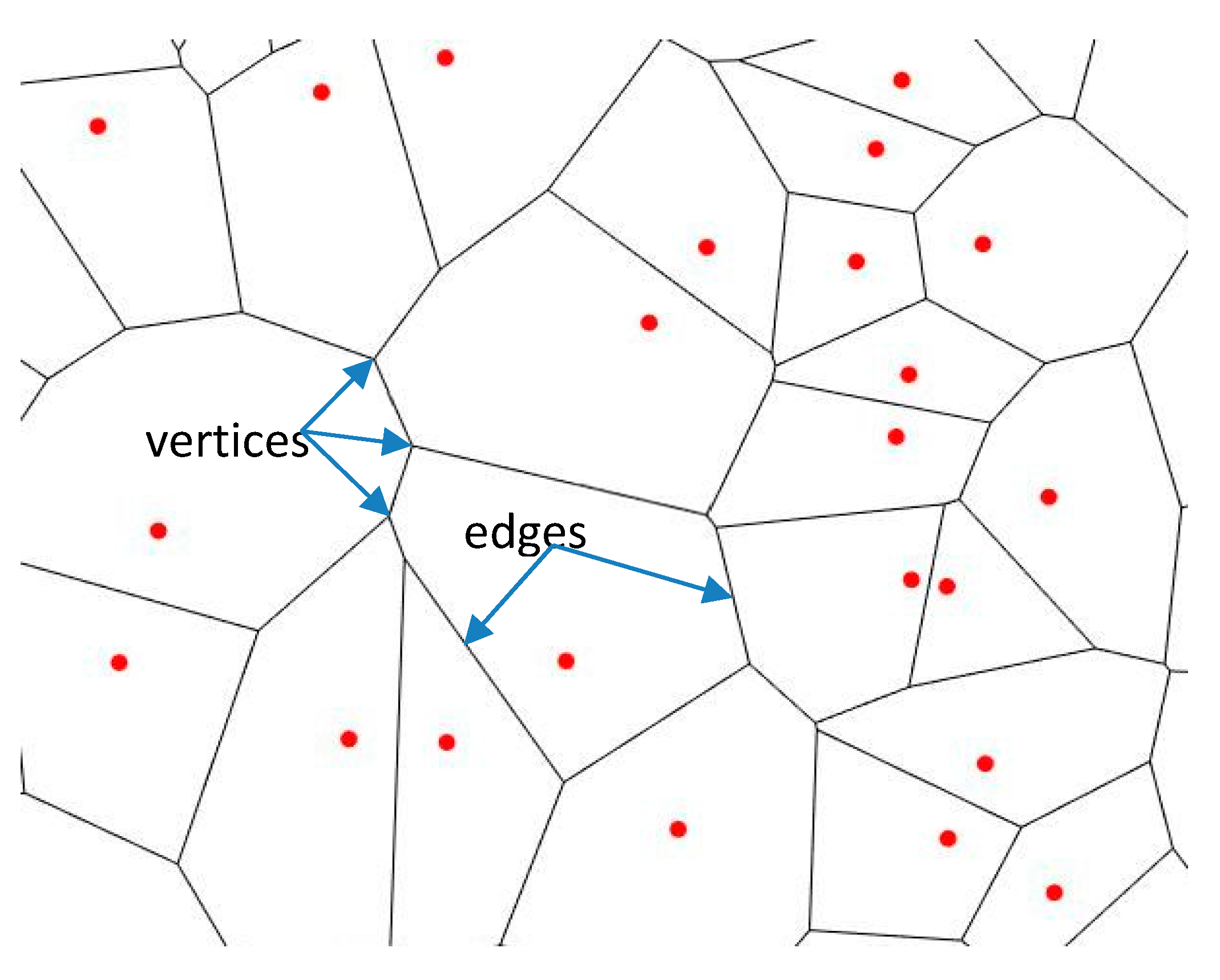
2. Topological and Scaling Properties of Voronoi Diagrams and Entropy
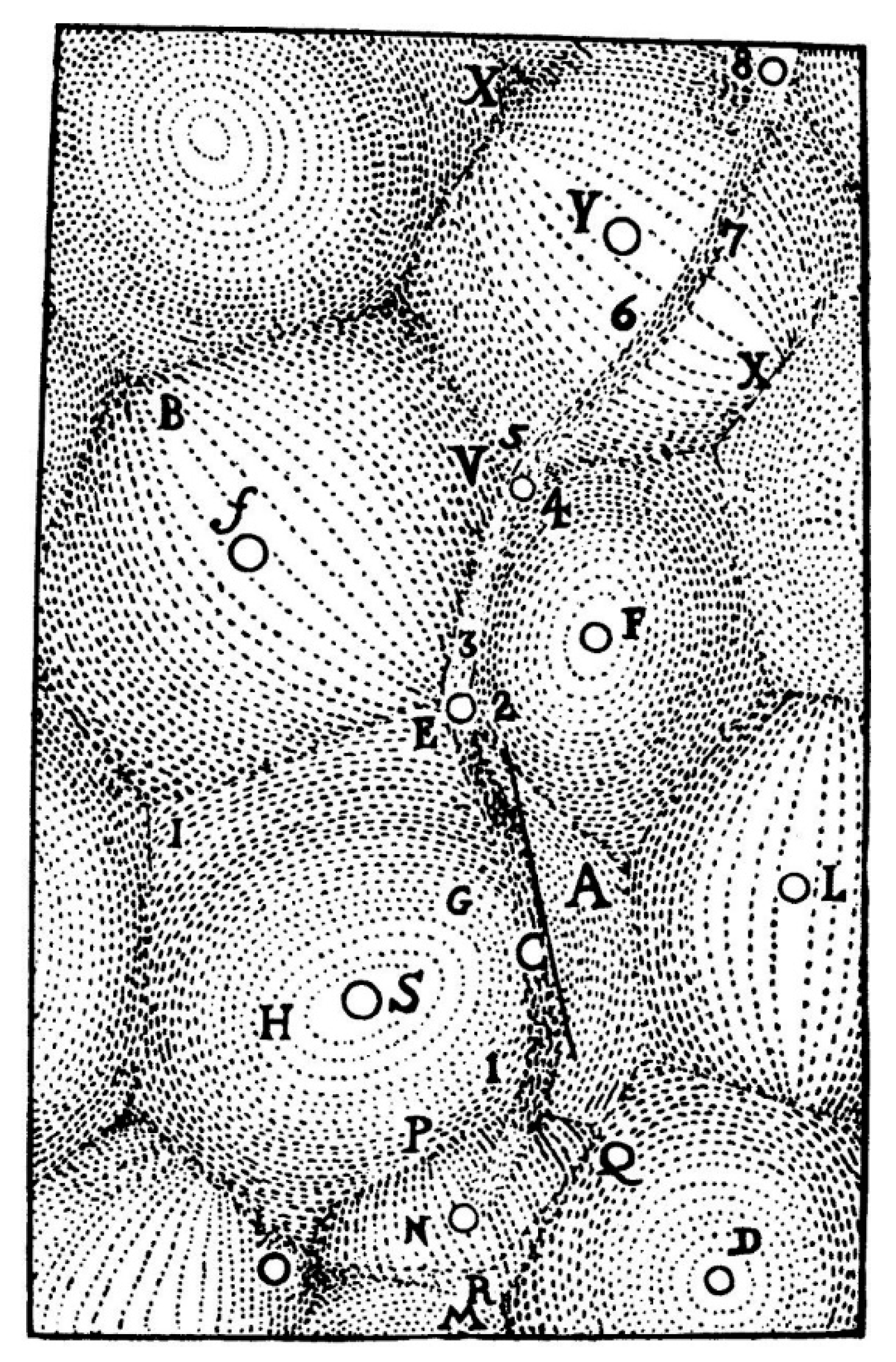
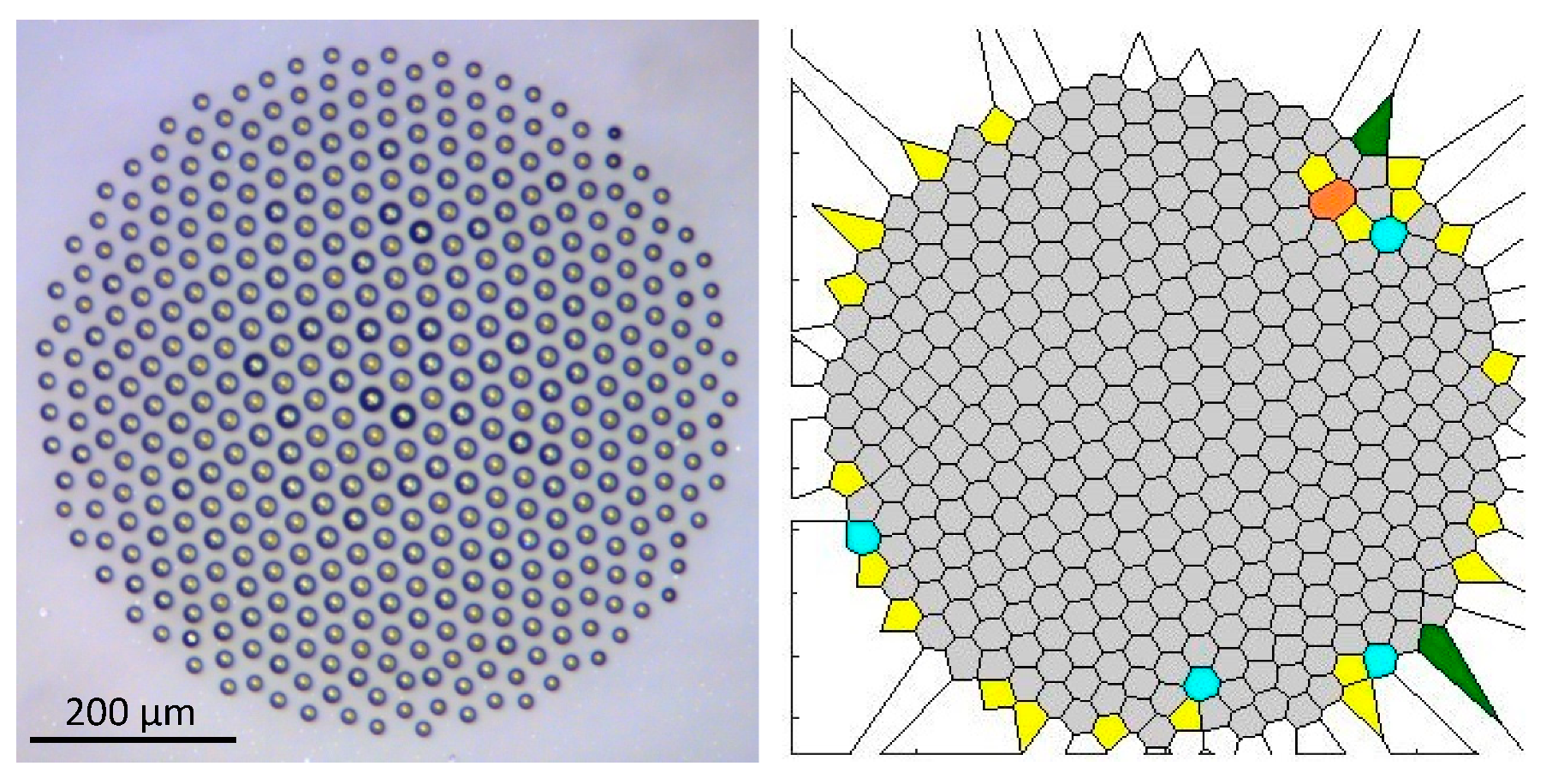
3. Analysis of 2D Self-Assembled Surface Patterns with 2D Voronoi Diagrams
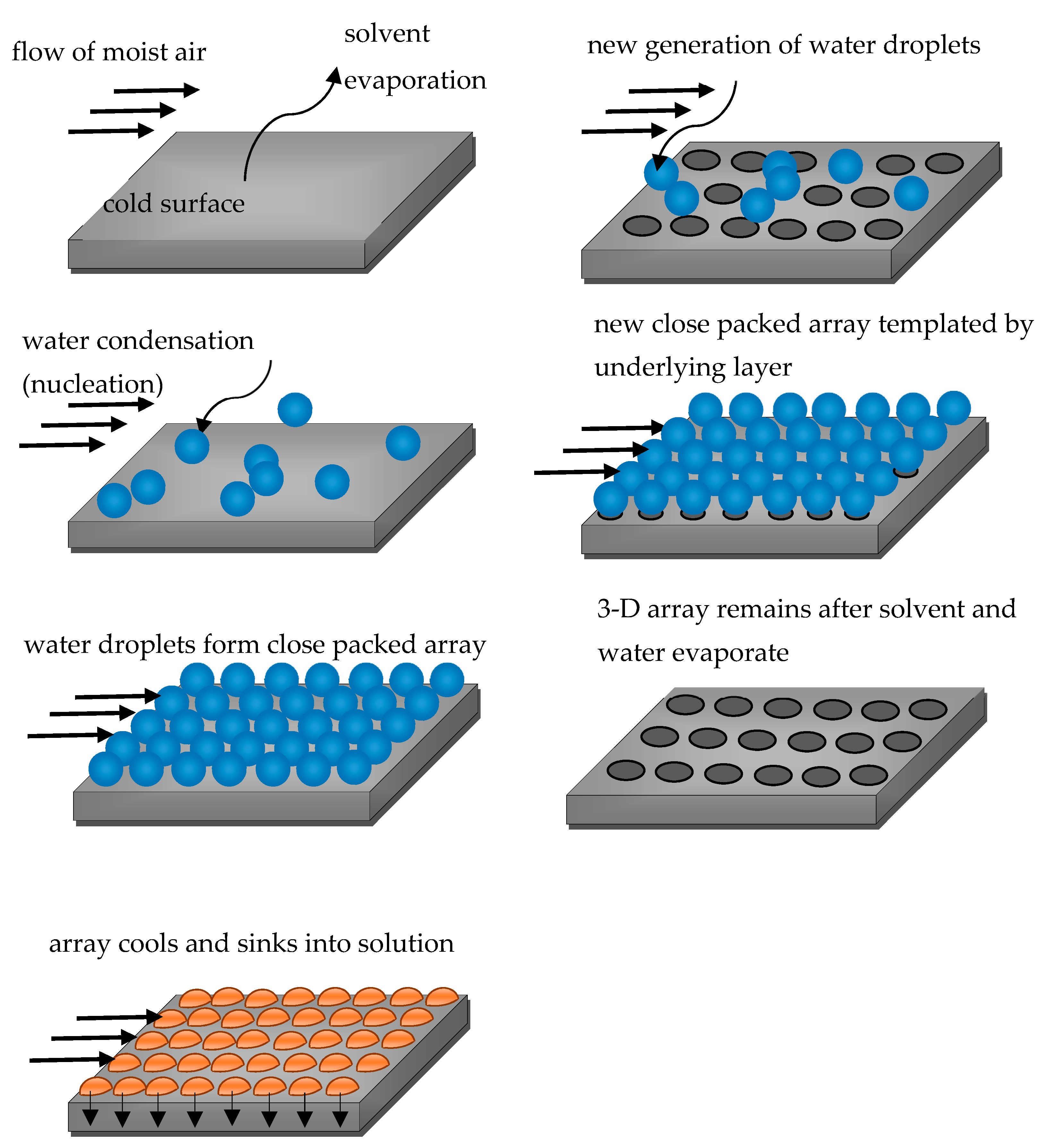
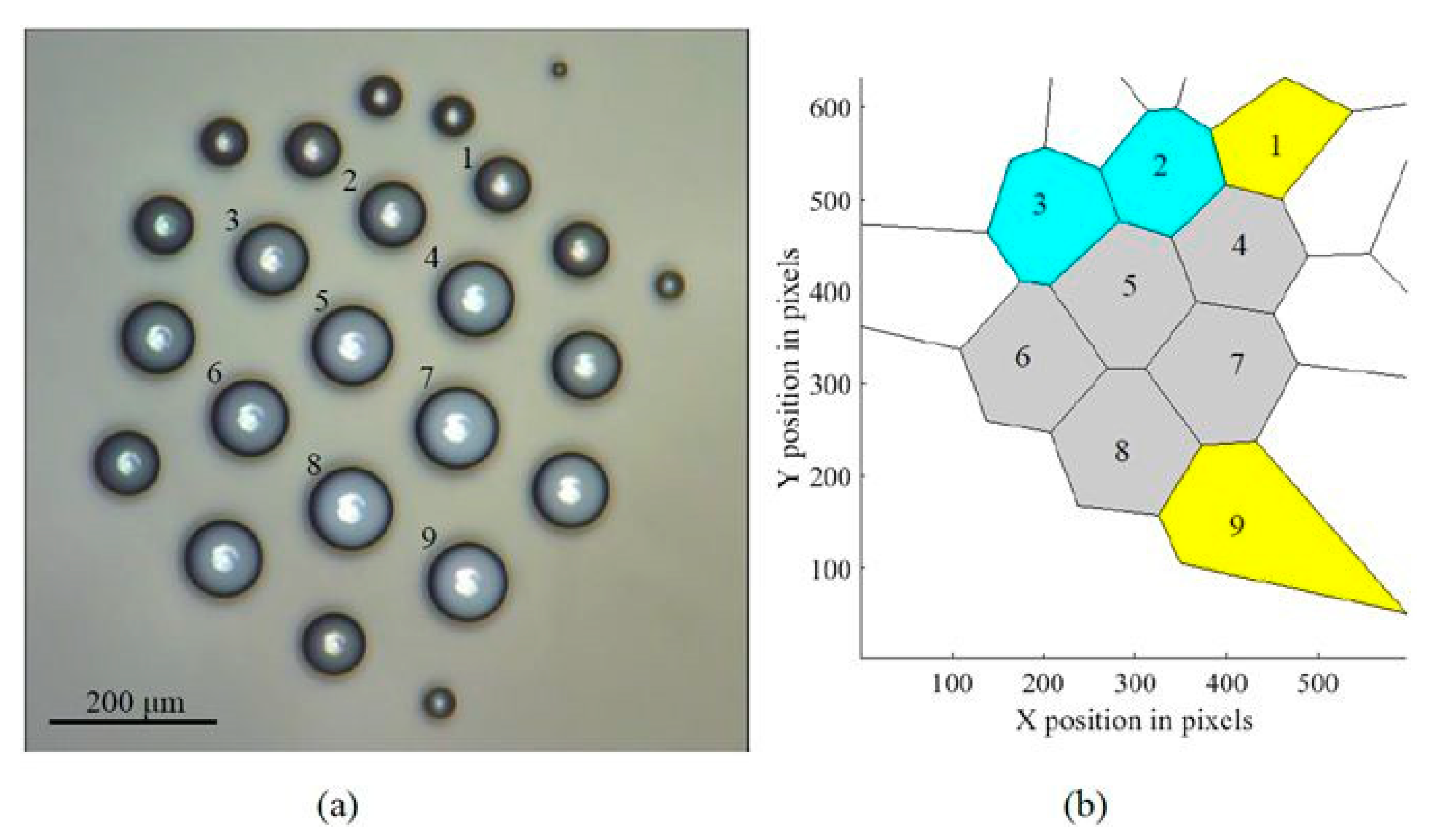
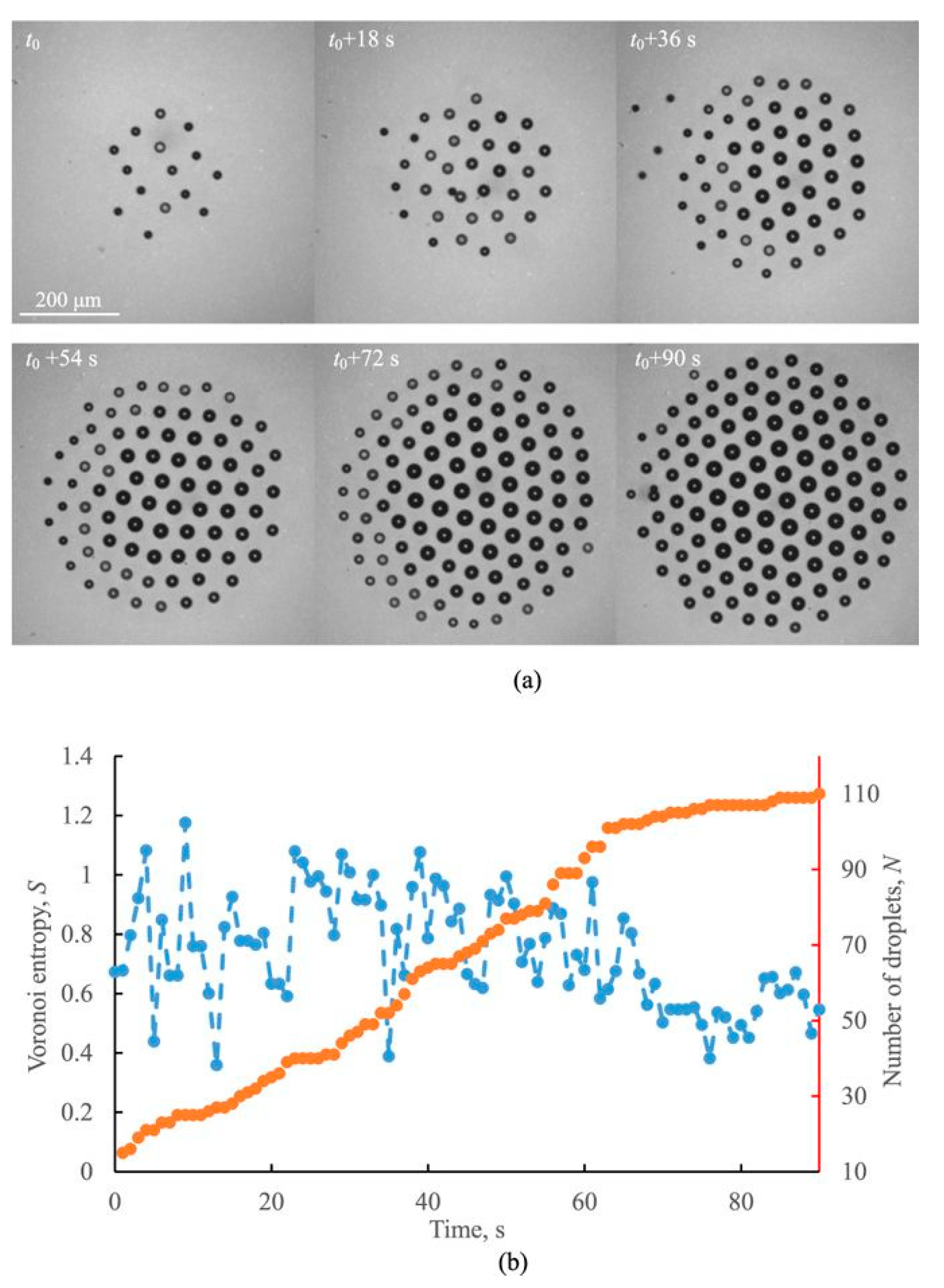
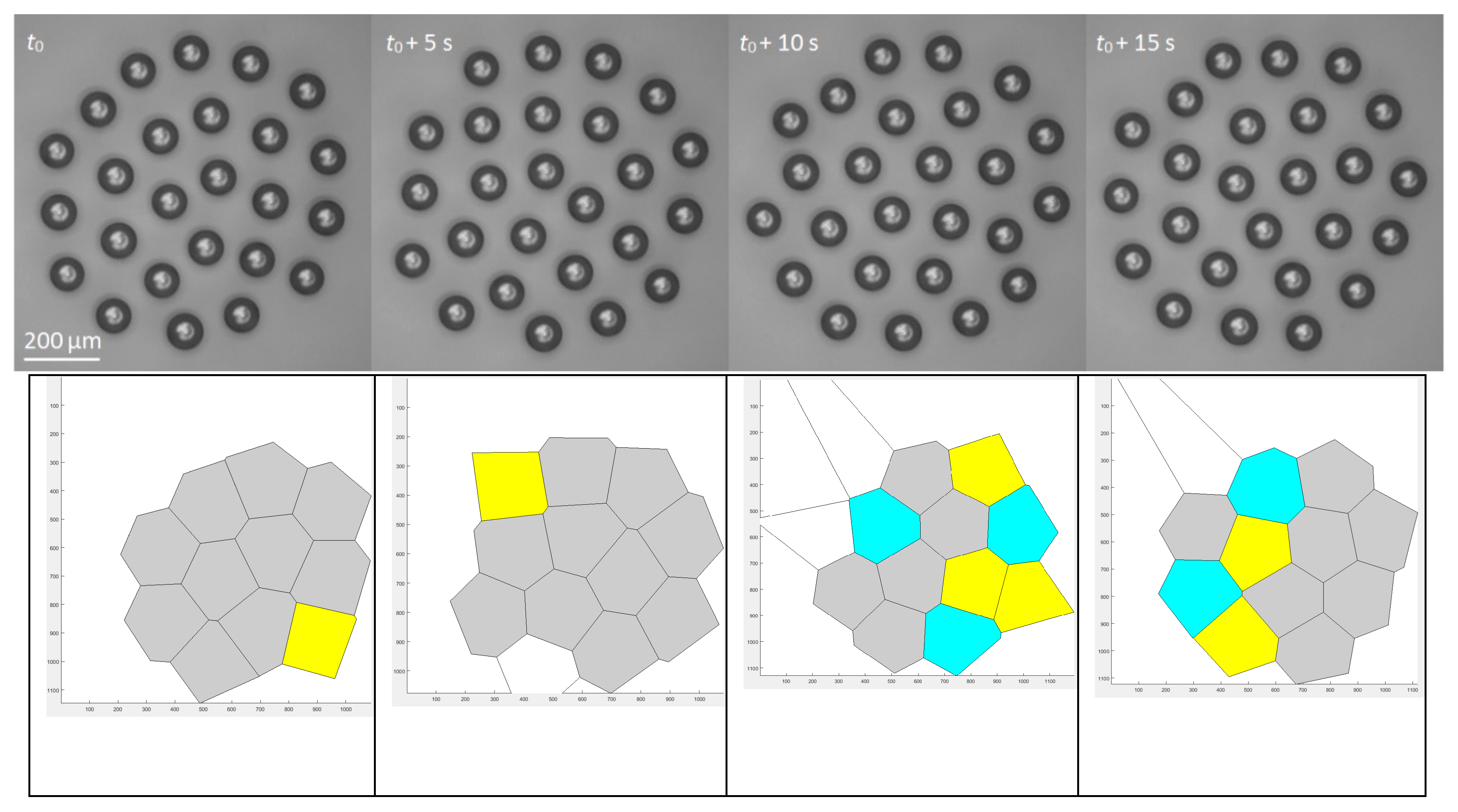
4. Droplet Clusters and Their Analysis with Voronoi Diagrams.
5. The Relation between Voronoi Entropy and Thermodynamic Entropy
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Widawski, G.; Rawiso, M.; Francois, B. Self-organized honeycomb morphology of star-polymer polystyrene films. Nature 1994, 369, 387–389. [Google Scholar] [CrossRef]
- Pitois, J.; Francois, B. Formation of ordered micro-porous membranes. Eur. Phys. J. B 1999, 8, 225–231. [Google Scholar] [CrossRef]
- Karthaus, O.; Cieren, X.; Shimomura, M.; Hasegawa, T. Water-assisted formation of micrometer-size honeycomb patterns of polymers. Langmuir 2000, 16, 6071–6076. [Google Scholar] [CrossRef]
- Bormashenko, E. Breath-figure Self-assembly, a Versatile Method of manufacturing membranes and porous structures: physical, chemical and technological aspects. Membranes 2017, 73, 45. [Google Scholar] [CrossRef]
- Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Recherches sur les paralléloèdres primitifs. Reine Angew. Math. 1908, 134, 198–287. [Google Scholar] [CrossRef]
- Descartes, R. Principia Philosophiae; Ludovicus Elzevirius: Amsterdam, The Netherlands, 1644; ISBN 978-90-277-1754-2. [Google Scholar]
- Liebling, T.M.; Pournin, L. Voronoi diagrams and Delaunay triangulations: Ubiquitous Siamese Twins. Doc. Math. 2012, Extra Volume ISMP, 419–431. [Google Scholar]
- Snow, J. Report on the Cholera Outbreak in the Parish of St. James, Westminster: during the autumn of 1854; Metropolitan Commission of Sewers: Westminster, UK, 1855.
- Dirichlet, G.L. Über die Reduction der positiven quadratischen Formen mit drei unbestimmten ganzen Zahlen. J. Reine Angew. Math. 1850, 40, 209–227. [Google Scholar] [CrossRef]
- Kumar, V.S.; Kumaran, V. Voronoi cell volume distribution and configurational entropy of hard-spheres. J. Chem. Phys. 2005, 123, 114501. [Google Scholar] [CrossRef]
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef]
- Weaire, D.; Rivier, N. Soap, cells and statistics—random patterns in two dimensions. Contemporary Phys. 1984, 25, 59–99. [Google Scholar] [CrossRef]
- Blatov, V.A. Voronoi–Dirichlet polyhedra in crystal chemistry: theory and applications. Crystallography Reviews 2004, 10, 249–318. [Google Scholar] [CrossRef]
- Limaye, A.V.; Narhe, R.D.; Dhote, A.M.; Ogale, S.B. Evidence for convective effects in breath figure formation on volatile fluid surfaces. Phys. Rev. Lett. 1996, 76, 3762–3765. [Google Scholar] [CrossRef] [PubMed]
- Lewis, E.T. The correlation between cell division and the shapes and sizes of prismatic cell in the epidermis of Cucumis. Anat. Rec. 1928, 38, 341–376. [Google Scholar] [CrossRef]
- Lewis, F.T. A volumetric study of growth and cell division in two types of epithelium-the longitudinally prismatic cells of Tradescantia and the radially prismatic epidermal cells of Cucumis. Anat. Rec. 1930, 47, 59–99. [Google Scholar] [CrossRef]
- Lewis, E.T. The geometry of growth and cell division in epithelial mosaics. Am. J. Bot. 1943, 30, 766–776. [Google Scholar] [CrossRef]
- Lewis, F.T. The geometry of growth and cell division in columnar parenchyma. Am. J Bot. 1944, 31, 619–629. [Google Scholar] [CrossRef]
- Chiu, S.N. Aboav-Weaire’s and Lewis’ laws—A review. Mater. Charact. 1995, 34, 149–165. [Google Scholar] [CrossRef]
- Rivier, N.; Lissowski, A. On the correlation between sizes and shapes of cells in epithelial mosaics. J. Phys. A Math. Gen. 1982, 15, L143–L148. [Google Scholar] [CrossRef]
- Sánchez-Gutiérrez, D.; Tozluoglu, M.; Barry, J.D.; Pascual, A.; Mao, Y.; Escudero, L.M. Fundamental physical cellular constraints drive self-organization of tissues. EMBO J. 2016, 35, 77–88. [Google Scholar] [CrossRef]
- Saraiva, J.; Pina, P.; Bandeira, L.; Antunes, J. Polygonal networks on the surface of Mars; applicability of Lewis, Desch and Aboav–Weaire laws. Phil. Mag. Lett. 2009, 89, 185–193. [Google Scholar] [CrossRef]
- Steyer, A.; Guenoun, P.; Beysens, D.; Knobler, C.M. Two-dimensional ordering during droplet growth on a liquid surfaceth on a liquid surface. Phys Rev. B 1990, 42, 1086–1089. [Google Scholar] [CrossRef]
- Pietsch, T.; Gindy, N.; Fahmi, A. Nano- and micro-sized honeycomb patterns through hierarchical self-assembly of metal-loaded diblock copolymer vesicles. Soft Matter 2009, 5, 2188–2197. [Google Scholar] [CrossRef]
- Park, M.S.; Kim, J.K. Breath figure patterns prepared by spin coating in a dry environment. Langmuir 2004, 20, 5347–5352. [Google Scholar] [CrossRef] [PubMed]
- Bormashenko, E.; Musin, A.; Whyman, G.; Barkay, Z.; Zinigrad, M. Revisiting the fine structure of the triple line. Langmuir 2013, 29, 14163–14167. [Google Scholar] [CrossRef] [PubMed]
- Madej, W.; Budkowski, A.; Raczkowska, J.; Rysz, J. Breath figures in polymer and polymer blend films spin-coated in dry and humid ambience. Langmuir 2008, 24, 3517–3524. [Google Scholar] [CrossRef] [PubMed]
- Rivier, N. Statistical crystallography structure of random cellular networks. Phil. Mag.B 1985, 52, 795–819. [Google Scholar] [CrossRef]
- Aboav, D.A. The arrangement of grains in a polycrystal. Metallography 1970, 3, 383–390. [Google Scholar] [CrossRef]
- Weaire, D. Some remarks on the arrangement of grains in a polycrystal. Metallography 1974, 7, 157–160. [Google Scholar] [CrossRef]
- Mombach, J.C.M.; de Almeida, R.M.C.; Iglesias, J.R. Mitosis and growth in biological tissues. Phys.Rev. E 1993, 48, 598–602. [Google Scholar] [CrossRef]
- Jarai-Szabo, F.; Zoltan, N. On the size distribution of Poisson Voronoi cells. Phys. A 2007, 385, 518–526. [Google Scholar] [CrossRef]
- Zhu, H.X.; Thorpe, S.M.; Windle, A.H. The geometrical properties of irregular two-dimensional. Phil. Mag. A 2001, 81, 2765–2783. [Google Scholar] [CrossRef]
- Shirriff, K. Generating fractals from Voronoi diagrams. Comput. Graph. 1998, 17, 165–167. [Google Scholar] [CrossRef]
- Delaunay, B. Sur la sphère vide. Bulletin de l’Académie des Sciences de l’URSS, Classe des Sciences Mathématiques et Naturelles 1934, 6, 793–800. [Google Scholar]
- Sung, B.J.; Yethiraj, A. Structure of void space in polymer solutions. Phys Rev E Stat Nonlin. Soft Matter Phys. 2010, 81, 031801. [Google Scholar] [CrossRef]
- Danielsson, M.; Parks, D.M.; Boyce, M.C. Three-dimensional micromechanical modeling of voided polymeric materials. J. Mech. Phys. Solids 2002, 50, 51–379. [Google Scholar] [CrossRef]
- Bigioni, T.P.; Lin, X.M.; Nguyen, T.T.; Corwin, E.I.; Witten, T.A.; Jaeger, H.M. Kinetically driven self assembly of highly ordered nanoparticle monolayers. Nat. Mater. 2006, 5, 265–270. [Google Scholar] [CrossRef]
- Yun, S.-H.; Yoo, S.; Jung, J.C.; Zin, W.-C.; Sohn, B.-H. Highly Ordered Arrays of Nanoparticles in Large Areas from Diblock Copolymer Micelles in Hexagonal Self-Assembly. Chem. Mater. 2006, 18, 5646–5648. [Google Scholar] [CrossRef]
- Arora, H.; Du, P.; Tan, K.W.; Hyun, J.K.; Grazul, J.; Xin, H.L.; Muller, D.A. Block Copolymer Self-Assembly–Directed Single-Crystal Homo- and Heteroepitaxial Nanostructures. Science 2010, 330, 214–219. [Google Scholar] [CrossRef]
- Xu, J.; Russell, T.P.; Ocko, B.M.; Checco, A. Block copolymer self-assembly in chemically patterned squares. Soft Matter. 2011, 7, 3915–3919. [Google Scholar] [CrossRef]
- Zámbó, D.; Suzuno, K.; Pothorszk, S.; Bárdfalvy, D.; Holló, G.; Nakanishi, H.; Wang, D.; Ueyama, D.; Deák, A.; Lagz, I. Self-assembly of like-charged nanoparticles into Voronoi diagrams. Phys. Chem. Chem. Phys. 2016, 18, 25735–25740. [Google Scholar] [CrossRef]
- Martin, C.P.; Blunt, M.O.; Pauliac-Vaujour, E.; Stannard, A.; Moriarty, P.; Vancea, I.; Thiele, U. Controlling Pattern Formation in Nanoparticle Assemblies via Directed Solvent Dewetting. Phys. Lett. 2007, 99, 116103. [Google Scholar] [CrossRef] [PubMed]
- Lim, J.S. Two Dimensional Signal and Image Processing; Prentice Hall: Upper Saddle River, NJ, USA, 1990; ISBN 0-13-935322-4. [Google Scholar]
- Parker, J.; Sherman, E.; van de Raa, M.; van der Meer, D.; Samelson, L.E.; Losert, W. Automatic sorting of point pattern sets using Minkowski functionals. Phys. Rev. E 2013, 88, 022720. [Google Scholar] [CrossRef] [PubMed]
- Mantz, H.; Jacobs, K.; Mecke, K. Utilizing Minkowski functionals for image analysis: A marching square algorithm. J. Stat. Mech. Theor. Exp. 2008, 2008, P12015. [Google Scholar] [CrossRef]
- Bormashenko, E.; Malkin, A.; Musin, A. Mesoscopic patterning in evaporated Polymer solutions: Poly (ethylene glycol) and room-temperature-vulcanized Polyorganosilanes/-siloxanes Promote formation of honeycomb structures. Macromol. Chem. Phys. 2008, 209, 567–576. [Google Scholar] [CrossRef]
- Aitken, J. Breath Figures. Proc. R. Soc. Edinb. 1895, 20, 94–97. [Google Scholar] [CrossRef]
- Aitkek, J. Breath figures. Nature 1911, 86, 516–517. [Google Scholar] [CrossRef]
- Rayleigh, L. Breath figures. Nature 1911, 86, 416–417. [Google Scholar] [CrossRef]
- Rayleigh, L. Breath figures. Nature 1912, 90, 436–438. [Google Scholar] [CrossRef]
- Bormashenko, E.; Pogreb, R.; Stanevsky, O.; Bormashenko, Y.; Stein, T.; Gendelman, O. Mesoscopic patterning in evaporated polymer solutions: new experimental data and physical mechanisms. Langmuir 2005, 21, 9604–9609. [Google Scholar] [CrossRef]
- Bormashenko, E.; Pogreb, R.; Musin, A.; Stanevsky, O.; Bormashenko, Y.; Whyman, G.; Gendelman, O.; Barkay, Z. Self-assembly in evaporated polymer solutions: Influence of the solution concentration. J. Colloid Interface Sci. 2006, 297, 534–540. [Google Scholar] [CrossRef]
- Alinchenko, M.G.; Anikeenko, A.V.; Medvedev, N.N.; Voloshin, V.P.; Mezei, M.; Jedlovszky, P. Morphology of Voids in Molecular Systems. A Voronoi-Delaunay analysis of a simulated DMPC membrane. J. Phys. Chem. B 2004, 108, 19056–19067. [Google Scholar] [CrossRef]
- Sánchez-Gutiérrez, D.; Sáez, A.; Gómez-Gálvez, P.; Paradas, C.; Escudero, L.M. Rules of tissue packing involving different cell types: human muscle organization. Sci. Rep. 2017, 7, 40444. [Google Scholar] [CrossRef] [PubMed]
- Fedorets, A.A.; Frenkel, M.; Shulzinger, E.; Dombrovsky, L.A.; Bormashenko, E.; Nosonovsky, M. Self-assembled levitating clusters of water droplets: pattern-formation and stability. Sci. Rep. 2017, 7, 1888. [Google Scholar] [CrossRef] [PubMed]
- Fedorets, A.A.; Frenkel, M.; Bormashenko, E.; Nosonovsky, M. Small levitating ordered droplet clusters: stability, symmetry, and Voronoi Entropy. J. Phys. Chem. Lett. 2017, 8, 5599–5602. [Google Scholar] [CrossRef] [PubMed]
- Fedorets, A.A. Droplet cluster. JETP Lett. 2004, 79, 372–374. [Google Scholar] [CrossRef]
- Fedorets, A.A. On the Mechanism of non-coalescence in a droplet cluster. JETP 2005, 81, 437–441. [Google Scholar] [CrossRef]
- Fedorets, A.A. Mechanism of stabilization of location of a droplet cluster above the liquid–gas interface. Tech. Phys. Lett. 2012, 38, 988–990. [Google Scholar] [CrossRef]
- Fedorets, A.A.; Dombrovsky, L.A. Generation of levitating droplet clusters above the locally heated water surface: A thermal analysis of modified installation. Int. J. Heat Mass Transf. 2017, 104, 1268–1274. [Google Scholar] [CrossRef]
- Tagawa, Y.; Mercado, J.M.; Prakash, V.N.; Calzavarini, E.; Sun, C.; Lohse, D. Three-dimensional Lagrangian Voronoi analysis for clustering of particles and bubbles in turbulence. J. Fluid Mech. 2012, 693, 201–215. [Google Scholar] [CrossRef]
- Tolman, R.C. Relativity, Themodynamics and Cosmology; Oxford University Press: Oxford, UK, 1934; ISBN 978-0486653839. [Google Scholar]
- Bormashenko, E. Entropy of relativistic mono-atomic gas and temperature relativistic transformation in thermodynamics. Entropy 2007, 9, 113–117. [Google Scholar] [CrossRef]
- Wigner, E.; Seitz, F. On the Constitution of metallic Sodium. Phys. Rev. 1933, 43, 804–810. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Holt, Rinehart and Winston: New York, NY, USA, 1976; ISBN 9780030493461. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bormashenko, E.; Frenkel, M.; Vilk, A.; Legchenkova, I.; Fedorets, A.A.; Aktaev, N.E.; Dombrovsky, L.A.; Nosonovsky, M. Characterization of Self-Assembled 2D Patterns with Voronoi Entropy. Entropy 2018, 20, 956. https://doi.org/10.3390/e20120956
Bormashenko E, Frenkel M, Vilk A, Legchenkova I, Fedorets AA, Aktaev NE, Dombrovsky LA, Nosonovsky M. Characterization of Self-Assembled 2D Patterns with Voronoi Entropy. Entropy. 2018; 20(12):956. https://doi.org/10.3390/e20120956
Chicago/Turabian StyleBormashenko, Edward, Mark Frenkel, Alla Vilk, Irina Legchenkova, Alexander A. Fedorets, Nurken E. Aktaev, Leonid A. Dombrovsky, and Michael Nosonovsky. 2018. "Characterization of Self-Assembled 2D Patterns with Voronoi Entropy" Entropy 20, no. 12: 956. https://doi.org/10.3390/e20120956
APA StyleBormashenko, E., Frenkel, M., Vilk, A., Legchenkova, I., Fedorets, A. A., Aktaev, N. E., Dombrovsky, L. A., & Nosonovsky, M. (2018). Characterization of Self-Assembled 2D Patterns with Voronoi Entropy. Entropy, 20(12), 956. https://doi.org/10.3390/e20120956








