A Novel Multi-Exposure Image Fusion Method Based on Adaptive Patch Structure
Abstract
1. Introduction
- It uses texture entropy to evaluate image information, which has strong adaptability and robustness.
- It implements the adaptive selection of image patch size by measuring texture entropy, which enables the fused image to retain more detailed information of the source images.
- It combines image cartoon-texture decomposition, image patch structure decomposition, and SSIM index optimization to adjust the local brightness and makes fused images sharper and more smooth.
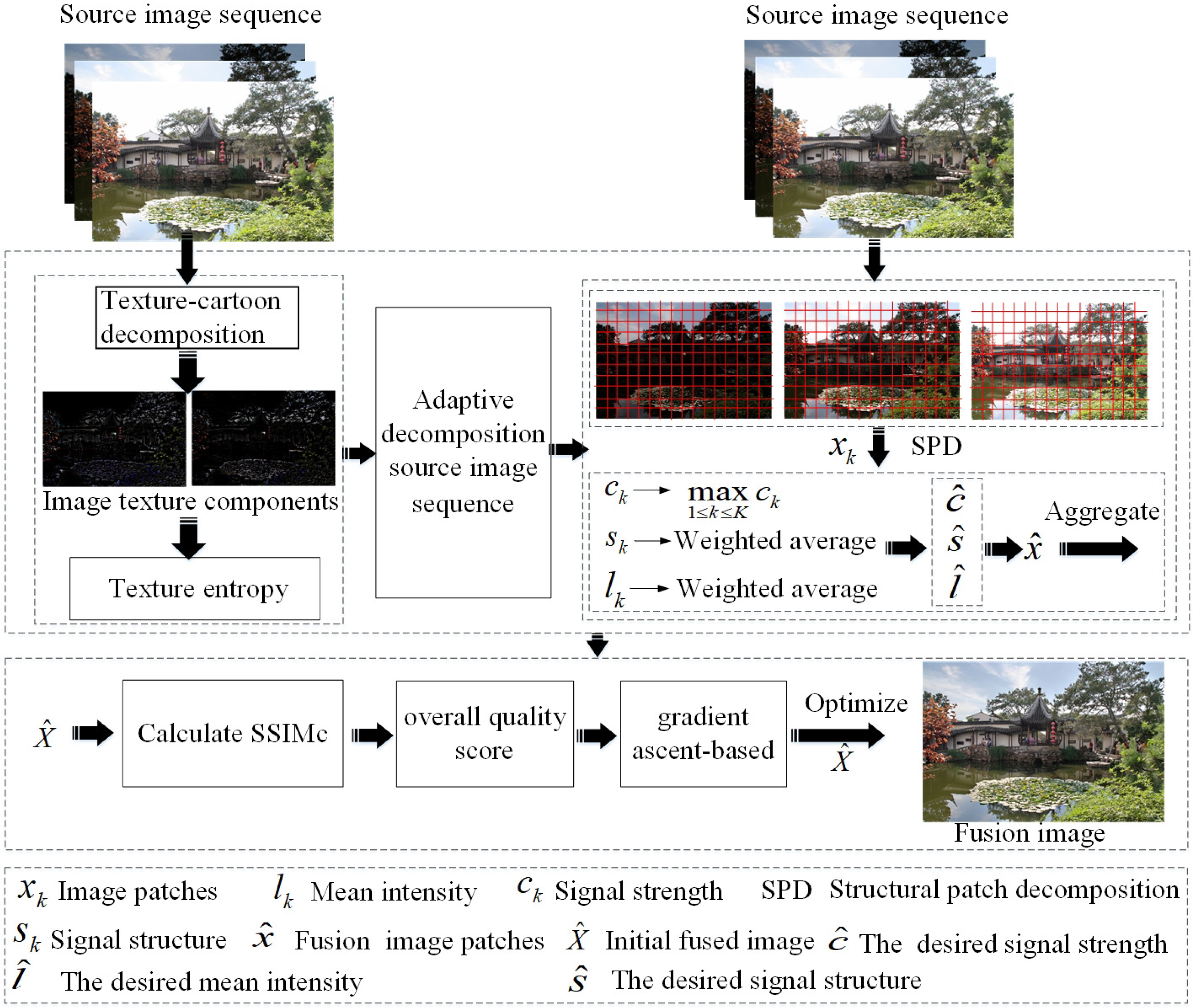
2. MEF Framework Based on the Adaptive Selection of Image Patch Size
2.1. Image Cartoon-Texture Decomposition
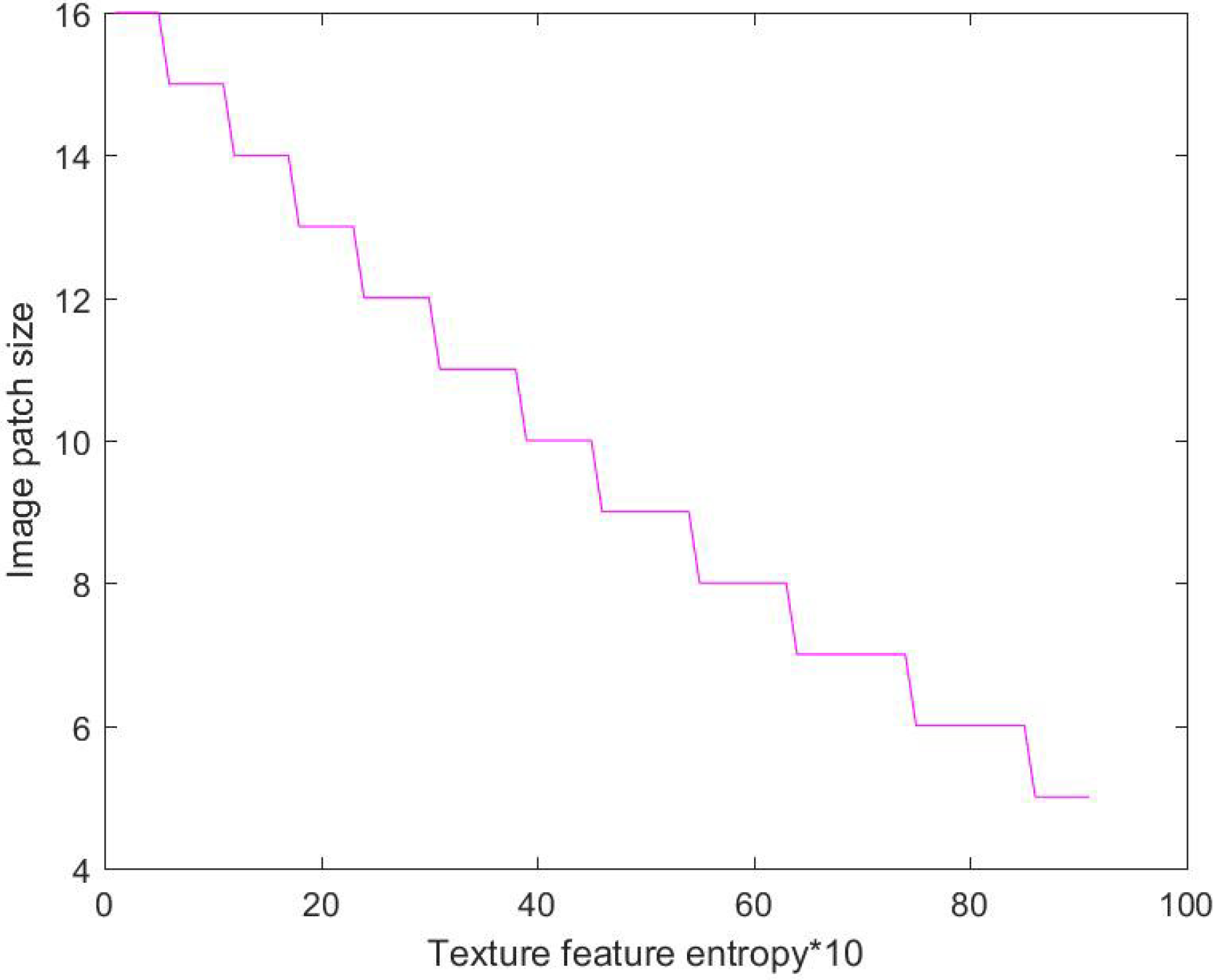
2.2. Adaptive Selection of Image Patch Size
2.3. Structure Patch Decomposition and Structural Similarity Optimization for MEF
3. Experiments and Analyses
3.1. Experiment Preparation
Objective Evaluation Metrics
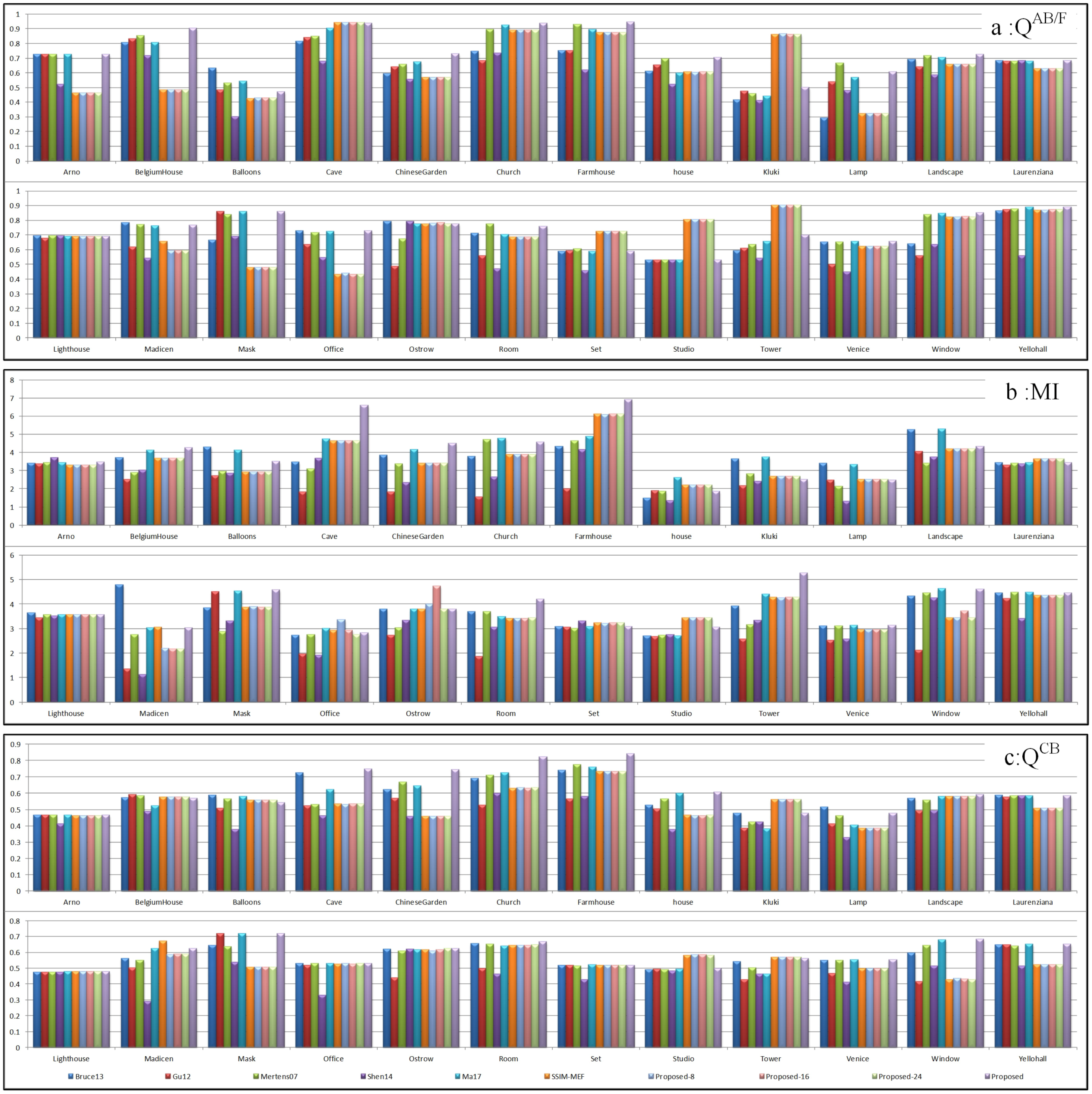
3.2. Experiment Results and Analyses
Experiment Results of Six MEF Methods
3.3. Objective Evaluation Metrics
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Reinhard, E.; Ward, G.; Pattanaik, S.; Debevec, P.E. High Dynamic Range Imaging: Acquisition, Display, and Image-Based Lighting; Princeton University Press: Princeton, NJ, USA, 2005; pp. 2039–2042. [Google Scholar]
- Zhu, Z.; Qi, G.; Chai, Y.; Yin, H.; Sun, J. A Novel Visible-infrared Image Fusion Framework for Smart City. Int. J. Simul. Process Model. 2018, 13, 144–155. [Google Scholar] [CrossRef]
- Ma, K.; Li, H.; Yong, H.; Wang, Z.; Meng, D.; Zhang, L. Robust Multi-Exposure Image Fusion: A Structural Patch Decomposition Approach. IEEE Trans. Image Process. 2017, 26, 2519–2532. [Google Scholar] [CrossRef] [PubMed]
- Artusi, A.; Richter, T.; Ebrahimi, T.; Mantiuk, R.K. High Dynamic Range Imaging Technology [Lecture Notes]. IEEE Signal Process. Mag. 2017, 34, 165–172. [Google Scholar] [CrossRef]
- Qi, G.; Zhu, Z.; Chen, Y.; Wang, J.; Zhang, Q.; Zeng, F. Morphology-based visible-infrared image fusion framework for smart city. Int. J. Simul. Process Model. 2018, 13, 523–536. [Google Scholar] [CrossRef]
- Oh, T.H.; Lee, J.Y.; Tai, Y.W.; Kweon, I.S. Robust High Dynamic Range Imaging by Rank Minimization. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1219–1232. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Qiu, H.; Yu, Z.; Li, B. Multifocus image fusion via fixed window technique of multiscale images and non-local means filtering. Signal Process. 2017, 138, 71–85. [Google Scholar] [CrossRef]
- Li, S.; Kang, X.; Fang, L.; Hu, J.; Yin, H. Pixel-level image fusion: A survey of the state of the art. Inf. Fusion 2017, 33, 100–112. [Google Scholar] [CrossRef]
- Zhu, Z.; Chai, Y.; Yin, H.; Li, Y.; Liu, Z. A novel dictionary learning approach for multi-modality medical image fusion. Neurocomputing 2016, 214, 471–482. [Google Scholar] [CrossRef]
- Mertens, T.; Kautz, J.; Van Reeth, F. Exposure Fusion: A Simple and Practical Alternative to High Dynamic Range Photography. Comput. Graph. Forum 2010, 28, 161–171. [Google Scholar] [CrossRef]
- Li, S.; Kang, X.; Hu, J. Image fusion with guided filtering. IEEE Trans. Image Process. 2013, 22, 2864–2875. [Google Scholar] [PubMed]
- Bruce, N.D.B. ExpoBlend: Information preserving exposure blending based on normalized log-domain entropy. Comput. Graph. 2014, 39, 12–23. [Google Scholar] [CrossRef]
- Kou, F.; Wei, Z.; Chen, W.; Wu, X.; Wen, C.; Li, Z. Intelligent Detail Enhancement for Exposure Fusion. IEEE Trans. Multimed. 2017, 20, 484–485. [Google Scholar] [CrossRef]
- Shen, J.; Zhao, Y.; Yan, S.; Li, X. Exposure Fusion Using Boosting Laplacian Pyramid. IEEE Trans. Cybern. 2014, 44, 1579–1590. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Sun, Y.; Huang, X.; Qi, G.; Zheng, M.; Zhu, Z. An Image Fusion Method Based on Sparse Representation and Sum Modified-Laplacian in NSCT Domain. Entropy 2018, 20, 522. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Wang, Z. A general framework for image fusion based on multi-scale transform and sparse representation. Inf. Fusion 2015, 24, 147–164. [Google Scholar] [CrossRef]
- Huafeng, L.; Jinting, Z.; Dapeng, T. Asymmetric Projection and Dictionary Learning with Listwise and Identity Consistency Constraints for Person Re-Identification. IEEE Access 2018, 6, 37977–37990. [Google Scholar]
- Zhu, Z.; Qi, G.; Chai, Y.; Li, P. A Geometric Dictionary Learning Based Approach for Fluorescence Spectroscopy Image Fusion. Appl. Sci. 2017, 7, 161. [Google Scholar] [CrossRef]
- Wang, K.; Qi, G.; Zhu, Z.; Chai, Y. A Novel Geometric Dictionary Construction Approach for Sparse Representation Based Image Fusion. Entropy 2017, 19, 306. [Google Scholar] [CrossRef]
- Shen, R.; Cheng, I.; Shi, J.; Basu, A. Generalized Random Walks for Fusion of Multi-Exposure Images. IEEE Trans. Image Process. 2011, 20, 3634–3646. [Google Scholar] [CrossRef]
- Qi, G.; Zhu, Z.; Erqinhu, K.; Chen, Y.; Chai, Y.; Sun, J. Fault-diagnosis for reciprocating compressors using big data and machine learning. Simul. Model. Pract. Theory 2018, 80, 104–127. [Google Scholar] [CrossRef]
- Shen, R.; Cheng, I.; Basu, A. QoE-based multi-exposure fusion in hierarchical multivariate Gaussian CRF. IEEE Trans. Image Process. 2013, 22, 2469–2478. [Google Scholar] [CrossRef] [PubMed]
- Gu, B.; Li, W.; Wong, J.; Zhu, M.; Wang, M. Gradient field multi-exposure images fusion for high dynamic range image visualization. J. Vis. Commun. Image Represent. 2012, 23, 604–610. [Google Scholar] [CrossRef]
- Li, S.; Kang, X. Fast multi-exposure image fusion with median filter and recursive filter. IEEE Trans. Consum. Electron. 2012, 58, 626–632. [Google Scholar] [CrossRef]
- Song, M.; Tao, D.; Chen, C.; Bu, J.; Luo, J.; Zhang, C. Probabilistic Exposure Fusion. IEEE Trans. Image Process. 2012, 21, 341. [Google Scholar] [CrossRef] [PubMed]
- Bertalmío, M.; Levine, S. Variational approach for the fusion of exposure bracketed pairs. IEEE Trans. Image Process. 2013, 22, 712–723. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Hu, S.; Liu, K. Patch-Based Correlation for Deghosting in Exposure Fusion. Inf. Sci. 2017, 415, 19–27. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Ma, K.; Duanmu, Z.; Yeganeh, H.; Wang, Z. Multi-Exposure Image Fusion by Optimizing A Structural Similarity Index. IEEE Trans. Comput. Imag. 2017, 4, 60–72. [Google Scholar] [CrossRef]
- Qi, G.; Wang, J.; Zhang, Q.; Zeng, F.; Zhu, Z. An Integrated Dictionary-Learning Entropy-Based Medical Image Fusion Framework. Future Internet 2017, 9, 61. [Google Scholar] [CrossRef]
- Li, H.; Li, X.; Yu, Z.; Mao, C. Multifocus image fusion by combining with mixed-order structure tensors and multiscale neighborhood. Inf. Sci. 2016, 349–350, 25–49. [Google Scholar] [CrossRef]
- Li, H.; He, X.; Tao, D.; Tang, Y.; Wang, R. Joint medical image fusion, denoising and enhancement via discriminative low-rank sparse dictionaries learning. Pattern Recognit. 2018, 79, 130–146. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Yin, H.; Chai, Y.; Li, Y.; Qi, G. A Novel Multi-modality Image Fusion Method Based on Image Decomposition and Sparse Representation. Inf. Sci. 2018, 432, 516–529. [Google Scholar] [CrossRef]
- Vese, L.A.; Osher, S.J. Image Denoising and Decomposition with Total Variation Minimization and Oscillatory Functions. J. Math. Imaging Vis. 2004, 20, 7–18. [Google Scholar] [CrossRef]
- Chamorro-Martinez, J.; Martinez-Jimenez, P. A comparative study of texture coarseness measures. In Proceedings of the IEEE International Conference on Image Processing, Cairo, Egypt, 7–10 November 2010; pp. 1329–1332. [Google Scholar]
- Zhang, W.; He, K.; Meng, C. Texture synthesis method by adaptive selecting size of patches. Comput. Eng. Appl. 2012, 48, 170–173. [Google Scholar]
- Qi, G.; Zhang, Q.; Zeng, F.; Wang, J.; Zhu, Z. Multi-focus image fusion via morphological similarity-based dictionary construction and sparse representation. CAAI Trans. Intell. Technol. 2018, 3, 83–94. [Google Scholar] [CrossRef]
- Petrović, V. Subjective tests for image fusion evaluation and objective metric validation. Inf. Fusion 2007, 8, 208–216. [Google Scholar] [CrossRef]
- Zhu, Z.; Qi, G.; Chai, Y.; Chen, Y. A Novel Multi-Focus Image Fusion Method Based on Stochastic Coordinate Coding and Local Density Peaks Clustering. Future Internet 2016, 8, 53. [Google Scholar] [CrossRef]
- Qu, G.; Zhang, D.; Yan, P. Information measure for performance of image fusion. Electron. Lett. 2002, 38, 313–315. [Google Scholar] [CrossRef]
- Zhu, Z.; Sun, J.; Qi, G.; Chai, Y.; Chen, Y. Frequency Regulation of Power Systems with Self-Triggered Control under the Consideration of Communication Costs. Appl. Sci. 2017, 7, 688. [Google Scholar] [CrossRef]
- Liu, Z.; Blasch, E.; Xue, Z.; Zhao, J.; Laganiere, R.; Wu, W. Objective Assessment of Multiresolution Image Fusion Algorithms for Context Enhancement in Night Vision: A Comparative Study. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 94–109. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Blum, R.S. A new automated quality assessment algorithm for image fusion. Image Vis. Comput. 2009, 27, 1421–1432. [Google Scholar] [CrossRef]








| Image Set | Patch Size | Image Set | Patch Size |
|---|---|---|---|
| Arno | 13 | Balloons | 15 |
| BelgiumHouse | 8 | Cave | 10 |
| Chinese Garden | 14 | Church | 9 |
| Farmhouse | 17 | House | 10 |
| Kluki | 12 | Lamp | 13 |
| Landscape | 12 | Laurenziana | 12 |
| Lighthouse | 12 | MadisonCapitol | 9 |
| Mask | 10 | Office | 17 |
| Ostrow | 18 | Room | 15 |
| Set | 13 | Studio | 12 |
| Tower | 15 | Venice | 10 |
| Window | 15 | Yello wHall | 18 |
| QAB/F | MI | QCB | Time | |
|---|---|---|---|---|
| Bruce13 | 0.66684 | 3.67199 | 0.57956 | 17.30 s |
| Gu12 | 0.64301 | 2.61998 | 0.50975 | 13.60 s |
| Mertens07 | 0.71941 | 3.26387 | 0.57021 | 10.20 s |
| Shen14 | 0.57109 | 2.93935 | 0.46300 | 57.27 s |
| Ma17 | 0.71470 | 3.85767 | 0.57580 | 13.64 s |
| SSIM-MEF | 0.72586 | 3.67061 | 0.57730 | 15.93 s |
| Proposed-8 | 0.65852 | 3.50575 | 0.53225 | 9.50 s |
| Proposed-16 | 0.65863 | 3.53180 | 0.53234 | 14.11 s |
| Proposed-24 | 0.65814 | 3.47528 | 0.53253 | 21.13 s |
| Proposed | 0.73623 | 3.91869 | 0.60737 | 14.12 s |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Sun, Y.; Zheng, M.; Huang, X.; Qi, G.; Hu, H.; Zhu, Z. A Novel Multi-Exposure Image Fusion Method Based on Adaptive Patch Structure. Entropy 2018, 20, 935. https://doi.org/10.3390/e20120935
Li Y, Sun Y, Zheng M, Huang X, Qi G, Hu H, Zhu Z. A Novel Multi-Exposure Image Fusion Method Based on Adaptive Patch Structure. Entropy. 2018; 20(12):935. https://doi.org/10.3390/e20120935
Chicago/Turabian StyleLi, Yuanyuan, Yanjing Sun, Mingyao Zheng, Xinghua Huang, Guanqiu Qi, Hexu Hu, and Zhiqin Zhu. 2018. "A Novel Multi-Exposure Image Fusion Method Based on Adaptive Patch Structure" Entropy 20, no. 12: 935. https://doi.org/10.3390/e20120935
APA StyleLi, Y., Sun, Y., Zheng, M., Huang, X., Qi, G., Hu, H., & Zhu, Z. (2018). A Novel Multi-Exposure Image Fusion Method Based on Adaptive Patch Structure. Entropy, 20(12), 935. https://doi.org/10.3390/e20120935







