1. Introduction
Rotor is a key element of rotary machine and its working condition affects the reliability and safety of whole mechanical system. Accurate identification of rotor faults is very helpful for reducing economic losses and ensuring production safety [
1,
2,
3,
4].
As the vibration signal of rotors carries plentiful fault information, a lot of rotor fault diagnosis approaches were developed based on vibration signal analysis [
5,
6]. Due to the non-stationary and non-linear characteristics of rotor vibration signals, classical signal analysis methods based on Fourier transform fail to extract the fault features of rotors accurately [
7]. In recent years, the application of time–frequency analysis to rotor failure detection has attracted considerable attention as the time–frequency analysis approaches are able to reflect the characteristic information in both time domain and frequency domain [
8]. Among these developed time–frequency analysis approaches, wavelet transform (WT) is one of the most effective one for its high time–frequency resolution [
9,
10]. However, an appropriate basis function should be selected or designed in every use of WT to ensure a satisfactory result, which reduces the adaptability of WT [
11]. Considering the drawback of WT, Huang et al. developed a novel adaptive time–frequency technique called Hilbert-Huang transform (HHT) [
12], which is the combination of empirical mode decomposition (EMD) and Hilbert transform (HT). EMD is used to adaptively decompose a multi-component signal into several intrinsic mode functions (IMFs) that carry the useful information of different frequency bands. Then the instantaneous amplitude (IA) and instantaneous frequency (IF) of each IMF are calculated by HT. Consequently, the HHT time–frequency spectrum (TFS) can be obtained by integrating the IAs and IFs of all IMFs. HHT has an extensive application in detecting mechanical faults owing to its priorities of extracting non-stationary characteristics of signals.
The HHT TFS demonstrates the energy–frequency–time distribution of a signal. For different mechanical faults, the corresponding energy–frequency–time distribution varies greatly. To implement the automatic identification of different mechanical fault types, it is of great significance to exploit an effective index to measure the differences of the corresponding energy–frequency–time distribution. Shannon Entropy is a satisfactory indicator for measuring the complexity and regularity of a signal and the diversity of any distribution [
13,
14,
15]. Therefore, some entropy-based indicators were developed to evaluate the fault features of rotating machinery. For example, the Teager energy entropy ration (TEER) was proposed as an impulsive feature evaluation index to select the optimal sub-band component obtained by performing wavelet transform decomposition on the vibration signal of rolling bearings in [
16]. The TEER index is the combination of the Teager energy entropy in time domain and frequency domain. However, it cannot reflect the information of the time–frequency domain. Yu et al. proposed a time–frequency entropy (TFE) method by combing the merits of entropy and HHT for gear fault diagnosis [
17]. The TFE gives an indicator that can estimate the information of time–frequency domain. However, the TFE has two main shortcomings. One is originated from EMD. EMD is troubled by mode mixing [
18], which makes the obtained HHT TFS cannot accurately reflect the time–frequency information of a signal. On the other hand, the TFE index is a measure of the whole information of the HHT TFS, it is not able to extract the local energy–frequency–time distribution of the TFS, which leads the calculation of TFE to be relatively complex. In conclusion, the TFE can be improved from two aspects: (a) Improve the HHT method to obtain a more accurate TFS; (b) Develop a novel index which can reflect the local characteristics of the TFS.
To improve the accuracy of HHT, some other advanced signal decomposition approaches, such as ensemble empirical mode decomposition (EEMD) [
19], complementary ensemble empirical mode decomposition (CEEMD) [
20], empirical wavelet transform [
21], variable mode decomposition (VMD) [
22], and adaptive local iterative filtering (ALIF) [
23] have been employed to replace EMD to extract the sub-components of a signal. Despite these methods have a better performance over EMD in data decomposition, the premise of obtaining ideal results by using these methods is the good choice of parameters, the process of which is very complex. Singular spectrum decomposition (SSD) is a new adaptive data decomposition method [
24], the basic principle of which is based on singular spectrum analysis (SSA). It could choose the parameters automatically and retrieve the construction components accurately. Moreover, the existence of non-meaningful components could be minimized to a large extend. However, the problem of end effects still has not been solved in the original SSD algorithm, which needs to be studied further. Some useful techniques such as extreme value point extension [
25], data prediction [
26] and waveform matching extension method [
27] have been studied by scholars for restraining the end effect of EMD. However, these developed approaches have some drawbacks. For example, the extreme value point extension method only considers the information of several extreme value points near signal endpoint but does not take into account the internal law of the signal, so the effect of this method for complex non-stationary signals is not ideal. The data prediction method is on the base of the intelligent prediction techniques such as neural work [
28] and support vector regression [
29]. Its improvement effect depends largely on the parameter setting of the prediction tool itself, and the operation time is also long, which decreases the practicability of this method. The waveform matching extension method takes into account the internal laws and trends of signal and has high computation efficiency. However, how to choose the best matching waveform adaptively is a difficult problem. In view of the above problems, a novel adaptive waveform matching extension approach was introduced for solving the end effects and improving the decomposition accuracy of SSD. The improved SSD (ISSD) method was employed to replace EMD to extract the sub-component signals of the rotor vibration signal. Several sub-component signals called singular spectrum components (SSCs) can be extracted after the ISSD decomposition. Then an ISSD-HT TFS can be produced by using HT to demodulate every SSC. The ISSD-HT TFS is more accurate than the HHT TFS due to the advantages of ISSD over EMD. Considering that the main fault features of rotors locate in the former harmonics of rotary frequency of the TFS, a new index called characteristic frequency band energy entropy (CFBEE) was proposed in this paper to extract the local characteristics of the ISSD-HT TFS corresponding to different working conditions of rotors. After extracting the CFBEE as the feature vector, an outstanding machine-learning classifier called support vector machine (SVM) [
30], which is especially suitable for the classification problem of small samples was used in this paper to achieve the fault identification of rotors.
This organization of this paper is as follows: In
Section 2, basic theory background of ISSD, characteristic frequency band energy entropy and SVM is introduced.
Section 3 describes the framework of the proposed method. Simulation and experiment signals are analyzed in
Section 4 and
Section 5, respectively. Besides, comparison is performed among the proposed method and three other methods to demonstrate the effectiveness and superiority of the proposed method. Conclusion is summarized in
Section 6.
2. Theory Background
2.1. Singular Spectrum Decomposition
SSD is a novel signal decomposition approach derived from SSA. While SSA has a powerful capability of recovering sub-component signal from the multi-component signals [
31], how to properly choose the embedding dimension and select the principal components for reconstructing a specific sub-component are its two main obstacles. The use of SSD improves the process by allowing the SSA fundamental parameters to be selected adaptively. Given an original multi-component signal
y(
n),
n = 1,2,…,
N, its sub-component signals, referred to as SSCs, can be iteratively extracted using the following steps:
(a) Embedding.
If the embedding dimension is selected as
K, 1 <
K <
N, a
K ×
L matrix
Y named Hankel matrix can be generated. The Hankel matrix consists of
K lagged vectors
yi = [
y(
i),…,
y(
N),
y(1),…,
y(
i−1)],
i = 1, 2,…,
N −
K + 1. Taking the one-dimensional signal
y(
n) = {1, 2, 3, 4, 5} as an example, if the embedding dimension
K is set to 3, the corresponding Hankel matrix becomes:
In the SSD method, the embedding dimension is adaptively selected as K = fs/fmax, where fmax represents the dominant frequency in the power spectral density (PSD) of y(n) and fs indicates the sampling frequency.
(b) Decomposition.
The Hankel matrix
Y is then decomposed using singular value decomposition (SVD):
where
U ∈
RK × K,
D ∈
RL × L and
V ∈
RN × N. Both
U and
V are orthogonal matrices, which contains the left and right vectors, respectively. The main diagonal of
D carries the singular values.
After the SVD process, the Hankel matrix Y is decomposed into K principle components.
(c) Grouping.
The R (R < K) principle components, whose left eigenvectors reflect a domain frequency in the range [fmax − Δf, fmax + Δf], are selected out to reconstruct the sub-component signal. Δf is determined by the Gaussian interpolation of the PSD of y(n).
(d) Reconstruction.
The selected
R principal components are employed to generate a rank-R approximation of
Y. Then the corresponding sub-component can be recovered by applying diagonal averaging to the adjusted version of this matrix. For instance, the adjusted version of the above matrix shown in Equation (1) can be described as:
The detailed introduction to SSD can refer to [
24].
2.2. Improved Singular Spectrum Decomposition
As reported in [
24], a limitation of SSD is that the decomposed components are always affected by end effects. This requires the extension of both ends of the original signal to isolate the distortion as far as possible from the outside of the signal to be analyzed. However, this extension cannot be blind extension, but to make the extended waveform conform to the natural trend of the original signal as much as possible, to maximize the maintenance of the change trend of the original signal and achieve a smooth transition between the extended waveform and the original signal. Thus, a novel waveform matching degree evaluation index was proposed by combing the correlation coefficient and root mean square error to adaptively perform the waveform matching extension. An improved singular spectrum decomposition (ISSD) approach was developed by using this waveform matching extension method to improve the decomposition accuracy.
The extension of the signal includes the left and right ends, and the following is an example of the extension of the left side to illustrate the proposed adaptive waveform matching extension method.
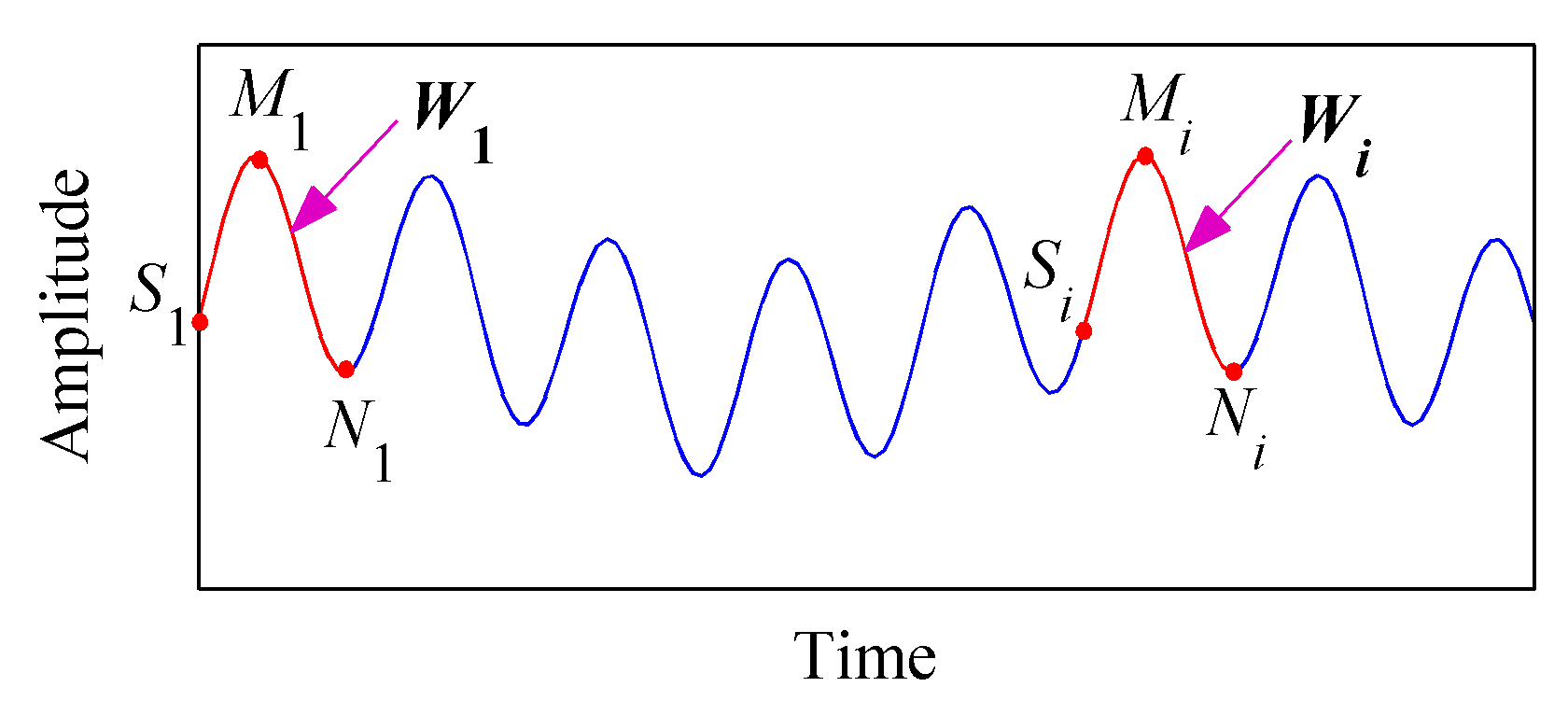
Assume the original signal is
x(
t),
Mi and
Ni (
i = 1, 2, 3,…) are the maximum and minimum points of
x(
t), respectively.
and
correspond to the time of the maximum and minimum points, respectively. The left end of the signal is defined as
S1. The signal shown in
Figure 1 was taken as an example, the first extreme point of which is a maximum point. The waveform
S1-
M1-
N1 is targeted as the characteristic waveform
W1. Then the optimal matching waveform will be searched within the whole data. Finally, the left data of the optimal matching waveform will be extended to the left of the data. The specific steps are given as follows:
(1) Find out the starting point of all matched waveform
Si (
i = 1,2,3…), whose corresponding time can be calculated as:
The waveform Si-Mi-Ni is defined as the matched waveform Wi.
(2) Calculate the proposed matching degree of the characteristic waveform and the matching waveform by using the following equation:
where,
and
represent the cross-correlation coefficient and root mean square error between
W1 and
Wi, respectively. If the correlation between the two waveforms is stronger and the root mean square error is smaller, the matching degree is higher.
(3) Treat the matching waveform which has the largest value of Di as the optimal matching waveform. When there are multiple optimal matching waveforms, the one which is farthest from the starting point is regarded as the optimal matching waveform.
(4) Extend the data on the left side of the optimal matching waveform to the left side of S1.
Similarly, the same steps can be used to complete the right extension of the data. The extended data will be decomposed by SSD to generate a series of SSCs with physical meanings. Finally, the SSCs with the same length as the original signal data can be obtained by intercepting based on the pre-extension position. As the ISSD will be combined with HT to conduct the time–frequency analysis for the rotor fault signal in this paper and HT also has end effects, the interception process will take place after the HT process.
2.3. Time–frequency Analysis Bsed on Improved Singular Spectrum Decomposition and Hilbert Transform
ISSD was combined with HT to perform the time–frequency on rotor vibration signal in this work. The process of this time–frequency analysis is as follows. Firstly, the original signal is decomposed into a series of SSCs by ISSD. Then, the obtained SSCs are demodulated by HT to derive their instantaneous frequency (IF) and IA.
For a given singular spectrum component
SSC(
t), its HT is defined as follows [
32]:
We can further get the analytical signal:
where,
a(
t) represents the IA of
SSC(
t) and
φ(
t) is the instantaneous phase. Their specific expressions are given in Equations (8) and (9), respectively:
The IF of
SSC(
t) can be derived as:
The IA and IF reflects the time–frequency information of SSC(t). By integrating the time–frequency information all SSCs, the ISSD-HT TFS can be derived.
2.4. Characteristic Frequency Band Energy Entropy
The time–frequency analysis can be an effective tool for extracting the fault signatures of rotors. However, to classify the rotor fault types automatically, some indexes must be developed to evaluate the useful information carried by the TFS. Time–frequency entropy (TFE) was thus introduced by Yu et al. [
17] to measure the energy distribution characteristics of the HTT TFS to distinguish different gear fault types. To highlight the innovation of the proposed method, the principle of the TFE would be given briefly before introducing the proposed CFBEE in this work.
In the principle of the TFE method, the whole TFS plane is divided into
N small time–frequency blocks with the same area, and the normalized energy of each block
Qi can be calculated as:
where,
Wi and
A represent the energy of the time–frequency block and the energy of the whole TFS plane, respectively.
Equation (12) gives the definition of TFE based on HHT:
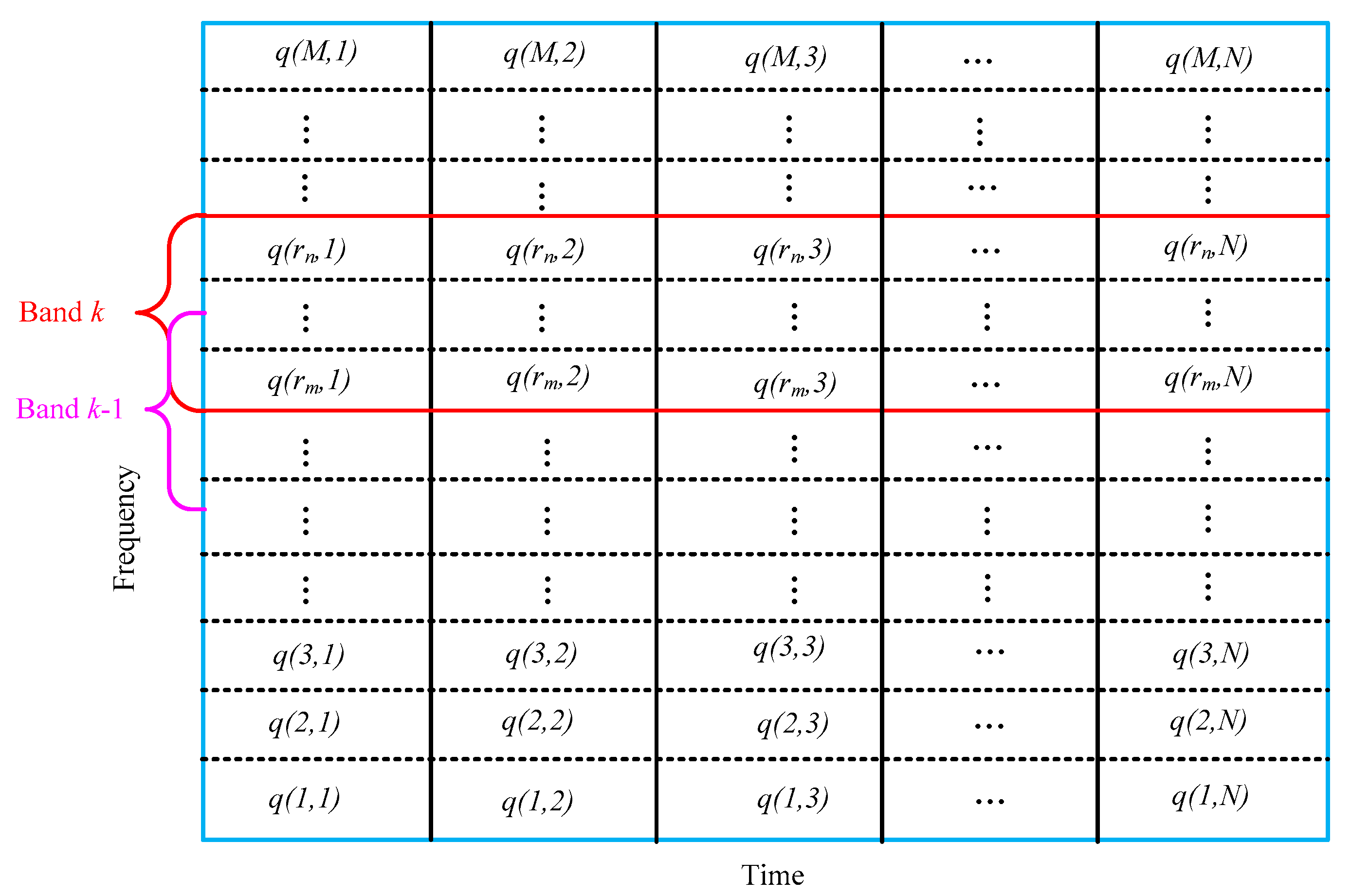
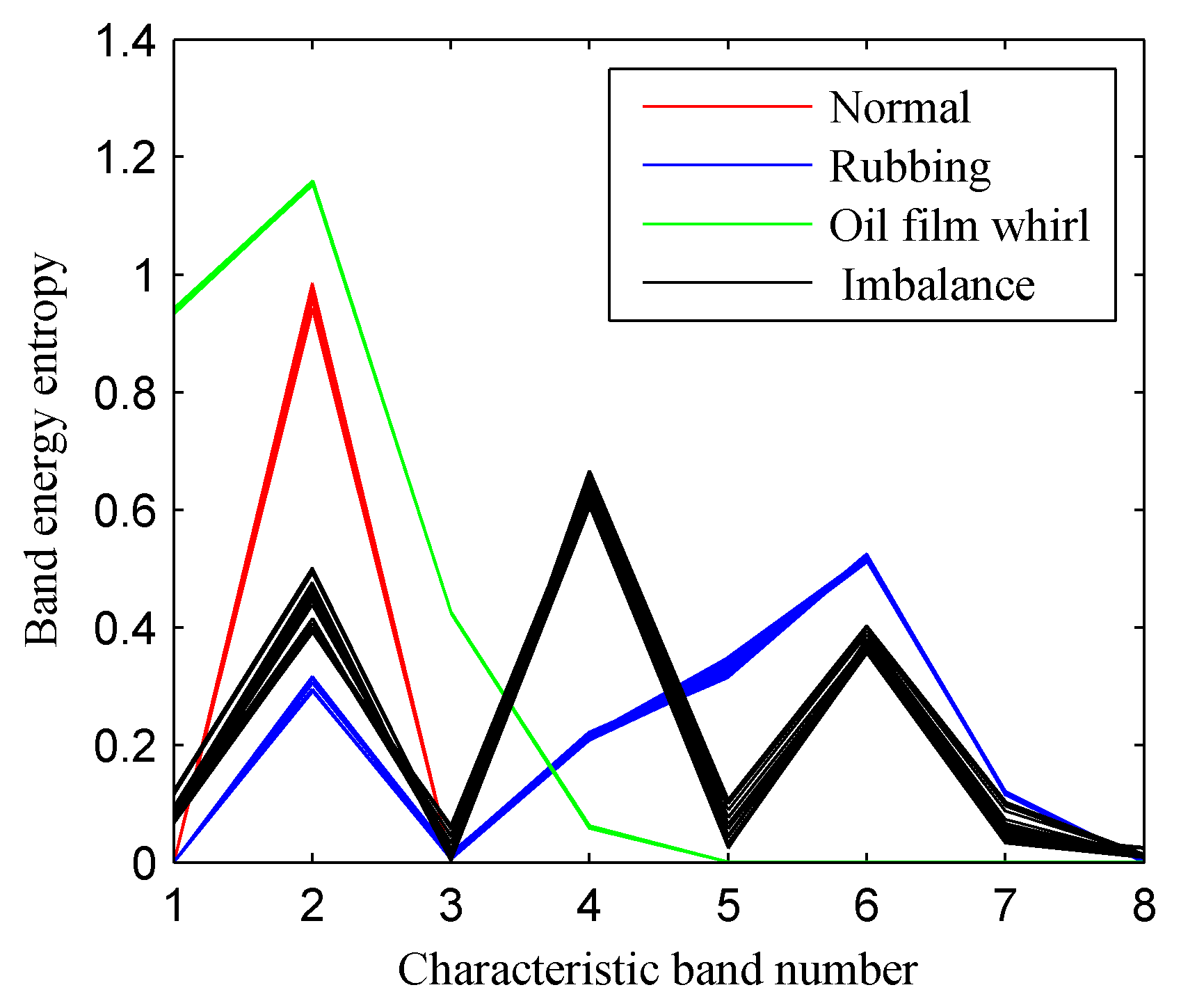
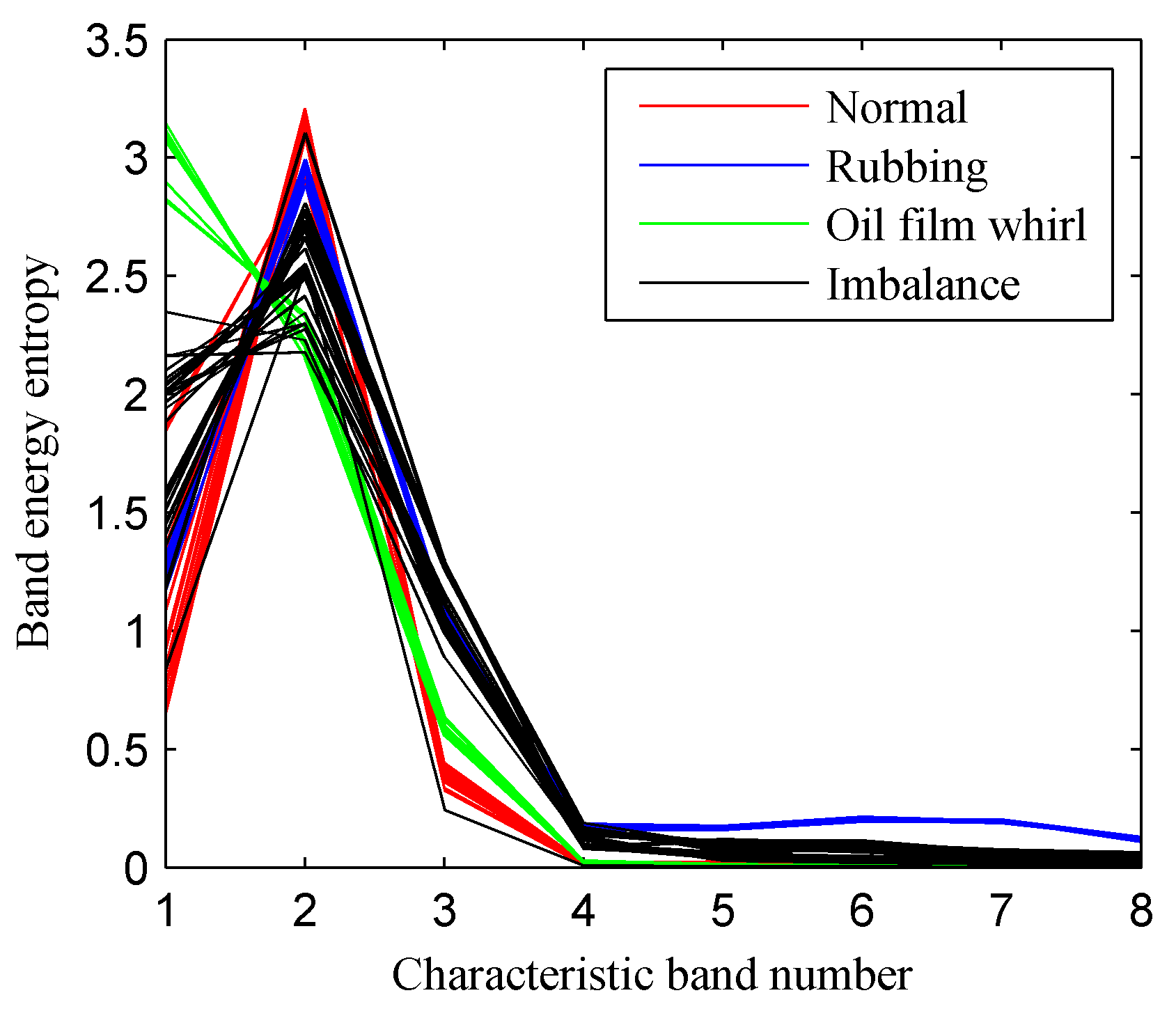
From the definition of TFE, we can deduce that it is a measure of the whole TFS. Therefore, some redundant information may be wrongly considered in the TFE index when the rotor vibration signal is affected by noise and other abnormal disturbances. Previous studies demonstrated that some sub-harmonics and sup-harmonics of the rotational speed, which is called the fault characteristic frequencies in this paper, would be generated when rotor defects occur. Hence, it is very critical to takes some measures to extract the fault features around the sub-harmonics and sup-harmonics of the rotational speed. Considering the characteristic information of rotor faults is always concentrated in the former fault characteristic frequencies, we proposed the CFBEE index, which is used to mainly reflect the local characteristic information around the eight former characteristic frequencies, i.e., the 0.5X, 1X, 1.5X, 2X, 2.5X, 3X, 3.5X, 4X of the rotational frequency. Firstly, the time–frequency spectrum plane is divided into M × N blocks. Then, eight characteristic frequency bands of [0.1X–0.9X], [0.6X–1.4X], [1.1X–1.9X], [1.6X–2.4X], [2.1X–2.9X], [2.6X–3.4X], [3.1X–3.9X], [3.6X–4.4X], which respectively take the eight former characteristic frequencies as the center frequency are defined as characteristic frequency bands. Finally, the energy entropy of the eight characteristic frequency bands is calculated as the characteristic frequency band energy entropy.
Figure 2 shows the division result of the TFS plane corresponding to the CFBEE method. For the
kth characteristic frequency band (
),
and
represent its start and end row. Supposing the energy of the time–frequency block in the
kth characteristic frequency band is
W(
i,
j) and
Wk is the total energy of the
kth characteristic frequency band. The normalized energy of any time–frequency block can be described as follows:
Then, the total energy of the
ith row in the
kth characteristic frequency band can be derived as:
The CFBEE of
kth characteristic frequency band is defined as:
After calculating the CFBEE of all the eight characteristic frequency bands, a fault feature vector, i.e., {CFBEE1, CFBEE2, CFBEE3, CFBEE4, CFBEE5, CFBEE6, CFBEE7, CFBEE8}, is obtained to characterize the fault types. From the principle of CFBEE, we can find that it is a direct measure of the local information around the fault characteristic frequency. Previous studies indicate that the background noise can generate high-frequency components in the time–frequency spectrum. Hence, the CFBEE index can exclude some redundant information corresponding to the high-frequency noise.
2.5. Support Vcetor Machine
SVM is a machine-learning algorithm based on the structural risk minimization principle of statistical learning theory [
33]. For the two-class problem, SVM maps the non-linear separable problem in low-dimensional space to high-dimensional space through a certain non-linear kernel function mapping, making it linear separable. The core of SVM is to seek a hyper plane in high-dimensional space as the segmentation of two classifications to ensure the minimum classification error rate.
For a given training sample
, where
d represents the dimension of the space,
yi is the pattern label of
xi. The hyper plane can be described as:
where,
ω and
k represent the weighting vector and the bias, respectively.
The optimal classification plane in the feature space can be constructed by solving the following quadratic programming problem:
where,
C is a penalty factor which can indicates the penalty level for classification errors and
represents a slack factor. According to quadratic programming, Equation (16) is equivalent to solve the following optimization problem:
where
λi is Lagrange multiplier and
K(
xi,
xj) represents the kernel function. The optimal classification decision function can be derived as:
To deal with multi-class fault diagnosis problems, ‘one-against-others’ SVM algorithm illustrated in [
30] is adopted in this paper.
3. The Framework of the Proposed Method
Figure 3 displays the framework of the proposed method, which can be introduced in detail as:
(1) Decompose the signal collected by the sensors mounted on the rotor by the ISSD method to obtain the decomposed SSCs.
(2) Perform Hilbert transform on the SSCs to derive the ISSD-HT TFS plane.
(3) Divide the ISSD-HT TFS plane into eight frequency bands, namely, [0.1X–0.9X], [0.6X–1.4X], [1.1X–1.9X], [1.6X–2.4X], [2.1X–2.9X], [2.6X–3.4X], [3.1X–3.9X], [3.6X–4.4X], and the characteristic frequency band energy entropy of each band is calculated with the method mentioned above.
(4) Identify the rotor fault types with the SVM classification method.
4. Simulation Signal Analysis
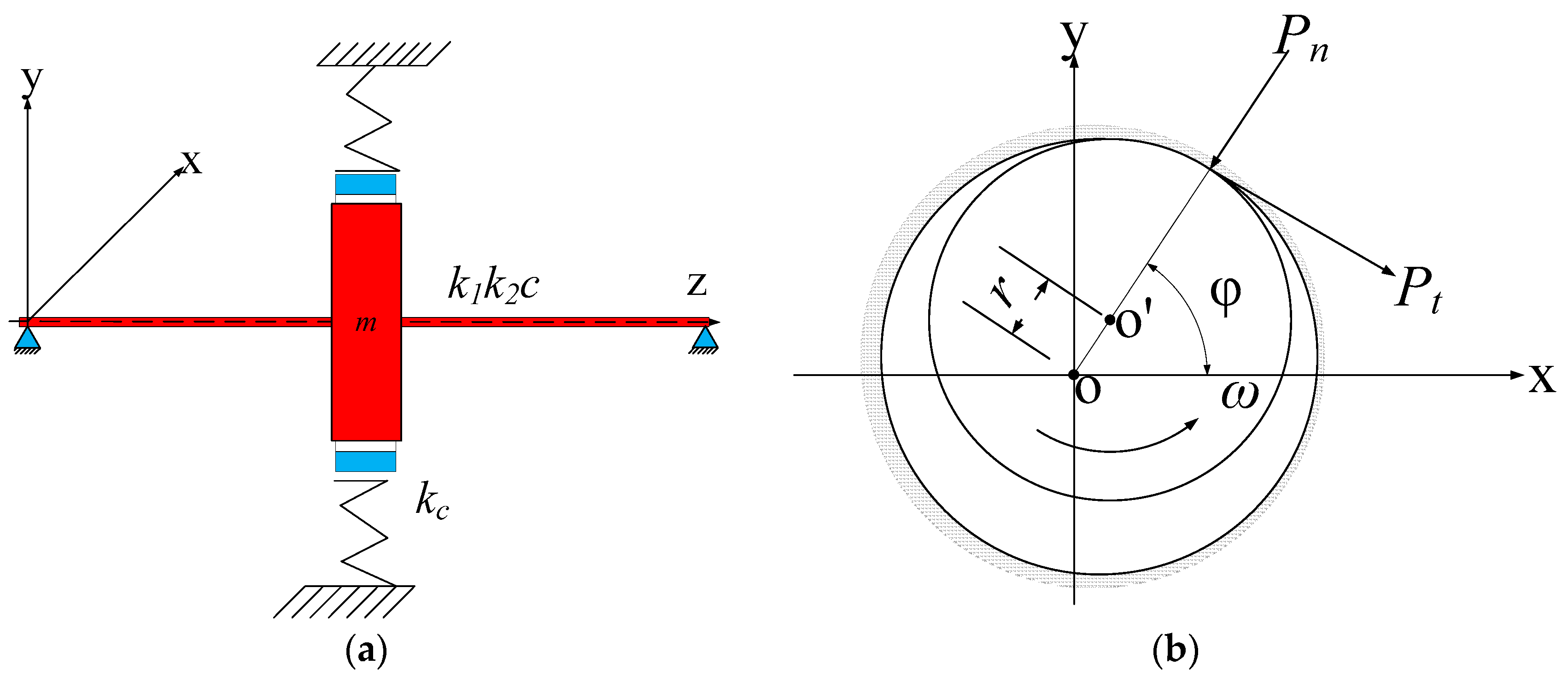
To validate the superiority of ISSD in processing rotor fault signals, a Jeffcott rotor rub-impact model was established to construct simulation signal firstly. Then the signal is analyzed by EMD, SSD and ISSD respectively for comparison. The rotor rubbing model is shown in
Figure 4a. A single disc rotor, the mass of which is
m, is fixed in the middle of a simply supported shaft with the angular speed of
ω. The mass of the shaft is neglected. It is assumed that the linear bending stiffness of the rotating shaft is
k1 and the non-linear bending stiffness of the rotating shaft is
k2.
c and
kc are the damping coefficient and the radial stiffness of the stator, respectively.
Figure 4b shows a schematic diagram of the rotor rubbing force. Assuming that the rubbing force between the rotor and the stator conforms to Coulomb’s law and
is the radial displacement of the geometric center of the rotor, the normal contact force
Pn and tangential rubbing forces
Pt can be calculated as follows [
34]:
where,
δ is the minimum gap between rotor and stator,
is the relative sliding speed between the moving and stationary parts,
f is the friction coefficient and
α is the speed influence factor. If the angle between the point of occurrence of rubbing and the
x-axis is
φ, the normal and tangential rubbing forces can be expressed in the X-Y coordinate system as follows:
Then, the equation of motion of the rotor can be established as Equation (22) shows:
where,
μ represents eccentricity of the rotor.
With the transformation of
,
,
,
,
,
,
, the differential equations of motion for the rotor are obtained:
Using the four order Runge-Kutta method to solve Equation (23), we can get the vibration response of the signal in the direction of X and Y. For the simulated signal in this paper, the specific parameters were initialized to: , , , , , , and .
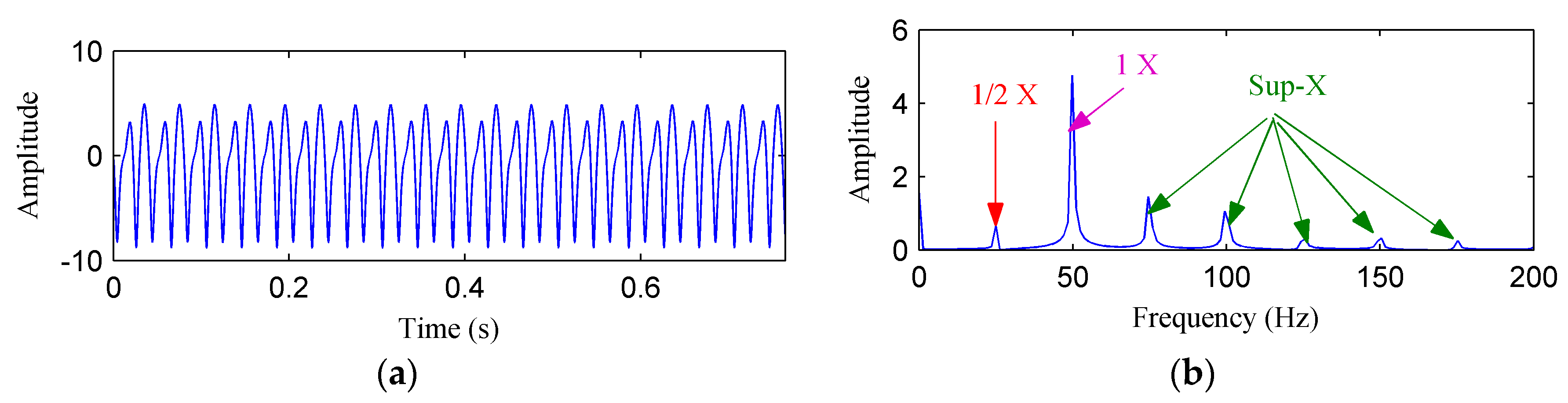
Figure 5a,b shows the waveform and frequency spectrum of the simulated rubbing signal in the Y direction, respectively. As can be seen from
Figure 5b, the fundamental frequency, fractional harmonics and high harmonics are all clearly presented.
Then, the simulation signal is processed by EMD, SSD and ISSD respectively, and the results are shown in
Figure 6,
Figure 7 and
Figure 8, respectively.
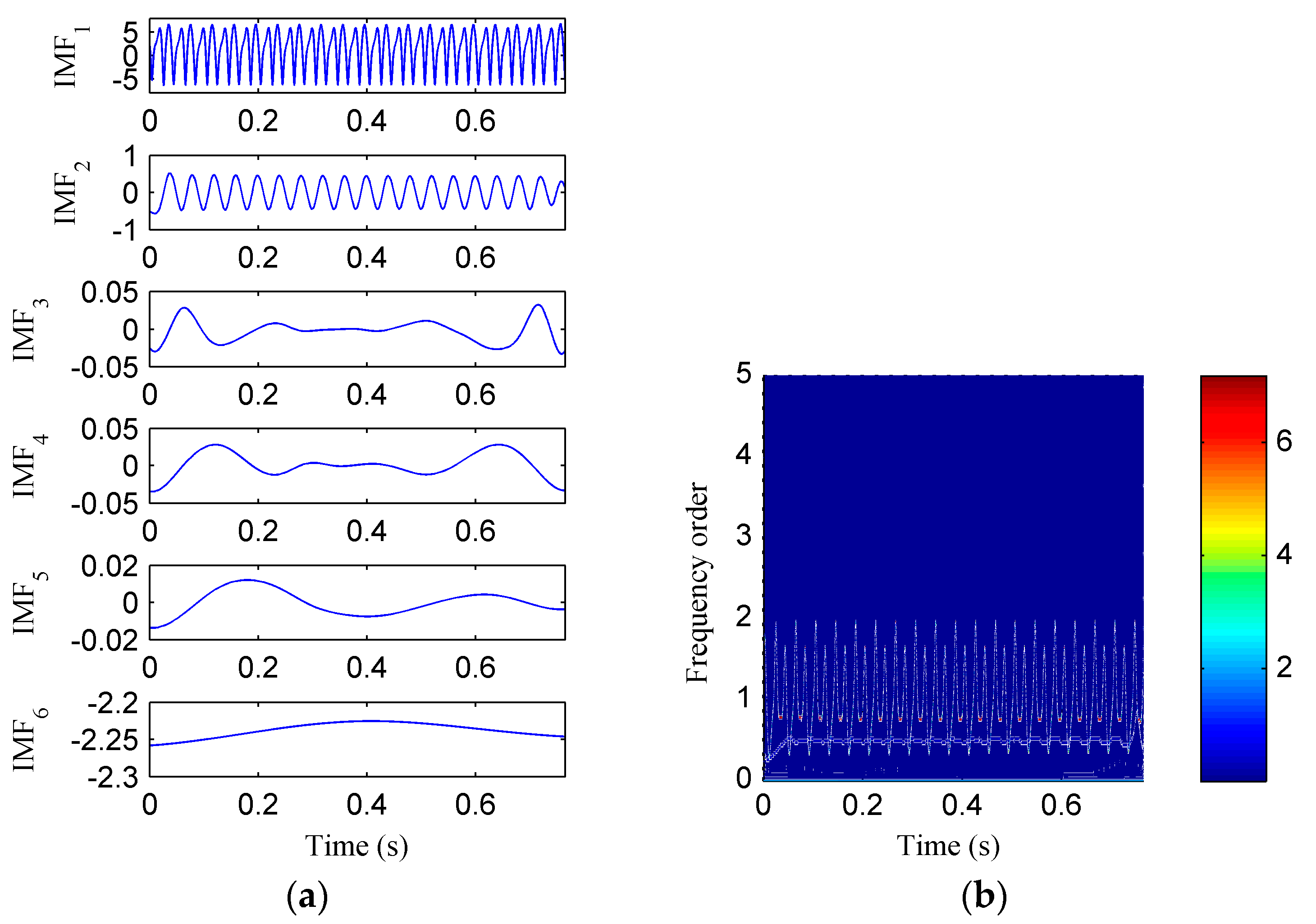
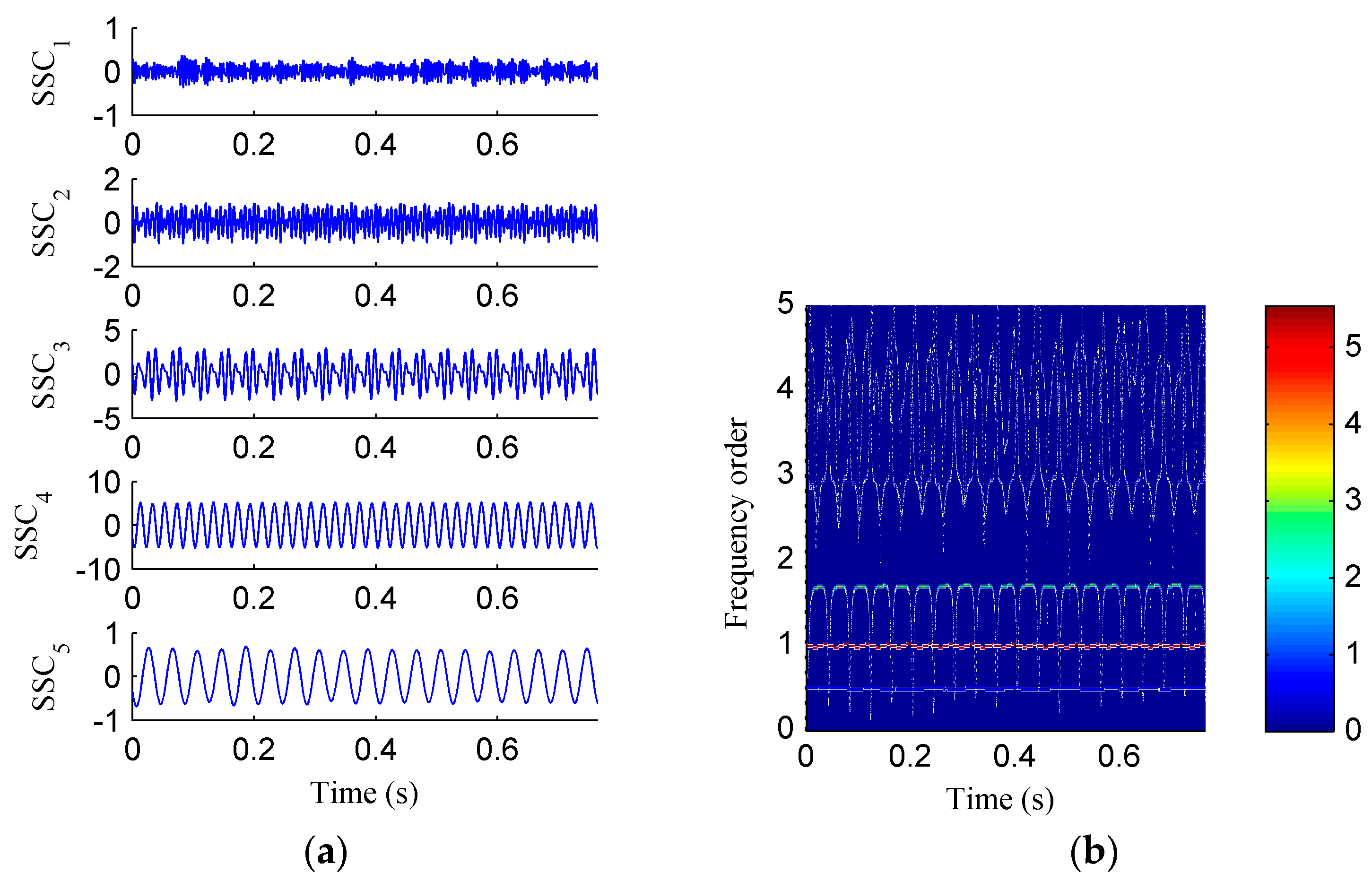
Figure 6a displays the decomposed sub-components using EMD and
Figure 6b depicts the corresponding HHT TFS, i.e., the EMD-HT TFS. To clearly reveal the relationship between the frequency components exhibited in the TFS and the rotation frequency, the y-axis of the TFS in this paper was described using the frequency order, which is defined as the ratio of the actual frequency to the rotation frequency. Six sub-components were extracted after the EMD decomposition, but some of them are false components without physical meaning. The model aliasing problem appeared on the HHT TFS, which makes the HTT TFS cannot accurately reflect the fault information. As shown in
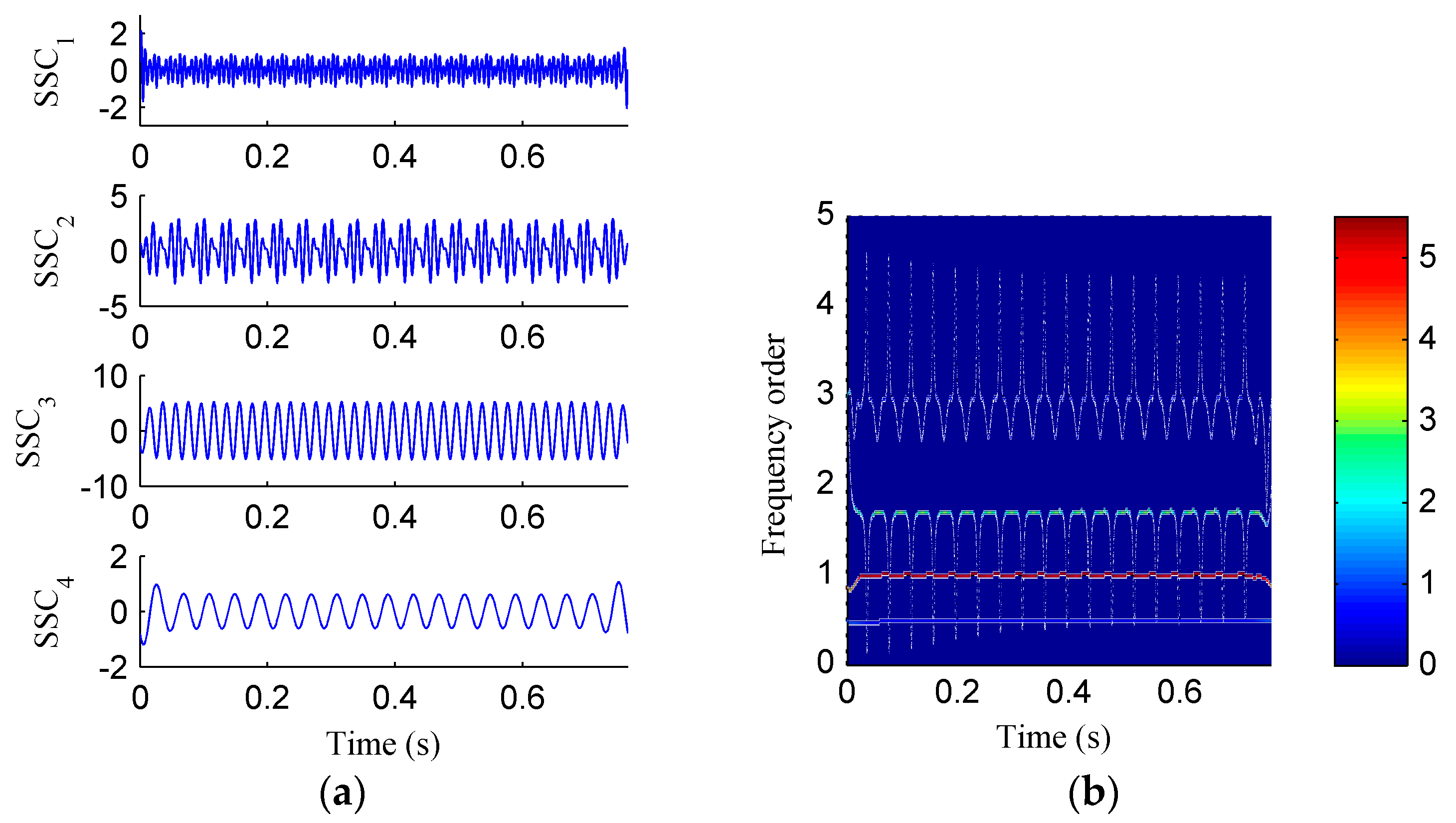
Figure 7a, four sub-components were derived after the SSD decomposition. The corresponding SSD-HT TFS as depicted in
Figure 7b reflects the characteristic frequencies of the simulated rubbing fault. Moreover, the “intrawave frequency modulation” phenomenon which is one of the characteristics of rubbing fault as reported in [
35] was clearly extracted. However, the end effects can also be found from the SSD-HT TFS. The appearance of the end effect can cause the change of the energy–frequency–time distribution in the TFS to some extent. Consequently, the energy–frequency–time distribution of the TFS will lose its real regularity. To ensure a more accurate measure of the energy distribution characteristics of the TFS by using the CFBEE index, the end effect problem should be solved. Compared with
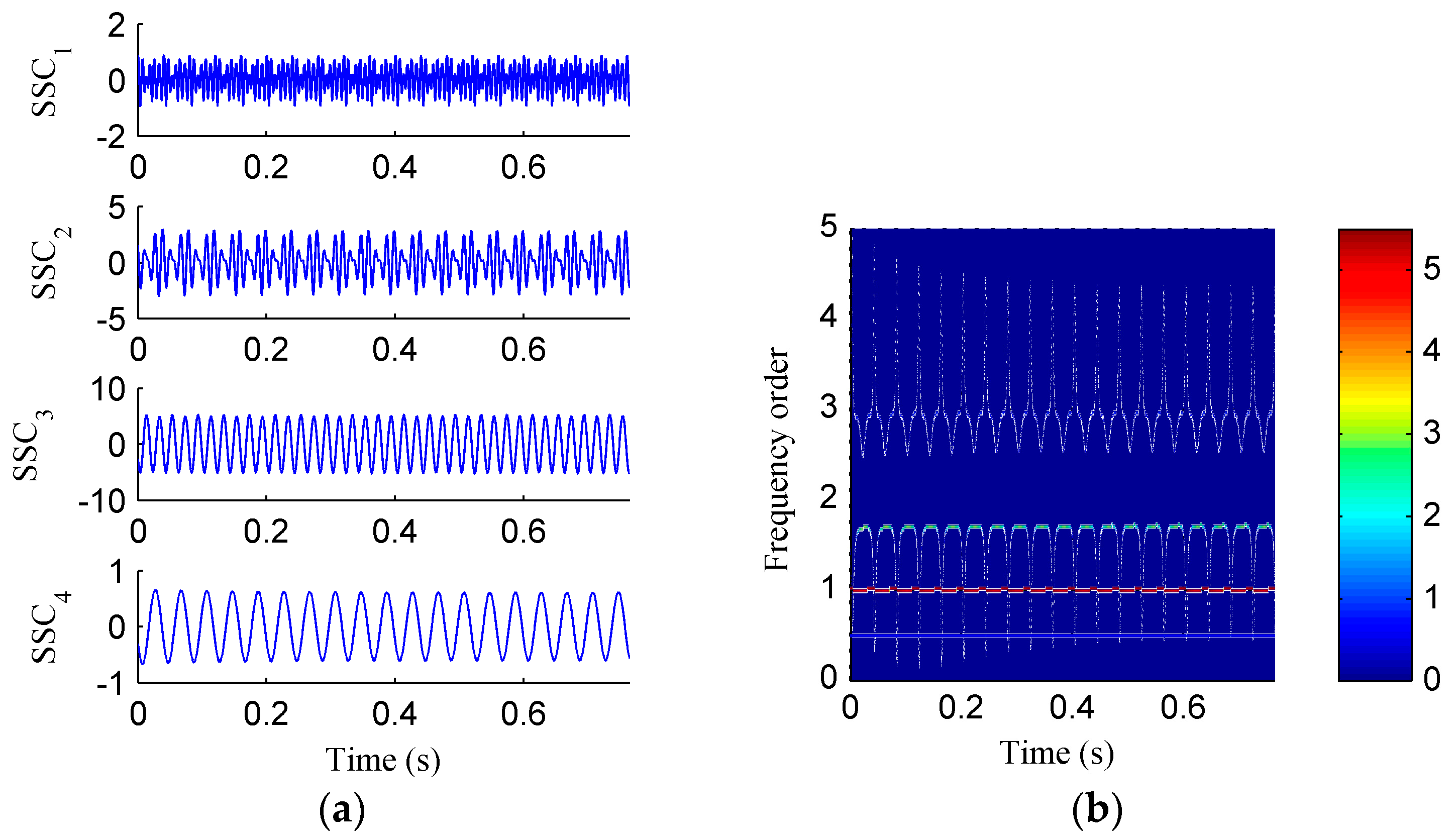
Figure 7a, the sub-components obtained by using ISSD as shown in
Figure 8a overcome the end effects. The corresponding ISSD-HT TFS displayed in
Figure 8b is also away from the end effects. Hence, the superiority of ISSD method over the other two methods can be demonstrated from the simulated results.
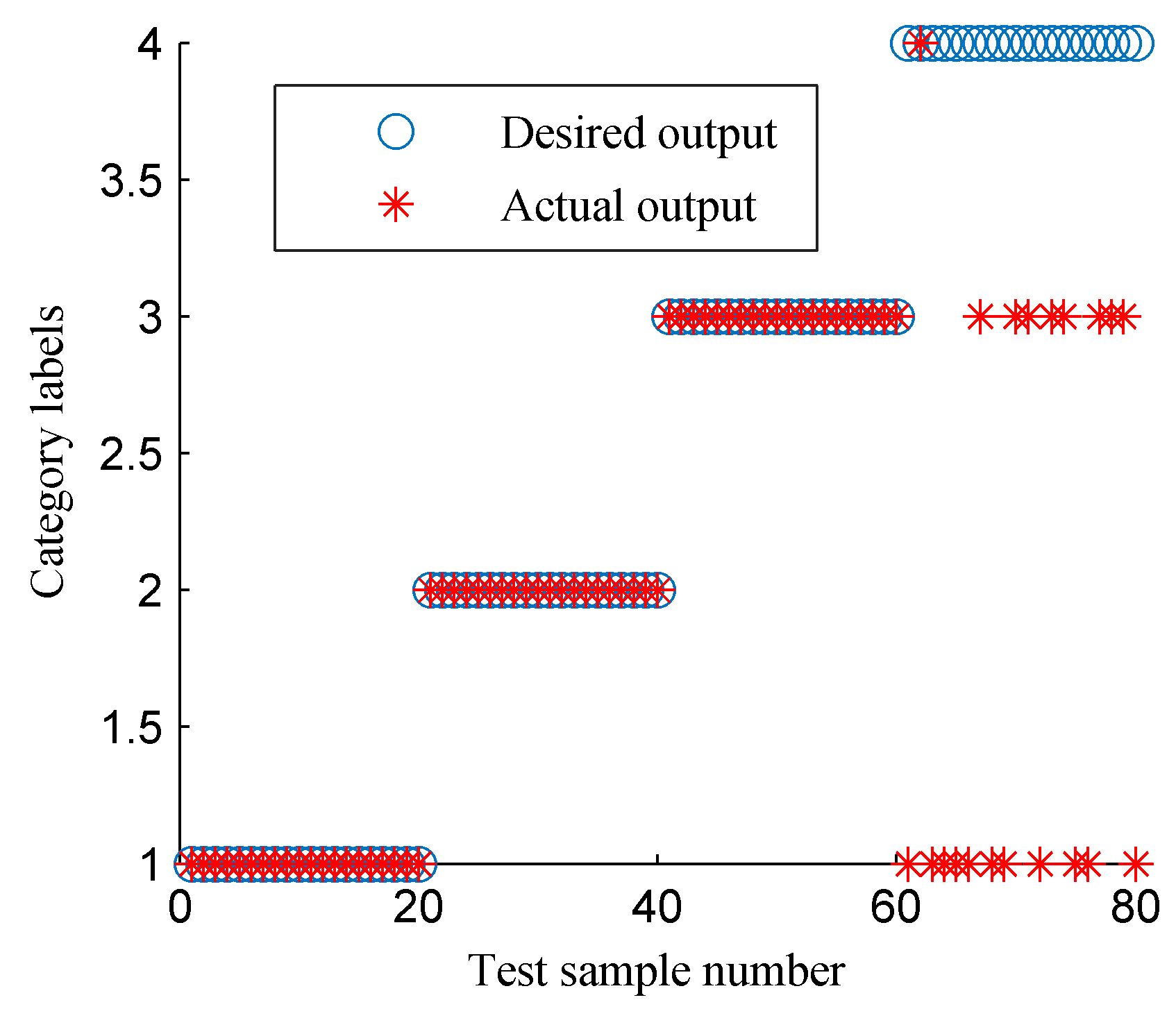
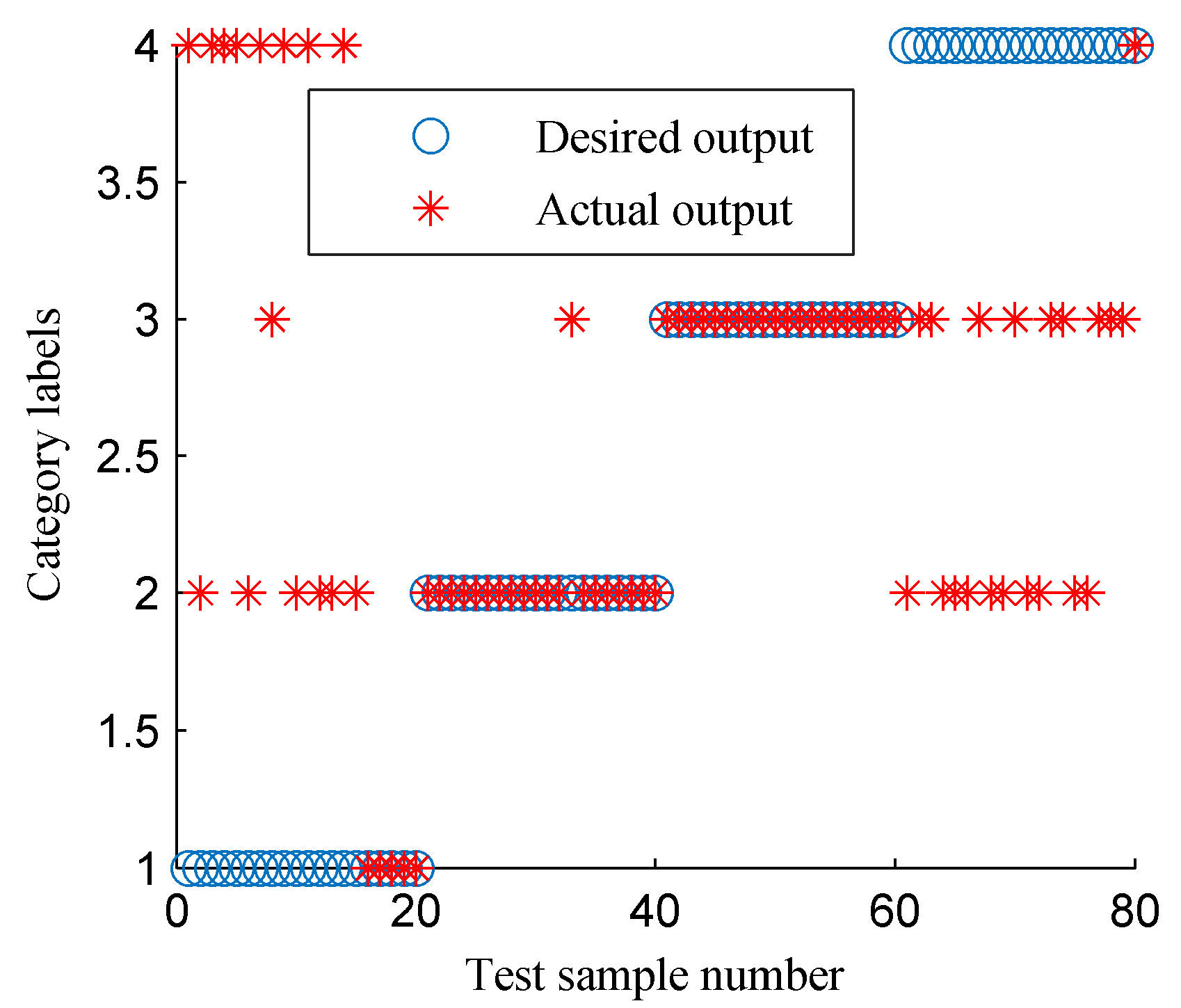
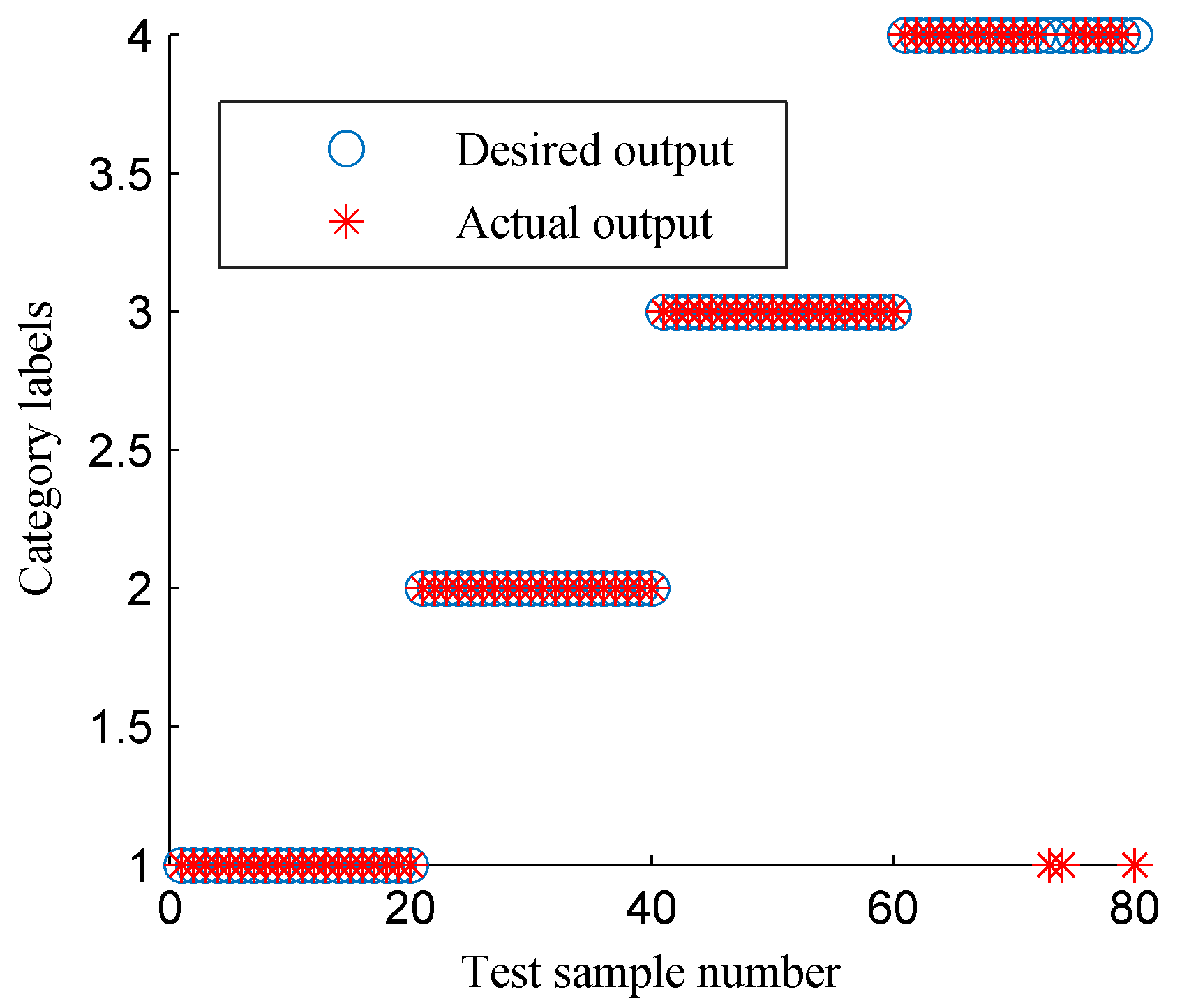
Finally, the CFBEE of the ISSD-HT time–frequency spectrum shown in
Figure 8b was calculated as [0.0111, 0.2689, 0.1326 1.1420, 0.0544, 0.3804, 0.7641, 0.0169]. It is visible that the values of the energy entropy of different characteristic frequency bands are different. As the regularity and complexity of the normalized energy sequences of different characteristic frequency bands are different and the entropy index can measure the regularity and complexity of the signal [
13,
14,
16,
30], the local information of the energy distribution around the characteristic frequency bands can be measured by the CFBEE indicator. Sometimes, the frequency components in the time–frequency spectrums of different rotor states are similar and difficult to distinguish by naked eyes, the CFBEE indicator can be used as an automatic fault feature extraction method to estimate the differences between different rotor states.
The vibration signal of the rotor collected in the practical operating condition is frequently influenced by external noise [
6]. To further verify the effectiveness of the developed method in extracting the fault characteristics from the noisy vibration signals. Additive Gaussian random noise
n(
t) was simulated by employing the following equation:
where
N represent the length of
n(
t).
Figure 9 shows the waveform of the additive Gaussian random noise. Then, the obtained noise was added to the simulated rubbing fault signal shown in
Figure 5a to generate a mixed signal, which was shown in
Figure 10a.
Figure 10b describes the FFT spectrum of the mixed signal. Some harmonics of the rotation frequency disappeared compared to
Figure 5b due to the influence of noise. It indicates that the adding noise weakened the fault features.
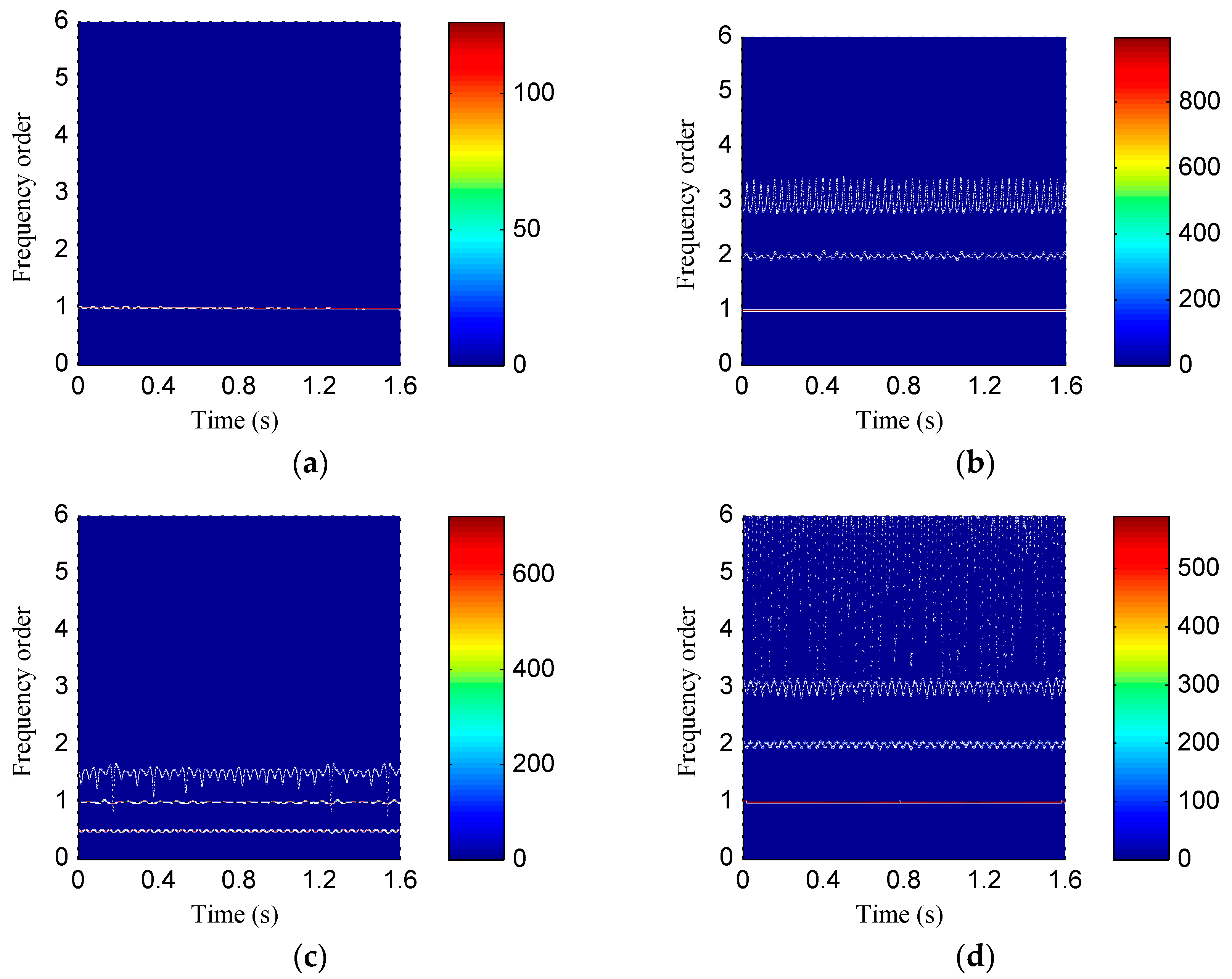
The mixed signal was analyzed by EMD and ISSD, and the corresponding results can be found from
Figure 11 and
Figure 12, respectively. Nine sub-components were generated by performing EMD on the mixed signal as
Figure 11a shows. That means the additive noise leads to the appearance of more decomposition components without physical meaning. Consequently, the problem of mode aliasing in the corresponding EMD-HT TFS displayed in
Figure 11b becomes more serious. As shown in
Figure 12a, five sub-components were derived after the ISSD decomposition, the first sub-component represents the noise and the other four components belong to the fault feature components.
Figure 12b shows the corresponding ISSD-HT TFS. Despite some high-frequency noise appeared on the ISSD-HT TFS, the fault characteristic frequencies and the “intrawave frequency modulation” characteristics can be clearly identified. It demonstrated that ISSD is more robust to noise compared to EMD.