Tight Bounds on the Rényi Entropy via Majorization with Applications to Guessing and Compression
Abstract
1. Introduction
2. Notation and Preliminaries
- P be a probability mass function defined on a finite set ;
- and be, respectively, the maximal and minimal positive masses of P;
- be the sum of the k largest masses of P for (note that and );
- , for an integer , be the set of all probability mass functions defined on with ; without any loss of generality, let ;
- , for and an integer , be the subset of all probability measures such that
- If , then
- By the continuous extension of ,where in the right side of (8) is the relative entropy (a.k.a. Kullback-Leibler divergence).
3. A Tight Lower Bound on the Rényi Entropy
- (1)
- , and ;
- (2)
- .
- (a)
- If , thenand
- (b)
- If , then
- (c)
- For all ,
- For every , and ,
4. Bounds on the Rényi Entropy of a Function of a Discrete Random Variable
- and be finite sets of cardinalities and with ; without any loss of generality, let and ;
- X be a random variable taking values on with a probability mass function ;
- be the set of deterministic functions ; note that is not one to one since .
- (a)
- For , if , let be the equiprobable random variable on ; otherwise, if , let be a random variable with the probability mass functionwhere is the maximal integer such thatThen, for every ,where
- (b)
- There exists an explicit construction of a deterministic function such thatwhere is independent of α, and it is obtained by using Huffman coding (as in [12] for ).
- (c)
- Let be a random variable with the probability mass functionThen, for every ,
- (1)
- Start from the probability mass function with ;
- (2)
- Merge successively pairs of probability masses by applying the Huffman algorithm;
- (3)
- Stop the merging process in Step 2 when a probability mass function is obtained (with );
- (4)
- Construct the deterministic function by setting for all probability masses , with , being merged in Steps 2–3 into the node of .
- is an aggregation of X, i.e., the probability mass function of satisfies () where partition into m disjoint subsets as follows:
- By the assumption , it follows that for every such ;
- From (35), where the function is given by for all , and for all . Hence, is an element in the set of the probability mass functions of with which majorizes every other element from this set.
5. Information-Theoretic Applications: Non-Asymptotic Bounds for Lossless Compression and Guessing
5.1. Guessing
5.1.1. Background
5.1.2. Analysis
- be i.i.d. with taking values on a set with ;
- , for every , where is a deterministic function with ;
- and be, respectively, ranking functions of the random vectors and .
- (a)
- The lower bound in (67) holds for every deterministic function ;
- (b)
- The upper bound in (69) holds for the specific , whose construction relies on the Huffman algorithm (see Steps 1–4 of the procedure in the proof of Theorem 2);
- (c)
- The gap between these bounds, for and sufficiently large k, is at most
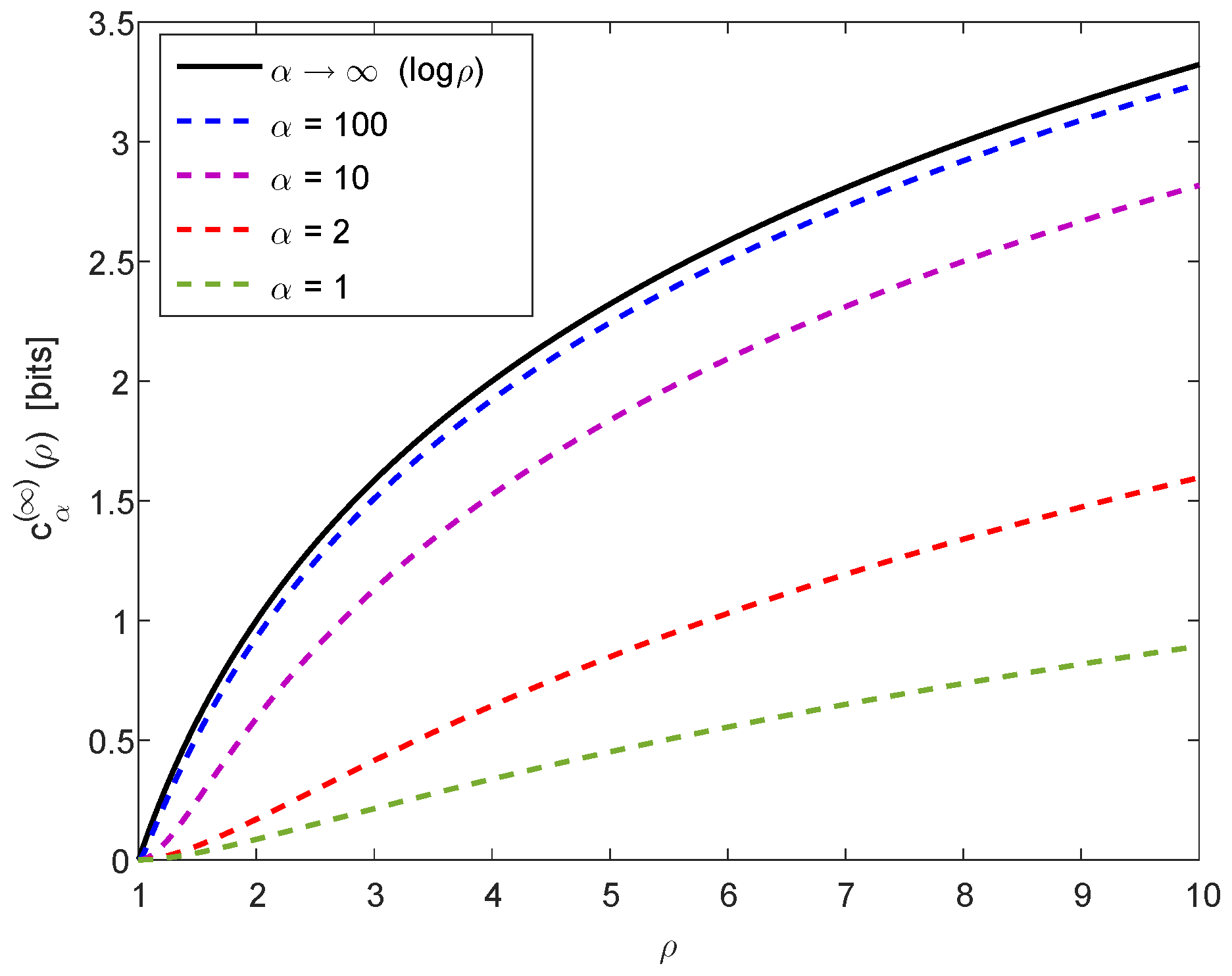
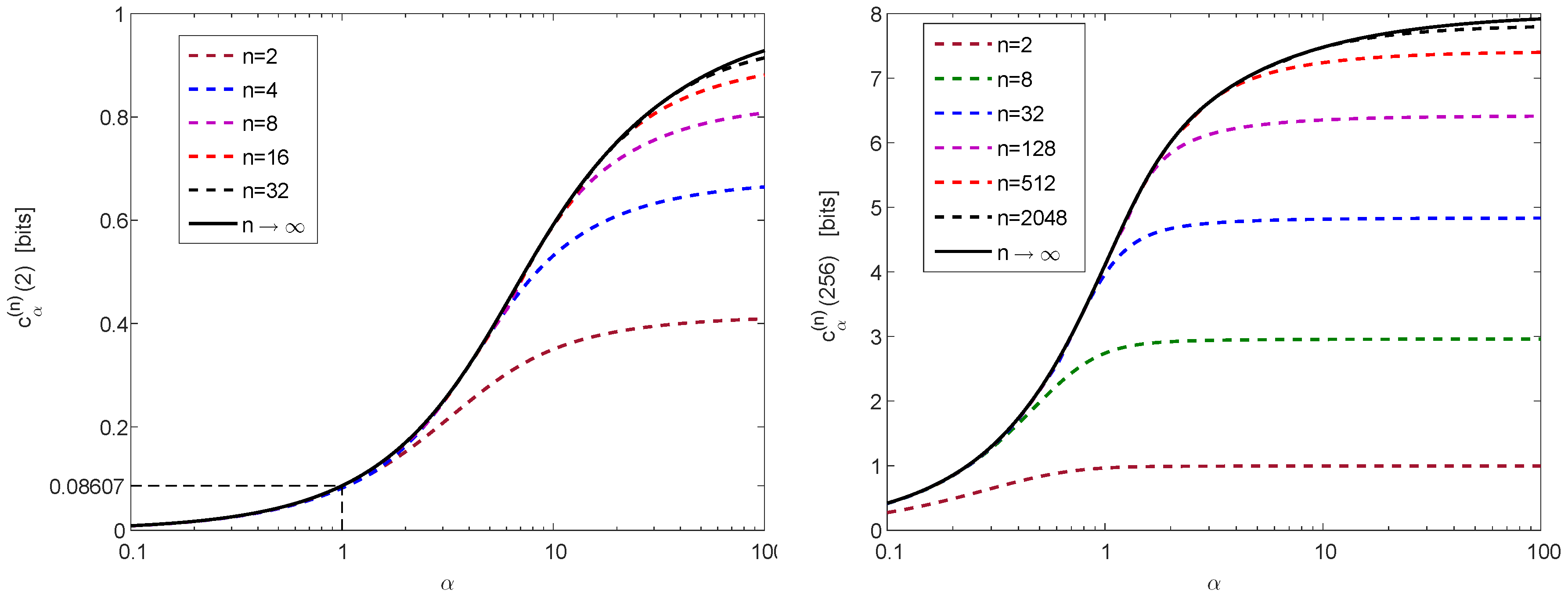
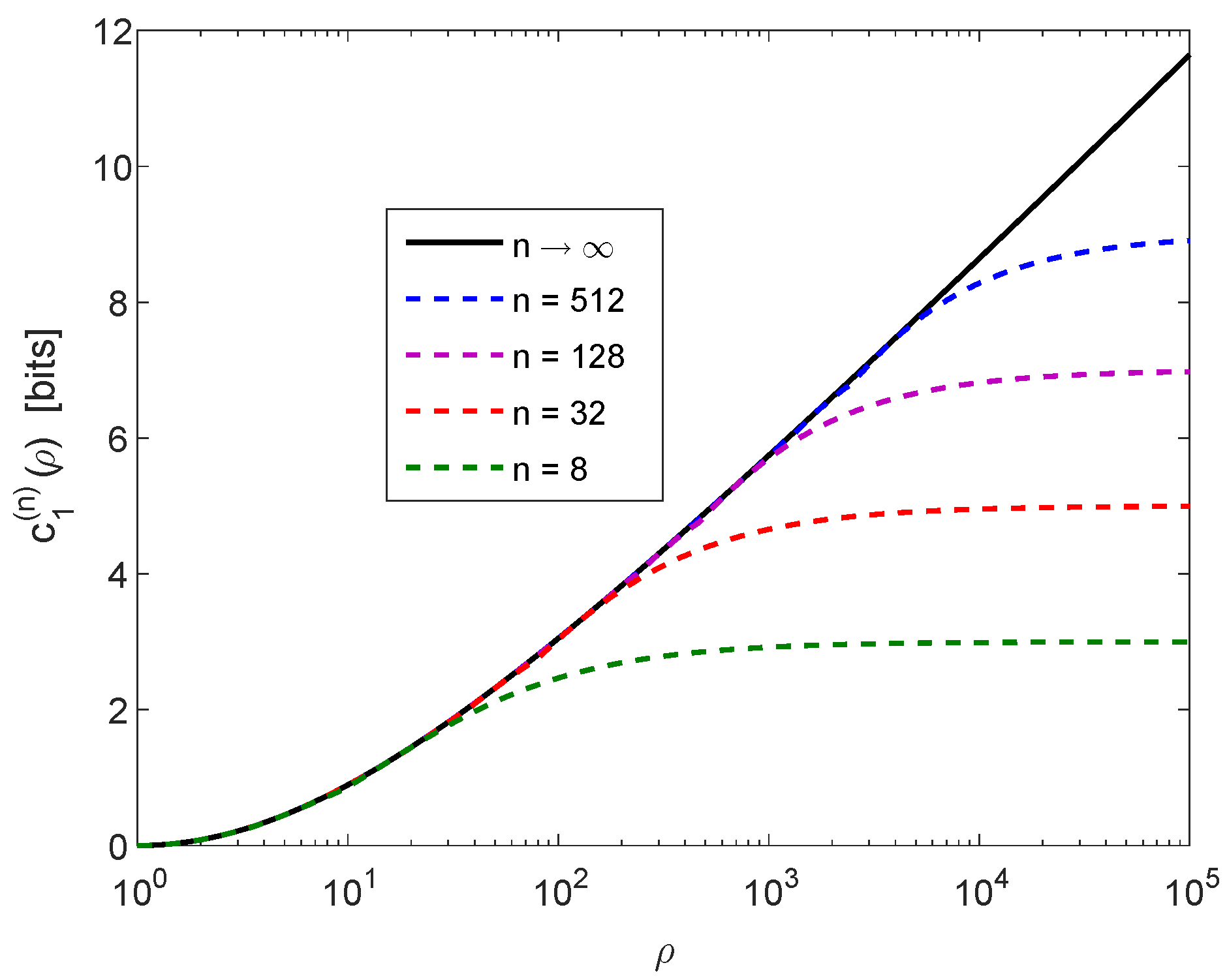
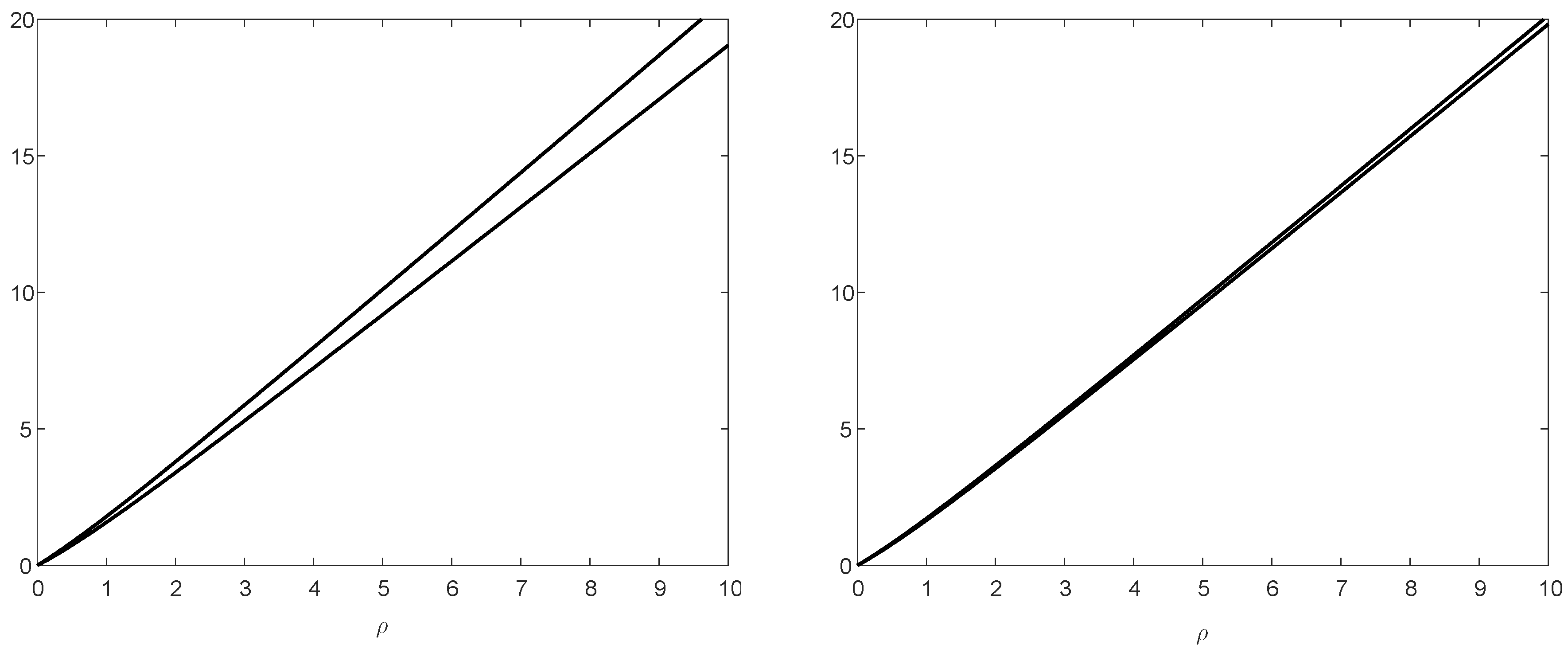
5.1.3. Numerical Result
5.2. Lossless Source Coding
5.2.1. Background
- (a)
- Converse result:
- (b)
- Achievability result: there exists a UD source code, for which
5.2.2. Analysis
- be i.i.d. symbols which are emitted from a DMS according to a probability mass function whose support is a finite set with ;
- Each symbol be mapped to where is the deterministic function (independent of the index i) with , as specified by Steps 1–4 in the proof of Theorem 2 (borrowed from [12]);
- Two UD fixed-to-variable source codes be used: one code encodes the sequences , and the other code encodes their mappings ; let the common size of the alphabets of both codes be D;
- and be, respectively, the scaled cumulant generating functions of the codeword lengths of the k-length sequences in (see (72)) and their mapping to .
- (a)
- There exists a UD source code for the sequences in such that the upper bound in (79) is satisfied for every UD source code which operates on the sequences in ;
- (b)
- (c)
- (d)
- The UD source codes in Items (a) and (b) for the sequences in and , respectively, can be constructed to be prefix codes by the algorithm in Remark 11.
- (1)
- As a preparatory step, we first calculate the probability mass function from the given probability mass function and the deterministic function which is obtained by Steps 1–4 in the proof of Theorem 2; accordingly, for all . We then further calculate the probability mass functions for the i.i.d. sequences in and (see (73)); recall that the number of types in and is polynomial in k (being upper bounded by and , respectively), and the values of these probability mass functions are fixed over each type;
- (2)
- The sets of codeword lengths of the two UD source codes, for the sequences in and , can (separately) be designed according to the achievability proof in Campbell’s paper (see [51] (p. 428)). More explicitly, let ; for all , let be given bywithand let , for all , be given similarly to (83) and (84) by replacing with , and with . This suggests codeword lengths for the two codes which fulfil (75) and (80), and also, both satisfy Kraft’s inequality;
- (3)
- The separate construction of two prefix codes (a.k.a. instantaneous codes) based on their given sets of codeword lengths and , as determined in Step 2, is standard (see, e.g., the construction in the proof of [84] (Theorem 5.2.1)).
Funding
Conflicts of Interest
Appendix A. Proof of Lemma 2
Appendix B. Proof of Lemma 3
Appendix C. Proof of Lemma 4
References
- Hardy, G.H.; Littlewood, J.E.; Pólya, G. Inequalities, 2nd ed.; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Marshall, A.W.; Olkin, I.; Arnold, B.C. Inequalities: Theory of Majorization and Its Applications, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Arnold, B.C. Majorization: Here, there and everywhere. Stat. Sci. 2007, 22, 407–413. [Google Scholar] [CrossRef]
- Arnold, B.C.; Sarabia, J.M. Majorization and the Lorenz Order with Applications in Applied Mathematics and Economics; Statistics for Social and Behavioral Sciences; Springer: New York, NY, USA, 2018. [Google Scholar]
- Cicalese, F.; Gargano, L.; Vaccaro, U. Information theoretic measures of distances and their econometric applications. In Proceedings of the 2013 IEEE International Symposium on Information Theory, Istanbul, Turkey, 7–12 July 2013; pp. 409–413. [Google Scholar]
- Steele, J.M. The Cauchy-Schwarz Master Class; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Bhatia, R. Matrix Analysis Graduate Texts in Mathematics; Springer: New York, NY, USA, 1997. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Ben-Bassat, M.; Raviv, J. Rényi’s entropy and probability of error. IEEE Trans. Inf. Theory 1978, 24, 324–331. [Google Scholar] [CrossRef]
- Cicalese, F.; Vaccaro, U. Bounding the average length of optimal source codes via majorization theory. IEEE Trans. Inf. Theory 2004, 50, 633–637. [Google Scholar] [CrossRef]
- Cicalese, F.; Gargano, L.; Vaccaro, U. How to find a joint probability distribution with (almost) minimum entropy given the marginals. In Proceedings of the 2017 IEEE International Symposium on Information Theory, Aachen, Germany, 25–30 June 2017; pp. 2178–2182. [Google Scholar]
- Cicalese, F.; Gargano, L.; Vaccaro, U. Bounds on the entropy of a function of a random variable and their applications. IEEE Trans. Inf. Theory 2018, 64, 2220–2230. [Google Scholar] [CrossRef]
- Cicalese, F.; Vaccaro, U. Maximum entropy interval aggregations. In Proceedings of the 2018 IEEE International Symposium on Information Theory, Vail, CO, USA, 17–20 June 2018; pp. 1764–1768. [Google Scholar]
- Harremoës, P. A new look on majorization. In Proceedings of the 2004 IEEE International Symposium on Information Theory and Its Applications, Parma, Italy, 10–13 October 2004; pp. 1422–1425. [Google Scholar]
- Ho, S.W.; Yeung, R.W. The interplay between entropy and variational distance. IEEE Trans. Inf. Theory 2010, 56, 5906–5929. [Google Scholar] [CrossRef]
- Ho, S.W.; Verdú, S. On the interplay between conditional entropy and error probability. IEEE Trans. Inf. Theory 2010, 56, 5930–5942. [Google Scholar] [CrossRef]
- Ho, S.W.; Verdú, S. Convexity/concavity of the Rényi entropy and α-mutual information. In Proceedings of the 2015 IEEE International Symposium on Information Theory, Hong Kong, China, 14–19 June 2015; pp. 745–749. [Google Scholar]
- Joe, H. Majorization, entropy and paired comparisons. Ann. Stat. 1988, 16, 915–925. [Google Scholar] [CrossRef]
- Joe, H. Majorization and divergence. J. Math. Anal. Appl. 1990, 148, 287–305. [Google Scholar] [CrossRef]
- Koga, H. Characterization of the smooth Rényi entropy using majorization. In Proceedings of the 2013 IEEE Information Theory Workshop, Seville, Spain, 9–13 September 2013; pp. 604–608. [Google Scholar]
- Puchala, Z.; Rudnicki, L.; Zyczkowski, K. Majorization entropic uncertainty relations. J. Phys. A Math. Theor. 2013, 46, 1–12. [Google Scholar] [CrossRef]
- Sason, I.; Verdú, S. Arimoto-Rényi conditional entropy and Bayesian M-ary hypothesis testing. IEEE Trans. Inf. Theory 2018, 64, 4–25. [Google Scholar] [CrossRef]
- Verdú, S. Information Theory, 2018; in preparation.
- Witsenhhausen, H.S. Some aspects of convexity useful in information theory. IEEE Trans. Inf. Theory 1980, 26, 265–271. [Google Scholar] [CrossRef]
- Xi, B.; Wang, S.; Zhang, T. Schur-convexity on generalized information entropy and its applications. In Information Computing and Applications; Lecture Notes in Computer Science; Springer: New York, NY, USA, 2011; Volume 7030, pp. 153–160. [Google Scholar]
- Inaltekin, H.; Hanly, S.V. Optimality of binary power control for the single cell uplink. IEEE Trans. Inf. Theory 2012, 58, 6484–6496. [Google Scholar] [CrossRef]
- Jorshweick, E.; Bosche, H. Majorization and matrix-monotone functions in wireless communications. Found. Trends Commun. Inf. Theory 2006, 3, 553–701. [Google Scholar] [CrossRef]
- Palomar, D.P.; Jiang, Y. MIMO transceiver design via majorization theory. Found. Trends Commun. Inf. Theory 2006, 3, 331–551. [Google Scholar] [CrossRef]
- Roventa, I. Recent Trends in Majorization Theory and Optimization: Applications to Wireless Communications; Editura Pro Universitaria & Universitaria Craiova: Bucharest, Romania, 2015. [Google Scholar]
- Sezgin, A.; Jorswieck, E.A. Applications of majorization theory in space-time cooperative communications. In Cooperative Communications for Improved Wireless Network Transmission: Framework for Virtual Antenna Array Applications; Information Science Reference; Uysal, M., Ed.; IGI Global: Hershey, PA, USA, 2010; pp. 429–470. [Google Scholar]
- Viswanath, P.; Anantharam, V. Optimal sequences and sum capacity of synchronous CDMA systems. IEEE Trans. Inf. Theory 1999, 45, 1984–1993. [Google Scholar] [CrossRef]
- Viswanath, P.; Anantharam, V.; Tse, D.N.C. Optimal sequences, power control, and user capacity of synchronous CDMA systems with linear MMSE multiuser receivers. IEEE Trans. Inf. Theory 1999, 45, 1968–1983. [Google Scholar] [CrossRef]
- Viswanath, P.; Anantharam, V. Optimal sequences for CDMA under colored noise: A Schur-saddle function property. IEEE Trans. Inf. Theory 2002, 48, 1295–1318. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the 4th Berkeley Symposium on Probability Theory and Mathematical Statistics, Berkeley, CA, USA, 8–9 August 1961; pp. 547–561. [Google Scholar]
- Arikan, E. An inequality on guessing and its application to sequential decoding. IEEE Trans. Inf. Theory 1996, 42, 99–105. [Google Scholar] [CrossRef]
- Arikan, E.; Merhav, N. Guessing subject to distortion. IEEE Trans. Inf. Theory 1998, 44, 1041–1056. [Google Scholar] [CrossRef]
- Arikan, E.; Merhav, N. Joint source-channel coding and guessing with application to sequential decoding. IEEE Trans. Inf. Theory 1998, 44, 1756–1769. [Google Scholar] [CrossRef]
- Burin, A.; Shayevitz, O. Reducing guesswork via an unreliable oracle. IEEE Trans. Inf. Theory 2018, 64, 6941–6953. [Google Scholar] [CrossRef]
- Kuzuoka, S. On the conditional smooth Rényi entropy and its applications in guessing and source coding. arXiv, 2018; arXiv:1810.09070. [Google Scholar]
- Merhav, N.; Arikan, E. The Shannon cipher system with a guessing wiretapper. IEEE Trans. Inf. Theory 1999, 45, 1860–1866. [Google Scholar] [CrossRef]
- Sundaresan, R. Guessing based on length functions. In Proceedings of the 2007 IEEE International Symposium on Information Theory, Nice, France, 24–29 June 2007; pp. 716–719. [Google Scholar]
- Salamatian, S.; Beirami, A.; Cohen, A.; Médard, M. Centralized versus decentralized multi-agent guesswork. In Proceedings of the 2017 IEEE International Symposium on Information Theory, Aachen, Germany, 25–30 June 2017; pp. 2263–2267. [Google Scholar]
- Sundaresan, R. Guessing under source uncertainty. IEEE Trans. Inf. Theory 2007, 53, 269–287. [Google Scholar] [CrossRef]
- Bracher, A.; Lapidoth, A.; Pfister, C. Distributed task encoding. In Proceedings of the 2017 IEEE International Symposium on Information Theory, Aachen, Germany, 25–30 June 2017; pp. 1993–1997. [Google Scholar]
- Bunte, C.; Lapidoth, A. Encoding tasks and Rényi entropy. IEEE Trans. Inf. Theory 2014, 60, 5065–5076. [Google Scholar] [CrossRef]
- Shayevitz, O. On Rényi measures and hypothesis testing. In Proceedings of the 2011 IEEE International Symposium on Information Theory, Saint Petersburg, Russia, 31 July–5 August 2011; pp. 800–804. [Google Scholar]
- Tomamichel, M.; Hayashi, M. Operational interpretation of Rényi conditional mutual information via composite hypothesis testing against Markov distributions. In Proceedings of the 2016 IEEE International Symposium on Information Theory, Barcelona, Spain, 10–15 July 2016; pp. 585–589. [Google Scholar]
- Harsha, P.; Jain, R.; McAllester, D.; Radhakrishnan, J. The communication complexity of correlation. IEEE Trans. Inf. Theory 2010, 56, 438–449. [Google Scholar] [CrossRef]
- Liu, J.; Verdú, S. Rejection sampling and noncausal sampling under moment constraints. In Proceedings of the 2018 IEEE International Symposium on Information Theory, Vail, CO, USA, 17–22 June 2018; pp. 1565–1569. [Google Scholar]
- Yu, L.; Tan, V.Y.F. Wyner’s common information under Rényi divergence measures. IEEE Trans. Inf. Theory 2018, 64, 3616–3632. [Google Scholar] [CrossRef]
- Campbell, L.L. A coding theorem and Rényi’s entropy. Inf. Control 1965, 8, 423–429. [Google Scholar] [CrossRef]
- Courtade, T.; Verdú, S. Cumulant generating function of codeword lengths in optimal lossless compression. In Proceedings of the 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014; pp. 2494–2498. [Google Scholar]
- Courtade, T.; Verdú, S. Variable-length lossy compression and channel coding: Non-asymptotic converses via cumulant generating functions. In Proceedings of the 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014; pp. 2499–2503. [Google Scholar]
- Hayashi, M.; Tan, V.Y.F. Equivocations, exponents, and second-order coding rates under various Rényi information measures. IEEE Trans. Inf. Theory 2017, 63, 975–1005. [Google Scholar] [CrossRef]
- Kuzuoka, S. On the smooth Rényi entropy and variable-length source coding allowing errors. In Proceedings of the 2016 IEEE International Symposium on Information Theory, Barcelona, Spain, 10–15 July 2016; pp. 745–749. [Google Scholar]
- Sason, I.; Verdú, S. Improved bounds on lossless source coding and guessing moments via Rényi measures. IEEE Trans. Inf. Theory 2018, 64, 4323–4346. [Google Scholar] [CrossRef]
- Tan, V.Y.F.; Hayashi, M. Analysis of ramaining uncertainties and exponents under various conditional Rényi entropies. IEEE Trans. Inf. Theory 2018, 64, 3734–3755. [Google Scholar] [CrossRef]
- Tyagi, H. Coding theorems using Rényi information measures. In Proceedings of the 2017 IEEE Twenty-Third National Conference on Communications, Chennai, India, 2–4 March 2017; pp. 1–6. [Google Scholar]
- Csiszár, I. Generalized cutoff rates and Rényi information measures. IEEE Trans. Inf. Theory 1995, 41, 26–34. [Google Scholar] [CrossRef]
- Polyanskiy, Y.; Verdú, S. Arimoto channel coding converse and Rényi divergence. In Proceedings of the Forty-Eighth Annual Allerton Conference on Communication, Control and Computing, Monticello, IL, USA, 29 September–1 October 2010; pp. 1327–1333. [Google Scholar]
- Sason, I. On the Rényi divergence, joint range of relative entropies, and a channel coding theorem. IEEE Trans. Inf. Theory 2016, 62, 23–34. [Google Scholar] [CrossRef]
- Yu, L.; Tan, V.Y.F. Rényi resolvability and its applications to the wiretap channel. In Lecture Notes in Computer Science, Proceedings of the 10th International Conference on Information Theoretic Security, Hong Kong, China, 29 November–2 December 2017; Springer: New York, NY, USA, 2017; Volume 10681, pp. 208–233. [Google Scholar]
- Arimoto, S. On the converse to the coding theorem for discrete memoryless channels. IEEE Trans. Inf. Theory 1973, 19, 357–359. [Google Scholar] [CrossRef]
- Arimoto, S. Information measures and capacity of order α for discrete memoryless channels. In Proceedings of the 2nd Colloquium on Information Theory, Keszthely, Hungary, 25–30 August 1975; Csiszár, I., Elias, P., Eds.; Colloquia Mathematica Societatis Janós Bolyai: Amsterdam, The Netherlands, 1977; Volume 16, pp. 41–52. [Google Scholar]
- Dalai, M. Lower bounds on the probability of error for classical and classical-quantum channels. IEEE Trans. Inf. Theory 2013, 59, 8027–8056. [Google Scholar] [CrossRef]
- Leditzky, F.; Wilde, M.M.; Datta, N. Strong converse theorems using Rényi entropies. J. Math. Phys. 2016, 57, 1–33. [Google Scholar] [CrossRef]
- Mosonyi, M.; Ogawa, T. Quantum hypothesis testing and the operational interpretation of the quantum Rényi relative entropies. Commun. Math. Phys. 2015, 334, 1617–1648. [Google Scholar] [CrossRef]
- Simic, S. Jensen’s inequality and new entropy bounds. Appl. Math. Lett. 2009, 22, 1262–1265. [Google Scholar] [CrossRef]
- Jelineck, F.; Schneider, K.S. On variable-length-to-block coding. IEEE Trans. Inf. Theory 1972, 18, 765–774. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completness; W. H. Freedman and Company: New York, NY, USA, 1979. [Google Scholar]
- Boztaş, S. Comments on “An inequality on guessing and its application to sequential decoding”. IEEE Trans. Inf. Theory 1997, 43, 2062–2063. [Google Scholar] [CrossRef]
- Bracher, A.; Hof, E.; Lapidoth, A. Guessing attacks on distributed-storage systems. In Proceedings of the 2015 IEEE International Symposium on Information Theory, Hong-Kong, China, 14–19 June 2015; pp. 1585–1589. [Google Scholar]
- Christiansen, M.M.; Duffy, K.R. Guesswork, large deviations, and Shannon entropy. IEEE Trans. Inf. Theory 2013, 59, 796–802. [Google Scholar] [CrossRef]
- Hanawal, M.K.; Sundaresan, R. Guessing revisited: A large deviations approach. IEEE Trans. Inf. Theory 2011, 57, 70–78. [Google Scholar] [CrossRef]
- Hanawal, M.K.; Sundaresan, R. The Shannon cipher system with a guessing wiretapper: General sources. IEEE Trans. Inf. Theory 2011, 57, 2503–2516. [Google Scholar] [CrossRef]
- Huleihel, W.; Salamatian, S.; Médard, M. Guessing with limited memory. In Proceedings of the 2017 IEEE International Symposium on Information Theory, Aachen, Germany, 25–30 June 2017; pp. 2258–2262. [Google Scholar]
- Massey, J.L. Guessing and entropy. In Proceedings of the 1994 IEEE International Symposium on Information Theory, Trondheim, Norway, 27 June–1 July 1994; p. 204. [Google Scholar]
- McEliece, R.J.; Yu, Z. An inequality on entropy. In Proceedings of the 1995 IEEE International Symposium on Information Theory, Whistler, BC, Canada, 17–22 September 1995; p. 329. [Google Scholar]
- Pfister, C.E.; Sullivan, W.G. Rényi entropy, guesswork moments and large deviations. IEEE Trans. Inf. Theory 2004, 50, 2794–2800. [Google Scholar] [CrossRef]
- De Santis, A.; Gaggia, A.G.; Vaccaro, U. Bounds on entropy in a guessing game. IEEE Trans. Inf. Theory 2001, 47, 468–473. [Google Scholar] [CrossRef]
- Yona, Y.; Diggavi, S. The effect of bias on the guesswork of hash functions. In Proceedings of the 2017 IEEE International Symposium on Information Theory, Aachen, Germany, 25–30 June 2017; pp. 2253–2257. [Google Scholar]
- Gan, G.; Ma, C.; Wu, J. Data Clustering: Theory, Algorithms, and Applications; ASA-SIAM Series on Statistics and Applied Probability; SIAM: Philadelphia, PA, USA, 2007. [Google Scholar]
- Campbell, L.L. Definition of entropy by means of a coding problem. Probab. Theory Relat. Field 1966, 6, 113–118. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Kontoyiannis, I.; Verdú, S. Optimal lossless data compression: Non-asymptotics and asymptotics. IEEE Trans. Inf. Theory 2014, 60, 777–795. [Google Scholar] [CrossRef]
- Van Erven, T.; Harremoës, P. Rényi divergence and Kullback-Leibler divergence. IEEE Trans. Inf. Theory 2014, 60, 3797–3820. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sason, I. Tight Bounds on the Rényi Entropy via Majorization with Applications to Guessing and Compression. Entropy 2018, 20, 896. https://doi.org/10.3390/e20120896
Sason I. Tight Bounds on the Rényi Entropy via Majorization with Applications to Guessing and Compression. Entropy. 2018; 20(12):896. https://doi.org/10.3390/e20120896
Chicago/Turabian StyleSason, Igal. 2018. "Tight Bounds on the Rényi Entropy via Majorization with Applications to Guessing and Compression" Entropy 20, no. 12: 896. https://doi.org/10.3390/e20120896
APA StyleSason, I. (2018). Tight Bounds on the Rényi Entropy via Majorization with Applications to Guessing and Compression. Entropy, 20(12), 896. https://doi.org/10.3390/e20120896




