Higher Order Geometric Theory of Information and Heat Based on Poly-Symplectic Geometry of Souriau Lie Groups Thermodynamics and Their Contextures: The Bedrock for Lie Group Machine Learning
Abstract
“Inviter les savants géomètres à traiter nos problèmes avec le soucis de la commodité et de l’agrément: qu’ils écartent tout ce qui n’a rien à voir avec la pénétration de l’esprit, seule qualité dont nous faisons grand cas et que nous nous sommes proposé d’éprouver et de couronner”—Blaise Pascal—Deuxième Lettre sur la roulette, Paris, 19 Juillet 1658 [1]
“Nous avons fait de la Dynamique un cas particulier de la Thermodynamique, une Science qui embrasse dans des principes communs tous les changements d’état des corps, aussi bien les changements de lieu que les changements de qualités physiques”—Pierre Duhem, Sur les équations générales de la Thermodynamique, 1891 [2]
“Nous prenons le mot mouvement pour désigner non seulement un changement de position dans l’espace, mais encore un changement d’état quelconque, lors même qu’il ne serait accompagné d’aucun déplacement… De la sorte, le mot mouvement s’oppose non pas au mot repos, mais au mot équilibre.”—Pierre Duhem, Commentaire aux principes de la Thermodynamique, 1894 [3]
1. Introduction
- In Section 1, we introduce seminal idea on Symplectic geometry used in mechanics and in statistical mechanics, as introduced by Jean-Marie-Souriau during the 60s. From previous work of François Gallissot extending Cartan’s results on integral invariant (theorem on types of differential forms generating equations of movement of a material point invariant in the transformations of the Galilean group), we present the Lagrange 2-form and moment map elaborated by Souriau to build a geometric mechanics theory, where a dynamical system is then represented by a foliation of the evolution, determined by an antisymmetric covariant second order tensor. Souriau has applied this tool for mechanical statistics to build a thermodynamics of dynamical systems, where the classical notion of Gibbs canonical ensemble is extended for a homogeneous symplectic manifold on which a Lie group (dynamical group) has a symplectic action. In case of Galileo group, the symmetry is broken, and new “co-homological” Souriau relations should be verified in Lie algebra of the group.
- In Section 2, we synthetize results on higher order thermodynamics based on higher order temperatures and heats, as introduced by Ingarden and Jaworski for mesoscopic systems. This model is based on higher order maximum entropy Gibbs density definition constraining solution with respects to higher order moments.
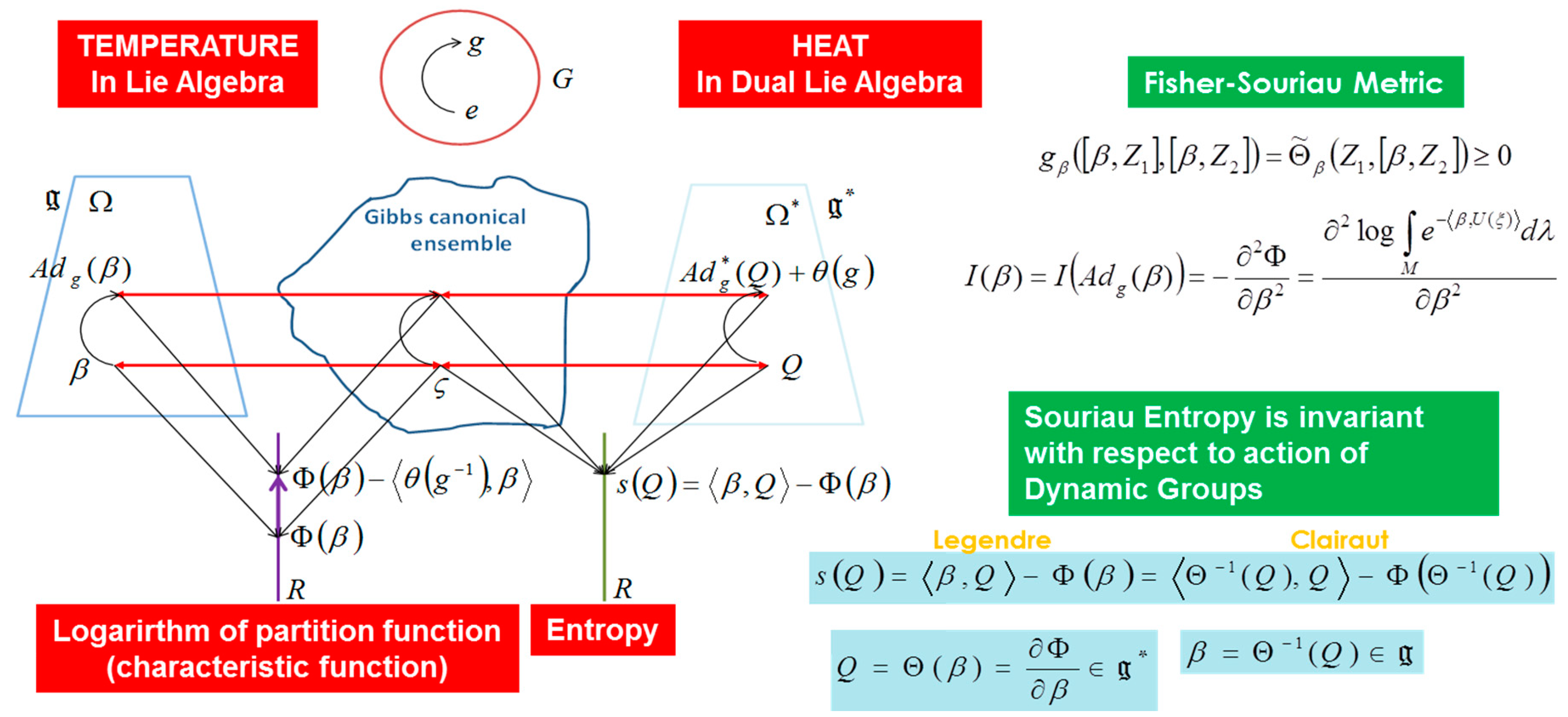
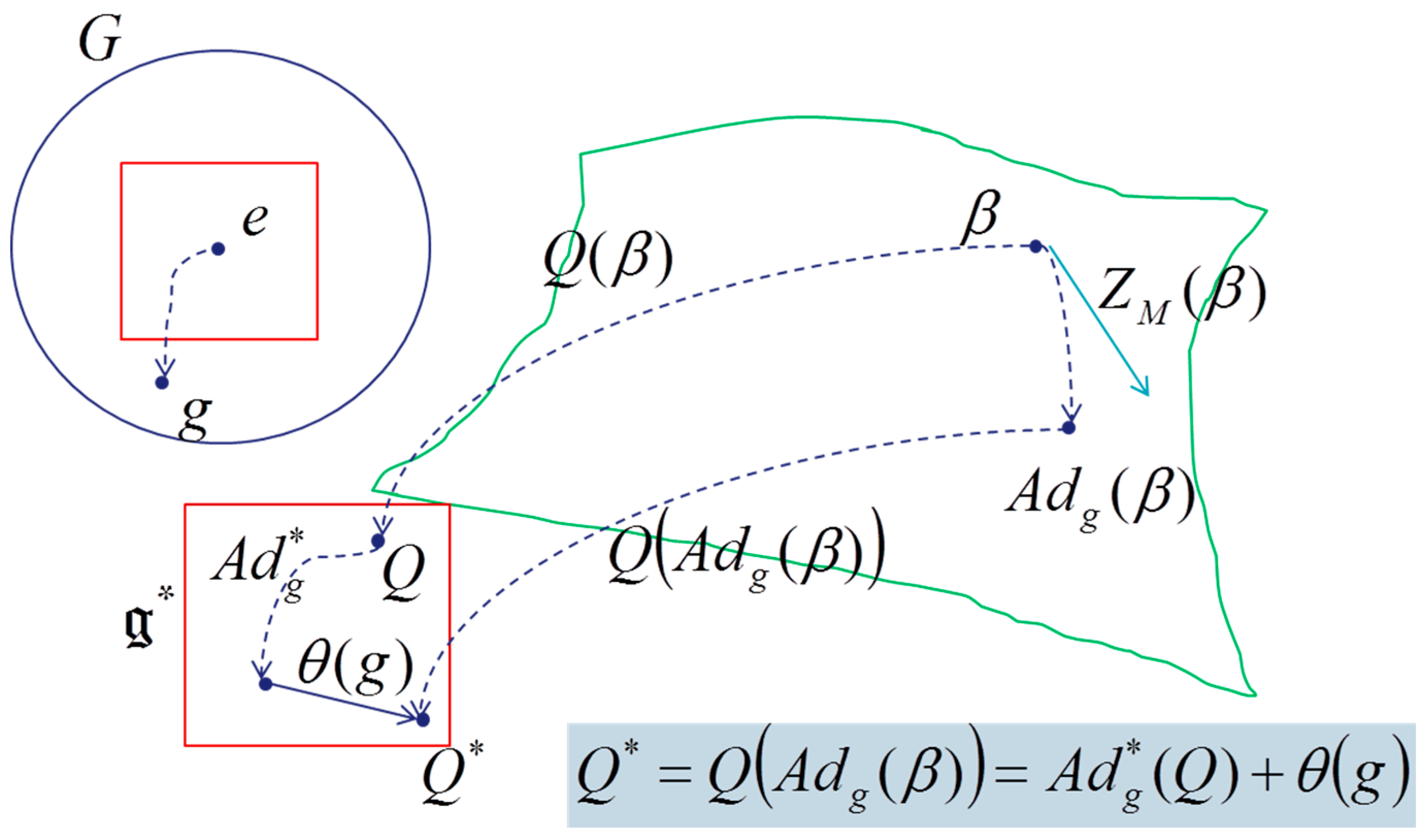
- In Section 3, we develop “Lie groups thermodynamics” model, developed to describe Gibbs state for dynamical systems, where Souriau introduced the concept of co-adjoint action of a group on its momentum space that allows designing physical observables like energy, heat and momentum or moment as pure geometrical objects. The Souriau model then generalizes the Gibbs equilibrium state to all symplectic manifolds that have a dynamical group, with a “geometric” (Planck) temperature as an element of the Lie algebra and “geometric heat” as an element of the dual Lie algebra. We have observed that Souriau has introduced a symmetric tensor that is an extension of classical Fisher metric in information geometry. This new Fisher-Souriau metric is invariant with respect to the action of the group. These equations are universal, because they are not dependent on the symplectic manifold but only on the dynamical group and its associated two-cocycle. Souriau called it “Lie groups thermodynamics”.
- In Section 4, we give an extended Koszul study of Souriau’s non-equivariant model associated to a class of co-homology. Koszul has deepened the Souriau model, considering purely algebraic and geometric developments of geometric mechanics. Koszul has defined a skew symmetric bilinear form by a closed expression depending only on the cocycle and related to the Souriau antisymmetric bilinear map introduced previously in Section 3. This Koszul study of the moment map non-equivariance, and the existence of an affine action of G on g* is at the cornerstone of Souriau theory of Lie groups thermodynamics.
- In Section 5, at the step of the Souriau Lie groups thermodynamics presentation, we will introduce a generalized Souriau definition of entropy, as the Legendre transform of the logarithm of the Laplace transform, making the connection with information geometry. This definition is a general contexture that can be extended to highly abstract spaces preserving Legendre structure, if we are able to generalize the Laplace transform.
- In Section 6, we illustrate Souriau’s Lie groups thermodynamics for a centrifuge system. The main Souriau idea was to define the Gibbs states for one-parameter subgroups of the Galilean group, because he proved that the action of the full Galilean group on the space of motions of an isolated mechanical system is not related to any equilibrium Gibbs state (the open subset of the Lie algebra, associated to this Gibbs state, is empty).
- In Section 7, we have defined an higher-order model of Lie groups thermodynamics based on a poly-symplectic vector valued approach. This multi-symplectic extension, is based on a multi-valued one that preserve the notion of (poly-)moment map built by Günther based on an n-symplectic model. We replace the symplectic form of the Souriau model by a vector valued form that is called poly-symplectic. We consider the non-equivariance of poly-moment map by introducing poly-cocycle. We finally conclude with poly-symplectic definition extension of the Fisher-Souriau metric.
- In Section 8, we conclude with potential extension to Lie group machine learning.
- In Appendix A, we recall a synthesis of Günther’s poly-symplectic model with initial notation
- In Appendix B, we develop computation of the Fisher metric for multivariate Gaussian density, to establish links with Souriau’s Lie groups Gibbs density model.
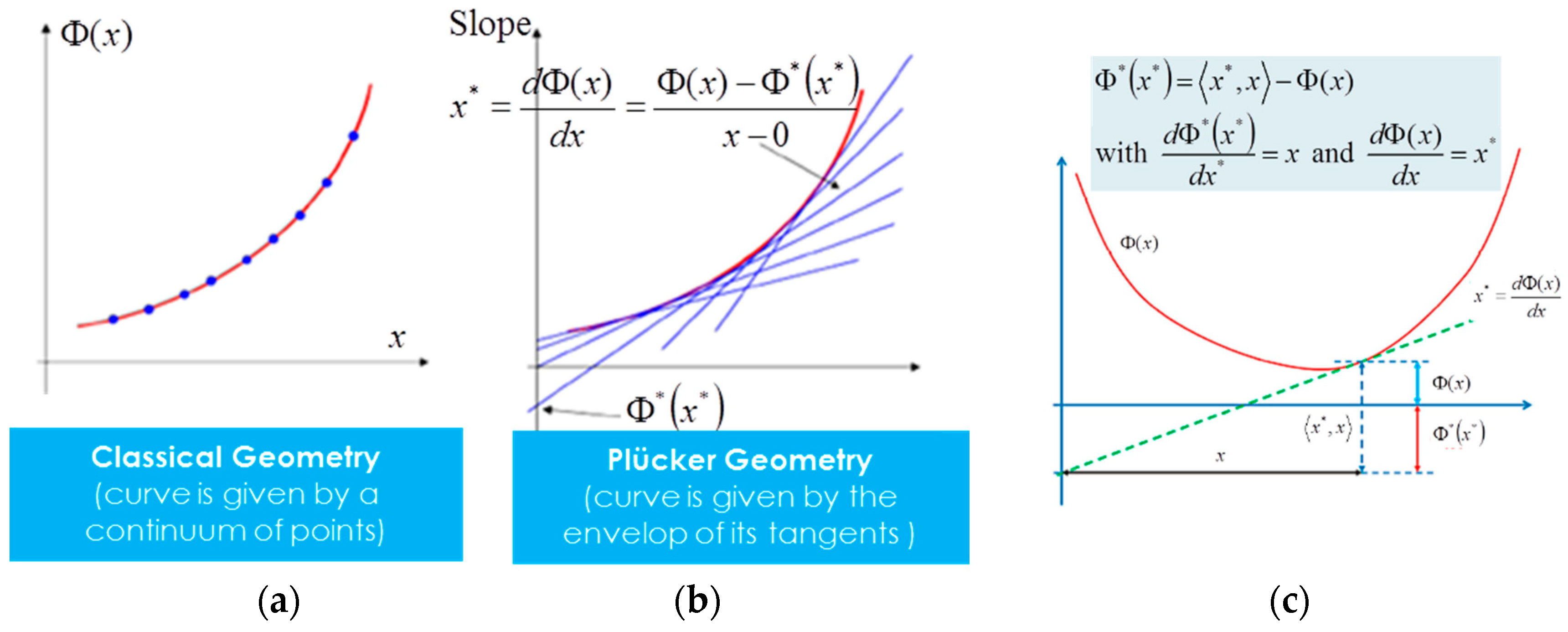
- In Appendix C, we give more details on the Legendre transform, the basic tool of information geometry and Souriau Lie groups thermodynamics. More especially, we give a definition of the Legendre transform with projective geometry definition by Chasles as reciprocal polar with respect to a paraboloid.
- In Appendix D, we give solution of a centrifuge system thermodynamics, given by Roger Balian based on a classical approach, to make the link with the Souriau approach.
- In Appendix E, we recall the main proofs of Souriau’s Lie groups thermodynamics and its poly-symplectic extension.
- In Appendix F, we present another Souriau statistical physics model, developed for relativistic thermodynamics of continua, which preserves the Legendre transform, where temperature is given by a killing vector.
2. Seminal Idea of Symplectic Geometry in Mechanics and in Statistical Mechanics by Gallissot and Souriau
“Plaçons-nous d’abord dans le cadre de la mécanique classique. Étudions un système mécanique isolé, non dissipatif—nous dirons brièvement une «chose». L’ensemble des mouvements de cette «chose» est une variété symplectique. Pourquoi? Il suffit de se reporter à la Mécanique Analytique de Lagrange (1811); l’espace des mouvements y est traité comme variété différentiable; les coordonnées covariantes et contravariantes de la forme symplectique y sont écrites (Ce sont les “parenthèses“ et “crochets“ de Lagrange). Évoquons maintenant la géométrie du 20 éme siècle. Soit G un groupe difféologique (par exemple un groupe de Lie); μ un moment de G (un moment, c’est une 1-forme invariante à gauche sur G); alors l’action du groupe sur μ engendre canoniquement un espace symplectique (ces groupes pourront avoir une dimension infinie). Présomption épistémologique: derrière chaque «chose» est caché un groupe G (sa “source“), et les mouvements de la «chose» sont simplement des moments de G (doublet latin mnémotechnique : momentum-movimentum). L’isolement de la «chose» indique alors que le groupe de Poincaré (respectivement de Galilée-Bargman) est inséré dans G; voilà l’origine des grandeurs conservées relativistes (respectivement classiques) associées à un mouvement x: elles constituent simplement le moment induit sur le groupe spacio-temporel par le moment-mouvement x.” (In English: Let’s put ourselves first in the framework of classical mechanics. Let’s study an isolated, non-dissipative mechanical system—we will briefly say a “thing”. The set of movements of this “thing” is a symplectic manifold. Why? It is enough to refer to the Analytical Mechanics of Lagrange (1811); the space of movements is treated as a differentiable manifold; the covariant and contravariant coordinates of the symplectic form are written there (these are the “parentheses” and “brackets” of Lagrange). Let’s now talk about the geometry of the 20th century. Let G be a diffeological group (for example a Lie group); μ a moment of G (a moment is a left invariant 1-form on G); then the action of the group on μ canonically generates a symplectic space (these groups can have an infinite dimension). Epistemological presumption: behind each “thing” is hidden a group G (its “source”), and the movements of the “thing” are simply moments of G (mnemonic Latin doublet: momentum-movimentum). The isolation of the “thing” then indicates that the group of Poincaré (respectively Galileo-Bargman) is inserted in G; here is the origin of the relativistic (respectively classical) conserved magnitudes associated with a movement x: they simply constitute the moment induced on the spacio-temporal group by the moment-motion x.)
“Il y a un théorème qui remonte au XXème siècle. Si on prend une orbite coadjointe d’un groupe de Lie, elle est pourvue d’une structure symplectique. Voici un algorithme pour produire des variétés symplectiques: prendre des orbites coadjointes d’un groupe. Donc cela laisse penser que derrière cette structure symplectique de Lagrange, il y avait un groupe caché. Prenons le mouvement classique d’un moment du groupe, alors ce groupe est très «gros» pour avoir tout le système solaire. Mais dans ce groupe est inclus le groupe de Galilée, et tout moment d’un groupe engendre des moments d’un sous-groupe. On va retrouver comme cela les moments du groupe de Galilée, et si on veut de la mécanique relativiste, cela va être du groupe de Poincaré. En fait avec le groupe de Galilée, il y a un petit problème, ce ne sont pas les moments du groupe de Galilée qu’on utilise, ce sont les moments d’une extension centrale du groupe de Galilée, qui s’appelle le groupe de Bargman, et qui est de dimension 11. C’est à cause de cette extension, qu’il y a cette fameuse constante arbitraire figurant dans l’énergie. Par contre quand on fait de la relativité restreinte, on prend le groupe de Poincaré et il n’y a plus de problèmes car parmi les moments il y a la masse et l’énergie c’est mc2. Donc le groupe de dimension 11 est un artéfact qui disparait, quand on fait de la relativité restreinte.” (In Engish: There is a theorem dating back to the twentieth century. If we take a coadjoint orbit of a Lie group, it is provided with a symplectic structure. Here is an algorithm to produce symplectic manifolds: take coadjoint orbits from a group. So it suggests that behind this symplectic structure of Lagrange, there was a hidden group. Take the classic movement of a moment of the group, so this group is very “big” to have the whole solar system. But in this group is included the Galileo group, and any moment of a group generates moments of a subgroup. We will find like that the moments of the group of Galileo, and if we want relativistic mechanics, it will be Poincaré group. In fact with Galileo group, there is a small problem, it is not the moments of the Galileo group that are used, it is the moments of a central extension of the Galileo group, which is called the Bargman group, and that is of dimension 11. It is because of this extension, that there is this famous arbitrary constant appearing in the energy. On the other hand, when we do special relativity, we take Poincaré group and there are no more problems because among the moments there is the mass and the energy is mc2. So the 11-dimensional group is an artifact that disappears, when we do special relativity.)
- if classical mechanics cannot benefit from these models by placing an exterior form of degree two at its base
- if thanks to the notion of manifold, the notion of connection cannot be introduced in a more natural way
- if the paradoxal indeterminations/impossibilities in the Lagrangian framework could be explained more clearly
- if the problem of integration of equations of motion could be enlightened, generated by a form of degree two.
3. Higher Order Thermodynamics Based on Higher Order Temperatures
4. Model of Souriau Lie Groups Thermodynamics
- Action of Lie group on Lie algebra:
- Characteristic function after Lie group action:
- Invariance of entropy with respect to action of Lie group:
- Action of Lie group on geometric heat:
5. Extended Koszul Study of Souriau Non-Equivariant Model Associated to a Class of Cohomology
6. Souriau Model of Generalized Entropy Based on Legendre and Laplace Transforms
- -
- is semi-definite convex function,
- -
- is convex and semi-continuous
- -
- Letan interior point ofthen:
“Il est évident que l’on ne peut définir de valeurs moyennes que sur des objets appartenant à un espace vectoriel (ou affine); donc—si bourbakiste que puisse sembler cette affirmation—que l’on n’observera et ne mesurera de valeurs moyennes que sur des grandeurs appartenant à un ensemble possédant physiquement une structure affine. Il est clair que cette structure est nécessairement unique—sinon les valeurs moyennes ne seraient pas bien définies.” (In English: It is obvious that one can only define average values on objects belonging to a vector (or affine) space; Therefore—so this assertion may seem Bourbakist—that we will observe and measure average values only as quantity belonging to a set having physically an affine structure. It is clear that this structure is necessarily unique—if not the average values would not be well defined.)
7. Illustration of Souriau Thermodynamics of a Centrifuge System
8. Higher-Order Model of Lie Groups Thermodynamics Based on Poly-Symplectic Vector Valued Model
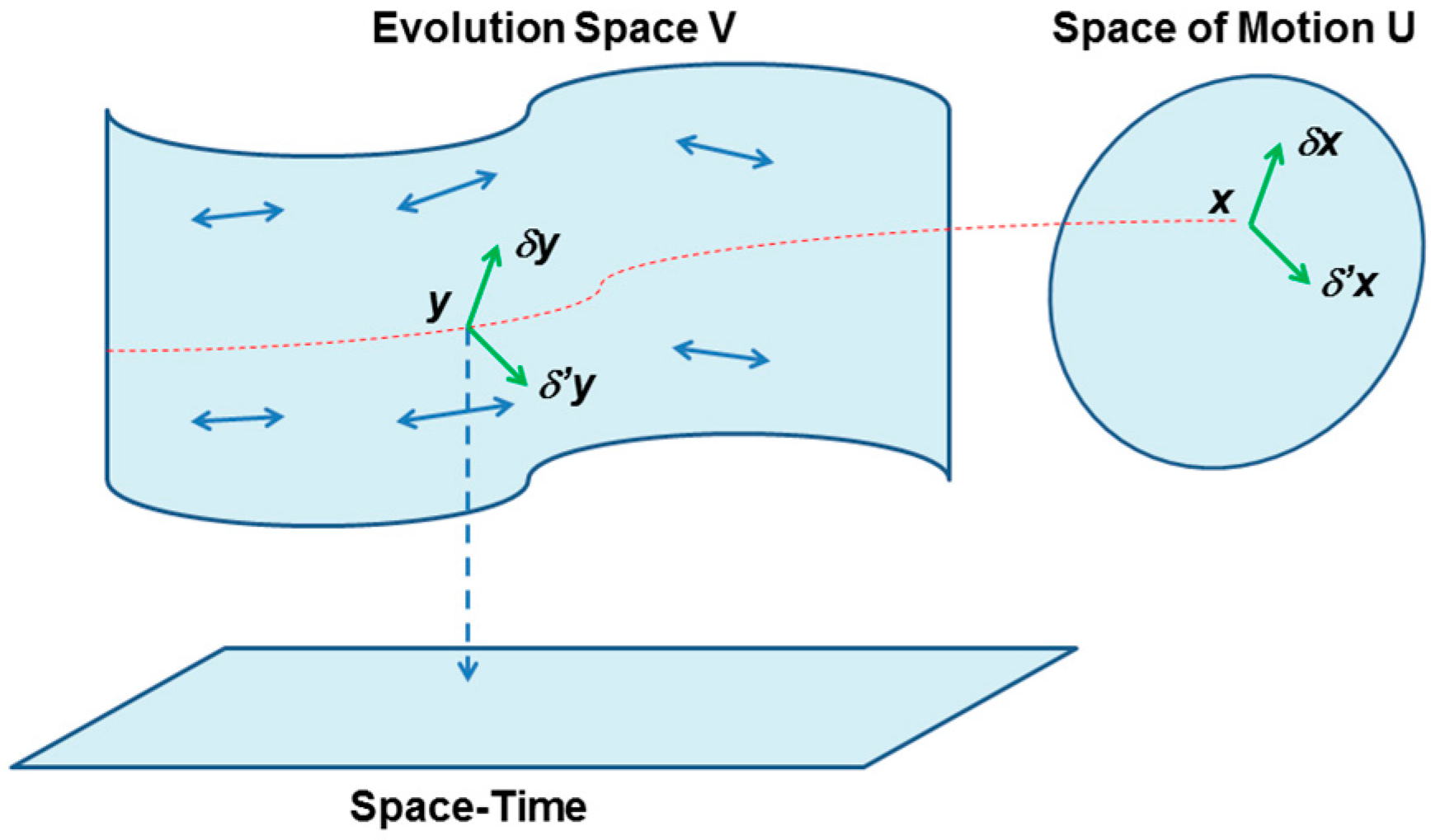
- C0: For each field system, an evolution space can be constructed, which describes the states of the system completely.
- C1: The evolution space carries a geometric structure, which assigns to each function (Hamiltonian density) its Hamiltonian equations.
- C2: The geometry of the evolution space gives ‘canonical transformations’, i.e., the general symmetry group of a system independently of the choice of Hamiltonian density.
- C3: The formalism is covariant, i.e., no special coordinates or coordinate systems on the parameter space are used to construct the Hamiltonian equations.
- C4: There is an equivalence between regular Lagrange systems and certain (regular) Hamiltonian systems.
- C5: For one dimensional parameter space the theory reduces to the ordinary Hamiltonian formalism on symplectic manifolds in classical mechanics.
- the evolution space of a classical field will appear as the dual of a jet bundle, which carries naturally a polysymplectic structure.
- canonical transformations are bundle isomorphisms leaving this poly-symplectic form invariant.
- one-form: (canonical one-form):
- two-form: closed & non-degenerate (canonical polysymplectic form)
- A closed nondegenerate Rn-valued two-form Ω on a manifold M is called a polysymplectic form. The pair (M, Ω) is a polysymplectic manifold.
- A polysymplectic form Ω on a manifold M is called a standard form iff M has an atlas of canonical charts for Ω, i.e., charts in which locally Ω is written as the canonical evaluation form on P x Lin (P,Rn). (M, Ω) is called a standard polysymplectic manifold.
9. Conclusions and Possible Extensions
- Geometry of Erich Kähler: Study of differential manifolds geometry equipped with a unitary structure satisfying a condition of integrability. The homogeneous Kähler case studied by André Lichnerowicz [130].
- In robotics, the special Euclidean group SE(3) which is the homogeneous Galileo group (robotics also consider the group of similitudes SIM(3)):
- In information geometry, the general affine group is involved A(n,R) for exponential family:with particular case of Gaussian density, associated by Cholesky factorisation of covariance matrix, where covariance matrix square root is triangular matrix with positive elements on its diagonal (it is a group):
- In the study of homogeneous bounded domains, as the simplest one given by Poincaré upper-half plane:
“Je me suis dit, à force de rencontrer des groupes, il y a quelque chose de caché là-dessous. La catégorie métaphysique des groupes qui plane dans l’empyrée des mathématiques, que nous découvrons et que nous adorons, elle doit se rattacher à quelque chose de plus proche de nous. En écoutant de nombreux exposés faits par des neurophysiologistes, j’ai fini par apprendre le rôle primitif du déplacement des objets. Nous savons manipuler ces déplacements mentalement avec une très grande virtuosité. Ce qui nous permet de nous manipuler nous-même, de marcher, de courir, de sauter, de nous rattraper quand nous tombons, etc. Ce n’est pas vrai seulement pour nous, c’est vrai aussi pour les singes ; ils sont beaucoup plus adroits que nous pour anticiper les résultats d’un déplacement. Pour certaines opérations élémentaires de «lecture», ils vont même dix fois plus vite que nous. Beaucoup de neurophysiologistes pensent qu’il y a une structure spéciale génétiquement inscrite dans le cerveau, le câblage d’un groupe … Lorsque il y un tremblement de terre, nous assistons à la mort de l’Espace. … Nous vivons avec nos habitudes que nous pensons universelles. … La neuroscience s’occupe rarement de la géométrie … Pour les singes qui vivent dans les arbres, certaines propriétés du groupe d’Euclide sont mieux câblées dans leurs cerveaux.” (In Engish: “I said to myself, because of meeting groups everywhere, there is something hidden there. The metaphysical category of groups that hovers in the empyrean of mathematics, which we discover and adore, must be connected with something closer to us. Listening to many presentations by neurophysiologists, I ended up learning the primitive role of moving objects. We know how to manipulate these movements mentally with great virtuosity. That allows us to manipulate ourselves, to walk, run, jump, catch up when we fall, and so on. This is not true only for us, it is true also for monkeys; they are much more adroit than we are to anticipate the results of a trip. For some basic “reading” operations, they are even ten times faster than us. Many neurophysiologists think that there is a special structure genetically inscribed in the brain, the wiring of a group… When there is an earthquake, we witness the death of Space. … We live with our habits that we think universal. … Neuroscience rarely deals with geometry … For monkeys living in trees, some of Euclid’s group properties are better wired in their brains.)
“Il est une Cosmologie avec laquelle la Thermodynamique générale présente une analogie non-méconnaissable; cette Cosmologie, c’est la Physique péripatéticienne … Parmi les attributs de la substance, la Physique péripatéticienne confère une égale importance à la catégorie de la quantité et à la catégorie de la qualité; or, par ses symboles numériques, la Thermodynamique générale représente également les diverses grandeurs des quantités et les diverses intensités des qualités. Le mouvement local n’est, pour Aristote, qu’une des formes du mouvement général, tandis que les Cosmologies cartésienne, atomistique et newtonienne concordent en ceci que le seul mouvement possible est le changement de lieu dans l’espace. Et voici que la Thermodynamique générale traite, en ses formules, d’une foule de modifications telles que les variations de températures, les changements d’état électrique ou d’aimantation, sans chercher le moins du monde à réduire ces variations au mouvement local”—Pierre Duhem—La théorie Physique: son objet, sa structure [132].
“Pour la théorie de la connaissance mais aussi pour les sciences est fondamentale la notion de perspective. Or, les expériences faites dans la géométrie algébriques, dans la théorie des nombres, et dans l’algèbre abstraite m’induisent à tenter une formulation mathématique de cette notion pour surmonter ainsi au moyen de raisonnements d’origine géométrique la géométrie. Il me semble en effet, que la tendance vers l’abstraction observée dans les mathématiques d’aujourd’hui, loin d’être l’ennemi de l’intuition ait le sens profond de quitter l’intuition pour la faire renaitre dans une alliance entre «esprit de géométrie» et «esprit de finesse», alliance rendue possible par les réserves énormes des mathématiques pures dont Pascal et Goethe ne pouvaient pas encore se douter”—Erich Kähler—Sur la théorie des corps purement algébriques, 1952.
Funding
Conflicts of Interest
Appendix A. Günther’s Polysymplectic Model
- one-form: (canonical one-form)
- two-form: closed & non-degenerate (canonical polysymplectic form)
- is a 1-cocyle for allthen
- bilinear map on : is a 2 cocycle
Appendix B. Fisher Metric for Multivariate Gaussian Density

Appendix C. Geometric Definition of Legendre Transform by Chasles as Reciprocal Polar with Respect to a Paraboloid
Appendix D. Centrifuge Thermodynamics by Roger Balian Based on Classical Approach
Appendix E. Proof of Convergence for Poly-Symplectic Model Based on Souriau Proof
- neighborhoods respectively of
- positive integrable function on such that:
Appendix F. Relativistic Souriau Thermodynamics of Continua

- specific molecular volume:
- specific mass:
- pressure:
- Heat Flux:
- Specific Mass-Energy:with:
References
- Chatelain, J.M. Pascal, le Coeur et la Raison; Bibliothèque nationale de France: Paris, France, 2016. [Google Scholar]
- Duhem, P. Sur les équations générales de la thermodynamique. In Annales Scientifiques de l’École Normale Supérieure; Ecole Normale Supérieure: Paris, France, 1891; Volume 8, pp. 231–266. (In French) [Google Scholar]
- Duhem, P. Commentaire aux principes de la Thermodynamique—Troisième partie. J. Math. Appl. 1894, 10, 207–286. (In French) [Google Scholar]
- Needham, P. Commentary on the Principles of Thermodynamics by Pierre Duhem; Boston Studies in the Philosophy of Science; Needham, P., Ed.; Springer: Berlin, Germany, 2011. [Google Scholar]
- Duhem, P. Commentaire aux principes de la Thermodynamique—Première partie. J. Math. Appl. 1892, 8, 269–330. (In French) [Google Scholar]
- Bordoni, S. From thermodynamics to philosophical tradition: Pierre Duhem’s research between 1891 and 1896. Lettera Matematica 2017, 5, 261–266. [Google Scholar] [CrossRef]
- Stoffel, J.-F. Pierre Duhem: Un savant-philosophe dans le sillage de Blaise Pascal. Revista Portuguese de Filosofia 2007, 63, 275–307. [Google Scholar] [CrossRef]
- Le Ferrand, H.; Mazliak, L. Pierre Duhem (1861–1916) et ses Contemporains Institut Henri Poincaré, 14 Septembre 2016; Organisée par Hervé Le Ferrand (Dijon)—Laurent Mazliak: Paris, France, 2016. [Google Scholar]
- Barbaresco, F. Jean-Louis Koszul and the elementary structures of Information Geometry. In Geometric Structures of Information Geometry; Nielsen, F., Ed.; Springer: Berlin, Germany, 2018. [Google Scholar]
- Barbaresco, F. Koszul Lecture Contemporaneity: Elementary Structures of Information Geometry and Geometric Heat Theory. In Introduction to Symplectic Geometry; Koszul, J.L., Ed.; Springer: Berlin, Germany, 2018. [Google Scholar]
- Barbaresco, F. Jean-Louis Koszul et les Structures Elémentaires de la Géométrie de l’Information. Revue SMAI Matapli. SMAI, Ed.; 2018, Volume 116. Available online: https://www.see.asso.fr/pdf_viewer/22381/m (accessed on 2 November 2018).
- Duhem, P. Recherches sur l‘élasticité. Ann. Ecole Norm. 1905, 22, 143–217. [Google Scholar] [CrossRef]
- Souriau, J.M. Thermodynamique Relativiste des Fluides; Rendiconti del Seminario Matematico; Università Politecnico di Torino: Torino, Italy, 1978; Volume 35, pp. 21–34. [Google Scholar]
- Souriau, J.M. Milieux continus de dimension 1, 2 ou 3: Statique et dynamique. In Proceedings of the 13eme Congrès Français de Mécanique, Poitiers, France, 1–5 September 1997; pp. 41–53. [Google Scholar]
- Amari, S.I. Natural gradient works efficiently in learning. Neural Comput. 1998, 10, 251–276. [Google Scholar] [CrossRef]
- Amari, S.I.; Nagaoka, H. Methods of Information Geometry; Harada, D., Ed.; Translations of Mathematical Monographs; American Mathematical Society: Providence, RI, USA, 2000; Volume 191. [Google Scholar]
- Pascanu, R.; Bengio, Y. Natural gradient revisited. arXiv 2013, arXiv:1301.3584v1. [Google Scholar]
- Martens, J. New insights and perspectives on the natural gradient method. arXiv 2014, arXiv:1412.1193. [Google Scholar]
- Ollivier, Y. Riemannian metrics for neural networks I: Feedforward networks. Inf. Inference 2015, 4, 108–153. [Google Scholar] [CrossRef]
- Amari, S.I. Information Geometry and Its Applications; Applied Mathematical Sciences; Springer: Berlin, Germany, 2016. [Google Scholar]
- Ollivier, Y.; Arnold, L.; Auger, A.; Hansen, N. Information-geometric optimization algorithms: A unifying picture via invariance principles. J. Mach. Learn. Res. 2017, 18, 1–65. [Google Scholar]
- Ollivier, Y.; Marceau-Caron, G. Natural Langevin dynamics for neural networks. In Geometric Science of Information (GSI 2017); Nielsen, F., Barbaresco, F., Eds.; Lecture Notes in Computer Science 10589; Springer: Berlin, Germany, 2017; pp. 451–459. [Google Scholar]
- Marle, C.-M. From Tools in Symplectic and Poisson Geometry to J.-M. Souriau’s Theories of Statistical Mechanics and Thermodynamics. Entropy 2016, 18, 370. [Google Scholar] [CrossRef]
- Balian, R.; Valentin, P. Hamiltonian structure of thermodynamics with gauge. Eur. Phys. J. B 2001, 21, 269–282. [Google Scholar] [CrossRef]
- Balian, R. From Microphysics to Macrophysics, 2nd ed.; Springer: Berlin, Germany, 2007; Volume I. [Google Scholar]
- Der Schaft, A.; Maschke, B. Homogeneous Hamiltonian Control Systems Part I: Geometric Formulation; Elsevier: Amsterdam, The Netherlands, 2018; Volume 51, pp. 1–6. [Google Scholar]
- Jaworski, W. Information thermodynamics with the second order temperatures for the simplest classical systems. Acta Phys. Pol. 1981, 60, 645–659. [Google Scholar]
- Jaworski, W. Higher-order moments and the maximum entropy inference: The thermodynamical limit approach. J. Phys. A Math. Gen. 1987, 20, 915–926. [Google Scholar] [CrossRef]
- Ingarden, H.S.; Meller, J. Temperatures in linguistics as a model of thermodynamics. Open Syst. Inf. Dyn. 1994, 2, 211–230. [Google Scholar] [CrossRef]
- Ingarden, R.S.; Nakagomi, T. The second order extension of the Gibbs state. Open Syst. Inf. Dyn. 1992, 1, 259–268. [Google Scholar] [CrossRef]
- Ingarden, R.S.; Kossakowski, A.; Ohya, M. Information Dynamics and Open Systems; Classical and Quantum Approach, Fundamental Theories of Physics; Springer: Berlin, Germany, 1997; Volume 86. [Google Scholar]
- Jaworski, W.; lngarden, R.S. On the partition function in information thermodynamics with higher order temperatures. Bull. Acad. Pol. Sci. Sér. Phys. Astron. 1980, 1, 28–119. [Google Scholar]
- Jaworski, W. On Information Thermodynamics with Temperatures of the Second Order. Master’s Thesis, Institute of Physics, Nicolaus Copernicus University, Torun, Poland, 1981. (In Polish). [Google Scholar]
- Jaworski, W. On the thermodynamic limit in information thermodynamics with higher-order temperatures. Acta Phys. Pol. 1983, A63, 3–19. [Google Scholar]
- Jaworski, W. Investigation of the Thermodynamic Limit for the States Maximizing Entropy under Auxiliary Conditions for Higher-Order Statistical Moments. Ph.D. Thesis, Institute of Physics, Nicolaus Copernicus University, Torun, Poland, 1983. (In Polish). [Google Scholar]
- Ingarden, R.S.; Kossakowski, A. Statistical thermodynamics with higher order temperatures for ideal gases of bosons and fermions. Acta Phys. Pol. 1965, 28, 499–511. [Google Scholar]
- Ingarden, R.S.; Tamassy, L. On parabolic geometry and irreversible macroscopic time. Rep. Math. Phys. 1993, 32, 11–33. [Google Scholar] [CrossRef]
- Ingarden, R.S. Towards mesoscopic thermodynamics: Small systems in higher-order states. Open Syst. Inf. Dyn. 1993, 1, 75–102. [Google Scholar] [CrossRef]
- Ingarden, R.S.; Janyszek, H.; Kossakowski, A.; Kawaguchi, T. Information geometry of quantum statistical systems. Tensor Ns 1982, 37, 105–111. [Google Scholar]
- Ingarden, R.S.; Kossakowski, A. On the connection of nonequilibrium information thermodynamics with non-hamiltonian quantum mechanics of open systems. Ann. Phys. 1975, 89, 451–485. [Google Scholar] [CrossRef]
- Casalis, M. Familles Exponentielles Naturelles Invariantes par un Groupe. Ph.D. Thesis, l’Université Paul Sabatier, Toulouse, France, 1990. [Google Scholar]
- Casalis, M. Familles Exponentielles Naturelles sur Rd Invariantes par un Groupe. Int. Stat. Rev. 1991, 59, 241–262. [Google Scholar] [CrossRef]
- Souriau, J.-M. Structures des Systèmes Dynamiques; Dunod: Paris, France, 1970. [Google Scholar]
- Koszul, J.L. Introduction to Symplectic Geometry; Science Press: Beijing, China, 1986. (In Chinese), translated by SPRINGER in English, 2018 [Google Scholar]
- Marle, C.M. Géométrie Symplectique et Géométrie de Poisson; Mathématiques en Devenir, Calvage & Mounet: Paris, France, 2018. [Google Scholar]
- Kostant, B. Quantization and Unitary Representations; Lecture Notes in Math. 170; Springer: Berlin, Germany, 1970. [Google Scholar]
- Koszul, J.L.; Travaux, D.B. Kostant sur les Groupes de Lie Semi-Simples; Séminaire Bourbaki: Paris, France, 1958–1960; pp. 329–337.
- Gunther, C. The polysymplectic Hamiltonian formalism in field theory and calculus of variations I: The local case. J. Differ. Geom. 1987, 25, 23–53. [Google Scholar] [CrossRef]
- Munteanu, F.; Rey, A.M.; Salgado, M. The Günther’s formalism in classical field theory: Momentum map and reduction. J. Math. Phys. 2004, 5, 1730–1751. [Google Scholar] [CrossRef]
- Awane, A. k-symplectic structures. J. Math. Phys. 1992, 33, 4046–4052. [Google Scholar] [CrossRef]
- Awane, A.M. Goze, Pfaffian Systems, k-Symplectic Systems; Springer: Berlin, Germany, 2000. [Google Scholar]
- Edelen, D.G.B. The invariance group for Hamiltonian systems of partial differential equations. Arch. Rational Mech. Anal. 1961, 5, 95–176. [Google Scholar] [CrossRef]
- De Donder, T. Théorie Invariante du Calcul des Variations, Nuov. ed.; Gauthiers–Villars: Paris, France, 1935. [Google Scholar]
- Lepage, T. Sur les champs géodésiques du calcul des variations. Bull. Acad. R. Belg. Classes Sci. 1936, 22. [Google Scholar]
- Hélein, F. Multisymplectic formalism and the covariant phase space. In Variational Problems in Differential Geometry; Bielawski, R., Houston, K., Speight, M., Eds.; London Mathematical Society Lecture Note Series 394; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Facchi, P.; Kulkarni, R.; Manko, V.I.G.; Marmo, S.E.C.G.; Ventriglia, F. Classical and quantum Fisher information in the geometrical formulation of quantum mechanics. Phys. Lett. A 2010, 374, 4801. [Google Scholar] [CrossRef]
- Contreras, E.; Schiavina, M. On the geometry of mixed states and the quantum information tensor. J. Math. Phys. 2016, 57, 062209. [Google Scholar] [CrossRef]
- Luati, A. Maximum Fisher information in mixed state quantum systems. Ann. Stat. 1770, 32, 2004. [Google Scholar] [CrossRef]
- Contreras, E.; Schiavina, M. Kähler fibrations in quantum information theory. arXiv 2018, arXiv:1801.09793. [Google Scholar]
- Souriau, J.-M. La structure symplectique de la mécanique décrite par Lagrange en 1811. Math. Sci. Hum. 1986, 94, 45–54. [Google Scholar]
- Marle, C.M. The inception of Symplectic Geometry: The works of Lagrange and Poisson during the years 1808–1810. Lett. Math. Phys. 2009, 90, 3. [Google Scholar] [CrossRef]
- Barbaresco, F.; Boyom, M. Foundations of Geometric Structure of Information. In Proceedings of the FGSI’19, IMAG lab (Institut Montpelliérain Alexander Grothendieck), Montpellier, France, 4–6 February 2019; Available online: https://fgsi2019.sciencesconf.org/ (accessed on 11 November 2018).
- Szczeciniarz, J.-J.; Iglesias-Zemmour, P. SOURIAU 2019 Conference, SPHERE, Université Paris-Diderot, Paris, France, 27–31 May 2019. Available online: http://souriau2019.fr/ (accessed on 1 November 2018).
- Souriau, J.-M. Mécanique statistique, groupes de Lie et cosmologie, Colloques int. du CNRS numéro 237. In Proceedings of the Géométrie Symplectique et Physique Mathématique, Aix-en-Provence, France, 24–28 June 1974; pp. 59–113. [Google Scholar]
- Obădeanu, V. Structures géométriques associées a certains systèmes dynamiques. Balkan J. Geom. Appl. 2000, 5, 81–89. [Google Scholar]
- Obădeanu, V. Systèmes Dynamiques et Structures Géométriques Associées; Universitatea din Timișoara, Facultatea de Matematică: Timișoara, Romania, 1999. [Google Scholar]
- Obădeanu, V. Systèmes Biodynamiques et Lois de Conservation Applications au Systèmes de Neurones; Universitatea din Timișoara, Facultatea de Matematicӑ: Timișoara, Romania, 1994. [Google Scholar]
- Gallissot, F. Les formes extérieures en mécanique. Annales de l’Institut Fourier 1952, 4, 145–297. [Google Scholar] [CrossRef]
- Gallissot, F. les formes extérieures et la mécaniques des milieux continus. Annales de l’Institut Fourier 1958, 8, 291–335. [Google Scholar] [CrossRef]
- Souriau, J.M. C’est quantique? Donc c’est Géométrique. Feuilletages—Quantification Géométrique: Textes des Journées D’étude des 16 et 17 Octobre 2003. Available online: http://semioweb.msh-paris.fr/f2ds/docs/feuilletages/Jean-Marie_Souriau3.pdf (accessed on 1 November 2018).
- Souriau, J.M. C’est Quantique? Donc c’est Géométrique. Feuilletages—Quantification Géométrique Video. 2003. Available online: https://www.youtube.com/watch?time_continue=417&v=vZeidrBPljM (accessed on 1 November 2018).
- Souriau, J.M. Géométrie et Relativité. Collection Enseignement des Sciences; Hermann: Paris, France, 1964. [Google Scholar]
- Souriau, J.M. Thermodynamique et géométrie. Lecture Notes Math. 1976, 676, 369–397. [Google Scholar]
- Souriau, J.M.; Iglesias, P. Le Chaud, le Froid et la Géométrie, Groupe de Contact de Géométrie Différentielle et de Topologie Algébrique du FNRS; Université de Liège: Liège, Belgium, 1980. [Google Scholar]
- Stueckelberg, E.C.G.; Wanders, G. Thermodynamique en Relativité Générale. Helv. Phys. Acta 1953, 26, 307–316. [Google Scholar]
- Lichnerowicz, A. Théories Relativistes de la Gravitation et de L’électromagnétisme; Relativité Générale et Théories Unitaires; Masson et Cie: Paris, France, 1955. [Google Scholar]
- Vallée, C. Lois de Comportement des Milieux Continus Dissipatifs Compatibles avec la Physique Relativiste. Ph.D. Thesis, University of Poitiers, Poitiers, France, 1978. [Google Scholar]
- Vallée, C. Relativistic thermodynamics of continua. Int. J. Eng. Sci. 1981, 19, 589–601. [Google Scholar] [CrossRef]
- Garrel, J. Tensorial Local-Equilibrium Axion and Operator of Evolution. Il Nuovo Cimento 1986, 94, 119–139. [Google Scholar] [CrossRef]
- Anile, A.; Choquet-Bruhat, Y. Relativistic Fluid Dynamics; Lecture Notes in Mathematics; Springer: Berlin, Germany, 1989. [Google Scholar]
- De Saxcé, G.; Vallée, C. Galilean Mechanics and Thermodynamics of Continua; Wiley-ISTE: Hoboken, NJ, USA, 2016. [Google Scholar]
- de Saxcé, G. 5-Dimensional Thermodynamics of Dissipative Continua. In Models, Simulation, and Experimental Issues in Structural Mechanics; Springer: Berlin, Germany, 2017. [Google Scholar]
- Ingarden, R.S. Information geometry in functional spaces of classical ad quantum finite statistical systems. Int. J. Eng. Sci. 1981, 19, 1609–1616. [Google Scholar] [CrossRef]
- Ingarden, R.S. Information Geometry of Thermodynamics. Trans. Tenth Prague Conf. 1988, 10, 421–428. [Google Scholar]
- Mrugala, R. On equivalence of two metrics in classical thermodynamics. Physica 1984, 125A, 631–639. [Google Scholar] [CrossRef]
- Mrugala, R. Riemannian and Finslerian geometry in thermodynamics. Open Syst. Inf. Dyn. 1992, 1, 379–396. [Google Scholar] [CrossRef]
- Mrugala, R. On a special family of thermodynamic processes and their invariants. Rep. Math. Phys. 2000, 46, 461–468. [Google Scholar] [CrossRef]
- Mrugała, R. On contact and metric structures on thermodynamic spaces. RIMS Kokyuroku 2000, 1142, 167–181. [Google Scholar]
- Mrugała, R. Structure group U(n) x 1 in thermodynamics. J. Phys. A Math. Gen. 2005, 38, 10905. [Google Scholar] [CrossRef]
- Arnold, V.I. Contact geometry: The geometrical method of Gibbs’s thermodynamics. In Proceedings of the Gibbs Symposium, New Haven, CT, USA, 15–17 May 1989; Caldi, D.G., Mostow, G.D., Eds.; Yale University: New Haven, CT, USA, 1989; pp. 163–179. [Google Scholar]
- Barbaresco, F. Geometric Theory of Heat from Souriau Lie Groups Thermodynamics and Koszul Hessian Geometry. Entropy 2016, 18, 386. [Google Scholar] [CrossRef]
- Kijowski, W. A finite dimensional canonical formalism in the classical field theory. Commun. Math. Phys. 1973, 30, 99–128. [Google Scholar] [CrossRef]
- Kijowski, W. Multiphase spaces and gauge in the calculus of variations. Bulletin de L Academie Polonaise des Sciences-Serie des Sciences Mathematiques Astronomiques et Physiques 1974, 22, 1219–1225. [Google Scholar]
- Kijowski, W.; Szczyrba, W. A canonical structure for classical field theories. Commun. Math Phys. 1976, 46, 183–206. [Google Scholar] [CrossRef]
- Nakagomi, T. Mesoscopic version of thermodynamic equilibrium condition. Another approach to higher order temperatures. Open Syst. Inf. Dyn. 1992, 1, 233–241. [Google Scholar] [CrossRef]
- Nencka, H.; Streater, R.F. Information Geometry for some Lie algebras. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 1999, 2, 441–460. [Google Scholar] [CrossRef]
- Sampieri, U. Lie group structures and reproducing kernels on homogeneous siegel domains. Annali di Matematica Pura ed Applicata 1988, 152, 1–19. [Google Scholar] [CrossRef]
- Alexeevsky, D. Vinberg’s Theory of Homogeneous Convex Cones: Developments and Applications; Transformation groups 2017. Conference dedicated to Prof. Ernest B. Vinberg on the occasion of his 80th birthday, Moscow, December 2017 [Video]. Available online: http://www.mathnet.ru/present19121 (accessed on 1 November 2018).
- Trépreau, J.-M. Transformation de Legendre et pseudoconvexité avec décalage. J. Fourier Anal. Appl. 1995, 1, 569–588. [Google Scholar]
- Leray, J. Le calcul differentiel et intégral sur une variété analytique complexe. Bull. Soc. Math. France 1952, 87, 81–180. [Google Scholar]
- Brenier, Y. Un algorithme rapide pour le calcul de transformées de Legendre-Fenchel discrètes. C. R. Acad. Sci. Paris 1989, 308, 587–589. [Google Scholar]
- Legendre, A.M. Mémoire Sur L’intégration de Quelques Equations aux Différences Partielles; Mémoires de l’Académie des Sciences: Paris, France, 1787; pp. 309–351. [Google Scholar]
- Konstantatou, M.; McRobie, A. Reciprocal constructions using conic sections and Poncelet duality. In Proceedings of the IASS 2016 Tokyo Symposium: Spatial Structures in the 21st Century—Graphic Statics, Tokyo, Japan, 26–30 September 2016. [Google Scholar]
- Benayoun, L. Méthodes Géométriques pour L’étude des Systèmes Thermodynamiques et la Génération D’équations D’état. Ph.D. Thesis, Institut National Polytechnique de Grenoble, Grenoble, France, 1999. [Google Scholar]
- Der Schaft, A.; Maschke, B. Homogeneous Hamiltonian Control Systems Part II: Application to thermodynamic systems. IFAC-PapersOnLine 2018, 51, 7–12. [Google Scholar]
- Delzant, T.; Wacheux, C. Action Hamiltoniennes: Invariants et Classification; Organisé par Michel Brion et Thomas Delzant, CIRM: Luminy, France, 2010; Volume 1, pp. 23–31. [Google Scholar]
- Moreau, J.J. Fonctions convexes duales et points proximaux dans un espace hilbertien. C. R. Acad. Sci. Paris 1962, 255, 2897–2899. [Google Scholar]
- Libermann, P. Legendre foliations on contact manifolds. Differ. Geom. Appl. 1991, 1, 57–76. [Google Scholar] [CrossRef]
- Kostant, B.; Sahi, S. The Capelli identity, tube domains, and the generalized Laplace transform. Adv. Math. 1991, 87, 71–92. [Google Scholar] [CrossRef]
- Duhem, P. Sur la stabilité d’un système animé d’un mouvement de rotation, Comptes rendus, t. CXXXII, séance du 29 Avril 1901. 1021.
- Duhem, P. Sur la stabilité de l’équilibre d’une masse fluide animée d’un mouvement de rotation. J. Math. 1901, VII, 311–330. [Google Scholar]
- Duhem, P. Stabilité pour des perturbations quelconques, d’un système animé d’un mouvement de rotation uniforme. C. R. 1902, CXXXIV, 23. [Google Scholar]
- Duhem, P. Sur la stabilité pour des perturbations quelconques, d’un système animé d’un mouvement de rotation uniforme. Journal de Mathématiques pures et Appliquées 1902, VIII, 5. [Google Scholar]
- Poincaré, H. Sur l’équilibre d’une masse fluide animée d’un mouvement de rotation, chap. 14, Stabilité des ellipsoïdes. Acta Mathematica 1885, VII, 366–367. [Google Scholar]
- Barbaresco, F. Poly-symplectic Model of Higher Order Souriau Lie Groups Thermodynamics for Small Data Analytics. In Geometric Science of Information; Springer: Berlin, Germany, 2017; Volume 10589, pp. 432–441. [Google Scholar]
- Volterra, V. Sulle Equazioni Differenziali che Provengono da Questiono di Calcolo delle Variazioni; Serise IV; Tip. della R. Accademia dei Lincei: Roma, Italy, 1890; Volume VI, pp. 42–54. [Google Scholar]
- Volterra, V. Sopra una Estensione della Teoria Jacobi-Hamilton del Calcolo delle Variazioni; Serise IV; Tip. della R. Accademia dei Lincei: Roma, Italy, 1890; Volume VI, pp. 127–138. [Google Scholar]
- Dedecker, P. Calcul des variations, formes différentielles et champs géodésiques. Géométrie Différentielle 1953, 52, 17. [Google Scholar]
- Dedecker, P. On the generalization of symplectic geometry to multiple integrals in the calculus of variations. In Differential Geometrical Methods in Mathematical Physics; Bleuler, K., Reetz, A., Eds.; Lect. Notes Maths; Springer: Berlin, Germany, 1977; Volume 570, pp. 395–456. [Google Scholar]
- Hélein, F.; Kouneiher, J. Covariant Hamiltonian formalism for the calculus of variations with several variables: Lepage–Dedecker versus De Donder–Weyl. Adv. Theor. Math. Phys. 2004, 8, 565–601. [Google Scholar] [CrossRef]
- Carathéodory, C. Uber die Extremalen und geod ätischen Felder in der Variationsrechnung der mehrfachen Integrale. Acta Sci. Math. (Szeged) 1929, 4, 193–216. [Google Scholar]
- Weyl, H. Geodesic fields in the calculus of variations. Ann. Math. 1935, 36, 607–629. [Google Scholar] [CrossRef]
- Edelen, D.G.B. Nonlocal Variations and Local Invariance of Fields; American Elsevier: New York, NY, USA, 1969. [Google Scholar]
- Rund, H. The Hamilton-Jacobi Theory in the Calculus of Variations; Van Nostrand: Princeton, NJ, USA, 1966. [Google Scholar]
- Cartan, E. Sur les espaces à connexion affine et la théorie de la relativité généralisée, partie I. Ann. Ec. Norm 1923, 40, 325–412. [Google Scholar]
- Cartan, E. Sur les espaces à connexion affine et la théorie de la relativité généralisée (suite). Ann. Ec. Norm. 1924, 41, 1–25. [Google Scholar]
- Cartan, E. Sur les espaces connexion affine et la théorie de la relativité généralisée partie II. Ann. Ec. Norm. 1925, 42, 17–88. [Google Scholar]
- Cartan, E. La Méthode du Repère Mobile, la Théorie des Groupes Continus et les Espaces Généralisés; Exposés de Géométrie, No. 5; Hermann: Paris, France, 1935. [Google Scholar]
- Alekseevsky, D. Vinberg’s Theory of Homogeneous Convex Cones: Developments and Applications, Transformation Groups 2017. Conference Dedicated to Prof. Ernest B. Vinberg on the Occasion of His 80th Birthday, Moscow, December 2017. Available online: https://www.mccme.ru/tg2017/slides/alexeevsky.pdf (accessed on 1 November 2018).
- Lichnerowicz, A.; Medina, A. On Lie groups with left-invariant symplectic or Kählerian structures. Lett. Math. Phys. 1988, 16, 225–235. [Google Scholar] [CrossRef]
- Scholz, E.E. Cartan’s attempt at bridge-building between Einstein and the Cosserats – or how translational curvature became to be known as torsion. arXiv 2018, arXiv:1810.03872v1 [math.HO]. [Google Scholar]
- Duhem, P. La théorie physique: Son objet, sa structure, Vrin Edition ed. 2007. Available online: https://books.openedition.org/enseditions/6077 (accessed on 2 November 2018).
- Conteras, I.; Alba, N.M. Poly-Poisson sigma models and their relational poly-symplectic groupoids. J. Math. Phys. 2018, 59, 072901. [Google Scholar] [CrossRef]
- Belgodère, P. Courbure moyenne généralisée. C. R. Acad. Sci. Paris 1944, 218, 739–740. [Google Scholar]
- Belgodère, P. Extremales d’une intégrale de surface Sg(p, q)dxdy. C. R. Acad. Sci. Paris 1944, 219, 272–273. [Google Scholar]






© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbaresco, F. Higher Order Geometric Theory of Information and Heat Based on Poly-Symplectic Geometry of Souriau Lie Groups Thermodynamics and Their Contextures: The Bedrock for Lie Group Machine Learning. Entropy 2018, 20, 840. https://doi.org/10.3390/e20110840
Barbaresco F. Higher Order Geometric Theory of Information and Heat Based on Poly-Symplectic Geometry of Souriau Lie Groups Thermodynamics and Their Contextures: The Bedrock for Lie Group Machine Learning. Entropy. 2018; 20(11):840. https://doi.org/10.3390/e20110840
Chicago/Turabian StyleBarbaresco, Frédéric. 2018. "Higher Order Geometric Theory of Information and Heat Based on Poly-Symplectic Geometry of Souriau Lie Groups Thermodynamics and Their Contextures: The Bedrock for Lie Group Machine Learning" Entropy 20, no. 11: 840. https://doi.org/10.3390/e20110840
APA StyleBarbaresco, F. (2018). Higher Order Geometric Theory of Information and Heat Based on Poly-Symplectic Geometry of Souriau Lie Groups Thermodynamics and Their Contextures: The Bedrock for Lie Group Machine Learning. Entropy, 20(11), 840. https://doi.org/10.3390/e20110840




