Cross Entropy of Neural Language Models at Infinity—A New Bound of the Entropy Rate
Abstract
1. Introduction
2. Entropy Rate Estimation of Natural Language
3. Model
3.1. Neural Language Model
3.2. n-Gram Language Model
3.3. Dataset
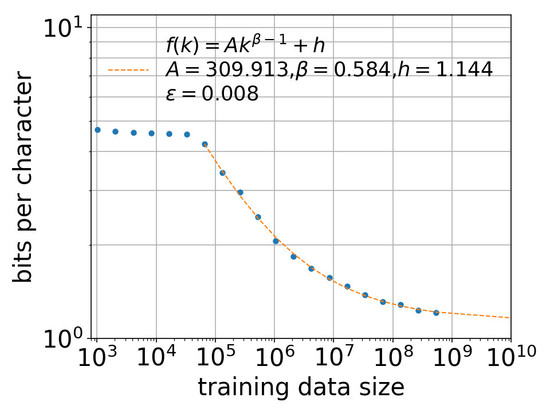
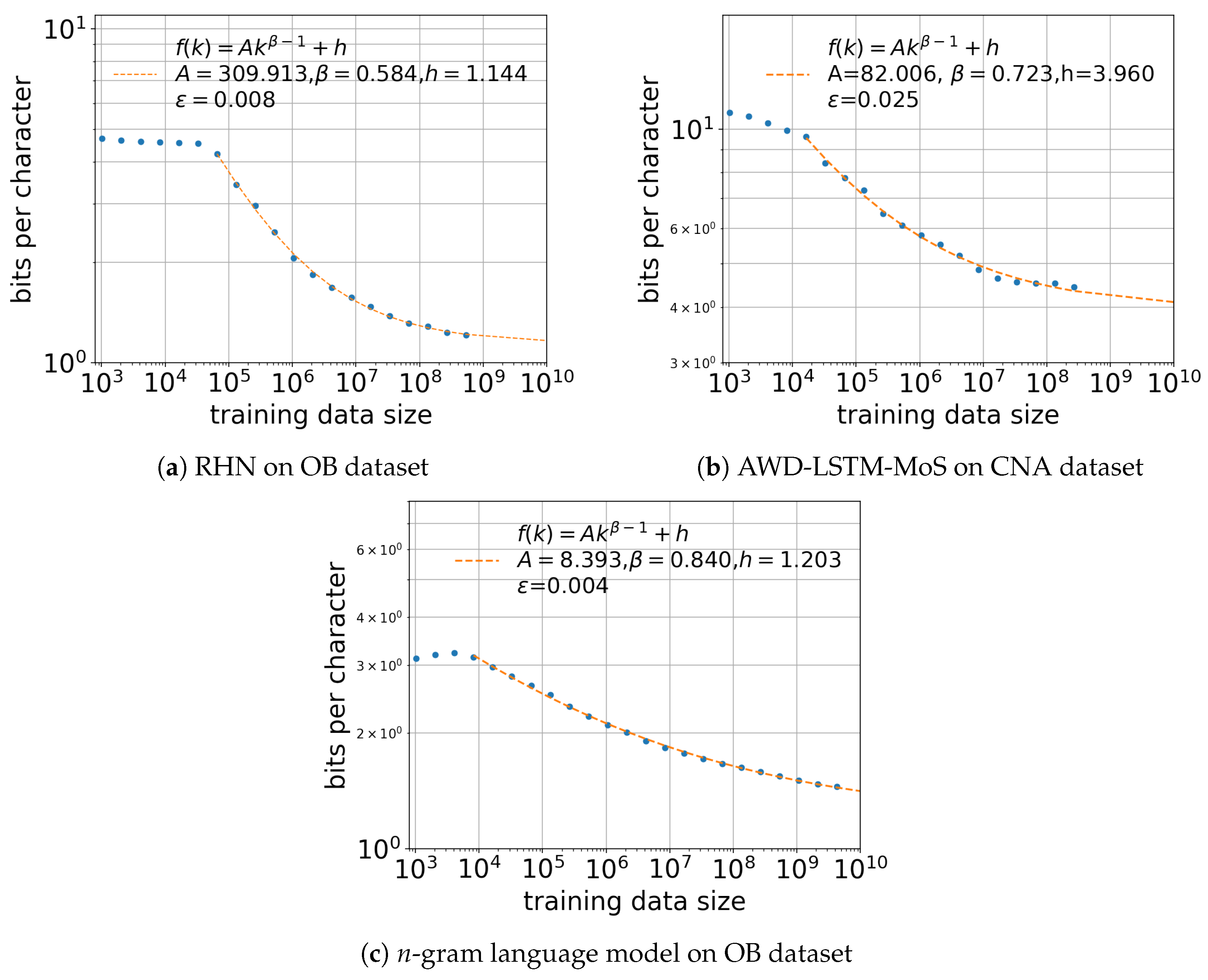
4. Estimating Entropy Rate Through Extrapolation
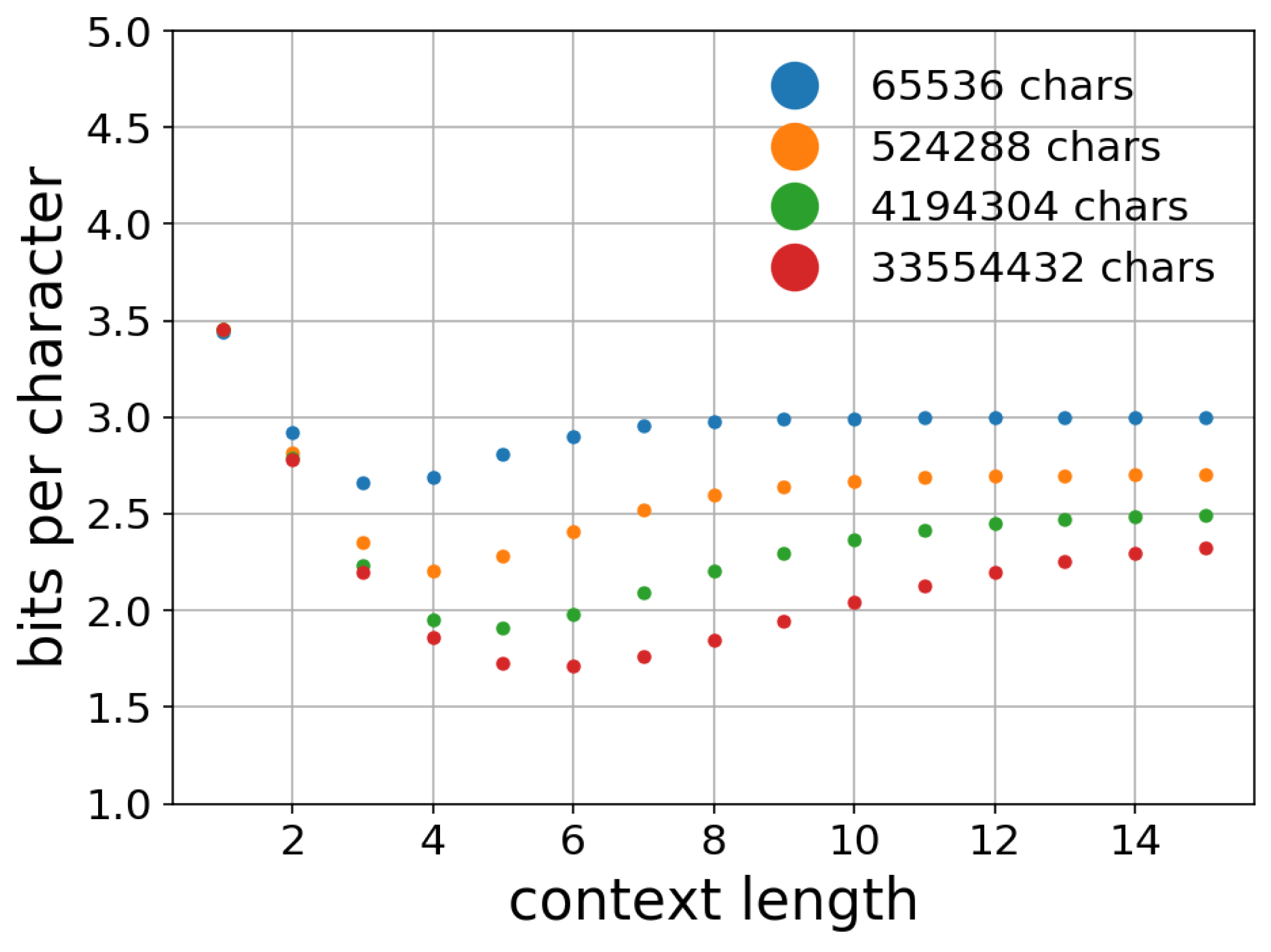
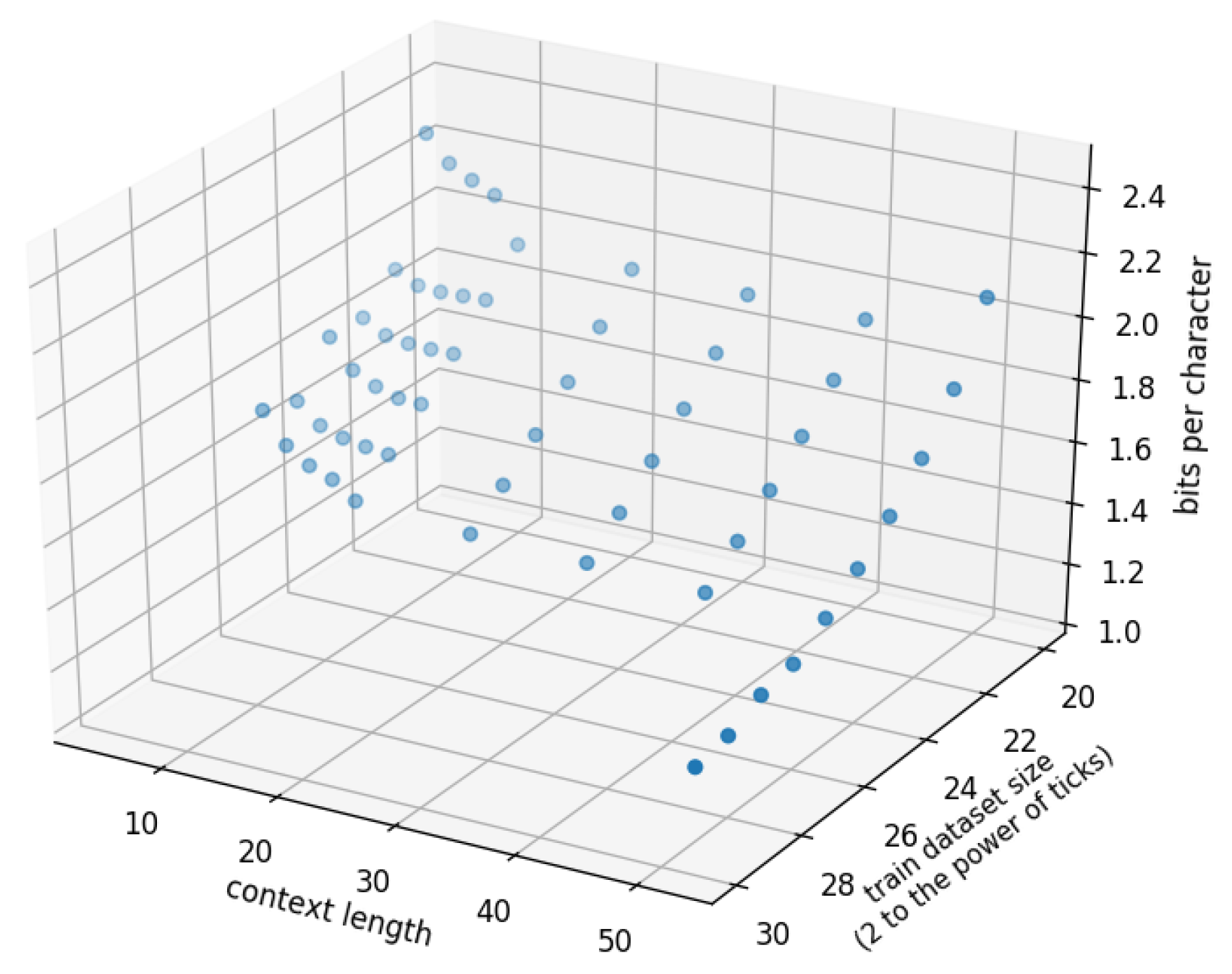
5. Effect of Parameters
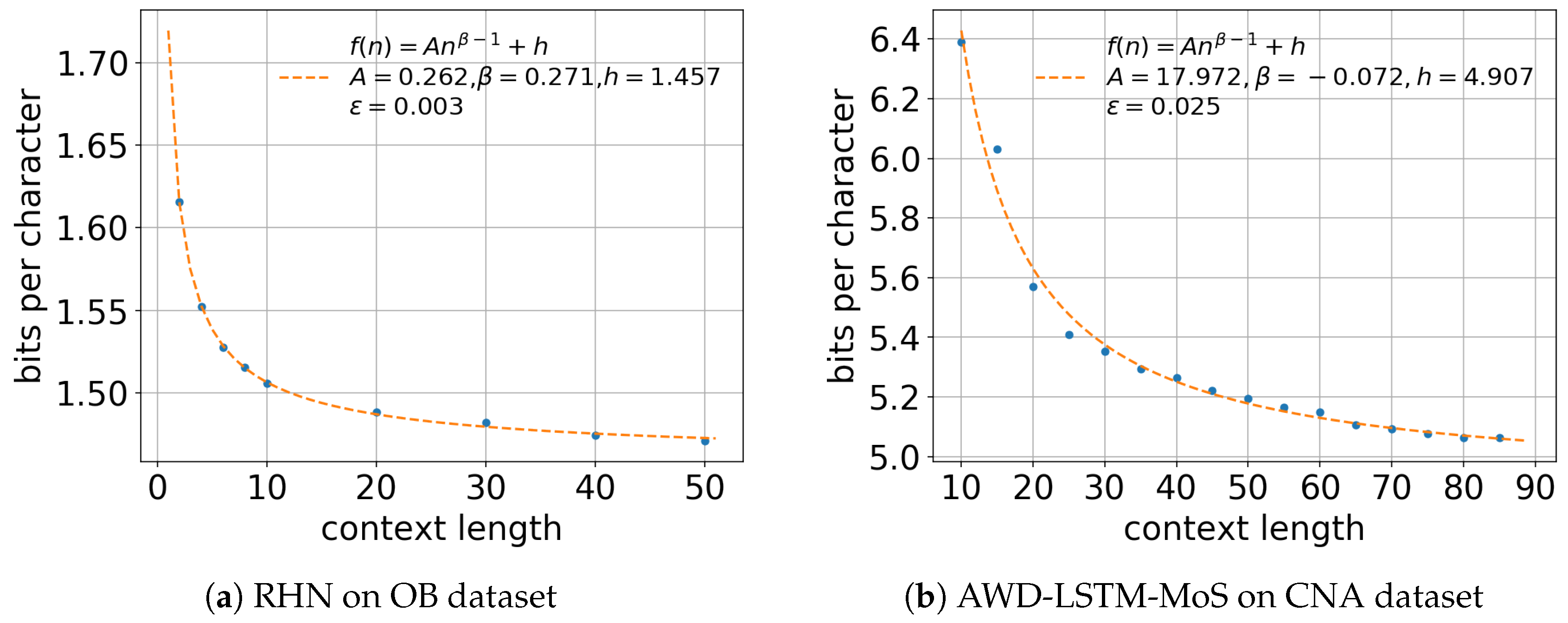
5.1. Effect of Context Length n
5.2. Effect of Training Data Size k
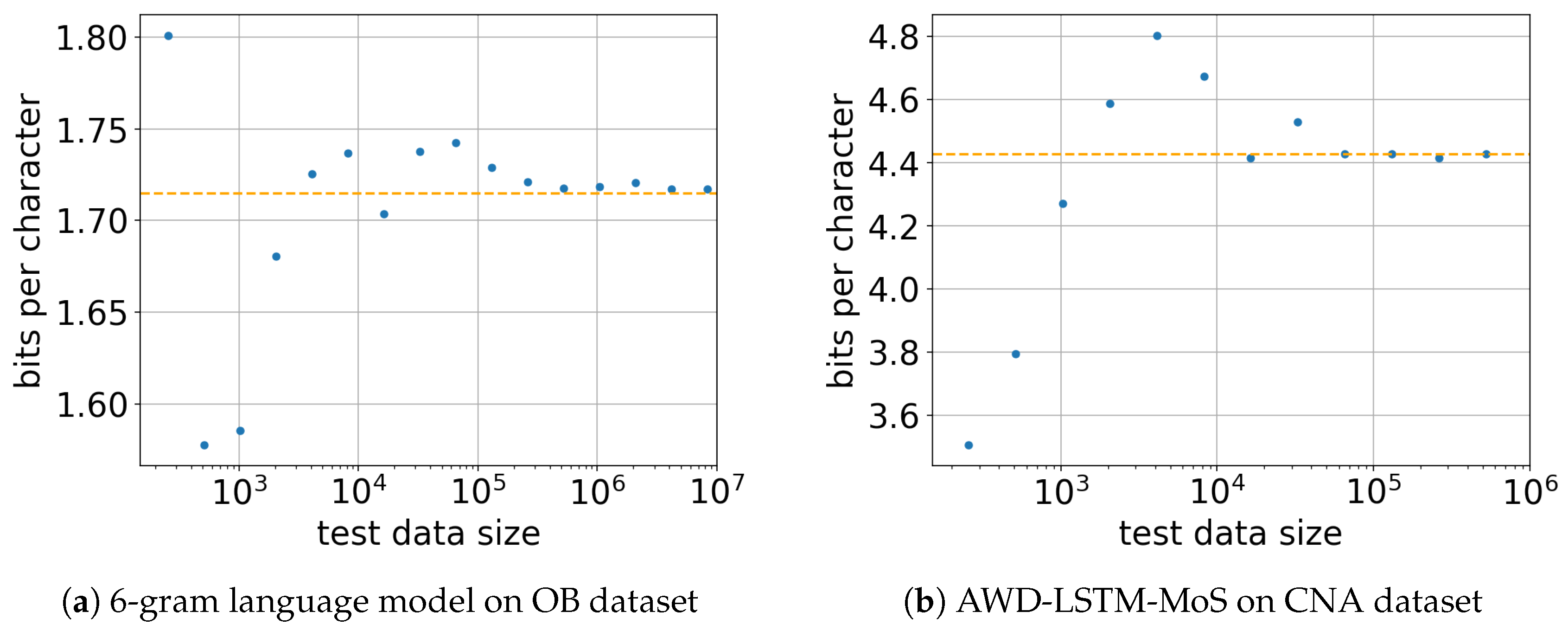
5.3. Effect of Test Data Size m
5.4. Effect of Parameter Size
6. Entropy Rate Estimated with Neural Language Models
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Neural Language Models
Appendix A.1. Embedding Representation
Appendix A.2. Enriched Architectures of Recurrent Neural Networks
Appendix A.3. Training Strategy
Appendix A.4. Recurrent Highway Networks
Appendix A.5. AWD-LSTM-MoS
References
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the Difficulty of Training Recurrent Neural Networks. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. III1310–III1318. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Mikolov, T.; Karafiát, M.; Burget, L.; Cernocký, J.; Khudanpur, S. Recurrent neural network based language model. In Proceedings of the 11th Annual Conference of the International Speech Communication Association, Chiba, Japan, 26–30 September 2010; pp. 1045–1048. [Google Scholar]
- Zilly, J.G.; Srivastava, R.K.; Koutník, J.; Schmidhuber, J. Recurrent highway networks. arXiv, 2016; arXiv:1607.03474. [Google Scholar]
- Melis, G.; Dyer, C.; Blunsom, P. On the state of the art of evaluation in neural language models. In Proceedings of the 6th International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Merity, S.; Keskar, N.S.; Socher, R. Regularizing and optimizing LSTM language models. In Proceedings of the 6th International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Yang, Z.; Dai, Z.; Salakhutdinov, R.; Cohen, W.W. Breaking the softmax bottleneck: A high-rank RNN language model. In Proceedings of the 6th International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Merity, S.; Keskar, N.; Socher, R. An Analysis of Neural Language Modeling at Multiple Scales. arXiv, 2018; arXiv:1803.08240. [Google Scholar]
- Han, Y.; Jiao, J.; Lee, C.Z.; Weissman, T.; Wu, Y.; Yu, T. Entropy Rate Estimation for Markov Chains with Large State Space. arXiv, 2018; arXiv:1802.07889. [Google Scholar]
- Manning, C.D. Computational linguistics and deep learning. Comput. Linguist. 2015, 41, 701–707. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv, 2018; arXiv:1810.04805. [Google Scholar]
- Darmon, D. Specific Differential Entropy Rate Estimation for Continuous-Valued Time Series. Entropy 2016, 18, 190. [Google Scholar] [CrossRef]
- Bentz, C.; Alikaniotis, D.; Cysouw, M.; Ferrer-i Cancho, R. The Entropy of Words—Learnability and Expressivity across More than 1000 Languages. Entropy 2017, 19, 275. [Google Scholar] [CrossRef]
- Shannon, C. Prediction and entropy of printed English. Bell Syst. Tech. J. 1951, 30, 50–64. [Google Scholar] [CrossRef]
- Cover, T.M.; King, R.C. A Convergent Gambling Estimate of the Entropy of English. IEEE Trans. Inf. Theory 1978, 24, 413–421. [Google Scholar] [CrossRef]
- Brown, P.F.; Pietra, S.A.D.; Pietra, V.J.D.; Lai, J.C.; Mercer, R.L. An Estimate of an Upper Bound for the Entropy of English. Comput. Linguist. 1992, 18, 31–40. [Google Scholar]
- Schümann, T.; Grassberger, P. Entropy estimation of symbol sequences. Chaos 1996, 6, 414–427. [Google Scholar] [CrossRef] [PubMed]
- Takahira, R.; Tanaka-Ishii, K.; Dębowski, Ł. Entropy Rate Estimates for Natural Language—A New Extrapolation of Compressed Large-Scale Corpora. Entropy 2016, 18, 364. [Google Scholar] [CrossRef]
- Hilberg, W. Der bekannte Grenzwert der redundanzfreien Information in Texten—eine Fehlinterpretation der Shannonschen Experimente? Frequenz 1990, 44, 243–248. [Google Scholar] [CrossRef]
- Dębowski, Ł. Maximal Repetitions in Written Texts: Finite Energy Hypothesis vs. Strong Hilberg Conjecture. Entropy 2015, 17, 5903–5919. [Google Scholar]
- Dębowski, Ł. A general definition of conditional information and its application to ergodic decomposition. Stat. Probabil. Lett. 2009, 79, 1260–1268. [Google Scholar]
- Ornstein, D.; Weiss, B. Entropy and data compression schemes. IEEE Trans. Inf. Theory 1993, 39, 78–83. [Google Scholar] [CrossRef]
- Ebeling, W.; Nicolis, G. Entropy of Symbolic Sequences: The Role of Correlations. Europhys Lett. 1991, 14, 191–196. [Google Scholar] [CrossRef]
- Hestness, J.; Narang, S.; Ardalani, N.; Diamos, G.; Jun, H.; Kianinejad, H.; Patwary, M.; Yang, Y.; Zhou, Y. Deep Learning Scaling is Predictable, Empirically. arXiv, 2017; arXiv:1712.00409. [Google Scholar]
- Khandelwal, U.; He, H.; Qi, P.; Jurafsky, D. Sharp Nearby, Fuzzy Far Away: How Neural Language Models Use Context. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics, Melbourne, Australia, 15–20 July 2018; pp. 284–294. [Google Scholar]
- Katz, S. Estimation of probabilities from sparse data for the language model component of a speech recognizer. Trans. Acoust. Speech Signal Process. 1987, 35, 400–401. [Google Scholar] [CrossRef]
- Kneser, R.; Ney, H. Improved backing-off for m-gram language modeling. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Detroit, MI, USA, 9–12 May 1995. [Google Scholar]
- Chelba, C.; Mikolov, T.; Schuster, M.; Ge, Q.; Brants, T.; Koehn, P.; Robinson, T. One Billion Word Benchmark for Measuring Progress in Statistical Language Modeling. arXiv, 2013; arXiv:1312.3005. [Google Scholar]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [PubMed]
- Amari, S.-i.; Fujita, N.; Shinomoto, S. Four Types of Learning Curves. Neural Comput. 1992, 4, 605–618. [Google Scholar] [CrossRef]
- Gal, Y.; Ghahramani, Z. A Theoretically Grounded Application of Dropout in Recurrent Neural Networks. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 1027–1035. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. Available online: http://download.tensorflow.org/paper/whitepaper2015.pdf (accessed on 24 October 2018).
- Srivastava, R.K.; Greff, K.; Schmidhuber, J. Training Very Deep Networks. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 2377–2385. [Google Scholar]
- Sutskever, I.; Martens, J.; Dahl, G.E.; Hinton, G.E. On the importance of initialization and momentum in deep learning. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. III1139–III1147. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in PyTorch. In Proceedings of the Neural Information Processing Systems Autodiff Workshop, Long Beach, CA, USA, 9 December 2017. [Google Scholar]
- Polyak, B.T.; Juditsky, A.B. Acceleration of Stochastic Approximation by Averaging. SIAM J. Control Optim. 1992, 30, 838–855. [Google Scholar] [CrossRef]

| Dataset | Character Tokens | Word Tokens | Vocabulary | Unique Characters | Test Character Tokens |
|---|---|---|---|---|---|
| One Billion (English) | 4,091,497,941 | 768,648,885 | 81,198 | 139 | 37,811,222 |
| Central News Agency (Chinese) | 743,444,075 | 415,721,153 | 1,694,159 | 9171 | 493,376 |
| Dataset | Model | Smallest Cross-Entropy |
|---|---|---|
| OB | RHN | 1.210 |
| OB | n-gram model | 1.451 |
| OB | PPM-d | 1.442 |
| CNA | AWD-LSTM-MoS | 4.429 |
| CNA | n-gram model | 4.678 |
| CNA | PPM-d | 4.753 |
| Dataset | Model | Drop Point | ||||
|---|---|---|---|---|---|---|
| A | h | |||||
| OB | RHN | 358.997 | 0.570 | 1.144 | 0.008 | |
| OB | n-gram model | 8.393 | 0.840 | 1.210 | 0.004 | |
| OB | PPM-d | 12.551 | 0.791 | 1.302 | 0.015 | - |
| CNA | AWD-LSTM-MoS | 82.006 | 0.723 | 3.960 | 0.025 | |
| CNA | n-gram model | 388.338 | 0.647 | 4.409 | 0.018 | |
| CNA | PPM-d | 35.602 | 0.766 | 4.295 | 0.078 | - |
| Dataset | Model | g | |||||
|---|---|---|---|---|---|---|---|
| h | |||||||
| 1B | RHN | 89.609 | 0.661 | 0.324 | 0.294 | 1.121 | 0.006 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takahashi, S.; Tanaka-Ishii, K. Cross Entropy of Neural Language Models at Infinity—A New Bound of the Entropy Rate. Entropy 2018, 20, 839. https://doi.org/10.3390/e20110839
Takahashi S, Tanaka-Ishii K. Cross Entropy of Neural Language Models at Infinity—A New Bound of the Entropy Rate. Entropy. 2018; 20(11):839. https://doi.org/10.3390/e20110839
Chicago/Turabian StyleTakahashi, Shuntaro, and Kumiko Tanaka-Ishii. 2018. "Cross Entropy of Neural Language Models at Infinity—A New Bound of the Entropy Rate" Entropy 20, no. 11: 839. https://doi.org/10.3390/e20110839
APA StyleTakahashi, S., & Tanaka-Ishii, K. (2018). Cross Entropy of Neural Language Models at Infinity—A New Bound of the Entropy Rate. Entropy, 20(11), 839. https://doi.org/10.3390/e20110839